В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и m будут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
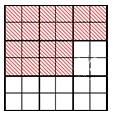
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Цикл статей “Дроби”
Первая часть
Вторая часть
Третья часть
ОСНОВНОЕ СВОЙСТВО ДРОБИ
Вторая статья цикла «Дроби» — «Почему дроби называют правильными и неправильными» закончилась сравнением правильных и неправильных дробей. Однако, прежде чем дальше развивать тему сравнения дробей необходимо рассмотреть основное свойство дроби, являющееся основой (фундаментом) преобразований обыкновенных дробей, используемых как при сравнении, так и при сложении и вычитании дробей с разными знаменателями.
Начну, как обычно, с определения:
ОСНОВНОЕ СВОЙСТВО ДРОБИ — это свойство обыкновенной дроби сохранять своё значение при одновременном умножении или делении её числителя и знаменателя на натуральное число.
В буквенном виде это определение при умножении имеет вид:
СЛЕДСТВИЕ. Две равные дроби являются различными записями одного и того же числа!
Так дроби
выражают одно и то же число, которое, как мы уже знаем, имеет словесную форму «половина».
ПРИМЕР. Пользуясь основным свойством дроби, найдите значение а, при котором верно равенство
РЕШЕНИЕ. Поскольку знаменатель первой дроби в 2 раза больше знаменателя второй, то и числитель первой дроби должен быть в 2 раза больше числителя второй. Умножая и числитель, и знаменатель второй дроби на 2, получаем
откуда а = 6.
ОТВЕТ. 6.
Основное свойство дроби служит для «сокращения» дроби, а также для приведения к заранее выбранному числу знаменателя (или числителя, что используется гораздо реже) обыкновенной дроби, что можно использовать и для сравнения обыкновенных дробей, что и послужит темой следующей статьи цикла.
В заключение приведу пример использования приведения к нужному числу числителя дроби, который может быть интересен ученикам старших, начиная с 8-го класса, поскольку подобные примеры могут встретиться и на ОГЭ, и на ЕГЭ. Его решение взято из моей статьи «Математический концерт» в которой этот пример является первым из двух примеров «На бис».
Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_математика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Цикл статей “Дроби”
1 статья
2 статья
3 статья
4 статья [Текущая]
Основное свойство дроби
Все обыкновенные дроби обладают следующим свойством:
Если числитель и знаменатель обыкновенной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
Это свойство называется основным свойством дроби. С его помощью можно получать новые дроби, равные данной дроби.
В общем виде основное свойство дроби можно выразить так:
где a — нуль или натуральное число, b и m — натуральные числа.
Согласно данному свойству, одну и ту же часть единицы можно выразить с помощью дробей в разных формах.
Пример. Рассмотрим три круга, у которых жёлтым цветом закрашена некоторая одинаковая часть:
У первого круга закрашено 


Все три дроби равны между собой 
Можно заметить, что члены второй дроби в 2 раза больше числителя и знаменателя первой дроби, а члены третьей — в 3 раза.
Умножив оба члена дроби 

Умножив оба члена дроби 

Или наоборот, разделив числитель и знаменатель дроби 

Разделив члены дроби 

Умножение числителя и знаменателя дроби на одно и то же число называют расширением дроби. Деление числителя и знаменателя на одно и то же число называют сокращением дроби.
Основное свойство дроби обычно применяется при сокращении дробей и при приведении дробей к общему знаменателю.
ОБЫКНОВЕННАЯ ДРОБЬ
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
- Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю;
- сравнить полученные дроби.
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
- разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
- Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
- При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.
Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Десятичная дробь
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Основное свойство рациональной дроби
Главное определение свойства дробей: при умножении или делении числителя, или знаменателя дроби получается дробное значение равное ей по значению. Иными словами, значение дроби остается неизменным.
Определение
Преобразование дробного значения к новому знаменателю – это вычисление заданной дроби, которая равна дроби, но с наиболее большим значением в числителе и знаменателем.
Для того чтобы привести любую дробь к новому значению знаменателя, необходимо числитель и знаменатель перемножить на простое действительное число.
Выполнять преобразования обыкновенных дробей без приведения их общему наименьшему знаменателю были бы невозможны.
Определение
Сокращение дроби – перечень основных действий, проводимых с дробями, которые приводят к преобразованию дробных значений, и приведению к наименьшему знаменателю.
При сокращении дроби необходимо числитель и знаменатель разделить на общее простое натуральное число. Иначе данное значение еще называют общим знаменателем.
Не все дроби можно сократить, так как значения в числителе и знаменателе могут быть несократимыми.
Это означает, что значение дроби не изменится.
Пример №1: Необходимо дробь [frac{1}{2}] перемножить на одно и тоже число, которое равно 2.
Для этого составим и запишем следующее выражение: [frac{1}{2}=frac{1 times 2}{2 times 2}=frac{2}{4}].
В ходе вычисления получаем дробь равную [frac{2}{4}]. Согласно основному свойству дроби [frac{2}{4}=frac{1}{2}].
Пример №2:
Числитель и знаменатель дробного значения, которое равно [frac{4}{8}] разделим на одинаковое значение равное 2.
Составим и решим выражение следующего вида: [frac{4}{8}=frac{4 times 2}{8 times 2}=frac{2}{4}]. Проведя необходимые вычисления получаем ответ [frac{2}{4}]. Снова применяя основное свойство дроби получаем, что [frac{2}{4}=frac{4}{8}].
Определение
Дополнительный множитель — численное значение, на которое можно умножить числитель и знаменатель дроби и получить число равное дроби.
Свойство сокращения дроби
Любое дробное выражение можно сокращать, тем самым преобразовывая его в более простое значение. Процесс сокращения дробного значения опирается на правило основного свойства дроби.
Определение
Сокращение дробного значения — это процесс деления числителя и знаменателя на значение, которое является общим для двух данных.
Пример №1:
Нужно заданное числовое значение равное сократить.
Для это необходимо выполнить следующие действия:
- все числовые значения данной дроби умножить на максимальное значение (общий числовой делитель) для значений 2 и 4.
- определяется наименьший общий делитель, для значений 2 и 4.
- числитель и знаменатель нужно разделить на НОД, равный 2.
[frac{2}{4}=frac{2 div 2}{4 div 2}=frac{1}{2}]
После выполнения всех необходимых вычислений и преобразований, получаем сокращенную дробь [frac{2}{4}=frac{1}{2}].
При этом исходное значение не изменилось, так как сокращение дроби сопровождалось делением значения числителя и знаменателя простое действительное число.
Пример №2:
В данном примере подробно рассмотрим сокращение дроби [frac{20}{40}]. Чтобы преобразовать дробь в более удобный вид, для последующих вычислений, определим наименьший общий делитель (НОД). Так как числитель равен 20, а знаменатель — 40, общим делителем будет число 20.
Запишем выражение: [frac{20}{40}=frac{20 div 20}{40 div 20}=frac{1}{2}].
Из решения видно, что довольна не удобная дробь [frac{20}{40}] благодаря сокращению, преобразовалась в упрощенный вид.
Пример №3:
В данном примере нужно сократить заданную дробь [frac{32}{36}], которая имеет значения в числителе и в знаменателе, неудобные для последующих вычислений в задачах разного типа.
Как в предыдущих примерах нужно выполнить идентичные действия согласно основному свойству дроби. Для заданной дроби определим общий делитель. В данном случае это будет значение равное 4. Числитель и знаменатель нужно разделить на наименьший делитель [frac{32}{36}=frac{32 div 4}{36 div 4}=frac{8}{9}].
Однако существуют случаи, когда сократить дроби невозможно. Так как в числителе может быть задано простое число, которое делится только на единичное значение или на само себя. Следовательно, они сокращаются.
В алгебре такие значения называются несократимыми.
К несократимым дробям относятся значения вида: [frac{1}{2} ; frac{3}{4} ; frac{3}{5} frac{5}{7} ; frac{7}{13}].
Сокращать дроби можно и иным способом. Он заключается в том, чтобы пропускать и не разъяснять подробно на какое значение делится числитель и знаменатель.
Если рассмотреть значение дроби [frac{32}{36}], то можно сделать вывод, что при упрощении дроби, ее разделили на число 4. А именно: числитель и знаменатель привели к общему делителю. [frac{32}{36}=frac{32 div 4}{36 div 4}=frac{8}{9}].
Более сокращенная версия будет выглядеть так, что часть выражения: [frac{32 div 4}{36 div 4}] опускается. И окончательный вариант при сокращении будет иметь следующий вид: [frac{32}{36}=frac{8}{9}].
Основная суть данного способа — это делитель сохранять в памяти и не переписывать его. В вышеприведенном примере значение 4 не записывалось, а в конечном итоге был записан только окончательный ответ.
Нет времени решать самому?
Наши эксперты помогут!
Сокращение дроби упрощенным способом
Важно выполнить следующие действия:
- Числитель нужно разделить на общий делитель.
- Полученное значение записывается около числителя, при этом значение числителя необходимо перечеркнуть.
- Аналогичным образом нужно поступить и со знаменателем.
- Следующим действием, нужно все вычисленные значения собрать и получить новое значение дроби.
Выполнив все пункты алгоритма, можно сделать вывод, что произошло преобразование одной дроби в другую. Значения составленной дроби равно значению заданной, согласно основным правилам при решении дробных значений.
Существует способ сокращения дробей, который предварительно нужно разложить на простые числа значение числителя и знаменателя.
Пример №4:
Нужно сократить заданную дробь: [frac{9}{27}]. Для этого изначально разложим на простые множители значение которое задано в числителе и знаменателе. Составим и запишем следующее выражение: .[frac{9}{27}=frac{3 times 3}{3 times 3 times 3}].
Затем нужно применить второй упрощенный способ сокращения дроби. В числителе и в знаменателе определяем по одному простому числу и затем делим все множители на наименьший общий делитель для этих значений.
Затем нужно сократить значение равное трем в числителе и знаменателе. Для этого нужно значение три разделить на НОД. Выполнив все вычисления получим и запишем выражение: [frac{9}{27}=frac{3}{3 times 3}]
Следующим действие снова сократим числитель и знаменатель на три и получим выражение: [frac{9}{27}=frac{1}{3}].
Так как больше сокращать не имеет смысла, получаем окончательное выражение равное [frac{1}{3}].
Значение три в знаменателе сократить нельзя, так как знаменатель необходимо сокращать совместно с числителем, а значение числителя равно единице.
Окончательный ответ будет выглядеть так: [frac{9}{27}=frac{1}{3}].
Когда необходимо применять основные правила и свойства дробей
- Основное свойство нужно применять в тех случаях, когда дробное число необходимо привести к наименьшему значению для знаменателя и числителя.
- Данное свойство играет огромную роль при сокращении дробей и приведения из более простому и удобному виду.
- Основное свойство дробей применяется только в случаях когда дроби являются сократимыми в числителе и в знаменателе нет простых чисел следующего типа: [frac{1}{3}].