Как найти основные элементы параллелепипеда

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 мая 2022 года; проверки требуют 4 правки.

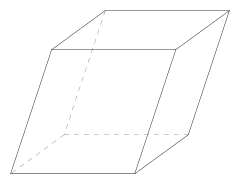
Параллелепи́пед (др.-греч. παραλληλ-επίπεδον^[1] от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — четырёхугольная призма, все грани которой являются параллелограммами.

Типы параллелепипеда[править | править код]

Различается несколько типов параллелепипедов:

• Наклонный — боковые грани не перпендикулярны основанию.
• Прямой — боковые грани перпендикулярны основанию.
• Прямоугольный — все грани являются прямоугольниками.
• Ромбоэдр — все грани являются равными ромбами.
• Куб — все грани являются квадратами.

Основные элементы[править | править код]

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства[править | править код]

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Основные формулы[править | править код]

Прямой параллелепипед[править | править код]

Площадь боковой поверхности
S_б=Р_о*h, где Р_о — периметр основания, h — высота

Площадь полной поверхности
S_п=S_б+2S_о, где S_о — площадь основания

Объём
V=S_о*h

Прямоугольный параллелепипед[править | править код]

Площадь боковой поверхности
S_б=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности
S_п=2(ab+bc+ac)

Объём
V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Куб[править | править код]

Площадь поверхности:

Объём: , где  — ребро куба.

Произвольный параллелепипед[править | править код]

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения^[2]:215.

В математическом анализе[править | править код]

В математическом анализе под n-мерным прямоугольным параллелепипедом понимают множество точек вида

Сечение параллелепипеда плоскостью[править | править код]

В зависимости от расположения секущей плоскости и параллелепипеда сечение параллелепипеда может быть треугольником, четырехугольником, пятиугольником и шестиугольником.

Примечания[править | править код]

Ссылки[править | править код]

• Прямоугольный параллелепипед Архивная копия от 21 февраля 2020 на Wayback Machine

В данной публикации мы рассмотрим определение, элементы, виды и основные свойства параллелепипеда, в т.ч. прямоугольного. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

• Определение параллелепипеда
• Виды параллелепипедов

• Свойства параллелепипеда

Определение параллелепипеда

Параллелепипед – это геометрическая фигура в пространстве; шестигранник, гранями которого являются параллелограммы. Фигура имеет 12 ребер и 6 граней.

Параллелепипед – это разновидность призмы с параллелограммом в качестве оснований. Основные элементы фигуры те же, что и у призмы.

Примечание: Формулы для расчета площади поверхности (для прямоугольной фигуры) и объема параллелепипеда представлены в отдельных публикациях.

Виды параллелепипедов

1. Прямой параллелепипед – боковые грани фигуры перпендикулярны ее основаниям и являются прямоугольниками.
2. Прямой параллелепипед может быть прямоугольным – основаниями являются прямоугольники.
3. Наклонный параллелепипед – боковые грани не перпендикулярны основаниям.
4. Куб – все грани фигуры являются равными квадратами.
5. Если все грани параллелепипеда – это одинаковые ромбы, он называется ромбоэдром.

Свойства параллелепипеда

1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами.

2. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам.

3. Квадрат диагонали (d) прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины (a), ширины (b) и высоты (c).

d² = a² + b² + c²

Примечание: к параллелепипеду, также, применимы свойства призмы.

Параллелепипед — тело строгих геометрических форм, противоположные грани которого находятся в параллельных плоскостях. Все плоскости, или грани, включая основание, параллелограммы. Научно определение параллелепипеда — призма, основанием которой служит параллелограмм. Часто ученики затрудняются ответить, чем отличается параллелограмм от параллелепипеда. Отличие в том, что параллелограмм — фигура плоская, двухмерная, а параллелепипед — объемное геометрическое тело, протяженное в трех измерениях, имеющее ширину, высоту и длину. Как выглядит параллелепипед, посмотрите на рисунке:

Виды параллелепипеда

Параллелепипед — многогранник. Его ограничивают шесть плоскостей, два основания, и четыре боковые грани. Линии, по которым соединяются грани, называются ребрами, а точки, в которых сходятся три ребра — вершинами. У фигуры 8 вершин.

Если грани имеют общее ребро, то их называют смежными, а те, у которых такого ребра нет — противоположными. Это же касается и вершин, если они не лежат на одной грани, то их тоже называют противоположными. Высота, ширина и длина прямоугольного  параллелепипеда называются измерениями, они выходят из одной вершины. Если фигура не прямоугольная, то измерения и ребра не совпадают.

При построении параллелепипеда на рисунке можно провести ряд дополнительных линий, которые помогают при вычислении объема, площади поверхности, неизвестных длин и других параметров. Если линии проходят через противоположные вершины, то их называют диагоналями. У параллелепипеда их насчитывается четыре.

В геометрии выделяют несколько типов параллелепипедов, которые отличаются некоторыми свойствами:

• Прямой — фигура, у которой боковые грани являются прямоугольниками;
• Прямоугольный — все грани прямоугольники, не только боковые, но и основания. Объемный прямоугольник — это т есть такой параллелепипед.
• Наклонный — боковые грани находятся по отношению к основанию под углами, отличными от 90⁰;
• Ромбоэдр — все грани представляют собой равные ромбы;
• Куб — все грани квадратны.

Свойства параллелепипеда

Для всех типов параллелепипедов можно выделить общие свойства, характеризующие фигуру. Таких свойств немного, запомнить их не сложно:

• Диагонали параллелепипеда в точке пересечения делятся пополам;
• Параллелепипед симметричен относительно точки пересечения диагоналей;
• Любой отрезок, соединяющий две точки на гранях параллелепипеда и проходящий через точку пересечения диагоналей, делится пополам;
• Противоположные грани равны и параллельны (вытекает из определения);
• Сумма квадратов измерений равна квадрату диагонали.

Твердо запомнив эти свойства несложно решить большинство задач школьной геометрии.

Основные формулы параллелепипеда

Кроме свойств этой фигуры нужно запомнить ряд несложных формул. Конечно, в процессе решения задачи можно вывести эти выражения самостоятельно. Но часто на это нет времени, лучше воспользоваться готовыми шаблонами.

Формула площади боковой поверхности прямого параллелепипеда — одна из самых простых. S_б=Р_о∙h. В этой формуле только три величины, но одна из них составная:

H – высота параллелепипеда;

Р – периметр, АВ+ВС+АD+ CD.

Воспользоваться такой формулой можно только в том случае, если известны длины сторон основы и высота.

Площадь полной поверхности параллелепипеда определяется по формуле S_п=S_б+2S_о.

Как найти площадь боковой поверхности мы знаем из предыдущего пункта, а площадь S_о рассчитывается в зависимости от вида четырехугольника, лежащего в основании.

Объем прямого параллелепипеда тоже найти несложно, для этого достаточно умножить площадь основания на высоту. Объём V=S_о∙h

Формулы для прямоугольного параллелепипеда тоже не отличаются сложностью:

S_б=2c(a+b) в этой формуле а и b – стороны основания, с – высота, равна длине бокового ребра.

Площадь полной поверхности равна S_п=2(ab+bc+ac);

Объем V=abc, то есть, произведение всех трех измерений.

Когда же приходится вычислять площади и объем произвольного параллелепипеда, то показанные формулы не всегда срабатывают. Необходимо использовать законы векторной геометрии. При вычислении объема параллелепипеда через длину диагонали, необходимо использовать проекции на разные оси. Видимая простота формул — это только основа для сложной работы, требующей пространственного воображения и смекалки.

Материал урока.

Прежде чем
приступить к изучению нового материала, давайте вспомним, какая фигура
называется тетраэдром, вспомним элементы тетраэдра и виды тетраэдра.

С параллелепипедом
мы уже знакомы. Напомним, что в курсе геометрии базовой школы мы определяли параллелепипед
как четырехугольную призму, основаниями которой являются параллелограммы.

Сегодня мы дадим
немного другое определение параллелограмма.

Рассмотрим два
равных параллелограмма ABCD и A₁B₁C₁D₁, которые расположены в параллельных плоскостях
так, что отрезки AA₁, BB₁,
CC₁, DD₁
параллельны.

Получили
четырехугольники ABB₁A₁,
BCC₁B₁, CDD₁C₁, DAA₁D₁.
Рассмотрим один из этих четырехугольников. Например, четырехугольник ABB₁A₁. Стороны
AA₁ и BB₁
параллельны по условию. По свойству параллельных плоскостей стороны AB и A₁B₁
параллельны. То есть, четырехугольник ABB₁A₁ – параллелограмм, аналогично, параллелограммами
будут каждый из четырехугольников BCC₁B₁, CDD₁C₁, DAA₁D₁.

Поверхность,
составленная из двух равных параллелограммов ABCD и A₁B₁C₁D₁ и четырех
параллелограммов ABB₁A₁,
BCC₁B₁, CDD₁C₁, DAA₁D₁называется
параллелепипедом и обозначается так: ABCDA₁B₁C₁D₁

Параллелограммы, из
которых составлен параллелепипед, называются гранями.

На рисунке
изображен параллелепипед ABCDA₁B₁C₁D₁. Обратите внимание, все шесть граней параллелепипеда
– параллелограммы.

Стороны
параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами
параллелепипеда. Две грани параллелепипеда называются противолежащими,
если они не имеют общего ребра. Например, грани AA₁B₁B и DD₁C₁C –
противолежащие.

Грани имеющие общее
ребро называются смежными. Например, грани AA₁D₁D и DD₁C₁C – смежные, ребро DD₁ у них общее.

Иногда какие-нибудь
две противолежащие грани параллелепипеда выделяются и называются основаниями,
тогда остальные грани – боковыми гранями, а их стороны, соединяющие
вершины оснований параллелепипеда, – его боковыми ребрами. В нашем
случае у параллелепипеда ABCDA₁B₁C₁D₁ грани ABCD и A₁B₁C₁D₁– его
основания. Остальные же грани являются боковыми гранями.

Две вершины,
которые не принадлежат одной грани, называются противоположными.

Отрезок, который
соединяет противоположные вершины, называется диагональю параллелепипеда.
Соответственно у параллелепипеда есть четыре диагонали.

То есть, если в
качестве оснований выбрать грани ABCDиA₁B₁C₁D₁, то боковыми гранями будут параллелограммы ABB₁A₁, BCC₁B₁, CDD₁C₁, DAA₁D₁, а
боковыми рёбрами будут отрезки AA₁, BB₁, CC₁, DD₁.

Мы уже знаем, как
изображается параллелепипед. Как и в прочих пространственных фигурах, невидимые
рёбра и другие отрезки изображаются штриховыми линиями.

Со свойствами
параллелепипеда мы уже знакомы. Повторим их еще раз и докажем с учетом нового
определения параллелепипеда.

Первое свойство
звучит так: противоположные грани параллелепипеда параллельны и равны.
Сразу отметим, что две грани параллелепипеда будут параллельны, если их
плоскости параллельны.

Докажем,
например, параллельность и равенство граней ABB₁A₁ и DCC1D₁
параллелепипеда ABCDA₁B₁C₁D₁. Поскольку
эти грани являются параллелограммами, то можно записать, что AB
параллельно DC и AA₁
параллельно DD₁. То есть две пересекающиеся
прямые AB и AA₁ одной
грани соответственно параллельны двум пересекающимся прямым CD
и DD₁ другой грани. Значит, по признаку
параллельности плоскостей получим, что грани ABB₁A₁ и DCC₁D₁ параллельны.

Поскольку все грани
параллелепипеда – параллелограммы, то можно записать, что AB
равно DC и AA₁равно DD₁. По этой же причине стороны углов A₁AB и D₁DC соответственно сонаправлены, и, значит, эти углы равны.
Таком, образом мы доказали, что две смежные стороны и угол между ними
параллелограмма ABB₁A₁
соответственно равны двум смежным сторонам и углу между ними параллелограмма DCC₁D₁, поэтому
параллелограммы ABB₁A₁
и DCC₁D₁
равны.

Перейдем ко второму
свойству. Диагонали параллелепипеда пересекаются в одной точке и делятся
этой точкой пополам.

Доказательство
этого утверждения основывается на следующем факте: если две прямые в
пространстве параллельны третьей прямой, то они параллельны.

Мы знаем, что
диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Итак, на экране
изображен прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Поскольку грани ABCDи AA₁D₁D – параллелограммы, то BC
параллельно AD, BC равно AD, A₁D₁
параллельно AD, A₁D₁ равно AD. Из этого
следует, что A₁D₁
параллельно BC и A₁D₁ равно BC. Поэтому
четырехугольник A₁D₁CB – параллелограмм. А значит, его диагонали A₁C и D₁B пересекаются в некоторой точке О и делятся этой точкой
пополам. Заметим, что эти же диагонали A₁C и D₁B
являются также диагоналями параллелепипеда.

Поскольку грани ABCDиDD₁C₁C– параллелограммы, то AB параллельно
CD, AB равно CD,
C₁D₁
параллельно CD, C₁D₁ равно CD. Из этого
следует, что C₁D₁
параллельно AB и C₁D₁ равно AB. Поэтому
четырехугольник C₁D₁AB – параллелограмм. И,
следовательно, его диагонали C₁A и D₁B
пересекаются и точкой пересечения делятся пополам. Но серединой диагонали D₁B является точка О.
Таким образом, диагонали A₁C,
D₁B и C₁A параллелепипеда
пересекаются в точке О и делятся этой точкой пополам.

Поскольку грани ABCDи AA₁B₁B – параллелограммы, то CD
параллельно AB, CD равно AB, A₁B₁
параллельно AB, A₁B₁ равно AB. Из этого
следует, что A₁B₁
равно CD и A₁B₁ параллельно CD. Поэтому
четырехугольник A₁B₁CD – параллелограмм. И,
следовательно, его диагонали A₁C и B₁D
пересекаются и точкой пересечения делятся пополам. Но серединой диагонали A₁C является точка О.
Таким образом, все четыре диагонали A₁C, B₁D,
C₁A и D₁B параллелепипеда
пересекаются в точке О и делятся этой точкой пополам. Что и требовалось
доказать.

Слово
параллелепипед происходит от древнегреческих слов паралелос –
параллельный, и епипед – плоскость.

Если все боковые
ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые
грани – прямоугольники, то такой параллелепипед называется прямым.

Если параллелепипед
не является прямым, то есть если все его боковые ребра не перпендикулярны к
плоскостям оснований, то он называется наклонным.

Если же и
основаниями прямого параллелепипеда служат прямоугольники, то такой
параллелепипед называется прямоугольным.

Параллелепипед
очень часто встречается в жизни, практически все здания имеют форму
параллелепипеда. И многие предметы имеют форму параллелепипеда.

Решим несколько
задач.

Задача. Дан
параллелепипед . Доказать, что
диагональ  параллельна .

Доказательство.

Что и требовалось доказать.

Задача. Сумма
всех рёбер параллелепипеда  равна  cм.
Найдите каждое ребро параллелепипеда, если ,
а .

Решение.

Из соотношений
выразим длины ребер AB и BB1
через длину ребра BC.

Получим, что ABравно , BB₁ равно .

У параллелепипеда
двенадцать ребер, из них четыре ребра равны ребру AB,
четыре ребра равны ребру BB₁, четыре ребра
равны ребру BC. Заменим ребра AB
и BB₁ и их выражением через ребро BC, получим, что 12BC=120. Тогда получим,
что длина ребра BC= 10. Подставим это значение в
формулу для нахождения длин ребер AB и BB1, получим, что AB= 8, а BB₁= 12.

Кратко запишем
решение задачи.

Подведем итоги
урока. Сегодня на уроке мы познакомились с еще одним пространственнымтелом
– параллелепипедом. Познакомились с элементами параллелепипеда, решили
несколько задач по данной теме.