Как найти основные системы счисления

Всем привет! Это первая лекция базового курса для подготовки к ЕГЭ по информатике. Базовый курс – это набор лекций для подготовки к ЕГЭ с самого нуля. Он создан для тех кто только начал свою подготовку к экзамену. Подписывайтесь на мой канал и будет вам счастье!

Система Счисления(СС) -это способ записи числа с помощью символов. Символы еще называют алфавитом СС.

Системы Счисления бывают позиционные и непозиционные . На картинке выше символьная и римская СС являются хорошим примером непозиционной системы счисления. Как не переставляйте кружочки, смысл не поменяется их все равно будет десять.

Нам же с вами для сдачи ЕГЭ по информатике нужно разобраться в принципах и правилах позиционной системы счисления.

В позиционной СС от позиции(разряда) цифры зависит ее значение. Например число 685 = 600(сотни) + 80(десятки) + 5(единицы), можно записать иначе 685 = 6 * 100 + 8 * 10 + 5 * 1. Если бы число 685 было непозиционным, то мы бы записали так, 685 = 6+8+5 = 19.

С тем что такое системы счисления мы с вами разобрались. Теперь предлагаю рассмотреть основные системы счисления и классические способы перевода с одной системы счисления в другую.

Важно запомнить что в любой позиционной системе счисления все работает так же как в десятичной системе счисления. Для того чтобы в этом убедится и понять, нужно как можно больше практиковаться!

Двоичная система счисления

(0, 1)

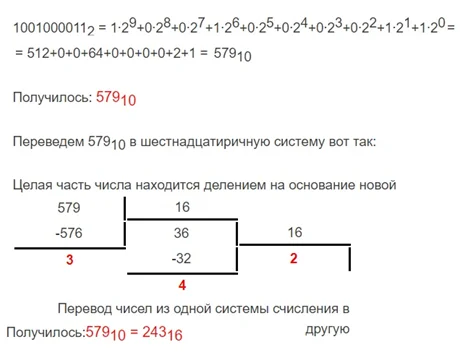
Для перевода десятичного числа в двоичную систему счисления нам нужно разделить это число на 2(основание двоичной системы счисления) столбиком и выписать остатки от деления в обратном порядке.

Давайте теперь переведем получившееся число в двоичной СС обратно в десятичную. Заодно проверим, правильно ли мы посчитали.

Восьмеричная система счисления

(0, 1, 2, 3, 4, 5, 6, 7)

Для перевода числа из десятичной в восьмеричную систему счисления, будем делить наше число на 8 (основание системы счисления). Точно так же как и в двоичной СС

Переведем получившееся число обратно в десятичную систему счисления

Шестнадцатиричная система счисления

(1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15))

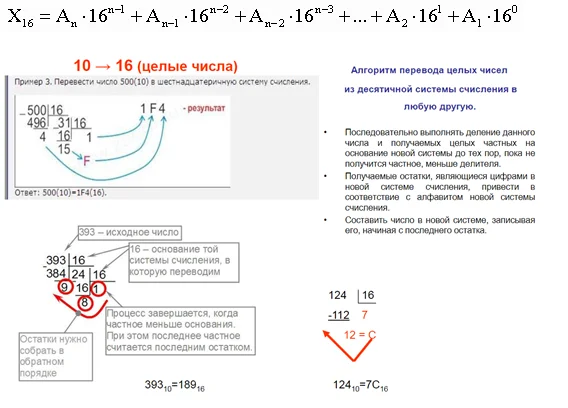
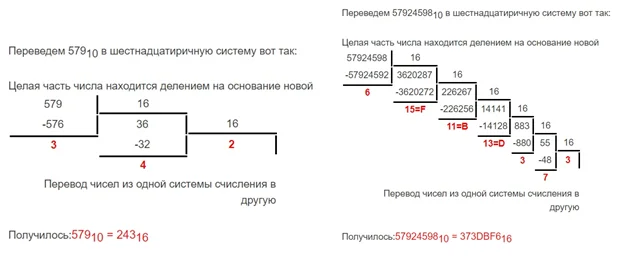
Для перевода числа из десятичной СС в шестнадцатиричную СС делаем все то же самое. Делим число уголком на 16 (основание системы счисления)

И так же переведем число обратно

Мы с вами рассмотрели основные системы счисления и стандартный способ перевода из одной СС в другую. Конечно существуют другие способы и мы их с вами в дальнейшем обязательно рассмотрим. Но я вам настоятельно рекомендую потренироваться переводить числа именно таким способом.

Для перевода числа из десятичной системы счисления в любую другую, необходимо это число разделить уголком на основание системы счисления. А в ответ записать остатки от деления в обратном порядке.

Другие статьи по теме:

План урока:

Системы счисления – виды, особенности

Непозиционные системы счисления, их особенности

Основные позиционные системы счисления, правила перевода

Шестандцатеричная система счисления

Арифметические операции в двоичной системе

Сравнение систем

Таблицы истинности

Развиваясь, древний человек стал испытывать потребность в способах выражения количества. Подсчет убитых животных, количество врагов или соседей – причин становилось все больше. Сначала люди использовали только понятия «один», «много». После стали использовать понятие «пара», чтобы обозначить два предмета, это намного облегчило жизнь.

Постепенно перешли к использованию подручных средств – пальцев на руках и ногах, зарубок на коре дерева, кости животного или узелков на канате. Именно такие примитивные «счетные машины» позволили через тысячи лет узнать, что предки умели не просто считать, но даже умудрялись фиксировать результаты подсчета.

Кроме зарубок и узелков появилась потребность в символах, выражающих большее количество чего-либо, чем «один». Тогда были придуманы первые знаки для выражения больших значений. Так, египтяне, использовали знаки для цифр 1, 5, 10. Число 324 в их системе выглядело так: 

А описание чисел при помощи специальных знаков и является системой счисления.

Системы счисления – виды, особенности

Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.

Источник

Все существующие системы делят на 2 группы:

1. Позиционные системы счисления – такие, в которых, в зависимости от положения, цифры будет иметь разное значение. К этой группе относится арабская СС, в которой на первом месте справа цифра будет обозначать единицы, на втором – десятки, на третьем – сотни и так далее.

Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.

К этой группе также относятся СС с различными основаниями (2,8,16).

1. Непозиционные СС – имеет значение именно знак, а не его положение. Единицы, десятки, сотни обозначаются определенными символами. Яркий представитель этой группы – римская СС.

Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.

12 – XII

8 – VIII или IIX

Правильным считается тот вариант, при котором получается меньше символов.

Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.

Алфавит СС – знаки, которые используются для обозначения цифр.

Основание – количество знаков, которыми кодируются числа.  Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.

Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 1254₈, 01100111₂. Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).

Разряд – положение, позиция обозначения цифры в числе. Пример?

Непозиционные СС, их особенности

Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).

Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.

Источник

Римская СС

В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.

Основные рекомендации при пользовании римскими цифрами:

1. Символы следует писать по убыванию слева направо.
2. Нежелательно записывать подряд более 3 одинаковых знаков.
3. Положение цифры обозначает, какой ее вклад – отрицательный, если она стоит слева от большего числа, положительный – справа.

Таблица римских цифр 

Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.

Основные позиционные СС, правила перевода

Двоичная система счисления

Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.

Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.

Алгоритм перевода чисел из десятичной в двоичную систему:

1. Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
2. Записать остатки, от последнего к первому.
3. Первый ноль можно не писать.

0111 0100 1100₂ 

Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток < или равен =.

Обратный алгоритм перевода из двоичной в десятичную систему счисления:

Записать число развернуто, то есть, сколько сотен, десятков и единиц в нем, но учитывая основу – 2

Объяснение. Развернутая форма записи 579: 5*10²+7*10¹+9*10⁰ = 579₁₀.

Источник

Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.

1. Умножить и суммировать полученные значения.

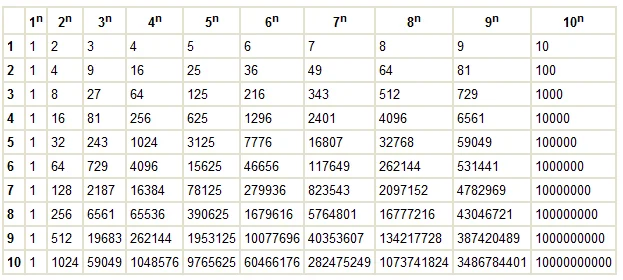
А чтобы было легче, пользуются готовой таблицей степеней 2.

Альтернативный способ преобразования для гуманитариев

Для начала нужно написать степени двойки, начиная с самой большой:

Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет.
Перевод числа 579

Обратно еще проще. Подсчитать количество знаков – это будет степень 2 в степени -1. И так далее. А проще при помощи той же таблицы:

Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.

Восьмеричная СС

Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).

Пример: Перевести 579₈ из десятичной в восьмеричную систему счисления:

Обратный перевод из восьмеричной СС в десятичную:

1103₈ = 1∙8³+1∙8²+0∙8¹+3∙8⁰ = 512+64+0+3 = 579₁₀

Таблица степеней

Альтернативный вариант таблицы степеней 

Шестнадцатеричная СС

Это целочисленная система с основанием 16 (символы шестнадцатеричной системы счисления 0-9 и буквы A – F). Используется в реализации компьютерного программирования и документации на низком уровне, так как 8-битный байт, для записи которого удобно использовать 2 цифры из шестнадцатеричной системы.

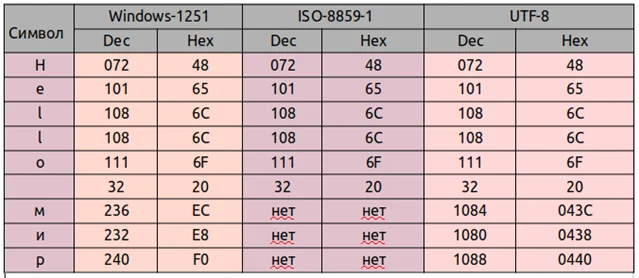
Стандарт Юникод использует 4 и более символов 16-ой СС.

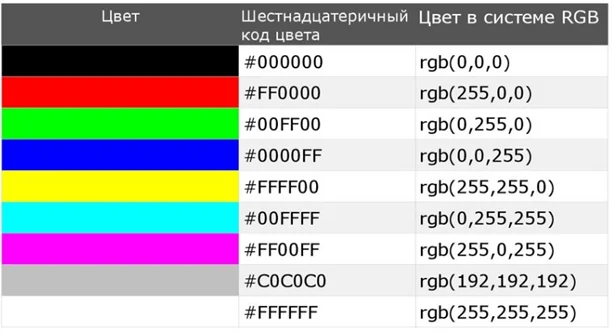
Для записи цвета из красного, зеленого и синего (R, G и B) также используют эту систему.

Алгоритм преобразования чисел в 16СС

Способ преобразования аналогичный предыдущим – расписывание числа как многочлена с учетом степеней 16. Для этого число делится на 16, в итоге – перечень остатков от деления, записанных наоборот.

В сети есть калькуляторы, способные выполнять преобразование чисел в различные СС и обратно (некоторые даже с детальным описанием процесса).

Арифметика для 2СС

Принципы выполнения простейших арифметических операций одинаковы для любых позиционных систем, независимо от основы:

Особенности арифметики СС с разными основами:

• при сложении чисел двух 1 в двоичной системе переполняется младший разряд (сумма = или ˃ основания СС), то единица переходит к большему разряду;
• если есть 0-1=1, идет заимствование из старшего разряда;
• умножать 2СС удобнее всего в столбик, учитывая 4 основные правила;
• заем единиц в 2СС при отнимании/делении, тогда она дает промежуточным разрядам по 1, а для занимаемого разряда сразу 11.

Примеры арифметических операций:

Для удобства разработаны готовые таблицы сложения в различных системах:

Сложение в 8-ой СС                                              в 16СС

С их помощью можно быстро суммировать в различных СС.

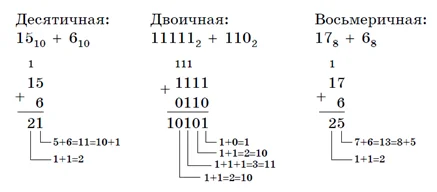
Сложение для разных СС на примере 15 и 6:

Если необходимо сложить числа из разных систем, их приводят к одной основе. Самым простым вариантом будет перевод в десятичную систему, решение простого примера и перевод результата в любую из систем.

Рассмотрим сумму 43₈ и 56₁₆. Результат можно выразить в любой СС, но проще привести к 8- или 16-ричной:

 Переводим число 56 в восьмеричную через двоичную:

Умножение в 8-ой СС

в 16СС

Сравнение систем

СС могут быть с произвольной основой, но популярны 2,8,10,16-ые.

Сравнительная таблица разных систем счисления:

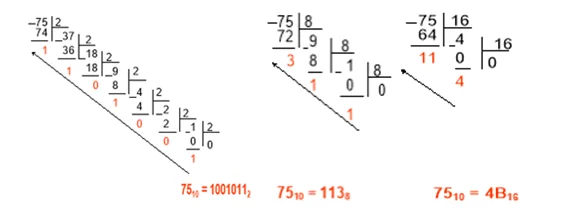
Перевод числа 75 в разные системы:

Источник

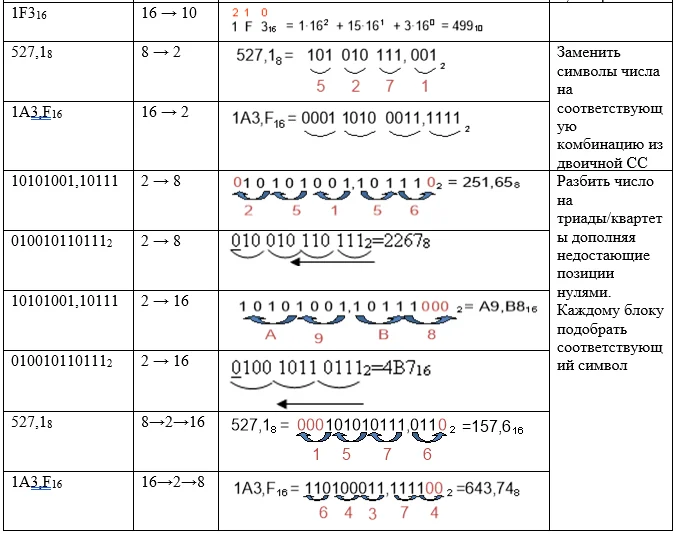
Правила перевода из двоичной, восьмеричной и шестнадцатеричной в 10СС:

Исходный вариант следует разделить на тройки цифр, с крайней справа. Если не хватает, старший разряд дополнить 0. Далее под каждой триадой ставится подходящий символ из 8‑ой системы.

Рассмотрим перевод на примере числа 579, которое соответствует 1001000011₂ 

001 001 000 011

Правила перевода из двоичной в шестнадцатеричную систему счисления:

Число разбивается по 4 знака, начиная справа (с меньшего разряда). Если не будет хватать символов у старшего разряда, тетраду дополняют нулями.

1001000011₂

0010 0100 0011

Сравнительный перевод дробей в СС

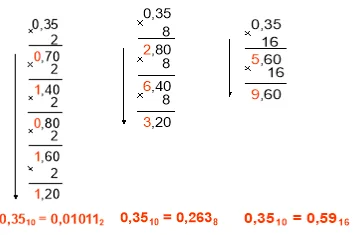
Чтобы перевести правильные дроби из 10-ой СС в другие позиционные, следует придерживаться правила, которое хорошо видно на примере перевода числа 0,35:

Удобно писать над каждой цифрой порядок, а дальше ее умножить на основу СС в степени разряда.

Перевод целых и дробей в 2СС, 8СС, 16СС:

Таблицы истинности

При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.

Основные логические операции

Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.

Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

Фрагмент таблицы истинности для конъюнкции.

Так выражаются условия для всех логических операций.

Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.

При составлении урока был использован некоторый материал из сайта: https://studylib.ru/doc/6220932/sistemy-schisleniya

 3.1.
Основные понятия систем счисления

 3.2.
Виды систем счисления

 3.3.
Правила перевода чисел из одной системы
счисления в другую

 3.4.
Иллюстрированный вспомогательный
материал

 3.5.
Тестирование

 3.6.
Контрольные вопросы

Разные народы в разные
времена использовали разные системы
счисления. Следы древних систем счета
встречаются и сегодня в культуре многих
народов. К древнему Вавилону восходит
деление часа на 60 минут и угла на 360
градусов. К Древнему Риму – традиция
записывать в римской записи числа I, II,
III и т. д. К англосаксам – счет дюжинами:
в году 12 месяцев, в футе 12 дюймов, сутки
делятся на 2 периода по 12 часов.

По современным данным,
развитые системы нумерации впервые
появились в древнем Египте. Для записи
чисел египтяне применяли иероглифы
один, десять, сто, тысяча и т.д. Все
остальные числа записывались с помощью
этих иероглифов и операции сложения.
Недостатки этой системы – невозможность
записи больших чисел и громоздкость.

В конце концов, самой
популярной системой счисления оказалась
десятичная система. Десятичная система
счисления пришла из Индии, где она
появилась не позднее VI в. н. э. В ней всего
10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 но информацию
несет не только цифра, но также и место
позиция, на которой она стоит. В числе
444 три одинаковых цифры обозначают
количество и единиц, и десятков, и сотен.
А вот в числе 400 первая цифра обозначает
число сотен, два 0 сами по себе вклад в
число не дают, а нужны лишь для указания
позиции цифры 4.

3.1. Основные понятия систем счисления

Система счисления
– это совокупность правил и приемов
записи чисел с помощью набора цифровых
знаков. Количество цифр, необходимых
для записи числа в системе, называют
основанием системы
счисления. Основание
системы записывается в справа числа в
нижнем индексе:
;;и
т. д.

Различают два типа систем счисления:

позиционные, когда значение каждой
цифры числа определяется ее позицией
в записи числа;

непозиционные, когда значение цифры
в числе не зависит от ее места в записи
числа.

Примером непозиционной системы счисления
является римская: числа IX, IV, XV и т.д.

Примером позиционной
системы счисления является десятичная
система, используемая повседневно.

Любое целое число в позиционной системе
можно записать в форме многочлена:

где S –
основание системы счисления;

–
цифры числа, записанного в данной системе
счисления;

n – количество разрядов числа.

Пример. Число
запишется
в форме многочлена следующим образом:

3.2. Виды систем счисления

Римская система счисленияявляется
непозиционной системой. В ней для записи
чисел используются буквы латинского
алфавита. При этом буква I всегда означает
единицу, буква – V пять, X – десять, L –
пятьдесят, C – сто, D – пятьсот, M – тысячу
и т.д. Например, число 264 записывается в
виде CCLXIV. При записи чисел в римской
системе счисления значением числа
является алгебраическая сумма цифр, в
него входящих. При этом цифры в записи
числа следуют, как правило, в порядке
убывания их значений, и не разрешается
записывать рядом более трех одинаковых
цифр. В том случае, когда за цифрой с
большим значением следует цифра с
меньшим, ее вклад в значение числа в
целом является отрицательным. Типичные
примеры, иллюстрирующие общие правила
записи чисел в римской система счисления,
приведены в таблице.

Таблица 2.
Запись чисел в римской
системе счисления

1	2	3	4	5
I	II	III	IV	V
6	7	8	9	10
VI	VII	VIII	IX	X
11	13	18	19	22
XI	XIII	XVIII	XIX	XXII
34	39	40	60	99
XXXIV	XXXIX	XL	LX	XCIX
200	438	649	999	1207
CC	CDXXXVIII	DCXLIX	CMXCIX	MCCVII
2045	3555	3678	3900	3999
MMXLV	MMMDLV	MMMDCLXXVIII	MMMCM	MMMCMXCIX

Недостатком римской системы
является отсутствие формальных правил
записи чисел и, соответственно,
арифметических действий с многозначными
числами. По причине неудобства и большой
сложности в настоящее время римская
система счисления используется там,
где это действительно удобно: в литературе
(нумерация глав), в оформлении документов
(серия паспорта, ценных бумаг и др.), в
декоративных целях на циферблате часов
и в ряде других случаев.

Десятичня система счисления– в
настоящее время наиболее известная и
используемая. Изобретение десятичной
системы счисления относится к главным
достижениям человеческой мысли. Без
нее вряд ли могла существовать, а тем
более возникнуть современная техника.
Причина, по которой десятичная система
счисления стала общепринятой, вовсе не
математическая. Люди привыкли считать
в десятичной системе счисления, потому
что у них по 10 пальцев на руках.

Древнее изображение
десятичных цифр (рис. 1) не случайно:
каждая цифра обозначает число по
количеству углов в ней. Например, 0 –
углов нет, 1 – один угол, 2 – два угла и т.д.
Написание десятичных цифр претерпело
существенные изменения. Форма, которой
мы пользуемся, установилась в XVI веке.

Десятичная система впервые
появилась в Индии примерно в VI веке
новой эры. Индийская нумерация использовала
девять числовых символов и нуль для
обозначения пустой позиции. В ранних
индийских рукописях, дошедших до нас,
числа записывались в обратном порядке
– наиболее значимая цифра ставилась
справа. Но вскоре стало правилом
располагать такую цифру с левой стороны.
Особое значение придавалось нулевому
символу, который вводился для позиционной
системы обозначений. Индийская нумерация,
включая нуль, дошла и до нашего времени.
В Европе индусские приёмы десятичной
арифметики получили распространение
в начале ХIII в. благодаря работам
итальянского математика Леонардо
Пизанского (Фибоначчи). Европейцы
заимствовали индийскую систему счисления
у арабов, назвав ее арабской. Это
исторически неправильное название
удерживается и поныне.

Десятичная система использует
десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также
символы “+” и “–” для обозначения
знака числа и запятую или точку для
разделения целой и дробной частей числа.

В вычислительных машинах
используется двоичная
система счисления,
её основание – число 2. Для записи чисел
в этой системе используют только две
цифры – 0 и 1. Вопреки распространенному
заблуждению, двоичная система счисления
была придумана не инженерами-конструкторами
ЭВМ, а математиками и философами задолго
до появления компьютеров, еще в ХVII – ХIХ
веках. Первое опубликованное обсуждение
двоичной системы счисления принадлежит
испанскому священнику Хуану Карамюэлю
Лобковицу (1670 г.). Всеобщее внимание к
этой системе привлекла статья немецкого
математика Готфрида Вильгельма Лейбница,
опубликованная в 1703 г. В ней пояснялись
двоичные операции сложения, вычитания,
умножения и деления. Лейбниц не
рекомендовал использовать эту систему
для практических вычислений, но
подчёркивал её важность для теоретических
исследований. Со временем двоичная
система счисления становится хорошо
известной и получает развитие.

Выбор двоичной системы для применения
в вычислительной технике объясняется
тем, что электронные элементы – триггеры,
из которых состоят микросхемы ЭВМ, могут
находиться только в двух рабочих
состояниях.

С помощью двоичной системы кодирования
можно зафиксировать любые данные и
знания. Это легко понять, если вспомнить
принцип кодирования и передачи информации
с помощью азбуки Морзе. Телеграфист,
используя только два символа этой азбуки
– точки и тире, может передать практически
любой текст.

Двоичная система удобна
для компьютера, но неудобна для человека:
числа получаются длинными и их трудно
записывать и запоминать. Конечно, можно
перевести число в десятичную систему
и записывать в таком виде, а потом, когда
понадобится перевести обратно, но все
эти переводы трудоёмки. Поэтому
применяются системы счисления, родственные
двоичной – восьмеричная
и шестнадцатеричная.
Для записи чисел в этих системах требуется
соответственно 8 и 16 цифр. В 16-теричной
первые 10 цифр общие, а дальше используют
заглавные латинские буквы. Шестнадцатеричная
цифра A соответствует десятеричному
числу 10, шестнадцатеричная B – десятичному
числу 11 и т. д. Использование этих систем
объясняется тем, что переход к записи
числа в любой из этих систем от его
двоичной записи очень прост. Ниже
приведена таблица соответствия чисел,
записанных в разных системах.

Таблица 3. Соответствие чисел, записанных
в различных системах счисления

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
1	001	1	1
2	010	2	2
3	011	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

• даёт представления множества чисел (целых и/или вещественных);
• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);
• отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на:

• позиционные (англ. positional system, place-value notation);
• непозиционные;
• смешанные.

Позиционные системы счисления[править | править код]

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у арабов.

Под позиционной системой счисления обычно понимается -ичная система счисления, которая определяется целым числом , называемым основанием системы счисления. Целое число без знака в -ичной системе счисления представляется в виде конечной линейной комбинации степеней числа :

, где  — это целые числа, называемые цифрами, удовлетворяющие неравенству .

Каждая степень в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя (номером разряда). Обычно в записи ненулевых чисел начальные нули опускаются.

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число записывают в виде последовательности его -ичных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

Например, число сто три представляется в десятичной системе счисления в виде:

Наиболее часто употребляемыми в настоящее время позиционными системами являются:

• 2 — двоичная (в дискретной математике, информатике, программировании);
• 3 — троичная;
• 8 — восьмеричная;
• 10 — десятичная (используется повсеместно);
• 12 — двенадцатеричная (счёт дюжинами);
• 16 — шестнадцатеричная (используется в программировании, информатике);
• 20 — двадцатеричная;
• 60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

В позиционных системах чем больше основание системы счисления, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

Смешанные системы счисления[править | править код]

Смешанная система счисления является обобщением -ичной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел , и каждое число в ней представляется как линейная комбинация:

, где на коэффициенты , называемые как и прежде цифрами, накладываются некоторые ограничения.

Записью числа в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса , начиная с первого ненулевого.

В зависимости от вида как функции от смешанные системы счисления могут быть степенными, показательными и т. п. Когда для некоторого , смешанная система счисления совпадает с показательной -ичной системой счисления.

Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина « дней, часов, минут, секунд» соответствует значению секунд.

Факториальная система счисления[править | править код]

В факториальной системе счисления основаниями являются последовательность факториалов , и каждое натуральное число представляется в виде:

, где .

Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: номер перестановки (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе будет обозначать число инверсий для элемента в том множестве, в котором производятся перестановки (число элементов меньших , но стоящих правее его в искомой перестановке).

Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём перестановку с номером 100:

положим  — коэффициент при числе , тогда , , , , тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, перестановка с номером 100 будет иметь вид: (5,3,1,2,4)
Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.

Фибоначчиева система счисления[править | править код]

Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число в ней представляется в виде:

, где  — числа Фибоначчи, , при этом в коэффициентах есть конечное количество единиц и не встречаются две единицы подряд.

Непозиционные системы счисления[править | править код]

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

К наиболее распространённым сегодня непозиционным системам счисления относятся римские цифры.

Биномиальная система счисления[править | править код]

В биномиальной системе счисления^[en] число x представляется в виде суммы биномиальных коэффициентов:

, где

При всяком фиксированном значении каждое натуральное число представляется уникальным образом.^[1]

Система остаточных классов (СОК)[править | править код]

Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором попарно взаимно простых модулей с произведением так, что каждому целому числу из отрезка ставится в соответствие набор вычетов , где

…

При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка .

В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в .

Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленных в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям .

Система счисления Штерна-Броко[править | править код]

Система счисления Штерна-Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна-Броко.

См. также[править | править код]

• История математики
• Алфавитная запись чисел
• Число
• Счёты
• Логарифмическая система счисления

Примечания[править | править код]

Ссылки[править | править код]

• Гашков С. Б. Системы счисления и их применение. — М.: МЦНМО, 2004. — (Библиотека «Математическое просвещение»). Архивная копия от 12 января 2014 на Wayback Machine
• Фомин С. В. Системы счисления. — М.: Наука, 1987. — 48 с. — (Популярные лекции по математике).
• Яглом И. Системы счисления // Квант. — 1970. — № 6. — С. 2—10.
• Цифры и системы счисления. Онлайн Энциклопедия Кругосвет.
• Стахов А. Роль систем счисления в истории компьютеров. Архивировано 1 мая 2009 года.
• Микушин А. В. Системы счисления. Курс лекций «Цифровые устройства и микропроцессоры»
• Butler J. T., Sasao T. Redundant Multiple-Valued Number Systems В статье рассмотрены системы счисления, использующие цифры больше единицы и допускающие избыточность в представлении чисел