Как найти особые точки системы дифференциальных уравнений - Сайт, где вы сможете решить свои вопросы

Особые решения дифференциальных уравнений

Решение y=varphi(x) дифференциального уравнения

F(x,y,y')=0

(1)

называется особым, если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку (x_0,y_0) кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение y=varphi(x) , но не совпадающее с ним в сколь угодно малой окрестности (x_0,y_0) . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция F(x,y,y') и ее частные производные $frac{partial F}{partial y}$ и $frac{partial F}{partial y'}$ непрерывны по всем аргументам x,,y,,y' , то любое особое решение уравнения (1) удовлетворяет также уравнению

$frac{partial}{partial y'}F(x,y,y')=0.$

(2)

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

psi(x,y)=0

(3)

называется p-дискриминантом уравнения (1), а кривая, определяемая уравнением (3), называется p-дискриминантной кривой (коротко mathsf{PDK} ).

Часто бывает так, что mathsf{PDK} распадается на несколько ветвей. Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Пример 1. Найти особые решения дифференциального уравнения

xy'+(y')^2-y=0.

(4)

Решение.

а) Находим p-дискриминантную кривую. В данном случае F(x,y,y')equiv xy'+(y')^2-y и условие (2) принимает вид $frac{partial F}{partial y'}equiv x+2y'=0$ , отсюда $y'=-frac{x}{2}$ . Подставляя это выражение для в уравнение (4), получаем

$y=-frac{x^2}{4}$

(5)

Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.

б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что $y=-frac{x^2}{4}$ есть решение уравнения (4).

в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде y=xy'+(y')^2 . Это уравнение Клеро. Его общее решение

y=Cx+C^2

(6)

Выпишем условие касания двух кривых y=y_1(x) и y=y_2(x) в точке с абсциссой x=x_0 :

y_1(x_0)=y_2(x_0), quad y'_1(x_0)=y'_2(x_0).

(7)

Огибающая семейства прямых как особое решение дифференциального уравнения

Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой x-x_0 .

Полагая $y_1(x)=-frac{x^2}{4},~y_2(x)=Cx+C^2$ , находим, что условия (7) принимают вид

$-frac{x_0^2}{4}=Cx_0+C^2, quad -frac{x_0}{2}=C.$

(8)

Подставляя $C=-frac{x_0}{2}$ в первое из равенств (8), получаем $-frac{x_0^2}{4}=-frac{x_0^2}{2}+frac{x_0^2}{4}$ или $-frac{x_0^2}{4}=-frac{x_0^2}{4},,$ т.е. при $C=-frac{x_0}{2}$ первое равенство выполняется тождественно, так как x_0 есть абсцисса произвольной точки.

Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой $C=-frac{x_0}{2}$ . Значит, $y=-frac{x^2}{4}$ есть особое решение уравнения (4).

г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).

Огибающей семейства кривых

Phi(x,y,C)=0

(9)

называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые Gamma_1 и Gamma_2 касаются в точке M_0 , если они имеют в этой точке общую касательную.

Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения x,,y,,y' совпадают со значениями для интегральной кривой, касающейся огибающей в точке (x,y) , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению F(x,y,y')=0 , т.е. огибающая является интегральной кривой.

Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.

Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений

$begin{cases}Phi(x,y,C)&=0,\[3pt] dfrac{partial}{partial C}Phi(x,y,C)&=0.end{cases}$

(10)

Некоторая ветвь СДК заведомо будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные

$left|frac{partialPhi}{partial x}right|leqslant M, quad left|frac{partialPhi}{partial y}right|leqslant N,$

(11)

где и — постоянные;

2) $frac{partialPhi}{partial x}ne0 quad text{or} quad frac{partialPhi}{partial y}ne0.$

Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.

Пример 2. Найти особые решения дифференциального уравнения

x(y')^2-2yy'+4x=0, quad x>0,

(13)

зная его общий интеграл

x^2=C(y-C).

(14)

Решение.

а) Находим C-дискриминантную кривую. Имеем Phi(x,y,C)equiv C(y-C)-x^2 , так что $frac{partialPhi}{partial C}equiv y-2C,,$ отсюда $C=frac{y}{2}$ . Подставляя это значение в (14), получаем $x^2=frac{y}{2}!left(y-frac{y}{2}right)!,$ откуда

(y-2x)(y+2x)=0 quad Rightarrow quad y=pm2x.

(15)

Это и есть C-дискриминантная кривая: она состоит из двух прямых y=2x и y=-2x .

б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).

в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как $frac{partialPhi}{partial x}=-2x$ и $frac{partialPhi}{partial y}=C$ , то на каждой ветви СДК имеем $left|frac{partialPhi}{partial x}right|=|-2x|leqslant2b$ (предполагаем, что решение y(x) уравнения (13) рассматривается на отрезке 0<aleqslant xleqslant b ).

$left|frac{partialPhi}{partial y}right|=|C|leqslant N,$ здесь $N=max_{Cin G}|C|,$

где — область допустимых значений .

Заметим, что на любой из ветвей СДК $frac{partialPhi}{partial x}=-2xne0$ в области x>0 , так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).

Итак, установлено, что каждое из решений (15) есть особое решение.

В вопросах отыскания особых решений оказываются полезными следующие символические схемы:

$mathsf{PDKequiv Ocdot Zcdot P^2=0,}$

(16)

$mathsf{CDKequiv Ocdot Y^2cdot Z^3=0.}$

(17)

Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:

1) mathsf{O=0} — уравнение огибающей;

2) mathsf{Z=0} — уравнение геометрического места точек заострения (возврата);

3) mathsf{P=0} — уравнение геометрического места точек прикосновения интегральных линий, причем множитель mathsf{P} входит в mathsf{PDK} в квадрате.

Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:

1) mathsf{O=0} — уравнение огибающей;

2) mathsf{Y=0} — уравнение геометрического места узловых точек, причем множитель mathsf{Y} входит в mathsf{CDK} в квадрате;

3) mathsf{Z=0} — уравнение геометрического места точек заострения, причем множитель mathsf{Z} входит в mathsf{CDK} в кубе.

Не обязательно, чтобы для каждой задачи все составные части mathsf{PDK} и mathsf{CDK} фигурировали в соотношениях (16) и (17).

Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.

В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в mathsf{PDK} в квадрате (и совсем не входит в mathsf{CDK} ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в mathsf{PDK} ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в mathsf{CDK} — в третьей, то возможно наличие геометрического места точек заострения.

Пример 3. Найти особое решение дифференциального уравнения

2y(y'+2)-x(y')^2=0.

(18)

Решение. Особое решение, если оно существует, определяется системой

$left{!!!begin{array}{r}2y(y'+2)-x(y')^2=0,\2y-2xy'=0,end{array}right.$

(19)

где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую y^2+2xy=0 , которая распадается на две ветви

y=0,

(20)

y=-4x.

(21)

Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).

Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства

Cy-(C-x)^2=0,

(22)

являющегося общим интегралом для (18).

Выпишем систему для определения C-дискриминантной кривой $begin{cases}Cy-(C-x)^2=0,\y-2(C-x)=0,end{cases}$ откуда, исключая , получаем y^2+4xy=0 , или y=0 и y=-4x , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии y=0 и y=-4x являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.

Интегральные кривые (22) суть параболы $y=frac{(C-x)^2}{C}$ , а линии y=0,~y=-4x – огибающие этого семейства парабол (рис. 20).

Огибающие семейства парабол

Пример 4. Найти особые решения дифференциального уравнения

(y')^2=4x^2.

(23)

Решение. Дифференцируем (23) по y':

2y'=0.

(24)

Исключая из (23) и (24), получим x^2=0 . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.

Решениями уравнения (23) являются параболы y=x^2+C,~y=-x^2+C и те гладкие кривые, которые можно составить из их частей (рис. 21).

Из чертежа видно, что прямая x=0 действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).

Пример 5. Найти особые решения дифференциального уравнения

(y')^2(2-3y)^2=4(1-y).

(25)

Решение. Найдем mathsf{PDK} . Исключая из системы уравнений $begin{cases}(y')^2(2-3y)^2-4(1-y)=0,\y'(2-3y)^2=0,end{cases}$ получаем

(2-3y)^2(1-y)=0.

(26)

Преобразовав уравнение (25) к виду $frac{dx}{dy}=pmfrac{2-3y}{2sqrt{1-y}}$ , находим его общий интеграл y^2(1-y)=(x-C)^2 .

Найдем mathsf{CDK} . Исключая из системы уравнений $begin{cases}y^2(1-y)-(x-C)^2=0,\2(x-C)=0,end{cases}$ будем иметь

y^2(1-y)=0.

(27)

Итак, из (26) и (27) имеем

$mathsf{PDK}equiv(1-y)(2-3y)^2=0, quad mathsf{CDK}equiv(1-y)y^2=0.$

Множитель 1-y входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция y=1 есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что y=1 действительно удовлетворяет уравнению.

Уравнение 2-3y=0 , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения $(mathsf{P^2})$ .

Наконец, уравнение y=0 , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек $(mathsf{Y^2})$ (рис.22).

Особые решения дифференциального уравнения

Пример 6. Найти особые решения дифференциального уравнения

$3y=2xy'-frac{2}{x}(y')^2.$

(28)

Решение.

а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем $0=2x-frac{4}{x}y'$ , откуда

$y'=frac{x^2}{2},.$

(29)

Подставляя (29) в (28), найдем уравнение mathsf{PDK} :

$mathsf{PDK}equiv6y-x^3=0.$

(30)

б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде

$3y=2xp-frac{2}{x}p^2.$

(31)

Дифференцируя обе части (28) по и учитывая, что y'=p , будем иметь

$px^2-2p^2=(2x^3-4px)frac{dp}{dx},,$ откуда $(x^2-2p)!left(p-2xfrac{dp}{dx}right)=0.$

Огибающая семейства полукубических парабол

Приравнивая нулю первый множитель x^2-2p=0 , получаем (29), а соотношение $p-2xfrac{dp}{dx}=0$ дает

Cx=p^2.

(32)

Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):

(3y+2C)^2=4Cx^3.

(33)

в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь

2C=x^3-3y.

(34)

Подставляя (34) в (33), получаем уравнение $mathsf{CDK}equiv(6y-x^3)x^3=0$ .

Согласно символическим схемам (16) и (17) заключаем, что 6y-x^3=0 есть огибающая семейства полукубических парабол (33), а x=0 есть геометрическое место точек заострения (множитель входит в уравнение mathsf{CDK} в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что y=x^3slash6 есть решение, а x=0 решением не является (при x=0 уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Особые решения дифференциальных уравнений

Решение дифференциального уравнения

называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Пример 1. Найти особые решения дифференциального уравнения

а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем

Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.

б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).

в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение

Выпишем условие касания двух кривых и в точке с абсциссой :

Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .

Полагая , находим, что условия (7) принимают вид

Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.

Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).

Огибающей семейства кривых

называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.

Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.

Некоторая ветвь СДК заведомо будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные

где и — постоянные;

Пример 2. Найти особые решения дифференциального уравнения

а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда

Это и есть C-дискриминантная кривая: она состоит из двух прямых и .

б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).

в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке

где — область допустимых значений .

Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==” />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).

Итак, установлено, что каждое из решений (15) есть особое решение.

В вопросах отыскания особых решений оказываются полезными следующие символические схемы:

Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места точек заострения (возврата);

3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.

Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;

3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.

Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).

В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.

Пример 3. Найти особое решение дифференциального уравнения

Решение. Особое решение, если оно существует, определяется системой

где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви

Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).

Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства

являющегося общим интегралом для (18).

Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.

Интегральные кривые (22) суть параболы , а линии – огибающие этого семейства парабол (рис. 20).

Пример 4. Найти особые решения дифференциального уравнения

Решение. Дифференцируем (23) по

Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.

Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).

Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).

Пример 5. Найти особые решения дифференциального уравнения

Решение. Найдем . Исключая из системы уравнений получаем

Преобразовав уравнение (25) к виду , находим его общий интеграл .

Найдем . Исключая из системы уравнений будем иметь

Итак, из (26) и (27) имеем

Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.

Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .

Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).

Пример 6. Найти особые решения дифференциального уравнения

а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда

Подставляя (29) в (28), найдем уравнение :

б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде

Дифференцируя обе части (28) по и учитывая, что , будем иметь

Приравнивая нулю первый множитель , получаем (29), а соотношение дает

Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):

в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь

Подставляя (34) в (33), получаем уравнение .

Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).

ЛЕКЦИЯ 4

Модели, описываемые системами двух автономных дифференциальных уравнений.

Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр. Пример: химические реакции первого порядка.

Наиболее интересные результаты по качественному моделированию свойств биологических систем получены на моделях из двух дифференциальных уравнений, которые допускают качественное исследование с помощью метода фазовой плоскости. Рассмотрим систему двух автономных обыкновенных дифференциальных уравнений общего вида

(4.1)

P(x,y), Q(x,y) – непрерывные функции, определенные в некоторой области G евклидовой плоскости ( x,y ‑ декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первого.

Область G может быть как неограниченной, так и ограниченной. Если переменные x, y имеют конкретный биологический смысл (концентрации веществ, численности видов) чаще всего область G представляет собой положительный квадрант правой полуплоскости:

Концентрации веществ или численности видов также могут быть ограничены сверху объемом сосуда или площадью ареала обитания. Тогда область значений переменных имеет вид:

Переменные x, y во времени изменяются в соответствии с системой уравнений (4.1), так что каждому состоянию системы соответствует пара значений переменных ( x, y) .

Изображающая точка на фазовой плоскости

Обратно, каждой паре переменных ( x, y) соответствует определенное состояние системы.

Рассмотрим плоскость с осями координат, на которых отложены значения переменных x,y. Каждая точка М этой плоскости соответствует определенному состоянию системы. Такая плоскость носит название фазовой плоскости и изображает совокупность всех состояний системы. Точка М(x,y) называется изображающей или представляющей точкой.

Пусть в начальный момент времени t=t₀ координаты изображающей точки М₀( x( t₀) , y( t₀)) . В каждый следующий момент времени t изображающая точка будет смещаться в соответствии с изменениями значений переменных x( t) , y( t) . Совокупность точек М( x( t) , y(t)) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t), y(t) согласно уравнениям (4.1), называется фазовой траекторией.

Совокупность фазовых траекторий при различных начальных значениях переменных дает легко обозримый “портрет” системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x, y без знания аналитических решений исходной системы уравнений (4.1).

Для изображения фазового портрета необходимо построить векторное поле направлений траекторий системы в каждой точке фазовой плоскости. Задавая приращение D t>0, получим соответствующие приращения D x и D y из выражений:

Направление вектора dy/dx в точке ( x, y) зависит от знака функций P(x, y), Q(x, y) и может быть задано таблицей:

Задача построения векторного поля упрощается, если получить выражение для фазовых траекторий в аналитическом виде. Для этого разделим второе из уравнений системы (4.1) на первое:

. (4.2)

Решение этого уравнения y = y( x, c) , или в неявном виде F( x,y) =c, где с – постоянная интегрирования, дает семейство интегральных кривых уравнения (4.2) ‑ фазовых траекторий системы (4.1) на плоскости x, y.

Для построения фазового портрета пользуются методом изоклин – на фазовой плоскости наносят линии, которые пересекают интегральные кривые под одним определенным углом. Уравнение изоклин легко получить из (4.2). Положим

где А – определенная постоянная величина. Значение А представляет собой тангенс угла наклона касательной к фазовой траектории и может принимать значения от – ¥ до + ¥ . Подставляя вместо dy/dx в (4.2) величину А получим уравнение изоклин:

. (4.3)

Уравнение (4.3) определяет в каждой точке плоскости единственную касательную к соответствующей интегральной кривой за исключением точки, где P (x,y) = 0, Q ( x,y) = 0, в которой направление касательной становится неопределенным, так как при этом становится неопределенным значение производной:

Эта точка является точкой пересечения всех изоклин – особой точкой. В ней одновременно обращаются в нуль производные по времени переменных x и y.

Таким образом, в особой точке скорости изменения переменных равны нулю. Следовательно, особая точка дифференциальных уравнений фазовых траекторий (4.2) соответствует стационарному состоянию системы (4.1), а ее координаты – суть стационарные значения переменных x, y.

Особый интерес представляют главные изоклины:

dy/dx=0, P ( x,y) =0 – изоклина горизонтальных касательных и

dy/dx= ¥ , Q ( x,y) =0 – изоклина вертикальных касательных.

Построив главные изоклины и найдя точку их пересечения (x,y), координаты которой удовлетворяют условиям:

мы найдем тем самым точку пересечения всех изоклин фазовой плоскости, в которой направление касательных к фазовым траекториям неопределенно. Это – особая точка, которая соответствует стационарному состоянию системы (рис. 4.2).

Система (4.1) обладает столькими стационарными состояниями, сколько точек пересечения главных изоклин имеется на фазовой плоскости.

Каждая фазовая траектория соответствует совокупности движений динамической системы, проходящих через одни и те же состояния и отличающихся друг от друга только началом отсчета времени.

Рис. 4.2. Пересечение главных изоклин на фазовой плоскости.

Таким образом, фазовые траектории системы – это проекции интегральных кривых в пространстве всех трех измерений x, y, t на плоскость x, y (рис.4.3).

Рис. 4.3. Траектории системы в пространстве ( x, y, t).

Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.

Устойчивость стационарного состояния

Пусть система находится в состоянии равновесия.

Тогда изображающая точка находится в одной из особых точек системы, в которых по определению:

Устойчива или нет особая точка, определяется тем, уйдет или нет изображающая точка при малом отклонении от стационарного состояния. Применительно к системе из двух уравнений определение устойчивости на языке e , d выглядит следующим образом.

Состояние равновесия устойчиво, если для любой заданной области отклонений от состояния равновесия ( e ) можно указать область d ( e ) , окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области d , никогда не достигнет границы e . (рис. 4.4)

Иллюстрация к определению устойчивости области e и d на плоскости ( x,y)

Для большого класса систем – грубых систем – характер поведения которых не меняется при малом изменении вида уравнений, информацию о типе поведения в окрестности стационарного состояния можно получить, исследуя не исходную, а упрощенную линеаризованную систему.

Рассмотрим систему двух линейных уравнений:

. (4.4)

Здесь a, b, c, d – константы, x, y ‑ декартовы координаты на фазовой плоскости.

Общее решение будем искать в виде:

. (4.5)

Подставим эти выражения в (4.4) и сократим на e l t :

(4.6)

Алгебраическая система уравнений (4.6) с неизвестными A, B имеет ненулевое решение лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, равен нулю:

Раскрывая этот определитель, получим характеристическое уравнение системы:

. (4.7)

Решение этого уравнения дает значения показателя l _1,2 , при которых возможны ненулевые для A и B решения уравнения (4.6). Эти значения суть

. (4.8)

Если подкоренное выражение отрицательно, то l _1,2 комплексно сопряженные числа. Предположим, что оба корня уравнения (4.7) имеют отличные от нуля действительные части и что нет кратных корней. Тогда общее решение системы (4.4) можно представить в виде линейной комбинации экспонент с показателями l ₁ , l ₂ :

_(4.9)

Для анализа характера возможных траекторий системы на фазовой плоскости используем линейное однородное преобразование координат, которое позволит привести систему к каноническому виду:

, (4.10)

допускающее более удобное представление на фазовой плоскости по сравнению с исходной системой (4.4). Введем новые координаты ξ , η по формулам:

(4.1)

Из курса линейной алгебры известно, что в случае неравенства нулю действительных частей l ₁ , l ₂ исходную систему (4.4) при помощи преобразований (4.11) всегда можно преобразовать к каноническому виду (4.10) и изучать ее поведение на фазовой плоскости ξ , η . Рассмотрим различные случаи, которые могут здесь представиться.

Корни λ ₁ , λ ₂ – действительны и одного знака

В этом случае коэффициенты преобразования действительны, мы переходим от действительной плоскости x,y к действительной плоскости ξ, η. Разделив второе из уравнений (4.10) на первое, получим :

. (4.12)

Интегрируя это уравнение, находим :

, где . (4.13)

Условимся понимать под λ ₂ корень характеристического уравнения с большим модулем, что не нарушает общности нашего рассуждения. Тогда, поскольку в рассматриваемом случае корни λ ₁ , λ ₂ – действительны и одного знака, a >1 , и мы имеем дело с интегральными кривыми параболического типа.

Все интегральные кривые (кроме оси η, которой соответствует ) касаются в начале координат оси ξ, которая также является интегральной кривой уравнения (4.11). Начало координат является особой точкой.

Выясним теперь направление движений изображающей точки вдоль фазовых траекторий. Если λ ₁ , λ ₂ – отрицательны, то, как видно из уравнений (4.10), |ξ|, |η| убывают с течением времени. Изображающая точка приближается к началу координат, никогда, однако, не достигая его. В противном случае это противоречило бы теореме Коши, которая утверждает, что через каждую точку фазовой плоскости проходит лишь одна фазовая траектория.

Такая особая точка, через которую проходят интегральные кривые, подобно тому, как семейство парабол проходит через начало координат, носит название узла (рис. 4.5)

Рис. 4.5. Особая точка типа узел на плоскости канонических координат ξ, η

Состояние равновесия типа узел при λ ₁ , λ ₂ 0 устойчиво по Ляпунову, так как изображающая точка по всем интегральным кривым движется по направлению к началу координат. Это устойчивый узел. Если же λ ₁ , λ ₂ > 0, то |ξ|, |η| возрастают с течением времени и изображающая точка удаляется от начала координат. В этом случае особая точка – неустойчивый узел .

На фазовой плоскости x, y общий качественный характер поведения интегральных кривых сохранится, но касательные к интегральным кривым не будут совпадать с осями координат. Угол наклона этих касательных будет определяться соотношением коэффициентов α , β , γ , δ в уравнениях (4.11).

Корни λ ₁ , λ ₂ – действительны и разных знаков.

Преобразование от координат x,y к координатам ξ, η опять действительное. Уравнения для канонических переменных снова имеют вид (4.10), но теперь знаки λ ₁ , λ ₂ различны. Уравнение фазовых траекторий имеет вид :

где , (4.14)

Интегрируя (4.14), находим

(4.15)

Это уравнение определяет семейство кривых гиперболического типа, где обе оси координат – асимптоты (при a=1 мы имели бы семейство равнобочных гипербол) . Оси координат и в этом случае являются интегральными кривыми – это будут единственные интегральные кривые, проходящие через начало координат. Каждая из них состоит из трех фазовых траекторий : из двух движений к состоянию равновесия (или от состояния равновесия) и из состояния равновесия. Все остальные интегральные кривые – суть гиперболы, не проходящие через начало координат (рис. 4.6) Такая особая точка носит название «седло ». Линии уровня вблизи горной седловины ведут себя подобно фазовым траекториям в окрестности седла.

Рис. 4.6. Особая точка типа седло на плоскости канонических координат ξ , η

Рассмотрим характер движения изображающей точки по фазовым траекториям вблизи состояния равновесия. Пусть, например, λ ₁ >0 , λ ₂ . Тогда изображающая точка, помещенная на оси ξ, будет удаляться от начала координат, а помещенная на оси η – будет неограниченно приближаться к началу координат , не достигая его за конечное время . Где бы ни находилась изображающая точка в начальный момент (за исключением особой точки и точек на асимптоте η =0), она в конечном счете будет удаляться от состояния равновесия, даже если в начале она движется по одной из интегральных кривых по направлению к особой точке .

Очевидно, что особая точка типа седла всегда неустойчива . Только при специально выбранных начальных условиях на асимптоте η =0 система будет приближаться к состоянию равновесия. Однако это не противоречит утверждению о неустойчивости системы. Если считать , что все начальные состояния системы на фазовой плоскости равновероятны, то вероятность такого начального состояния, которое соответствует движению по направлению к особой точке, равна нулю. Поэтому всякое реальное движение будет удалять систему от состояния равновесия. Переходя обратно к координатам x,y, мы получим ту же качественную картину характера движения траекторий вокруг начала координат.

Пограничным между рассмотренными случаями узла и седла является случай, когда один из характеристических показателей, например λ ₁ , обращается в нуль, что имеет место, когда определитель системы – выражение ad-bc=0 (см. формулу 4.8 ). В этом случае коэффициенты правых частей уравнений (4.4) пропорциональны друг другу :

и система имеет своими состояниями равновесия все точки прямой :

Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом , по которым изображающие точки либо приближаются к состоянию равновесия, либо удаляются от него в зависимости от знака второго корня характеристического уравнения λ ₂ = a+d. (Рис.4. 7 ) В этом случае координаты состояния равновесия зависят от начального значения переменных.

Рис. 4.7. Фазовый портрет системы, один из характеристических корней которой равен нулю, а второй отрицателен.

В этом случае при действительных x и y мы будем иметь комплексные сопряженные ξ , η ( 4.10) . Однако , вводя еще одно промежуточное преобразование, можно и в этом случае свести рассмотрение к действительному линейному однородному преобразованию. Положим :

(4.16)

где a,b, и u,v – действительные величины. Можно показать, что преобразование от x,y к u,v является при наших предположениях действительным, линейным, однородным с детерминантом, отличным от нуля. В силу уравнений (4.10, 4.16) имеем :

(4.17)

Разделив второе из уравнений на первое , получим :

которое легче интегрируется , если перейти к полярной системе координат ( r, φ ) . После подстановки получим , откуда :

. (4.18)

Таким образом, на фазовой плоскости u, v мы имеем дело с семейством логарифмических спиралей, каждая из которых имеет асимптотическую точку в начале координат. Особая точка, которая является асимптотической точкой всех интегральных кривых, имеющих вид спиралей , вложенных друг в друга, называется фокусом ( рис.4.8 ) .

Рис. 4.8. Фазовый портрет системы в окрестности особой точки типа фокус на плоскости координат u, v .

Рассмотрим характер движения изображающей точки по фазовым траекториям. Умножая первое из уравнений (4.17) на u , а второе на v и складывая , получаем :

где

Пусть a ₁ 0 ( a ₁ = Re λ ) . Изображающая точка тогда непрерывно приближается к началу координат, не достигая его в конечное время. Это означает, что фазовые траектории представляют собой скручивающиеся спирали и соответствуют затухающим колебаниям переменных. Это – устойчивый фокус .

В случае устойчивого фокуса, как и в случае устойчивого узла, выполнено не только условие Ляпунова, но и более жесткое требование. Именно, при любых начальных отклонениях система по прошествии времени вернется как угодно близко к положению равновесия. Такая устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю, называют абсолютной устойчивостью .

Если в формуле (4.18) a₁ >0 , то изображающая точка удаляется от начала координат, и мы имеем дело с неустойчивым фокусом . При переходе от плоскости u,v к фазовой плоскости x , y спирали также останутся спиралями, однако будут деформированы.

Рассмотрим теперь случай, когда a ₁ =0 . Фазовыми траекториями на плоскости u, v будут окружности которым на плоскости x,y соответствуют эллипсы :

Таким образом, при a₁ =0 через особую точку x= 0 , y=0 не проходит ни одна интегральная кривая. Такая изолированная особая точка, вблизи которой интегральные кривые представляют собой замкнутые кривые, в частности, эллипсы, вложенные друг в друга и охватывающие особую точку, называется центром.

Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.

Рис. 4.9. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений (4.4).

Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей уравнений (4.4). При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.

Бифуркационная диаграмма

. (4.11)

Тогда характеристическое уравнение запишется в виде:

. (4.12)

Рассмотрим плоскость с прямоугольными декартовыми координатами s , D и отметим на ней области, соответствующие тому или иному типу состояния равновесия, который определяется характером корней характеристического уравнения

. (4.13)

Условием устойчивости состояния равновесия будет наличие отрицательной действительной части у l ₁ и l ₂ . Необходимое и достаточное условие этого – выполнение неравенств s > 0, D > 0 . На диаграмме (4.15) этому условию соответствуют точки, расположенные в первой четверти плоскости параметров. Особая точка будет фокусом, если l ₁ и l ₂ комплексны. Этому условию соответствуют те точки плоскости, для которых , т.е. точки между двумя ветвями параболы s 2 = 4 D . Точки полуоси s = 0, D >0, соответствуют состояниям равновесия типа центр. Аналогично, l ₁ и l ₂ – действительны, но разных знаков, т.е. особая точка будет седлом, если D , и т.д. В итоге мы получим диаграмму разбиения плоскости параметров s , D , на области, соответствующие различным типам состояния равновесия.

Рис. 4.10. Бифуркационная диаграмма

для системы линейных уравнений 4.4

Если коэффициенты линейной системы a, b, c, d зависят от некоторого параметра, то при изменении этого параметра будут меняться и величины s , D . При переходе через границы характер фазового портрета качественно меняется. Поэтому такие границы называются бифуркационными – по разные стороны от границы система имеет два топологически различных фазовых портрета и, соответственно два разных типа поведения.

На диаграмме видно, как могут проходить такие изменения. Если исключить особые случаи – начало координат, – то легко видеть, что седло может переходить в узел, устойчивый или неустойчивый при пересечении оси ординат. Устойчивый узел может перейти либо в седло, либо в устойчивый фокус, и т.д. Отметим, что переходы устойчивый узел – устойчивый фокус и неустойчивый узел – неустойчивый фокус не являются бифуркационными, так как топология фазового пространства при этом не меняется. Более подробно мы поговорим о топологии фазового пространства и бифуркационных переходах в лекции 6.

При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация называется бифуркацией Андронова-Хопфа по именам исследовавших ее ученых. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной (см. лекцию 8).

Пример. Система линейных химических реакций

Вещество Х притекает извне с постоянной скоростью, превращается в вещество Y и со скоростью, пропорциональной концентрации вещества Y, выводится из сферы реакции. Все реакции имеют первый порядок, за исключением притока вещества извне, имеющего нулевой порядок. Схема реакций имеет вид:

(4.14)

и описывается системой уравнений:

(4.15)

Стационарные концентрации получим, приравняв правые части нулю:

. (4.16)

Рассмотрим фазовый портрет системы. Разделим второе уравнение системы (4.16) на первое. Получим:

. (4.17)

Уравнение (4.17) определяет поведение переменных на фазовой плоскости. Построим фазовый портрет этой системы. Сначала нарисуем главные изоклины на фазовой плоскости. Уравнение изоклины вертикальных касательных:

Уравнение изоклины горизонтальных касательных:

Особая точка (стационарное состояние) лежит на пересечении главных изоклин.

Теперь определим, под каким углом пересекаются координатные оси интегральными кривыми.

Если x=0, то .

Таким образом, тангенс угла наклона касательной к интегральным кривым y=y(x), пересекающим ось ординат x=0, отрицателен в верхней полуплоскости (вспомним, что переменные x, y имеют значения концентраций, и поэтому нас интересует только правый верхний квадрант фазовой плоскости). При этом величина тангенса угла наклона касательной увеличивается с удалением от начала координат.

Рассмотрим ось y=0 . В месте пересечения этой оси интегральными кривыми они описываются уравнением

При тангенс угла наклона интегральных кривых, пересекающих ось абсцисс, положителен и увеличивается от нуля до бесконечности с увеличением x.

при .

Затем при дальнейшем увеличении тангенс угла наклона уменьшается по абсолютной величине, оставаясь отрицательным и стремится к -1 при x ® ¥ . Зная направление касательных к интегральным кривым на главных изоклинах и на осях координат, легко построить всю картину фазовых траекторий.

Рис. 4.12. Фазовый портрет системы линейных химических реакций (4.15)

Особые точки кривой

Понятие частной производной используется при исследовании кривых.

Пусть кривая задана уравнением

Угловой коэффициент касательной к кривой определяется по формуле

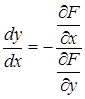Если в данной точке М(х, у) рассматриваемой кривой по крайней мере одна из частных производных 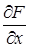и 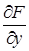не обращается в нуль, то в этой точке вполне определяется 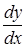или или 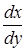. Кривая F(х, у) = 0 в такой точке имеет вполне определенную касательную. В этом случае точка М(х, у) называется обыкновенной точкой.

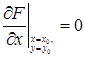или ,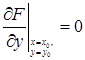

то угловой коэффициент касательной становится неопределенным.

Определение. Если в точке М₀(х₀, у₀) кривой F(х, у) = 0 обе частные производные 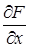и 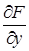обращаются в нуль, то такая точка называется особой точкой кривой. Следовательно, особая точка кривой определяется системой уравнений

F = 0, , .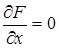

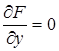Естественно, что не всякая кривая имеет особые точки. Так, например, для эллипса

, , ,

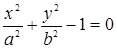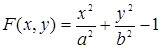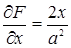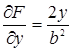производные 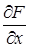и 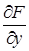обращаются в нуль только при х = 0, у = 0, но эти значения х и у не удовлетворяют уравнению эллипса. Следовательно, эллипс не имеет особых точек.

Не предпринимая подробного исследования поведения кривой вблизи особой точки, рассмотрим несколько примеров кривых, имеющих особые точки.

Пример 45. Исследовать особые точки кривой

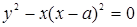, (а > 0).

Решение. В данном случае 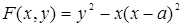, поэтому

, .

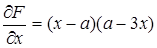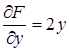Решая совместно три уравнения

F = 0, , ,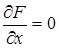

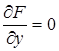находим единственную удовлетворяющую им систему значений х и у:

Следовательно, точка М₀(а, 0) есть особая точка кривой.

Исследуем поведение кривой вблизи особой точки и построим кривую. Перепишем данное уравнение в виде 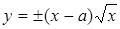. Из этой формулы следует, что кривая: 1) определена лишь при х ³ 0; 2) симметрична относительно оси Ох; 3) пересекает ось Ох в точках (0, 0) и (а, 0). Последняя точка, как было указано, является особой.

Мы рассмотрим сначала ту часть кривой, которая соответствует знаку +: . Найдем первую и вторую производные от у по х:

, .

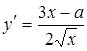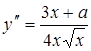При х = 0 имеем 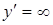. Следовательно, кривая касается оси Оу в начале координат. При х = а/3 имеем 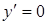, , 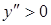т.е. при х = а/3 функция у имеет минимум: 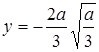. На отрезке 0 а/3 будет 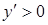; при х ® ¥ будет у ® ¥. При х = а имеем 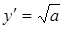, т.е. в особой точке М₀(а, 0) ветвь кривой имеет касательную .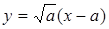

Так как вторая ветвь кривой 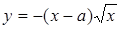симметрична с первой относительно оси Ох, то, следовательно, в особой точке кривая имеет и вторую касательную (ко второй ветви) .

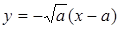Через особую точку кривая проходит дважды. Такая точка называется узловой точкой.

Рассмотренная кривая изображена на рис. 10.

Пример 46. Исследовать на особые точки кривую (полукубическая парабола) у 2 – х 3 = 0.

Решение. Координаты особых точек определяются из системы уравнений: у 2 – х 3 = 0, 3х 2 = 0, 2у = 0. Следовательно, М₀(0, 0) есть особая точка.

Перепишем данное уравнение в виде . Для построения кривой исследуем сначала ветвь, которой в уравнении соответствует знак плюс; ветвь кривой, соответствующая знаку минус, симметрична с первой относительно оси Ох.

Функция у определена только при х ³ 0, неотрицательна и возрастает при возрастании х.

Найдем первую и вторую производные от функции :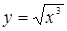

, .

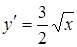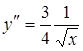При х = 0 имеем у = 0, у¢ = 0. Следовательно, рассматриваемая ветвь кривой имеет в начале координат касательную у = 0. Вторая ветвь кривой 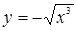также проходит через начало координат и имеет ту же касательную у = 0. Таким образом, две различные ветви кривой встречаются в начале координат, имеют одну и ту же касательную и расположены от касательной по разные стороны. Такая особая точка называется точкой возврата первого рода (рис. 11).

Заметим, что кривую у 2 – х 3 = 0 можно рассматривать как предельный случай кривой у 2 = х(х – а) 2 (рассмотренной в примере 45), когда а ® 0, т.е. когда петля кривой стягивается в точку.

Пример 47. Исследовать кривую (у – х 2 ) 2 – х 5 = 0.

Решение. Координаты особых точек определяются системой уравнений

которая имеет единственное решение: х = 0, у = 0. Следовательно, начало координат есть особая точка.

Перепишем данное уравнение в виде 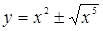. Из этого уравнения следует, что х может принимать значения от 0 до +¥.

Определим производные первого и второго порядка:

, .

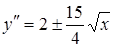Исследуем ветви кривой, соответствующие знакам плюс и минус, в отдельности. В обоих случаях при х = 0 имеем: у = 0, у¢ = 0, т.е. для обеих ветвей оси Ох является касательной. Рассмотрим сначала ветвь 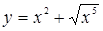. При возрастании х от 0 до ¥, у возрастает от 0 до ¥. Вторая ветвь 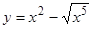пересекает ось Ох в точках (0, 0) и (1, 0).

При х = 16/25 функция 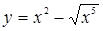имеет максимум. Если х ® +¥, то у ® -¥.

Таким образом, в данном случае в начале координат встречаются две ветви кривой; обе ветви имеют одну и ту же касательную и расположены по одну сторону от касательной вблизи точки касания. Такая особая точка называется точкой возврата второго рода. График рассматриваемой функции изображен на рис. 12.

Пример 48. Исследовать кривую у 2 – х 4 + х 6 = 0.

Решение. Начало координат есть особая точка. Для исследования кривой вблизи этой точки перепишем уравнение кривой в виде .

Так как уравнение кривой содержит только четные степени переменных, то кривая симметрична относительно осей координат и, следовательно, достаточно исследовать часть кривой, соответствующую положительным значениям х и у. Из последнего уравнения следует, что х может изменяться на отрезке от 0 до 1, т.е. 0 £ х £ 1.

Вычислим первую производную для той ветви кривой, которая является графиком функции :

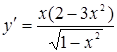При х = 0 имеем у = 0, у¢ = 0. Следовательно, в начале координат кривая касается оси Ох.

При х = 1 имеем у = 0, у¢ = ¥; следовательно, в точке (1, 0) касательная параллельна оси Оу. При функция имеет максимум (рис. 13).

В начале координат (в особой точке) две ветви кривой, соответствующие знакам плюс и минус перед корнем, взаимно касаются. Такая особая точка называется точкой соприкосновения.

Пример 49. Исследовать кривую у 2 – х 2 (х – 1) = 0.

Решение. Напишем систему уравнений, определяющих особые точки:

Эта система имеет решение х = 0, у = 0. Следовательно, точка (0, 0) есть особая точка кривой. Перепишем данное уравнение в виде . Очевидно, что х может изменяться от 1 до +¥, а также принимать значение 0 (в последнем случае у = 0).

Исследуем ветвь кривой, соответствующую знаку плюс перед корнем. При увеличении х от 1 до ¥ у увеличивается от 0 до ¥. Производная 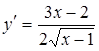. При х = 1 имеем у¢ = ¥; следовательно, в точке (1, 0) касательная параллельна оси Оу.

Вторая ветвь кривой, соответствующая знаку минус, симметрична с первой относительно оси Ох.

Точка (0, 0) имеет координаты, удовлетворяющие уравнению, и, следовательно, принадлежит кривой, но вблизи нее нет других точек кривой (рис. 14). Такая особая точка называется изолированной особой точкой.

Задание для самостоятельной работы

Исследовать на особые точки кривые:

156. 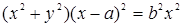(a > 0, b > 0) (конхоида). Рассмотреть три случая:

Дата добавления: 2015-07-24 ; просмотров: 2365 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

[spoiler title=”источники:”]

http://www.library.biophys.msu.ru/LectMB/Lect04.htm

http://helpiks.org/4-26553.html

[/spoiler]

Источник

http://profbeckman.narod.ru/

Каждая динамическая система имеет свой фазовый портрет. На фазовом портрете изображаются особые точки (точки положения равновесия, критические, неподвижные точки), которые позволяют без решения дифференциального уравнения или отображений предсказать поведение динамической системы.

Мы уже неоднократно упоминали особые точки. В этой главе мы рассмотрим способы их нахождения и их свойства несколько подробнее.

12.1 Дифференциальные уравнения и особые точки

Через каждую точку фазовой плоскости проходит только одна фазовая траектория: если эту точку выбрать в качестве начального состояния системы, дальнейшее движение системы будет определено однозначно. Это движение идёт вдоль фазовой траектории, проходящей через данную точку фазовой плоскости; фазовые траектории системы не пересекаются. Исключение составляют лишь отдельные, изолированные точки фазовой плоскости. Такие точки, через которые проходит более одной фазовой траектории или не проходит ни одной траектории, называются особыми. Фазовый портрет даёт наглядное графическое представление о возможных движениях изучаемой динамической системы.

Если фазовое пространство X представляет собой многомерное пространство или область в нем, а время непрерывно и если известна скорость движется каждой точки x фазового пространства (известна вектор-функция скорости v(x)), то траектория точки х0 Х

будет решением автономного дифференциального уравнения dx v(x) с начальным dt

условием x(0). Заданная таким образом динамическая система называется фазовым потоком для автономного дифференциального уравнения. В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями 1-го порядка в матричной форме.

Особая точка векторного поля – определяет положение равновесия. Это точка, в которой векторное поле равно нулю; положение равновесия или точка покоя динамической системы, определяемая данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая – прямая, параллельная оси времени.

Критическая (неподвижная) точка дифференцируемой функции действительной или комплексной переменной f:D R, где R – область в Rn, – любое её значение х0, при котором все частные производные f равны нулю, f(x0)=0. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума дифференцируемой функции. Значение функции в критической точке называется критическим значением. Для дифференцируемой функции нескольких переменных критическая точка там, где все частные производные равны нулю.

Точка равновесия – такая точка в пространстве координат динамической системы,

генерируемой автономной системой ОДУ, которая характеризует ее состояние равновесия в

данный момент. Это одна из стационарных точек функции, описывающей поведение

системы; все частные производные функции обращаются в точке равновесия в нуль. Решение, которое со временем не меняется.

Сингулярная особая точка — точка, в которой математическая функция стремится к бесконечности или имеет какие-либо иные нерегулярности поведения.

Интерес к неподвижным точкам заключается в том, что точки, где функция имеет локальные экстремумы являются критическими точками.

http://profbeckman.narod.ru/

В критической точке график f(x) имеет горизонтальную касательную и производная от функции равна нулю. Если g(x,y) – дифференцируемая функция двух переменных, то g(x,y)=0 – неявное уравнение кривой. Критическая точка такой кривой для проекции,

параллельной оси y (отображение (x,y)→x), является точкой кривой, где g x, y 0 .y

Здесь касательная к кривой параллельна оси y и в этой точке g не определяет неявную функцию от x до y. Критическая точка (x0,y0) – одновременно точка бифуркации, так как, как правило, при изменении х есть две ветви кривой на

стороне х0 и ноль с другой стороны.

Рис. 1. Абсциссы (координаты х) красных кружков – стационарные точки, голубые квадраты – точки перегиба.

Функция f(x) имеет критическую точку x0 с критическим значением y0, тогда и только тогда, когда (x0,y0) является критической точкой ее графа для проекции, параллельной x– оси с тем же критическим

значением y0.Например, критические точки единичной окружности уравнения x2+y2-1=0 равны (0, 1) и (0, -1) для проекции, параллельной оси y, и (1, 0) и (-1, 0) для направления, параллельного оси х. Если рассматривать верхнюю половину круга как график функции

f (x)

1 x2 то x=0 – единственная критическая точка с критическим значением 1.

Критические точки окружности для проекции, параллельной оси y, точно соответствуют точкам, где производная от f не определена.

Пример 1. Функция f(x)=x2+2x+3 всюду дифференцируема, производная f‘(x)=2x+2. Функция имеет единственную критическую точку -1, т. к. именно это значение х0 получается из 2x0+2=0. Точка х0 – глобальный минимум f, критическое значение f(-1)=2. График f – вогнутая парабола, критической точкой является абсцисса экстремума, где касательная линия горизонтальна, а критическое значение – ордината экстремума: пересечение этой касательной с осью y.

Пример 2. Функция f(x)=x2/3 определена для всех x и дифференцируема при x≠0, производная f‘(x)=2x-1/3/3. Так как f‘(x)≠0 для x≠0, то единственно возможной критической точкой f является x=0.

Поскольку производная не существует в 0, то одни авторы считают её критической, а другие нет. График функции f имеет точку возврата в этой точке с вертикальной касательной. Соответствующим критическим значением f(0)=0.

Пример 3. Функция f(x)=x3-3x+1 всюду дифференцируема, причём производная f‘(x)=3x2-3. Она имеет две критические точки при x=-1 и x=1 соответствующими критическими значениями: f(-1)=3

– локальное максимальное значение, и f(1)=-1 – локальное минимальное значение f. Эта функция не имеет глобального максимума или минимума. Так как f(2)=3, то критическое значение может быть достигнуто и в некритической точке. Геометрически это означает, что горизонтальная касательная линия к графу в одной точке (x=-1) пересекает график под острым углом в другой точке (x=2).

Пример 4. Функция f(x)=1/x не имеет критических точек. Точка x=0 не рассматривается как критическая точка, потому что она не включена в область определения функции.

Рис. 2. График f(y) (слева) и его фазовая линия

(справа). Здесь а и с – стоки, а b – источник.

В любой малой окрестности фазового пространства, не содержащей особых точек, векторное поле можно выпрямить подходящей заменой координат – тем самым, поведение системы вне особых точек устроено одинаково и очень просто. Напротив, в окрестности особой

http://profbeckman.narod.ru/

точки система может обладать очень сложной динамикой. Говоря о свойствах особых точек векторных полей, обычно подразумевают свойства соответствующей системы в малой окрестности особой точки.

В простейшем случае однопараметрического автономного ОДУ dy f ( y) фазовая dx

плоскость вырождается в прямую линию (её строят вертикально, рис.1 справа) или горизонтально. Это даёт простой метод анализа поведения динамической системы.

Фазовая линия, представляет собой интервал области производной. Критические точки (т.е. корни производной, точки у) такие, что , а интервалы между критическими точками обозначены стрелками: интервал, на котором производная положительна, имеет стрелку, указывающую в положительном направлении вдоль линии (вверх) и интервал, на котором производная отрицательно имеет стрелку, указывающую в отрицательном направлении вдоль линии (вниз).

Примеры – фазовые линии, соответствующие функциям, не меняющие знак: если , то каждая точка – устойчивое равновесие (не меняется); еслидля всех , то всегда увеличивается, и если тогда всегда уменьшается. Простейшими нетривиальными примерами являются экспоненциальная модель роста/радиоактивный распад (одно неустойчивое/устойчивое равновесие) и модель логистического (два равновесия, одно устойчиво, одно неустойчиво).

Приведём несколько примеров анализа простых ОДУ с использованием фазовой

линии.

Рис. 3. К задаче 1: б – фазовая линия; в – типичные интегральные кривые.

Пример 5. Для ОДУ y‘=3y: найти критические точки, нарисовать фазовую линию, классифицировать критические точки по стабильности и нанести на график некоторые решения. Для y‘=3y единственная критическая точка y=0. График f(y) – прямая линия, причём y‘>0 при у>0 и у‘<0 при y<0. Поместим большую точку в критической точке. Так как y‘>0 в интервале y>0, то по вертикальной линии направляем стрелку вверх, аналогично для интервала y<0 откладываем стрелку вниз. Поскольку стрелки идут в разные стороны от критической точки, равновесие неустойчиво. Рядом с фазовой линией построим график кривых для самой функции f(t)=t3+c (для простоты считаем c=0). Равновесное решение соответствует критической точке: это горизонтальная линия y(t)=0. Решения расходятся от абсциссы в разные стороны при увеличении t. Положение равновесия неустойчиво, о чём и свидетельствовала фазовая линия.

Рис. 4. К примеру 1: а – график f(y): б – фазовая линия; в – типичные интегральные

кривые.

http://profbeckman.narod.ru/

Пример 6. Фазовая линия для логистического уравнения y‘=k0(1-y/M)y. Критические точки: y=0 и y=M. Решения сдвинуты во времени. Точка равновесия у=0 неустойчива, точка у=М – устойчива. Пример 7. Полу-устойчивое и полу-неустойчивое положение равновесия. ОДУ y‘=y2 имеет одну полустабильную точку равновесия при у=0, y‘ – всегда положителен (за исключением у=0).

Критическая точка может быть устойчивой, неустойчивой или полуустойчивой, что демонстрируют исходящие (или входящие) в них стрелки. Если обе стрелки направлены на критическую точку, она устойчива (сток): близкие решения асимптотически сходятся к критической точке, а решение устойчиво при малых возмущениях, что означает, что если решение нарушено, оно снова вернется к устойчивой точке. Если обе стрелки указывают направление от критической точки, она неустойчива (источник): близкие решения будут расходиться от критической точки, а решение будет неустойчивым, при малых возмущениях решение обратно не вернётся. Если одна стрелка направлена на критическую точку и одна – от нее, то она полустабильна (узел): она устойчива в одном

направлении (где стрелка направлена на точку) и неустойчива в другом направлении (где стрелка направлена от точки).

Рис. 5. К примеру 2: а – график f(y): б – фазовая линия; в – типичные интегральные кривые.

Поскольку нелинейные уравнения не имеют аналитического решения, то в теории динамики существенное внимание уделяется методам линеаризации,

которые позволяют найти критические точки и дать им разумную интерпретацию. Переход от нелинейной к линейной системе упирается в проблему топологической эквивалентности.

Особая точка (неподвижная точка, положение равновесия, стационарная точка, точка покоя, критическая точка) динамической системы описываемое системой ОДУ – решение, которое не изменяется со временем. Геометрически равновесие – точка в

фазовом пространстве.
Система ОДУ	(1)

x F(x)

имеет равновесное решение x(t)=x0, если F(x0)=0.

Нахождение равновесия, т.е. решение уравнения F(x)=0 просто только в некоторых специальных случаях.

Если х0 – особая точка дифференцируемого векторного поля F(x), являющегося правой частью автономной системы Ур.1, а F/ x – производная отображения F, то система линейных дифференциальных уравнений

	A	F	x0	,	y x x0	(1а)

y Ay,	x

называется линеаризацией системы (1) в особой точке x0, поле Ау – линейной частью поля F в точке х0, а А – оператор этой линейной части или оператор линеаризации.

Две системы дифференциальных уравнений (или, что то же самое – два векторных поля) топологически эквивалентны в окрестности особых точек, если существует гомеоморфизм (взаимно однозначное и взаимно непрерывное отображение), переводящий особую точку первой системы и траектории, лежащие в некоторой ее окрестности, в особую точку и траектории второй системы с сохранением ориентации траекторий.

Гомеоморфизм – взаимно однозначное соответствие между двумя топологическими пространствами, при котором оба взаимнообратных отображения, определяемые этим

http://profbeckman.narod.ru/

соответствием, непрерывны. Эти отображения называются гомеоморфными, или топологическими, отображениями, а также гомеоморфизмами, а о пространствах говорят, что они принадлежат одному топологическому типу называемые гомеоморфными, или топологически эквивалентными. Они являются изоморфными объектами в категории топологических пространств и непрерывных отображений.

Топологическая эквивалентность – топологическое отношение между топологическими пространствами; топологические пространства X и Y называются топологически эквивалентными, если они гомеоморфны, т.е. если существует гомеоморфизм пространства X на пространство У. Топологическая эквивалентность является рефлексивным, симметричным и транзитивным бинарным отношением на классе всех топологических пространств. В соответствии с этим совокупность всех топологических пространств разбивается на попарно не пересекающиеся классы топологической эквивалентности.

Теорема Гробмана-Хартмана. Непрерывно дифференцируемое векторное поле с гиперболической особой точкой в некоторой окрестности этой точки топологически эквивалентно своей линейной части.

Локальный фазовый портрет гиперболической точки нелинейной системы эквивалентен таковому для линейной.

Из этой теоремы вытекает, что качественное поведение решений автономной системы дифференциальных Ур.(1) в окрестности гиперболической особой точки полностью определяется поведением решений системы линейных дифференциальных уравнений с постоянным оператором (матрицей) линейной части поля в этой точке.

Линейная система ОДУ называется гиперболической, если все её собственные значения якобиана (вообще говоря, комплексные) имеют отличные от нуля вещественные части. Особая точка (положение равновесия) системы дифференциальных уравнений (1) называется гиперболической, если ни одно собственное значение оператора линейной части поля в этой точке не лежит на мнимой оси, т.е. если её собственное значение отлично от нуля. Если собственное значение точки равно нулю, то точку называют негиперболической. В этом случае система неустойчива и возможны бифуркации.

Гиперболическая периодическая точка – периодическая точка, у которой все мультипликаторы (производная в неподвижной точке) по модулю отличны от единицы. Это периодическая точка, орбита которой является гиперболическим множеством. Важный частный случай – гиперболическая неподвижная точка.

Неподвижная точка гиперболична, если имеет производную, отличную от +, т.е. если среди всех мультипликаторов нет равных по модулю единице.

В одномерной (скалярной) динамической системе x‘=f(x) равновесие имеет место при f(x)=0 (рис. 6). Якобиан в каждом равновесии есть J=f‘(x). Равновесие асимптотически стабильно, когда f‘(x)<0; это означает, что наклон f отрицателен. Оно нестабильно, когда f‘(x)>0. Слева два равновесия на рис. 6 гиперболические (f‘(x) 0), другие негиперболические поскольку наклон (собственное значение) есть нуль. Тем не менее, негиперболическое равновесие системы устойчиво, если функция изменяет знак с положительного на отрицательный при равновесии.

Рис. 6. Равновесие одномерной системы x’=f(x) в точках где f(x)=0.

Как уже упоминалось, двумерную систему линейных дифференциальных уравнений можно записать в виде

http://profbeckman.narod.ru/

x, y

ax by

(2)

x, y y

cx dy

комплексно сопряжённые.

При равновесии

ax by 0

cx dy 0

(3)

Система (2) в матричной форме

d x

b x

(4)

dt y

d y

или Х

АХ

где А – 2х2 матрица коэффициентов

и (x,y) – вектор координат двух независимых

переменных .y

Для определения особых точек используют собственные значения уравнения Ах=х находят решением характеристического уравнения.

Обычно классификацию положений равновесия линейной системы, основанную на собственных значениях. Однако тип точки равновесия можно определить и без вычисления собственных значений 1,2, а зная лишь только определитель матрицы detA и её след trA.

Напомним, что следом матрицы называется число, равное сумме диагональных

элементов:	a	b	, trA=a+d, detA=ad–bc. Действительно, характеристическое уравнение


	c	d

матрицы имеет следующий вид:

λ2−(a+d)λ+ad−bc=0.

(5а)

или

λ2−trA λ+detA=0.

где р=a+d=tr(A), q=ad-bc, =detA=ad-bc

(5б)

Собственные значения 1 и 2

линейного оператора А находят по формуле

trA

2 4q

(6)

1,2

где дискриминант, D=(trA)2−4detA.

Собственные вектора: V1 и V2 – корни уравнения bV 2 (d a)V c 0.

Таким образом, бифуркационная кривая, разграничивающая различные режимы

trA 2

устойчивости, представляет собой параболу на плоскости (trA, detA): det A .2

Выше параболы находятся точки равновесия типа фокус и центр. Точки типа “центр” расположены на положительной полуоси 0y, т.е. при условии trA=0. Ниже параболы находятся точки типа “узел” или “седло”. Сама парабола содержит дикритические или вырожденные узлы. Устойчивые режимы движения существуют в левом верхнем квадранте бифуркационной диаграммы. Остальные три квадранта соответствуют неустойчивым положениям равновесия.

http://profbeckman.narod.ru/

Условие detА=0 определяет линию вырожденных особых точек, среди которых можно выделить вырожденный плоский седло-узел, имеющий, как правило, один узловой и два седловых сектора. Невырожденные седло, узел и фокус являются гиперболическими особыми точками. Центр к гиперболическому положению равновесия не относится. Гиперболичны те положения равновесия, для которых собственные значения матрицы коэффициентов detA линейной системы ОДУ лежат вне мнимой оси.

Особая точка означает, что в стационарном состоянии значения переменных в системе не меняются со временем, т.е. в одномерном случае скорость изменения значений dx/dt =0 (и следовательно) f(x)=0. Корни этого алгебраического уравнения – стационарные состояния.

В двумерном случае особая точка кривой, заданная уравнением F(x,y)=0, – точка

P0(x0,y0) такая, что	F			F	0 . Если при этом не все вторые частные
x	x0 , y0	y	x0 , y0

производные функции F(x, у) в точке P0 равны нулю, то особая точка называется двойной. Если наряду с обращением в нуль первых производных в точке М0 обращаются в нуль и все вторые производные, но не все третьи производные равны нулю, то особая точка называется тройной, и т.д.

Рис. 7. Точки равновесия линейной автономной системы и бифуркационные кривые.

Они же возникают и в нелинейных автономных системах при их линеаризации. а – виды фазовых портретов, б – демонстрация устойчивости особых точек. Здесь trA=a+d=р detA=ad-bc=q.

Рис. 8. Виды фазовой плоскости в зависимости от локализации собственных значений.

Из уравнения F(x,y)=0 ни одно из переменных x,y не может быть выражено как функция другого даже в как угодно малой окрестности точки P0. Если вторые частные

http://profbeckman.narod.ru/

производные не все одновременно обращаются в нуль в точке P0 (двойная особая точка), то поведение кривой в окрестности P0 во многом определяется знаком :

2 F			2 F		2 F	2	(7)


2				2
x				y
		P			P		x y	P0
	0		0

Если Δ>0, то особая точка называется изолированной; например, у кривой у- х4+4x2=0 начало координат есть изолированная особая точка (рис. 9.1). Если Δ<0, то особая точка называется узловой, или точкой самопересечения; например, у кривой (x2+y2+a2)2–4a2x2-a4=0 начало координат есть узловая особая точка (рис. 9.2); кривая x2– y3=0 имеет начало координат точкой самопересечения. Если Δ=0, то особая точка кривой является либо изолированной, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную, например: а) точка возврата 1-го рода – различные ветви кривой расположены по разные стороны от общей касательной и образуют остриё, как у кривой у2-х3=0 (рис. 9.3a); б) точка возврата 2-го рода – различные ветви кривой расположены по одну сторону от общей касательной, как у кривой (у-x2)2– х5=0 (рис. 9.3б); в) точка самоприкосновения (для кривой у2-х4=0 начало координат является точкой самоприкосновения (рис. 9.3в). Наряду с указанными особых точек имеется много других особых точек со специальными названиями; например, асимптотическая точка – вершина спирали с бесконечным числом витков (рис. 9.4), точка прекращения, угловая точка и т.д.

Рис. 9. Особые точки ОДУ.

Точка (0, 0) является узлом для уравнений у‘=2у/х (λ1=1, λ2=2; и y‘=у/х (λ1=λ2=1; седлом для уравнения у’=-у/х (λ1=-1, λ2=1; фокусом для уравнения у’=(х+у)/(х-у) (λ1=1-i, λ2=1+i; и центром для уравнения у’=-x/y (λ1=-i, λ2=i.

Рис. 10. Пример 8: зависимость y(x) как функция времени при большом числе начальных условий.

Пример 8. Двумерная система ОДУ

		t
x x 0	x(t) x(0)e

y 4y 0	y(t) y(0)e 4t

Фазовый портретстабильный седло, точка (0,0) – стабильная точка равновесия.

Рис. 11. К примеру 9.

Пример 9: Дана система ОДУ

		t
x x 0	x(t) x(0)e

y 4y 0	y(t) y(0)e4t

http://profbeckman.narod.ru/

Фазовый портрет – седло. Фазовая траектория попадает в точку (0,0) только если начальное условие было задано в начале кооордитат. Остальные траектории никогда не попадают в точку

(0,0).

Рис. 12. К примеру 10.

					Пример 10. Устойчивость седловой точки. Имеем
							2	1
	x 2x y 0
систему уравнений			x Ax	A
						2	1
	y 2x y 0
Собственное	значение 1	1,5616		2	2,5616
Собственные	вектора V1		0,2703		V2	0,8719

			0,9628			0,4896
		Стабильноеседло		Нестабильное седло
									1 1
Пример 11. У системы	x x y 0
			xAx A		. Собственные значения
								4	1
			y 4x y

равны +1,7321i. Так как реальные части собственных значений равны нулю, то реализуется фазовая плоскость, в которой точкой равновесия является центр.

Рис. 13. К примеру 11.

В анализе поведения решений дифференциальных уравнений на плоскости удобно пользоваться методом изоклин.

Изоклина – линия на плоскости, в каждой̆ точке которой, касательныӗ к фазовым траекториям исследуемой̆ системы уравнений имеют один угол наклона.

Главные изоклины – нуль-изоклины, фазовые траектории которых проходят под углом φ=0о (изоклина горизонтальных касательных) и φ=90о (изоклина вертикальных касательных). При уравнениях имеющих вид: dx/dt=f1(x, y), dy/dt=f2(x,y) уравнение изоклины записывается как: dy/dx=f2(x, y)/f1(x,y)=A=const. Для изоклины горизонтальных касательных уравнение принимает вид: dy/dx=(f2(x,y))/(f1(x,y))=tg0о=0 или f2(x,y)=0; для изоклины вертикальных касательных: dy/dx=(f2(x,y))/(f1(x,y)) tg90о=∞ или P(x,y)=0.

Коротко остановимся на линейных системах уравнений высоких порядков. При их решении обычно исходное уравнение представляют в виде системы линейных уравнений, решения которых довольно хорошо отработаны.

Пример 12. Линейное уравнение 2-го порядка

x ax bx 0

с постоянными вещественными коэффициентами a, b, можно свести к системе

x y,

y bx ay.

Фазовые траектории этой системы задают фазовые траектории на плоскости x, x .

Характеристическое уравнение: 2

a b 0, .

Можно показать, что практически всегда систему высокого порядка можно свести

к большой системе ОДУ первого порядка.

x1(t)

F1 (x1, x2 ,…,t

(x,t)

x2 (t)

F2 (x1, x2 ,…,t

F2 (x,t)

(8)

dt .

x (t)

(x , x ,…,t

(x,t)

1 2

http://profbeckman.narod.ru/

Поведение системы уравнений первого порядка можно визуально интерпретировать строя фазовые траектории x(t) для различных начальных условий

x(t 0).

Если местоположения всех неподвижных точек (точки, где dx 0 ) на фазовой dt

плоскости установлены, то их можно использовать как реперные точки, вокруг которых исследуется фазовое поведение. В каждой неподвижной точке, линеаризацию проводят,

разлагая Ур.(8) в ряд в виде x x fix

Если собственное значение вещественно, то любая точка, лежащая в направлении собственного вектора, будет развиваться по прямому пути, параллельному собственному вектору. Если действительное собственное значение отрицательно, то прямой путь будет асимптотически приближаться к началу координат; если собственное значение положительно, траектория будет расходиться по прямому пути к бесконечности. Если

собственное значение является мнимым, то траектория будет циркулировать вокруг неподвижной точки с частотой, пропорциональной величине собственного значения. Если собственное значение комплексно, его траектория будет циркулировать с частотой, пропорциональной ее мнимой части, и расходиться от или сходиться к неподвижной точке. Если какая-либо из неподвижных точек имеет собственное значение с положительной вещественной частью, неподвижная точка не может быть устойчивой – это потому, что «типичные» точки в окрестности неподвижных точек будут обладать некоторой компонентой неустойчивого собственного вектора.

Рис. 14. К примеру 13.

Пример 13. Построить фазовые траектории системы

x 0 ,

где

d 2 x

k можно

рассматривать,

как

dt2

частоту колебаний n.

dx dx

x 2C

Решение x

x ;

xdx k

xdx

;

C ; x

k 2

– эллиптическое уравнение.

A2k 2

Пример 14 . Определить фазовый портрет уравнения x

kx 0 , где k -положительно (колебания

маятника около верхнего положения неустойчивого равновесия).

x C1e

C2e

Решение:

y C

ke kt C

kt .

Рис. 15. К примеру 14.

Фазовые

траектории

задаются

уравнением

представляющее собой уравнение семейства гипербол (рис. 14). При

С=0 имеются две асимптоты этого семейства гипербол,

проходящие

через

начало координат:

. Начало

координат

является

k x

единственной особой точкой, причём, за исключением асимптот, ни

Источник

Особые решения дифференциальных уравнений

Особые решения дифференциальных уравнений

ЛЕКЦИЯ 4

Бифуркационная диаграмма

Особые точки кривой

12.1 Дифференциальные уравнения и особые точки

Вам также может понравиться

Как найти инн компании по огрн

Как найти сколько калорий в 1 грамме

Как найти наушники эппл дома

Добавить комментарий Отменить ответ