Содержание
- Как найти остатки при делении куба
- Решение
- Замечания
- math4school.ru
- Делимость целых чисел и остатки
- Немного теории
- Задачи с решениями
- Задачи без решений
Как найти остатки при делении куба
Докажите, что число
а) 97 97 ,
б) 1997 17
нельзя представить в виде суммы кубов нескольких идущих подряд натуральных чисел.
Решение
а) Куб числа, кратного 3, делится на 9. Если же число не делится на 3, то его можно записать в виде n = 3k ± 1. Тогда n³ = 9(3k³ ± 3k² + k) ± 1, то есть даёт остаток ±1 при делении на 9 (мы рассматриваем остаток –1 вместо остатка 8). Поэтому остатки при делении на 9 кубов последовательных натуральных чисел образуют последовательность 1, –1, 0, 1, –1, 0, . Отсюда сразу видно, что сумма любых трёх последовательных кубов делится на 9 и вообще сумма любого количества последовательных кубов может давать только остатки 0 и ±1 при делении на 9.
97 97 ≡ (–2) 97 ≡ (–2) 6·16+1 ≡ –2 (mod 9), так как 2 6 = 64 ≡ 1 (mod 9). Следовательно, 97 97 при делении на 9 даёт остаток –2, то есть не может быть суммой последовательных кубов.
б) Будем рассматривать остатки при делении кубов на 7. Снова воспользуемся отрицательными остатками (–3, –2, –1 вместо, соответственно, 4, 5, 6). Имеем: (±1)³ = ±1, (±2)³ = ±8, (±3)³ = ±27. Поэтому последовательность остатков при делении кубов натуральных чисел на 7 выглядит так: 1, 1, –1, 1, –1, –1, 0, 1, . Отсюда видно, что сумма последовательных кубов может давать при делении на 7 только остатки 0, ±1 и ±2.
1997 17 ≡ 2 17 ≡ 2 3·5+2 ≡ 4 (mod 7), так как 2³ ≡ 1 (mod 7). Следовательно, 1997 17 при делении на 7 даёт остаток 4 и не может быть суммой последовательных кубов.
Замечания
2. Ср. с задачей М1592 из Задачника «Кванта».
Источник
math4school.ru








Делимость целых чисел и остатки

Немного теории
В разнообразных задачах про целые числа используются основные понятия и теоремы, связанные с делимостью. Приведём некоторые из них.
Каждое целое число а можно разделить на натуральное число m с остатком, то есть представить в виде а = mq + r, где q и r – целые числа и r (остаток) не меньше 0, но меньше q.
Среди любых m последовательных целых чисел найдется ровно одно число, делящееся на m.
Различные натуральные числа при делении на натуральное m могут давать любой из остатков 0, 1, 2, . m–1. Однако степени натуральных чисел с фиксированным натуральным показателем n>1 не обязательно снова могут давать при делении на m любой из этих остатков. Так при делении на 3, 4, 5 и 8 четвёртые степени целых чисел могут давать остатки только 0 и 1. Ниже приведена таблица возможных остатков при делении квадратов, кубов, четвертых и пятых степеней на числа от 3 до 10.

Если два числа а и b при делении на число m дают одинаковые остатки, то говорят, что а сравнимо с b по модулю m. Записывают это так

Если a > b, то наибольший общий делитель a и b равен наибольшему общему делителю a – b и b.
Если а и b – натуральные числа и а = bq + r (r – остаток), то наибольший общий делитель d этих чисел равен наибольшему общему делителю b и r; пользуясь этим утверждением несколько раз, можно найти его как последний не равный нулю остаток в цепочке делений с остатком:
(алгоритм Евклида); отсюда следует, что существуют целые числа х и у, такие, что d = ах + by. В частности, если числа а и b взаимно просты, то есть не имеют общих делителей, больших 1, то существуют целые х и у, для которых ах + by = 1.
Каждое натуральное число единственным образом представляется в виде произведения простых чисел (основная теорема арифметики).
Количество простых чисел бесконечно; доказательство этого утверждения по Евклиду основано на том, что произведение нескольких простых чисел, сложенное с единицей, имеет отличные от всех этих простых чисел множители.
Если числа b1, b2, … , bn попарно взаимно просты, то для любых остатков r1, r2, … , rn (ri меньше bi) найдется число а, которое при делении на bi дает остаток ri (китайская теорема об остатках).
Задачи с решениями
1. Сколько существует натуральных чисел, меньших 1000, которые не делятся ни на 5, ни на 7?
Вычёркиваем из 999 чисел, меньших 1000, числа, кратные 5: их [999/5]=199. Далее вычёркиваем числа, кратные 7: их [999/7]=142. Но среди чисел, кратных 7, имеется [999/35]=28 чисел, одновременно кратных 5; они будут вычеркнуты дважды. Итого, нами должно быть вычеркнуто 199+142–28=313 чисел. Остаётся 999–313=686.
2. Номер автобусного билета – шестизначное число. Билет называется счастливым, если сумма трёх первых цифр номера равна сумме последних трёх цифр. Докажите, что сумма всех номеров счастливых билетов делится на 13.
Если счастливый билет имеет номер А, то билет с номером В=999999–А также счастливый, при этом А и В различны. Поскольку А+В=999999=1001·999=13·77·99 делится на 13, то и сумма номеров всех счастливых билетов делится на 13.
3. Докажите, что сумма квадратов трёх целых чисел не может при делении на 8 дать в остатке 7.
Любое целое число при делении на 8 имеет остатком одно из следующих восьми чисел 0, 1, 2, 3, 4, 5, 6, 7, поэтому квадрат целого числа имеет остатком при делении на 8 одно из трёх чисел 0, 1, 4. Чтобы при делении на 8 сумма квадратов трёх чисел имела остаток 7, необходимо, чтобы выполнялся один из двух случаев: либо один из квадратов, либо все три при делении на 8 имеют нечётные остатки.
В первом случае нечётный остаток есть 1, а сумма двух чётных остатков равна 0, 2, 4, то есть сумма всех остатков равна 1, 3, 5. Остатка 7 в этом случае получить нельзя. Во втором случае три нечётных остатка это три 1, и остаток всей суммы равен 3. Итак, 7 не может быть остатком при делении на 8 суммы квадратов трёх целых чисел.
4. Докажите, что при любом натуральном n:
а) число 5 5n+1 + 4 5n+2 + 3 5n делится на 11.
б) число 2 5n+3 + 5 n ·3 n+2 делится на 17.
а) Первоначально выполним следующее преобразование заданного выражения:
5 5n+1 +4 5n+2 +3 5n = 5(3125) n + 16(1024) n + (243) n = 5(11·284+1) n + 16(11·93+1) n + (11·22+1) n .
Принимая во внимание бином Ньютона n-й степени, можно записать: (х+1) n = Ах+1, где А – некоторое целое число при целых х. Тогда приведённое выше выражение принимает вид 11В+5+16+1 = 11С, очевидно делящееся на 11, где В и С – некоторые целые числа.
б) Выполним следующие преобразования, из которых следует доказываемое утверждение:
2 5n+3 + 5 n ·3 n+2 = 8·32 n + 9·15 n = 8(17+15) n + 9·15 n = 17А + 8·15 n + 9·15 n = 17А + 17·15 n = 17В,
где А, В – целые положительные числа.
а) если х 2 +у 2 делится на 3 и числа х, у целые, то х и у делятся на 3;
б) если сумма трёх целых чисел делится на 6, то и сумма кубов этих чисел делится на 6;
в) если p и q простые числа и p>3, q>3, то p 2 –q 2 делится на 24;
г) если a, b, c – любые целые числа, то найдутся такие взаимно простые k и t, что ak+bt делится на c.
а) Пусть х=3а+r1, у=3b+r2, где r1 и r2 – остатки от деления на 3, то есть какие-то из чисел 0, 1, 2. Тогда х 2 +у 2 =3(3а 2 +3b 2 +2аr1+2br2)+(r1) 2 +(r2) 2 . Так как х 2 +у 2 делится на 3, первое слагаемое последней суммы делится на 3, то (r1) 2 +(r2) 2 делится на 3, что возможно, с учётом вышесказанного, только при r1=r2=0.
Таким образом, х=3а и у=3b, то есть х и у делятся на 3, что и требовалось доказать.
б) Достаточно показать, что x 3 +y 3 +z 3 –(x+y+z) делится на 6. Это так и есть, ведь каждое из слагаемых x 3 –x, y 3 –y и z 3 –z делится на 6, поскольку а 3 –а=а(а–1)(а+1) – произведение трёх последовательных целых чисел, которое обязательно делится на 2, 3, а, значит, и 6.
в) Кратность p 2 –q 2 числу 3 можно доказать так. При делении на 3 квадраты целых чисел дают остатки 0 или 1. Так как p и q простые числа больше 3, то это p 2 и q 2 при делении на 3 имеют одинаковые остатки – единицу. Тогда p 2 –q 2 делится на 3.
С другой стороны, p 2 –q 2 =(p+q)(p–q). Так как p и q нечётные и при делении на 4 имеют остатки 1 или 3, то выражение в одних скобках делится на 4, а в других – на 2, а разность квадратов p и q – на 8.
Так как p 2 –q 2 делится на взаимно простые числа 3 и 8, то p 2 –q 2 делится на 3·8=24, что и требовалось доказать.
г) Пусть наибольший общий делитель чисел b и c–a равен d, b=k·d и c–a=t·d. Тогда числа k и t взаимно просты.
а) наибольший общий делитель чисел 2n+3 и n+7;
б) все пары натуральных чисел х, у таких, что 2х+1 делится на у и 2у+1 делится на х;
в) все целые k, для которых k 5 +3 делится на k 2 +1;
г) хотя бы одно натуральное число n такое, что каждое из чисел n, n+1, n+2, . , n+20 имеет с числом 30030=2·3·5·7·11·13 общий делитель, больший единицы.
а) Заметим, что если m > n, то НОД (m; n) = НОД (m – n; n).
Иначе говоря, наибольший общий делитель двух натуральных чисел равен наибольшему общему делителю модуля их разности и меньшего числа. Легко доказать это свойство.
Пусть k – общий делитель m u n (m > n). Это значит, что m = ak, n = bk, где a, b – натуральные числа, причем a > b. Тогда m – n = k(a – b), откуда следует, что k – делитель числа m – n. Значит, все общие делители чисел m и n являются делителями их разности m – n, в том числе и наибольший общий делитель.
НОД (2n+3; n+7) = НОД (n+7; 2n+3 – (n+7)) = НОД (n+7; n–4) = НОД (n–4; 11).
Так как 11 – простое число, то искомый наибольший общий делитель равен 1 либо 11. Если n–4 = 11d, то есть n = 4+11d, то наибольший общий делитель равен 11, в противном случае – 1.
Ответ: НОД (2n+3; n+7) = 11, при n равных 4+11d; НОД (2n+3; n+7) = 1, при n не равных 4+11d.
б) Число 2х+1 нечётное и делится на у, поэтому у тоже нечётное. Аналогично х – нечётное.
Числа х и у взаимно простые. Действительно, пусть k – общий делитель х и у, тогда 2х делится на k, и (2х+1) тоже делится на k (k – делитель у, а у – делитель 2х+1). Значит, 1 делится на k, то есть k=1.
Число 2х+2у+1 делится и на х и на у, а значит, – на ху. Тогда 2х+2у+1 не меньше ху.
Пусть х 5 +3 = (k 3 –k)( k 2 +1) + (k+3), то k 5 +3 делится на k 2 +1, если k+3 делится на k 2 +1. Когда это возможно? Рассмотрим варианты:
2) k+3 = k 2 +1; решая, находим k = –1, k = 2;
3) проверим целые k при которых k+3 > k 2 +1; после проверки: k = 0, k = 1.
г) пусть m = 2·3·5·7·k. Подбирая k так, чтобы m–1 делилось на 11, а m+1 – на 13, получим, что число n = m–10 удовлетворяет условию задачи.
7. Существует ли десятизначное число, делящееся на 11, в записи которого каждая цифра встречается по одному разу?
I способ. Выписывая трёхзначные числа, делящиеся на 11, можно среди них найти три числа, в записи которых участвуют все цифры от 0 до 9. Например, 275, 396,418. С их помощью можно составить десятизначное число, делящееся на 11. Например:
2753964180 = 275·10 7 + 396·10 7 + 418·10 = 11·(25·10 7 + 36·10 4 + 38·10).
II способ. Для нахождения требуемого числа воспользуемся признаком делимости на 11, согласно которому числа n=a1a2a3…a10 (в данном случае аi не множители, а цифры в записи числа n) и S(n)=a1–a2+a3–…–a10 одновременно делятся на 11.
Пусть А – сумма цифр, входящая в S(n) со знаком «+», В – сумма цифр, входящая в S(n) со знаком «–». Число А–В, согласно условию задачи, должно делиться на 11. Положим В–А=11, кроме того, очевидно, А+В=1+2+3+…+9=45. Решая полученную систему В–А=11, А+В=45, находим, А=17, В=28. Подберём группу из пяти различных цифр с суммой 17. Например, 1+2+3+5+6=17. Эти цифры возьмём в качестве цифр с нечётными номерами. В качестве цифр с чётными номерами возьмём оставшиеся – 4, 7, 8, 9, 0.
Мы видим, что условию задачи удовлетворяет, например, число 1427385960.
8. Два двузначных числа, записанных одно за другим, образуют четырёхзначное число, которое делится на их произведение. Найти эти числа.
Пусть a и b – два двузначных числа, тогда 100a+b – четырёхзначное число. По условию 100a+b = k·ab, отсюда b = a(kb–100), то есть b делится на a.
Итак, b = ma, но a и b двузначные числа, поэтому m однозначное.
Так как 100a+b = 100a+ ma = а(100+m) и 100a+b = kab, то а(100+m) = kab,
то есть 100+m = kb или 100+m = kma, откуда 100 = m(ka–1).
Таким образом, m – делитель числа 100, кроме того, m – однозначное число, значит, m = 1, 2, 4, 5.
Так как ka = 1+100/m, причём а двузначно, то отпадают для m значения 1 и 5, ибо
при m = 1 число 100/1+1 = 101 не делится ни на какое двузначное число а;
при m = 5 число 100/5+1 = 21 и имеем а=21, при котором b = ma = 5·21 – трёхзначное число.
При m = 2 имеем, ka = 51, a = 17, b = 17·2 = 34;
при m = 4 имеем, ka = 26, a = 13, b = 13·4 = 52.
9. Докажите, что при любых натуральных k и n число 1 2k+1 + 2 2k+1 + . . . + n 2k+1 не делится на n + 2.
Воспользуемся тем, что сумма одинаковых нечётных степеней двух чисел делится на сумму этих чисел, что следует из известного алгебраического тождества. Можно записать:
3 2k+1 + (n – 1) 2k+1 = (3 + (n – 1))·А2 = (2 + n)·А2,
4 2k+1 + (n – 2) 2k+1 = (4 + (n – 2))·А3 = (2 + n)·А3 и так далее, где Аi – некоторые целые числа.
В зависимости от чётности n возможна нехватка числа для образования последней пары, избежать этого позволит умножение на 2, рассматриваемой в условии суммы. Итак,
2(1 2k+1 + 2 2k+1 +. +n 2k+1 ) = 2·1 2k+1 + (2 2k+1 + n 2k+1 ) + (3 2k+1 + (n – 1) 2k+1 ) +. + (n 2k+1 + 2 2k+1 ) =
= 2 + (n + 2)·А, где А – некоторое целое число.
Одно из слагаемых последней суммы делится на n + 2, другое при любых натуральных n – нет. Итак, рассматриваемая в условии сумма не делится на n при любых натуральных n и k.
10. Докажите, что для любого простого числа р > 2 числитель m дроби

Заметим, что число р–1 чётное, и преобразуем дробь m/n к виду

Приводя полученное выражение к общему знаменателю


из которого вытекает равенство m(p–1)!=pqn. Поскольку ни одно из чисел 1, 2, 3, … , р–1 не делится на простое число р, то последнее равенство возможно лишь в случае, если m делится на р, что и требовалось доказать.
Задачи без решений
1. Докажите, что при любом натуральном n:
а) число 4 n + 15n – 1 делится на 9;
б) число 3 2n+3 + 40n – 27 делится на 64;
в) число 5 n (5 n + 1) – 6 n (3 n + 2 n ) делится на 91.
а) натуральные значения n такие, что n 5 – n делится на 120;
б) наименьшее натуральное число n такое, что n делится на 19, а n + 2 делится на 82.
3. Пусть m, n – различные натуральные числа, причём m – нечётное. Докажите, что 2 m –1 и 2 n +1 взаимно простые.
4. Четыре различных целых трёхзначных числа, начинающиеся с одной и той же цифры, обладают тем свойством, что их сумма делится на три из них без остатка. Найдите эти числа.
5. Докажите, что для каждого натурального n > 1 число n n – n 2 + n – 1 делится на (n – 1) 2 .
Источник
26.05.2016, 12:10. Показов 3459. Ответов 2
Метки нет (Все метки)

Доказать, что кубы натуральных чисел при делении на 9 могут давать только остатки 0,1 или 8.
Как решала: Рассмотрела кубы чисел от 0 до 9: 0,1,8,27,64,125,216,343,512,729
Заметим, что {0, 27, 216, 729} при делении на 9 r=0
{1,64, 343}при делении на 9 r=1
{8, 125, 512}при делении на 9 r=8
Преположение подтверждается. Но как доказать в общем виде? Вот в чем вопрос
0

Метод анализа остатков
В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.
В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.
Пример №19.
Найти частное и остаток от деления числа (— 23) на 7.
Решение:
Согласно формуле деления с остатком, получаем:
— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.
Пример №20.
Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.
Решение:
Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:
- остаток от деления на 2 равен 1;
- остаток от деления на 4 равен 1;
- остаток от деления на 5 равен 3;
- остаток от деления на 9 равен 0;
- остаток от деления на 10 равен 3;
- остаток от деления на 25 равен 23.
Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.
Пример №21.
Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа 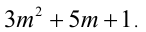
Решение:
Из условия следует, что число m имеет вид: 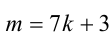 . Тогда
. Тогда
Таким образом, остаток от деления числа 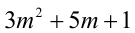 на 7 равен 1.
на 7 равен 1.
Пример №22.
Доказать, что при любых целых X число 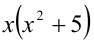 делится нацело на 6.
делится нацело на 6.
Решение:
Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:
1) Пусть 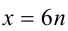 , тогда
, тогда 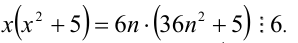
2) Пусть 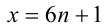 , тогда
, тогда 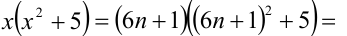
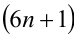
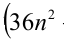
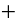
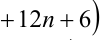
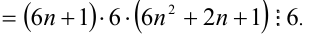
3) Пусть 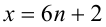 , тогда
, тогда 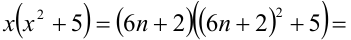
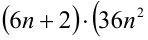
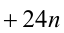
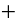
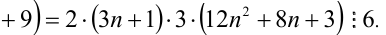
4) Пусть 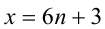 , тогда
, тогда 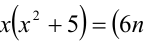
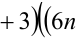
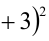
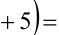
5) Пусть 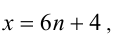 тогда
тогда 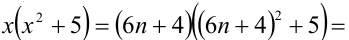
![]()
6) Пусть 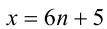 , тогда
, тогда 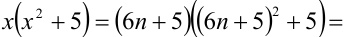
Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 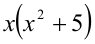 кратно 6.
кратно 6.
Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:
Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.
Пример №23.
Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?
Решение:
Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе
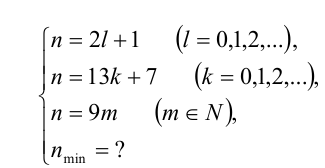
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности 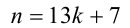 число k должно быть чётным, т.е.
число k должно быть чётным, т.е. 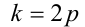
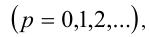 причём меньшему n соответствует меньшее р , но тогда имеем
причём меньшему n соответствует меньшее р , но тогда имеем 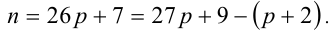 Поскольку числа п и
Поскольку числа п и 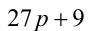 делятся нацело на 9, то, следовательно, число
делятся нацело на 9, то, следовательно, число 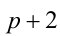 также должно быть кратно 9 (и при этом быть минимальным). Наименьшее целое неотрицательное р , для которого выполняются эти условия, равно 7, откуда находим
также должно быть кратно 9 (и при этом быть минимальным). Наименьшее целое неотрицательное р , для которого выполняются эти условия, равно 7, откуда находим
Ответ: самое меньшее — 189 счётных палочек.
Пример №24.
После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.
Решение:
Обозначим 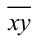 — искомое число
— искомое число 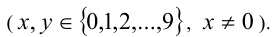 Тогда, по условию, имеем систему уравнений
Тогда, по условию, имеем систему уравнений
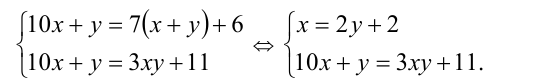
Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.
Пример №25.
Целые числа m, n,k не делятся нацело на 3. Доказать, что число 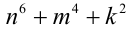 делится на 3.
делится на 3.
Доказательство. Если 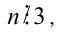 то возможны два случая:
то возможны два случая: 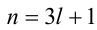 и
и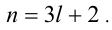 . В первом случае
. В первом случае 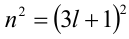 — делится на 3 с остатком 1, а значит,
— делится на 3 с остатком 1, а значит, 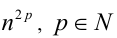 , также делится на 3 с остатком 1. Аналогично во втором случае:
, также делится на 3 с остатком 1. Аналогично во втором случае: 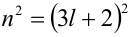 делится на 3 с остатком
делится на 3 с остатком 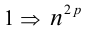 делится на 3 с остатком 1. Таким образом, если целое число не делится нацело на 3, то его квадрат (любая чётная степень) при делении на 3 дают остаток 1. Но тогда сумма трёх таких чётных степеней кратна 3.
делится на 3 с остатком 1. Таким образом, если целое число не делится нацело на 3, то его квадрат (любая чётная степень) при делении на 3 дают остаток 1. Но тогда сумма трёх таких чётных степеней кратна 3.
Пример №26.
Доказать, что если 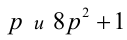 — простые числа, то
— простые числа, то 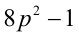 — тоже простое число.
— тоже простое число.
Доказательство. Если 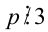 , то остаток от деления
, то остаток от деления 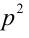 на 3 равен 1. Но тогда
на 3 равен 1. Но тогда 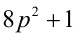 делилось бы на 3, что противоречит условию. Следовательно,
делилось бы на 3, что противоречит условию. Следовательно, 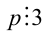
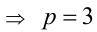 , тогда действительно
, тогда действительно 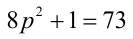 — простое число, и при этом
— простое число, и при этом 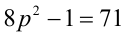 тоже является простым.
тоже является простым.
Пример №27.
Решить уравнение в целых числах
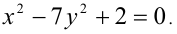
Решение:
Перепишем уравнение в виде: 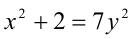 . Заметим, что правая часть уравнения при любом целом Y делится нацело на 7. Выясним, какие остатки при делении на 7 даёт левая часть данного уравнения. Для этого разобьём множество всех целых X на 7 групп в зависимости от остатка при делении на 7:
. Заметим, что правая часть уравнения при любом целом Y делится нацело на 7. Выясним, какие остатки при делении на 7 даёт левая часть данного уравнения. Для этого разобьём множество всех целых X на 7 групп в зависимости от остатка при делении на 7: 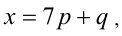 где
где 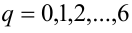 , и рассмотрим каждый из этих случаев в отдельности.
, и рассмотрим каждый из этих случаев в отдельности.
1) Если 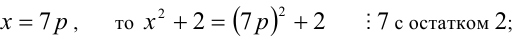
2) если 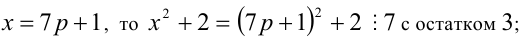
3) если 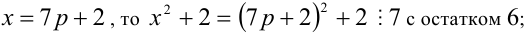
4) если 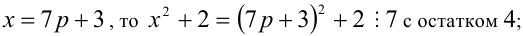
5) если 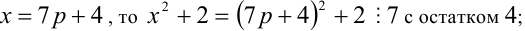
6) если 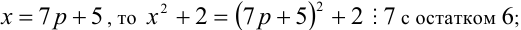
7) если 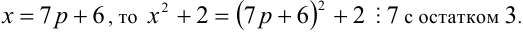
Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.
Пример №28.
Найти все пары целых чисел (x;y), удовлетворяющие уравнению
и доказать, что для каждой такой пары сумма 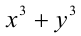 является нечётным числом.
является нечётным числом.
Решение:
Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:
1) Если 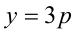 , то уравнение примет вид
, то уравнение примет вид 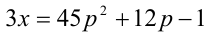 . Это равенство невозможно, так как его левая часть кратна 3, а правая — нет.
. Это равенство невозможно, так как его левая часть кратна 3, а правая — нет.
2) Если 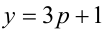 , то получим аналогичную ситуацию.
, то получим аналогичную ситуацию.
3) Наконец, если 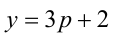 , то, подставляя в уравнение, получим
, то, подставляя в уравнение, получим
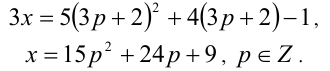
Следовательно, общий вид решений: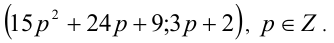 Осталось показать, что
Осталось показать, что 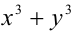 — нечётно. В самом деле, если
— нечётно. В самом деле, если 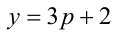 чётно, то
чётно, то 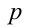 — чётно и, значит,
— чётно и, значит, 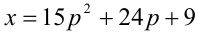 — нечётно. Если, наоборот,
— нечётно. Если, наоборот, 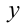 — нечётно, то
— нечётно, то 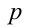 также нечётно, а значит,
также нечётно, а значит,  — чётно. Таким образом, числа
— чётно. Таким образом, числа  и
и 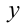 , а значит и их кубы, имеют всегда разную чётность, поэтому их сумма есть нечётное число.
, а значит и их кубы, имеют всегда разную чётность, поэтому их сумма есть нечётное число.
Ответ: 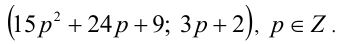
Пример №29.
Решить в целых числах уравнение
Решение:
Так как произвольное целое число  представимо в виде
представимо в виде 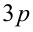 ,
, 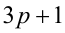 или
или 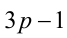 где
где 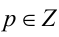 , а
, а
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 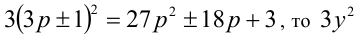 даёт при делении на 9 остаток 0 или 3. Итак, правая часть уравнения может делиться на 9 с остатками 2 или 5, а левая — 0, 1 или 8. Следовательно, уравнение не имеет решений в целых числах.
даёт при делении на 9 остаток 0 или 3. Итак, правая часть уравнения может делиться на 9 с остатками 2 или 5, а левая — 0, 1 или 8. Следовательно, уравнение не имеет решений в целых числах.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:

Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Lana67 |
Заголовок сообщения: Количество остатков
|
||
|
Здравствуйте! Подскажите, пожалуйста, для этой задачи существует какая-либо формула или нужно применить метод перебора, т.е. просто возвести в куб и узнать какой остаток, а в результате и сколько их: (13q)[math]^{3}[/math], (13q+1)[math]^{3}[/math], …, (13q+12)[math]^{3}[/math]? Задача такая:
|
||
| Вернуться к началу |
|
||
|
Lana67 |
Заголовок сообщения: Re: Количество остатков
|
|
michel,да, нет не трудно, я их уже перебрала. Просто стало интересно, может быть это можно сделать по какой-то формуле?
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Lana67 “Спасибо” сказали: Andy |
|
|
Lana67 |
Заголовок сообщения: Re: Количество остатков
|
|
Andy, их оказалось пять: 0, 1, 5, 8, 12.
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Lana67 “Спасибо” сказали: Andy |
|
|
Lana67 |
Заголовок сообщения: Re: Количество остатков
|
|
Я вот, что нашла в интернете.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти количество остатков от деления
в форуме Теория чисел |
taxol |
7 |
654 |
11 фев 2021, 14:37 |
|
Сумма остатков
в форуме Ряды |
Volodislavir |
2 |
291 |
23 фев 2018, 23:28 |
|
Регрессия при автокорреляции остатков
в форуме Математическая статистика и Эконометрика |
kuzojlberg |
9 |
323 |
18 апр 2019, 18:26 |
|
Уравнение из равенства остатков
в форуме Теория чисел |
math_user |
13 |
445 |
17 авг 2019, 17:30 |
|
Вычислить интеграл с помощью остатков
в форуме Комплексный анализ и Операционное исчисление |
Daria1999 |
0 |
123 |
22 окт 2019, 19:48 |
|
Теорема 75 теория чисел – равность остатков
в форуме Теория чисел |
afraumar |
5 |
671 |
23 авг 2013, 19:40 |
|
Количество способов
в форуме Комбинаторика и Теория вероятностей |
tovarz |
1 |
514 |
03 апр 2014, 18:58 |
|
Количество отношений
в форуме Дискретная математика, Теория множеств и Логика |
lolliker228 |
7 |
132 |
23 ноя 2020, 02:40 |
|
Найти количество n
в форуме Алгебра |
Mathnew |
12 |
778 |
21 янв 2015, 02:23 |
|
Количество способов
в форуме Дискретная математика, Теория множеств и Логика |
sedlitskas |
3 |
210 |
16 апр 2020, 17:04 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Значит, даёт кубы этих остатков:
.
Действительно,
Для отрицательных чисел можно заметить, что . Тогда остатки будут аналогичные.





