Как найти остаток от деления числа формула

Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом^[1]. Пусть и — целые числа, причём bneq 0. Деление с остатком («делимого») на («делитель») означает нахождение таких целых чисел и , что выполняется равенство:

Таким образом, результатами деления с остатком являются два целых числа: называется неполным частным от деления, а — остатком от деления. На остаток налагается дополнительное условие: то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения при заданных выше условиях. Если остаток равен нулю, говорят, что нацело делится на

Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).

Примеры

Проверка:

Проверка:

Проверка:

Проверка:

Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.

Определение[править | править код]

Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль^[2], либо теория сразу формулируется для целых чисел, как указано выше^[1].

Для вычисления неполного частного от деления на положительное число следует разделить (в обычном смысле) на и округлить результат до ближайшего целого в меньшую сторону:

${displaystyle q=leftlfloor {frac {a}{b}}rightrfloor ,}$

когда

где полускобки обозначают взятие целой части. Значение неполного частного позволяет вычислить значение остатка по формуле:

Для отрицательного делителя нужно округлять частное в большую сторону:

${displaystyle q=leftlceil {frac {a}{b}}rightrceil ,}$

когда

Операция «mod» и связь со сравнениями[править | править код]

Величина остатка может быть получена бинарной операцией «взятия остатка» от деления на , обозначаемой mod:

Не следует путать это обозначение с обозначением сравнения по модулю . Формула для влечёт выполнение сравнения:

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства , необходимого для того, чтобы было остатком.

В программировании[править | править код]

Операция вычисления неполного частного и остатка в различных языках программирования

Язык	Неполное частное	Остаток	Знак остатка
ActionScript		`%`	Делимое
Ada		`mod`	Делитель
`rem`	Делимое
Бейсик		`MOD`	Не определено
Си (ISO 1990)	`/`	`%`	Не определено
Си (ISO 1999)	`/`	`%`	Делимое^[3]
C++ (ISO 2003)	`/`	`%`	Не определено^[4]
C++ (ISO 2011)	`/`	`%`	Делимое^[5]
C#	`/`	`%`	Делимое
ColdFusion		`MOD`	Делимое
Common Lisp		`mod`	Делитель
	`rem`	Делимое
D	`/`	`%`	Делимое^[6]
Delphi	`div`	`mod`	Делимое
Eiffel	`//`	`\`	Делимое
Erlang	`div`	`rem`	Делимое
Euphoria		`remainder`	Делимое
Microsoft Excel (англ.)	`QUOTIENT()`	`MOD()`	Делитель
Microsoft Excel (рус.)	`ЧАСТНОЕ()`	`ОСТАТ()`
FileMaker	`Div()`	`Mod()`	Делитель
Fortran		`mod`	Делимое
	`modulo`	Делитель
GML (Game Maker)	`div`	`mod`	Делимое
Go	`/`	`%`	Делимое
Haskell	`div`	`mod`	Делитель
`quot`	`rem`	Делимое
J		`\|~`	Делитель
Java	`/`	`%`	Делимое^[7]
`Math.floorDiv`	`Math.floorMod`	Делитель (1.8+)
JavaScript	.toFixed(0)	`%`	Делимое
Lua		`%`	Делитель
Mathematica	`Quotient`	`Mod`	Делитель
MATLAB	`idivide(?, ?, 'floor')`	`mod`	Делитель
`idivide`	`rem`	Делимое
MySQL	`DIV`	`MOD` `%`	Делимое
Oberon	`DIV`	`MOD`	+
Objective Caml		`mod`	Не определено
Pascal	`div`	`mod`	Делимое^[8]
Perl	Нет	`%`	Делитель
PHP	Нет^[9]	`%`	Делимое
PL/I		`mod`	Делитель (ANSI PL/I)
Prolog (ISO 1995)		`mod`	Делитель
PureBasic	`/`	`Mod` `%`	Делимое
Python	`//`	`%`	Делитель
QBasic		`MOD`	Делимое
R	%/%	`%%`	Делитель
RPG		`%REM`	Делимое
Ruby	`/`	`%`	Делитель
Scheme		`modulo`	Делитель
SenseTalk		`modulo`	Делитель
`rem`	Делимое
Tcl		`%`	Делитель
Verilog (2001)		`%`	Делимое
VHDL		`mod`	Делитель
`rem`	Делимое
Visual Basic		`Mod`	Делимое

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:

78 mod 33 = 12
78 div 33 = 2

Знак остатка[править | править код]

Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
Знак остатка совпадает со знаком делителя: неполное частное округляет к .

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти^[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.

Как запрограммировать, если такой операции нет?[править | править код]

Неполное частное можно вычислить через деление и взятие целой части: $q=left[{frac {a}{b}}right]$ , где [x] , в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды mod остаток программируется как a-qb .

Если положительно, а знак совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой .

Неполное частное и неотрицательный остаток от деления на степень двойки $2^{n}$ — это битовый сдвиг (для чисел со знаком — арифметический) и ${displaystyle aoperatorname {&} (2^{n}-1)}$ .

Обобщения[править | править код]

Вещественные числа[править | править код]

Если два числа и (отличное от нуля) относятся к множеству вещественных чисел, может быть поделено на без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.

Формально:

если

, то

, где

Пример

Деление 7,9 на 2,1 с остатком даёт:

${displaystyle leftlfloor {frac {7{,}9}{2{,}1}}rightrfloor =3}$

(неполное частное);

(остаток).

Гауссовы целые числа[править | править код]

Гауссово число — это комплексное число вида a+bi , где a,b — целые числа. Для них можно определить деление с остатком: любое гауссово число можно разделить с остатком на любое ненулевое гауссово число , то есть представить в виде:

где частное и остаток — гауссовы числа, причём
Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, можно разделить на тремя способами:

{displaystyle 7+2i=(3-i)(2+i)+i=(3-i)(1+i)+3=(3-i)(2+2i)+(-1-2i).}

Многочлены[править | править код]

При делении с остатком двух многочленов f(x) и g(x) для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:

, причём

Пример: ${frac {2x^{2}+4x+5}{x+1}}=2x+2$ (остаток 3), так как: ${displaystyle 2x^{2}+4x+5=(x+1)(2x+2)+3}$ .

См. также[править | править код]

Алгоритм Евклида
Делимость
Наибольший общий делитель
Непрерывная дробь
Сравнение по модулю

Примечания[править | править код]

↑ ¹ ² Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
↑ ISO/IEC 9899:TC2: When integers are divided, the result of the / operator is the algebraic quotient with any fractional part discarded. [This is often called «truncation toward zero».]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится.
↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
↑ N3242=11-0012 (Working draft), текст совпадает с C99
↑ D language specification (англ.). dlang.org. Дата обращения: 29 октября 2017. Архивировано из оригинала 3 октября 2017 года.
↑ Арнолд, Кен, Гослинг, Дж., Холмс, Д. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
↑ Стандарт 1973 года: div — division with truncation.
↑ PHP: Arithmetic Operators — Manual. Дата обращения: 27 ноября 2014. Архивировано 19 ноября 2014 года.
↑ DIV — Unsigned Divide

Источник

Бывает, он сопряжен с некоторыми неудобствами, но это лучше, чем ничего.

Именно в древней Греции зародилась теория делимости

Приветствую Вас, уважаемые Читатели! Сегодня хочу немного погрузиться в теорию делимости, а именно в вычисление остатков от деления. Эта задача является и практически важной, ведь такие операции применяются буквально повсюду: от криптографии до телекоммуникационных систем. Поехали!

Итак, начнем с определения:

Как найти остаток от деления ? Универсальный способ

Так же такие числа называются сравнимыми по модулю m.

Для равноостаточных чисел работает такая теорема:

Если при делении на m числа a1,a2,a3… an соответственно равноостаточны числам b1,b2.b3…bn, то равноостаточными будут суммы a1+a2+a3+…+an и b1+b2+b3+…bn, а также произведения a1a2a3…an и b1b2b3…bn.
Как следствие, если числа a и b равноостаточны, то такими же являются и числа a^n и b^n при любо натуральном n.

Формулировка весь запутанная, поэтому разберем два пример. Итак:

Теперь пример посложнее с многоступенчатым решением:

В итоге мы получаем хоть и меньшее, но всё равно трудно вычисляемое вручную число, поэтому продолжаем дальше:

На третьем шаге уже нет смысла вычислять все остатки, как прежде. Можно было и вычислить вручную. Получаем, что первоначальное число и число 56 равноостаточны при делении на 37. Ответ получен! Спасибо за внимание!

Формула деления с остатком

Деление с остатком, как это?

Разделить с остатком число a на число b – значит найти два таких числа: c – частное и n – остаток, и сложить их.

Данную формулу так же можно прочитать следующим образом:

Разделить с остатком число a на число b – значит найти два таких числа c и n (частное и остаток), что:

Правило деления с остатком

Что бы разделить число с остатком, нужно:

1. Подобрать близкое к делимому число, которое меньше делимого и делителя на делитель без остатка;

2. Выполнить деление;

3. Найти остаток – из делимого вычесть число, которое разделили. Остаток всегда должен быть меньше делителя.

Примеры

9 : 4 = 2 (остаток 1), 9 = 4 • 2 + 1;

19 : 4 = 4 (остаток 1), 19 = 4 • 4 + 3;

23 : 3 = 7 (остаток 2), 23 = 7 • 3 + 2.

Объясним правило на примере 19 : 4

1. Подбираем близкое к 19 число, которое меньше 19 и делится на 4 без остатка. Это число 16;

2. Делим 16 на 4, получаем 4;

3. Находим остаток: 19 – 16 = 3. Сравниваем остаток с делителем: 3 < 4. Значит, частное найдено верно.

4. Значит, 19 : 4 = 4 + 3 (остаток).

Проверка деления с остатком

Что бы проверить деление с остатком нужно:

1. Остаток сравнить с делителем (остаток должен быть меньше делителя);

2. Частное умножить на делитель и к полученному произведению прибавить остаток. Если получится делимое, то пример решен верно.

Пример №1

31 : 4 = 7 (остаток 3)

Проверяем:

1. 4 < 3;

2. 7 • 4 + 3 = 23.

Пример №2

50 : 15 = 3 (остаток 5)

Проверяем:

1. 5 < 15;

2. 3 • 15 + 5 = 50.

Источник

Деление с остатком.

Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.

Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?

Решение:
Поделим число 16 на 5 столбиком получим:

Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.

16=5⋅3+1

a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.

Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.

Остаток от деления

Остаток всегда должен быть меньше делителя.

Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.

Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.

Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.

Остаток может быть равен делителю?
Ответ: нет.

Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)

Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8

Решение:
а) Делим столбиком:

258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.

Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258

б) Делим столбиком:

1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.

Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873

Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.

Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.

Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)

Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22

б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107

Задача:

Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?

Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400

Ответ: 30 кусков получиться и 10 см. проволоки останется.

Источник

Формула деления с остатком

При делении числа а на число b
устанавливается, сколько раз по b
содержится в а:

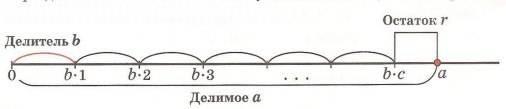
Если получилось с откладываний и осталось
r единиц (r < b), то а
= b • c + r. Это равенство называют
формулой деления с остатком. В нём
показана взаимосвязь между делимым,
делителем, частным и остатком:

Итак, при делении с остатком делимое
равно произведению делителя и частного
плюс остаток (остаток меньше делителя).

Задача.

Некоторое число разделили на 8. Получилось
частное 6 и остаток 3. Найти делимое.

Решение:

b = 8, с = 6, r = 3, Надо
найти а. По формуле деления с остатком
имеем:

а = b • с + r = 8 • 6 + 3 = 51.

Порядок выполнения
совместных действий. Скобки.

Рассмотренные нами четыре действия —
сложение, вычитание, умножение и деление
— принято делить на две ступени. Первые
два действия, т. е. сложение и вычитание,
называются действиями первой ступени,
а последние два, т. е. умножение и деление,
— действиями второй ступени. В каждой
ступени, следовательно, имеется одно
прямое и одно обратное ему действие.

Мы будем называть арифметическим
выражением всякую совокупность
чисел и знаков, указывающих, какие
действия над этими числами нужно
произвести.

Если в выражении встречаются только
действия первой ступени, то их принято
выполнять в том порядке, в каком они
написаны слева направо.

23 + 12— 5 = 35 — 5 = 30; 38— 18 + 11 = 20 + 11 = 31.

Если в выражении встречаются только
действия второй ступени, то их принято
выполнять в том порядке, в каком они
написаны, слева направо. Например:

60 24 : 8 = 1 440 : 8 =
180; 100 : 5  6 = 20 
6 = 120.

Если в выражении встречаются действия
и первой, и второй ступени, то сначала
принято выполнять действия второй
ступени, а потом первой.

1) 80  20 + 10 = 1 600 +
10 = 1 610,

2) 90 + 60 : 4 = 90 + 15 = 105.

Всякое отклонение от этого порядка
должно быть обозначено скобками.

Например: (15 + 10)  4 —
(27 — 9) : 3 = 25  4 —
18 : 3 = 100 — 6 = 94.

Средним арифметическим нескольких
чисел называется частное от деления
суммы этих чисел на их число.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение[править | править код]

Операция «mod» и связь со сравнениями[править | править код]