Как найти остаток от деления многочленов

Как найти остаток от деления многочленов

Теорема Безу и следствия из неё

19 июля 2022

Теорема Безу позволяет решать уравнения высших степеней, которые на первый взгляд не решаются, и раскладывать на множители многочлены, которые не раскладываются.:)

Формулировка теоремы довольно проста:

Терема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x- color{red}{a}$ равен значению этого многочлена в точке $x= color{red}{a}$:

[r=Pleft( color{red}{a} right)]

На практике нас интересует не сама теорема Безу, а некоторые следствия из неё — именно они помогают решать уравнения и раскладывать многочлены на множители. В этом уроке мы рассмотрим все такие следствия и станем настоящими мастерами в работе с многочленами.

Содержание

  1. Деление с остатком
  2. Разложение на множители
  3. Целые корни многочленов
  4. Рациональные корни многочленов
  5. Доказательства

В разных учебниках теорему Безу проходят то в 9-м классе, то в 10-м. Этот урок построен так, что вы поймёте его вне зависимости от школы, класса и учебника.

1. Деление с остатком

Итак, есть многочлен $Pleft( x right)$ и двучлен $x- color{red}{a}$. Разделим $Pleft( x right)$ на $x- color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x- color{red}{a} right)+r]

Теперь найдём значение многочлена $Pleft( x right)$ в точке $x= color{red}{a}$:

[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}- color{red}{a} right)+r=r]

Собственно, мы только что доказали теорему Безу. А заодно подготовили основу для первого важного следствия.

Следствие 1. Деление на произвольный двучлен

Теорема Безу прекрасно работает не только для двучлена $x-color{red}{a}$, но и для любого линейного выражения вида $color{blue}{k}x+color{red}{b}$.

Следствие 1. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $color{blue}{k}x+color{red}{b}$ равен значению этого многочлена в точке $x=-color{red}{b}/ color{blue}{k};$:

[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]

На практике для большей надёжности рекомендуется приравнять двучлен $color{blue}{k}x+color{red}{b}$ к нулю:

[begin{align} color{blue}{k}x+color{red}{b} &=0 \ x &=-frac{color{red}{b}}{color{blue}{k}} \ end{align}]

Затем подставить найденное значение $x=-{color{red}{b}}/{color{blue}{k}};$ в многочлен $Pleft( x right)$ и таким образом найти $Pleft( -{color{red}{b}}/{color{blue}{k}}; right)$:

[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]

Пример 1. Стандартный многочлен

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)=4{{x}^{3}}-3{{x}^{2}}+5x-6]

на двучлен $Tleft( x right)=x-2$.

Решение. Это стандартный двучлен вида $x-color{red}{a}$, поэтому решаем по стандартной теореме Безу, согласно которой остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{2}$ равен $Pleft( color{red}{2} right)$:

[begin{align}r &=Pleft( color{red}{2} right)= \ &=4cdot {color{red}{2}^{3}}-3cdot {color{red}{2}^{2}}+5cdotcolor{red}{2}-6 \ &=32-12+10-6=24 end{align}]

Ответ: 24.

Пример 2. Более сложный многочлен

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)={{left( {{x}^{3}}-2{{x}^{2}}+5 right)}^{3}}{{left( 2x+1 right)}^{5}}]

на двучлен $Tleft( x right)=x+1$.

Решение. Многочлен $Pleft( x right)$ представлен в виде произведения двух других многочленов, которые ещё и возведены в степени. Если раскрыть скобки и привести подобные слагаемые, получится обычный многочлен вида

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

По свойствам степеней найдём степень такого многочлена:

[deg Pleft( x right)=3cdot 3+1cdot 5=14]

Раскрывать скобки и приводить подобные в многочлене 14-й степени долго и трудно, а главное — в этом нет никакой необходимости. Ведь по теореме Безу остаток от деления $Pleft( x right)$ на двучлен $x-color{red}{a}$ всегда равен $Pleft( color{red}{a} right)$ — и не важно, как записан исходный многочлен $Pleft( x right)$.

Для надёжности, чтобы найти $color{red}{a}$, приравняем к нулю двучлен $Tleft( x right)=x+1$:

[begin{align}x+1 &=0 \ x &=color{red}{-1} \ end{align}]

Теперь подставим $x=color{red}{-1}$ в многочлен $Pleft( x right)$ и найдём остаток:

[begin{align}r &=Pleft( color{red}{-1} right)= \ &={{left( {{left( color{red}{-1} right)}^{3}}-2cdot {{left( color{red}{-1} right)}^{2}}+5 right)}^{3}}cdot {{left( 2cdot left( color{red}{-1} right)+1 right)}^{5}}= \ &={{left( -1-2+5 right)}^{3}}cdot {{left( -2+1 right)}^{5}}=-8 end{align}]

Ответ: −8.

Пример 3. Рациональные коэффициенты

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)=3{{x}^{20}}+{{x}^{19}}-7x+1]

на двучлен $Tleft( x right)=3x+1$.

Решение. Воспользуемся Следствием 1 из теоремы Безу. Для надёжности приравняем к нулю двучлен $Tleft( x right)$ и найдём $color{red}{a}$:

[begin{align}3x+1 &=0 \ x &=color{red}{-{1}/{3};} end{align}]

Подставим найденное $x=color{red}{-{1}/{3};}$ в многочлен $Pleft( x right)$ и найдём остаток:

[begin{align} Pleft( color{red}{-frac{1}{3}} right) &=3cdot {{left( color{red}{-frac{1}{3}} right)}^{20}}+{{left( color{red}{-frac{1}{3}} right)}^{19}}-7cdot left( color{red}{-frac{1}{3}} right)+1= \ &=frac{1}{{{3}^{19}}}-frac{1}{{{3}^{19}}}+frac{7}{3}+1=frac{10}{3} end{align}]

Ответ: ${10}/{3};$.

Пример 4. Иррациональные коэффициенты

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)={{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}+64]

на двучлен $Tleft( x right)=left( 1-sqrt{3} right)x+2$.

Решение. Вновь воспользуемся Следствием 1 из теоремы Безу. Приравняем двучлен $Tleft( x right)$ к нулю и найдём $color{red}{a}$:

[left( 1-sqrt{3} right)x+2=0]

Это линейное уравнение с иррациональными коэффициентами. Такое уравнение решается стандартно (см. урок «Линейные уравнения»):

[x=-frac{2}{1-sqrt{3}}=frac{2}{sqrt{3}-1}]

Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряжённое:

[x=frac{2color{blue}{left( sqrt{3}+1 right)}}{left( sqrt{3}-1 right) color{blue}{left( sqrt{3}+1 right)}}=frac{2left( sqrt{3}+1 right)}{2}= color{red}{sqrt{3}+1}]

Степень исходного многочлена: $deg Pleft( x right)=6$. Если подставить в такой многочлен иррациональное число, то это число придётся возводить в шестую степень. Это слишком долго и трудно, поэтому перепишем многочлен $Pleft( x right)$ так:

[begin{align} Pleft( x right) &=left( {{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}-64 right)+128= \ &={{left( {{x}^{2}}-4 right)}^{3}}+128 end{align}]

Мы выделили точный куб разности — классическую формулу сокращённого умножения. Как это работает — см. уроки «Формулы сокращённого умножения» и «Куб суммы и разности».

В такую формулу намного проще подставить $x=color{red}{sqrt{3}+1}$:

[begin{align}Pleft( color{red}{sqrt{3}+1} right) &={{left( {{left( color{red}{sqrt{3}+1} right)}^{2}}-4 right)}^{3}}+128= \ &={{left( {{left( sqrt{3} right)}^{2}}+2sqrt{3}+{{1}^{2}}-4 right)}^{3}}+128= \ &={{left( 2sqrt{3} right)}^{3}}+128= \ &=24sqrt{3}+128 end{align}]

Ответ получился некрасивым, но это и есть искомый остаток от деления.

Ответ: $24sqrt{3}+128$.

2. Разложение на множители

Сейчас будет немного теории, которая может показаться непонятной, но далее на примерах всё встанет на свои места.

Рассмотрим ещё раз деление многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

По теореме Безу мы легко найдём остаток $r=Pleft( color{red}{a} right)$. В частности, при $Pleft( color{red}{a} right)=0$ многочлен примет вид

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

А это значит, что многочлен $Pleft( x right)$ разделился на двучлен $x-color{red}{a}$ без остатка, и мы получили разложение на множители.

Кроме того, равенство $Pleft( color{red}{a} right)=0$ означает, что число $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. И это ещё одно замечательное следствие теоремы Безу.

Следствие 2. Корни многочлена и деление

Следствие 2. Число $x=color{red}{a}$ является корнем многочлена $Pleft( x right)$ тогда и только тогда, когда $Pleft( x right)$ делится без остатка на $left( x-color{red}{a} right)$.

На практике это означает, что для разложения многочлена на множители мы просто перебираем разные числа $x=color{red}{a}$ до тех пор, пока не окажется, что $Pleft( color{red}{a} right)=0$. В этот момент многочлен перепишется в виде

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Такой перебор особенно эффективен в сочетании со схемой Горнера (см. урок «Схема Горнера»). Потому что параллельно с вычислением $Pleft( color{red}{a} right)$ мы получаем ещё и коэффициенты нового многочлена $Qleft( x right)$.

Пример 10. Обычный многочлен

Разложите на множители многочлен

[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}-11x-6]

Решение. Для наглядности отметим синим цветом коэффициенты многочлена $Pleft( x right)$:

[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-11} right)cdot x+left( color{blue}{-6} right)]

Составим из них таблицу для схемы Горнера:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline{} & {} & {} & {} & {} & {}\ end{array}]

Все коэффициенты целые, поэтому логично проверять целые $x=color{red}{a}$, начиная с самых простых и маленьких чисел:

[x=pm 1; pm 2; pm 3; ldots ]

Проверим $x=color{red}{1}$ и $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline color{red}{1} & 1 & 4 & 1 & -10 & color{red}{-16}\ hline color{red}{-1} & 1 & 2 & -5 & -6 & color{green}{0}\ end{array}]

Проверка числа $x=color{red}{1}$ окончилась неудачей: остаток $r=color{red}{-16}$. Зато проверка $x=color{red}{-1}$ дала остаток $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ является корнем многочлена $Pleft( x right)$, и сам многочлен можно переписать так:

[begin{align}Pleft( x right) &=Qleft( x right)cdot left( x-left( color{red}{-1} right) right) \ &=left( {{x}^{3}}+2{{x}^{2}}-5x-6 right)left( x+1 right) end{align}]

Теперь разложим многочлен $Qleft( x right)$ по схеме Горнера. Проверим ещё раз число $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r}{} & 1 & 3 & -3 & -11 & -6\ hline color{red}{-1} & color{blue}{1} & color{blue}{2} & color{blue}{-5} & color{blue}{-6} & color{green}{0}\ hline color{red}{-1} & 1 & 1 & -6 & color{green}{0} & {}\ end{array}]

И вновь получили $r=color{green}{0}$. Исходный многочлен примет вид

[Pleft( x right)=left( {{x}^{2}}+x-6 right){{left( x-1 right)}^{2}}]

В первой скобке стоит квадратный трёхчлен. Разложим его на множители по теореме Виета:

[{{x}^{2}}+x-6=left( x+3 right)left( x-2 right)]

Итого окончательное разложение многочлена $Pleft( x right)$:

[left( x+3 right)left( x-2 right){{left( x-1 right)}^{2}}]

Однако это было довольно простое задание: теорема Безу использовалась лишь в качестве обоснования, почему вместо $Pleft( x right)$ мы пишем $Qleft( x right)left( x-color{red}{a} right)$.

Следующее задание будет намного интереснее.:)

Пример 11. Многочлен с двумя переменными

Разложите на множители многочлен

[Pleft( x,y right)=y{{x}^{2}}+3yx+x-4y-1]

Решение. Это многочлен от двух переменных. Он квадратный относительно переменной $x$ и линейный относительно $y$. Чтобы разложить такой многочлен на множители, сгруппируем его слагаемые относительно переменной $x$:

[Pleft( x,y right)= color{blue}{y}cdot {{x}^{2}}+left( color{blue}{3y+1} right)cdot x+left( color{blue}{-4y-1} right)]

Составляем таблицу:

[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline {} & {} & {} & {}\ end{array}]

Чтобы воспользоваться теоремой Безу, нужно найти такое $x=color{red}{a}$, чтобы $r=Pleft( color{red}{a} right)= color{green}{0}$. Поскольку в роли коэффициентов выступают выражения, содержащие переменную $y$, вновь рассмотрим самые простые варианты, которые приходят в голову:

[x=pm 1; pm y]

Проверим, например, $x=color{red}{1}$:

[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline color{red}{1} & y & 4y+1 & color{green}{0}\ end{array}]

Первая же попытка привела к успеху: $r=color{green}{0}$, поэтому $x=color{red}{1}$ — крень многочлена $Pleft( x,y right)$. Разложим этот многочлен на множители согласно Следствию 2 теоремы Безу:

[Pleft( x,y right)=left( ycdot x+4y+1 right)cdot left( x-color{red}{1} right)]

В первой скобке стоит новый многочлен, линейный по $x$ и по $y$. Его уже нельзя разложить на множители, поэтому ответ окончательный:

[Pleft( x,y right)=left( xy+4y+1 right)left( x-1 right)]

Важное замечание. Строго говоря, линейность многочлена по каждой переменной ещё не означает, что его нельзя разложить на множители. Простой контрпример:

[xy-x+y-1=left( x+1 right)left( y-1 right)]

Однако в нашем случае дальнейшее применение теоремы Безу и проверки по схеме Горнера не даст никаких новых множителей.

3. Целые корни многочленов

До сих пор мы подставляли числа наугад. И если удавалось найти число $x=color{red}{a}$ такое, что $Pleft( color{red}{a} right)=0$, мы объявляли его корнем, а многочлен $Pleft( x right)$ переписывали в виде

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Однако с помощью теоремы Безу можно значительно ускорить отыскание корней, отбросив заведомо неподходящие варианты. В этом нам поможет следующее утверждение.

Следствие 3. Целочисленные корни

Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:

[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.

Обратите внимание: старший коэффициент при ${{x}^{n}}$ равен единице. Именно поэтому многочлен $Pleft( x right)$ называется приведённым. Кроме того, все коэффициенты ${{a}_{n-1}},ldots ,{{a}_{0}}$ должны быть целыми числами.

И вот тогда целые корни следует искать среди делителей свободного члена ${{a}_{0}}$.

Пример 5. Простое уравнение

Решите уравнение

[{{x}^{3}}-2{{x}^{2}}-x+2=0]

Решение. Это приведённое кубическое уравнение с целыми коэффициентами. Рассмотрим многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-2} right)cdot {{x}^{2}}+left( color{blue}{-1} right)cdot x+color{blue}{2}]

Если у него есть целые корни, то по Следствию 3 теоремы Безу все они находятся среди делителей свободного члена ${{a}_{0}}=2$. Таких делителей всего четыре:

[x=pm 1; pm 2]

Подставим эти числа в схему Горнера:

[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-2} & color{blue}{-1} & color{blue}{2}\ hline color{red}{1} & 1 & -1 & -2 & color{green}{0}\ hline color{red}{-1} & 1 & -2 & color{green}{0} & {}\ end{array}]

Уже на первом шаге мы получили $r=color{green}{0}$. Следовательно, $x=color{red}{1}$ — корень многочлена $Pleft( x right)$, и сам многочлен можно переписать так:

[Pleft( x right)=left( {{x}^{2}}-x-2 right)left( x-color{red}{1} right)]

Впрочем, если учесть третью строку таблицы, то можно вообще записать

[Pleft( x right)=left( x-2 right)left( x-left( color{red}{-1} right) right)left( x-color{red}{1} right)]

В любом случае, корни многочлена, как и корни уравнения — это числа 2, 1 и −1.

Ответ: $x=1$, $x=-1$, $x=2$.

Формула понижения степени

Итак, с помощью теоремы Безу мы можем:

  1. Найти целый корень многочлена;
  2. Разложить исходный многочлен на множители;
  3. Далее искать корни многочлена степени на единицу меньше.

В самом деле, если $Pleft( color{red}{a} right)=0$, тогда по Следствию 2 теоремы Безу мы переписываем многочлен $Pleft( x right)$ в виде

[Pleft( x right)=Qleft( x right)left( x-color{red}{a} right)]

Далее мы ищем корни многочлена $Qleft( x right)$, степень которого на единицу меньше $Pleft( x right)$.

Этот приём называется понижением степени. Он помогает свести исходный многочлен к квадратному, корни которого легко считаются, например, через дискриминант.

Пример 6. Среднее уравнение

Решите уравнение

[{{x}^{3}}-3{{x}^{2}}-4x+12=0]

Решение. Это уравнение третьей степени. Достаточно найти один корень — далее останется решить квадратное уравнение. Заметим, что многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-4} right)cdot x+color{blue}{12}]

является приведённым с целочисленными коэффициентами. По Следствию 3 теоремы Безу все целые корни этого многочлена содержатся среди делителей свободного члена ${{a}_{0}}=12$. Таких делителей довольно много:

[x=pm 1; pm 2; pm 3; pm 4; pm 6; pm 12]

Впрочем, нам достаточно найти всего один корень. Воспользуемся схемой Горнера:

[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-3} & color{blue}{-4} & color{blue}{12}\ hlinecolor{red}{1} & 1 & -2 & -7 & color{red}{5}\ hlinecolor{red}{-1} & 1 & -4 & 0 & color{red}{12}\ hlinecolor{red}{2} & 1 & -1 & -6 & color{green}{0}\ end{array}]

Проверка закончилась неудачей для $x=color{red}{1}$ и $x=color{red}{-1}$. Но для $x=color{red}{2}$ мы нашли то, что искали: остаток $r=color{green}{0}$. Следовательно, $x=color{red}{2}$ — корень многочлена $Pleft( x right)$.

Разложим многочлен на множители согласно теореме Безу:

[Pleft( x right)=left( {{x}^{2}}-x-6 right)left( x-color{red}{2} right)]

В первой скобке стоит квадратный трёхчлен. Его корни легко найти по теореме Виета:

[Pleft( x right)=left( x-3 right)left( x+2 right)left( x-2 right)]

Приравниваем полученное произведение к нулю и решаем уравнение: $x=3$, $x=-2$, $x=2$.

Ответ: $x=2$, $x=-2$, $x=3$.

Пример 7. Сложное уравнение

Решите уравнение

[{{x}^{4}}-{{x}^{3}}-5{{x}^{2}}+3x+2=0]

Решение. Слева приведённый многочлен с целочисленными коэффициентами, поэтому все целые корни находятся среди делителей свободного члена ${{a}_{0}}=2$:

[x=pm 1; pm 2]

Достаточно подобрать два корня — далее уравнение сведётся к квадратному. Воспользуемся схемой Горнера:

[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{-1} & color{blue}{-5} & color{blue}{3} & color{blue}{2}\ hlinecolor{red}{-1} & 1 & -2 & -3 & 6 & color{red}{-4}\ hlinecolor{red}{1} & 1 & 0 & -5 & -2 & color{green}{0}\ hlinecolor{red}{-2} & 1 & -2 & -1 & color{green}{0} & {}\ end{array}]

Получили корни $x=color{red}{1}$ и $x=color{red}{-2}$. Разложим многочлен на множители:

[left( {{x}^{2}}-2x-1 right)left( x-color{red}{1} right)left( x-left( color{red}{-2} right) right)=0]

Решим квадратного уравнение из первой скобки:

[{{x}^{2}}-2x-1=0]

Дискриминант положителен:

[begin{align} D &={{left( -2 right)}^{2}}-4cdot 1cdot left( -1 right)= \ &=4+4=8 end{align}]

Следовательно, уравнение имеет два корня:

[x=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]

Ответ: $x=1$, $x=-2$, $x=1pm sqrt{2}$.

4. Рациональные корни

До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.

Рассмотрим уравнение

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.

Следствие 4. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.

Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

имеют вид $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.

Пример 8. Простой многочлен

Найдите рациональные корни многочлена

[Pleft( x right)=2{{x}^{5}}-{{x}^{4}}+4x-2]

Решение. Делители свободного члена ${{a}_{0}}=-2$:

[p=pm 1; pm 2]

Положительные делители старшего коэффициента ${{a}_{4}}=2$:

[q=1; 2]

Возможные рациональные корни многочлена $Pleft( x right)$ по Следствию 4 теоремы Безу:

[x=pm 1; pm 2; pm {1}/{2};]

Проверять числа $x=color{red}{pm 1}$ нет смысла, поскольку все коэффициенты многочлена $Pleft( x right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.

Остальные числа проверим по схеме Горнера:

[begin{array}{r|r|r|r|r|r|r}{} & color{blue}{2} & color{blue}{-1} & color{blue}{0} & color{blue}{0} & color{blue}{4} & color{blue}{-2}\ hlinecolor{red}{2} & 2 & 3 & 6 & 12 & 28 & color{red}{54}\ hlinecolor{red}{-2} & 2 & -5 & 10 & -20 & 44 & color{red}{-90}\ hline color{red}{{1}/{2};} & 2 & 0 & 0 & 0 & 4 & color{green}{0}\ hline color{red}{-{1}/{2};} & 2 & -2 & 1 & -{1}/{2}; & {17}/{4}; & color{red}{-{33}/{8};}\ end{array}]

Подошло лишь одно число: $x=color{red}{{1}/{2};}$. Следовательно, многочлен имеет лишь один рациональный корень.

Ответ: $x={1}/{2};$.

Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами. При таких обстоятельствах получить $r=color{green}{0}$ уже невозможно.

Пример 9. Сложный многочлен

Найдите рациональные корни многочлена

[Pleft( x right)=3{{x}^{7}}+2{{x}^{6}}-5{{x}^{5}}+3{{x}^{3}}-{{x}^{2}}-7x+5]

Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:

[p=pm 1; pm 5]

Положительные делители старшего коэффициента ${{a}_{7}}=3$:

[q=1; 3]

Кандидаты в корни согласно Следствию 4 теоремы Безу:

[x=pm 1; pm 5; pm {1}/{3};; pm {1}/{5};]

Всего восемь кандидатов. Проверим их все по схеме Горнера:

[begin{array}{r|r|r|r|r|c|c|c|c}{} & color{blue}{3} & color{blue}{2} & color{blue}{-5} & color{blue}{0} & color{blue}{3} & color{blue}{-1} & color{blue}{-7} & color{blue}{5}\ hlinecolor{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & color{green}{0}\ hlinecolor{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & color{red}{-6} & {}\ hlinecolor{red}{5} & 3 & 20 & 100 & color{red}{500} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-5} & 3 & -10 & 50 & color{red}{-250} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{1}/{3};} & 3 & 6 & 2 & color{red}{{2}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{1}/{3};} & 3 & 4 & color{red}{-{4}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{5}/{3};} & 3 & 10 & color{red}{{50}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{5}/{3};} & 3 & 0 & 0 & 0 & 3 & -3 & color{green}{0} & {}\ end{array}]

Обратите внимание: для чисел $x=color{red}{5}$ и $x=color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти.

При проверке $x=color{red}{{1}/{3};}$, $x=color{red}{-{1}/{3};}$ и $x=color{red}{{5}/{3};}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.

Итого найдены два рациональных корня: $x=color{red}{1}$ и $x=color{red}{-{5}/{3};}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)

5. Доказательства

Рассмотрим доказательства всех ключевых утверждений сегодняшнего урока.

5.1. Теорема Безу

Мы сформулировали эту теорему в самом начале урока:

Терема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x-color{red}{a}$ равен значению этого многочлена в точке $x=color{red}{a}$:

[r=Pleft( color{red}{a} right)]

Доказательство. Разделим многочлен $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

Такое представление всегда однозначно (см. урок «Деление многочленов с остатком»). Здесь многочлен $Qleft( x right)$ — неполное частное, $r$ — остаток, причём

[begin{align}deg r lt deg left( x-color{red}{a} right) &=1 \ deg r &=0 \ end{align}]

Другими словами, остаток $r$ — это просто число.

Теперь найдём значение $Pleft( x right)$ в точке $x=color{red}{a}$:

[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}-color{red}{a} right)+r=r]

Теорема Безу доказана. Однако её доказательство опирается на единственность деления с остатком.

5.2. Целочисленные корни

Целочисленные корни приведённого многочлена с целыми коэффициентами следует искать среди делителей свободного члена.

Следствие 3. Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:

[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.

Доказательство. Пусть $color{red}{b}in mathbb{Z}$ — корень многочлена $Pleft( x right)$, т.е. $Pleft( color{red}{b} right)=0$. Подставим число $x=color{red}{b}$ в формулу многочлена и получим уравнение:

[{color{red}{b}^{n}}+{{a}_{n-1}}{color{red}{b}^{n-1}}+ldots +{{a}_{1}}color{red}{b}+{{a}_{0}}=0]

Перенесём последнее слагаемое вправо, а слева из оставшихся слагаемых вынесем множитель $color{red}{b}$ за скобку:

[color{red}{b}cdot left( {color{red}{b}^{n-1}}+{{a}_{n-1}}{color{red}{b}^{n-2}}+ldots +{{a}_{1}} right)=-{{a}_{0}}]

Поскольку $-{{a}_{0}}in mathbb{Z}$, а слева стоят два целочисленных множителя, получаем, что число $-{{a}_{0}}$ делится на $color{red}{b}$. Следовательно, свободный член ${{a}_{0}}$ тоже делится на $color{red}{b}$, что и требовалось доказать.

5.3. Рациональные корни

Рассмотрим уравнение

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.

Утверждение. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения $Pleft( x right)=0$, то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.

Доказательство. Подставим число $x=color{red}{p}/color{blue}{q};$ в исходное уравнение. Поскольку $x=color{red}{p}/color{blue}{q};$ — корень, уравнение обратится в верное числовое равенство:

[{{a}_{n}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n}}+{{a}_{n-1}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n-1}}+ldots +{{a}_{1}}cdot frac{color{red}{p}}{color{blue}{q}}+{{a}_{0}}=0]

Домножим обе части на ${color{blue}{q}^{n}}$. Получим

[{{a}_{n}}{color{red}{p}^{n}}+{{a}_{n-1}}{color{red}{p}^{n-1}}color{blue}{q}+ldots +{{a}_{1}}color{red}{p}{color{blue}{q}^{n-1}}+{{a}_{0}}{color{blue}{q}^{n}}=0]

Перенесём последнее слагаемое ${{a}_{0}}{color{blue}{q}^{n}}$ вправо, а в левой части из оставшихся слагаемых вынесем множитель $color{red}{p}$ за скобку:

[color{red}{p}left( {{a}_{n}}{color{red}{p}^{n-1}}+{{a}_{n-1}}{color{red}{p}^{n-2}}color{blue}{q}+ldots +{{a}_{1}}{color{blue}{q}^{n-1}} right)=-{{a}_{0}}{color{blue}{q}^{n}}]

Слева и справа от знака равенства стоят целые числа, поскольку все слагаемые и множители являются целыми. Мы видим, что левая часть делится на $color{red}{p}$. Следовательно, правая часть тоже делится на $color{red}{p}$:

[-{{a}_{0}}{color{blue}{q}^{n}} vdots color{red}{p}]

По условию теоремы дробь $color{red}{p}/color{blue}{q};$ несократима. Следовательно, числа $color{blue}{q}$ и $color{red}{p}$ не имеют общих делителей, и единственный возможный вариант — это когда ${{a}_{0}}$ делится на $color{red}{p}$.

Аналогично доказывается, что старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$. Теорема доказана.

Вот и всё.:)

Смотрите также:

  1. Схема Горнера
  2. Деление многочленов уголком
  3. Теорема Виета
  4. Задача B3 — работа с графиками
  5. Метод коэффициентов, часть 2
  6. Нестандартная задача B2: студенты, гонорары и налоги
Источник

В данной публикации мы рассмотрим теорему Безу, с помощью которой можно найти остаток от деления многочлена на двучлен, а также, научимся применять ее на практике для решения примеров.

  • Формулировка теоремы Безу

  • Решение примеров

Формулировка теоремы Безу

Остаток от деления многочлена P(x) на двучлен (x-a) равняется P(a).

Pn(x) = a0xn + a1xn-1 + … + an-1x + an

Следствие из теоремы:

Число a является корнем многочлена P(x) исключительно в том случае, если многочлен P(x) без остатка делится на двучлен (x-a).

Из этого следствия вытекает следующее утверждение: множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения P(x)=0.

Решение примеров

Пример 1
Найдите остаток от деления многочлена 5x2 – 3x + 7 на двучлен (x – 2).

Решение
Чтобы найти остаток от деления, согласно теореме Безу, требуется найти значение многочлена в точке a (т.е. вместо x подставляем значение a, которое в нашем случае равняется числу 2).
5 ⋅ 22 – 3 ⋅ 2 + 7 = 21.

Т.е. остаток равен 21.

Пример 2
Используя теорему Безу выясните, делится ли многочлен 3x4 + 15x – 11 на двучлен (x + 3) без остатка.

Решение
В данном случае a = -3. Подставляем это число вместо x в многочлен и получаем:
3 ⋅ (-3)4 + 15 ⋅ (-3) – 11 = 187.

Это значит, что деление без остатка невозможно.

Пример 3
Выясните, при каком значении y, многочлен x23 + yx + 16 без остатка делится на двучлен (x + 1).

Решение
Применив теорему Безу, находим нулевой остаток от деления:
(-1)23 + y ⋅ (-1) + 16 = 0
-1 – y + 16 = 0
y = 15

Таким образом, при y, равном 15, остаток будет равен 0.

Источник

Деление многочленов — операция деления с остатком в евклидовом кольце многочленов от одной переменной над некоторым полем. Наивный алгоритм, реализующий эту операцию, представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов f(x) и g(x), g(x) ne 0, существуют единственные многочлены q(x) и r(x), такие что

frac{f(x)}{g(x)}=q(x) + frac{r(x)}{g(x)},

причем r(x) имеет более низкую степень, чем g(x).

Целью алгоритмов деления многочленов является нахождение частного q(x) и остатка r(x) для заданных делимого f(x) и ненулевого делителя g(x)[1].

Постановка задачи[править | править код]

Задача о делении многочленов с остатком может быть сформулирована в следующих эквивалентных постановках[2].

Частное и остаток[править | править код]

Многочлены {displaystyle S(x)=s_{0}+s_{1}x+dots +s_{m}x^{m}} степени m и {displaystyle T(x)=t_{0}+t_{1}x+dots +t_{n}x^{n}} степени n, заданы своими коэффициентами. Необходимо найти частное {displaystyle Q(x)=q_{0}+q_{1}x+dots +q_{m-n}x^{m-n}} и остаток {displaystyle R(x)=r_{0}+r_{1}x+dots +r_{n-1}x^{n-1}}, такие что[2]

{displaystyle S(x)=T(x)Q(x)+R(x).} (1)

Определённые таким образом многочлены Q(x) и R(x) единственны — если допустить, что у уравнения (1) существует два решения {displaystyle Q_{1}(x),R_{1}(x)} и {displaystyle Q_{2}(x),R_{2}(x)}, то

{displaystyle T(x)left(Q_{1}(x)-Q_{2}(x)right)=R_{1}(x)-R_{2}(x),}

из чего следует, что либо {displaystyle Q_{1}(x)=Q_{2}(x)}, что также влечёт {displaystyle R_{1}(x)=R_{2}(x)}, либо степень {displaystyle R_{1}(x)-R_{2}(x)} не меньше степени T(x), что невозможно по определению R(x)[3].

Матричная постановка[править | править код]

Данную задачу можно переписать в матричном виде, если считать, что даны {displaystyle s_{0},s_{1},dots ,s_{m}} и {displaystyle t_{0},t_{1},dots ,t_{n}}, а посчитать нужно {displaystyle q_{0},q_{1},dots ,q_{m-n}} и {displaystyle r_{0},r_{1},dots ,r_{n-1}} такие что[2]

{displaystyle {begin{bmatrix}s_{m}\vdots \s_{n+1}\s_{n}\s_{n-1}\vdots \s_{0}end{bmatrix}}={begin{bmatrix}t_{n}&dots &0&0\vdots &ddots &vdots &vdots \dots &dots &t_{n}&0\dots &dots &t_{n-1}&t_{n}\dots &dots &t_{n-2}&t_{n-1}\vdots &ddots &vdots &vdots \0&dots &0&t_{0}end{bmatrix}}{begin{bmatrix}q_{m-n}\vdots \q_{1}\q_{0}end{bmatrix}}+{begin{bmatrix}0\vdots \0\0\r_{n-1}\vdots \r_{0}end{bmatrix}}_{textstyle .}} (2)

Обратная тёплицева матрица[править | править код]

В силу того, что {displaystyle R(x)=S(x)-T(x)Q(x)}, для решения задачи достаточно найти {displaystyle q_{m-n},dots ,q_{0}} по первым {displaystyle m-n+1} уравнениям системы. Если рассматривать только эти уравнения, задача принимает вид

{displaystyle {begin{bmatrix}s_{m}\vdots \s_{n+1}\s_{n}end{bmatrix}}={begin{bmatrix}t_{n}&dots &0&0\vdots &ddots &vdots &vdots \dots &dots &t_{n}&0\dots &dots &t_{n-1}&t_{n}end{bmatrix}}{begin{bmatrix}q_{m-n}\vdots \q_{1}\q_{0}end{bmatrix}}_{textstyle .}} (3)

Матрица данной системы уравнений является нижнетреугольной и тёплицевой, составленной из старших коэффициентов {displaystyle T(x)} и нулей, а решение системы эквивалентно нахождению обратной к ней[2].

Обратный многочлен по модулю[править | править код]

Пусть {displaystyle S^{R}(x)=x^{m}S(x^{-1})=s_{m}+s_{m-1}x+dots +s_{0}x^{m}} и {displaystyle T^{R}(x)=x^{n}T(x^{-1})=t_{n}+t_{n-1}x+dots +t_{0}x^{n}} — многочлены, полученные из S(x) и T(x) разворотом последовательности коэффициентов. Систему уравнений (3) можно сформулировать как

{displaystyle S^{R}(x)equiv T^{R}(x)Q^{R}(x){pmod {x^{k}}},}

где {displaystyle k=m-n+1}, а {displaystyle {bmod {x}}^{m-n}} означает, что остатки от деления многочленов {displaystyle S^{R}(x)} и {displaystyle T^{R}(x)Q^{R}(x)} на x^{k} равны. Деление многочлена P(x) на x^{k} может быть представлено как {displaystyle P(x)=x^{k}Q(x)+R(x)}, поэтому остаток R(x) равен многочлену, полученному из первых k коэффициентов P(x), то есть,

{displaystyle R(x)=p_{0}+p_{1}x+dots +p_{k-1}x^{k-1}.}

Если многочлены {displaystyle S^{R}(x)} и {displaystyle T^{R}(x)} известны, то {displaystyle Q^{R}(x)equiv S^{R}(x)T^{R}(x)^{-1}{pmod {x^{k}}}}, где {displaystyle T^{R}(x)^{-1}} — обратный к {displaystyle T^{R}(x)} многочлен в кольце остатков по модулю x^{k}. Таким образом, поиск Q(x) может быть сведён к нахождению {displaystyle V(x)=v_{0}+v_{1}x+dots +v_{k}x^{k}}, такого что

{displaystyle V^{R}(x)equiv T^{R}(x)^{-1}{pmod {x^{k}}}.} (4)

Данная постановка позволяет также находить обратную матрицу в системе (3):

Пусть T — матрица размера k из (3). Тогда {displaystyle T^{-1}} — нижнетреугольная тёплицева матрица, первый столбец которой равен {displaystyle {begin{bmatrix}v_{k-1}&v_{k-2}&dots &v_{0}end{bmatrix}}^{T}}, где {displaystyle v_{0},dots ,v_{k-1}} — коэффициенты V(x) из (4).

Доказательство

Система (3) эквивалентна уравнению {displaystyle S^{R}(x)equiv T^{R}(x)Q^{R}(x){pmod {x^{k}}}}. Соответственно, система

{displaystyle {begin{bmatrix}v_{m-n}&dots &0&0\vdots &ddots &vdots &vdots \v_{1}&dots &v_{m-n}&0\v_{0}&dots &v_{m-n-1}&v_{m-n}end{bmatrix}}{begin{bmatrix}s_{m}\vdots \s_{n+1}\s_{n}end{bmatrix}}={begin{bmatrix}q_{m-n}\vdots \q_{1}\q_{0}end{bmatrix}}}

может быть представлена в виде {displaystyle V^{R}(x)S^{R}(x)equiv Q^{R}(x){pmod {x^{k}}}}, что в случае (4) эквивалентно системе (3).■

В силу произвольности многочлена T(x), определяющего элементы T, данный факт позволяет находить обратную к произвольной тёплицевой нижнетреугольной матрице[2].

Формальные степенные ряды[править | править код]

Уравнение {displaystyle S^{R}(x)=T^{R}(x)Q^{R}(x)} можно рассматривать не только по модулю {displaystyle x^{m-n}}, но и как равенство в кольце формальных степенных рядов. Пусть {displaystyle s(x)} и t(x) — формальные степенные ряды, совпадающие с многочленами {displaystyle S^{R}(x)} и {displaystyle T^{R}(x)}. Если в таких терминах найти формальный ряд

{displaystyle q(x)={frac {s(x)}{t(x)}},} (5)

то его коэффициенты при младших {displaystyle m-n+1} степенях будут соответствовать искомому многочлену {displaystyle Q^{R}(x)}. Такой подход также позволяет рассмотреть задачу (2) как систему с бесконечно продлённой тёплицевой матрицей и бесконечно продлённым столбцом q, в которой исключён столбец остатков r. Решение первых h строк такой системы даст первые h коэффициентов ряда q(x), а именно {displaystyle q_{m-n},q_{m-n-1},dots ,q_{m-n-h+1}}. В то же время, работа со степенными рядами в целом, при которой интерес представляют только первые h коэффициентов ряда (например, из-за ограниченности доступной памяти), эквивалентна работе с многочленами, операции над которыми производятся в кольце остатков по модулю {displaystyle x^{h}}[4]. В частности, поиск первых h коэффициентов q(x) эквивалентен решению уравнения {displaystyle s(x)equiv t(x)q(x){pmod {x^{h}}}}[2].

Методы решения[править | править код]

Деление столбиком[править | править код]

В ходе алгоритма, коэффициенты при старших степенях S(x) последовательно зануляются за счёт вычитания из него T(x), умноженного на некоторую степень x с коэффициентами, которые затем образуют частное Q(x). Изначально, коэффициент {displaystyle q_{m-n}} определяется равным {textstyle {frac {s_{m}}{t_{n}}}}. Если разложить {displaystyle Q(x)=q_{m-n}x^{m-n}+Q'(x)}, то

{displaystyle S(x)=T(x)(q_{m-n}x^{m-n}+Q'(x))+R(x).}

С помощью замены {displaystyle S'(x)=S(x)-q_{m-n}x^{m-n}T(x)}, данное уравнение приобретает вид

{displaystyle S'(x)=T(x)Q'(x)+R(x),}

аналогичный уравнению (1). При этом m-й коэффициент {displaystyle S'(x)}, по определению {displaystyle q_{m-n}}, равен {displaystyle 0}, поэтому степень {displaystyle S'(x)} будет меньше, чем степень S(x). Процедура повторяется, пока степень {displaystyle S'(x)} не станет меньше степени T(x), что будет означать, что очередной {displaystyle S'(x)} равен R(x) и для него {displaystyle Q'(x)=0}[3].

Пример[править | править код]

Пусть {displaystyle S(x)=x^{3}-12x^{2}-42} и {displaystyle T(x)=x-3}. Для данных многочленов, деление столбиком S(x) на T(x) может быть записано как

{displaystyle {begin{array}{rr}-{begin{array}{llll}x^{3}&-12x^{2}&{color {gray}+0x}&-42\x^{3}&-3x^{2}&&\hline end{array}}&{begin{array}{|l}x-3\hline x^{2}-9x-27end{array}}\-{begin{array}{lll}-9x^{2}&&-42\-9x^{2}&+27x&\hline end{array}}&\-{begin{array}{ll}-27x&-42\-27x&+81\hline end{array}}&\-123end{array}}}

Таким образом,

{displaystyle {frac {x^{3}-12x^{2}-42}{x-3}}=x^{2}-9x-27-{frac {123}{x-3}},}

то есть, многочлен {displaystyle Q(x)=x^{2}-9x-27} — частное деления, а {displaystyle R(x)=-123} — остаток.

Алгоритм Зивекинга — Кона[править | править код]

В 1972 году Мальте Зивекинг предложил алгоритм для поиска решения B(x) уравнения {displaystyle A(x)cdot B(x)=C(x){pmod {x^{n+1}}}} при заданных A(x) и C(x)[5]. В 1974 году Кон Сянчжун[en] показал, что при {displaystyle C(x)=1} алгоритм представляет собой итерацию метода Ньютона для {displaystyle f(V)=V^{-1}-A}[6]. При таком подходе, итерация принимает вид

{textstyle V_{k+1}=V_{k}-{frac {f(V_{k})}{f'(V_{k})}}=2V_{k}-AV_{k}^{2},}

Где {displaystyle f'(V_{k})=-V_{k}^{-2}} обозначает производную функции {displaystyle f(V)} в точке V_{k}. Для оценки точности алгоритма, можно оценить разность

{textstyle V_{k+1}-B=A(2V_{k}A^{-1}-V_{k}^{2}-A^{-2})=-A(V_{k}-B)^{2},}

из чего следует, что если {displaystyle V_{k}-B} делится на {displaystyle x^{t}} (что равносильно тому, что первые t коэффициентов V_{k} определены корректно), то {displaystyle V_{k+1}-B} будет делиться уже на {displaystyle x^{2t}}. Таким образом, при начальном условии {displaystyle V_{0}=b_{0}=a_{0}^{-1}}, каждая итерация удваивает число точно определённых коэффициентов B(x). Поэтому для вычисления {displaystyle A(x)^{-1}{pmod {x^{n+1}}}} достаточно O(log n) итераций. Применение быстрого преобразования Фурье к умножению многочленов в формуле выше позволяет прийти к итоговому времени работы O(nlog n), что существенно улучшает оценку для обычного длинного умножения[7].

Пример[править | править код]

Пусть {displaystyle S(x)=x^{3}-12x^{2}-42} и {displaystyle T(x)=x-3}. В силу (4), необходимо найти {displaystyle Q^{R}(x)=(-42x^{3}-12x+1)(-3x+1)^{-1}{pmod {x^{3}}}}. Обратный многочлен {displaystyle V(x)=(-3x+1)^{-1}{pmod {x^{3}}}} ищется следующим образом:

  1. Начальное приближение определяется как {textstyle V_{0}={frac {1}{T^{R}(0)}}=1};
  2. Первое приближение определяется как {displaystyle V_{1}=V_{0}(2-(-3x+1)V_{0})=3x+1};
  3. Второе приближение определяется как {displaystyle V_{2}=(3x+1)(2-(-3x+1)(3x+1))=(3x+1)(9x^{2}+1)=27x^{3}+9x^{2}+3x+1}.

В силу свойств метода Ньютона, первые 2^{2}=4 коэффициента {displaystyle V_{2}(x)} определены верно. Так как дальнейшие вычисления происходят по модулю x^{3}, коэффициенты при более высоких степенях можно отбросить. Отсюда

{displaystyle Q^{R}(x)equiv (-12x+1)(9x^{2}+3x+1)equiv -108x^{3}-27x^{2}-9x+1equiv -27x^{2}-9x+1{pmod {x^{3}}},}

в силу чего {displaystyle Q(x)=x^{2}-9x-27}.

Анализ алгоритмов[править | править код]

Для оценки эффективности различных методов используется арифметическая схемная сложность[en] — суммарное количество операций сложения, умножения, вычитания и деления над полем комплексных чисел, которые необходимо произвести в ходе работы алгоритма. Также оценивается количество параллельных шагов, требуемых для многопроцессорной реализации алгоритма, в предположении, что каждый процессор на любом шаге может выполнять не более одной операции[7].

Каждая итерация алгоритма деления столбиком заключается в вычитании смещённого на некоторую величину T(x) из S(x), что может быть выполнено за O(n). Так как степень S(x), изначально равная m, уменьшается, пока она не станет меньше n, общее время работы алгоритма можно оценить как {displaystyle O(kn)}, где k=m-n[2].

См. также[править | править код]

  • Теорема Безу
  • Правило Руффини
  • Базис Грёбнера
  • Наибольший общий делитель двух многочленов[en]
  • Синтетическое деление[en]

Примечания[править | править код]

  1. ↑
    Сканави М. И. Элементарная математика. — 2-е изд., перераб. и доп. — М.: Наука, 1972. — С. 142—147. — 592 с.
  2. ↑ 1 2 3 4 5 6 7 Bini, Pan, 1986, pp. 184—186
  3. ↑ 1 2 Knuth, 1997, pp. 420—421
  4. ↑ Knuth, 1997, pp. 525—533
  5. ↑ Sieveking, 1972
  6. ↑ Kung, 1974
  7. ↑ 1 2 Bini, Pan, 1986, pp. 186—188

Литература[править | править код]

  • Bini D., Pan V. Polynomial division and its computational complexity (англ.) // Journal of Complexity — Elsevier BV, 1986. — Vol. 2, Iss. 3. — P. 179—203. — ISSN 0885-064X; 1090-2708 — doi:10.1016/0885-064X(86)90001-4
  • Knuth D. The Art of Computer Programming (англ.): Seminumerical Algorithms — 3 — Addison-Wesley, 1997. — Vol. 2. — 784 p. — ISBN 978-0-201-89684-8
  • Kung H. T. On computing reciprocals of power series (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1974. — Vol. 22, Iss. 5. — P. 341—348. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01436917
  • Sieveking M. An algorithm for division of powerseries (англ.) // Computing — Springer Science+Business Media, 1972. — Vol. 10, Iss. 1-2. — P. 153—156. — ISSN 0010-485X; 1436-5057 — doi:10.1007/BF02242389
  • Schönhage A. Variations on Computing Reciprocals of Power Series (англ.) // Algorithms Seminar, 2000-2001 / F. Chyzak — Institut National de Recherche en Informatique et en Automatique, 2001. — P. 81—84. — 197 p.
Источник

Продолжаем изучать многочлены. В данном уроке мы научимся их делить.

Деление многочлена на одночлен

Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.

Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:

многочлен деление пр 1

Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:

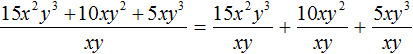
многочлен деление пр 1 шаг 2

Получили привычное для нас деление одночленов. Выполним это деление:

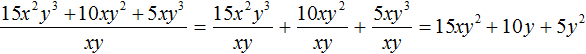многочлен деление пр 1 решениеТаким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.

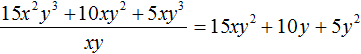
многочлен деление пр 1 решение шаг 2

При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.

В нашем примере произведение полученного многочлена 15xy2 + 10y + 5y2 и делителя xy должно быть равно многочлену 15x2y3 + 10xy2 + 5xy3, то есть исходному делимому. Проверим так ли это:

(15xy2 + 10y + 5y2)xy = 15x2y3 + 10xy2 + 5xy3

Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.

Например, чтобы сложить дроби одна четвертая, две четвертых и три четвёртых нужно записать следующее выражение:

деление многочленов пример 3

Если мы вычислим выражение деление многочленов рисунок 3, то получим дробь 6 на 4, значение которой равно 1,5.

При этом выражение деление многочленов рисунок 3 мы можем вернуть в исходное состояние деление многочленов рисунок 4, и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5

дмо рис 1

Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x

дмо рис 4

Вычисление каждой дроби даст в результате многочлен a + b + c

дмо рис 3

Пример 2. Разделить многочлен 8m3n + 24m2n2 на одночлен 8m2n

деление многочленов пример 2

Пример 3. Разделить многочлен 4c2d − 12c4d3 на одночлен −4c2d

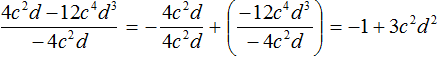
деление многочленов пример 4

Деление одночлена на многочлен

Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.

Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.

дм рис 4

Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.

Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.

Например, найдём значение выражения деление многочленов пример 5 при x = 2.

Выражение деление многочленов пример 5 представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:

деление многочленов пример 5 решение

Деление многочлена на многочлен

Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x2 + 8x + 15

(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15

(x + 5)(x + 3) = x2 + 8x + 15

Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.

Тогда согласно этому правилу, деление полученного нами многочлена x2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.

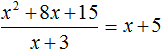
дмм рис 4

Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.

Выполним уголком деление многочлена x2 + 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.

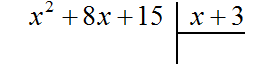
дм пр 1 шаг 1

В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.

Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.

Сейчас наша задача найти первый член нового многочлена. Как это сделать?

Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:

дмм рис 5

Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.

Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.

Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.

Если первый член делимого (в нашем случае это x2) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:

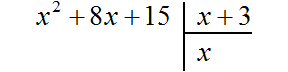
дм пр 1 шаг 2

Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x2 + 3x. Записываем этот многочлен под делимым x2+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:

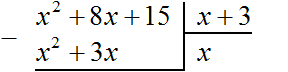
дм пр 1 шаг 3

Теперь из делимого x2 + 8x + 15 вычитаем x2 + 3x. Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x

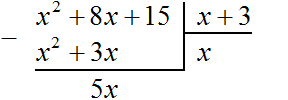
дм пр 1 шаг 4

Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:

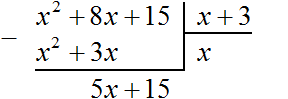
дм пр 1 шаг 5

Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)

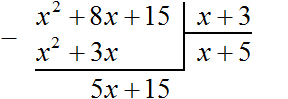
дм пр 1 шаг 6

Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15

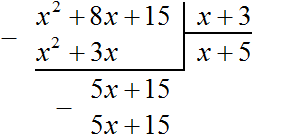
дм пр 1 шаг 7

Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.

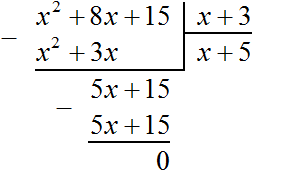
дм пр 1 шаг 8

На этом деление завершено.

После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x2 + 8x + 15

(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15

Пример 2. Разделить многочлен x2 − 8x + 7 на многочлен x − 7

Записываем уголком данное деление:

дм пр 2 шаг 1

Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:

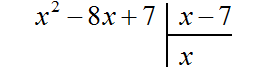
дм пр 2 шаг 2

Умножаем x на x − 7, получаем x2 − 7x. Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:

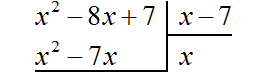
дм пр 2 шаг 3

Вычитаем из x2 − 8x + 7 многочлен x2 − 7x. При вычитании x2 из x2 получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7

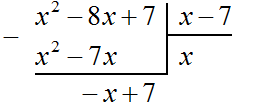
дм пр 2 шаг 4

Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:

дм пр 2 шаг 4 1

Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:

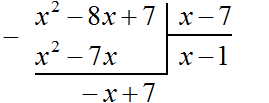
дм пр 2 шаг 5

Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7

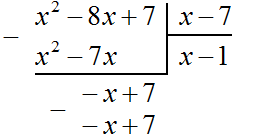
дм пр 2 шаг 6

Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0

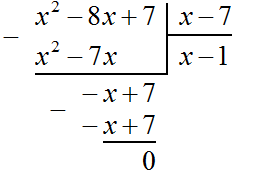
дм пр 2 шаг 7

Деление завершено. Таким образом, частное от деления многочлена x2 − 8x + 7 на многочлен x − 7 равно x − 1

дмм пример 2 шаг последний

Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x2 − 8x + 7

(x − 1)(x − 7) = x2 − x − 7x + 7 = x2 − 8x + 7

Пример 3. Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3

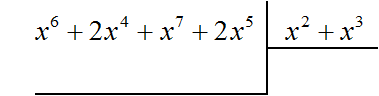
дмм пример 3 шаг 1

Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x4

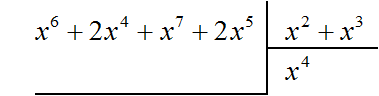
дмм пример 3 шаг 2

Умножаем x4 на делитель x2 + x3 и полученный результат записываем под делимым. Если x4 умножить на x2 + x3 получится x6 + x7. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:

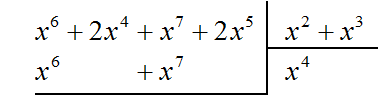
дмм пример 3 шаг 3

Теперь из делимого вычитаем многочлен x6 + x7. Вычитание x6 из x6 даст в результате 0. Вычитание x7 из x7 тоже даст в результате 0. Оставшиеся члены 2x4 и 2x5 снесём:

дмм пример 3 шаг 4

Получилось новое делимое 2x4 + 2x5. Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7

дмм пример 3 вычитание скобки

Разделим многочлен 2x4 + 2x5 на делитель x2 + x3. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x2. Записываем этот член в частном:

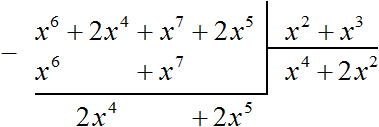
дмм пример 3 шаг 5

Умножаем 2x2 на делитель x2 + x3 и полученный результат записываем под делимым. Если 2x2 умножить на x2 + x3 получится 2x4 + 2x5. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:

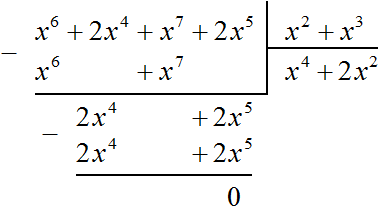
дмм пример 3 шаг 6

Вычитание многочлена 2x4 + 2x5 из многочлена 2x4 + 2x5 дало в результате 0, поэтому деление успешно завершилось.

В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.

Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.

Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x6 + 2x4 + x7 + 2x5 упорядочить в порядке убывания степеней, то получим многочлен x7 + x6 + 2x5 + 2x4. А если члены многочлена x2 + x3 упорядочить в порядке убывания степеней, то получим многочлен x3 + x2

Тогда деление уголком многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 примет следующий вид:

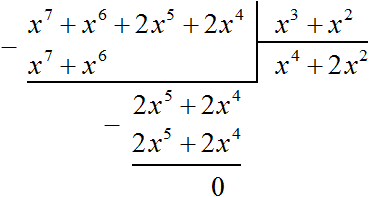
дмм пример 4 решение

Деление завершено. Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2

дмм пример 3 шаг последний

Выполним проверку. Умножим частное x4 + 2x2 на делитель x2 + x3. У нас должен получиться многочлен x6 + 2x4 + x7 + 2x5

(x4 + 2x2)(x2 + x3) = x4 (x2 + x3) + 2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5

При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.

Перепишем умножение (x4 + 2x2)(x2 + x3) упорядочив члены многочленов в порядке убывания степеней.

(x4 + 2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2) = x7 + x6 + 2x5 + 2x4

Пример 4. Разделить многочлен 17x2 − 6x4 + 5x3 − 23x + 7 на многочлен 7 − 3x2 − 2x

Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:

дмм пример 5

Значит,

дм рис 5

Пример 5. Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2

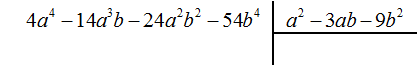
дмм пример 5 шаг 1

Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a2. Записываем 4a2 в частном:

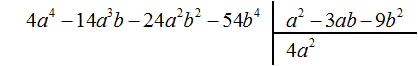
дмм пример 5 шаг 2

Умножим 4a2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым:

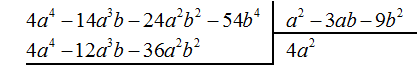
дмм пример 5 шаг 3

Вычтем из делимого полученный многочлен 4a4 − 12a3b − 36a2b2

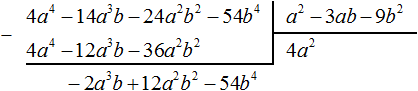
дмм пример 5 шаг 4

Теперь делим −2a3b + 12a2b2 − 54b4 на делитель a2 − 3ab − 9b2. Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:

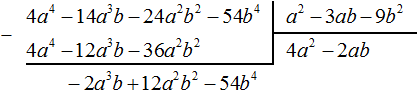
дмм пример 5 шаг 5

Умножим −2ab на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым −2a3b + 12a2b2 − 54b4

дмм пример 5 шаг 6

Вычтем из многочлена −2a3b + 12a2b2 − 54b4 многочлен −2a3b + 12a2b2 − 18ab3. При вычитании подобных членов обнаруживаем, что члены −54b4 и 18ab3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a3b из −2a3b и 6a2b2 из 12a2b2, а вычитание 18ab3 из −54b4 запишем в виде разности −54b4 − (+18ab3) или −54b4 − 18ab3

дмм пример 5 шаг 7

Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:

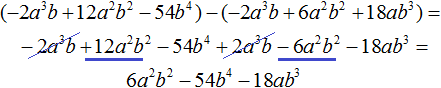
дмм пример 5 шаг 8

Вернёмся к нашей задаче. Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:

дмм пример 5 шаг 9

Умножим 6b2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым 6a2b2 − 54b4 − 18ab3. Сразу вычтем этот полученный результат из делимого 6a2b2 − 54b4 − 18ab3

дмм пример 5 шаг 10

Деление завершено. Таким образом, частное от деления многочлена 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 равно 4a2 − 2ab + 6b2.

дм рис 6

Выполним проверку. Умножим частное 4a2 − 2ab + 6b2 на делитель a2 − 3ab − 9b2. У нас должен получиться многочлен 4a4 − 14a3b − 24a2b2 − 54b4

дмм пример 5 шаг 11

Деление многочлена на многочлен с остатком

Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.

Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:

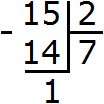
15 на 2 решение

То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:

15 на 2 дробный вид

Рациональное число семь целых одна вторая читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.

Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:

дмм рис 6

Например, разделим многочлен 2x3 − x2 − 5x + 4 на многочлен x − 3

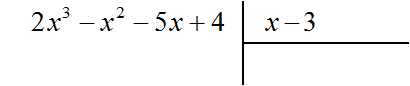
дммо пример 1 шаг 1

Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:

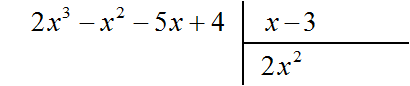
дммо пример 1 шаг 2

Умножим 2x2 на делитель x − 3 и полученный результат запишем под делимым:

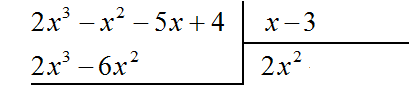
дммо пример 1 шаг 3

Вычтем из делимого полученный многочлен 2x3 − 6x2

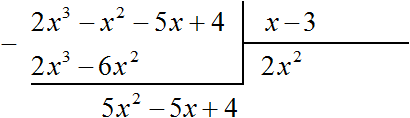
дммо пример 1 шаг 4

Теперь делим 5x2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:

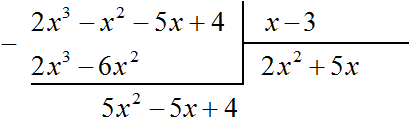
дммо пример 1 шаг 5

Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x2 − 5x + 4

дммо пример 1 шаг 6

Вычтем из многочлена 5x2 − 5x + 4 многочлен 5x2 − 15x

дммо пример 1 шаг 7

Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:

дммо пример 1 шаг 8

Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4

дммо пример 1 шаг 10

Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.

Поэтому при делении многочлена 2x3 − 2x2 − 5x + 4 на многочлен x − 3 получается 2x2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:

дммо рис 2

Когда деление многочленов невозможно

Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.

Например, нельзя разделить многочлен x3 + x на многочлен x4 + x2, поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.

Вопреки этому запрету можно попробовать разделить многочлен x3 + x на многочлен x4 + x2, и даже получить частное x−1, которое при перемножении с делителем будет давать делимое:

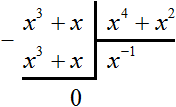
дм рис 2

дм рис 3

Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x−1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x−1 это дробь 1 na x, которая не является произведением.

Пусть имеется прямоугольник со сторонами 4 и 2

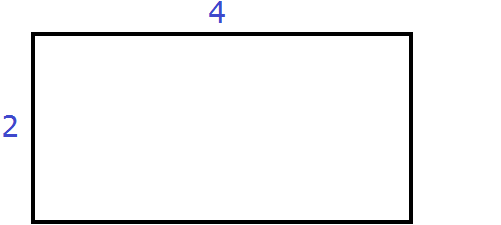
пр 42x рис 1

Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.

Увеличим длину и ширину этого прямоугольника на x

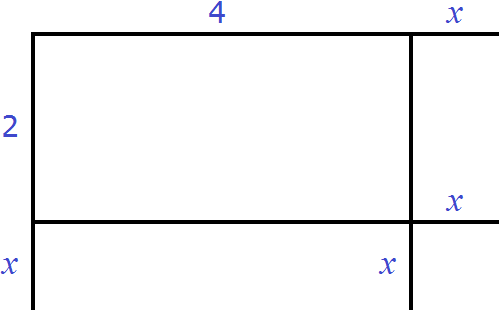
пр 42x рис 2

Достроим отсутствующие стороны:

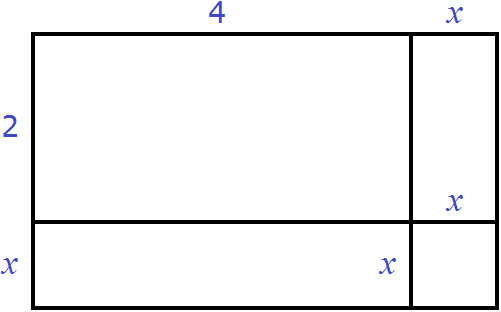
пр 42x рис 3

Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x2 + 6x + 8

(x + 4)(x + 2) = x2 + 4x + 2x + 8 = x2 + 6x + 8

При этом мы можем выполнить обратную операцию, а именно разделить площадь x2 + 6x + 8 на ширину x + 2 и получить длину x + 4.

дм рис 1

Степень многочлена x2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Задание 2. Выполните деление:

Решение:

Задание 3. Выполните деление:

Решение:

Задание 4. Выполните деление:

Решение:

Задание 5. Выполните деление:

Решение:

Задание 6. Выполните деление:

Решение:

Задание 7. Выполните деление:

Решение:

Задание 8. Выполните деление:

Решение:

Задание 9. Выполните деление:

Решение:

Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:

Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:

Задание 14. Выполните деление:

Решение:

Задание 15. Выполните деление:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже


Источник

Содержание:

  • Формулировка теоремы Безу
  • Следствия из теоремы Безу
  • Примеры решения задач

Формулировка теоремы Безу

Теорема

Остаток от деления многочлена $P(x)$ на двучлен $(x-a)$ равен $P(a)$ .

Следствия из теоремы Безу

  1. Число $a$ – корень многочлена $P(x)$ тогда и только тогда, когда $P(x)$ делится без остатка на двучлен $x-a$ .

    Отсюда, в частности, следует, что множество корней многочлена $P(x)$ тождественно множеству корней соответствующего уравнения $P(x)=0$ .

  2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами
    (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
  3. Пусть $a$ – целый корень приведенного многочлена
    $P(x)$ с целыми коэффициентами. Тогда для любого целого $k$ число $P(k)$ делится на $a-k$ .

Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на
единицу меньше: если $P(a)=0$, то заданный многочлен $P(x)$ можно представить в виде:

$$P(x)=(x-a) Q(x)$$

Таким образом, один корень найден и далее находятся уже корни многочлена $Q(x)$, степень которого на единицу меньше степени исходного
многочлена. Иногда этим приемом – он называется понижением степени – можно найти все корни заданного многочлена.

Примеры решения задач

Пример

Задание. Найти остаток от деления многочлена $f(x)=3 x^{2}-4 x+6$ на двучлен $(x-1)$

Решение. Согласно теореме Безу искомый остаток равен значению многочлена в точке
$a=1$ . Найдем тогда $f(1)$, для этого значение $a=1$ подставим в выражение для многочлена $f(x)$ вместо $x$ . Будем иметь:

$$f(1)=3 cdot 1^{2}-4 cdot 1+6=3-4+6=5$$

Ответ. Остаток равен 5

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. С помощью теоремы Безу доказать, что многочлен
$f(x)=17 x^{3}-13 x^{2}-4$ делится на двучлен $x=1$ без остатка.

Решение. Указанный многочлен делится на заданный двучлен без остатка, если число
$x=1$ – корень данного многочлена, то есть имеет место равенство: $f(1)=0$ . Найдем значение многочлена в точке $x=1$ :

$$f(1)=17 cdot 1^{3}-13 cdot 1^{2}-4=17-13-4=0$$

Что и требовалось доказать

Источник

Добавить комментарий