Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть 






Таким образом, результатами деления с остатком являются два целых числа: 





Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).
- Примеры
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Определение[править | править код]
Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше[1].
Для вычисления неполного частного от деления 



когда
.
где полускобки 


Для отрицательного делителя нужно округлять частное в большую сторону:
когда
.
Операция «mod» и связь со сравнениями[править | править код]
Величина остатка может быть получена бинарной операцией «взятия остатка» от деления 

Не следует путать это обозначение с обозначением сравнения по модулю 

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства 

В программировании[править | править код]
| Язык | Неполное частное |
Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % |
Делимое | |
| Ada | mod |
Делитель | |
rem |
Делимое | ||
| Бейсик | |
MOD |
Не определено |
| Си (ISO 1990) | / |
% |
Не определено |
| Си (ISO 1999) | / |
% |
Делимое[3] |
| C++ (ISO 2003) | / |
% |
Не определено[4] |
| C++ (ISO 2011) | / |
% |
Делимое[5] |
| C# | / |
% |
Делимое |
| ColdFusion | MOD |
Делимое | |
| Common Lisp | mod |
Делитель | |
rem |
Делимое | ||
| D | / |
% |
Делимое[6] |
| Delphi | div |
mod |
Делимое |
| Eiffel | // |
\ |
Делимое |
| Erlang | div |
rem |
Делимое |
| Euphoria | remainder |
Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() |
MOD()
|
Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() |
ОСТАТ()
|
|
| FileMaker | Div() |
Mod() |
Делитель |
| Fortran | mod |
Делимое | |
modulo |
Делитель | ||
| GML (Game Maker) | div |
mod |
Делимое |
| Go | / |
% |
Делимое |
| Haskell | div
|
mod |
Делитель |
quot
|
rem |
Делимое | |
| J | |~ |
Делитель | |
| Java | /
|
%
|
Делимое[7] |
Math.floorDiv
|
Math.floorMod
|
Делитель (1.8+) | |
| JavaScript | .toFixed(0) | % |
Делимое |
| Lua | % |
Делитель | |
| Mathematica | Quotient
|
Mod |
Делитель |
| MATLAB | idivide(?, ?, 'floor') |
mod |
Делитель |
idivide |
rem |
Делимое | |
| MySQL | DIV |
MOD% |
Делимое |
| Oberon | DIV |
MOD |
+ |
| Objective Caml | mod |
Не определено | |
| Pascal | div |
mod |
Делимое[8] |
| Perl | Нет | % |
Делитель |
| PHP | Нет[9] | % |
Делимое |
| PL/I | mod |
Делитель (ANSI PL/I) | |
| Prolog (ISO 1995) | mod |
Делитель | |
| PureBasic | / |
Mod% |
Делимое |
| Python | // |
% |
Делитель |
| QBasic | |
MOD |
Делимое |
| R | %/% | %% |
Делитель |
| RPG | %REM |
Делимое | |
| Ruby | /
|
% |
Делитель |
| Scheme | modulo |
Делитель | |
| SenseTalk | modulo |
Делитель | |
rem |
Делимое | ||
| Tcl | % |
Делитель | |
| Verilog (2001) | % |
Делимое | |
| VHDL | mod |
Делитель | |
rem |
Делимое | ||
| Visual Basic | |
Mod |
Делимое |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
78 mod 33 = 12 78 div 33 = 2
Знак остатка[править | править код]
Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
- Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
- Знак остатка совпадает со знаком делителя: неполное частное округляет к
.
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.
Как запрограммировать, если такой операции нет?[править | править код]
Неполное частное можно вычислить через деление и взятие целой части: ![q=left[{frac {a}{b}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a5108d8efbb2b9259f9487fc6f9f7bb61aa7337)
![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
При отсутствии команды mod остаток программируется как 
Если 


Неполное частное и неотрицательный остаток от деления на степень двойки 


Обобщения[править | править код]
Вещественные числа[править | править код]
Если два числа 



Формально:
- если
, то
, где
.
- Пример
Деление 7,9 на 2,1 с остатком даёт:
(неполное частное);
(остаток).
Гауссовы целые числа[править | править код]
Гауссово число — это комплексное число вида 



,
где частное 

Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, 

Многочлены[править | править код]
При делении с остатком двух многочленов 

, причём
.
- Пример
(остаток 3), так как:
.
См. также[править | править код]
- Алгоритм Евклида
- Делимость
- Наибольший общий делитель
- Непрерывная дробь
- Сравнение по модулю
Примечания[править | править код]
- ↑ 1 2 Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
- ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
- ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the
/operator is the algebraic quotient with any fractional part discarded. [This is often called «truncation toward zero».]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится. - ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
- ↑ N3242=11-0012 (Working draft), текст совпадает с C99
- ↑ D language specification (англ.). dlang.org. Дата обращения: 29 октября 2017. Архивировано из оригинала 3 октября 2017 года.
- ↑ Арнолд, Кен, Гослинг, Дж., Холмс, Д. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
- ↑ Стандарт 1973 года: div — division with truncation.
- ↑ PHP: Arithmetic Operators — Manual. Дата обращения: 27 ноября 2014. Архивировано 19 ноября 2014 года.
- ↑ DIV — Unsigned Divide
Бывает, он сопряжен с некоторыми неудобствами, но это лучше, чем ничего.
Приветствую Вас, уважаемые Читатели! Сегодня хочу немного погрузиться в теорию делимости, а именно в вычисление остатков от деления. Эта задача является и практически важной, ведь такие операции применяются буквально повсюду: от криптографии до телекоммуникационных систем. Поехали!
Итак, начнем с определения:
Так же такие числа называются сравнимыми по модулю m.
Для равноостаточных чисел работает такая теорема:
- Если при делении на m числа a1,a2,a3… an соответственно равноостаточны числам b1,b2.b3…bn, то равноостаточными будут суммы a1+a2+a3+…+an и b1+b2+b3+…bn, а также произведения a1a2a3…an и b1b2b3…bn.
- Как следствие, если числа a и b равноостаточны, то такими же являются и числа a^n и b^n при любо натуральном n.
Формулировка весь запутанная, поэтому разберем два пример. Итак:
Теперь пример посложнее с многоступенчатым решением:
В итоге мы получаем хоть и меньшее, но всё равно трудно вычисляемое вручную число, поэтому продолжаем дальше:
На третьем шаге уже нет смысла вычислять все остатки, как прежде. Можно было и вычислить вручную. Получаем, что первоначальное число и число 56 равноостаточны при делении на 37. Ответ получен! Спасибо за внимание!
Читайте также:
В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.
Общее представление о делении с остатком
Ранее мы указывали, что сам процесс деления сводится к разъединению одного множества на два или несколько. Чаще всего мы встречаемся с делением на равные части, то есть множества, получившиеся в результате, будут одинаковыми. Но так разделить возможно далеко не всегда. К примеру, 8 конфет разделить поровну на троих детей не выйдет: у каждого будет по 2 конфеты, а две останутся лишними. В данном случае мы имеем остаток 2, то есть остались две конфеты. Этот пример отображает основной смысл деления с остатком. Запишем определение:
Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.
В чем состоит смысл деления с остатком?
В случае натуральных чисел деление с остатком имеет следующий смысл. Мы уже знаем, что понятие натурального числа тесно связано с количеством чего-либо. Допустим, у нас есть некое число предметов (обозначим его a), а после его деления образуется остаток, условно d. У нас остались числа b и c. Есть два основных подхода к их обозначению:
1) если b –количество элементов в каждом равном множестве, полученном после деления, то c – это количество множеств, которое у нас получилось.
2) если b – это количество множеств, то c – это число предметов в каждом из них.
Поясним нашу мысль на конкретных числах. Допустим, натуральное число 13 было разделено на 4. В итоге мы имеем два числа – 3 и 1. Мы можем рассмотреть эту ситуацию с двух сторон:
1) тринадцать предметов были сгруппированы по 4. У нас получилось 3 группы, а в исходном множестве остался всего 1 предмет;
2) тринадцать предметов разложили по 4 группам. У нас получилось, что в каждой группе по 3 предмета, а остаток равен 1.
Если натуральное число a всегда можно разделить с остатком на любое натуральное b, то можно выделить следующие ситуации:
1. A можно разделить на b без остатка, то есть все предметы можно разделить на равные множества. При этом «лишних» у нас не останется, тогда d будет равно 0. Получается, что деление без остатка – это частный случай деления с остатком.
2. A может быть меньше b. Тогда ни одного требуемого множества мы из него составить не можем, и число c будет равно нулю, а остаток равен a (то есть числу предметов в исходном множестве).
3. A может делиться на b с остатком. Тогдазначения a, b, c и d будут натуральными числами.
Подводим итог:
Результат деления натуральных чисел a и b с остатком – это два числа c и d, которые либо оба являются натуральными, либо одно из них равно нулю.
Основные понятия, используемые при делении с остатком
Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.
То натуральное число, которое делят на части, принято называть делимым, а то, на которое делят – делителем. Получившиеся в результате два числа мы называем соответственно остатком и неполным частным. К примеру, если мы разделим 8 на 3, то в итоге неполным частным будет 2, и остатком тоже 2.
Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение «÷», смысл которого тот же самый. Так, числовое выражение 16:3 означает деление одного натурального числа на другое с остатком.
Обозначим неполное частное буквой с, остаток – d, исходное число – a, а делитель – b. Тогда суть процесса деления в буквенном виде мы можем выразить как a:b=c (ост. d).
Также можно записать это в виде схемы: делимое: делитель = неполное частное (ост. остаток).
Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.
Задачи, в которых используется деление с остатком
В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:
1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.
Например:
У нас есть 67 шаров, которыми мы будем наряжать елки. Если на каждую елку нужно 15 шаров, сколько всего елок можно нарядить? Результат мы получим после деления с остатком.
Другой пример:
У нас есть 162 книги, которые нужно упаковать в 40 ящиков. Число книг, которое мы будем класть в каждую коробку, можно определить в результате деления 162 на 40.
Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)
Например, на заводе произведено 6 113 л молока. Его нужно разлить в бутылки по 2 л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится 3 часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.
2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.
Например:
У нас есть 197 конфет, которые раскладываются по коробкам. Мы знаем число этих коробок – оно равно 20. Деление 197 на 20 подскажет нам, сколько конфет остались неупакованными.
Чтобы изготовить бетонную плиту, надо израсходовать 750 кг цемента. Если мы закупили 12 900 кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.
Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления
Для установления этих связей сразу разберем конкретный пример.
У нас есть некоторое множество предметов, обозначим его буквой a. Распределим его по кучкам, количество которых равно b. Всего в каждой кучке у нас будет c предметов. Остаток обозначим d. В буквенном виде это выражение можно записать как a:b=c (ост. d). Теперь проанализируем связи, которые есть в этом равенстве.
Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.
Учитывая смысл умножения и сложения натуральных чисел, мы можем записать это в виде равенства c·b+d=a. А наличие у умножения и сложения переместительных свойств позволяет нам переформулировать его как a=b·c+d. Получается следующее правило:
Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.
Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:
Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.
Решение
Имеем b=7, c=11 и d=2. Это все данные, которые нам нужны для вычислений. Подставим нужные значения: b·c+d=7·11+2. Следуя правильному порядку выполнения математических действий, получим в итоге 7·11+2=77+2=79 (если нужно, повторите основы умножения и сложения натуральных чисел).
Ответ: делимое будет равно 79.
Если нужно проверить верность результата действия деления с остатком, то для этого мы также проверяем справедливость равенства a=b·c+d.
Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.
Вспомним, что остаток от деления, который мы выше договорились обозначить буквой d, представляет собой число элементов, оставшееся в исходном множестве после его разделения на равные части. Значит, d=a−b·c. Записать это равенство мы можем благодаря свойствам умножения и вычитания натуральных чисел. Сформулируем определение:
Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.
У нас получилось буквенное выражение d=a−b·c, которое будет нам полезно при нахождении остатка от деления. Разберем такую задачу.
Мы разделили 67 на 15 и получили неполное частное 4. Вычислите остаток от деления.
Решение
Имеем a=67, b=15, c=4. Если мы подставим в выражение a−b·c исходные значения, то сможем подсчитать остаток: 67−15·4. Поскольку 15·4=60, то 67−15·4=67−60=7.
Ответ: остаток от деления равен 7.
Мы также можем найти неполное частное, если знаем значение делимого, делителя и остатка. Исключим из исходного множества те элементы, которые образуют остаток. Благодаря свойствам вычитания натуральных чисел количество элементов в множестве мы теперь можем записать как a−d. После этого уже можно произвести деление без остатка, в результате которого получится b множеств по c элементов в каждом. Мы получили равенство (a−d):b=c. Его также можно записать в виде c=(a−d):b.
Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.
Мы разделили 221 на 52 и получили остаток 13. Вычислите неполное частное.
Решение
Отнимем остаток от делимого и результат разделим на делитель. Считаем: (221−13):52=208:52=4 (для подсчета мы использовали метод подбора частного).
Ответ: неполное частное равно 4.
Осталось разобрать последний случай: как быть, если нужно найти делитель при известных значениях делимого, остатка и неполного частного? Начнем опять же с исключения остатка из делимого, то есть запишем a-d. Вспомнив смысл деления одного натурального числа на другое, запишем следующее равенство: (a−d):c=b. Также будет верно b=(a−d):c. Сформулируем правило:
Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.
Возьмем пример решения такой задачи.
Было выполнено деление 877 на некоторое число с остатком 2, неполное частное при этом составило 35. Найдите значение делителя.
Решение
Вычтем остаток из делимого и получим 875. Результат нужно разделить на известное нам неполное частное 35. В итоге получится нужное нам значение делителя. Вычислим столбиком:
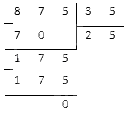
Ответ: делитель равен 25.
Деление c остатком (деление по модулю) — арифметическая операция, играющая большую роль в арифметике, теории чисел и алгебре. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть  и
и  — целые числа, причём
— целые числа, причём  Деление с остатком
Деление с остатком  («делимого») на
(«делимого») на  («делитель») означает нахождение таких целых чисел
(«делитель») означает нахождение таких целых чисел  и
и  , что выполняется равенство:
, что выполняется равенство:
Таким образом, результатами деления с остатком являются два целых числа:  называется неполным частным от деления, а
называется неполным частным от деления, а  — остатком от деления. На остаток налагается дополнительное условие:
— остатком от деления. На остаток налагается дополнительное условие:  то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел. Если остаток равен нулю, говорят, что
то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел. Если остаток равен нулю, говорят, что  нацело делится на
нацело делится на 
Примеры.
-
- Проверка:

- Проверка:
-
- Проверка:

- Проверка:
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Содержание
- 1 Определение
- 1.1 Натуральные и целые числа
- 1.2 Обобщения
- 1.2.1 Вещественные числа
- 1.2.2 Гауссовы целые числа
- 1.2.3 Многочлены
- 2 В программировании
- 2.1 Знак остатка
- 2.2 Как запрограммировать, если такой операции нет?
- 3 См. также
- 4 Примечания
- 5 Ссылки
Определение[править | править вики-текст]
Натуральные и целые числа[править | править вики-текст]
Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше.
Для практического выполнения целочисленного деления  на
на  с остатком следует разделить (в обычном смысле)
с остатком следует разделить (в обычном смысле)  на
на  как вещественные числа и округлить результат до ближайшего целого в меньшую сторону, это будет неполное частное
как вещественные числа и округлить результат до ближайшего целого в меньшую сторону, это будет неполное частное  :
:
Здесь скобки  означают округление до ближайшего целого в меньшую сторону. Далее найдём остаток от деления:
означают округление до ближайшего целого в меньшую сторону. Далее найдём остаток от деления:
Обобщения[править | править вики-текст]
Вещественные числа[править | править вики-текст]
Если два числа  и
и  (отличное от нуля) относятся к множеству вещественных чисел,
(отличное от нуля) относятся к множеству вещественных чисел,  может быть поделено на
может быть поделено на  без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.
без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.
Формально:
- если
 , то
, то  , где
, где 
Пример:
 (остаток 1,6)
(остаток 1,6)
Гауссовы целые числа[править | править вики-текст]
Гауссово число — это комплексное число вида  , где
, где  — целые числа. Для них можно определить деление с остатком: любое гауссово число
— целые числа. Для них можно определить деление с остатком: любое гауссово число  можно разделить с остатком на любое ненулевое гауссово число
можно разделить с остатком на любое ненулевое гауссово число  , то есть представить в виде:
, то есть представить в виде:
где частное  и остаток
и остаток  — гауссовы числа, причём
— гауссовы числа, причём  Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например,
Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например,  можно разделить на
можно разделить на  тремя способами:
тремя способами:
Многочлены[править | править вики-текст]
При делении с остатком двух многочленов  и
и  для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:
для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:
 , причём
, причём 
Пример:
 (остаток 3), так как 2x² + 4x + 5 = (x + 1)(2x + 2) + 3
(остаток 3), так как 2x² + 4x + 5 = (x + 1)(2x + 2) + 3
В программировании[править | править вики-текст]
| Язык | Неполное частное |
Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % |
Делимое | |
| Ada | mod | Делитель | |
| rem | Делимое | ||
| ASP | Mod |
Не определено | |
| Бейсик | |
MOD |
Не определено |
| Си (ISO 1990) | / |
% |
Не определено |
| Си (ISO 1999) | / |
% |
Делимое[3] |
| C++ (ISO 2003) | / |
% |
Не определено[4] |
| C++ (ISO 2011) | / |
% |
Делимое[5] |
| C# | / |
% |
Делимое |
| ColdFusion | MOD |
Делимое | |
| Common Lisp | mod |
Делитель | |
rem |
Делимое | ||
| Delphi | div |
mod |
Делимое |
| Eiffel | // |
\ |
Делимое |
| Erlang | div |
rem |
Делимое |
| Euphoria | remainder |
Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() |
MOD() |
Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() |
ОСТАТ() |
|
| FileMaker | Div() |
Mod() |
Делитель |
| Fortran | mod |
Делимое | |
modulo |
Делитель | ||
| GML (Game Maker) | div |
mod |
Делимое |
| Go | / |
% |
Делимое |
| Haskell | div |
mod |
Делитель |
quot |
rem |
Делимое | |
| J | |~ |
Делитель | |
| Java | / |
% |
Делимое[6] |
Math.floorDiv |
Math.floorMod |
Делитель (1.8+) | |
| JavaScript | % |
Делимое | |
| Lua | % |
Делитель | |
| Mathematica | Mod |
Делитель | |
| MATLAB | idivide(?, ?, 'floor') |
mod |
Делитель |
idivide |
rem |
Делимое | |
| MySQL | DIV |
MOD% |
Делимое |
| Objective Caml | mod |
Не определено | |
| Pascal | div |
mod |
Делимое[7] |
| Perl | Нет | % |
Делитель |
| PHP | Нет[8] | % |
Делимое |
| PL/I | mod |
Делитель (ANSI PL/I) | |
| Prolog (ISO 1995) | mod | Делитель | |
| PureBasic | / |
Mod% |
Делимое |
| Python | // |
% |
Делитель |
| QBasic | |
MOD | Делимое |
| R | %% | Делитель | |
| RPG | %REM | Делимое | |
| Ruby | % | Делитель | |
| Scheme | modulo | Делитель | |
| SenseTalk | modulo | Делитель | |
| rem | Делимое | ||
| Tcl | % | Делитель | |
| Verilog (2001) | % | Делимое | |
| VHDL | mod | Делитель | |
| rem | Делимое | ||
| Visual Basic | |
Mod |
Делимое |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получении случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа. Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
78 mod 33 = 12 78 div 33 = 2
Знак остатка[править | править вики-текст]
Важно отметить, что операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
- Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
- Знак остатка совпадает со знаком делителя: неполное частное округляет к −∞.
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
- Есть сумма n копеек, положительная или отрицательная. Перевести её в рубли и копейки. —
n div 100иn mod 100. Знак остатка совпадает со знаком делимого. - Есть бесконечное клеточное поле, каждая клетка — 16×16 пикселей. В какую клетку попадает точка (x, y), и каковы координаты относительно верхнего левого угла клетки? —
(x div 16, y div 16)и(x mod 16, y mod 16)соответственно. Знак остатка совпадает со знаком делителя.
Как запрограммировать, если такой операции нет?[править | править вики-текст]
Неполное частное можно запрограммировать как ![q = left[frac{a}{b}right]](https://web.archive.org/web/20160430141554im_/https://upload.wikimedia.org/math/f/7/1/f714da379d07864de682eaaf2754b14a.png) (с тем или иным видом округления к целому). Однако деление получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).
(с тем или иным видом округления к целому). Однако деление получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).
При отсутствии команды mod остаток программируется как  .
.
Если b положительно, а знак r совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой  .
.
См. также[править | править вики-текст]
- Алгоритм Евклида
- Делимость
- Наибольший общий делитель
- Непрерывная дробь
- Сравнение по модулю
Примечания[править | править вики-текст]
- ↑ Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
- ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
- ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the
/operator is the algebraic quotient with any fractional part discarded. [This is often called “truncation toward zero”.]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится. - ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
- ↑ N3242=11-0012 (Working draft), текст совпадает с C99
- ↑ К. Арнолд, Дж. Гослинг, Д. Холмс. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
- ↑ Стандарт 1973 года: div — division with truncation.
- ↑ PHP: Arithmetic Operators – Manual
Ссылки[править | править вики-текст]
- Деление с остатком: онлайн-калькулятор
Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.
Что такое деление?
Деление это действие, позволяющее что-либо разделить.
Деление состоит из трёх параметров: делимого, делителя и частного.
Делимое это то что делят;
Делитель это число, показывающее на сколько частей нужно разделить делимое.
Частное это собственно результат.
Пусть у нас имеются 4 яблока:

Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:
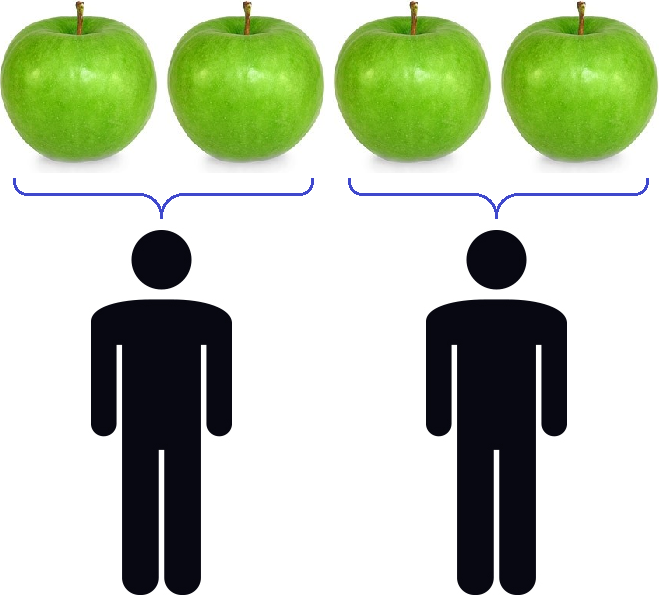
Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:
![]()
В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.
Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4
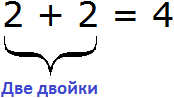
В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».

Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
![]()
Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2
Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷
На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.
Деление с остатком
Остаток — это то что осталось от действия деления неразделённым.
Например, пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Можно проверить это умножением:
(2 × 2) + 1 = 5
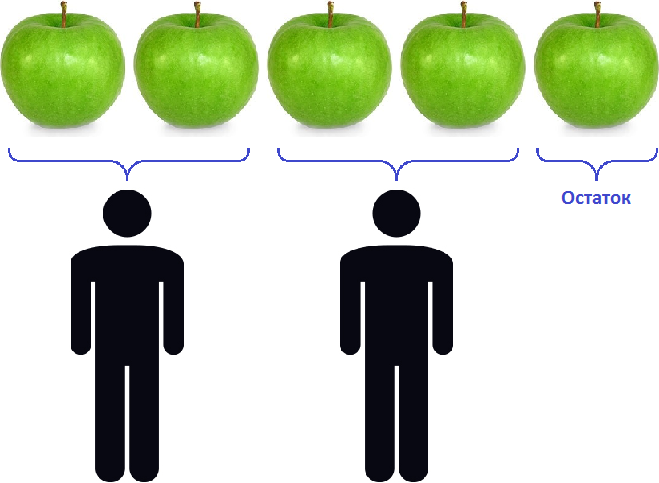
Допустим, имеются пять яблок:

Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не полýчится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:
Деление уголком
Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.
Прежде чем делить уголком, человек должен знать:
- обычное деление маленьких чисел;
- деление с остатком;
- умножение в столбик;
- вычитание в столбик.
Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:
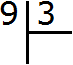
Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
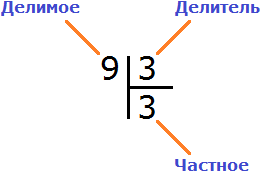
Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:
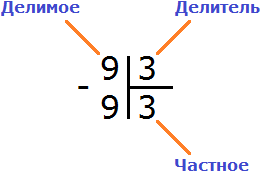
Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:
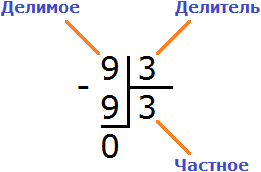
Пример 2. Найти значение выражения 8 : 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.
Сначала запишем данное выражение уголком:
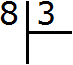
Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:
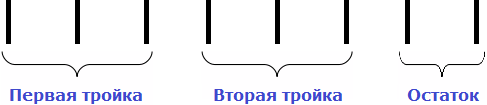
В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:
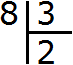
Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:
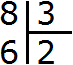
Далее из 8 вычитаем 6. Полученное число и будет остатком:
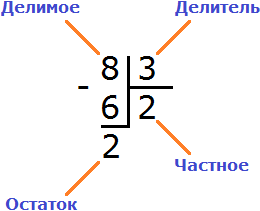
8 : 3 = 2 (2 в остатке)
Проверка:
(2 × 3) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то её надо разделить на делитель, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то надо разделить их на делитель, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1. Найти значение выражения 25 : 3
25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше чем три? Да. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:
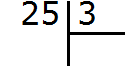
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:
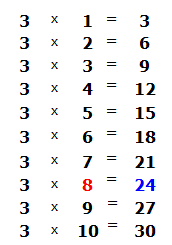
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
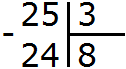 Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
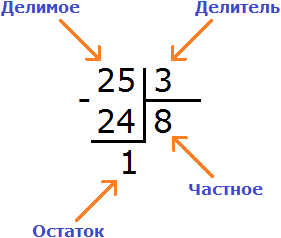
25 : 3 = 8 (1 в остатке)
Проверка:
(8 × 3) + 1 = 24 + 1 = 25
Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.
В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше чем три, поэтому деление завершено. Последний остаток мéньший делителя говорит о том, что он не содержит чисел равных делителю.
В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек.
Пример 2. Разделить 326 на 4.
Смóтрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да. Значит можно выполнять деление.
Записываем уголком данное выражение:

Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:
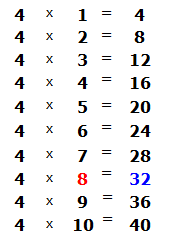
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
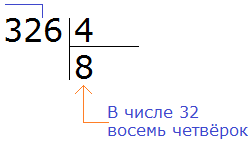 Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
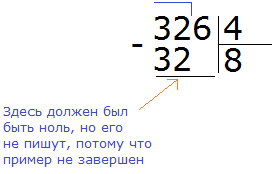 Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
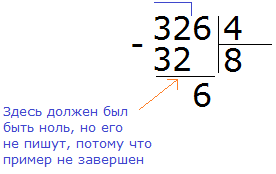
Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:
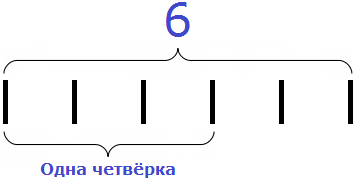
Записываем единицу в правом уголке нашего ответа:
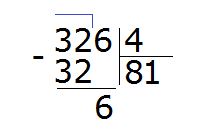 Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
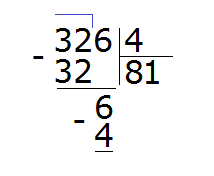
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
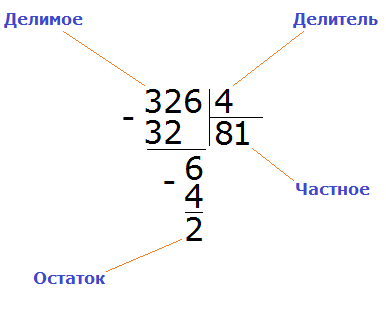
Получили 326 : 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.
Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.
А в примере 25 : 3 первое неполное делимое было 25.
Пример 3. Найти значение выражения 384 : 5
Записываем данное выражение в уголком:
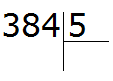
Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:
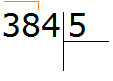
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:
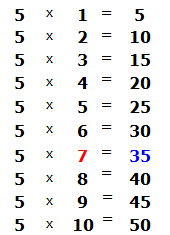
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
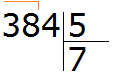 Умножаем 7 на 5, получаем 35 и записываем его под 38:
Умножаем 7 на 5, получаем 35 и записываем его под 38:

Теперь из 38 вычитаем 35, получим 3:
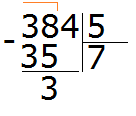
Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:
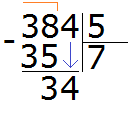
Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:
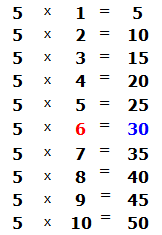
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
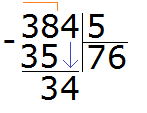
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
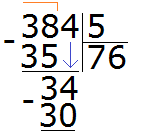
Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5
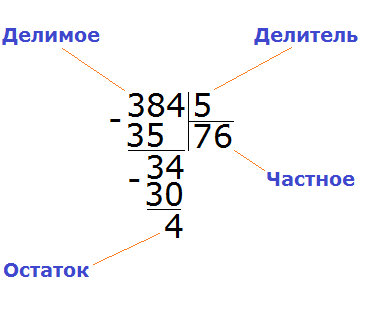
384 : 5 = 76 (и 4 в остатке)
Проверка:
(76 × 5) + 4 = 380 + 4 = 384
Пример 4. Найти значение выражения 8642 : 4
Этот пример немного посложнее. Записываем уголком данное выражение:
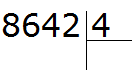
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2
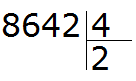 Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
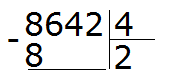
Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.
Далее сносим цифру 6 и делим её на делитель, получаем 1
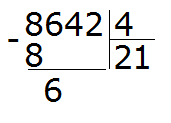 Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
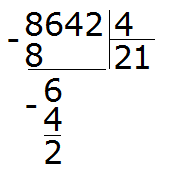
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6
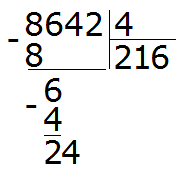
Умножаем 6 на 4, получаем 24. Записываем это число под 24
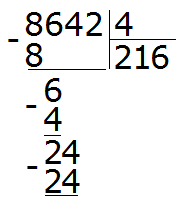
Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2
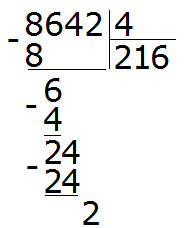
Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.
Поэтому два разделить на четыре это ноль:
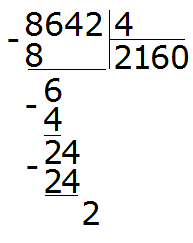 Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
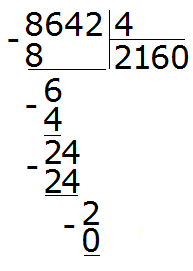
Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:
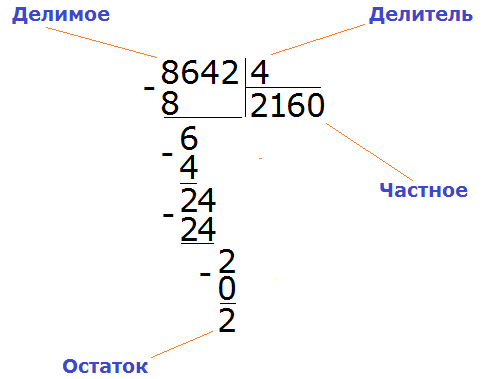
8642 : 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел, у которых на конце 0
Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.
Например, разделим 120 : 3
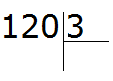
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
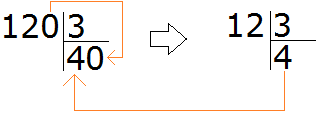
Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.
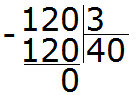
120 : 3 = 40
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12 : 3 = 4 (делимое без нулей на конце)
120 : 3 = 40 (здесь у делимого один ноль)
1200 : 3 = 400 (здесь у делимого два нуля)
12000 : 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5
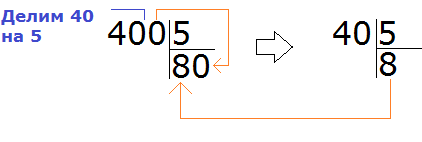 Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
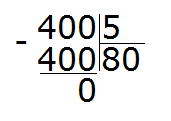 Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
1000 + 400 = 1400
Можно по-отдельности разделить 1000 на 5 и 400 на 5:
1000 : 5 = 200
400 : 5 = 80
и сложить полученные результаты:
200 + 80 = 280
Итого: 1400 : 5 = 280
Решим этот же пример уголком:
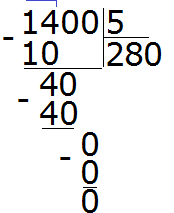
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так-то просто.
Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первую цифру, образующую самый старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.
Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Превратим число 13735 в круглое число. Первая цифра 1 образуют старший разряд (разряд десятков тысяч) — эту цифру оставляем без изменений, а остальные цифры заменяем нулями. В итоге получаем 10000.
Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут рассмотрены более подробно.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.
Пример 1. Найти значение выражения 88 : 12
Записываем данное выражение уголком:
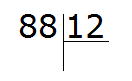 Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».
Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число которое меньше делимого, но очень близко к нему или равно ему.
Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12
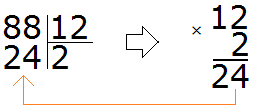
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.
Пробуем следующее число. Допустим частное равно 5
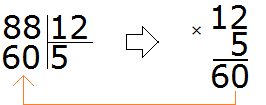
Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.
Попробуем сразу взять по 8
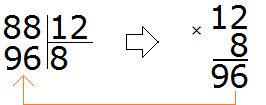
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7
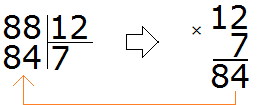
Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.
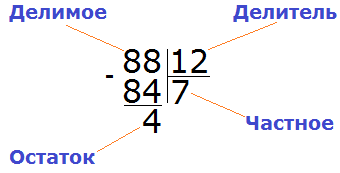
88 : 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.
В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)
320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.
Для начала превращаем делимое и делитель в круглые числа.
Круглым числом для 88 будет число 80.
А круглым числом для 12 будет число 10.
Теперь делим полученные круглые числа:
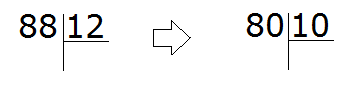 80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
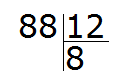
Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.
Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:

Как видно, этим способом мы решили этот пример намного быстрее.
Пример 2. Найти значение выражения 1296 : 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
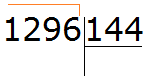 Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144
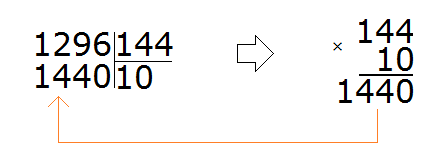
Десятка не подходит, поскольку при умножении получается число, которое больше делимого.
Попробуем взять по 9, уменьшив десятку на единицу.
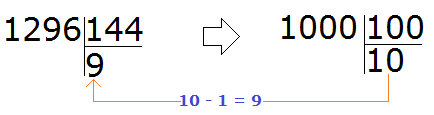
Проверяем девятку. Для этого умножаем её на делитель:
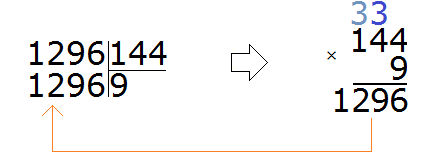
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296
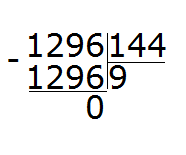 1296 : 144 = 9
1296 : 144 = 9
Проверка: 144 × 9 = 1296
Пример 3. Попробуем решить большой и сложный пример 227 492 : 331
Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300
 Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
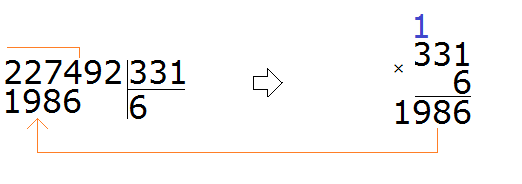 Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
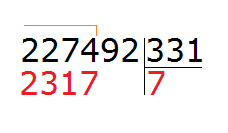 Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
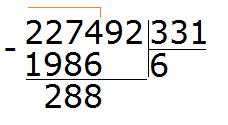
288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
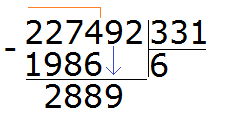
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:
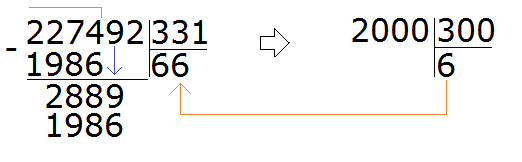 Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
 Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:
Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:

Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241
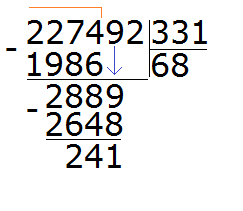
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
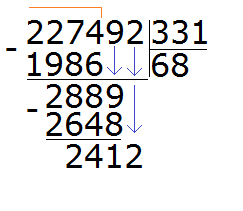
Теперь делим 2412 на 331. Возьмём по 7
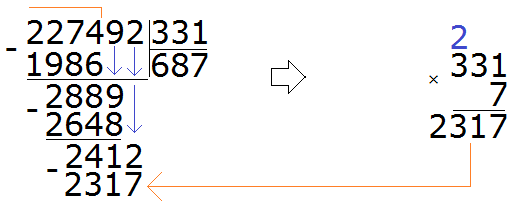
Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:

227 492 : 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.
Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.
Задания для самостоятельного решения
Задание 1. Выполните деление:
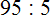
Решение:
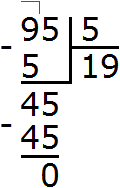
Задание 2. Выполните деление:

Решение:

Задание 3. Выполните деление:

Решение:

Задание 4. Выполните деление:
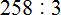
Решение:

Задание 5. Выполните деление:

Решение:
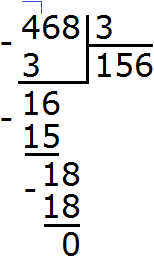
Задание 6. Выполните деление:

Решение:
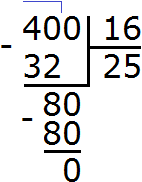
Задание 7. Выполните деление:
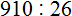
Решение:

Задание 8. Выполните деление:
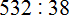
Решение:

Задание 9. Выполните деление:
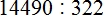
Решение:

Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:
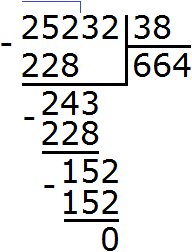
Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:
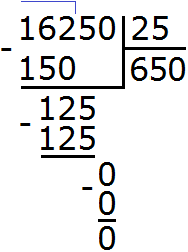
Задание 14. Выполните деление:
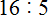
Решение:
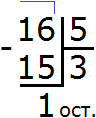
Задание 15. Выполните деление:
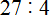
Решение:

Задание 16. Выполните деление:
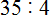
Решение:
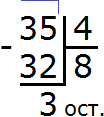
Задание 17. Выполните деление:
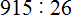
Решение:
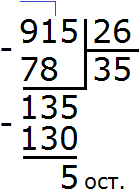
Задание 18. Выполните деление:

Решение:
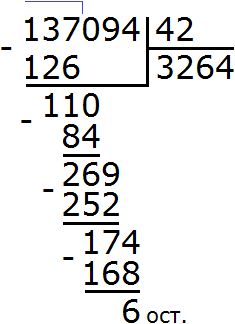
Задание 19. Выполните деление:

Решение:

Задание 20. Выполните деление:
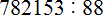
Решение:
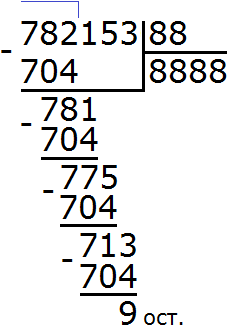
Задание 21. Выполните деление:

Решение:
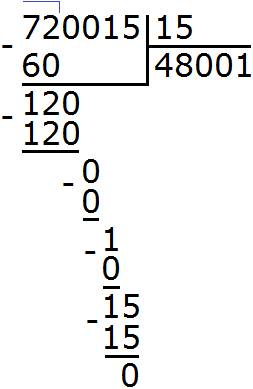
Задание 22. Выполните деление:
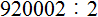
Решение:
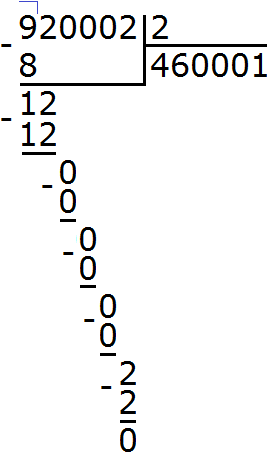
Задание 23. Выполните деление:

Решение:
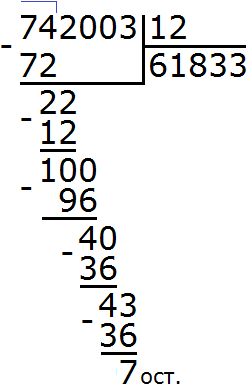
Задание 24. Выполните деление:
Решение:
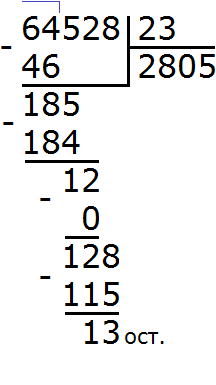
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
















