Ряд, полученный отбрасыванием от исходного n первых членов, называется n-м остатком ряда.
Обозначение:
Все члены, кроме тех, что входят в n-й остаток ряда, в сумме дают т. н. n-ю частичную сумму ряда.
Свойства[править | править код]
Для остатка ряда справедливы следующие утверждения:
- Если ряд сходится, то сходится любой его остаток.
- Если хотя бы один остаток ряда сходится, то и сам ряд сходится.
- Если ряд сходится, то
Существуют способы оценки остатка ряда с помощью интегрального признака Коши (для знакоположительного ряда) и Признака сходимости Лейбница (для знакочередующегося ряда).
|
|
Это статья-заготовка по математике. Помогите Википедии, дополнив эту статью, как и любую другую. |
Последовательности и ряды |
|
|---|---|
| Последовательности |
|
| Ряды, основное |
|
| Числовые ряды (действия с числовыми рядами) |
|
| Функциональные ряды |
|
| Другие виды рядов |
|
|
|
Для улучшения этой статьи желательно:
После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки. |
Остаток ряда и его оценка
Рассмотрим
сходящийся ряд ![]() .
.
Как было отмечено ранее, вычисление его
суммы
![]()
непосредственно
по определению очень неудобно, однако
для достаточно больших n
имеет место
приближенное равенство
![]() ,
,
точность которого возрастает с увеличениемn.
Для оценки точности этого приближенного
равенства введем понятие остатка
сходящегося ряда.
Определение.
Разность между суммой
![]() иn-й
иn-й
частичной суммой
![]() ряда называетсяn-м
ряда называетсяn-м
остатком
сходящегося ряда:
![]() .
.
Очевидно
![]() ,
,
т. е.![]() представляет собой сумму сходящегося
представляет собой сумму сходящегося
ряда, который получен из данного![]() исключением
исключением
первых n
членов. Так как по определению
![]() ,
,
то
![]() .
.
Абсолютная
погрешность при замене
![]() частичной суммой
частичной суммой![]() равна
равна![]() .
.
Таким образом, если требуется найти
сумму ряда с точностью до
![]() ,
,
то надо взять столько первых членов
ряда, чтобы выполнялось условие
![]() .
.
Однако, отметим еще раз, остаток
![]() – также сумма ряда, и находить его мы в
– также сумма ряда, и находить его мы в
большинстве случаев не умеем. Поэтому
выясним, как найти номер ос
татка
n,
чтобы
![]() ,
,
т. е. как произвести только оценку
остатка, не находя его самого. Это
позволит нам вовремя остановиться при
вычислении частичных сумм ряда, когда
уже будет получено приближение требуемой
точности.
Не
формулируя теорем об оценке остатка,
отметим следующие вполне очевидные
факты:
1)
если
![]() и
и![]() – сходящиеся знакоположительные ряды
– сходящиеся знакоположительные ряды
и
![]() то
то
![]() ,
,
где![]() ,
,![]() ;
;
2)
если знакочередующийся ряд
![]() ,
,
сходится по признаку Лейбница, то![]() ,
,
т. е. абсолютная величина остатка такого
ряда меньше модуля первого отброшенного
члена ряда.(Это
следует из того, что по теореме Лейбница
сумма ряда
![]() ).
).
Если
данный ряд знакоположительный, то его
остаток
![]() ,
,
составленный из отброшенных членов,
чаще всего сравнивают с бесконечно
убывающей геометрической прогрессией,
т. к. ее сумма вычисляется по известной
формуле![]() .
.
Пример
11. Вычислить
сумму ряда
![]() с точностью
с точностью![]() ,
,
если
|
а) |
|
б) |
|
Решение.
а)
![]() – ряд геометрической
– ряд геометрической
прогрессии
со знаменателем
![]() .
.
По
определению
![]()
является
также рядом геометрической прогрессии
с
![]() и первым членом
и первым членом![]() .
.
Найдем сумму этой прогрессии, т. е.
![]() :
:
 .
.
Путем
подбора определим, при каком значении
n
будет выполняться неравенство
![]() .
.
Положим, например,![]() .
.
Получим![]() ,
,
т. е.
![]() .
.
Так как ![]() ,
,
то три слагаемых не дают приближение
требуемой
точности. Пусть
![]() ,
,
отсюда![]() ,
,
т. е.![]() .
.
Итак,
принимаем
![]() .
.
Это означает, что
![]() с
с
точностью
![]() .
.
Неравенство
![]() можно было решить и не прибегая к подбору:
можно было решить и не прибегая к подбору:
![]() ,
,
поэтому
![]() или
или![]() .
.
Приближенное
значение полученной дроби можно вычислить
на калькуляторе.
б)
Знакоположительный ряд
![]()
геометрической
прогрессией не является, но при всех
![]() справедливо неравенство:
справедливо неравенство:![]() .
.
![]() –ряд
–ряд
геометрической прогрессии со знаменателем
![]() .
.
Очевидно,
![]() ,
,
где![]() –n-й
–n-й
остаток исследуемого ряда, а
![]() .
.
Поэтому
 .
.
Так
как
![]() ,
,
то![]() .
.
Значит,![]() также меньше
также меньше![]() и
и
 с
с
заданной точностью
![]() .
.
Пример
12. Вычислить
сумму ряда
![]() с заданной точностью:
с заданной точностью:
|
а) |
|
|
б) |
|
|
|
в) |
|
|
г) |
|
|
а)
Ряд
![]() сходится по
сходится по
признаку Лейбница. Сумма n
первых
членов
этого ряда
![]() отличается от его суммы
отличается от его суммы
![]() на
на
величину меньшую, чем
![]() .
.
Поэтому, отбросив десятый и следующие
за ним члены, получим![]() с точностью
с точностью
![]() .
.
б)
Для того, чтобы вычислить приближенно
сумму ряда
![]() с такой же
с такой же
точностью
![]() ,
,
придется взять не 9, как в примере а), а
99
первых
слагаемых, т. к.
![]() и
и![]() .
.
Сравнение
результатов, полученных в примерах а)
и б), приводит к понятию скорости
сходимости рядов: очевидно, ряд
![]() сходится
сходится
быстрее, чем
![]() ,
,
т. к. для вычисления суммы с одной и той
же точностью в первом случае необходимо
взять меньше слагаемых, чем во втором.
в)
Знакочередующийся ряд
![]() удовлетворяет
удовлетворяет
условиям признака Лейбница, а поэтому
допускаемая погрешность
![]() .
.![]() ,
,
значит,
![]()
с
заданной точностью
![]() .
.
г)
Данный ряд также сходится по признаку
Лейбница. Абсолютная величина
его
седьмого члена
![]() ,
,
следовательно, частичная сумма![]()
отличается
от суммы ряда менее, чем на
![]() ,
,
и
![]() .
.
Соседние файлы в папке ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
Рассмотрим сходящийся ряд

Как известно, его сумма S является пределом последовательности его частичных сумм  при
при 

Поэтому для достаточно больших  имеем приближенное равенство
имеем приближенное равенство

Точность этого равенства возрастает с увеличением  . Для оценки точности приближенного равенства (45) введем понятие остатка сходящегося ряда.
. Для оценки точности приближенного равенства (45) введем понятие остатка сходящегося ряда.
Определение. Разность между суммой ряда S и его  частичной суммой
частичной суммой  называется
называется  остатком сходящегося ряда (44), Остаток ряда обозначается
остатком сходящегося ряда (44), Остаток ряда обозначается 

Как видно из равенства (46), остаток ряда представляет собой сумму сходящегося ряда, полученного из данного ряда отбрасыванием  его первых членов:
его первых членов:

Из определения остатка ряда ясно, что

Действительно,
 (X)
(X)
Абсолютная погрешность при замене суммы ряда S его частичной суммой  очевидно, равна модулю остатка ряда:
очевидно, равна модулю остатка ряда:

Таким образом, если требуется найти сумму ряда с точностью до  то надо взять сумму такого числа
то надо взять сумму такого числа  первых членов ряда, чтобы выполнялось неравенство
первых членов ряда, чтобы выполнялось неравенство  Однако в большинстве случаев находить остаток
Однако в большинстве случаев находить остаток  точно мы не умеем. Поэтому выясним, как выбирать номер остатка
точно мы не умеем. Поэтому выясним, как выбирать номер остатка  , чтобы его модуль не превосходил заданного числа
, чтобы его модуль не превосходил заданного числа  .
.
Оценка остатка знакоположительного ряда
Теорема 1. Если все члены сходящегося знакоположительного ряда

не превосходят соответствующих членов другого сходящегося знакоположительного ряда

то  остаток ряда (49) не превосходит
остаток ряда (49) не превосходит  остатка ряда (50).
остатка ряда (50).
Доказательство. Обозначим через  и
и  остатки рядов (49) и (50)
остатки рядов (49) и (50)

Каждый из этих остатков является суммой сходящегося знакоположительного ряда.
Так как по условию  , то на основании признака сравнения (п. 5, теорема 1) сумма первого ряда не превосходит суммы второго ряда, т. е.
, то на основании признака сравнения (п. 5, теорема 1) сумма первого ряда не превосходит суммы второго ряда, т. е.

Определение. Если даны два сходящихся ряда

причем члены ряда (Y) больше соответствующих членов ряда (U), то ряд (V) называется мажорирующим рядом по отношению к ряду 
Из предыдущей теоремы следует, что остаток мажорирующего ряда всегда больше или равен остатку основного ряда.
Обычно в качестве мажорирующего ряда берут ряд, остаток которого  можно легко вычислить (например, геометрическую прогрессию).
можно легко вычислить (например, геометрическую прогрессию).
Тогда, по только что доказанной теореме, мы легко оценим остаток  данного ряда.
данного ряда.
Пример 1. Оценить третий остаток ряда

Решение. Каждый член этого ряда меньше соответствующего члена геометрической прогрессии

со знаменателем  . Следовательно, третий остаток
. Следовательно, третий остаток  данного ряда меньше третьего остатка
данного ряда меньше третьего остатка  этой прогрессии:
этой прогрессии:

Таким образом, сумма данного ряда отличается от суммы его трех первых членов меньше, чем на 
Оценка остатка знакопеременного ряда
Теорема 2. Пусть дан абсолютно сходящийся знакопеременный ряд

Тогда абсолютная величина его  остатка не превосходит
остатка не превосходит  остатка ряда, составленного из абсолютных величин членов этого ряда. Доказательство. Пусть знакопеременный ряд
остатка ряда, составленного из абсолютных величин членов этого ряда. Доказательство. Пусть знакопеременный ряд

сходится абсолютно. Это значит, что сходится и ряд

Рассмотрим  остатки этих рядов
остатки этих рядов

При любом  имеем:
имеем:

Переходя в этом неравенстве к пределу при  , получим
, получим

или

Пример 2. Оценить третий остаток  ряда
ряда

Решение. Данный ряд знакопеременный, так как, например,

Рассмотрим ряд

Этот ряд сходится, так как его члены не превосходят соответствующих членов геометрической прогрессии 

Поэтому данный ряд сходится абсолютно.
Обозначая остатки данного ряда, ряда, составленного из абсолютных величин, и геометрической прогрессии соответственно через  , имеем
, имеем

Таким образом, находим оценку третьего остатка данного ряда

Оценка остатка знакочередующегося ряда сходящегося по признаку Лейбница
Особенно проста оценка остатка в случае знакочередующегося ряда.
Теорема 3. Если знакочередующийся ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит первого из отброшенных членов.
Доказательство. Пусть ряд

сходится по признаку Лейбница.
Тогда  остаток ряда
остаток ряда

сам является суммой знакочередующегося ряда. На основании признака Лейбница остаток  по абсолютной величине должен быть не больше первого члена ряда, т. е.
по абсолютной величине должен быть не больше первого члена ряда, т. е.

Пример 3. Вычислить с точностью до 0,01 сумму ряда

Решение. Данный ряд сходится по признаку Лейбница, поэтому

Так как сумма ряда должна быть вычислена с точностью до 0,01, то достаточно, чтобы выполнялось неравенство  или
или

Это неравенство выполняется, начиная с  . Таким образом,
. Таким образом,


Пусть дан ряд
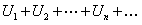 (12.1.5)
(12.1.5)
ОПРЕДЕЛЕНИЕ 12.1.5 Сумма, членами которой являются члены ряда (12.1.5), начиная с 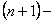 го, взятые в том же порядке, что и в исходном ряде, называется n-м остатком ряда и обозначается
го, взятые в том же порядке, что и в исходном ряде, называется n-м остатком ряда и обозначается
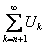 или
или 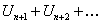
Частичная сумма сходящегося ряда отличается от его суммы на величину суммы остатка. Поэтому чем меньше сумма остатка ряда, тем точнее описывает соответствующая частичная сумма ряда сумму всего ряда.
ТЕОРЕМА 12.1.1 Если ряд (12.1.5) сходится, то сумма его 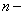 го остатка при
го остатка при 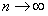 стремится к нулю.
стремится к нулю.
Доказательство. Обозначим 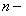 й остаток ряда через
й остаток ряда через 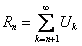 и будем для краткости называть просто остатком ряда, тогда
и будем для краткости называть просто остатком ряда, тогда
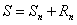 .(12.1.6)
.(12.1.6)
В (12.1.6) перейдем к пределу при 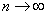 :
:
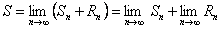 , так как ряд (12.1.5) по условию сходится, то
, так как ряд (12.1.5) по условию сходится, то 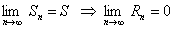 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Помощь по математике. Решение задач и контрольных работ
Остаток ряда
Материал из Большого Справочника
Ряд, полученный отбрасыванием от исходного n первых членов, называется n-м остатком ряда.
Обозначение:
Все члены, кроме тех, что входят в n-й остаток ряда, в сумме дают т. н. n-ю частичную сумму ряда.
Свойства
Для остатка ряда справедливы следующие утверждения:
- Если ряд сходится, то сходится любой его остаток.
- Если хотя бы один остаток ряда сходится, то и сам ряд сходится.
- Если ряд сходится, то
Существуют способы оценки остатка ряда с помощью интегрального признака Коши (для знакоположительного ряда) и Признака сходимости Лейбница (для знакочередующегося ряда).


