 Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
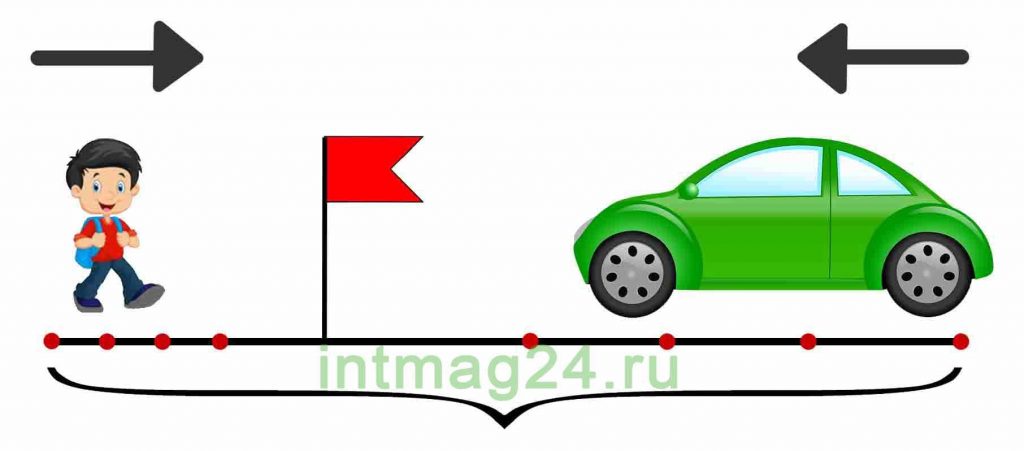
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
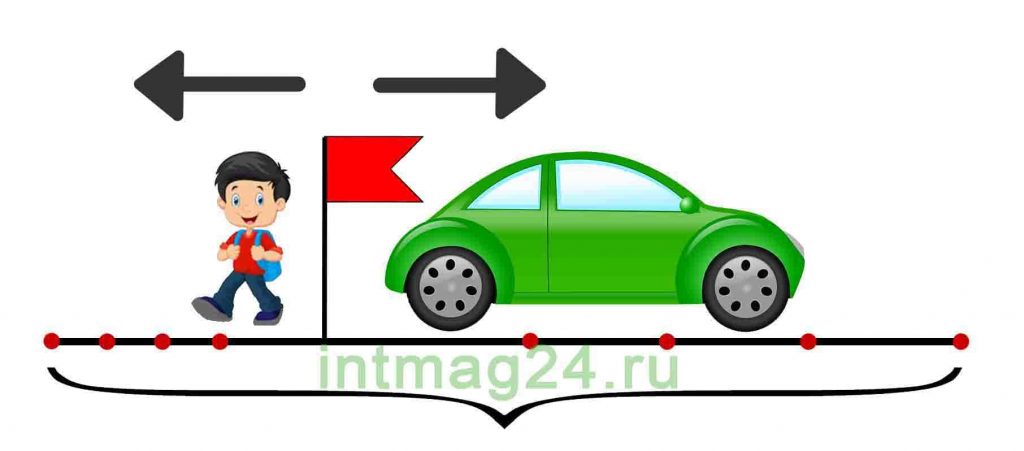
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.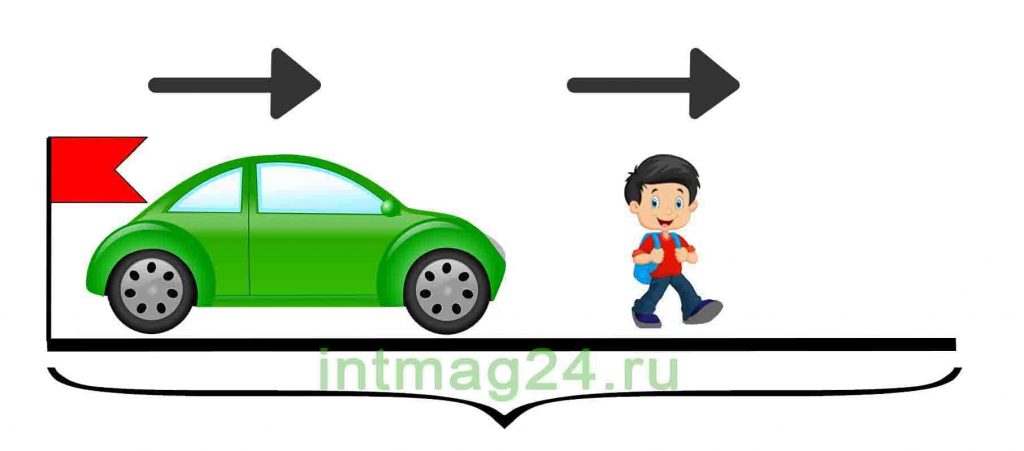
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
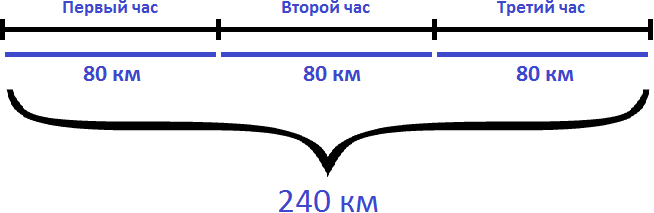
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
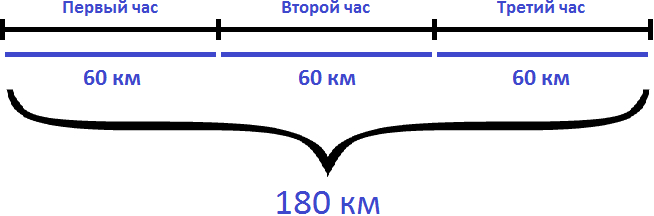
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
![]()
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
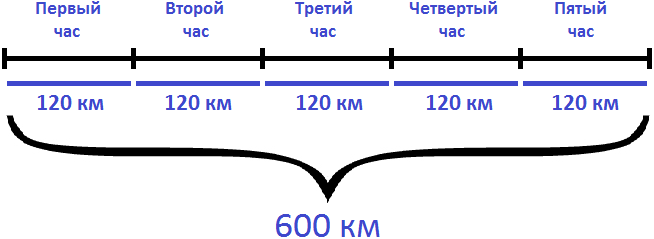
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
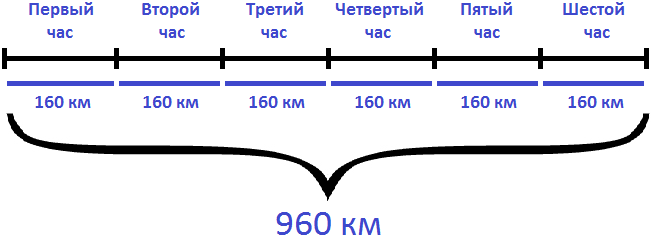
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
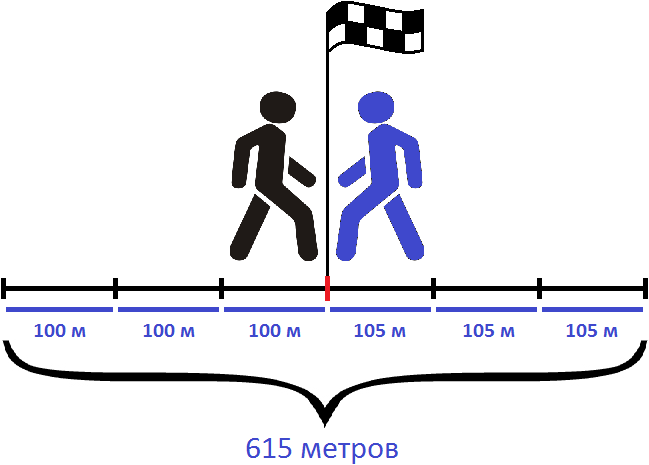
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
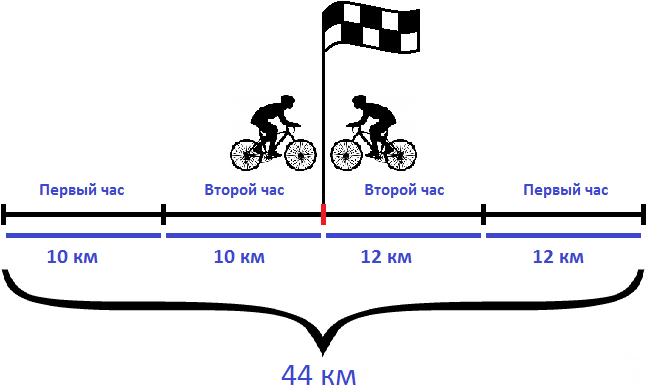
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
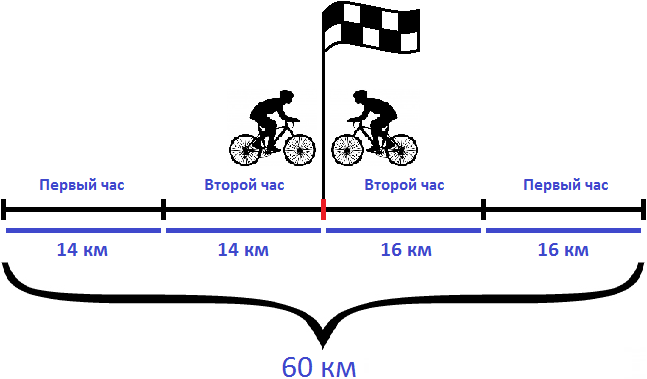
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
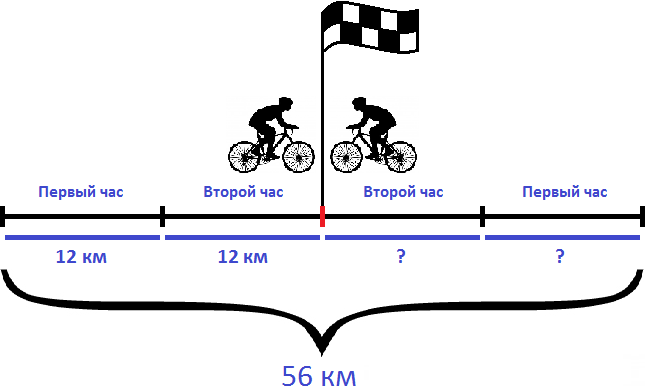
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
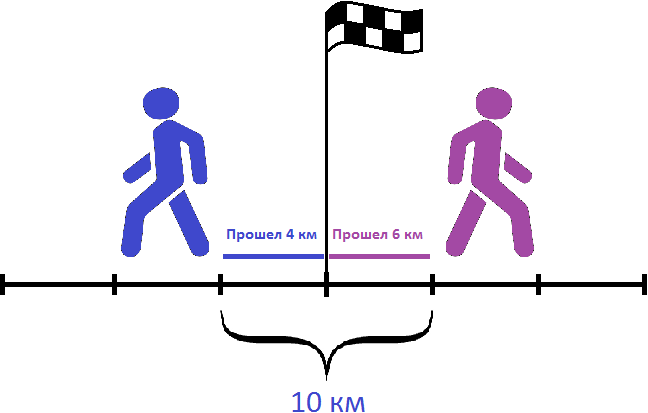
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
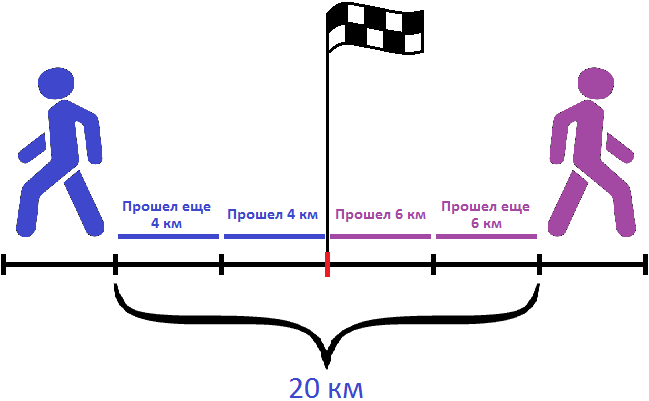
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
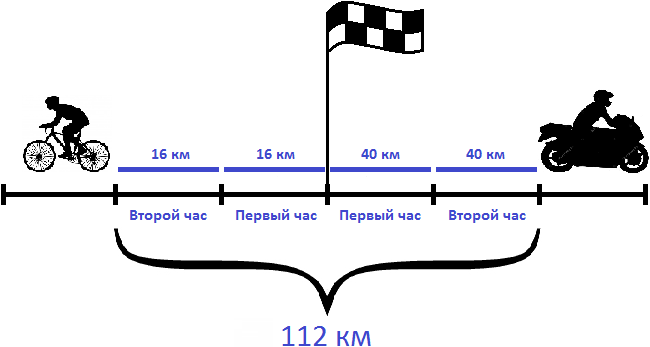
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
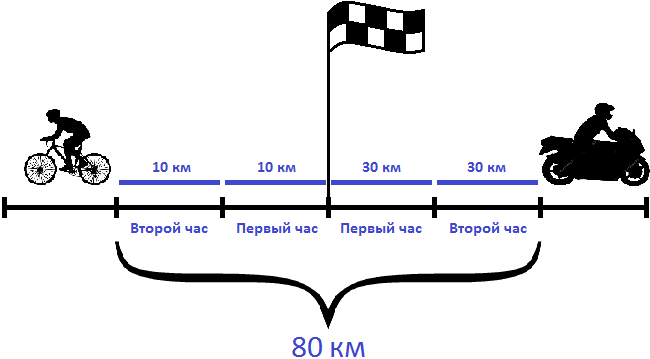
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
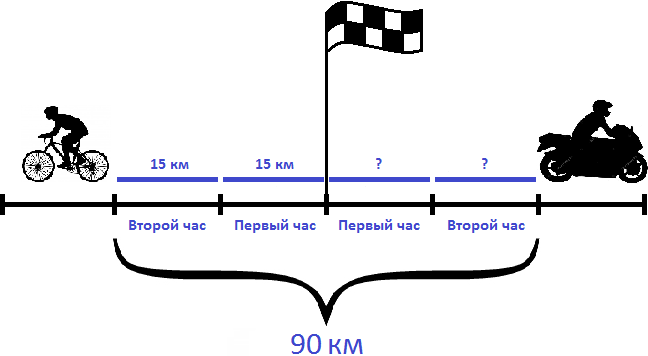
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
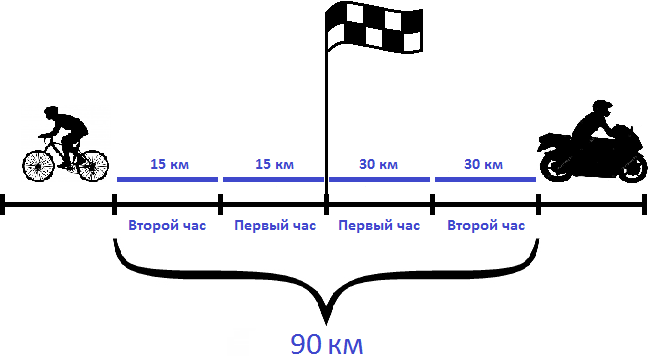
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние

Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние

Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
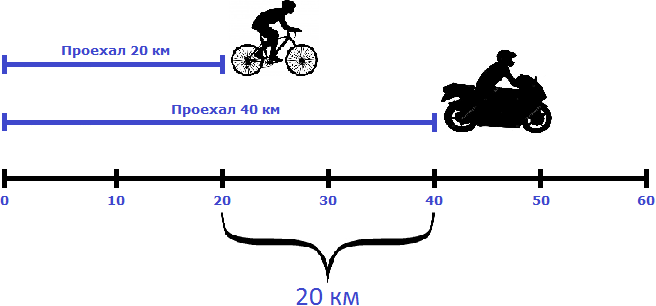
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
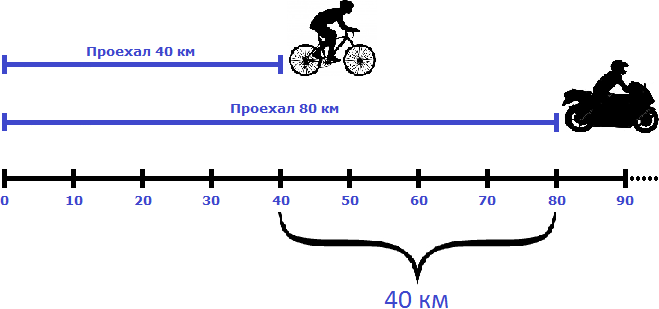
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
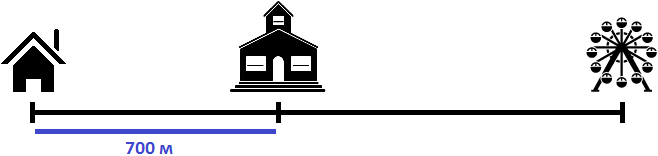
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
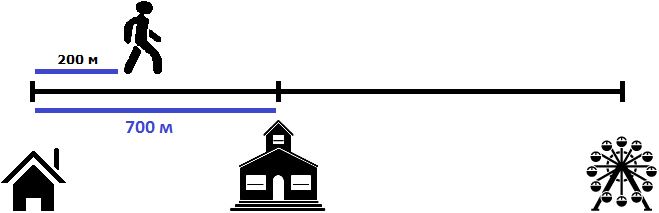
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
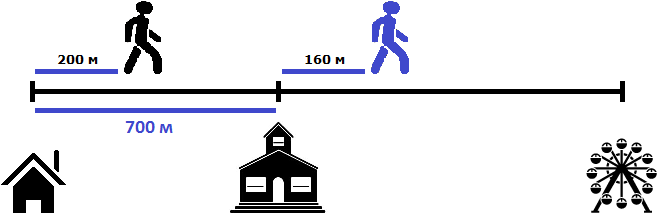
Теперь нужно найти расстояние между пешеходами
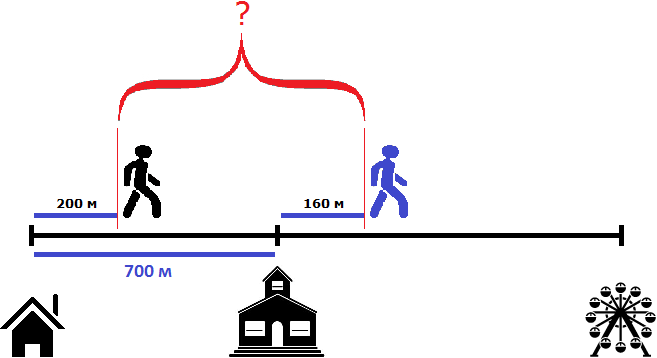
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
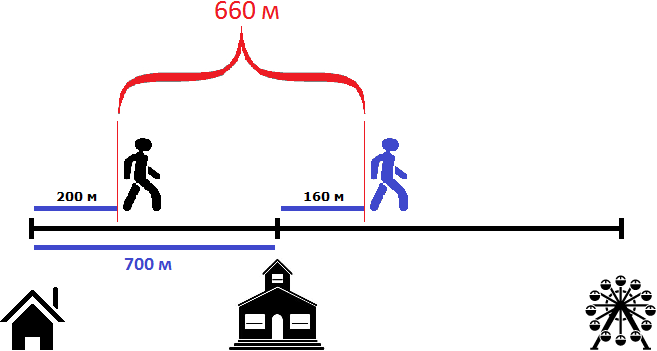
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
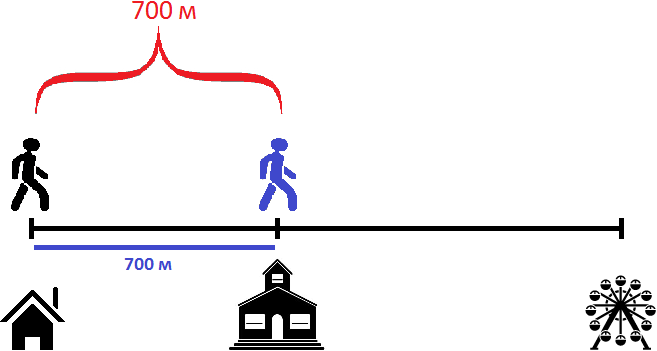
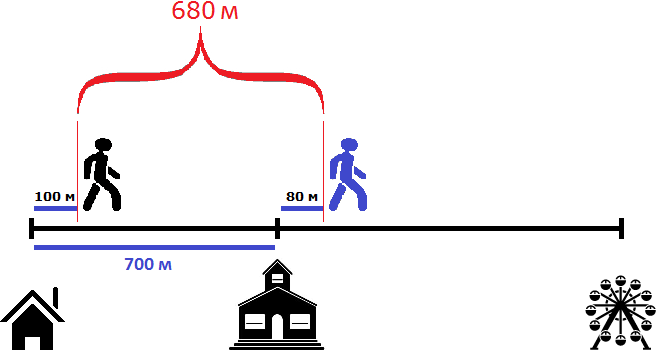
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м

Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
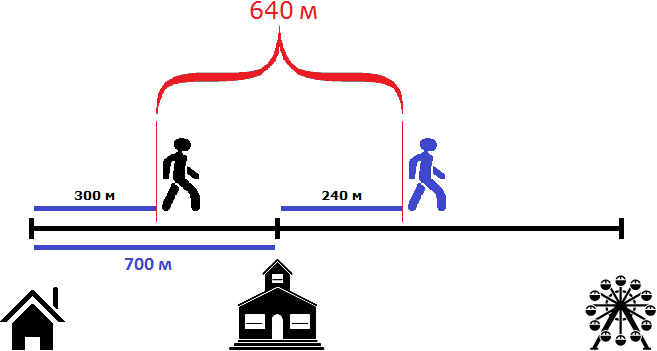
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
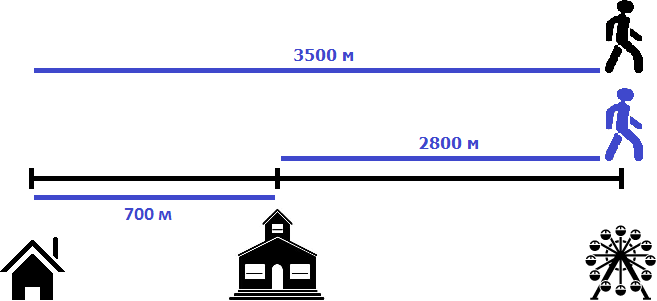
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
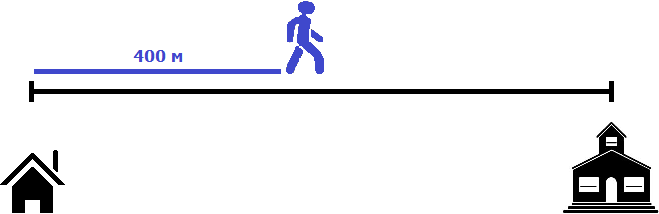
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
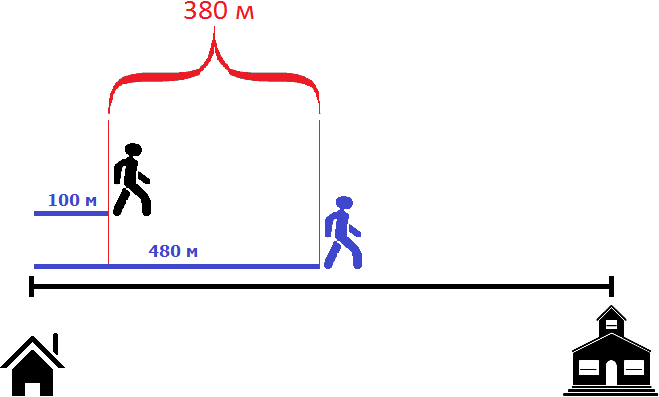
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
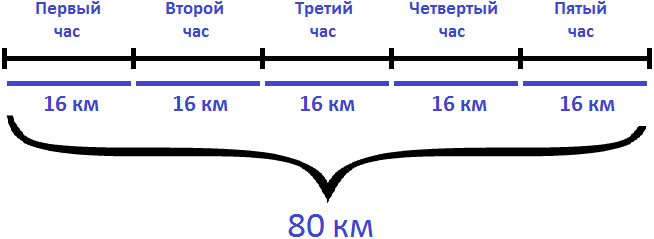
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
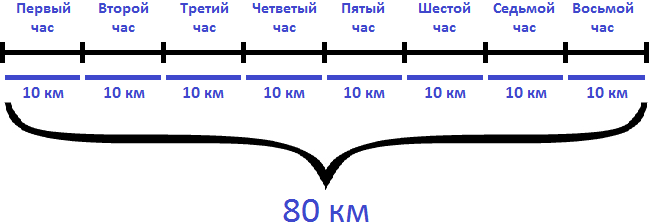
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
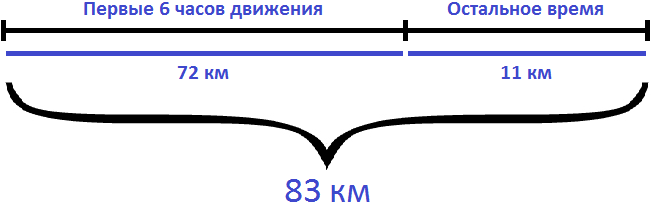
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
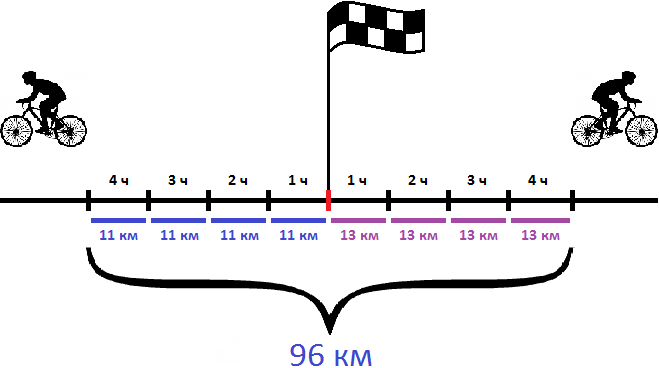
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет 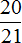 скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
Решение
Найдем скорость ростовского поезда. Она составляет 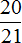 скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти
скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти 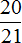 от 63 км
от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
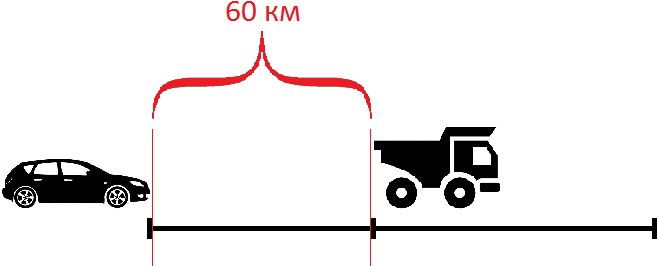
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
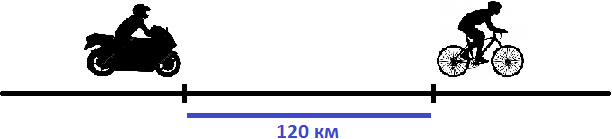
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
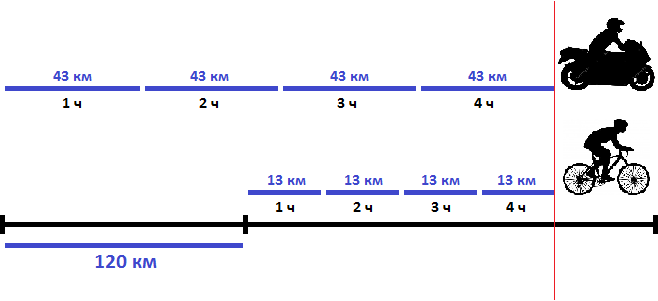
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение

Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
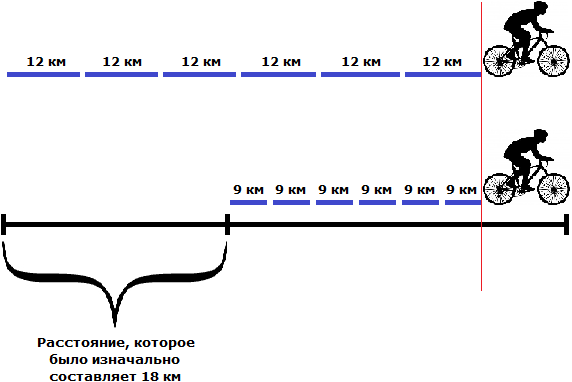
Ответ: между велосипедистами первоначально было 18 км.
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение

Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения

Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
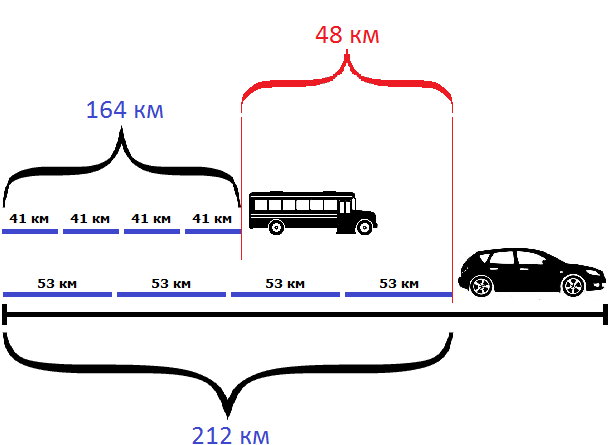
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Задачи на движение
 Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.
Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
- на больше
- в пять раз больше
- на меньше, чем
- меньше в раза
- на меньше, чем
- частное от деления на в полтора раза больше
- квадрат суммы и равен
- составляет процентов от
- больше на процентов
Пока не напишете — в ответы не подглядывайте! 🙂
Казалось бы, на первые три вопроса ответит и второклассник. Но почему-то у половины выпускников они вызывают затруднения, не говоря уже о вопросах и . Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Итак, правильные ответы:
- больше, чем . Разница между ними равна пяти. Значит, чтобы получить большую величину, надо к меньшей прибавить разницу.
- больше, чем , в пять раз. Значит, если умножить на , получим .
- меньше, чем . Разница между ними равна . Чтобы получить меньшую величину, надо из большей вычесть разницу.
- меньше, чем . Значит, если из большей величины вычтем разницу, получим меньшую.
- На всякий случай повторим терминологию:
Сумма — результат сложения двух или нескольких слагаемых.
Разность — результат вычитания.
Произведение — результат умножения двух или нескольких множителей.
Частное — результат деления чисел. - Мы помним, что .
- Если принять за , то на процентов больше, то есть .
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
- Все эти задачи решаются по одной-единственной формуле: , то есть расстояние скорость время. Из этой формулы можно выразить скорость или время .
- В качестве переменной удобнее всего выбирать скорость. Тогда задача точно решится!
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
. Из пункта в пункт , расстояние между которыми км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт на часа позже автомобилиста. Ответ дайте в км/ч.
Что здесь лучше всего обозначить за ? Скорость велосипедиста. Тем более, что ее и надо найти в этой задаче. Автомобилист проезжает на километров больше, значит, его скорость равна .
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
Его мы найдем по формуле: . Для велосипедиста получим , для автомобилиста .
Эти данные тоже запишем в таблицу.
Вот что получится:
| велосипедист |
| автомобилист |
Остается записать, что велосипедист прибыл в конечный пункт на часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит, что на четыре больше, чем , то есть
Приведем дроби в левой части к одному знаменателю.
Первую дробь домножим на , вторую — на .
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение. ), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю» или «Как раскрывать скобки» — вы получите нужный вам конкретный ответ. Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Разделим обе части нашего уравнения на . В результате уравнение станет проще. Но почему-то многие учащиеся забывают это делать, и в результате получают сложные уравнения и шестизначные числа в качестве дискриминанта.
Умножим обе части уравнения на . Получим:
Раскроем скобки и перенесем всё в левую часть уравнения:
Мы получили квадратное уравнение. Напомним, что квадратным называется уравнение вида . Решается оно стандартно — сначала находим дискриминант по формуле , затем корни по формуле .
В нашем уравнении , , .
Найдем дискриминант и корни:
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Следующая задача — тоже про велосипедиста.
2 . Велосипедист выехал с постоянной скоростью из города в город , расстояние между которыми равно км. На следующий день он отправился обратно со скоростью на км/ч больше прежней. По дороге он сделал остановку на часа. В результате он затратил на обратный путь столько же времени, сколько на путь из в . Найдите скорость велосипедиста на пути из в . Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из в равна . Тогда его скорость на обратном пути равна . Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
На обратном пути велосипедист сделал остановку на часа и в результате затратил столько же времени, сколько на пути из в . Это значит, что на обратном пути он крутил педали на часа меньше.
Значит, на три меньше, чем . Получается уравнение:
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Разделим обе части уравнения на .
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать». Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Умножим обе части уравнения на , раскроем скобки и соберем все в левой части.
Находим дискриминант. Он равен .
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ не подходит, так как скорость велосипедиста должна быть положительна.
Ты нашел то, что искал? Поделись с друзьями!
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад. Теперь скорость течения будет вычитаться из собственной скорости судна.
3 . Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна .
Тогда скорость движения моторки по течению равна , а скорость, с которой она движется против течения .
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению , при движении против течения , причем на два часа больше, чем .
| по течению |
| против течения |
Условие « на два часа больше, чем » можно записать в виде:
Приводим дроби в левой части к одному знаменателю
Делим обе части на , чтобы упростить уравнение
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и (оба этих числа при возведении в квадрат дают ). Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
4 . Теплоход проходит по течению реки до пункта назначения км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна км/ч, стоянка длится часов, а в пункт отправления теплоход возвращается через часов после отплытия из него. Ответ дайте в км/ч.
Снова обозначим за скорость течения. Тогда скорость движения теплохода по течению равна , скорость его движения против течения равна . Расстояния — и туда, и обратно — равны км.
Теперь графа «время».
Поскольку , время движения теплохода по течению равно , которое теплоход затратил на движение против течения, равно .
| по течению |
| против течения |
В пункт отправления теплоход вернулся через часов после отплытия из него. Стоянка длилась часов, следовательно, часов теплоход плыл — сначала по течению, затем против.
Прежде всего разделим обе части уравнения на . Оно станет проще!
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — приводим дроби в левой части к одному знаменателю, умножаем обе части уравнения на , получаем квадратное уравнение . Поскольку скорость течения положительна, получаем: .
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
5 . Баржа в вышла из пункта в пункт , расположенный в км от . Пробыв в пункте — час минут, баржа отправилась назад и вернулась в пункт в . Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.
Пусть скорость течения равна . Тогда по течению баржа плывет со скоростью , а против течения со скоростью .
Сколько времени баржа плыла? Ясно, что надо из вычесть , а затем вычесть время стоянки. Обратите внимание, что час минут придется перевести в часы: час минут часа. Получаем, что суммарное время движения баржи (по течению и против) равно часа.
| по течению |
| против течения |
Возникает вопрос — какой из пунктов, или , расположен выше по течению? А этого мы никогда не узнаем! 🙂 Да и какая разница — ведь в уравнение входит сумма , равная .
Решим это уравнение. Число в правой части представим в виде неправильной дроби: .
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Работать с дробными коэффициентами неудобно! Если мы разделим обе части уравнения на и умножим на , оно станет значительно проще:
Поскольку скорость течения положительна, .
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м , а второго — 105 м/м , то скорость сближения будет составлять 100 + 105 , то есть 205 м/м . Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
Найдем расстояние, пройденное вторым велосипедистом:
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Решение
Найдем скорость удаления велосипедистов
Узнаем какое расстояние будет между ними через 4 часа
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
Ответ: 510 км между автобусами будет через 5 часов.
Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
20 thoughts on “Задачи на движение”
Здравствуйте. Как решить такую задачу? Она вроде, и на движение, и на уравнение, но никак не мог понять как ее составить и решить.
Моторная лодка прошла против течения реки 297 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.
Задача на составление уравнения, содержащего рациональные выражения. В данном уроке такие задачи не рассмотрены. Обычно их решают в процессе изучения рациональных выражений.
x — скорость лодки в неподвижной воде
x — 2 — скорость лодки против течения
x + 2 — скорость лодки по течению
297/x-2 — время движения против течения
297/x+2 — время движения по течению
Тогда 297/x-2 = 297/x+2 + 3
Ответ: скорость лодки в неподвижной воде 20 км/ч
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-11-ege-zadachi-na-dvijenie/
[/spoiler]
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:

Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Задачи на встречное движение
Рассмотрим задачи, в которых речь идёт о встречном движении. В таких задачах два каких-нибудь объекта движутся навстречу друг другу. Задачи на встречное движение можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй — со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?

Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:
400 + 280 = 680 (км).
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч — это скорость сближения автомобилей. За 4 часа они проехали расстояние:
170 · 4 = 680 (км).
Таким образом, задачу на встречное движение можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Населённые пункты находятся на расстоянии 680 км.
Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?

Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
20 + 25 = 45 (км).
Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:
70 – 45 = 25 (км).
У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:
4 + 5 = 9 (км/ч).
Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):
9 · 5 = 45 (км).
А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:
70 – 45 = 25 (км).
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 70 – 45 = 25 (км) |
| 4) 70 – 45 = 25 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 25 км.
