Как найти остовное дерево минимального веса

Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.

Формальная постановка задачи

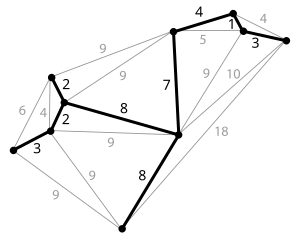
Имеется следующий неориентированный взвешенный граф. Назовем остовным деревом подграф, содержащий все вершины исходного графа, который является деревом. И задача состоит в том, чтобы найти такое остовное дерево, сумма рёбер которого минимальна.

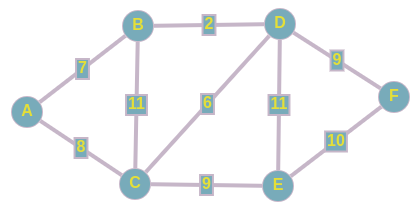
Неформальная постановка задачи

Представьте исходный граф без рёбер, теперь вам нужно как-то соединить все вершины между собой, чтобы можно было бы попасть из любой вершины в другую, не имея при этом циклов в получившемся графе с минимально возможной суммой весов включенных рёбер.

Алгоритм Краскала

Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.

• Вначале мы производим сортировку рёбер по неубыванию по их весам.

• Добавляем i-ое ребро в наш подграф только в том случае, если данное ребро соединяет две разные компоненты связности, одним из которых является наш подграф. То есть, на каждом шаге добавляется минимальное по весу ребро, один конец которого содержится в нашем подграфе, а другой – еще нет.

• Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.

Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.

Разбор конкретного примера по шагам

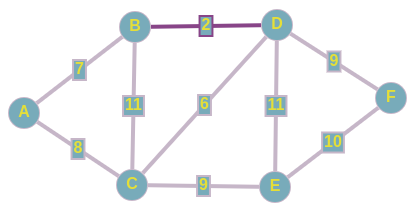
При добавлении в наше остовное дерево ребра A <--> C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.

По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.

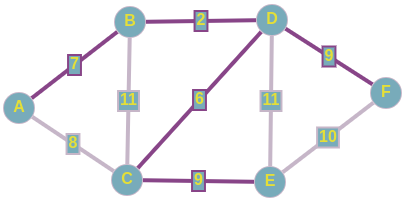
Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.

Суммарный вес искомого MST равен 33.

Реализация

Псевдокод

vector<int> parent, rank;

void make_set(int v) {
    parent[v] = v;
    rank[v] = 0;
}

int find_set(int v) {
    if (v == parent[v])
        return v;
    return parent[v] = find_set(parent[v]);
}

void union_sets(int a, int b) {
    a = find_set(a);
    b = find_set(b);
    if (a != b) {
        if (rank[a] < rank[b])
            swap(a, b);
        parent[b] = a;
        if (rank[a] == rank[b])
            rank[a]++;
    }
}

struct Edge {
    int u, v, weight;
    bool operator<(Edge const& other) {
        return weight < other.weight;
    }
};

int n;
vector<Edge> edges;

int cost = 0;
vector<Edge> result;
parent.resize(n);
rank.resize(n);
for (int i = 0; i < n; i++)
    make_set(i);

sort(edges.begin(), edges.end());

for (Edge e : edges) {
    if (find_set(e.u) != find_set(e.v)) {
        cost += e.weight;
        result.push_back(e);
        union_sets(e.u, e.v);
    }
}

Алгоритм Прима

Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.

• Изначально наш подграф состоит из одной любой вершины исходного графа.

• Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.

• Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.

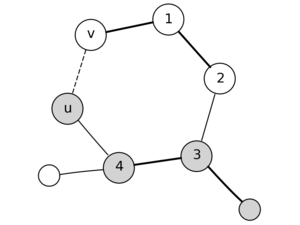
Разбор конкретного примера

Выбираем чисто случайно вершину E,далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C <--> E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее:

Теперь выборка производится из рёбер:
D <--> C; w = 6
A <--> C; w = 8
F <--> E; w = 10
B <--> C; w = 11
D <--> E; w = 11

То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.

Добавляем в наш подграф реброD <--> C и по аналогии добаляем ребро D <--> B. Получаем следующее:

Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины:
A и F.

Проводим последние штрихи и получили тот же самый подграф в качестве минимального остовного дерева. Но как мы раннее говорили, сам подграф ничего не решает, главное тут – множество рёбер, которые включены в наше остовное дерево.

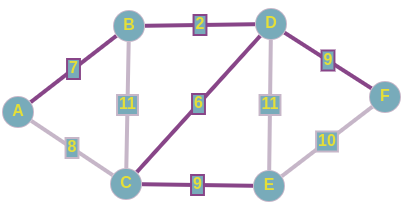
Суммарный вес искомого MST равен 33.

Источники

Инструмент для работы с графами
Лекция Павла Маврина

Насколько подробно я расписываю? (Учтите, что приоритетом данных статей является разжевывание)

Проголосовали 33 пользователя.

Воздержались 6 пользователей.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 ноября 2020 года; проверки требуют 5 правок.

Минимальное остовное дерево (или минимальное покрывающее дерево) в (неориентированном) связном взвешенном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

Пример[править | править код]

Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: допустим, есть n городов, которые необходимо соединить дорогами так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой такой дороги. Требуется решить, какие именно дороги нужно строить, чтобы минимизировать общую стоимость строительства.

Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, рёбра — это пары городов, между которыми можно проложить прямую дорогу, а вес ребра равен стоимости строительства соответствующей дороги.

Алгоритмы[править | править код]

Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них перечислены ниже:

• Алгоритм Прима,
• Алгоритм Краскала (или алгоритм Крускала),
• Алгоритм Борувки,
• Алгоритм обратного удаления (получение минимального остовного дерева из связного рёберно взвешенного графа).

Родственные задачи[править | править код]

На задачу о нахождении минимального остовного дерева похожа задача о дереве Штейнера. В ней задано несколько точек на плоскости и требуется проложить между ними граф путей так, чтобы минимизировать сумму длин путей. Главное отличие от задачи о минимальном остовном дереве при этом заключается в том, что разрешается добавлять дополнительные точки ветвления с целью ещё сильнее уменьшить сумму длин рёбер. Задача о дереве Штейнера является NP-полной.

Литература[править | править код]

• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 23. Минимальные остовные деревья // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4.

const int maxn = 1e5, inf = 1e9;
vector from, to, weight;
bool used[maxn]

// считать все рёбра в массивы

used[0] = 1;
for (int i = 0; i < n-1; i++) {
    int opt_w = inf, opt_from, opt_to;
    for (int j = 0; j < m; j++)
        if (opt_w > weight[j] && used[from[j]] && !used[to[j]])
            opt_w = weight[j], opt_from = from[j], opt_to = to[j]
    used[opt_to] = 1;
    cout << opt_from << " " << opt_to << endl;
}

const int maxn = 1e5, inf = 1e9;
bool used[maxn];
vector< pair<int, int> > g[maxn];
int min_edge[maxn] = {inf}, best_edge[maxn];
min_edge[0] = 0;

// ...

for (int i = 0; i < n; i++) {
    int v = -1;
    for (int u = 0; u < n; j++)
        if (!used[u] && (v == -1 || min_edge[u] < min_edge[v]))
            v = u;

    used[v] = 1;
    if (v != 0)
        cout << v << " " << best_edge[v] << endl;

    for (auto e : g[v]) {
        int u = e.first, w = e.second;
        if (w < min_edge[u]) {
            min_edge[u] = w;
            best_edge[u] = v;
        }
    }
}

set< pair<int, int> > q;
int d[maxn];

while (q.size()) {
    v = q.begin()->second;
    q.erase(q.begin());

    for (auto e : g[v]) {
        int u = e.first, w = e.second;
        if (w < d[u]) {
            q.erase({d[u], u});
            d[u] = w;
            q.insert({d[u], u});
        }
    }
}

int _p[maxn];

int p(int v) {
    if (_p[v] == v)
        return v;
    else
        return p(_p[v]);
}

void unite(int a, int b) {
    a = p(a), b = p(b);
    _p[a] = b;
}

for (int i = 0; i < n; i++)
    _p[i] = i;

int _p[maxn], s[maxn];

int p (int v) { return (_p[v] == v) ? v : _p[v] = p(_p[v]); }

void unite(int a, int b) {
    a = p(a), b = p(b);
    if (s[a] > s[b])
        swap(a, b);
    s[b] += s[a];
    _p[a] = b;
}

// где-то в main:

for (int i = 0; i < n; i++)
    _p[i] = i;

// (w, (a, b))
vector< pair< int, pair<int, int> > > edges;

sort(edges.begin(), edges.end());

for (auto e : edges) {
    int a = e.first.first, b = e.first.second;
    // компоненты разные, если лидеры разные
    if (p(a) != p(b)) {
        // добавим ребро (a, b)
        unite(a, b);
    }
}

Minimum spanning Tree (MST) is an important topic for GATE. Therefore, we will discuss how to solve different types of questions based on MST. Before understanding this article, you should understand basics of MST and their algorithms (Kruskal’s algorithm and Prim’s algorithm).

Type 1. Conceptual questions based on MST –
There are some important properties of MST on the basis of which conceptual questions can be asked as:

• The number of edges in MST with n nodes is (n-1).
• The weight of MST of a graph is always unique. However there may be different ways to get this weight (if there edges with same weights).
• The weight of MST is sum of weights of edges in MST.
• Maximum path length between two vertices is (n-1) for MST with n vertices.
• There exists only one path from one vertex to another in MST.
• Removal of any edge from MST disconnects the graph.
• For a graph having edges with distinct weights, MST is unique.

Que – 1. Let G be an undirected connected graph with distinct edge weight. Let emax be the edge with maximum weight and emin the edge with minimum weight. Which of the following statements is false? (GATE CS 2000)
(A) Every minimum spanning tree of G must contain emin.
(B) If emax is in a minimum spanning tree, then its removal must disconnect G
(C) No minimum spanning tree contains emax
(D) G has a unique minimum spanning tree

Solution: As edge weights are unique, there will be only one edge emin and that will be added to MST, therefore option (A) is always true.
As spanning tree has minimum number of edges, removal of any edge will disconnect the graph. Therefore, option (B) is also true.
As all edge weights are distinct, G will have a unique minimum spanning tree. So, option (D) is correct.
Option C is false as emax can be part of MST if other edges with lesser weights are creating cycle and number of edges before adding emax is less than (n-1).

Type 2. How to find the weight of minimum spanning tree given the graph –
This is the simplest type of question based on MST. To solve this using kruskal’s algorithm,

• Arrange the edges in non-decreasing order of weights.
• Add edges one by one if they don’t create cycle until we get n-1 number of edges where n are number of nodes in the graph.

Que – 2. Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry Wij in the matrix W below is the weight of the edge {i, j}. What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T? (GATE CS 2010)

(A) 7
(B) 8
(C) 9
(D) 10

Solution: In the adjacency matrix of the graph with 5 vertices (v1 to v5), the edges arranged in non-decreasing order are:

(v1,v2), (v1,v4), (v4,v5), (v3,v5), (v1,v5), 
(v2,v4), (v3,v4), (v1,v3), (v2,v5), (v2,v3) 

As it is given, vertex v1 is a leaf node, it should have only one edge incident to it. Therefore, we will consider it in the end. Considering vertices v2 to v5, edges in non decreasing order are:

(v4,v5), (v3,v5), (v2,v4), (v3,v4), (v2,v5), (v2,v3)

Adding first three edges (v4,v5), (v3,v5), (v2,v4), no cycle is created. Also, we can connect v1 to v2 using edge (v1,v2). The total weight is sum of weight of these 4 edges which is 10.

Type 3. How many minimum spanning trees are possible using Kruskal’s algorithm for a given graph –

• If all edges weight are distinct, minimum spanning tree is unique.
• If two edges have same weight, then we have to consider both possibilities and find possible minimum spanning trees.

Que – 3. The number of distinct minimum spanning trees for the weighted graph below is ____ (GATE-CS-2014)

(A) 4
(B) 5
(C) 6
(D) 7

Solution: There are 5 edges with weight 1 and adding them all in MST does not create cycle.
As the graph has 9 vertices, therefore we require total 8 edges out of which 5 has been added. Out of remaining 3, one edge is fixed represented by f.

For remaining 2 edges, one is to be chosen from c or d or e and another one is to be chosen from a or b. Remaining black ones will always create cycle so they are not considered. So, possible MST are 3*2 = 6.

Type 4. Out of given sequences, which one is not the sequence of edges added to the MST using Kruskal’s algorithm –
To solve this type of questions, try to find out the sequence of edges which can be produced by Kruskal. The sequence which does not match will be the answer.

Que – 4. Consider the following graph:

Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm? (GATE-CS-2009)
(A) (b,e), (e,f), (a,c), (b,c), (f,g), (c,d)
(B) (b,e), (e,f), (a,c), (f,g), (b,c), (c,d)
(C) (b,e), (a,c), (e,f), (b,c), (f,g), (c,d)
(D) (b,e), (e,f), (b,c), (a,c), (f,g), (c,d)

Solution: Kruskal algorithms adds the edges in non-decreasing order of their weights, therefore, we first sort the edges in non-decreasing order of weight as:

(b,e), (e,f), (a,c), (b,c), (f,g), (a,b), (e,g), (c,d), (b,d), (e,d), (d,f).

First it will add (b,e) in MST. Then, it will add (e,f) as well as (a,c) (either (e,f) followed by (a,c) or vice versa) because of both having same weight and adding both of them will not create cycle.
However, in option (D), (b,c) has been added to MST before adding (a,c). So it can’t be the sequence produced by Kruskal’s algorithm.

Среди всех
каркасов графа в практическом плане
часто интересует каркас
минимального
веса.
Например, если граф является моделью
для решения задачи проектирования сети
связи между несколькими населенными
пунктами – требуется минимизировать
длину (стоимость) кабеля связи. В этом
случае граф G
=
(V,E)
будет связным взвешенным неориентированным,
таким образом, каждому
ребру приписано некоторое число (вес)
(рис.7.4) и необходимо найти каркас с
минимальным суммарным весом A
=
(V,B),
где BE
(рис.7.5).

Рассмотрим общую
схему работы алгоритмов построения
минимального остовного дерева с
использованием жадной
стратегии.
Итак, пусть дан связный неориентированный
граф G
c n
вершинами и весовая функция w:
E →
R.

Искомый остов
строится постепенно. Алгоритм использует
некоторый ациклический подграф А
исходного графа G,
который называется промежуточным
остовным лесом. Изначально G
состоит из
n вершин-компонент,
не соединенных друг с другом (n
деревьев из
одной вершины). На каждом шаге в A
добавляется одно новое ребро. Граф A
всегда является подграфом некоторого
минимального остова. Очередное добавляемое
ребро e=(u,v)
выбирается так, чтобы не нарушить этого
свойства: A
U
{e}
тоже должно быть подграфом минимального.
Такое ребро
называется безопасным
(ребро
G
называется безопасным (safe),
если для некоторой компоненты A
это ребро является самым лёгким из всех
рёбер, соединяющих вершины этой компоненты
с оставшимися вершинами).

Вот как выглядит
общий алгоритм
построения минимального остовного
дерева:

MIN_OSTOV(G,w)
1:
A
← 0
2:
While
(пока) A
не является остовом
3:
    Do
найти безопасное ребро (u,v)
∈
E
для A
4:
         A
← A
U
{(u,v)}
5:
Return
A

По определению A,
он должен оставаться подграфом некоторого
минимального остова после любого числа
итераций. Конечно, главный вопрос состоит
в том, как искать безопасное ребро на
шаге 3. Понятно, что такое ребро всегда
существует, если A
еще не является минимальным остовом
(любое ребро остова, не входящее в A).
Заметим, что так как A
не может содержать циклов, то на каждом
шаге ребром соединяются различные
компоненты связности (изначально все
вершины в отдельных компонентах, в конце
A –
одна компонента). Таким образом цикл
выполняется (n-1)
раз.

У
задачи построения минимального остовного
дерева длинная и богатая история[2
]R.
L.
Graham
and
P.
Hell.
On the
history of the minimum spanning tree problem. Annals of the History
of Computing, 7(1): 43-57, 1985.

Впервые
работа на эту тему был опубликован в
1926 году Отакаром Борувкой в качестве
метода нахождения оптимальной
электрической сети в Моравии.

В
настоящее время наиболшую известность
получили алгоритмы Крускала и Прима.

Алгоритм
Крускала.
Первый из предлагаемых алгоритмов
принадлежи классу так называемых жадных
алгоритмов. Этот
алгоритм пытается найти решение
поставленной задачи в лоб, стараясь
найти минимальное остовное дерево
последовательным отбором ребер с
минимальным весом, следя за тем, чтобы
получающийся граф не имел циклов.
Разумеется, для этого необходимо сначала
отсортировать все ребра графа по
возрастанию их весов. Лучше всего, если
граф с самого начала представлен списком
ребер, в этом случае сортировка будет
наиболее естественной. Но даже и в других
случаях сортировка ребер графа по весу
занимает не слишком много времени – в
худшем случае mlog₂m,
где m
– количество ребер графа.

После сортировки
ребер по весу строящееся остовное дерево
организуется в виде отдельных фрагментов
этого дерева, в которые в каждый момент
времени включены все вершины графа. В
начале работы каждая вершина графа
представляет собой отдельную компоненту,
а соединяющих их ребер пока вообще нет.
Каждое вновь включаемое ребро соединяет
две отдельные компоненты в одну, таким
образом, полное остовное дерево будет
построено после n-1
включения ребра.
Разумеется,
очередное ребро можно включить в дерево,
только если его концы принадлежат разным
компонентам, в противном случае в
компоненте образуется цикл. Таким
образом, если очередное ребро соединяет
вершины, принадлежащие одной связной
компоненте, то такое ребро не включается
в строящееся остовное дерево и игнорируется
алгоритмом.

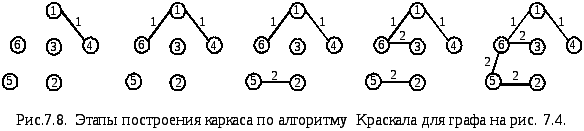
Рассмотрим
реализацию алгоритма на примере графа
на рис.7.4[Окулов].
Потребуется массив
меток вершин графа
и массив
ребер отсортированных по весам
(рис.
7.6).

Начальные значения
элементов массива
меток
M
равны номерам соответствующих вершин.
Ребро выбирается в каркас в том случае,
если вершины, соединяемые им, имеют
разные значения меток. В этом случае
циклы не образуются. Для примера,
приведенного выше, процесс изменения
Mark показан на рис.
.

Реализация
алгоритма:

1.
Ищем ребро <
v,
w
> с различными
метками инцидентных ему вершин.

2.
Копируем метку М[
v]

M[w]
, если
М[v]
< M[w]
и, наоборот,

М[w]

M[v]
, если
М[w]
< M[v].

3.
Повторяем эти действия n-1
раз (по числу
ребер, которые образуют каркас).

В конце концов все
элементы массива М
приобретут значение метки равной 1
(рис.
7.7)

Процесс разметки
начинается и распространяется с ребер,
имеющих меньший вес, поэтому именно они
в первую очередь будут включаться в
каркас. Кроме того, ребра имеющие
одинаковые метки в вершинах, инцидентных
ему, исключаются в текущий момент из
рассмотрения. При реализации алгоритма
используется дополнительная процедура
Marker.

На рис. рис.
7.8.
представлена последовательность этапов
при построении компонент остовного
дерева согласно жадному алгоритму. В
качестве исходного графа выбран граф
рис.7.4.
Первоначально остовное дерево состоит
из отдельных вершин исходного графа,
жадный алгоритм постепенно добавляет
к нему ребра, начиная с ребер с наименьшим
весом. На рис.
7.8, б показаны
5 последовательных этапов построения
остовного дерева согласно жадному
алгоритму. На каждом этапе в остовное
дерево включается новое ребро. Ребра,
замыкающие цикл в уже построенной части,
игнорируются алгоритмом.

Procedure
Marker
( a,
b
:Integer
); { меньшую
метку распространяет на все

вершины,
инцидентные данному ребру (a,b)}

Var
i, c :Integer;

Begin

If
a > b Then
Begin
c := a; a := b; b := c; End;
{ делаем
а
<b }

For
i := 1 To n Do

If
M[ i ] = b Then
M[ i ] := a;

End;

Procedure
Kruskal;

Var
i, j, v, w :Integer;

Begin

СОРТИРОВКА
ребер R
по возрастанию их весов;

For
i :=1 To
n Do

M[ i ] := i;

For
i :=1 To
n-1 Do
Begin

For
j := 1 To
n Do
Begin

v :=R[
1, j ]; w := R[ 2, j ];

If
M[ v ] < > M[ w ] Then
Break;

End;

Write(
v:3, w:3); {вывод
ребра}

Marker
( M[
v
], M[
w
] ); { меньшую
метку распространяет на все}

End;
{вершины,
инцидентные данному ребру (a,b)}

End;

Общее
время работы алгоритма Крускала
составляет O(ElogE)
(основное время уходит на сортировку).
Скорость работы жадного алгоритма
определяется скоростью, с которой будут
выбраны и отсортированы все ребра графа,
т. к. вся остальная работа обычно занимает
меньше времени. Тем не менее для больших
графов, построение и проверка деревьев
компонент строящегося остовного дерева
может занимать значительное время, если
они вырождаются в линейные списки
вершин, что вполне возможно в некоторых
специфических ситуациях.

Алгоритм
Прима.
В этом алгоритме построение остовного
дерева начинается с одной вершины, к
которой затем добавляются ребра таким
образом, чтобы каждое новое ребро одним
своим концом опиралось в уже построенную
часть дерева, а другой конец лежал бы в
множестве еще не присоединенных к дереву
вершин. Из всех таких ребер на каждом
шаге выбирается ребро с наименьшим
весом. Алгоритм Прима следует общей
схеме алгоритма построения минимального
остовного дерева: на каждом шаге мы
добавляем к строящемуся остову безопасное
ребро. Как и прежде воспользуемся
«жадным»
алгоритмом. Жадные алгоритмы действуют,
используя в каждый момент лишь часть
исходных данных и принимая лучшее
решение на основе этой части. В нашем
случае мы будем на каждом шаге рассматривать
множество ребер, допускающих присоединение
к уже построенной части остовного
дерева, и выбирать из них ребро с
наименьшим весом. Повторяя эту процедуру,
мы получим остовное дерево с наименьшим
весом. Отличие
этого метода от метода Крускала
заключается в том, что на каждом шаге
строится дерево, а не ациклический граф
(граф без циклов).

Для
реализации введем две переменные
множественного типа S0
и
S1.
Первоначально в S1
находятся все вершины графа, кроме
начальной, а в S0
только начальная. Далее ищется ребро
минимального веса, соединяющего вершину
из S0

и одну из вершин v,
принадлежащую
S1.
Найденное ребро включается в Q,
а вершина v
исключается из S1
и включается в S0.
Далее повторяется поиск следующего
ребра до тех пор, пока S1
не станет пустым.

На рис.
7.9 приведен
пример построения каркаса по алгоритму
Прима. Программная реализация алгоритма
приведена ниже. В ней используется
вспомогательная функция Extract_Min,
которая ищет кратчайшее ребро, соединяющее
вершины из S0
и
S1.

S0,
S1
:Set
Of
Byte;
{ S0
– множество выбранных вершин; }

{
S1
– множество невыбранных вершин;}

Function
Extract_Min
:Byte;
{возвращает
вершину v
из S1
–
самую }

Var
i,
j,
w,
v,
Min
:Integer;
{
« близкую»
к множеству вершин
S0
}

Begin
Min := MaxInt;

For
i := 0 To n-1 Do {перебор
вершин
в
S0}

If

i
In
S0

Then
For
j := 0 To n-1 Do {перебор
вершин
в
S1}

If
j In
S1

Then
If
( A[ i, j ] <> 0 ) And
( A[ i, j ] < Min )

Then
Begin

Min := A[
i, j ];

w
:= i; v:=j;

End;

WriteLn( w :3, v
:3 );

Extract_Min
:= v;

End;

Procedure
Prima ( s :Byte ); {
s
– начальная
вершина}

Var
v :Byte;

Begin

S0 := [ s ];

S1 := [ 0..n – 1 ] – [ s
];

While
S1 <> [ ] Do
Begin

v
:= Extract_Min;

S0
:= S0 + [ v ];

S1
:= S1 – [ v ];

End;

End;

Время работы
алгоритма Прима зависит от того, как
реализована функция Extract_Min.
Если вместо множеств S0
и S1
использовать очередь с приоритетами,
то это время составит O(ElogV).

Алгоритмы имеют
разную производительность на различных
графах. Скорость работы алгоритма
Крускала зависит, прежде всего, от
количества ребер в графе и слабо зависит
от количества вершин. Напротив, скорость
работы алгоритма Прима определяется
количеством вершин и слабо зависит от
числа ребер. Следовательно, алгоритм
Крускала следует применять в случае
неплотных или разреженных графов, у
которых количество ребер мало по
сравнению с количеством ребер у полного
графа. Если известно, что ребер в графе
достаточно много, то для поиска
минимального остовного дерева лучше
применять алгоритм Прима.

Конечно, реальная
скорость работы зависит и от представления
графа, и от реализации основных операций
над ним, и от реализации самих алгоритмов
нахождения минимального остовного
дерева, так что приведенные выше
рекомендации носят очень приблизительный
характер. Лучше всего поэкспериментировать
немного самому, пробуя применить разные
алгоритмы к различным графам.

9

Соседние файлы в папке Lektsii_TRPO

• #
• #
• #
• #
• #
• #
• #