
Номер задания № 661 из решебника ГДЗ на учебник по Геометрии 7, 8, 9 классов от авторов Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев. Готовое домашнее задание актуально на 2014-2018 годы.
Условие
Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащей вне окружности, если дуги, заключенные между секущими, равны 140° и 52°.
Другие задания из этого решебника
- Ответкин
- Решебники
- 7 класс
- Геометрия
- Атанасян
- Номер №661


ГДЗ (готовое домашние задание из решебника) на Номер №661 по учебнику Геометрия 7-9 классы: учебник для общеобразовательных организаций / Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 2-е издание. Просвещение, 2014-2019г.
Условие
Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащей вне окружности, если дуги, заключенные между секущими, равны 140° и 52°.
Решение 1
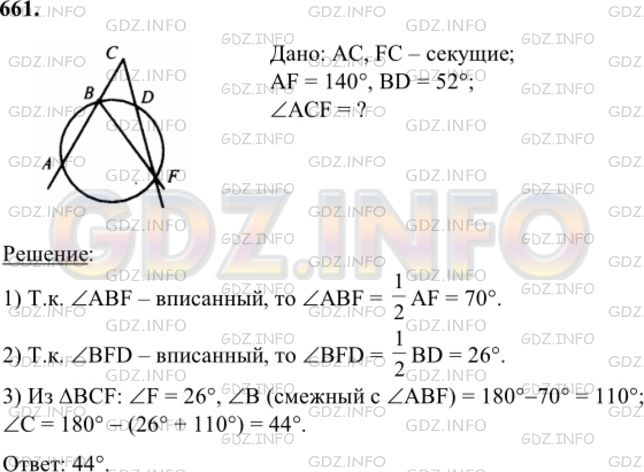
Решение 2

Решение 3

Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
Доказательства теорем об углах, связанных с окружностью
Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).




Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства



и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства



что и завершает доказательство теоремы 1.
Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства


что и требовалось доказать.
Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство . Рассмотрим рисунок 9.


Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства


что и требовалось доказать.
Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство . Рассмотрим рисунок 10.


Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства


что и требовалось доказать
Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство . Рассмотрим рисунок 11.


Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства


что и требовалось доказать.
Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.
Доказательство . Рассмотрим рисунок 12.


Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство
Углы, связанные с окружностью.
Центральный угол — угол, вершина которого совпадает с центром окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают её.
Вписанный угол в два раза меньше центрального , опирающегося на ту же дугу.

Все вписанные углы , опирающиеся на одну и ту же дугу равны.

Все вписанные углы , опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.

Все вписанные углы , опирающиеся на диаметр, прямые.

Любые два вписанных угла , опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.

Угол между пересекающимися хордами измеряется полусуммой дуг, заключенных между его сторонами.

Угол между секущими, пересекающимися вне окружности, измеряется полуразностью дуг, заключенных между его сторонами.

Угол между касательной и секущей, пересекающимися вне окружности, измеряется полуразностью дуг, заключенных между его сторонами.

Угол между касательными к окружности измеряется полуразностью дуг, заключенных между его сторонами.

Угол между касательной и хордой, проходящей через точку касания, равняется половине центрального угла, опирающегося на данную хорду:
Угол между секущими
Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.
Проведём хорду AN.
Для треугольника APN ∠ANC — внешний угол при вершине N.
Так как внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним,
∠ANC — вписанный угол, опирающийся на дугу AC,
∠PAN — вписанный угол, опирающийся на дугу MN.
Так как вписанный угол равен половине дуги, на которую он опирается, то
[spoiler title=”источники:”]
http://anasta8ia.ru/angles-associated-with-the-circle/
[/spoiler]
Геометрия,
вопрос задал iEzeVyachik,
4 года назад
iEzeVyachik:
Все пацаны спасибо больше ненадо, отдуши!)
math448:
Если бы я была пацаном ..
iEzeVyachik:
Ахах, извиняюсь не знал, Спасибо девушка!
artamonjounior123:
Просто я ещё не знаю такого свойства или это теоремы. И он тоже может быть тоже.
math448:
А ты в каком классе?
artamonjounior123:
Этой теоремы*
artamonjounior123:
8 класс
artamonjounior123:
Как раз мой ответ внизу его тоже можно посмотреть.
math448:
Молодец, оригинально решил
Ответы на вопрос
Угол между секущими, равен полуразность друг, заключёнными между этими секущими: 150-38=112
112*0,5=56 Градусов
Ответил artamonjounior123
1
Ответ:
Дано:
AC=150
DF=38
Решение:
Так как угол Adc вписанный то он равен 1/2*AC=75
Так как угол Dcf вписанный то он равен 1/2*DF=19
Из треугольника DBC угол C=19 угол D(смежный с углом Adc) значит угол D=180-75=105
Угол C=180-(19+105)=56
Ответ: угол C=56.
Ну так более подробней.
Объяснение:
Приложения:
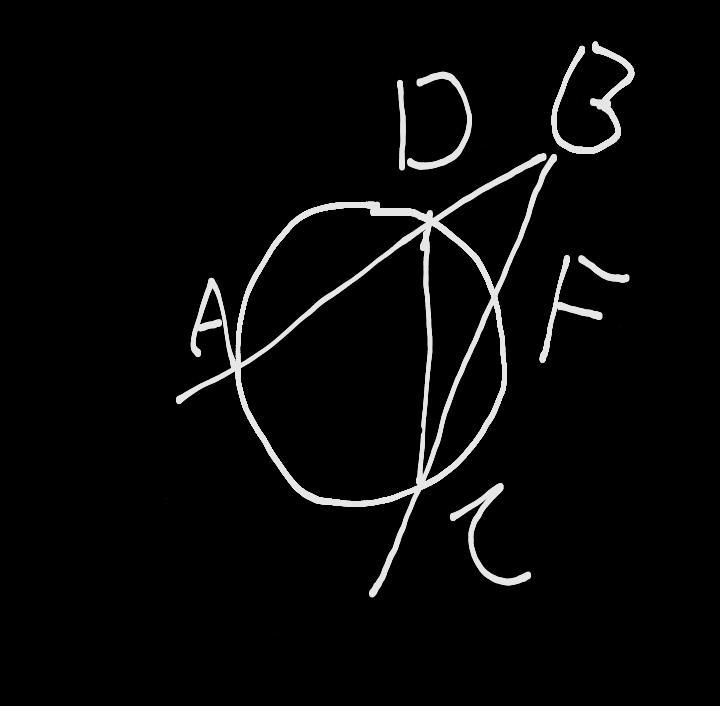
artamonjounior123:
Ребят допустил описку в ответе угол B а не C.
math448:
Ничего страшного, бывает
Новые вопросы
Помогите решить задачу!
максим зайцев
Профи
(611),
на голосовании
4 года назад
найдите острый угол образованный двумя секущими проведенными из точки лежащей внутри окружности если дуги заключённые между секущей равны 54 и 42
Голосование за лучший ответ
Serg
Мыслитель
(8131)
4 года назад
Выполним дополнительные построения. Соединим точки пересечения секущих с окружностью. Получим четырехугольник, вокруг которого описана окружность.
Углы EDC и EFC равны половине дуги, на которую они опираются, или 21
Углы DCF и FED равны половине дуги, на которую они опираются, или 27
В треугольнике CFB угол CDF = 180 – 21 – 27 = 132. Это тупой угол между секущими. Острый, соответственно, 180 – 132 = 48

