Как найти освещенность звезды

При этом пока все еще не так просто. Звезда или иной объект излучает (или отражает) свет разных длин волн – а человек их воспринимает по-разному. При одной и той же интенсивности зеленый свет воспринимается ярче, красный – тусклее, а инфракрасный, разумеется, не воспринимается вовсе. 

Абсолютные звёздные величины

Видимый блеск и видимая звёздная величина звезды зависят от её расстояния до наблюдателя – r. Чтобы освободиться от влияния расстояния, введено понятие об абсолютном блеске и абсолютной величине звезды.

Абсолютным блеском звезды L называется тот блеск, который она имела бы, будучи удалена от наблюдателя на расстояние равное 10 парсекам.

Так как освещённость убывает обратно пропорционально квадрату расстояния, то абсолютный блеск L и видимый блеск l связаны соотношением:

L/l = r²/100 = 2,512^m-M 

m – видимая звёздная величина, М – абсолютная звёздная величина, под которой понимают ту звёздную величину, которую бы имела звезда, будучи удалённой на расстояние, равное 10 парсекам.

Из указанного соотношения получаем формулу:

М = m + 5 – 5lg r 

С учётом межзвёздного поглощения:

М = m + 5 – 5lg r – А(r)

где А(r) – поглощение света, пропорциональное расстоянию до звезды.

Эта формула позволяет вычислить абсолютную звёздную величину звезды, если известно расстояние, и вычислить расстояние, если известна абсолютная величина, по формуле:

lg r = (m – M)/5 + 1

Абсолютные звёздные величины могут быть болометрическими, визуальными, фотографическими.

Солнце имеет абсолютную звёздную величину +4,7^m.

Часто используют светимость звезды – отношение абсолютного блеска звезды к абсолютному блеску Солнца.

Самые яркие звёзды ярче Солнца на 14^m, они испускают больше энергии в 1 000 000 раз. Самые слабые слабее на 14^m. Они испускают меньше энергии в 300 000 раз.

Отношение светимостей самых ярких и самых слабых звёзд достигает около 100 млрд.

Источник

Светимость (блеск) звезд

Представьте, что где-то в море в ночной тьме тихо мерцает огонек. Если бывалый моряк не объяснит вам, что это, вы часто и не узнаете: то ли перед вами фонарик на носу проходящей шлюпки, то ли мощный прожектор далекого маяка.

В том же положении в темную ночь находимся и мы, глядя на мерцающие звезды. Их видимый блеск зависит и от их истинной силы света, называемой светимостью (полное количествл энергии, излучаемой по всем направлениям), и от их расстояния до нас. Только знание расстояния до звезды позволяет подсчитать ее светимость по сравнению с Солнцем. Так например, светимость звезды, в десять раз менее яркой в действительности, чем Солнце, выразится числом 0,1.

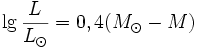
Истинную силу света звезды можно выразить еще иначе, вычислив, какой звездной величины она бы нам казалась, если бы она находилась от нас на стандартном расстоянии в 32,6 светового года, то есть на таком, что свет, несущийся со скоростью 300 000 км/сек, прошел бы его за это время.

где R – радиус звезды, Т – температура.

Принять такое стандартное расстояние оказалось удобным для различных расчетов. Яркость звезды, как и всякого источника света, изменяется обратно пропорционально квадрату расстояния от него. Этот закон позволяет вычислять абсолютные звездные величины или светимости звезд, зная расстояние до них.

Когда расстояния до звезд стали известны, то мы смогли вычислить их светимости, то есть смогли как бы выстроить их в одну шеренгу и сравнивать друг с другом в одинаковых условиях. Надо сознаться, что результаты оказались поразительными, поскольку раньше предполагали, что все звезды «похожи на наше Солнце». Светимости звезд оказались поразительно разнообразными, и их в нашей шеренге не сравнить ни с какой шеренгой пионеров.

Приведем только крайние примеры светимости в мире звезд.

Самой слабой из известных долго являлась звезда, которая в 50 тысяч раз слабее Солнца, и ее абсолютная величина светимости: +16,6. Однако, впоследствии были открыты и ещё более слабые звезды, светимость которых, по сравнению с солнцем, меньше в миллионы раз!

Размеры в космосе обманчивы: Денеб с Земли сияет ярче Антареса, а вот Пистолет — не виден совсем. Тем не менее, наблюдателю с нашей планеты и Денеб и Антарес кажутся просто незначительными точками, по сравнению с Солнцем. Насколько это неверно можно судить по простому факту: Пистолет выпускает в секунду столько же света, сколько Солнце — за год!

На другом краю шеренги звезд стоит «S» Золотой Рыбы, видимая только в странах Южного полушария Земли как звездочка восьмой величины (то есть даже не видимая без телескопа!). В действительности она в 400 тысяч раз ярче Солнца, и ее абсолютная величина светимости: —8,9.

Абсолютная величина светимости нашего Солнца равна +5. Не так уж и много! С расстояния в 32,6 светового года мы бы его плохо видели без бинокля.

Если яркость обычной свечи принять за яркость Солнца, то в сравнении с ней «S» Золотой Рыбы будет мощным прожектором, а самая слабая звезда слабее самого жалкого светлячка.

Итак, звезды — это далекие солнца, но их сила света может быть совершенно иной, чем у нашего светила. Образно выражаясь, менять наше Солнце на другое нужно было бы с оглядкой. От света одного мы ослепли бы, при свете другого бродили бы, как в сумерках.

     

Ви́димая звёздная величина́ (обозначается m) — мера яркости небесного тела (точнее, освещённости, создаваемой этим телом) с точки зрения земного наблюдателя. Обычно используют величину, скорректированную до значения, которое она имела бы при отсутствии атмосферы. Чем ярче объект, тем меньше его звёздная величина.

Уточнение «видимая» указывает только на то, что эта звёздная величина наблюдается с Земли; это уточнение нужно, чтобы отличить её от абсолютной звёздной величины (которая является характеристикой самого́ источника, а не условий его наблюдения). Оно не указывает на видимый диапазон: видимыми называют и величины, измеренные в инфракрасном или каком-либо другом диапазоне. Величина, измеренная в видимом диапазоне, называется визуальной^[1].

В видимой части спектра самая яркая звезда на ночном небе вне Солнечной системы, Сириус, имеет видимую звёздную величину −1,46^m

Самая близкая к нам звезда, Солнце, имеет видимую величину −26,74^m

Источник, излучающий в видимом диапазоне и создающий освещённость в 1 люкс (например, источник с силой света в 1 канделу, находящийся на расстоянии 1 м), имеет видимую звёздную величину −14,20^m[2][3].

История[править | править код]

Видны невооружённым глазом[4]	Видимая величина	Яркость относительно Веги	Число звёзд ярче этой видимой величины[5]
Да	−1,0	250 %	1
0,0	100 %	4
1,0	40 %	15
2,0	16 %	48
3,0	6,3 %	171
4,0	2,5 %	513
5,0	1,0 %	1 602
6,0	0,40 %	4 800
6,5	0,25 %	9 096[6]
Нет	7,0	0,16 %	14 000
8,0	0,063 %	42 000
9,0	0,025 %	121 000
10,0	0,010 %	340 000

Шкала, используемая для обозначения звёздной величины, возникла в эллинистической Греции и использовалась для разделения видимых невооружённым глазом звёзд на шесть величин. Самые яркие звезды на ночном небе имеют первую звездную величину (m = 1), а самые тусклые соответствуют шестой звёздной величине (m = 6), что является пределом человеческого зрительного восприятия (без помощи оптических инструментов). Каждая целая величина считалась обладающей вдвое большей яркости по сравнению с последующей величиной (то есть использовалась логарифмическая шкала), хотя это соотношение было субъективным из-за отсутствия фотодетекторов. Эта довольно грубая шкала яркости звёзд была популяризирована Птолемеем в его труде Альмагесте и, как принято считать, придумана Гиппархом. Это невозможно ни доказать, ни опровергнуть, поскольку исходный звёздный каталог Гиппарха был утерян. Единственный сохранившийся текст самого Гиппарха (комментарий к Арату) свидетельствует о том, что у него не было системы для численного описания яркости: он всегда использует такие термины, как «большой» или «маленький», «яркий» или «слабый» или даже такие описания, как «видны в полнолуние»^[7].

В 1856 году Норман Роберт Погсон дал более формальное определение, определив звезду первой величины как звезду, которая в 100 раз ярче звезды шестой звёздной величины, тем самым постулировав логарифмическую шкалу, используемую до сих пор. Это означает, что звезда со звёздной величиной m примерно в 2,512 раза ярче звезды со звёздной величиной m + 1. Эта цифра соответствует корню пятой степени из 100 и известна как коэффициент Погсона^[8]. Нулевую точку шкалы Погсона первоначально определяли, принимая видимую звёздную величину Полярной звезды равной в точности 2,00^m. Позже астрономы обнаружили, что Полярная является переменной звездой и немного изменяет свою яркость, поэтому они переключились на Вегу в качестве стандартной точки отсчёта, постулировав яркость Веги как определение нулевой звёздной величины для любой заданной длины волны.

Помимо небольших поправок, яркость Веги по-прежнему служит определением нулевой величины для видимой и ближней инфракрасной частей спектра, где её спектральное распределение энергии близко к излучению чёрного тела при температуре 11 000 K. Однако с появлением инфракрасной астрономии было обнаружено, что излучение Веги включает в себя избыток инфракрасного излучения, предположительно из-за околозвёздного диска, состоящего из пыли при высоких температурах (но намного более холодной, чем поверхность звезды). На более коротких (например, видимых) длинах волн при этих температурах наблюдается незначительное излучение пыли. Для того, чтобы правильно расширить шкалу звёздных величин на инфракрасный диапазон спектра, эта особенность Веги не должна влиять на определение шкалы звёздных величин. Поэтому шкала звёздных величин была экстраполирована на все длины волн на основе кривой излучения чёрного тела для идеальной поверхности звезды при температуре 11 000 K, не загрязнённой излучением из её окрестностей. На основе этой модели можно вычислить спектральную энергетическую освещённость (обычно выражаемую в янских) для точки, соответствующей нулевой звёздной величине, как функцию длины волны^[9]. Небольшие отклонения указываются между системами, использующими измерительные приборы, разработанные независимо, чтобы можно было должным образом сравнивать данные, полученные разными астрономами, но большее практическое значение имеет определение звёздной величины не на одной длине волны, а применительно к отклику стандартных спектральных фильтров, используемых в фотометрии, в различных диапазонах длин волн.

Предельные величины для визуального наблюдения при большом увеличении^[10]

Диаметр телескопа (мм)	Ограничение на звёздную величину
35	11,3
60	12,3
102	13,3
152	14.1
203	14,7
305	15.4
406	15,7
508	16,4

В современных системах звёздных величин яркость в очень широком диапазоне определяется в соответствии с логарифмическим определением, подробно описанным ниже, с использованием заданного эталона. На практике такие видимые звёздные величины не превышают 30 (для возможных наблюдаемых значений). Яркость Веги превосходят четыре звезды на ночном небе в видимом диапазоне длин волн (и больше в инфракрасном диапазоне), а также яркие планеты Венера, Марс и Юпитер, и их следует описывать отрицательными величинами. Например, Сириус, самая яркая звезда небесной сферы, имеет звёздную величину −1,4^m в видимом диапазоне. Отрицательные величины для других очень ярких астрономических объектов можно найти в таблице справа.

Астрономы разработали и другие фотометрические системы точки отсчета в качестве альтернативы системы основанной на яркости Веги. Наиболее широко используется система звёздных величин AB^[11], в которой фотометрические нулевые точки основаны на гипотетическом эталонном спектре, имеющем постоянный поток на единичный частотный интервал, а не на использовании звёздного спектра или кривой чёрного тела в качестве эталона. Нулевая точка величины AB определяется таким образом, чтобы величины объекта на основе AB и Веги были приблизительно равны в полосе фильтра V.

Разность звёздных величин[править | править код]

Если видимые звёздные величины объектов 1 и 2 равны m₁ и m₂, то их разность определяется как

где L₁, L₂ — освещённости от этих объектов. Это соотношение известно как уравнение Погсона. Его можно записать также в другом виде^[2]:

или

Таким образом, разница в 5 звёздных величин соответствует отношению освещённостей в 100 раз, а разница в одну звёздную величину — в 100^1/5 ≈ 2,512 раза.

Из уравнения Погсона можно получить освещённость в люксах, создаваемую источником с известной видимой звёздной величиной m₁ в видимом диапазоне. Поскольку освещённость L₂ = 1 люкс создаёт источник с видимой звёздной величиной m₂ = −14,20^m, то^[2]

люкс.

Обратив формулу, получаем видимую звёздную величину объекта, создающего освещённость L₁, выраженную в люксах:

Примеры[править | править код]

Видимая звёздная величина полной Луны равна −12,7^m; яркость Солнца составляет −26,7^m.

Разница звёздных величин Луны () и Солнца ():

Отношение освещённостей от Солнца и Луны:

Таким образом, Солнце примерно в 400 000 раз ярче полной Луны.

Освещённость, создаваемая звёздами с видимой звёздной величиной 1,0^m и 6,0^m в видимом диапазоне, равна соответственно 8,3×10⁻⁷ люкс и 8,3×10⁻⁹ люкс^[2].

Суммарная звёздная величина[править | править код]

Общая видимая звёздная величина (m_s) двух близко расположенных небесных светил с видимыми звёздными величинами m₁ и m₂ вычисляется путём преобразования величин m₁ и m₂ к освещённостям, сложению освещённостей и последующему обратному преобразованию к логарифмическому виду:^[12]

По тому же принципу может быть вычислена общая звёздная величина систем, которые обладают бо́льшими уровнями кратности.

Примечания[править | править код]

Ссылки[править | править код]

• The astronomical magnitude scale Архивная копия от 29 августа 2019 на Wayback Machine // International Comet Quarterly (англ.)

Звездная величина — числовая безразмерная величина, характеризирующая яркость звезды или другого космического тела по отношению к видимой площади. Другими словами, эта величина отображает количество электромагнитных волн, излучаемых телом, которые регистрируются наблюдателем. Поэтому данная величина зависит от характеристик наблюдаемого объекта и расстояния от наблюдателя до него. Термин охватывает лишь  видимый, инфракрасный и ультрафиолетовый спектры электромагнитного излучения.

По отношению к точечным источникам света используют также термин «блеск», а к протяженным – «яркость».

История

Древнегреческий ученый Гиппарх Никейский, который жил на территории Турции во II веке до н. э., считается одним из влиятельнейших астрономов античности. Он составил объемный каталог звезд, первый в Европе, описав расположения более чем тысячи небесных светил. Также Гиппарх ввел такую характеристику как звездная величина. Наблюдая невооруженным  глазом за звездами, астроном решил разделить их по яркости на шесть величин, где первая величина – самый яркий объект, а шестая — наиболее тусклый.

В XIX веке, британский астрономом Норман Погсон усовершенствовал шкалу измерений звездных величин. Он расширил диапазон ее значений и ввел логарифмическую зависимость. То есть с повышением звездной величины на единицу, яркость объекта уменьшается в 2.512 раза. Тогда звезда 1-й величины (1^m) в сто раз ярче, нежели светило 6-й величины (6^m).

За эталон небесного светила с нулевой звездной величиной изначально брался блеск Веги, самой яркой точки в созвездии Лиры. Несколько позже было изложено более точное определение объекта нулевой звездной величины – его освещённость должная равняться 2,54·10⁻⁶ люкс, а световой поток в видимом диапазон 10⁶ квантов/(см²·с).

Видимая звездная величина

Описанная выше характеристика, которую определил Гиппарх Никейский, впоследствии стала носить название «видимая» или «визуальная». Имеется в виду, что ее можно наблюдать как при помощи человеческих глаз в видимом диапазоне, так и с использованием различных инструментов вроде телескопа, включая ультрафиолетовый и инфракрасный диапазон. Звездная величина созвездия Большой Медведицы равна 2^m. Однако мы знаем, что Вега с нулевым блеском (0^m) не самая яркая звезда на небосводе (пятая по блеску, третья для наблюдателей с территории СНГ). Поэтому более яркие звезды могут иметь отрицательную звездную величину, к примеру, Сириус (-1.5^m). Также сегодня известно, что среди небесных светил могут быть не только звезды, но и тела, отражающие свет звезд – планеты, кометы или астероиды. Звездная величина полной Луны составляет −12,7^m.

Абсолютная звездная величина и светимость

Для того чтобы была возможность сравнить истинную яркость космических тел, была разработана такая характеристика как абсолютная звездная величина. Согласно ней вычисляется значение видимой звездной величины объекта, если бы этот объект располагался на за 10 парсек (32,62 световых лет) от Земли. В таком случае отсутствуют зависимость от расстояния до наблюдателя при сравнении различных звезд.

Абсолютная звездная величина для космических объектов в Солнечной системе использует иное расстояние от тела к наблюдателю. А именно 1 астрономическую единицу, при этом, в теории, наблюдатель должен находиться в центре Солнца.

Более современной и полезной величиной в астрономии стала «светимость». Эта характеристика определяет полную энергию, которую излучает космическое тело за определенный отрезок времени. Для ее вычисления как раз и служит абсолютная звездная величина.

Спектральная зависимость

Как уже говорилось ранее, звездная величина может быть измерена для различных видов электромагнитного излучения, а потому имеет разные значения для каждого диапазона спектра. Для получения картинки какого-либо космического объекта астрономы могут использовать фотопластинки, которые более чувствительны к высокочастотной части видимого света, и на изображении звезды получаются голубыми. Такая звездная величина называется «фотографической», m_Pv. Чтобы получилось значение близкое к визуальному («фотовизуальное», m_P), фотопластинку покрывают специальной ортохроматической эмульсией и используют желтый светофильтр.

Учеными была составлена так называемая фотометрическая система диапазонов, благодаря которой можно определять основные характеристики космических тел, такие как: температура поверхности, степень отражения света (альбедо, не для звезд), степень межзвездного поглощения света и прочие. Для этого производится фотографирование светила в разных спектрах электромагнитного излучения и последующие сравнение результатов. Для фотографии наиболее популярны следующие фильтры: ультрафиолетовый, синий (фотографическая звездная величина) и желтый (близкий к фотовизуальному диапазону).

Фотография с запечатленными энергиями всех диапазонов электромагнитных волн определяет так называемую болометрическую звездную величину (m_b). С ее помощью, зная расстояние и степень межзвездного поглощения, астрономы вычисляют светимость космического тела.

Звездные величины некоторых объектов

• Солнце = −26,7^m
• Полная Луна = −12,7^m
• Вспышка Иридиума = −9,5 ^m. Iridium – это система из 66 спутников, которых движутся по орбите Земли и служат для передачи голоса и прочих данных. Периодически поверхность каждого из трех главных аппаратов отсвечивает солнечный свет в сторону Земли, создавая ярчайшую плавную вспышку на небосводе до 10 секунд.

• Ярчайший взрыв сверхновой, в 1054-м году, вследствие которого, как считается, образовалась Крабовидная туманность = −6,0 ^m. Если верить записям китайских и арабских астрономов, сверхновую можно было наблюдать целых 23 дня, даже в дневное время невооруженным глазом.
• Венера во время максимума = −4,4 ^m
• Земля, для наблюдателя на Солнце = −3,84 ^m
• Марс во (макс.) = −3,0 ^m
• Юпитер (макс.) = −2,8 ^m
• МКС (макс.) = −2 ^m

• α Центавра = −0,27 ^m
• Вега = +0,03 ^m
• Галактика Андромеды = +3,4 ^m
• Тусклые звезды, которые еще может уловить человеческий глаз = +6 ^m — +7 ^m
• Проксима Центавра = +11,1 ^m
• Ярчайший квазар = +12,6 ^m
• Объекты, улавливаемые наземными телескопами (8-миметровыми) = +27 ^m
• Объекты, улавливаемые космическим телескопом Хаббл = +30 ^m 

Видимые звездные
величины ничего не говорят ни об общей
энергии, излучаемой звездой, ни о яркости
ее поверхности. Действительно, вследствие
различия в расстояниях маленькая,
сравнительно холодная звезда только
из-за своей относительно большой близости
к нам может иметь значительно меньшую
видимую звездную величину (т.е. казаться
ярче), чем далекий горячий гигант.

Если расстояния
до двух звезд известны, то на основании
их видимых звездных величин легко найти
отношение излучаемых ими действительных
световых потоков. Для этого достаточно
освещенности, создаваемые этими звездами,
отнести к общему для всех звезд
стандартному расстоянию. В качестве
такого расстояния принимается 10 пс.

Звездная величина,
которую имела бы звезда, если ее наблюдать
с расстояния в 10 пс,
называется абсолютной
звездной величиной.
Как и видимые, абсолютные звездные
величины могут быть визуальными,
фотографическими и т.д.

Пусть видимая
звездная величина некоторой звезды
равна m, а расстояние
ее от наблюдателя составляет r
пс. По определению, звездная
величина с расстояния 10 пс будет
равна абсолютной звездной величине М.
Применяя к m и М
формулу (5.5), получим:

_,
где Е и Е₁₀ —
соответственно освещенности от звезды
с расстояния r пс
и 10 пс. Поскольку освещенности
обратно пропорциональны квадратам
расстояний, то

.
Подставив это равенство в предыдущее
и выполнив преобразования, получим

M = m + 5  5 lg r.

(5.7)

Формула (5.7) позволяет
найти абсолютную звездную величину М,
если известна видимая звездная величина
объекта m
и расстояние до него r,
выраженное в парсеках. Если же абсолютная
звездная величина известна из каких-нибудь
других соображений, то, зная видимую
звездную величину, легко найти выраженное
в парсеках расстояние из условия

lg r = 1 + 0,2 (m — M).

(5.8)

Величина (m
— М) называется
модулем
расстояния.

Если
в соотношение (5.7) подставить видимую
звездную величину Солнца, а также
расстояние до него в парсеках, то получим,
что абсолютная звездная величина Солнца
М_=
4^m,8.

Найдем связь между
абсолютной звездной величиной и
светимостью звезды. Для этого поместим
две звезды на расстояние 10 пс от
наблюдателя и применим для них формулу
Погсона (5.5):

.

(5.9)

Если взять в
качестве второй звезды Солнце и принять
светимость Солнца за единицу, то с учетом
соотношения (5.9) получим

.

(5.10)

Отсюда
светимость звезды L
(выраженная в светимостях Солнца)

,

(5.11)

где
M
— абсолютная
звездная величина звезды.

§ 5.4. Основы колориметрии

Наиболее полной
информацией об излучении звезды является
распределение энергии в ее спектре,
выраженное в абсолютных энергетических
единицах. Однако достаточно точные
спектрофотометрические измерения можно
осуществить лишь для сравнительно
небольшого числа звезд, поток излучения
от которых наибольший. В тех случаях,
когда это удается сделать, оказывается,
что звезды излучают не по закону Планка,
причем нередко отличие сильнее, чем в
случае Солнца.

Для слабых звезд,
излучение которых удается зарегистрировать
лишь в широком участке спектра,
единственным источником информации
остается поток излучения, определяющий
их звездные величины.

Некоторое
представление о распределении энергии
в спектре звезд можно получить, если
измерять поток их излучения в различных
частях спектра, пользуясь светофильтрами.
Так получаются различные системы
звездных величин.

Звездные величины,
полученные в результате применения
визуальных фотометров или путем
глазомерных оценок, называются
визуальными.
До изобретения фотографии и применения
ее в астрономии визуальные методы
определения звездных величин были
единственным способом фотометрии звезд.
Сейчас этот метод играет меньшую роль,
хотя его и применяют при исследовании
переменных звезд.

Звездные величины,
которые получаются методом фотометрических
измерений изображений звезд, полученных
на фотопластинках, называются
фотографическими
звездными
величинами.

Наиболее точные
современные определения потока излучения
от звезд получаются фотоэлектрическими
или фотографическими методами с
применением специально подобранных
светофильтров в новой международной
системе U,
В, V,
что соответствует измерению потока в
трех участках спектра: ультрафиолетовой
области (ультрафиолетовая
звездная величина U),
синей и близкой ультрафиолетовой области
(синяя
звездная величина
В) и
желто-зеленой области (желтая
звездная величина
V).
Существуют и другие многоцветные
фотометрические системы, включающие,
например, измерения в красной или
инфракрасной областях спектра.

Обычно рассматривают
не длину волны максимума излучения, а
некоторую объективную характеристику
цвета звезды, называемую показателем
цвета,
и устанавливают эмпирическую зависимость
ее от эффективной температуры,
характеризующей суммарную энергию
излучения звезды. Судить о цвете можно,
сравнивая потоки излучения в различных
областях спектра. Поэтому показатель
цвета определяется как разность между
звездными величинами, измеренными в
двух каких-либо фотометрических системах,
например, фотографической и визуальной.
В этом случае обычный
показатель цвета
равен

,
где m_pg
и m_v
— соответственно
фотографическая и визуальная звездные
величины. В системе U,
В, V
обычно пользуются двумя показателями
цвета: основным
(В — V)
и ультрафиолетовым
(U
— В) или (U
— V).

Условились считать,
что все рассмотренные выше показатели
цвета равны нулю для звезд чисто белого
цвета. Показатели цвета звезд других
цветов могут быть как положительными,
так и отрицательными.

Раздел астрофизики,
посвященный изучению показателей цвета
звезд, называется колориметрией.
Его целью является измерение показателей
цвета различными методами и нахождение
других величин, характеризующих
спектральный состав излучения звезд,
а также установление связи между этими
характеристиками и температурой. 

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ВС, 01/09/2011 – 13:16 — mav Звёздная величина(из Википедии)  Звёздная величина – числовая характеристика объекта на небе, чаще всего звезды, показывающая, сколько света приходит от него в точку, где находится наблюдатель.   Видимая (визуальная)       Современное понятие видимой звёздной величины сделано таким, чтобы оно соответствовало величинам, приписанным звёздам древнегреческим астрономом Гиппархом во II веке до н. э. Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины. Промежуточные величины он распределил равномерно между оставшимися звёздами.      Видимая звёздная величина зависит не только от того, сколько света излучает объект, но и от того, на каком расстоянии от наблюдателя он находится. Видимая звёздная величина считается единицей измерения блеска звезды, причём чем блеск больше, тем величина меньше, и наоборот.       В 1856 году Н. Погсон предложил формализацию шкалы звёздных величин. Видимая звёздная величина определяется по формуле:    где I — световой поток от объекта, C — постоянная.      Поскольку данная шкала относительная, то её нуль-пункт (0m) определяют как яркость такой звезды, у которой световой поток равен 10³ квантов /(см²·с·Å) в зелёном свете (шкала UBV) или 106 квантов /(см²·с·Å) во всём видимом диапазоне света. Звезда 0m за пределами земной атмосферы создаёт освещённость в 2,54·10−6 люкс.      Шкала звёздных величин является логарифмической, поскольку изменение яркости в одинаковое число раз воспринимается как одинаковое (закон Вебера — Фехнера). Кроме того, поскольку Гиппарх решил, что величина тем меньше, чем звезда ярче, то в формуле присутствует знак минус. Следующие два свойства помогают пользоваться видимыми звёздными величинами на практике: Увеличению светового потока в 100 раз соответствует уменьшение видимой звёздной величины ровно на 5 единиц. Уменьшение звёздной величины на одну единицу означает увеличение светового потока в 101/2,5=2,512 раза.      В наши дни видимая звёздная величина используется не только для звёзд, но и для других объектов, например, для Луны и Солнца и планет. Поскольку они могут быть ярче самой яркой звезды, то у них может быть отрицательная видимая звёздная величина.      Видимая звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.) Визуальная звёздная величина (V или mv) определяется спектром чувствительности человеческого глаза (видимый свет), имеющего максимум чувствительности при длине волны 555 нм. или фотографически с оранжевым фильтром. Фотографическая или «синяя» звёздная величина (B или mp) определяется фотометрированием изображения звезды на фотопластинке, чувствительной к синим и ультрафиолетовым лучам, или при помощи сурьмяно-цезиевого фотоумножителя с синим фильтром. Ультрафиолетовая звёздная величина (U) имеет максимум в ультрафиолете при длине волны около 350 нм.     Разности звёздных величин одного объекта в разных диапазонах U−B и B−V являются интегральными показателями цвета объекта, чем они больше, тем более красным является объект. Болометрическая звёздная величина соответствует полной мощности излучения звезды, т. е. мощности, просуммированной по всему спектру излучения. Для её измерения применяется специальное устройство — болометр. абсолютная  Абсолютная звёздная величина (M) определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая звёздная величина Солнца +4,7. Если известна видимая звёздная величина и расстояние до объекта, можно вычислить абсолютную звёздную величину по формуле:   где d0 = 10 пк ≈ 32,616 световых лет . Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле  Абсолютная звёздная величина связана со светимостью следующим соотношением:    где  и  — светимость и абсолютная звёздная величина Солнца. Звёздные величины некоторых объектов Объект m Солнце −26,7 Луна в полнолуние −12,7 Вспышка Иридиума (максимум) −9,5 Сверхновая 1054 года (максимум) −6,0 Венера (максимум) −4,4 Земля (глядя с Солнца) −3,84 Марс (максимум) −3,0 Юпитер (максимум) −2,8 Международная космическая станция (максимум) −2 Меркурий (максимум) −1,9 Галактика Андромеды +3,4 Проксима Центавра +11,1 Самый яркий квазар +12,6 Самые слабые звёзды, наблюдаемые невооружённым глазом От +6 до +7 Самый слабый объект, заснятый в 8-метровый наземный телескоп +27 Самый слабый объект, заснятый в космический телескоп Хаббла +30 Самые яркие звёзды Объект Созвездие m Сириус Большой пёс −1,47 Канопус Киль −0,72 α Центавра Центавр −0,27 Арктур Волопас −0,04 Вега Лира 0,03 Капелла Возничий +0,08 Ригель Орион +0,12 Процион Малый пёс +0,38 Ахернар Эридан +0,46 Бетельгейзе Орион +0,50 Альтаир Орёл +0,75 Альдебаран Телец +0,85 Антарес Скорпион +1,09 Поллукс Близнецы +1,15 Фомальгаут Южная рыба +1,16 Денеб Лебедь +1,25 Регул Лев +1,35 Солнце с разных расстояний Местоположение наблюдателя m Икар (перигелий) −30,4 Меркурий (перигелий) −29,3 Венера (перигелий) −27,4 Земля −26,7 Марс (афелий) −25,6 Юпитер (афелий) −23,0 Сатурн (афелий) −21,7 Уран (афелий) −20,2 Нептун (афелий) −19,3 Плутон (афелий) −18,2 631 а. е. (яркость полной Луны) −12,7 Седна (афелий) −11,8 2006 SQ372 (афелий) −10,0 Комета Хякутакэ (афелий) −8,3 0,456 св. года (яркость Венеры) −4,4 Альфа Центавра 0,5 55 св. лет (порог видимости) 6,0 Ригель 12,0 Туманность Андромеды 29,3