|
|
Макеты страниц
В предыдущих главах мы ввели понятия случайной величины и вероятностного процесса и рассмотрели некоторые из их статистических свойств. В оставшихся главах этой книги мы используем развитые выше идеи для исследования результатов прохождения вероятностных процессов через системы различных видов. Так, например, в этой и двух последующих главах мы проведем такие исследования применительно к линейным системам; в частности, в настоящей главе мы рассмотрим основные понятия теории линейных систем, в следующей главе изучим вопросы, относящиеся к шумам в усилителях, и, наконец, в гл. 11 рассмотрим задачу оптимизации линейной системы.
9.1. Элементы теории линейных систем
Предполагается, что читатель в общем знаком с методами анализа линейных систем. Тем не менее мы приведем здесь обзор некоторых элементов этой теории.
Функция передачи системы. Предположим, что, как показано на фиг. 9.1,  — соответственно воздействие на линейную систему с фиксированными параметрами и отклик
— соответственно воздействие на линейную систему с фиксированными параметрами и отклик 

Фиг. 9.1. Линейная система.
Говоря, что система имеет фиксированные параметры, мы подразумеваем, что если воздействие  вызывает отклик
вызывает отклик  то воздействие
то воздействие  вызывает отклик
вызывает отклик  Называя систему линейной, мы подразумеваем, что если воздействие
Называя систему линейной, мы подразумеваем, что если воздействие  вызывает отклик
вызывает отклик  то воздействие
то воздействие

вызывает отклик

Примером такой системы может служить всякое устройство, описываемое системой линейных дифференциальных уравнений с постоянными коэффициентами.
Если на вход линейной системы с фиксированными параметрами в течение неограниченно долгого времени подавалось воздействие

где а» — действительное число, и если спустя это неограниченное время отклик существует, то он имеет ту же форму, т. е.

где А не зависит от  . В самом деле предположим, что воздействие вида
. В самом деле предположим, что воздействие вида  имеющее место, начиная с
имеющее место, начиная с  , создает на выходе вполне определенный отклик
, создает на выходе вполне определенный отклик  который называется стационарным откликом системы. Тогда, если система обладает фиксированными параметрами, воздействие
который называется стационарным откликом системы. Тогда, если система обладает фиксированными параметрами, воздействие

вызывает отклик  Так как
Так как  не зависит от t и система линейна, то воздействие
не зависит от t и система линейна, то воздействие  вызывает отклик
вызывает отклик  . Следовательно,
. Следовательно,

Положив  получаем, что
получаем, что

есть отклик системы на воздействие  и мы доказали наше утверждение при
и мы доказали наше утверждение при  Если теперь воздействие имеет комплексную амплитуду
Если теперь воздействие имеет комплексную амплитуду  т. е. если
т. е. если

то отклик имеет вид

что мы можем записать в виде

Отношение А комплексных амплитуд отклика  и воздействия
и воздействия  является функцией от
является функцией от  и мы будем обозначать его через
и мы будем обозначать его через  итак,
итак,

Функция  называется функцией передачи для данной линейной системы с фиксированными параметрами. Следует отметить, что в линейной системе с фиксированными параметрами может не существовать вполне определенного отклика, если на нее подается в течение неограниченно долгого времени воздействие вида
называется функцией передачи для данной линейной системы с фиксированными параметрами. Следует отметить, что в линейной системе с фиксированными параметрами может не существовать вполне определенного отклика, если на нее подается в течение неограниченно долгого времени воздействие вида  примером может служить LC-контур без потерь с резонансной частотой
примером может служить LC-контур без потерь с резонансной частотой  Это обстоятельство связано с понятием устойчивости, которое мы обсудим кратко несколько ниже.
Это обстоятельство связано с понятием устойчивости, которое мы обсудим кратко несколько ниже.
Предположим, что воздействие является периодической функцией времени, имеющей сходящийся ряд Фурье. Тогда мы можем написать

где

— основной период, а комплексные коэффициенты  определяются формулой
определяются формулой

Из (9.3) следует, что

есть отклик системы на компоненту воздействия

В силу линейности системы, полный отклик на воздействие  равен сумме компонент отклика
равен сумме компонент отклика  . Таким образом,
. Таким образом,

представляет собой стационарный отклик линейной системы с фиксированными параметрами на воздействие в форме периодической функции (9.4).
Пусть теперь воздействие является нестационарным и как функция времени имеет преобразование Фурье. Полученный нами выше результат для случая ряда Фурье можно эвристически распространить на этот случай следующим образом. Предположим, что мы заменили нестационарное воздействие  периодическим:
периодическим:

где коэффициенты  определяются по
определяются по  при помощи
при помощи
равенства (9.6). Соответствующий периодический отклик, согласно (9.7), будет иметь вид

Умножая и деля оба выражения на  и учитывая, что
и учитывая, что  является приращением для
является приращением для  получаем
получаем

и

Если мы теперь положим  так, чтобы
так, чтобы  то из (9.6) будет следовать, что
то из (9.6) будет следовать, что

где  — преобразование Фурье нестационарного воздействия, и, следовательно,
— преобразование Фурье нестационарного воздействия, и, следовательно,

и

Таким образом, отклик системы выражается преобразованием Фурье от

т. е. преобразование Фурье отклика линейной системы с фиксированными параметрами на нестационарное воздействие равно произведению преобразования Фурье этого воздействия на функцию передачи системы [в предположении, что интеграл (9.10) сходится].
Отклик на единичный импульс.
В теории линейных систем особую роль играет нестационарное воздействие в форме единичного импульса

Как показано в приложении I, преобразование Фурье от такой функции для всех  равно единице:
равно единице:

Преобразование Фурье от соответствующего отклика, согласно (9.11), равно

и, следовательно, сам отклик, согласно (9.10), равен

Итак, отклик на единичный импульс линейной системы с фиксированными параметрами выражается преобразованием Фурье от функции передачи системы  наоборот,
наоборот,

Если отклик на единичный импульс при отрицательных значениях t равен нулю, т. е. если

то соответствующая линейная система называется физически осуществимой.
Свертка.
Отклик линейной системы с фиксированными параметрами на нестационарное воздействие можно выразить через отклик системы на единичный импульс, подставляя в (9.10) выражение (9.16) для функции передачи. При этом мы получаем

Интеграл по  представляет собой обратное преобразование Фурье от
представляет собой обратное преобразование Фурье от  вычисленное при
вычисленное при  (т. е. воздействие в момент
(т. е. воздействие в момент  ). Следовательно,
). Следовательно,

С другой стороны, выражая  в (9.10) через
в (9.10) через  просто делая замену переменных в (9.18), получаем
просто делая замену переменных в (9.18), получаем

Эти интегралы, называемые свертками, показывают, что линейную систему с фиксированными параметрами можно охарактеризовать интегральным оператором. При этом отклик системы выражается как среднее от воздействия за истекшее время, взятое с весом, равным отклику системы на единичный импульс; поэтому отклик на единичный импульс иногда называют весовой функцией соответствующей линейной системы.

Фиг. 9 2. Свертка
Поскольку в физически осуществимой линейной системе отклик на единичный импульс при отрицательных значениях аргумента равен нулю, мы можем в равенстве (9.18) заменить бесконечный нижний предел интегрирования нулем:

Если мы, далее, предположим, что воздействие было равно нулю до момента  (как это показано на фиг. 9.2), то верхний предел со можно заменить на
(как это показано на фиг. 9.2), то верхний предел со можно заменить на  . Таким образом, отклик физически осуществимой линейной системы на воздействие, возникающее в момент
. Таким образом, отклик физически осуществимой линейной системы на воздействие, возникающее в момент  запишется в виде
запишется в виде

Дальнейшие рассуждения, быть может, помогут приобрести некоторую интуицию в обращении со свертками. Рассмотрим отклик физически осуществимой линейной системы в некоторый
фиксированный момент времени  Пусть воздействие
Пусть воздействие  в интервале
в интервале  , аппроксимировано совокупностью
, аппроксимировано совокупностью  неперекрывающихся прямоугольных импульсов ширины
неперекрывающихся прямоугольных импульсов ширины  причем
причем

Так как система линейна, то отклик ее в момент  равен сумме откликов, вызванных N предшествующими прямоугольными импульсами.
равен сумме откликов, вызванных N предшествующими прямоугольными импульсами.
Рассмотрим теперь отклик в момент  вызванный одним импульсом, поданным на вход в более ранний момент
вызванный одним импульсом, поданным на вход в более ранний момент  где
где  . При
. При  ширина входного импульса стремится к нулю
ширина входного импульса стремится к нулю  и вызванный этим импульсом отклик приближается к отклику, который имел бы место от единичного импульса, поданного на вход в тот же момент времени и равного по площади заданному прямоугольному импульсу, т. е. равного по площади
и вызванный этим импульсом отклик приближается к отклику, который имел бы место от единичного импульса, поданного на вход в тот же момент времени и равного по площади заданному прямоугольному импульсу, т. е. равного по площади  . Отклик системы в момент на единичный импульс, поданный в момент
. Отклик системы в момент на единичный импульс, поданный в момент  равен
равен  следовательно, отклик в момент
следовательно, отклик в момент  на рассматриваемый прямоугольный импульс равен приближенно
на рассматриваемый прямоугольный импульс равен приближенно  . Значит, общий отклик в момент равен приближенно
. Значит, общий отклик в момент равен приближенно

Если мы теперь положим  так, чтобы
так, чтобы  то получим
то получим

что при  совпадает с равенством (9.20).
совпадает с равенством (9.20).
Линейная система с фиксированными параметрами называется устойчивой, если всякое воздействие на систему, являющееся ограниченной функцией времени, вызывает отклик, также являющийся ограниченной функцией времени. Условия, которые надо наложить на отклик на единичный импульс, чтобы обеспечить устойчивость, можно получить следующим образом. Из равенства (9.18) вытекает, что

Если воздействие ограничено, то существует положительная константа А, такая, что для всех t

Следовательно, при таком воздействии для всех t

Таким образом, если отклик на единичный импульс абсолютно интегрируем, т. е. если

то отклик системы на ограниченное воздействие ограничен и система устойчива. С другой стороны, можно показать, что если функция  не интегрируема, то система неустойчива.
не интегрируема, то система неустойчива.
Часто оказывается полезным расширить введенное нами определение функции передачи системы и рассматривать ее как функцию комплексного переменного  Пусть
Пусть  определяется комплексным преобразованием Фурье
определяется комплексным преобразованием Фурье

в той области плоскости р, где этот интеграл существует. При  равенство (9.21) сводится к ранее выписанному выражению (9.16) для функции передачи системы. Если, в частности, система физически осуществима и устойчива, т. е. если функция
равенство (9.21) сводится к ранее выписанному выражению (9.16) для функции передачи системы. Если, в частности, система физически осуществима и устойчива, т. е. если функция  равна 0 при
равна 0 при  и интегрируема, то интеграл (9.21) сходится равномерно при всех
и интегрируема, то интеграл (9.21) сходится равномерно при всех  Следовательно, для всех
Следовательно, для всех  , у которых
, у которых  функция
функция  оказывается равномерно ограниченной (т. е.
оказывается равномерно ограниченной (т. е.  для всех
для всех  ). Обычными приемами можно показать, что при тех же условиях
). Обычными приемами можно показать, что при тех же условиях  является на самом деле аналитической функцией для всех
является на самом деле аналитической функцией для всех  , у которых
, у которых  Таким образом, ни на оси
Таким образом, ни на оси  ни в правой полуплоскости плоскости
ни в правой полуплоскости плоскости  функция
функция  не может иметь полюсов. Можно доказать и обратное утверждение: если
не может иметь полюсов. Можно доказать и обратное утверждение: если  является при всех
является при всех  , у которых
, у которых  ограниченной аналитической функцией и если
ограниченной аналитической функцией и если  удовлетворяет соответствующему условию, определяющему ее поведение при больших
удовлетворяет соответствующему условию, определяющему ее поведение при больших  , то преобразование Фурье от
, то преобразование Фурье от  будет функцией от t, обращающейся в нуль при
будет функцией от t, обращающейся в нуль при  иными словами, преобразование Фурье от
иными словами, преобразование Фурье от  будет откликом физически осуществимой системы на импульсное воздействие. Действительно, если
будет откликом физически осуществимой системы на импульсное воздействие. Действительно, если  интегрируема
интегрируема
Интересен тот частный случай, когда рассматриваемая система является  -полюсником, изображенным на фиг. 9.3. Нам желательно выразить функции передачи
-полюсником, изображенным на фиг. 9.3. Нам желательно выразить функции передачи  через более привычные величины импедансов и проводимостей схемы.
через более привычные величины импедансов и проводимостей схемы.

Фиг. 9.3.  -полюсник.
-полюсник.
Предполагая воздействие синусоидальным, мы можем написать

где  в общем случае являются комплексными функциями частоты. Соотношения между токами и напряжениями на
в общем случае являются комплексными функциями частоты. Соотношения между токами и напряжениями на  парах зажимов могут быть выражены системой
парах зажимов могут быть выражены системой  уравнений:
уравнений:

где коэффициенты  — так называемые переходные проводимости короткого замыкания. Если мы обратим в нуль все входные напряжения, кроме
— так называемые переходные проводимости короткого замыкания. Если мы обратим в нуль все входные напряжения, кроме  (т. е. закоротим все входы, кроме
(т. е. закоротим все входы, кроме  ), то уравнения (9.25) примут вид
), то уравнения (9.25) примут вид

Тогда, решая их относительно проводимостей  получим
получим

Итак, проводимость  равна отношению комплексной амплитуды
равна отношению комплексной амплитуды
тока короткого замыкания в  паре зажимов к комплексной амплитуде напряжения, приложенного к
паре зажимов к комплексной амплитуде напряжения, приложенного к  паре зажимов (когда все прочие пары зажимов замкнуты); отсюда и происходит название «переходная проводимость короткого замыкания». Если для всех значений
паре зажимов (когда все прочие пары зажимов замкнуты); отсюда и происходит название «переходная проводимость короткого замыкания». Если для всех значений 

то говорят, что многополюсник удовлетворяет условию взаимности.

Фиг. 9.4. Эквивалентная схема Тевенена.
На данном этапе удобно ввести для нашего многополюсника, рассматриваемого со стороны выходных зажимов, эквивалентную схему Тевенена. Такая эквивалентная схема, изображенная на фиг. 9.4, состоит из генератора, напряжение которого равно напряжению холостого хода на выходе исходного многополюсника, и включенного последовательно импеданса  равного импедансу исходного многополюсника со стороны выхода при всех короткозамкнутых входах. Из такого определения выходного импеданса и равенств (9.25) вытекает, что
равного импедансу исходного многополюсника со стороны выхода при всех короткозамкнутых входах. Из такого определения выходного импеданса и равенств (9.25) вытекает, что

и, следовательно,

т. е. выходной импеданс равен величине, обратной к проводимости короткого замыкания со стороны выходной пары зажимов.
Определим теперь выходное напряжение холостого хода, обусловленное входными напряжениями  Замыкая накоротко выходные зажимы, имеем, согласно эквивалентной схеме Тевенена,
Замыкая накоротко выходные зажимы, имеем, согласно эквивалентной схеме Тевенена,

Выходной ток короткого замыкания  протекающий под действием заданной системы входных напряжений, находится из первого из уравнений (9.25):
протекающий под действием заданной системы входных напряжений, находится из первого из уравнений (9.25):

Таким образом, выходное напряжение холостого хода  (XX)
(XX)
можно выразить через входные напряжения с помощью равенств

Из определения функций передачи системы  тогда следует, что
тогда следует, что

Сравнивая между собой последние два выражения, видим, что функции передачи можно следующим образом выразить через переходные проводимости короткого замыкания:

Мы используем эти результаты позже при изучении теплового шума в линейных цепях.
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. Системы связи и статистика
- 1.2. Эта книга
- Глава 2. ВЕРОЯТНОСТЬ
- 2.2. Основы
- 2.3. Совместные вероятности
- 2.4. Условные вероятности
- 2.5. Статистическая независимость
- 2.6. Примеры
- 2.7. Задачи
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 3.2. Функции распределения случайных величин
- 3.3. Дискретные случайные величины
- 3.4. Непрерывные случайные величины
- 3.5. Независимые случайные величины
- 3.6. Функции от случайных величин
- 3.7. Вероятностные процессы
- 3.8. Задачи
- Глава 4. СРЕДНИЕ ЗНАЧЕНИЯ
- 4.1. Математические ожидания
- 4.2. Моменты
- 4.3. Характеристические функции
- 4.4. Корреляция
- 4.5. Корреляционные функции
- 4.6. Сходимость
- 4.7. Интегралы от вероятностных процессов
- 4.8. Временные средние
- 4.9. Задачи
- Глава 5. ВЫБОР
- 5.2. Выборочное среднее
- 5.3. Сходимость выборочных средних
- 5.4. Центральная предельная теорема
- 5.5. Относительная частота
- 5.6. Задачи
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ
- 6.2. Спектральная плотность периодической функции
- 6.3. Спектральная плотность периодического вероятностного процесса
- 6.4. Разложение вероятностных процессов в ортогональные ряды
- 6.5. Спектральная плотность произвольной функции
- 6.6. Спектральный анализ стационарных в широком смысле вероятностных процессов
- 6.7. Взаимные спектральные плотности
- 6.8. Задачи
- Глава 7. ДРОБОВОЙ ШУМ
- 7.2. Распределение вероятностей для моментов вылета электронов
- 7.3. Средний ток в диоде, работающем в режиме насыщения
- 7.4. Спектральная плотность дробового шума диода, работающего в режиме насыщения
- 7.5. Плотность распределения вероятностей для дробового шума диода в режиме насыщения
- 7.6. Ток диода, работающего не в режиме насыщения
- 7.7 . Дробовой шум диода, работающего не в режиме насыщения
- 7.8 Дробовой шум триодов и пентодов, работающих не в режиме насыщения
- 7.9. Задачи
- Глава 8. ГАУССОВСКИЙ ПРОЦЕСС
- 8.2. Двумерное распределение
- 8.3. Многомерное распределение
- 8.4. Гауссовский вероятностный процесс
- 8.5. Узкополосный гауссовский вероятностный процесс
- 8.6. Сумма синусоидального сигнала и узкополосного гауссовского вероятностного процесса
- 8.7. Задачи
- Глава 9. ЛИНЕЙНЫЕ СИСТЕМЫ
- 9.2. Случайные воздействия
- 9.3. Корреляционная функция и спектр отклика
- 9.4. Тепловой шум
- 9.5. Распределения вероятностей отклика
- 9.6. Задачи
- Глава 10. ШУМФАКТОР
- 10.2. Шумфактор
- 10.3. Многокаскадный усилитель
- 10.4. Пример
- 10.5. Задачи
- Глава 11. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
- 11.2. Сглаживание и прогнозирование стационарных воздействий с использованием бесконечной предыстории (теория Винера)
- 11.3. Чистое прогнозирование: несингулярные процессы
- 11.4. Решение уравнения прогнозирования и фильтрации
- 11.5. Другие задачи фильтрации, использующие критерий среднеквадратичной ошибки
- 11.6. Сглаживание и прогнозирование при конечном времени наблюдения
- 11.7. Максимизация отношения сигнал/шум; согласованный фильтр
- 11.8. Задачи
- Глава 12. НЕЛИНЕЙНЫЕ СИСТЕМЫ; ПРЯМОЙ МЕТОД
- 12.2. Квадратичный детектор
- 12.3. Квадратичный детектор; сигнал плюс шум на входе
- 12.4. Однополупериодный линейный детектор
- 12.5. Задачи
- Глава 13. НЕЛИНЕЙНЫЕ СИСТЕМЫ; МЕТОД ПРЕОБРАЗОВАНИЙ
- 13.2. Устройства v-й степени
- 13.3. Корреляционная функция и спектральная плотность отклика
- 13.4. Спектральная плотность отклика
- 13.5. Узкополосное воздействие
- 13.6. Детекторы v-й степени
- 13.7. Задачи
- Глава 14. СТАТИСТИЧЕСКОЕ ОБНАРУЖЕНИЕ СИГНАЛОВ
- 14.1. Применение статистических понятий в вопросах радиосвязи и радиолокации
- 14.2. Проверка статистических гипотез
- 14.3. Критерии отношения правдоподобия
- 14.4. Статистические оценки
- 14.5. Передача информации фиксированными сигналами на фоне гауссовского шума
- 14.6. Сигналы с неизвестными параметрами в белом шуме
- 14.7. Радиолокационные сигналы на фоне гауссовского шума
- 14.8. Задачи
- ПРИЛОЖЕНИЕ 1. ИМПУЛЬСНЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 2. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- ЛИТЕРАТУРА
Импульсный отклик
системы.
По определению,
импульсными характеристиками систем
(второй широко используемый термин –
импульсный отклик систем) называются
функции h(t) для аналоговых и h(kt)
для цифровых систем, которые является
реакцией (откликом) систем на единичные
входные сигналы: дельта-функцию (t)
для аналоговых и импульс Кронекера
(kt)
для цифровых систем, поступающие на
вход систем соответственно при t=0 и k=0.
Эта реакция однозначно определяется
оператором преобразования:
y(t)
= T[(t)]
h(t).
(10.2.1)
y(kt)
= T[(kt)]
h(kt).
(10.2.1′)
Импульсный отклик
аналоговой системы, как результат
операции над дельта-функцией, в
определенной мере представляет собой
математическую абстракцию идеального
преобразования. С практической точки
зрения под импульсным откликом аналоговой
системы можно понимать математическое
отображение реакции системы на входной
сигнал произвольной формы с площадью,
равной 1, если длительность сигнала
пренебрежимо мала по сравнению со
временем реакции системы или с периодом
ее собственных колебаний. Под временем
(длиной) реакции системы обычно понимают
интервал, на котором значения функции
h(t) существенно отличаются от нуля после
прекращения действия единичного сигнала
на ее входе.
Для цифровых систем
импульсный отклик однозначно определяется
реакцией системы на импульс Кронекера
(kt)=1
при k=0. Функцию импульсного отклика
называют также весовой функцией системы.

Рис. 10.2.1. Импульсный отклик системы
h(t),
входной сигнал s(t) и выходная реакция
системы y(t).
На рисунке 10.2.1 приведен
пример импульсного отклика h(t) интегрирующей
RC-цепи. При подаче на вход RC-цепи импульса
заряда q
емкость С заряжается до напряжения Vо
= q/C
и начинает разряжаться через сопротивление
R, при этом напряжение на ней изменяется
по закону v(t) = Voe-t/RC
= (q/C)e-t/RC.
Отсюда, отклик RC-цепи по выходному
напряжению на входной сигнал q
= 1: h(t) = (1/C)e-t/RC.
По существу, импульсным откликом системы
h(t) определяется доля входного сигнала,
которая действует на выходе системы по
истечении времени t после поступления
сигнала на вход (запаздывающая реакция
системы).
Реакция системы
на произвольный сигнал.
Если функция
импульсного отклика системы известна,
то, с учетом принципа суперпозиции
сигналов в линейной системе, можно
выполнить расчет реакции системы в
любой произвольный момент времени на
любое количество входных сигналов с
любыми моментами времени их прихода
путем суммирования запаздывающих
реакций системы на эти входные сигналы,
как это показано на рис. 10.2.1 для трех
входных импульсов. В общем случае
произвольный сигнал на входе системы
может быть разложен в линейную
последовательность взвешенных единичных
импульсов:
y(t) = T[s(t)]
T[ s()(t-)
s()(t-)
d
На
основании принципа суперпозиции линейный
оператор Т может быть внесен под знак
интеграла, т.к. последний представляет
собой предельное значение суммы. При
этом операция преобразования действует
только по переменной t:
y(t) = s()
s()
Т[(t-)]
d s()
s()
h(t-)
d
Это выражение
представляет собой интеграл Дюамеля
или свертку (конволюцию) входного сигнала
с импульсной характеристикой системы.
Заменой переменных t-=
можно
убедиться в том, что эта операция, как
и положено свертке, коммутативна:
 s()
s()
h(t-)
d
 h()
h()
s(t-)
d.
Аналогично, для
дискретных сигналов:
y(kt)
= s(nt)
s(nt)
h(kt-nt)
 h(nt)
h(nt)
s(kt-nt).
(10.2.3′)
В символической
форме математического представления:
y(t) = s()
③
h(t-)
s(t-)
③
h()
s(t) ③
h(t).
В реальных физических
системах импульсный отклик h(t) равен
нулю при t<0 (реакция на выходе системы
не может опережать входной сигнал) и,
как правило, отличен от нуля только на
определенном интервале r, по которому
и ведется интегрирование или суммирование
в выражениях свертки. При обработке
данных на ЭВМ требований по односторонности
импульсного отклика не предъявляется,
равно как и по его размерам вперед и
назад от нуля по координатам.
Усиление постоянной
составляющей сигнала.
Подадим на
вход системы постоянный сигнал s(t) = A.
При этом сигнал на выходе системы:
y(t) = ![]() h()
h()
s(t-)
d
= А![]() h()
h()
dАКпс,
(10.2.4)
т.е. площадь
импульсного отклика (для цифровой
системы соответственно сумма коэффициентов
импульсного отклика) является коэффициентом
Кпс
усиления постоянной составляющей
входного сигнала. Если при обработке
сигналов должны изменяться только
динамические характеристики их формы
без изменения постоянной составляющей,
а равно и различных постоянных уровней
(фона, пьедесталов, региональных трендов
и т.п.), то площадь импульсного отклика
(сумма коэффициентов) должна нормироваться
к единице.

Рис. 10.2.2.
На рис. 10.2.2 приведен пример
выполнения свертки рассмотренной нами
выше RC-цепью при нормированной к 1 площади
импульсного отклика h().
Входной сигнал s(t) находится на постоянном
фоновом значении, в данном случае –
нулевом, при этом, как и следовало
ожидать, площадь выходного сигнала y(t)
равна площади входного сигнала.
Усиление шумов.
Критерием
качества системы при использовании
любого метода обработки информации
можно считать выполнение целевого
назначения с минимальным усилением
шумов (максимальным их подавлением).
Допустим, что система имеет нормированный
к 1 импульсный отклик h(k). Обозначим через
(k)
аддитивный шум с математическим ожиданием
M{(k)}=
![]()
= 0 и дисперсией D2,
который в сумме с сигналом поступает
на вход системы. Значения (k)
статистически независимы и некоррелированы
с сигналом. С учетом помехи во входном
сигнале значение сигнала на выходе
системы:
y(k) =
![]() h(n)[x(k-n)+(k-n)].
h(n)[x(k-n)+(k-n)].
Математическое
ожидание значений выходного сигнала:
M{y(k)}
= ![]()
h(n)[x(k-n)+M{(k-n)}]
= ![]()
h(n) x(k-n).
Вычислим дисперсию
распределения отсчетов выходного
сигнала:
D{y(k)}
=
M{[![]() h(n)[x(k-n)+(k-n)]-M{y(k)}]2}
h(n)[x(k-n)+(k-n)]-M{y(k)}]2}
= M{[![]() h(n)
h(n)
(k-n)]2}.
Если правую часть
последнего выражения представить в
виде
M{[![]() h(n)
h(n)
(k-n)][![]()
h(m) (k-m)]},
то в этом выражении
математические ожидания всех членов
произведения с сомножителями (n)(m)
при n
m равны 0 в силу статистической независимости
значений шума. Остаются только члены с
n = m, т.е.:
M{![]() h2(n)2(n)}
h2(n)2(n)}
= ![]()
h2(n)
M{2(n)}
= D![]()
h2(n)
= 2![]()
h2(n).
(10.2.5)
Отсюда следует,
что сумма квадратов значений нормированного
импульсного отклика системы представляет
собой коэффициент усиления аддитивных
шумов во входном сигнале.
Пример.
Сглаживающий фильтр: y(k) = 0.2![]() x(k-n).
x(k-n).
Коэффициент
усиления шумов: 5 (0.22)
= 0.2. Дисперсия шумов уменьшается в
1/0.2 = 5 раз.
Для систем с m
входами и n выходами аналогично
определяются парциальные импульсные
отклики hij(t),
i = {1,2, … ,n}, j = {1,2, … ,m}, каждым из которых
отображается сигнал на i-м выходе при
поступлении сигнала t)
на j-й вход. Полная совокупность импульсных
откликов образует матрицу:
 ,
,
а выражение свертки
приобретает вид:
![]() =
=
![]()
![]() d
d
Определение
импульсной реакциитребуется,
как правило, для рекурсивных систем,
так как импульсная реакция для НЦС
специального определения не требует:
h(k)
=![]() b(n)(k-n)
b(n)(k-n)
b(k).
Если выражение
для системы известно в общей форме
(10.1.2), определение импульсной реакции
производится подстановкой в уравнение
системы импульса Кронекера с координатой
k = 0 при нулевых начальных условиях, при
этом сигнал на выходе системы будет
представлять собой импульсную реакцию
системы: y(k)
h(k).
Пример. Уравнение
РЦС: yk =
xk
+ 0.5yk-1.
Входной сигнал: xk=
o=
{1,0,0,0,…}.
Расчет выходного
сигнала при нулевых начальных условиях:
yo
=
xo+0.5
y-1
=
1+0 = 1 = ho.
y1
=
x1+0.5
yo
=
0+0.5 = 0.5 = h1.
y2
=
x2+0.5
y1
=
0+0.25 = 0.25= h2
y3
=
x3+0.5
y2
=
0.125 = h3.
y4
=
x4+0.5
y3
=
0.0625 = h4,
т.д.
Импульсный
отклик
системы:
hk
=
{1, 0.5, 0.25, 0.125,
… }
(O.5)k,
k = 0,1,2….
Определение
импульсной реакции физических систем
обычно производится подачей на вход
систем ступенчатой функции uo(k)
= 1 при k
0, и uo(k)
= 0 при k < 0:
g(k) =![]() h(n)
h(n)
uo(k-n)
=![]() h(n).
h(n).
h(k)
= g(k) – g(k-1), k=0,1,2,…
Функция g(k) получила
название переходной характеристики
системы (перехода из одного статического
состояния в другое).
Отклик – линейная система
Cтраница 1
Отклик линейной системы зависит, во-первых, от оказываемого на систему воздействия, а во-вторых, от свойств самой системы. Из этого следует, что всякая формула, позволяющая найти отклик системы, должна содержать две функции, из которых одна выражает воздействие, а вторая характеризует свойства системы. Рассмотрим с этой точки зрения формулы интеграла Фурье и интеграла Дюамеля.
[1]
Величина отклика линейной системы прямо пропорциональна величине входной функции. Это позволяет нормализовать значение отклика и пользоваться графическими методами расчета систем.
[2]
Итак, отклик линейной системы на линейную комбинацию внешних воздействий равен линейной комбинации откликов на каждое отдельное воздействие.
[3]
Фурье; зная отклик линейной системы на синусоидальное воздействие, можно, разлагая воздействие произвольной формы в ряд Фурье или в интеграл Фурье, определить процессы в системе при этом произвольном воздействии с помощью обратного преобразования Фурье.
[4]
Сначала заметим, что отклик линейной системы на монохроматическое входное воздействие обязательно будет тоже монохроматическим, той же частоты. Это следует из того, что в системе все параметры постоянны ( иначе будет несправедливо свойство транспозиции), и нет причин, по которым частота входного воздействия может измениться. Кроме того, если фаза входного воздействия изменится, то точно на эту же величину должна измениться и фаза выходного воздействия, что является прямым следствием свойства транспозиции, так как фаза монохроматического сигнала может быть сведена к его задержке на соответствующую долю периода.
[5]
При наличии нескольких входных импульсов общий выходной отклик линейной системы – это просто сумма отдельных откликов.
[6]
Это и есть формула для нахождения отклика линейной системы на произвольное воздействие методом интеграла Фурье.
[7]
Данное определение свидетельствует о том, что отклик линейной системы с входными синусоидальными сигналами должен составляться из синусоидальных сигналов с теми же частотами, что и у входных сигналов; обычно подобная система задается частотной передаточной функцией ( частотной характеристикой), описывающей изменение амплитуды и фазы сигнала на выходе схемы в зависимости от частоты, как показано на рис. А.
[8]
Исходя из сформулированных математических свойств линейных систем, можно связать их с преобразованием Фурье и ввести функцию, полностью определяющую отклик линейной системы на любое входное воздействие.
[9]
При описании процесса рассеяния волн от протяженных объектов каждый отраженный сигнал представляет некоторую реализацию случайного процесса, которая может рассматриваться как отклик линейной системы на детерминированный зондирующий сигнал.
[10]
Частотный отклик линейной системы не зависит от амплитуды входного тестирующего сигнала. Следовательно, оценка нелинейности системы может быть проведена путем проверки реакции системы на синусоидальные воздействия. Как частота, так и амплитуда тестирующего синусоидального сигнала должна изменяться. В этом случае линейная система вырабатывает выходные сигналы той же частоты, что и входная синусоида, с амплитудой, пропорциональной амплитуде входного сигнала. Анализ преобразования Фурье на наличие дополнительных гармоник позволяет сделать предположение о нелинейности системы. При наличии возмущений ( измерительных шумов) рекомендуется проводить оценку усредненных по результатам нескольких экспериментов выходных последовательностей.
[11]
В большинстве физических линейных систем при данном воздействии на входе существует только один режим движения. Например, откликом линейной системы масса – пружина – демпфер на начальный импульс силы служит затухающее движение, в результате которого масса приходит в состояние покоя. У такой системы всего лишь один аттрактор, а именно точка равновесия. Однако у нелинейных систем может быть несколько положений равновесия или, как в случае некоторых самовозбуждающихся систем, может существовать несколько периодических или непериодических движений.
[12]
На рис. 3.7 показана связь между операцией взятия свертки и передаточной функцией. Весовая функция и передаточная функция являются эквивалентными способами представления отклика линейных систем, и каждая из них имеет свою область применения. Например, передаточные функции используются главным образом при анализе систем управления, когда приходится анализировать и комбинировать довольно сложные наборы подсистем.
[13]
На принципе наложения основаны сильные общие методы решения линейных задач. Рассмотрим одну из задач, сформулированных в предыдущем параграфе: найти отклик линейной системы на заданное воздействие при известных свойствах системы.
[14]
Поскольку систему с равным успехом можно охарактеризовать как в частотной, так и во временной области, для обоих областей были разработаны методы, позволяющие анализировать отклик линейной системы на произвольный входной сигнал. Использование временного анализа дает временной выход y ( t), и в процессе будет определена функция h ( t), импульсная характеристика, или импульсный отклик, сети. Предполагается, что система линейна и инвариантна относительно времени. Также предполагается, что система не имеет скрытой энергии на момент подачи сигнала на вход.
[15]
Страницы:
1
2
Dan’s answer — to compute $H(s)$ as normal, and then compute $1/H(s)$ — is equivalent to your suggestion of swapping the $x$ and $y$ (or doing it in one step by solving for $H_{yx}(s) = frac{X(s)}{Y(s)}$).
In the Laplace domain it’s justified by noting that
$$frac{H(s)}{H(s)} = H(s)H_{yx}(s) = 1$$
In theory this means that a system followed by its inverse system has an output equal to its input. In practice you need to make sure that $H_{xy}$ is realizable, and you have to recognize that if you’re actually chaining real systems, then your $H(s)$ is just a model that may not capture all of your real-world system’s real-world dynamics. So the actual end-to-end equation is something like
$$hat X(s) = left(H(s) X(s) + N(s)right) hat H_{yx}(s)$$
where $hat X$ denotes that it’s just an estimate, $N(s)$ is whatever noise is injected in your measurement of $Y$ and your implementation of $hat H_{yx}$, and $hat H_{yx}$ emphasizes that it’s a guess at your system model, not the real thing.
It’s also useful to note that doing this in the Laplace domain immediately lets you know whether what you’re trying is practical. If $H(s) = 1 / (tau_0 s + 1)$, for instance, you’d immediately see that $1 / H(s)$ is, strictly, unrealizable (because you can’t have a true naked differentiator).
However, as long as noise is negligible you could approach it arbitrarily closely by setting $hat H_{xy}(s) = frac{tau_0 s + 1}{tau_1 s + 1}$, which basically says you’re approximating a derivative as $frac{s}{tau_1 s + 1}$ — then you could use my end-end equation above, along with your knowledge of the nature of $X(s)$ and an estimate of the noise you’re going to inject at $N(s)$ to estimate your end-end system fidelity.
Мы можем проанализировать реакцию систем управления как во временной, так и в частотной областях. Мы обсудим анализ частотных характеристик систем управления в следующих главах. Давайте теперь обсудим анализ времени отклика систем управления.
Что такое время отклика?
Если выходной сигнал системы управления для входа изменяется во времени, то он называется временной реакцией системы управления. Время отклика состоит из двух частей.
- Переходный ответ
- Устойчивый государственный ответ
Реакция системы управления во временной области показана на следующем рисунке.
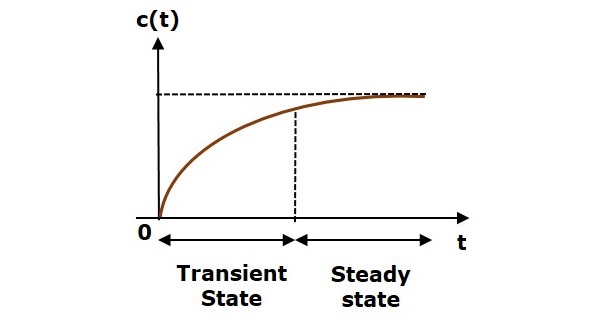
Здесь как переходные, так и стационарные состояния указаны на рисунке. Ответы, соответствующие этим состояниям, известны как ответы переходного и стационарного состояний.
Математически мы можем записать временную характеристику c (t) как
C(T)=Cтр(т)+Cсс(т)
Куда,
- c tr (t) – переходный ответ
- c ss (t) – реакция устойчивого состояния
Переходный ответ
После подачи ввода в систему управления, выходу требуется определенное время для достижения устойчивого состояния. Таким образом, выходной сигнал будет в переходном состоянии, пока он не перейдет в устойчивое состояние. Следовательно, ответ системы управления во время переходного состояния называется переходным процессом .
Переходный отклик будет нулевым для больших значений «t». В идеале это значение ‘t’ равно бесконечности и практически в пять раз больше.
Математически мы можем записать это как
limt rightarrow inftyctr(t)=0
Устойчивый государственный ответ
Часть временного отклика, которая остается даже после переходного отклика, имеет нулевое значение для больших значений «t», называется устойчивым откликом . Это означает, что переходный отклик будет нулевым даже в установившемся режиме.
пример
Найдем нестационарные и установившиеся состояния временной реакции системы управления c(t)=10+5e−t
Здесь второе слагаемое 5e−t будет равно нулю, так как t обозначает бесконечность. Итак, это переходный термин . И первый член 10 остается даже при приближении t к бесконечности. Итак, это термин устойчивого состояния .
Стандартные тестовые сигналы
Стандартные тестовые сигналы: импульсный, шаговый, линейный и параболический. Эти сигналы используются для определения производительности систем управления с использованием временной характеристики выхода.
Импульсный сигнал блока
Единичный импульсный сигнал δ (t) определяется как
delta(t)=0 для t neq0
и int0+0− delta(t)dt=1
На следующем рисунке показан единичный импульсный сигнал.
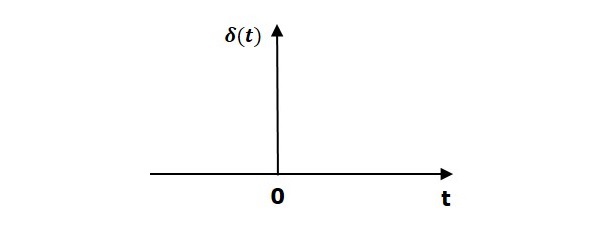
Итак, единичный импульсный сигнал существует только при ‘t’, равном нулю. Площадь этого сигнала при небольшом интервале времени вокруг ‘t’ равна нулю и равна единице. Значение единичного импульсного сигнала равно нулю для всех остальных значений «t».
Сигнал шага блока
Единичный шаговый сигнал u (t) определяется как
u(t)=1;t geq0
$ = 0; т <0 $
На следующем рисунке показан сигнал шага блока.
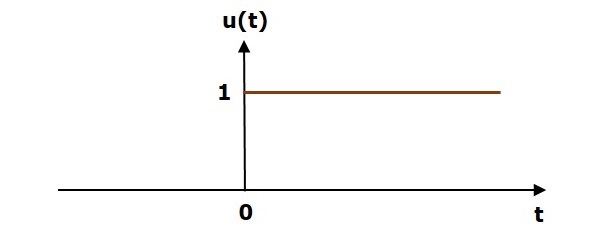
Таким образом, сигнал единичного шага существует для всех положительных значений ‘t’, включая ноль. И его значение равно единице за этот интервал. Значение сигнала единичного шага равно нулю для всех отрицательных значений ‘t’.
Сигнал рампы
Сигнал линейного изменения r (t) определяется как
$$ R (T) = т; t geq 0 $$
$ = 0; т <0 $
Мы можем записать единичный сигнал линейного изменения, r(t) через единичный сигнал шага, u(t) как
R(T)=TU(T)
На следующем рисунке показан сигнал линейного изменения.
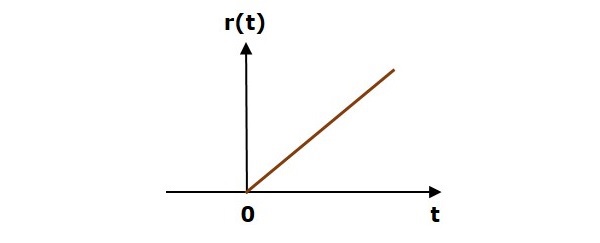
Таким образом, сигнал линейного изменения существует для всех положительных значений ‘t’, включая ноль. И его значение увеличивается линейно по отношению к ‘t’ в течение этого интервала. Значение единичного сигнала линейного изменения равно нулю для всех отрицательных значений ‘t’.
Единичный параболический сигнал
Единичный параболический сигнал p (t) определяется как,
$$ р (т) = гидроразрыва {т ^ 2} {2}; t geq 0 $$
$ = 0; т <0 $
Мы можем записать единичный параболический сигнал, p(t) через единичный сигнал шага, u(t) как,
р(т)= гидроразрыват22и(т)
На следующем рисунке показан блок параболического сигнала.
Таким образом, единичный параболический сигнал существует для всех положительных значений ‘t’, включая ноль. И его значение увеличивается нелинейно по отношению к ‘t’ в течение этого интервала. Значение единичного параболического сигнала равно нулю для всех отрицательных значений ‘t’.

