Как найти отклонение числа от среднего арифметического

Алгебра 7 класс. Что такое отклонение? например: 2,7,3,5,11,15

Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.
Пусть есть некий ряд (значения некоторой случайной величины — скажем, возраст детей в семье): 2,7,3,5,11,15.

1) находим среднее арифметическое: (2+7+3+5+11+15) / 6= 7,17
2) находим среднее арифметическое квадратов отклонений:
(2-7,17)^2+(7-7,17)^2+(3-7,17)^2+(5-7,17)^2+(11-7,17)^2+(15-7,17)^2/6=

Дисперсия характеризует разброс — чем больше дисперсия, тем сильнее «разбросан» (варьируется) признак относительно центрального значения.

Как посчитать среднее значение, квадратическое отклонение и погрешность

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 24 человек(а).

Количество просмотров этой статьи: 62 795.

После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.

Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.

Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.

Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)

Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.

Метод вычисления отклонений каждого значения от среднего арифметического

Для вычисления отклонений всех чисел выполним следующие действия:

. Находим среднее арифметическое;

2. Для вычисления отклонение из данного набора чисел вычитаем среднее арифметическое.

Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.

Среднее арифметическое находится по формуле

(2)

(3)

Найти отклонений всех чисел от среднего арифметического.

Сумма чисел в массиве (2):

Вычисление отклонения (3):

Блок схема 2 — Вычисление отклонений каждого значения от среднего арифметического

Описание методов создания, уничтожения и синхронизации потоков, примененных в программе

Создание потоков

Для создания многопоточных приложений в C++Builder реализован абстрактный класс TThread.- абстрактный класс, который допускает создание отдельных потоков выполняющихся в приложении.

Создайте потомка класса TThread, чтобы представить выполняемый поток в многопоточном приложении.

Каждый новый экземпляр потомка TThread — новый поток выполнения.

Множество экземпляров, полученные от класса TThread, делает C++Builder многопоточным приложением.

__fastcall TMyThread:: TMyThread (bool CreateSuspended)

// B метод объекта Execute (), вставьте код, который должен выполняться, когда поток выполняется.

void __fastcall TMyThread:: Execute ()

// — — Place thread code here — —

Для получения безопасного доступа куправлению свойствами и методами VCL-объектов в потоке предусмотрен метод Synchronize ()

ResetEvent (FMain->g_BusyEvent [1]); // запрещаем переформирование массива(FMain->g_BusyEvent [0]); // запрещаем переформирование массива

>++;(Terminated) break; // прекратить извне поток

Synchronize (&Mon); // блокирует одновременный доступ к компоненту нескольких потоков

SetEvent (FMain->g_BusyEvent [0]); // разрешаем параллельную обработку(FMain->g_BusyEvent [1]); // разрешаем параллельную обработку

Синхронизация потоков

Синхронизации потоков основывается на использовании событий (event). Объект типа событие может принимать одно из двух состояний: активное или пассивное. Когда событие находится в активном состоянии, его видят многие потоки одновременно. В результате такой объект можно использовать для управления работой сразу многих потоков. В библиотеке VCL события представлены классом TEvent.

Метод CreatEvents (): Создает объект класса TEvent, представляющий объект события.

Метод ResetEvent (): Переводит объект события в пассивное состояние.

Метод SetEvent (): Переводит объект события в активное состояние.

WaitForSingleObject (): Заставляет ждать, пока другой поток или процесс не пошлют сигнал об активизации объекта событие.

Завершение потоков

Потоки могут быть запущены и остановлены сколько угодно раз в процессе их выполнения. Для временной остановки запущенного потока можно обратиться к методу потока suspend. Для продолжения выполнения приостановленного потока вызовите метод потока Resume. Вы можете использовать вложенные вызовы вышеперечисленных методов, т.к. метод Suspend увеличивает внутренний счетчик потока, a Resume уменьшает. Поток не будет выполняться до тех пор, пока счетчик не обратиться в ноль, т.е., если вы вызвали пять раз метод Suspend, а затем четыре раза Resume, вам понадобится еще один (пятый) вызов метода Resume для продолжения выполнения потока.

Выполнение потока автоматически завершается после завершения функции Execute () или закрытии приложения.

Чтобы занятая потоком память освобождалась при завершении потока надо установить FreeOnTerminate=false.

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

• в финансах в качестве меры волатильности,
• в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

• А -> (19 + 21 + 19+ 21) / 4 = 20
• Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

• в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
• в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

• стандартное отклонение компании A = 1,
• стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ (“n” и “n–1”)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с “n–1”),
• полностью все данные – используется формула σ (с “n”).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 – μ = 15 – 20 = -5

x2 – μ = 26 – 20 = 6

x3 – μ = 15 – 20 = -5

x4 – μ = 24 – 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 – μ)² = (-5)² = 25

(x2 – μ)² = 6² = 36

(x3 – μ)² = (-5)² = 25

(x4 – μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi – μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:

1. Вычесть среднее значение из каждого числа
2. Возвести каждый результат в квадрат (так получатся квадраты разностей)
3. Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

• одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
• двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
• трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле “=СТАНДОТКЛОНА(“

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

• при <10% выборка слабо вариабельна,
• при 10% – 20 % — средне вариабельна,
• при >20 % — выборка сильно вариабельна.

Узнайте также про:

• Корреляции,
• Метод Крамера,
• Метод наименьших квадратов,
• Теорию вероятностей
• Интегралы.

Среднеквадратическое отклонение

Содержание:

• Определение среднеквадратического отклонения
• Расчет среднеквадратического отклонения
• Свойства среднеквадратического отклонения
• Прикладное значение среднеквадратического отклонения

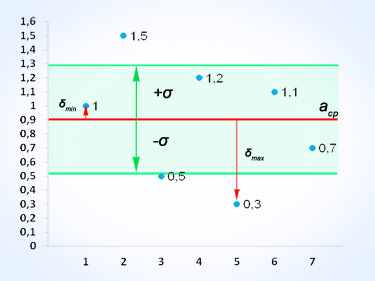
Среднеквадратическое отклонение σ в строгом смысле является частным случаем стандартного отклонения S₀ (стандартной ошибки), хотя зачастую их уравнивают как синонимы, но в случае среднеквадратического отклонения мы имеем дело с отклонением от среднего арифметического ^[1] значения конечного набора величин, а в случае стандартного отклонения – с отклонением от математического ожидания некой (чаще всего случайной) величины.

Среднеквадратическое отклонение значений множества заданных чисел от среднего арифметического определяется как число равное квадратному корню от суммы квадратов разности этих чисел и среднего арифметического, делённой на количество этих чисел:

σ = 

√

Расчет среднеквадратического отклонения

Для начала расчета среднеквадратического отклонения введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному – они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:
 

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднеквадратического отклонения в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднеквадратического отклонения и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Свойства среднеквадратического отклонения

1. Среднее квадратическое отклонение имеет всегда положительную или равную нулю величину:

0 ≤ σ.
 

2. Среднее квадратическое отклонение для заданного множества неотрицательных чисел лежит между минимальным и максимальным значением линейного отклонения от среднего значения этого множества.

3. Кроме того квадратическое отклонение подчиняется неравенству о средних, то есть для любого множества чисел оно не меньше среднего линейного отклонения:

δ ≤ σ

Прикладное значение среднеквадратического отклонения

Среднеквадратическое отклонение от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии, экспериментальной физике и статистике.
При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение^[3],[4] величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.

P.S. На этой странице используется Бета версия программы расчета среднеквадратического отклонения, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Среднее арифметическое значение (чаще используется термин, просто, “среднее арифметическое” или “среднее”) множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

a_{ср.арифм} =  

2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:

σ ² =  

3. Среднее линейное отклонение определяется как среднее от абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:

δ =  

4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:

V =  

  × 100%

5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:

R = a_max – a_min

● Главная
▸ Статьи
▸ Блог
▸ Копилка
✔ Среднеквадратическое отклонение

Как найти среднее квадратическое отклонение

Среднее квадратичное отклонение является важной количественной характеристикой в статистике, теории вероятностей и оценке точности измерений. Согласно определению средним квадратичным отклонением называется корень квадратный из дисперсии. Однако из этого определения не совсем понятно – что характеризует эта величина и как посчитать значение дисперсии.

Вам понадобится

• Калькулятор, компьютер

Инструкция

Пусть имеется несколько чисел, характеризующих какие-либо однородные величины. Например, результаты измереений, взвешиваний, статистических наблюдений и т.п. Все представленные величины должны измеряться одной и той же единицей измерения. Чтобы найти среднее квадратичное отклонение, проделайте следующие действия.

Определите среднее арифметическое всех чисел: сложите все числа и разделите сумму на общее количество чисел.

Найдите отклонение каждого числа от его среднего значения: вычтите от каждого числа среднее арифметическое значение, посчитанное в предыдущем пункте.

Определите дисперсию (разброс) чисел: сложите квадраты найденных ранее отклонений и разделите полученную сумму на количество чисел.

Извлеките из дисперсии квадратный корень. Полученное число и будет средним квадратическим отклонением данного множества чисел.

Пример.

В палате лежат семь больных с температурой 34, 35, 36, 37, 38, 39 и 40 градусов Цельсия.

Требуется определить среднее квадратическое отклонение от средней температуры.
Решение:
• «средняя температура по палате»: (34+35+36+37+38+39+40)/7=37 ºС;

• отклонения температур от среднего (в данном случае нормального значения): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, получается: -3, -2, -1, 0, 1, 2, 3 (ºС);

• дисперсия: ((-3)²+(-2)²+(-1)²+0²+1²+2²+3²)/7=(9+4+1+0+1+4+9)/7=4 (ºС²);

• среднее квадратическое отклонение: √4=2 (ºС);
Ответ: В среднем по палате температура – нормальная: 37 ºС, но среднее квадратическое отклонение температуры равняется 2 ºС, что указывает на серьезные проблемы у пациентов.

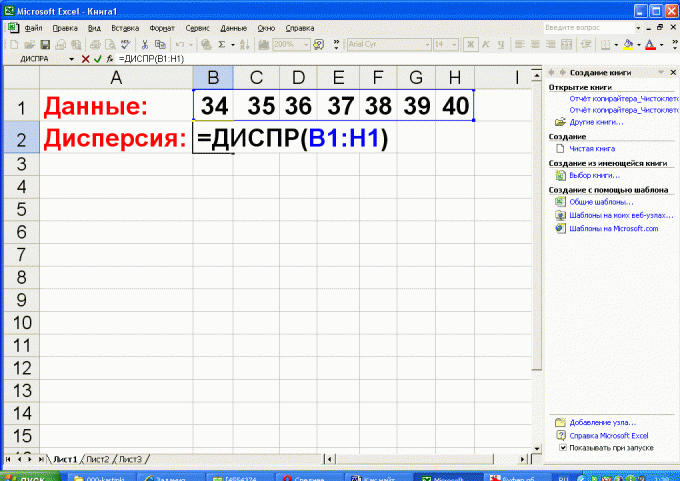
Если имеется возможность воспользоваться программой Excel, то вычисление дисперсии, а соответственно и среднего квадратического отклонения можно существенно упростить.
Для этого разместите данные измерений в один ряд (одну колонку) и воспользуйтесь статистической функцией ДИСПР. В качестве аргументов функции укажите диапазон ячеек таблицы, где размещены введенные числа.

Источники:

• как вычислить среднее квадратическое