Как найти отклонение точки от прямой

Отклонение точки от прямой

В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.

Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком “+”, если эта точка и начало координат лежат по разные стороны прямой, и со знаком “−”, если точка и начало координат лежат по одну сторону от прямой.

Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком “+”, если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком “−”, в противном случае.

Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M₁ от прямой L равно δ=+d₁, так как точка M₁ и начало координат O лежат по разные стороны прямой L, а отклонение точки M₂ от прямой L равно δ=−d₂, так как точка M₂ и начало координат O лежат по одну сторону от прямой L.

На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M₁ от прямой L равно δ=+d₁, так как точка M₁ лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M₂ от прямой L равно δ=−d₂, так как точка M₂ лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L

Рассмотрим нормальное уравнение прямой L (Рис.3):

где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.

Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:

Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.

Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.

Тогда

Но

где n− единичный нормальный вектор прямой L, α−угол между векторами n и .

Из (3) и (4) следует:

С другой стороны

так как нормальный вектор прямой имеет координаты n={cosφ, sinφ}, а точка M − M(x, y).

Сопоставляя (2), (5) и (6), получим:

Теорема доказана.

Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M₀(x₀, y₀) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M₀:

Заметим, расстояние от точки M₀ до прямой L будет равно модулю отклонения данной точки от прямой.

Пример 1. Задано нормальное уравнение прямой:

Найти отклонение точки M(5,-3) от прямой (7).

Решение. Подставим координаты точки M(5,−3) в левую часть уравнения (7):

Ответ. Отклонение точки M(5,−3) от прямой (7) равно:

Пример 2. Задано общее уравнение прямой:

Найти отклонение точки M(1,1) от прямой (8).

Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье “нормальное уравнение прямой”). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:

Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:

Умножив уравнение (8) на нормирующий множитель, получим:

Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):

Ответ. Отклонение точки M(1,1) от прямой (8) равно:

Пусть
– прямая, заданная уравнениеми– произвольная точка плоскости. Тогдарасстояние
от точкидо прямой
выражается формулой

(9)

Заметим,
что в знаменателе этой дроби стоит длина
вектора
– нормального вектора прямойТаким образом,чтобы
найти расстояние от точки до прямой,
надо подставить координаты точки в
уравнение прямой и разделить полученное
число на длину нормального вектора;
при этом мы получим число, которое может
быть отрицательным – в этом случае
берём его по абсолютной величине.

Решим несколько
задач.

Задача
10. Найти
расстояние от точки
до прямой

Решение.
Обозначим данную точку буквой
а прямую буквойПреобразуем уравнение прямой к видуполучим:Теперь применим формулу (9):

Задача
11. Найти
расстояние между параллельными прямыми
и

Решение.
Очевидно, расстояние между параллельными
прямыми равно расстоянию от какой-нибудь
точки первой прямой до второй прямой.
Найдём точку первой прямой. Возьмём,
например,
и подставим это число в уравнение прямойМы получим:Таким образом, точкапринадлежит прямойТеперь мы можем вычислить расстояниемежду прямыми:

Задача
12. На оси
абсцисс найти точку, равноудалённую от
прямых
и

Решение.
Общий вид точек, лежащих на оси абсцисс,
токов:
Обозначим данные прямые черезиПо условиюпоэтому по формуле (9) будем иметь:

Отсюда
получаем:
ЕслитоеслитоТаким образом, условию задачи удовлетворяют
две точки:и

Убрав
в формуле (9) знак абсолютной величины,
мы получим величину

(10)

называемую
отклонением
точки
от прямой
Как видно из формул (9) и (10), отклонение
лишь знаком может отличаться от
расстояния. Очевидно,и

Геометрический
смысл отклонения
следующий (см. рис. 13):

Рис.13.

отклонение
по абсолютной величине равно расстоянию,
причём
если точканаходится от прямойпо ту сторону, в которую направлен
нормальный векториесли она находится по другую сторону.

Замечание.
В ряде
учебников отклонение определяется чуть
по-другому, а именно,
еслииеслиТогда знакбудет положительный, если точканаходится по ту сторону от прямой, в
которой лежит начало координат, и
отрицательный, если по другую сторону.
Мы не будем пользоваться этим определением
отклонения, а будем использовать формулу
(10).

Покажем,
как с помощью отклонения просто решаются
задачи, которые с помощью расстояния
решаются гораздо сложнее.

Задача
13. Определить,
пересекает ли отрезок
прямуюеслиа прямаязадана уравнением

Решение.
Спросить, пересекает ли отрезок
прямую– это всё равно, что спросить, точкиилежат по одну иди по разные стороны от
прямойВычислим отклонения:

(знаменатели
дробей мы не вычисляем, так как нам нужны
не сами отклонения, а только их знаки).
Так как отклонения имеют одинаковые
знаки, то точки
илежат по одну сторону от прямойа значит, отрезокне пересекает прямую

Задача
14. Выяснить,
лежит ли точка
внутри треугольникаесли

Решение.
Составим уравнения прямых
и

уравнение:
т.е.

уравнение:
т.е.

уравнение:
т.е.

Для
того, чтобы точка лежала внутри
треугольника
необходимо и достаточно, чтобы она
лежала: 1) по ту же сторону от прямойгде лежит точка2) по ту же сторону от прямойгде лежит точкаи 3) по ту же сторону от прямойгде лежит точкаВычисляем отклонения:– одного знака. Далее,– одного знака. Наконец,– одного знака. Следовательно, точкалежит внутри

Задача
15. Определить,
лежит ли точка
между параллельными прямымии

Решение.
Обозначим данную точку через
а прямые –иПроверим, что эти прямые действительно
параллельны. Для этого вычислим их
нормальные векторы:Мы видим, чтоследовательно,(Заметим, что на самом деле тот факт, что
векторыиколлинеарны означает, что прямые
параллельныили
совпадают;
но мы не будем различать эти два случая,
здесь удобно считать, что любая прямая
параллельна самой себе). Преобразуем
одно из уравнений так, чтобы нормальные
векторы были одинаковы. Тогда получим:
Тогда они имеют один и тот же нормальный
вектор(см. рис. 14). Из рисунка видно, что точка
будет лежать между прямыми в точности
тогда, когда отклонения разных знаков.

Рис.14.

Вычисляем
отклонения:
Так как отклонения одного знака, то
точкане лежит между прямымии

Задача
16. Определить,
точка
лежит внутри тупого или внутри острого
угла, образованного прямымии

Решение.
Сначала обсудим принципиальный вопрос
о том, как различить ситуации острого
и тупого угла между прямыми. Пусть
– прямые,их нормальные векторы,– отклонения точкиот этих прямых. Если прямые не параллельны
и не перпендикулярны, то возможны два
случая: (а)– острый и (б)– тупой (см. рис. 15).

Рис.15.

В
перовом случае, как видно из рисунка,
для нахождения точки
внутри острого угла необходимо и
достаточно выполнение неравенстваа во втором случае нахождение внутри
острого угла равносильно неравенству

Применим
эти соображения к нашей ситуации. Имеем:
Так както имеет место случай (б). Вычислим
отклонения:Так какиразных знаков и имеет место случай (б),
то точкалежит внутри тупого угла.

Соседние файлы в папке СРС

• #
• #
• #
• #
• #
• #
• #
• #

Уравнением прямой называется такое уравнение первой степени с переменными х и у, которому удовлетворяют координаты любой точки этой прямой. Уравнение вида

называется общим уравнением прямой.
Уравнение прямой, разрешенное относительно переменной у, т. е. уравнение вида

называется уравнением с угловым коэффициентом. Параметр k называется угловым коэффициентом и равен тангенсу угла наклона прямой к оси Ox, k= tg φ.
Параметр b — величина отрезка, отсекаемая прямой (2) на оси Оу, считая от начала координат.
Уравнение вида

где а и b — величины отрезков, отсекаемых прямой на осях координат (рис. 1), называется уравнением прямой в отрезках.

Рис.1

Углом между двумя прямыми y=kx+b и y=k₁x+b₁ называется угол, на который надо повернуть прямую (с угловым коэффициентом k) до совпадения ее со второй прямой (с угловым коэффициентом k₁), против часовой стрелки (рис. 2).

Рис.2

Этот угол вычисляется по формуле:

Условие параллельности двух прямых

Условие перпендикулярности двух прямых:

Если прямые даны уравнениями в общем виде

то условием параллельности будет равенство

а перпендикулярности

Если прямая имеет угловой коэффициент k и проходит через данную точку то ее уравнение имеет вид:

Если в этом уравнении параметру k давать различные значения, то будем получать всевозможные прямые, проходящие через данную точку (х₁,у₁). Тогда уравнение (7) дает пучок прямых с центром в точке (х₁,у₁).
Если прямая проходит через две данные точки (х₁,у₁) и (х₂,у₂), то уравнение

называется уравнением прямой, проходящей через две данные точки.
Условием того, что три данные точки (х₁,у₁), (х₂,у₂) и (х₃,у₃) лежат на одной прямой, служит равенство:

Если две прямые даны общими уравнениями:

то координаты точки пересечения их определяются путем совместного решения этих уравнений:

Если то прямые имеют точку пересечения.
Если то прямые параллельны и не имеют точки пересечения.
Если то прямые совпадают и точка их пересечения становится неопределенной.
Уравнение вида

называется уравнением пучка прямых, проходящих через точку пересечения двух данных прямых:

Уравнение вида

называется нормальным уравнением прямой.
р — длина перпендикуляра (нормали), опущенного из начала координат на прямую, α — угол наклона этого перпендикуляра к оси Ох (рис. 3).

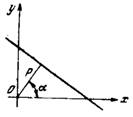
Рис.3

Всякое уравнение прямой общего вида Ах+Ву+С=0 можно привести к нормальному виду, умножая все его члены на нормирующий множитель.

взятый со знаком, противоположным знаку свободного члена С.
Отклонение δ данной точки от данной прямой есть длина перпендикуляра, опущенного из этой точки на прямую, взятая со знаком плюс, если точка и начало координат лежат по разные стороны от прямой, и со знаком минус, если они лежат по одну сторону от прямой.

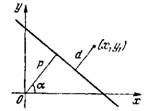
Рис.4

Чтобы найти отклонение точки М(х₁,у₁) от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки х₁ и у₁:

или

Для точек, лежащих на прямой, отклонение равно нулю. Расстояние d от точки до прямой есть абсолютная величина отклонения этой точки от прямой:

или

Положение прямой в полярной системе координат определяется длиною перпендикуляра р, опущенного из полюса на прямую, и углом α, образованным этим перпендикуляром и полярной осью ОР (рис. 5).

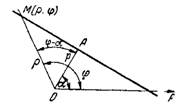
Рис.5

Уравнение прямой в полярных координатах имеет вид

р = ρcos(φ-α)                                  (16)

Обозначим через D расстояние от точки М до прямой L. Отклонением точки М от прямой L называется число D, если М и начало координат О лежат по разные стороны от прямой L, и число –D, если М и О лежат по одну сторону от L. Если О принадлежит L и П = (cos J, sin J) – нормальный вектор прямой L, то отклонение положим равным D, когда М лежит по ту же сторону от L, куда направлен вектор П, и –D – в противном случае.

Рис. 11

Пусть Q – проекция точки М = {X, Y} на ось, определяемую вектором П. Тогда отклонение точки М от прямой L равно

Поэтому

Отсюда

В силу того, что D = |D |, имеем

Пример 5. Даны координаты вершин треугольника А = {0,1}, B = {2,1} и C = {3,-1}. Найти длину высоты H, проведенной из вершины В на сторону АС.

Длина высоты равна расстоянию от точки В до прямой, проходящей через точки А и С. Найдем уравнение прямой, проходящей через эти точки:

Приведем это уравнение к нормальному виду:

Следовательно,

Упражнение 3. Найти расстояние от точек М1 = {-1,3} и М2 = {2,1} до прямой

3Х – 4У + 1 = 0

И выяснить, лежат ли эти точки по одну сторону от прямой или по разные стороны.

Решение.

Приведем уравнение прямой к нормальному виду:

И найдем отклонения данных точек от прямой:

Тогда

А поскольку отклонения точек от прямой имеют разные знаки, точки расположены по разные стороны от прямой.

Ответ: точки расположены по разные стороны от прямой.

Макеты страниц