Как найти отклонение в квадрате - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.^[1] Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.^[2] Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.^[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
2
Для вычисления среднего значения понадобятся все числа данного набора данных.^[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
3
Сложите все числа вашего набора данных.^[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.^[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.^[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.^[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 – 8 = 2; 8 – 8 = 0, 10 – 2 = 8, 8 – 8 = 0, 8 – 8 = 0, и 4 – 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.^[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.^[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.^[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.^[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.^[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.^[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама

Об этой статье

Эту страницу просматривали 64 743 раза.

Была ли эта статья полезной?

Источник

Среднеквадрати́ческое отклонение (среднеквадрати́чное отклонение, стандартное отклонение^[1]) — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания (аналога среднего арифметического с бесконечным числом исходов). Обычно означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.

В литературе обычно обозначают греческой буквой sigma (сигма). В статистике принято два обозначения: sigma — для генеральной совокупности и (с англ. standard deviation — стандартное отклонение) — для выборки.

Варианты определения[править | править код]

Обычно определяется как квадратный корень из дисперсии случайной величины: . Измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

В частности, если $x_{i}$ — -й элемент выборки, — объём выборки, — среднее арифметическое выборки (выборочное среднее — оценка математического ожидания величины):

${displaystyle {bar {x}}={frac {1}{n}}sum _{i=1}^{n}x_{i}={frac {1}{n}}(x_{1}+ldots +x_{n})}$

то два основных способа оценки стандартного отклонения записываются нижеследующим образом.

Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией^[2]):

${displaystyle S={sqrt {{frac {1}{n}}sum _{i=1}^{n}left(x_{i}-{bar {x}}right)^{2}}}}$

Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.

Оценка стандартного отклонения на основании несмещённой оценки дисперсии (подправленной выборочной дисперсии^[2], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):

${displaystyle S_{0}={sqrt {{frac {n}{n-1}}S^{2}}}={sqrt {{frac {1}{n-1}}sum _{i=1}^{n}left(x_{i}-{bar {x}}right)^{2}}}.}$

Само по себе, однако, $S_{0}$ не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Обе оценки являются состоятельными^[2].

Кроме того, среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки^[3]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии этой оценки.

Среднее значение выборки также является случайной величиной с оценкой среднеквадратичного отклонения^[3]^[]:

${displaystyle S_{bar {x}}=S_{0}/{sqrt {n}}={sqrt {{frac {1}{n(n-1)}}sum _{i=1}^{n}left(x_{i}-{bar {x}}right)^{2}}}.}$

Правило трёх сигм[править | править код]

Правило трёх сигм () гласит: вероятность того, что любая случайная величина отклонится от своего среднего значения менее чем на :

${displaystyle P(|xi -Exi mid <3sigma )geqslant {frac {8}{9}}}$

Практически все значения нормально распределённой случайной величины лежат в интервале , где — математическое ожидание случайной величины. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.

Интерпретация[править | править код]

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, для у всех трёх числовых множеств: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8} средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение[править | править код]

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы[править | править код]

Среднее квадратическое отклонение доходности портфеля отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Оценка рисков и критика[править | править код]

Среднеквадратическое отклонение широко распространено в финансовой сфере в качестве критерия оценки инвестиционного риска. По мнению американского экономиста Нассима Талеба, этого делать не следует. Так, по теории около двух третей изменений должны укладываться в определённые рамки (среднеквадратические отклонения −1 и +1) и что колебания свыше семи стандартных отклонений практически невозможны. Однако в реальной жизни, по мнению Талеба, всё иначе — скачки отдельных показателей могут превышать 10, 20, а иногда и 30 стандартных отклонений. Талеб считает, что риск-менеджерам следует избегать использования средств и методов, связанных со стандартными отклонениями, таких как регрессионные модели, коэффициент детерминации (R-квадрат) и бета-факторы. Кроме того, по мнению Талеба, среднеквадратическое отклонение — слишком сложный для понимания метод. Он считает, что тот, кто пытается оценить риск с помощью единственного показателя, обречён на неудачу^[4].

Климат[править | править код]

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт[править | править код]

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Пример[править | править код]

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

Тогда средняя оценка равна:

${displaystyle mu ={frac {2+4+4+4+5+5+7+9}{8}}=5}$

Вычислим квадраты отклонений оценок учеников от их средней оценки:

${displaystyle {begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\end{array}}}$

Среднее арифметическое этих значений называется дисперсией:

${displaystyle sigma ^{2}={frac {9+1+1+1+0+0+4+16}{8}}=4}$

Стандартное отклонение равно квадратному корню дисперсии:

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

${displaystyle sigma ^{2}={frac {9+1+1+1+0+0+4+16}{7}}approx 4{,}57}$

и стандартное отклонение равнялось бы:

{displaystyle sigma ={sqrt {4{,}57}}approx 2{,}14}

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Примечания[править | править код]

↑ Встречаются также различные синонимы: среднее квадратическое отклонение, стандартный разброс, стандартная неопределённость; термин «среднее квадратическое» означает «среднее степени 2»
↑ ¹ ² ³ Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
↑ ¹ ² C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — doi:10.1088/1674-1137/40/10/100001.
↑ Талеб, Гольдштейн, Шпицнагель, 2022, с. 46.

Литература[править | править код]

Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. — СПб.: Питер, 2003. — 688 с. — ISBN 5-272-00078-1..
Нассим Талеб, Дениэл Гольдштейн, Марк Шпицнагель. Шесть ошибок руководителей компаний при управлении рисками // Управление рисками (Серия «Harvard Business Review: 10 лучших статей») = On Managing Risk / Коллектив авторов. — М.: Альпина Паблишер, 2022. — С. 41—50. — 206 с. — ISBN 978-5-9614-8186-0.

Источник

Среднее квадратичное отклонение двух, трех, четырех и более чисел. Оно же стандартное отклонение, среднеквадратическое отклонение, среднеквадратичное отклонение, средняя квадратическая, стандартный разброс — показатель рассеивания значений случайной величины относительно её математического ожидания в теории вероятностей и статистике.

Как правило перечисленные термины равны квадратному корню дисперсии.

Пример вычисления стандартного отклонения по следующим формулам:
Вычислим среднюю оценку ученика: 2; 4; 5; 6; 8.

Cредняя оценка будет равна:

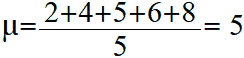
Вычисляем квадраты отклонений оценок от их средней оценки:

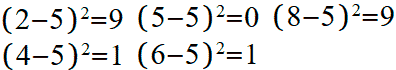
Вычислим среднее арифметическое (дисперсию) этих значений:

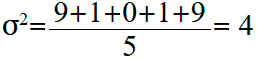
Стандартное отклонение равно квадратному корню дисперсии:

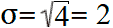
Эта формула справедлива только если эти пять значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки пяти случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 5 нужно было бы поставить n − 1 = 4:

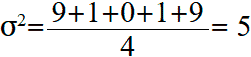
Тогда стандартное отклонение будет равняться:

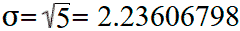
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

среднеквадратическое отклонение,
среднее квадратическое отклонение,
среднеквадратичное отклонение,
квадратичное отклонение,
стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

в финансах в качестве меры волатильности,
в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

А -> (19 + 21 + 19+ 21) / 4 = 20
Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

стандартное отклонение компании A = 1,
стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

стандартное отклонение формула, среднее квадратичное отклонение формула, среднеквадратическое отклонение формула, среднее квадратическое отклонение формула

Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение “xср” вместо “μ”.

Разница между формулами S и σ (“n” и “n–1”)

Состоит в том, что мы анализируем — всю выборку или только её часть:

только её часть – используется формула S (с “n–1”),
полностью все данные – используется формула σ (с “n”).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 – μ = 15 – 20 = -5

x2 – μ = 26 – 20 = 6

x3 – μ = 15 – 20 = -5

x4 – μ = 24 – 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 – μ)² = (-5)² = 25

(x2 – μ)² = 6² = 36

(x3 – μ)² = (-5)² = 25

(x4 – μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi – μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:

Вычесть среднее значение из каждого числа
Возвести каждый результат в квадрат (так получатся квадраты разностей)
Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Дисперсия и стандартное отклонение расчёт дисперсии формула

Где:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле “=СТАНДОТКЛОНА(“

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

при <10% выборка слабо вариабельна,
при 10% – 20 % — средне вариабельна,
при >20 % — выборка сильно вариабельна.

Узнайте также про:

Корреляции,
Метод Крамера,
Метод наименьших квадратов,
Теорию вероятностей
Интегралы.

Источник

Для определения
степени колеблемости признаков
используется среднее квадратическое
отклонение, широко применяемое в
экономических расчетах.

Среднее квадратическое
отклонение бывает простое и взвешенное.
Оно обозначается буквой σ.

—простое квадратическое
отклонение;
—взвешенное
квадратическое отклонение.

Рассмотрим порядок
вычисления взвешенного среднего
квадратического отклонения.

Вычисляют СА
взвешенную величину из ряда
.

Определяют
отклонения отдельных вариантов от
средней.

Полученные
отклонения возводят в квадрат.
Квадраты отклонений
делят на увеличивают на число случаев
в этих отклонениях, то есть на частоты
.
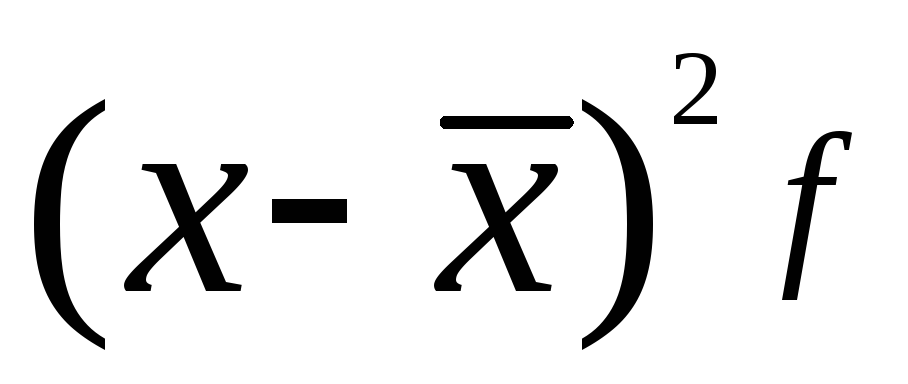Затем полученные отклонения суммируют.
Сумму квадратов
отклонений сумму всех чисел членов
ряда:

Таким
образом, получается дисперсия, или
средний квадрат отклонений.

Из величины,
выражающей дисперсию, извлекают
квадратный корень:

Пример. Произведем
вычисление простого и взвешенного
среднеквадратического отклонения. В
табл. 12 показано распределение кип
шерсти по массе при отгрузке.

Таблица
.12

Распределение кип шерсти при отгрузке

Масса одной кипы (), кг	Количество отгруженных кип (f), шт
86	10
90	20
94	10
96	30
100	15
110	15
ИТОГО	100

Требуется определить
СА простую и взвешенную, среднее
квадратическое отклонение простое и
взвешенное.

Определяем средний
вес одной кипы, для чего используем
формулу средней арифметической простой:

Подставим значения:

2. Среднее
квадратическое простое отклонение (не
взвешенное) определяем по формуле:

Для расчета
квадратического отклонения построим
расчетную таблицу(таб. .13).
Таблица .13

Данные для расчета квадратического отклонения

Масса кипы шерсти, кг	Отклонение от средней (= 96 кг)	Квадраты отклонений (х-х_а)²
86	-10(86-96)	100
90	-6	36
94	-2	4
96	0	0
100	+4	16
110	+14	196
ИТОГО

Что характеризует
полученное квадратическое отклонение?

Масса отдельных
кип шерсти отклоняется от средней (96
кг) в одних случаях на большую величину,
в других— на меньшую. В среднем это
отклонение от средней составляет ±7,7
кг. Из этих данных видно и другое: простое
среднее квадратическое отклонение
выражается в тех же именованных числах,
что и средняя величина. Поэтому оно
составляет так называемое абсолютное
отклонение от средней величины. По
данным примера рассчитаем также среднее
квадратическое отклонение (взвешенное)
для характеристики ряда распределения
с неравными частотами. Для этого примем
во внимание количество отгруженных
кип, которые будут составлять частоты(f).

Расчет производим
по формуле:

Построим расчетную
таблицу (табл. .14).

Сначала определяем
среднюю арифметическую взвешенную:

Рассчитаем среднее
квадратическое отклонение (взвешенное):

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.12.2018130.46 Кб297.docx
#
#
#
#
#
#
#
#
#
#

Источник

Об этой статье

Была ли эта статья полезной?

Варианты определения[править | править код]

Правило трёх сигм[править | править код]

Интерпретация[править | править код]

Практическое применение[править | править код]

Экономика и финансы[править | править код]

Оценка рисков и критика[править | править код]

Климат[править | править код]

Спорт[править | править код]

Пример[править | править код]

Примечания[править | править код]

Литература[править | править код]

Смотрите также

Использование и интерпретация величины среднеквадратического отклонения

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ (“n” и “n–1”)

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Пример 2 (с S)

Дисперсия и стандартное отклонение

Правило трёх сигм

Стандартное отклонение в excel

Коэффициент вариации

Распределение кип шерсти при отгрузке

Данные для расчета квадратического отклонения

Вам также может понравиться

Как составить график для еды

Отзывы как найти быстрей работу

Как найти плейкаст ко дню рождения

Добавить комментарий Отменить ответ