|
Известны данные за отчетный период и данные за аналогичный период предыдущего года.
Абсолютное отклонение это разница между отчетным и базовым периодом. Допустим, в прошлом году у нас было 3 яблока, а в этом 4. Абсолютное отклонение 4-3=1 яблоко Относительное отклонение – это соотношение отчетного к базовому периоду (обычно в процентах выражается, т.е. нужно еще на 100 умножить). Относительное отклонение (4/3)*100=133,3% (т.е. колическтво яблок увеличилось на 33,3 %=133,3%-100%) система выбрала этот ответ лучшим
Koriandr 17 4 года назад Абсолютным отклонением считается разница, которая имеется между отчетным и базовым периодом. Относительное отклонение – это соотношение отчетного к базовому периоду. Отчетный период – это определенный период в деятельности, по результатам которого составляются основные документы финансовой отчетности(например – отчет о прибылях и убытках ). Базовый период – период времени, с которым производится сравнение проектируемых или отчетных показателей(ВВП, прибыли и др.) какого-либо другого, обычно более позднего периода. Относительное отклонение – текущий период “a”, базовый период “b”. Aо = a-b. Относительное отклонение высчитывается в процентах 0о = a/b х 100% Вот так это решается и сложного ничего нет. А555АА 7 лет назад Для этого сначала вспомним что такое абсолютное отклонение и относительное отклонение. Абсолютное отклонение (Ао): это разница между отчетным периодом ( это цифры текущего отчетного года обозначим О) и базовым периодом( это цифры прошлого года обозначим буквой Б) И так: Ао = О – Б Относительное отклонение (выражается в процентах и обозначим Оо) и определяется делением отчетного периода на базовый и умножением на сто для перевода в проценты. И так это будет будет выглядеть вот так: Оо = (О/Б)*100 Примет: прошлом году выращено 50 тонн картошки, а в этом году 60 тонн картошки. Абсолютное отклонение будет равняться 10 тоннам. 60-50=10 Относительное отклонение будет составлять 20 процентов. (60/50)*100=20%
Peresvetik 8 лет назад Главной чертой такой, как показатель любого отклонения- будет тот факт, который позволит отклониться от определенного различия абсолютной величины. Это этот факт даст возможность сравнить всевозможные явления те, где абсолютное значение по своей сути является не сопоставимым. Данное отклонение является разностью между какими то величинами, и оно может быть как положительным,так и отрицательным. Любое относительное отклонение может быть рассчитано по отношению к другой величине. И оно будет выражаться либо в процентном исчислении, либо в долевом. Такой индекс исчисления повышает уровень для анализа,который проводится и позволит точно оценить все изменения.
Абсолютное отклонение это простое арифметическое действие с использованием знака (-) минус. К примеру; Вчера я выпил две бутылки лимонада, а сегодня три бутылки, абсолютное отклонение будет 3-2=1 равно 1 бутылка. Относительное отклонение выражается исключительно в процентах и определяется отношение отчетных цифр к базовым умножением на 100, в нашем случае это выглядит так; 3/2*100=150 то есть относительное отклонение составляет 50 процентов. Абсолютное отклонение равно: рентабельность по факту минус рентабельность по плану. Это отклонение может быть как положительным, так и отрицательным. Относительное отклонение равно: абсолютное отклонение разделить на рентабельность по плану и умножить на 100%, тоже может быть как положительным, так и отрицательным.
Ниннелль 9 лет назад Абсолютное отклонение рассчитывается как разница между текущим (отчетным периодом) и аналогичным периодом прошлого года (АППГ), либо просто другим прошедшим периодом, который нужен нам для сравнения рентабельности предприятия. То есть из значения текущего периода мы отнимаем значение базового периода, полученная разница и будет являться абсолютным отклонением. А относительное отклонение – соотношение тех же показателей друг к другу, только выраженное в процентах. Показатели текущего периода надо разделить на показатели базового периода и умножить на 100. Так мы получаем в процентах относительное отклонение.
Ky3HEts 5 лет назад Абсолютное отклонение – это величина между двумя периодами, измеряется оно в единицах. Например: В позапрошлом месяце Вы заработали на БВ 10- кредитов, а в прошлом – 200 кредитов. Абсолютная отклонение будет высчитываться по схеме 200-100 = 100 кредитов. Относительное отклонение – это соотношение между периодами, которое измеряется в процентах и формула с тем же данными выглядела бы следующим образом: 200/100 = 2*100% = 200%-100% (Процент кредитов за предыдущий месяц) = 100%. Ровно на 100% увеличилась Ваша прибыль за прошлый месяц.
Kobayashi 3 месяца назад Абсолютные и относительные отклонения – это два важных показателя, используемых для количественной оценки того, насколько конкретное значение отличается от контрольного значения. Эти показатели обычно используются в таких областях, как статистика, финансы, инженерное дело и многие другие, чтобы понять изменчивость набора данных и принимать решения на основе результатов. Абсолютное отклонение: Абсолютное отклонение, также известное как абсолютная разница, – это разница между значением и эталонным значением. Он выражается как величина разницы между двумя значениями и вычисляется как: Абсолютное отклонение = |значение – исходное значение| Например, если значение равно 75, а исходное значение равно 100, то абсолютное отклонение равно |75-100| = 25. Абсолютное отклонение измеряет разницу между значением и эталонным значением в абсолютных величинах и не зависит от размера значения или эталонного значения. Относительное отклонение: Относительное отклонение, также известное как процентное отклонение, представляет собой абсолютное отклонение, выраженное в процентах от контрольного значения. Он рассчитывается как: Относительное отклонение = (Абсолютное отклонение / исходное значение) х 100% Например, если значение равно 75, а исходное значение равно 100, то абсолютное отклонение равно 25, а относительное отклонение равно (25/100) х 100% = 25%. Относительное отклонение измеряет процентную разницу между значением и эталонным значением, и оно обеспечивает более осмысленное представление отклонения, особенно при сравнении значений разных размеров. Использование абсолютного и относительного отклонения: Абсолютные и относительные отклонения используются в различных приложениях, таких как контроль качества, финансовый анализ и инженерное проектирование. При контроле качества абсолютное отклонение используется для определения точности измерения или продукта, в то время как относительное отклонение используется для определения изменчивости измерения или продукта по отношению к контрольному значению. В финансовом анализе абсолютное отклонение используется для определения разницы между фактическими и ожидаемыми значениями, в то время как относительное отклонение используется для определения процентной разницы между фактическими и ожидаемыми значениями. В инженерном проектировании абсолютное отклонение используется для определения разницы между желаемыми и фактическими значениями расчетного параметра, в то время как относительное отклонение используется для определения процентной разницы между желаемыми и фактическими значениями расчетного параметра. Вывод: В заключение, абсолютное и относительное отклонение – это два важных показателя, используемых для количественной оценки отклонения между значением и эталонным значением. Абсолютное отклонение измеряет отклонение в абсолютном выражении, в то время как относительное отклонение измеряет отклонение в процентах от контрольного значения. Эти показатели широко используются в различных приложениях для принятия обоснованных решений на основе отклонения между значениями и контрольными значениями.
Kin963 8 лет назад Можно показать на примере. Примем за условие, что:
Для того, чтобы узнать относительное отклонение между этими периодами, надо ((9/6) *100)-100=50%, то есть относительное отклонение за эти два периода 50%. Для расчета абсолютного отклонения между этими периодами нужно 9-6=3, то есть абсолютное отклонение 3 у.е. НеЯэто 4 года назад Есть фактическая (индекс 1) и базовая (инд 0) величина показателей. Вот разность между ними и будет абсолютное отклонение. Относительное – это соотношение между инд 0 и 1, умноженное на 100. В поликлинику обратились за прошлый год 2000 первичных, за отчетный – 2135, абс откл = 135 2 135/2000х100 = 106,75 – 100 = 6,75 – относ откл В отчетном периоде первичных обращений увеличилось на 6,75 процентов.
Андрей1961 6 лет назад Отклонение абсолютное выражено разницей между двумя периодами отчетным и периодом базовым. К примеру в прошлом месяце ваш уровень зарплаты составлял 20 тыс. рублей, в следующем месяце уже 21 тыс. рублей. Абсолютное отклонение выразится разницей месяцев и будет равна 1 тыс. рублей. А вот относительная-это уже соотношение 21/20х100=105, обычная единица измерения в данном случае-%
розовый фламинго 9 лет назад Абсолютное отклонение всегда выражено в точной математической цифре, дающую точную информацию о некоем промежутке времени между точкой отсета начала события до точки отсета конца события. Относительное отклонение никогда не выражено в точных цифрах. Информация в данном случае выдана в процентом показателе дающем косвенную информацию не точную, а приблизительную.
biggold 9 лет назад Если вычесть из фактической рентабельности плановую, то мы получим Абсолютное отклонение Очевидно что этот показатель может быть положительным если предприятие успешное, и наоборот. Если абсолютное отклонение разделить на плановую рентабельность, а затем умножить на сотню, то мы получим относительное отклонение выраженное в процентах.
nikumarina2011 9 лет назад Разница между текущим периодом и прошлогодним и будет считаться абсолютным отклонением. Эти цифры просто вычитаются. А результат может быть как положительным, так и отрицательным. А относительное отклонение соответственно выражается в процентном отношении этих показателей по отношению друг к другу, является всегда положительным. Анна Сергеевна Саченко 7 лет назад Для определения обсолютного отклонения нужно, от полученного показателя отнять базовый. Следовательно отчетный минус аналогичный.В модуле! Относительное отклонение исчисляется отношением обсолютного отклонения к базовой(аналогичной) величине и умножено на 100%.
ворчунов 9 лет назад Абсолютное отклонение – это разность между величинами, может быть положительной и отрицательной. Относительное отклонение – это отношение между величинами и соответственно его выражают в процентах и отрицательным оно быть не может. mister 4 года назад Абсолютное отклонение – это разница в количестве, выражается в абсолютной величине. А вот чтобы получить относительное отклонение, нужно разделить эту разницу на то количество, которое было, и умножить на 100 процентов.
Alen4uk 9 лет назад Абсолютное значение представляет собой разницу между начальным результатом и достигнутым. Если даны 2 показателя, между которыми необходимо найти абсолютное отклонение, нужно вычесть из большего меньшее. Например, в одном магазине товар стоит 50 руб, в другом – 55 руб. 55-50=5 . Это есть абсолютное отклонение цены. Абсолютное отклонение 2 параметров во времени. Например, Доход фирмы в январе -5000 руб, в феврале – 4000 руб. Абсолютное отклонение = 4000 – 5000 = (-1000). Берем модуль числа . Понятно, что прибыль предприятия уменьшилась. Относительные показатели представляют собой отношение одной абсолютной величины к другой. Расчет относительного отклонения производится для оценки деятельности предприятия. Валерий Валерьевич 4 года назад Абсолютное отклонение – это как правило разница между начальным этапом и достигнутым. Например, если вам известна стоимость услуги в двух парикмахерских.Допустим это 300 и 350 рублей за стрижку, рассчитаем разницу: 350-300=50 (рублей) – это абсолютное отклонение цены. Относительное отклонение – это соотношение тех же услуг только в процентном выражении. Т. е. (350/300)*100 Получим результат выраженный в процентах.Такой принцип расчетов позволяет более правильно анализировать и оценить все изменения. Если в этом разобраться то ничего сложного тут нет.
Cranium 5 лет назад относительное отклонение рассчитывают по отношению к другим данным(общему показателю или параметру) и оно выражается в процентах- т.е. одну величину делим на другую и еще*100%, носит дополнительную информативность и позволяет более точно оценить изменение контольной величины. А абсолютное отклонение – это разница(путем вычетания) между величинами- отчетным и базовым периодом. например, в прошлом году мы получили на урожай 50 огурцов, а в этом – 56. Абсолютное отклонение – 56-50=6; относительное – (56/50)*100=112%.
Скрепка 9 лет назад Абсолютное отклонение – разница между данными за отчетный период и данными за аналогичный период предыдущего года. Поскольку Вы не приводите самих данных, то будем оперировать именно этим термином. Данные (текущий период) – Данные (прошлый период) Относительное отклонение – это отношение данных текущего периода к данным предыдущего, выраженное в процентах. (Данные (текущий период) / Данные (предудыщий период))*100%-100
jarptica 9 лет назад Абсолютное отклонение выражается, как правило, в каких-то единицах, в абсолютном выражении (рублях, килограммах, метрах, штуках и прочим). То есть берем одну цифру и вычитаем из такой же цифры предыдущего периода. Получаем абсолютное отклонение. А относительное считается в процентах. То есть берем цифру текущего года и делим ее на цифру предыдущего года, получается выражение в процентах. Знаете ответ? |
Расчет среднего абсолютного отклонения
На чтение 6 мин. Просмотров 1.3k. Опубликовано 27.07.2021
Статистические данные позволяют измерить разброс или разброс. Хотя чаще всего используются диапазон и стандартное отклонение, есть и другие способы количественной оценки дисперсии. Мы посмотрим, как рассчитать среднее абсолютное отклонение для набора данных.
Содержание
- Определение
- Варианты
- Пример: Среднее абсолютное отклонение относительно среднего
- Пример: Среднее абсолютное отклонение от среднего
- Пример: среднее абсолютное отклонение относительно медианы
- Пример: Среднее абсолютное отклонение от медианы
- Быстрые факты
- Распространенное использование
Определение
Начнем с определения среднего абсолютного отклонения, которое также называется средним абсолютным отклонением. Формула, отображаемая в этой статье, является формальным определением среднего абсолютного отклонения. Возможно, имеет смысл рассматривать эту формулу как процесс или серию шагов, которые мы можем использовать для получения нашей статистики.
- Мы начинаем со среднего значения или измерения центра набора данных, которое мы обозначим m.
- Затем мы находим, насколько каждый из значения данных отклоняются от m. Это означает, что мы берем разницу между каждым из значений данных и m.
- После этого мы берем абсолютное значение каждого отличия от предыдущего шага. Другими словами, мы отбрасываем любые отрицательные знаки для любых различий. Причина в том, что есть положительные и отрицательные отклонения от m. Если мы не найдем способ устранить отрицательные знаки, все отклонения нейтрализуют друг друга, если мы сложим их вместе.
- Теперь мы сложим все эти абсолютные значений.
- Наконец, мы делим эту сумму на n , которое представляет собой общее количество значений данных. Результат – среднее абсолютное отклонение.
Варианты
Существует несколько вариантов описанного выше процесса. Обратите внимание, что мы не указали точно, что такое m . Причина этого в том, что мы можем использовать различные статистические данные для m. Обычно это центр нашего набора данных, поэтому можно использовать любое из измерений центральной тенденции.
Наиболее распространенными статистическими измерениями центра набора данных являются среднее значение, медиана и мода. Таким образом, любой из них может использоваться как m при вычислении среднего абсолютного отклонения. Вот почему принято относиться к среднему абсолютному отклонению относительно среднего или среднему абсолютному отклонению от медианы. Мы увидим несколько примеров этого.
Пример: Среднее абсолютное отклонение относительно среднего
Предположим, что мы начнем со следующего набор данных:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
Среднее значение этого набора данных равно 5. Следующая таблица организует нашу работу по вычислению среднего абсолютного отклонения от среднего..
| Значение данных | Отклонение от среднего | Абсолютное значение отклонения |
| 1 | 1-5 = -4 | | -4 | = 4 |
| 2 | 2 – 5 = -3 | | -3 | = 3 |
| 2 | 2 – 5 = -3 | | -3 | = 3 |
| 3 | 3-5 = -2 | | -2 | = 2 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 9 | 9 – 5 = 4 | | 4 | = 4 |
| Сумма абсолютных отклонений: | 24 |
Теперь разделим эту сумму на 10, поскольку всего имеется десять значений данных. Среднее абсолютное отклонение от среднего составляет 24/10 = 2,4.
Пример: Среднее абсолютное отклонение от среднего
Теперь мы начинаем с другого набора данных:
1, 1, 4, 5, 5, 5, 5, 7, 7, 10.
Как и в предыдущем наборе данных, среднее значение этого набора данных равно 5.
| Значение данных | Отклонение от среднего | Абсолютное значение отклонения |
| 1 | 1-5 = -4 | | -4 | = 4 |
| 1 | 1-5 = -4 | | -4 | = 4 |
| 4 | 4-5 = -1 | | -1 | = 1 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 10 | 10 – 5 = 5 | | 5 | = 5 |
| Сумма абсолютных отклонений: | 18 |
Таким образом, среднее абсолютное отклонение от среднего составляет 18/10 = 1,8. Сравним этот результат с первым примером. Хотя среднее значение было одинаковым для каждого из этих примеров, данные в первом примере были более разбросанными. Из этих двух примеров видно, что среднее абсолютное отклонение от первого примера больше, чем среднее абсолютное отклонение от второго примера. Чем больше среднее абсолютное отклонение, тем больше разброс наших данных.
Пример: среднее абсолютное отклонение относительно медианы
Начните с того же набора данных, что и в первом примере:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
Медиана набора данных равна 6. В следующей таблице мы показываем детали расчета среднего абсолютного отклонения от медианы.
| Значение данных | Отклонение от медианы | Абсолютное значение отклонения |
| 1 | 1-6 = -5 | | -5 | = 5 |
| 2 | 2-6 = -4 | | -4 | = 4 |
| 2 | 2-6 = -4 | | -4 | = 4 |
| 3 | 3-6 = -3 | | -3 | = 3 |
| 5 | 5-6 = -1 | | -1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 9 | 9 – 6 = 3 | | 3 | = 3 |
| Сумма абсолютных отклонений: | 24 |
Снова делим сумму на 10 и получить среднее среднее отклонение от медианы как 24/10 = 2,4.
Пример: Среднее абсолютное отклонение от медианы
Начните с того же набора данных, что и раньше:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
На этот раз мы обнаруживаем, что режим этого набора данных равен 7. В следующей таблице мы показываем детали вычисления среднего абсолютного отклонения для режима.
| Данные | Отклонение от режима | Абсолютное значение отклонения |
| 1 | 1-7 = -6 | | -5 | = 6 |
| 2 | 2-7 = -5 | | -5 | = 5 |
| 2 | 2-7 = -5 | | -5 | = 5 |
| 3 | 3-7 = -4 | | -4 | = 4 |
| 5 | 5-7 = -2 | | -2 | = 2 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 7 | 7-7 = 0 | | 0 | = 0 |
| 9 | 9-7 = 2 | | 2 | = 2 |
| Сумма абсолютных отклонений: | 22 |
Делим сумму абсолютных отклонений и видим, что у нас есть среднее абсолютное отклонение о режиме 22/10 = 2.2.
Быстрые факты
Есть несколько основных свойств, касающихся средних абсолютных отклонений
- Среднее абсолютное отклонение от медианы всегда меньше или равно среднему абсолютному отклонению около значение.
- Стандартное отклонение больше или равно среднему абсолютному отклонению относительно среднего.
- Среднее абсолютное отклонение иногда сокращается до MAD. К сожалению, это может быть неоднозначным, поскольку MAD может альтернативно относиться к среднему абсолютному отклонению.
- Среднее абсолютное отклонение для нормального распределения примерно в 0,8 раза превышает размер стандартного отклонения.
Распространенное использование
Среднее абсолютное отклонение имеет несколько применений. Первое применение состоит в том, что эту статистику можно использовать для обучения некоторым идеям, лежащим в основе стандартного отклонения. Среднее абсолютное отклонение относительно среднего намного легче вычислить, чем стандартное отклонение. Это не требует, чтобы мы возводили отклонения в квадрат, и нам не нужно находить квадратный корень в конце нашего расчета. Кроме того, среднее абсолютное отклонение более интуитивно связано с разбросом набора данных, чем стандартное отклонение. Вот почему иногда сначала изучают среднее абсолютное отклонение, прежде чем вводить стандартное отклонение.
Некоторые зашли так далеко, что утверждают, что стандартное отклонение должно быть заменено средним абсолютным отклонением. Хотя стандартное отклонение важно для научных и математических приложений, оно не так интуитивно понятно, как среднее абсолютное отклонение. Для повседневных приложений среднее абсолютное отклонение – более ощутимый способ измерить разброс данных.
-

Различия между стандартными отклонениями для совокупности и выборки
-

Как рассчитать образец стандарта Отклонение
-

Эмпирическая взаимосвязь между средним, медианным и модой
-

Разница между средним и медианным значением и Режим
-

Что такое диапазон в статистике?
-

Когда стандартное отклонение равно нулю?
-

Разница между описательной и выводимой статистикой
-

Как определяются выбросы в статистике?
-

-

Как рассчитать стандарт населения Отклонение
-

Что такое первый и третий квартили?
-

Расчет Коэффициент корреляции
-

Пример доверительного интервала для дисперсии совокупности
-

Что такое моменты в статистике?
-

Дисперсия и стандартное отклонение
-

Ярлык формулы суммы квадратов
Как правильно рассчитать отклонение, и для чего это нужно

Для эффективного анализа данных и для нахождения проблемных участков в производстве необходимо находить отклонения в показателях. Отклонения бывают нескольких видов и отличаются как единицами измерения, так и способом получения, среди них можно выделить:
- Стандартное отклонение;
- Абсолютное отклонение;
- Относительное отклонение;
- Селективное отклонение;
- Кумулятивное отклонение;
- Отклонение во временном разрезе.
Как рассчитать отклонение в каждом случае, вы узнаете из этой статьи.
Как определить динамику изменения значений при отклонении
Нередко для того, чтобы понять насколько плавно изменяется тот или иной показатель на нескольких отрезках времени, простого среднего значения, сравниваемого с наименьшим или наибольшим числом из ряда – недостаточно. В таких случаях для более глубоко анализа применяется нахождение стандартного отклонения, показывающего более четко динамику изменения значений.
Пример:
Даны показатели затрат на средства уборки для двух заведений: 10, 21, 49, 15, 59 и 31, 29, 34, 27, 32, где средним значением будет 30,8 и 30,6. Показатели в среднем приблизительно одинаковы, однако даже визуально видно, что значения в одном заведении изменяются не равномерно, что их контроль производится от случая к случаю. Но для более полного представления необходимо найти стандартное отклонение. Оно будет равно: 19,51 и 2,4. При среднем значении в первом заведении 30,8 показатели отклоняются от него более чем существенно – 21,8, соответственно у вас есть подтверждение небрежного отношения к работе.
Рассчитывается оно следующим образом:
- Необходимо рассчитать среднее значение для проверяемого ряда данных. (10+21+49+15+59)/5=30,8
- Найти разницу между каждым показателем и средним значением. 10-30,8=-20,8; 21-30,8=9,8; 49-30,8=18,2; 15-30,8=15,8; 59-30,8=28,2
- Возвести каждое значение разницы в квадрат. -20,82=432,64; 9,82=96,04; 18,22=331,24; 15,82=249,64; 28,22=795,24.
- Сложить полученные результаты. 432,64+96,04+331,24+249,64+795,24=1904,8
- Полученный результат делиться на количество значений в ряду. 1904,8/5=380,96
- Корень из полученного числа и будет средним отклонением √380,96=19,51
Обязательный минимум
Под понятием абсолютного отклонения принято подразумевать отличия одного показателя от другого в числовом значении. Например, разница выручки за два дня: 15-13=2, где 2 – абсолютное отклонение. Этот способ подходит для нахождения отклонения между фактическим и планируемым результатом.
Для правильного выбора уменьшаемого и вычитаемого, необходимо четко понимать, для чего находится отклонения, например в случае с прибылью, планируемая будет уменьшаемым, а фактическая – вычитаемым. Использование абсолютного отклонения редко помогает при глубоком анализе ситуации.

Существует проблема с постановкой знаков «+/-», для уменьшения фактических издержек, но в большинстве случаев необходимо использовать «-».
Процент воспринимается лучше
Относительным отклонением считают процентное отношение одного показателя к другому. Чаще всего его рассчитывают для понимания того, как тот или иной компонент относится к целому значению ли параметру, а также для нахождения отношения между планируемым показателем и фактическим. Это помогает найти отношение затрат на транспортировку к сумме всех затрат, или объясняет, как в процентах относится полученная выручка к планируемой.
Применение относительного отклонения позволяет повысить уровень наглядности проводимого анализа, что в свою очередь дает возможность более точно вычленить и оценить произошедшие в системе изменения.
Для примера можно найти абсолютное отклонение для полученной выручки относительно планируемой: при соответствующих значениях 1600 и 2000, оно составит 2000-1600=400. Это визуально воспринимается не так серьезно, как процентное отношение (2000-1600)/1600*100%=25%. Отклонение в 25% воспринимается более серьезно.
Как это поможет в сезонной работе
Селективное отклонение призвано помочь сравнить исследуемые данные за определенные промежутки времени. Данным отрезком времени могут быть кварталы, месяцы, не редко это сравнения дней. И для большей информативности необходимо сравнивать временные отрезки не в пределах одного года, а с такими же за прошлые года. Это более точно покажет общую тенденцию изменений величин на протяжении нескольких лет и поможет четче выявить влияющие на них факторы.
Наибольшую актуальность применение селективного отклонения находит в фирмах, доход которых неравномерно распределен на протяжении года. То есть поставщики сезонных продуктов или услуг.
Как выявить тренд отклонения
Сумма, исчисляемая нарастающим итогом, называется кумулятивным отклонением. Благодаря ему производится оценка параметра, его рост или падение за заданный промежуток времени, чаще всего месяц. А также позволяет спланировать конечный результат изменений за период. Благодаря этому можно игнорировать случайные, несистематические изменения параметра, не влияющие на долгосрочную перспективу (весь период) и давать более четкую тенденцию движения параметра. Она чаще всего показывается в виде прямой на графике, последовательно отмечающем все показатели параметра, и соединяющей начальную и конечную точки ломаной линии. Ее направление вниз или вверх и будет тенденцией.
Отклонение во временном разрезе
Зачастую с его помощью происходит сравнение фактического и планируемого показателя. Является крайне важным в случае негативного отклонения планового значения от фактического. Позволяет использовать в анализе реальный результат вместо планируемого или желаемого показателей.
Содержание материала
- Как посчитать относительно отклонение?
- Как вычислить стандартное отклонение в Excel?
- Среднеквадратическое отклонение
- Как рассчитать отклонение показателей?
- Абсолютное отклонение
- Отклонение в процентах при отрицательных величинах
- Как посчитать отклонение от среднего?
- Селективное отклонение
- Как рассчитать процент выполнения плана?
Как посчитать относительно отклонение?
А относительное отклонение — соотношение тех же показателей друг к другу, только выраженное в процентах. Показатели текущего периода надо разделить на показатели базового периода и умножить на 100. Так мы получаем в процентах относительное отклонение.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения. Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. …
- Введите знак равенства. …
- Наберите «СТАНДОТКЛОН». …
- Укажите диапазон данных. …
- Нажмите кнопку «Enter «.
19 окт. 2018 г.
Среднеквадратическое отклонение
Для превращения дисперсии в логично понятные баллы, килограммы или доллары используется среднеквадратическое отклонение, которое представляет собой квадратный корень из дисперсии. Давайте вычислим его для нашего примера:
S = sqrt(D) = sqrt(2,78) = 1,667
Мы получили баллы и теперь можем использовать их для связки с математически ожиданием. Наиболее вероятный результат выстрела в этом случае будет выражен как 7,75 плюс-минус 1,667. Этого достаточно для ответа, но так же мы можем сказать, что практически наверняка стрелок попадет в область мишени между 6,08 и 9,41.
Стандартное отклонение или сигма — информативный показатель, иллюстрирующий разброс величины относительно ее центра. Чем больше сигма, тем больший разброс демонстрирует выборка. Это хорошо изученный коэффициент и для нормального распределения известно занимательное правило трех сигм. Установлено, что 99,7 % значений нормально распределенной величины лежат в области плюс-минус трех сигм от среднего арифметического.
Как рассчитать отклонение показателей?
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%.
Абсолютное отклонение
Как рассчитать абсолютное отклонение? Абсолютным отклонением можно назвать разницу, получаемую при вычитании одной величины из другой, этот способ является выражением сложившихся положений вещей между плановым и фактическим параметрами.
Известно, что определенную проблему обычно вызывает такой показатель, как знак абсолютного отклонения. Обычно считается, что отклонение, которое позитивно сказывается на прибыли предприятия, считается положительным, и в вычислениях его ставят со знаком «+». Что же касается банальной математики, такой подход считается не совсем корректным, а это, в свою очередь, вызывает конфликты и разногласия среди специалистов. Исходя из этого, на практике вычисления абсолютного отклонения зачастую пользуются не базовой экономической, а математической моделью. Математическая модель заключается в том, что повышение фактического оборота в сравнении с запланированным обозначается знаком «+», а уменьшение фактических издержек в сравнении с плановыми обозначается знаком «-«.
Отклонение в процентах при отрицательных величинах
Что будет с изменением прибыли, если какие-то товары имеют отрицательное старое значение? Пусть в нашем примере в январе мы продавали в убыток и прибыль была негативной. А ведь это не такой уж и редкий случай!

Фактически, прибыль выросла, а по расчётам – нет. Исправим формулу, нужно знаменатель взять по модулю (отбросить знак минус). Это распространенный подход, многие его используют. Применим функцию ABS, которая возвращает модуль числа:
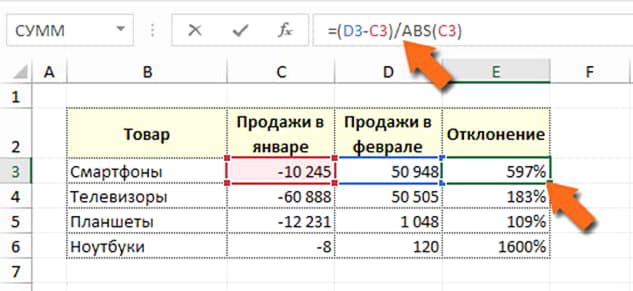
Проблема исправлена, этими результатами можно пользоваться. Однако, хочу вас предостеречь. Результаты могут быть недостаточно корректными. Взгляните на картинку еще раз. Прибыль от смартфонов выросла на 60 тысяч, и это 597%. А прибыль от телевизоров – на 110 тысяч, и это лишь 183%. Я использую такие результаты лишь для поверхностной оценки. Или можно не выводить отклонение для таких случаев.
Как посчитать отклонение от среднего?
Вычисление стандартного отклонения
- вычисляем среднее арифметическое выборки данных
- отнимаем это среднее от каждого элемента выборки
- все полученные разницы возводим в квадрат
- суммируем все полученные квадраты
- делим полученную сумму на количество элементов в выборке (или на n-1, если n>30)
12 авг. 2020 г.
Селективное отклонение
Как рассчитать отклонение такого рода? Этот способ расчета отклонения подразумевает сравнение контролируемых величин на определенном промежутке времени, это может быть такой показатель времени, как квартал или месяц, иногда даже это бывает день. Сравнивание интересующих нас величин за определенный промежуток времени (к примеру, месяц, давайте возьмем май) текущего года с тем же маем предыдущего года может дать нам более информативное сравнение с предыдущим месяцем, который рассматривается в плановом периоде.
Селективное отклонение актуальны для фирм, которые занимаются поставкой сезонных услуг. Далее будут описаны еще несколько видов отклонений, знание которых может существенно облегчить вашу жизнь.
Как рассчитать процент выполнения плана?
Для того, чтобы рассчитать процент выполнения плана, нужно воспользоваться формулой: %плана = (факт / план) * 100%. Эти показатели могут быть выражены как в количественных, так и в стоимостных единицах, а также складываться из нескольких компонентов.
Теги
Абсолютное
отклонение
– это разность между фактической и
базовой величиной показателя. Абсолютные
отклонения могут быть рассчитаны для
любых количественных и качественных
показателей (объема продукции,
количественных и качественных показателей,
характеризующих использование ресурсов,
величины активов, прибыли, финансовых
коэффициентов и т. п.). Например,
ΔN
= N1
– N0;
ΔR
= R1
– R0;
ΔD
= D1
– D0,
|
где |
N |
– |
объем |
|
R |
– |
среднесписочная |
|
|
D |
выработка |
Базовые
значения показателей в анализе принято
обозначать индексом 0, фактические –
1, отклонения (изменения) – символом Δ.
Относительное
отклонение позволяет
измерить прирост ресурса с учетом темпов
роста продукции, выпущенной с использованием
данного ресурса. Относительные отклонения
вычисляются только для количественных
показателей, характеризующих величину
потребленных ресурсов (затрат ресурсов).
Чтобы
найти относительное отклонение, нужно
из фактической величины ресурса вычесть
его базовую величину, скорректированную
на коэффициент
изменения объема продукции.
ΔR’
= R1
– R0
× kN;
kN
= N1
/ N0.
Величина
R0
× kN
показывает, сколько ресурсов было бы
необходимо для производства фактического
объема продукции, если бы не изменялись
качественные характеристики использования
ресурсов.
Отрицательное
относительное отклонение называется
относительной
экономией ресурса,
положительное – относительным
перерасходом.
Если
представить фактическую величину
ресурса через его базовую величину и
темп роста, формулу исчисления
относительного отклонения можно
преобразовать следующим образом:
ΔR’
= R1
– R0
× kN
= R0
× kR
– R0
× kN
= R0
× (kR
– kN).
Такое
представление демонстрирует, что
относительное отклонение возникает за
счет разницы темпов роста ресурса и
продукции. Если темп роста продукции
опережает темп роста ресурса, возникает
относительная экономия, что свидетельствует
о достаточно эффективном использовании
ресурса. Если же темп роста ресурса
превышает темп роста продукции, ресурс
используется неэффективно, о чем
свидетельствует относительный перерасход.
Если
же темпы роста ресурса и продукции
совпадают, относительное отклонение
равно нулю. Это означает, что прирост
продукции получен экстенсивным путем,
т. е. только за счет привлечения
дополнительных ресурсов. При этом
качественные показатели использования
ресурса не изменяются.
На
основании данных таблицы 3.1 оценим
эффективность использования трудовых
ресурсов.
Таблица
3.1
Исходные
данные для оценки эффективности
использования трудовых ресурсов
|
Показатель |
Предыдущий год |
Отчетный год |
Абсолютное отклонение |
Темп |
|
Объем |
4500 |
5000 |
500 |
111,1 |
|
Среднесписочная |
90 |
96 |
6 |
106,7 |
|
Выработка |
50 |
52,08 |
2,08 |
104,2 |
Относительное
отклонение может быть вычислено только
для показателя, характеризующего
численность работающих.
ΔR’
= R1
– R0
×∙kN
= 96 – 90 ×∙1,111 = 96 – 100 = -4.
Данные
таблицы 3.1, а также расчет относительного
отклонения позволяют сделать вывод,
что трудовые ресурсы использовались
достаточно эффективно. Об этом
свидетельствует опережающий темп роста
объема продукции по сравнению с темпом
роста численности работающих, что и
привело к относительной экономии данного
вида ресурса, а также к росту выработки
продукции на одного работающего.

