Просмотров 1.4к. Опубликовано 30.09.2022
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Отношения
Мы знаем это, чтобы ответить на вопрос, насколько часто одно число больше (или меньше) другого, или насколько одно число является дробью другого. найти частное данных чисел.
Частное двух чисел не равный нулю, называется отношением чисел , или отношением числа .
Где — члены отношения число перед термином отношенияследующий срок отношения.
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
количество
1,15 : 0,36 — отношение от числа 1,15 до числа 0,36.
Отношение двух чисел Показывает, как часто одно число больше другого или как сильно одно число зависит от другого. Это отношение чисел указывает, сколько раз число или сколько частей числа .
Помните, что деление можно заменить дробью, поэтому, отношение чисел можно записать двумя способами: и
Основное свойство отношения:
Отношение не меняется, когда его члены умножаются или делятся на одно и то же число, которое не равно нулю.
Запишем отношение от 3 до 10 и найти его значение:
То есть отношение двух чисел Он может быть выражен в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, какой процент число составляет от другого числа.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и добавить знак процента к результату.
Пример:
В каком проценте число 5 равно числу 10?
5 10 2 1 — 100 % = 1 2 — 100 % = 100 2 % = 50 % .
Ответ: 50% равно 5 умножить на 10.
Если значение двух величин выражено в одних и тех же единицах, то. их отношение называют также отношением. Если две величины выражены в разных единицах, то отношения эти величины должны быть сначала переведены в одну и ту же единицу измерения.
Например:
Дан прямоугольник длиной 12 см и шириной 1 м. Найти отношение длины сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 12 : 100 = 100.
Отношение ширины прямоугольника к его длине равно 100 : 12 =
Дробь взаимно обратная, поэтому и отношения 12 к 100 и 100 к 12 называются взаимно обратными.
На практике отношение Обратные дроби используются, например, при составлении чертежей и географических карт. В этом случае земельные участки рисуются на бумаге в уменьшенном виде, а на карте или картографии изображаются отношение, указывает, как часто длина отрезка на чертеже меньше длины соответствующего отрезка на местности.
Соотношение между длиной отрезка на карте и длиной соответствующего отрезка на местности называется масштабом карты (чертежа).
Предположим, что карта имеет масштаб
Давайте выясним, какова длина отрезка в 5 см на карте на земле.
Для решения обозначим длину отрезка на земле (в сантиметрах). Затем отношение длина отрезка на карте к длине отрезка на местности составляет: 5 :, данная отношение равна масштабу карты, что дает уравнение:
5 :
Решите это уравнение:
10 000;
50 000 см = 500 м = 0,5 км.
Ответ: Отрезок в 5 см на карте равен 0,5 км на местности.
Давайте выясним, какая длина на карте соответствует отрезку 9,5 км на карте.
Для решения обозначьте длину участка на карте (в километрах). Затем отношение длина отрезка на карте с длиной отрезка на местности: : 9,5, данная отношение равна масштабу карты, что дает уравнение:
Решите это уравнение:
0,00095 км = 0,95 м = 95 см.
Ответ: Отрезок 9,5 км на карте равен 95 см на карте.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Отношение чисел
Отношение чисел — это коэффициент от деления одного числа на другое.
Отношение чисел A и b можно записать двумя способами: со знаком деления или через косую черту (как дробь):
Эти признаки следующие: отношение a к b или отношение числа a к числу b.
Числа a и b, составляющие отношение a : b становятся терминами отношения. Делителем является предыдущий член отношения, а делитель — предпоследний член. отношения. Таким образом, a — предыдущий член, b — следующий.
Соотношение используется для сравнения двух чисел. Так, отношение a : b показывает, во сколько раз a больше b (если делитель больше делимого) или сколько процентов от числа b составляет a (если делитель меньше делимого).
Отношение 35 к 7 показывает, что число 35 в пять раз больше числа 7.
2)
Отношение 12 к 15 показывает, что число 12 в 0,8 раза больше числа 15.
Из основного свойства квоты следует, что. отношения :
Отношение не меняется, когда его члены умножаются или делятся на одно и то же ненулевое число.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Помните.
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Давайте на примере покажем, в чем суть концепции. отношение двух чисел.
В городе Липецке проходят соревнования по велоспорту. В прошлом году было 15 участников, в этом году — 75. На сколько больше участников в этом году, чем в прошлом?
Прежде чем решить проблему, давайте остановимся на самых важных фактах. Запишите отношение количество участников в этом году с количеством участников в прошлом году.
Помните.
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
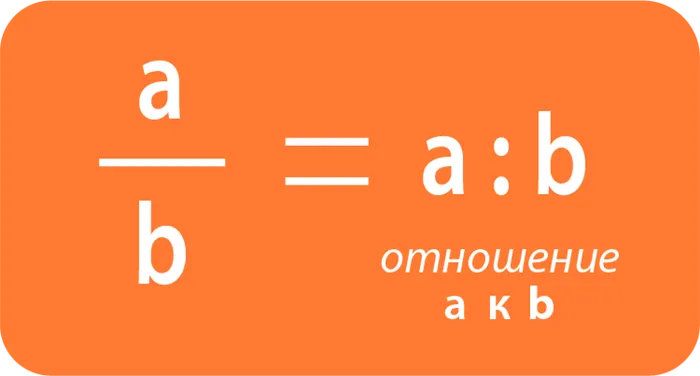
Помните.
Если вы умножите или разделите оба термина отношения на одно и то же число, которое не равно нулю, вы получите отношение, равное данному.
Если вы внимательно изучите приведенное выше правило, то обнаружите, что написанное выше правило — это не что иное, как основное свойство дробей, с помощью которого мы можем легко их сокращать.
Основное свойство коэффициента заключается в том, что он остается неизменным при умножении или делении делителя и делимого на одно и то же число.
Задания для самостоятельной работы
На пост президента претендовали два кандидата. Явка составила 120 человек. Распределение голосов соответствует соотношению 3:5. Необходимо определить количество голосов, полученных победителем.
Соотношение между количеством хвойных и лиственных деревьев в лесу можно представить как 1:4. Необходимо рассчитать долю лиственных деревьев.
На площади 24 га выращиваются сельскохозяйственные культуры. Зерновые и овощи распределяются в соответствии с с отношением 5:3. Необходимо рассчитать площадь возделывания овощных культур в гектарах.
Основное свойство отношения: Путем умножения или деления членов отношения на одно и то же число, отличное от нуля, данный отношение останется неизменным.
Отношения в задачах
Теперь давайте узнаем, как отношения в задачах.
Давайте сразу перейдем к примерам, чтобы увидеть, какой может быть формулировка отношения.
Проблема 1
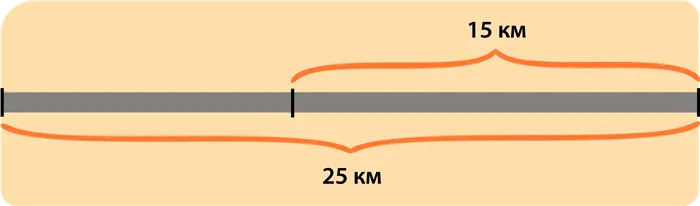
Протяженность дороги составляет 25 километров. Он освещен на протяжении 15 километров.
(α) Найдите, какая часть дороги освещена.
(b) Во сколько раз вся проезжая часть длиннее освещенной части?
Решение:
В начале урока мы обнаружили отношение меньшего числа в большее, определяя тем самым, какая часть первого числа содержится во втором.
Это первый вопрос.
Для нахождения отношения Отношение длины освещенного участка к длине всей дороги делится на единицу:
Значит, длина освещенного участка составляет (mathbf>) по всей длине дороги.
Второй вопрос: «Во сколько раз больше?». — соответствует отношению от большего числа к меньшему.
Чтобы найти это отношения это разделить длину всей дороги на длину освещенной части дороги:
Это отвечает на вопрос второго пункта.
Важно также всегда следить за тем, чтобы количество было одинаковым.
Так, если что-то дано нам в тоннах и килограммах, и мы хотим найти отношения Чтобы узнать эти количества, мы должны либо перевести тонны в килограммы, либо наоборот.
Проблема 2
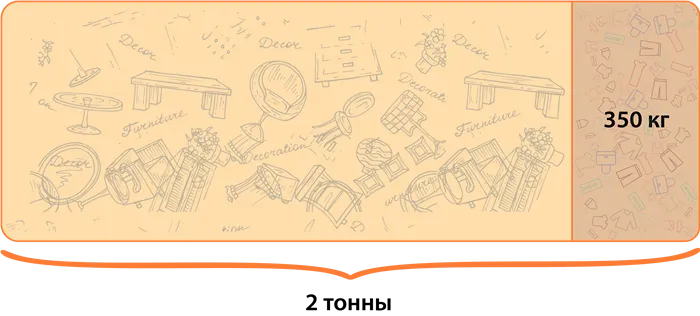
Масса груза составляет 2 тонны. Известно, что часть груза — это одежда, масса которой составляет 350 кг.
Определите, сколько процентов от массы груза составляет масса одежды.
Решение:
Давайте сначала переведем тонны в килограммы. Оказывается, что масса груза составляет 2000 кг.
Теперь давайте найдем неизвестное. отношение:
Теперь попробуйте решить задачу самостоятельно и воспользуйтесь подсказками, если у вас возникнут трудности.
Вы можете пройти тест и получить результат после того, как войдете в систему или зарегистрируетесь.
Интересная информация
Сегодня вы научитесь математическим фокусам!
Их идея заключается в том, что можно запутать людей с помощью математических преобразований, которые дают нам то, что нам нужно.
Уловка 1.
Попросите зрителя придумать число и никому его не называть.
Теперь попросите их умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть число в уме.
Теперь вы можете с уверенностью сказать, что зритель получил число 4.
Это происходит потому, что при преобразовании исходное число удаляется из арифметической цепочки, оставляя только четверку.
Попробуйте доказать это с помощью формул, вычитая исходное число X
Уловка 2
В этой игре вы можете угадать день рождения человека.
Попросите зрителя умножить количество дней рождения на 2. Затем попросите его прибавить к результату 5 и умножить целое число на 50. Затем попросите зрителя добавить номер месяца, в котором он родился (1 января, 2 февраля и т.д.).
Чтобы узнать день рождения человека по полученному числу, вычтите 250 из числа, указанного зрителем — вы получите трех- или четырехзначное число, где первые одна или две цифры обозначают день рождения, а последние две цифры — месяц.
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Эта информация доступна зарегистрированным пользователям
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf{a div b}) или же через дробную черту: (mathbf{frac{a}{b}})
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
(mathbf{256div8=32})
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
(mathbf{15div12=frac{15}{12}=frac{5cdot3}{4cdot3}=frac{5}{4}=1frac{1}{4}})
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf{1frac{1}{4}}) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
(mathbf{16div24=frac{16}{24}=frac{8cdot2}{8cdot3}=frac{2}{3}})
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf{frac{2}{3}}) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf{frac{2}{3}}) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
(mathbf{14div28=frac{14}{28}=frac{14cdot1}{14cdot2}=frac{1}{2}})
И посчитаем отношение 28 к 14
(mathbf{28div14=2})
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf{frac{2}{5}}), найдем отношение b к a
Для этого надо найти обратное число к (mathbf{frac{2}{5}})
(mathbf{1divfrac{2}{5}=frac{5}{2}=2frac{1}{2}})
Значит, отношение b к a равняется (mathbf{2frac{1}{2}})
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf{frac{1}{3}})
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf{frac{1}{3}})
Эта информация доступна зарегистрированным пользователям
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf{frac{3}{8}})
Перемножив, мы получим:
(mathbf{4cdotfrac{3}{8}=frac{4cdot3}{8}=frac{4cdot3}{4cdot2}=frac{3}{2}=1frac{1}{2}})
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
(mathbf{1frac{1}{2}div4=frac{3}{2}div4=frac{3}{2cdot4}=frac{3}{8}})
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf{2frac{1}{2}})
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
(mathbf{2frac{1}{2}div10=frac{2cdot2+1}{2}div10=frac{5}{2}div10=frac{5}{2cdot10}=frac{1}{2cdot2}=frac{1}{4}})
Ответ: дробь, взяв которую от 10 получили (mathbf{2frac{1}{2}}), равняется (mathbf{frac{1}{4}})
Пример 2
Отношение первого числа ко второму равно (mathbf{1frac{1}{5}}), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf{1frac{1}{5}})
(mathbf{1div1frac{1}{5}=1divfrac{6}{5}=1cdotfrac{5}{6}=frac{5}{6}})
Теперь можно найти второе число, домножим первое на эту дробь:
(mathbf{6cdotfrac{5}{6}=frac{6cdot5}{6}=5})
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
(mathbf{6div5=frac{6}{5}=1frac{1}{5}})
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf{1frac{1}{2}})
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
(mathbf{1div1frac{1}{2}=1divfrac{3}{2}=frac{2}{3}})
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
(mathbf{8divfrac{2}{3}=8cdotfrac{3}{2}=frac{8cdot3}{2}=4cdot3=12})
Ответ: число a равняется 12
Эта информация доступна зарегистрированным пользователям
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Эта информация доступна зарегистрированным пользователям
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
(mathbf{15div25=frac{15}{25}=frac{3cdot5}{5cdot5}=frac{3}{5}})
Значит, длина освещенного участка составляет (mathbf{frac{3}{5}}) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» – это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
(mathbf{25div15=frac{25}{15}=frac{5cdot5}{3cdot5}=frac{5}{3}=1frac{2}{3}})
Что отвечает на вопрос второго пункта.
Ответ: a) (mathbf{frac{3}{5}}), б) (mathbf{1frac{2}{3}})
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Эта информация доступна зарегистрированным пользователям
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
(mathbf{frac{350}{2000}=frac{35}{200}=frac{7cdot5}{5cdot40}=frac{7}{40}})
Ответ: (mathbf{frac{7}{40}}).
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 – получится трехзначное или четырехзначное число, где первые одна или две цифры – это день рождения, а последние две – месяц.
Чтобы узнать, на сколько процентов одно число больше или меньше другого, очень удобно воспользоваться следующими формулами:
Формула 1
если высчитывать, на сколько число больше другого, нужно
Формула 2
если высчитывать, на сколько число меньше другого, нужно
В обеих случаях выполняем примерно одинаковые действия и здесь нужно быть очень внимательным, чтобы ничего не напутать.
Почему нужно быть внимательным? – Потому что если сравнивать два два числа по разному – получим разные результаты.
Проверим это на примерах, которые уже есть в ответах на этот вопрос:
сравним числа 160 и 80
из первой формулы узнаем, что число 160 больше числа 80 на 100%
р%=(160-80)/80*100%=100%
из второй формулы узнаем, что число 80 меньше числа 160 на 50%
р%=(160-80)/160*100%=50%.
Аналогично узнаем, что число 20 больше числа 15 на 33,33%, а число 15 меньше числа 20 на 25%.
Если сравнивать числа, которые своими номиналами будут не очень сильно отличаться друг от друга (например числа 100 и 101) тогда процентная разница будет незаметна, но она все равно будет
101 больше 100 на 1% а число 100 меньше 101 на 0,99%
Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.
В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то». Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш» или если поменять местами яблоки и груши, то «соотношения груш и яблок».
В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам» или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам».
Соотношение выражается, как a к b (где вместо a и b любые числа), но также можно встретить запись, которая составлена с помощью двоеточия как a : b. Прочитать эту запись можно различными способами:
- a к b
- a относится к b
- отношение a к b
Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:
4 : 2
Это соотношение можно прочитать как «четыре к двум» либо «соотношение четырех яблок и двух груш» либо «четыре яблока относится к двум грушам»
Если же поменяем местами яблоки и груши, то будем иметь соотношение 2 : 4. Это соотношение можно прочитать как «два к четырем» либо «две груши к четырем яблокам» либо «две груши относятся к четырем яблокам».
В дальнейшем соотношение мы будем называть просто отношением.
Что такое отношение?
Отношение, как было сказано ранее, записывается в виде a : b. Также его можно записать в виде дроби 
. А мы знаем, что такая запись в математике означает деление. Тогда результатом выполнения отношения будет частное чисел a и b.
Отношением в математике называют частное двух чисел.
Отношение позволяет узнать сколько количества одной сущности приходится на единицу другой. Вернемся к отношению четырех яблок к двум грушам (4 : 2). Это отношение позволит нам узнать, сколько яблок приходится на единицу груши. Под единицей подразумевается одна груша. Сначала запишем отношение 4 : 2 в виде дроби:
Данное отношение представляет собой деление числа 4 на число 2. Если выполнить это деление, мы получим ответ на вопрос сколько яблок приходится на единицу груши
Получили 2. Значит четыре яблока и две груши (4 : 2) соотносятся (взаимосвязаны друг с другом) так, что на одну грушу приходится два яблока
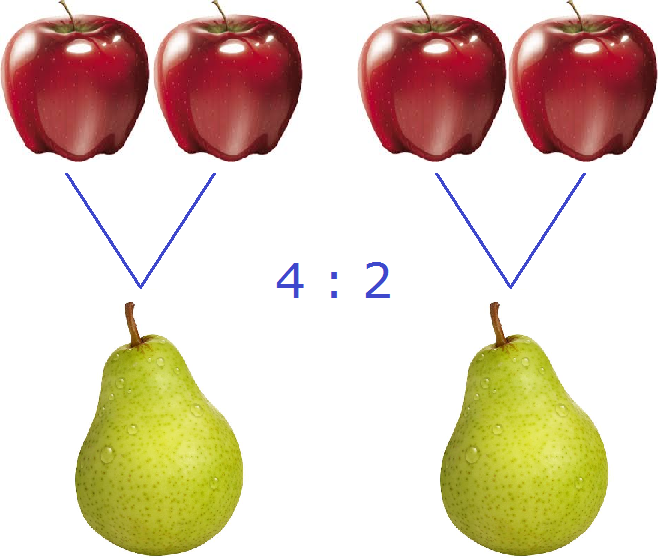
На рисунке показано, как четыре яблока и две груши соотносятся между собой. Видно, что на каждую грушу приходятся два яблока.
Отношение можно перевернуть, записав как 
. Тогда у нас получится соотношение двух груш и четырех яблок или «отношение двух груш к четырем яблокам». Это отношение покажет, сколько груш приходится на единицу яблока. Под единицей яблока подразумевается одно яблоко.
Чтобы найти значение дроби нужно вспомнить, как делить меньшее число на большее
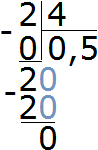
Получили 0,5. Переведём эту десятичную дробь в обыкновенную:
Сократим полученную обыкновенную дробь на 5
Получили ответ 
(половину груши). Значит две груши и четыре яблока (2 : 4) соотносятся (взаимосвязаны друг с другом) так, что на одно яблоко приходится половина груши
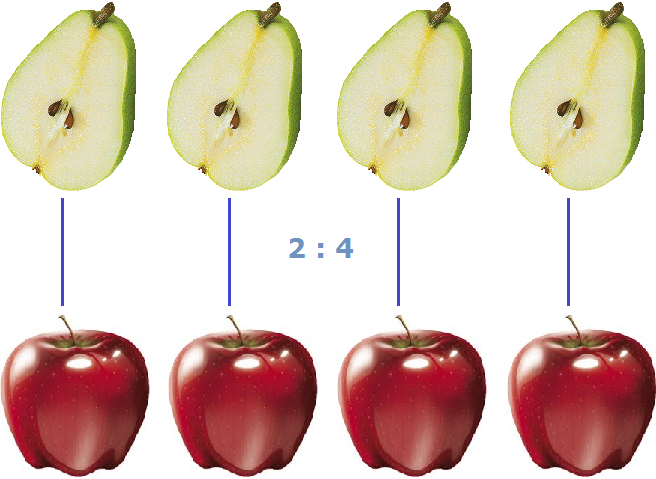
На рисунке показано, как две груши и четыре яблока соотносятся между собой. Видно, что на каждое яблоко приходится половинка груши.
Числа, из которых составлено отношение, называют членами отношения. Например, в отношении 4 : 2 членами являются числа 4 и 2.
Рассмотрим другие примеры соотношений. Для приготовления чего-либо составляется рецепт. Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).
Преобразуем соотношение 1 : 2 в дробь, получим . Вычислив эту дробь, получим 0,5. Значит один стакан хлопьев и два стакана молока соотносятся (взаимосвязаны друг с другом) так, что на один стакан молока приходится половина стакана хлопьев.
Если перевернуть соотношение 1 : 2 то получится соотношение 2 : 1 («два к одному» или «два стакана молока на один стакан хлопьев»). Преобразуем соотношение 2 : 1 в дробь, получим 
. Вычислив эту дробь, получим 2. Значит два стакана молока и один стакан хлопьев соотносятся (взаимосвязаны друг с другом) так, что на один стакан хлопьев приходятся два стакана молока.
Пример 2. В классе 15 школьников. Из них 5 – это мальчики, 10 – девочки. Можно записать соотношение девочек и мальчиков 10 : 5 и преобразовать это соотношение в дробь 
. Вычислив эту дробь получим 2. То есть девочки и мальчики соотносятся между собой так, что на каждого мальчика приходятся две девочки
На рисунке показано, как десять девочек и пять мальчиков соотносятся между собой. Видно, что на каждого мальчика приходятся две девочки.
Соотношение не всегда можно обращать в дробь и находить частное. В некоторых случаях это будет нелогично.
Так, если перевернуть отношение получится 
, а это уже отношение мальчиков к девочкам. Если вычислить эту дробь получается 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что на каждую девочку приходится половина мальчика. Математически это конечно верно, но с точки зрения реальности не совсем разумно, ибо мальчик это живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.
Умение построить правильное отношение — важный навык при решении задач. Так в физике, отношение пройденного расстояния ко времени есть скорость движения.
Расстояние обозначается через переменную S, время — через переменную t, скорость — через переменную v. Тогда фраза «отношение пройденного пути ко времени есть скорость движения» будет описываться следующим выражением:
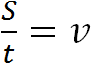
Предположим, что автомобиль проехал 100 километров за 2 часа. Тогда отношение пройденных ста километров к двум часам будет скоростью движения автомобиля:
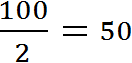
Скоростью принято называть расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. А отношение, как было сказано ранее, позволяет узнать сколько количества одной сущности приходится на единицу другой. В нашем примере отношение ста километров к двум часам показывает сколько километров приходится на один час движения. Видим, что на каждый час движения приходятся 50 километров
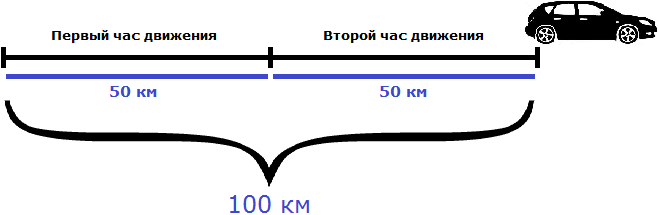
Поэтому скорость измеряется в км/ч, м/мин, м/с. Символ дроби ( / ) указывает на отношение расстояния ко времени: километров в час, метров в минуту и метров в секунду соответственно.
Пример 2. Отношение стоимости товара к его количеству есть цена одной единицы товара
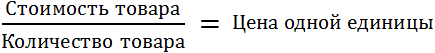
Если мы взяли в магазине 5 шоколадных батончиков и их общая стоимость составила 100 рублей, то мы можем определить цену одного батончика. Для этого нужно найти отношение ста рублей к количеству батончиков. Тогда получим, что на один батончик приходятся 20 рублей
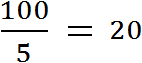
Сравнение величин
Ранее мы узнали, что отношение между величинами разной природы образуют новую величину. Так, отношение пройденного расстояния ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.
Но отношение можно использовать и для сравнения величин. Результат выполнения такого отношения есть число, показывающее во сколько раз первая величина больше второй или какую часть первая величина составляет от второй.
Чтобы узнать во сколько раз первая величина больше второй, в числитель отношения нужно записать большую величину, а в знаменатель меньшую величину.
Чтобы узнать какую часть первая величина составляет от второй, в числитель отношения нужно записать меньшую величину, а в знаменатель большую величину.
Рассмотрим числа 20 и 2. Давайте узнаем во сколько раз число 20 больше числа 2. Для этого находим отношение числа 20 к числу 2. В числителе отношения записываем число 20, а в знаменателе — число 2
Значение данного отношения равно десяти
Отношение числа 20 к числу 2 есть число 10. Это число показывает во сколько раз число 20 больше числа 2. Значит число 20 больше числа 2 в десять раз.
Пример 2. В классе 15 школьников. 5 из них это мальчики, 10 – девочки. Определить во сколько раз девочек больше мальчиков.
Записываем отношение девочек к мальчикам. В числителе отношения записываем количество девочек, в знаменатель отношения — количество мальчиков:
Значение данного отношения равно 2. Значит в классе из 15 человек девочек в два раза больше мальчиков.
Здесь уже не стоит вопрос о том, сколько девочек приходятся на одного мальчика. В данном случае отношение используется для сравнения количества девочек с количеством мальчиков.
Пример 3. Какую часть число 2 составляет от числа 20.
Находим отношение числа 2 к числу 20. В числителе отношения записываем число 2, а в знаменателе — число 20
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее
Значение отношения числа 2 к числу 20 есть число 0,1
В данном случае десятичную дробь 0,1 можно перевести в обыкновенную. Такой ответ будет проще для восприятия:
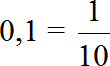
Значит число 2 от числа 20 составляет одну десятую часть.
Можно сделать проверку. Для этого найдём 
от числа 20. Если мы всё сделали правильно, то должны получить число 2
20 : 10 = 2
2 × 1 = 2
Получили число 2. Значит одна десятая часть от числа 20 есть число 2. Отсюда делаем вывод, что задача решена верно.
Пример 4. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества школьников составляют мальчики.
Записываем отношение мальчиков к общему количеству школьников. В числителе отношения записываем пять мальчиков, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 5 нужно разделить на число 15
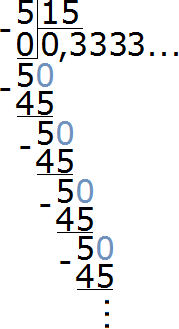
При делении 5 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную
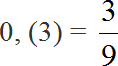
Сократим полученную дробь на 3
Получили окончательный ответ 
. Значит мальчики составляют одну треть от всего класса
На рисунке видно, что в классе из 15 школьников треть класса составляют 5 мальчиков.
Если для проверки найти от 15 школьников, то мы получим 5 мальчиков
15 : 3 = 5
5 × 1 = 5
Пример 5. Во сколько раз число 35 больше числа 5 ?
Записываем отношение числа 35 к числу 5. В числитель отношения нужно записать число 35, в знаменатель — число 5, но не наоборот
Значение данного отношения равно 7. Значит число 35 в семь раз больше числа 5.
Пример 6. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества составляют девочки.
Записываем отношение девочек к общему количеству школьников. В числителе отношения записываем десять девочек, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае, число 10 нужно разделить на число 15
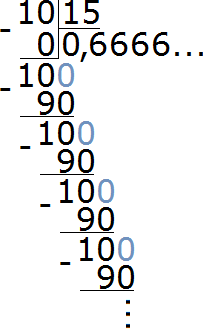
При делении 10 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную
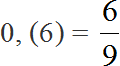
Сократим полученную дробь на 3
Получили окончательный ответ 
. Значит девочки составляют две трети от всего класса
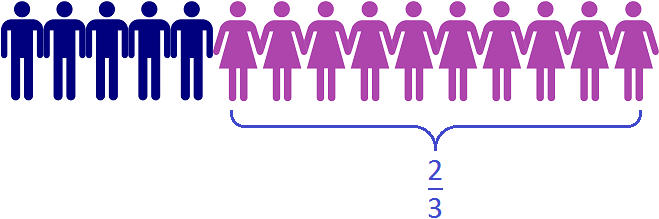
На рисунке видно, что в классе из 15 школьников две трети класса составляют 10 девочек.
Если для проверки найти от 15 школьников, то получим 10 девочек
15 : 3 = 5
5 × 2 = 10
Пример 7. Какую часть 10 см составляют от 25 см
Записываем отношение десяти сантиметров к двадцати пяти сантиметрам. В числителе отношения записываем 10 см, в знаменателе — 25 см
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 10 нужно разделить на число 25
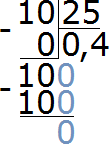
Переведём полученную десятичную дробь в обыкновенную
Сократим полученную дробь на 2
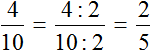
Получили окончательный ответ 
. Значит 10 см составляют от 25 см.
Пример 8. Во сколько раз 25 см больше 10 см
Записываем отношение двадцати пяти сантиметров к десяти сантиметрам. В числителе отношения записываем 25 см, в знаменателе — 10 см
Найдём значение данного отношения
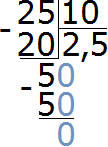
Получили ответ 2,5. Значит 25 см больше 10 см в 2,5 раза (в два с половиной раза)
Важное замечание. При нахождении отношения одноименных физических величин эти величины обязательно должны быть выражены в одной единице измерения, в противном случае ответ будет неверным.
Например, если мы имеем дело с двумя длинами и хотим узнать во сколько раз первая длина больше второй или какую часть первая длина составляет от второй, то обе длины сначала нужно выразить в одной единице измерения.
Пример 9. Во сколько раз 150 см больше 1 метра?
Сначала сделаем так, чтобы обе длины были выражены в одной единице измерения. Для этого переведем 1 метр в сантиметры. Один метр это сто сантиметров
1 м = 100 см
Теперь находим отношение ста пятидесяти сантиметров к ста сантиметрам. В числителе отношения записываем 150 сантиметров, в знаменателе — 100 сантиметров
Найдём значение данного отношения
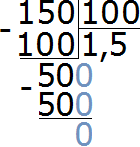
Получили ответ 1,5. Значит 150 см больше 100 см в 1,5 раза (в полтора раза).
А если бы не стали переводить метры в сантиметры и сразу попытались найти отношение 150 см к одному метру, то у нас получилось бы следующее:
Получилось бы, что 150 см больше одного метра в сто пятьдесят раз, а это неверно. Поэтому обязательно нужно обращать внимание на единицы измерения физических величин, которые участвуют в отношении. Если эти величины выражены в разных единицах измерения, то для нахождения отношения этих величин, нужно перейти к одной единице измерения.
Пример 10. В прошлом месяце зарплата человека составляла 25000 рублей, а в текущем месяце зарплата выросла до 27000 рублей. Определить во сколько раз выросла зарплата
Записываем отношение двадцати семи тысяч к двадцати пяти тысячам. В числителе отношения записываем 27000, в знаменателе — 25000
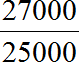
Найдём значение данного отношения
Получили ответ 1,08. Значит зарплата выросла в 1,08 раза. В будущем, когда мы познакомимся с процентами, такие показатели как зарплата будем выражать в процентах.
Пример 11. Ширина многоквартирного дома 80 метров, а высота 16 метров. Во сколько раз ширина дома больше его высоты?
Записываем отношение ширины дома к его высоте:
Значение данного отношения равно 5. Значит ширина дома в пять раз больше его высоты.
Свойство отношения
Отношение не изменится если его члены умножить или разделить на одно и тоже число.
Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.
Вернемся к отношению девочек к мальчикам (10 : 5). Данное отношение показало, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.
В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).
НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5
Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.
На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.
Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?
В обоих классах девочек в два раза больше мальчиков, поскольку отношения 
и 
равны одному и тому же числу.
Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.
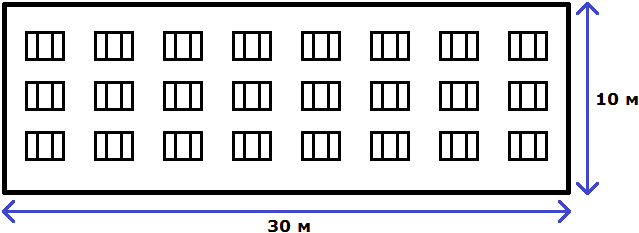
Чтобы нарисовать на бумаге похожий дом, нужно рисовать его в таком же отношении 30 : 10.
Разделим оба члена этого отношения на число 10. Тогда получим отношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3
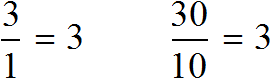
Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров
3 м = 300 см
1 м = 100 см
Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см
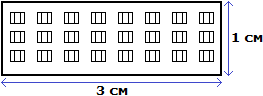
Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный
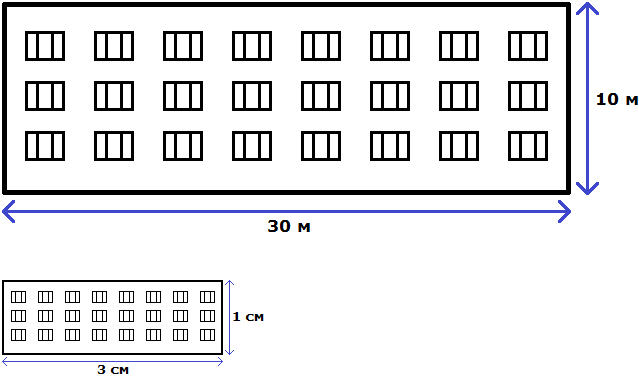
Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.
Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.
Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.
Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части
40 м : 4 = 10 м
Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.
Определим сколько метров приходится на ширину:
10 м × 3 = 30 м
Определим сколько метров приходится на высоту:
10 м × 1 = 10 м
Несколько членов отношения
Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.
Пример 1. Куплено 18 яблок. Эти яблоки разделили между мамой, папой и дочкой в отношении 2 : 1 : 3. Сколько яблок получил каждый?
Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:
Если сложить члены отношения 2 : 1 : 3, то можно узнать сколько всего частей имеется:
2 + 1 + 3 = 6 (частей)
Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6
18 : 6 = 3 (яблока на одну часть)
Теперь определим сколько яблок получил каждый. Умножая три яблока на каждый член отношения 2 : 1 : 3, можно определить сколько яблок получила мама, сколько получил папа и сколько получила дочка.
Узнаем сколько яблок получила мама:
3 × 2 = 6 (яблок)
Узнаем сколько яблок получил папа:
3 × 1 = 3 (яблока)
Узнаем сколько яблок получила дочка:
3 × 3 = 9 (яблок)
Пример 2. Новое серебро (альпака) — это сплав никеля, цинка и меди в отношении 3 : 4 : 13. Сколько килограммов каждого металла нужно взять, чтобы получить 4 кг нового серебра?
4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:
3 + 4 + 13 = 20 (частей)
Определим сколько килограммов будет приходиться на одну часть:
4 кг : 20 = 0,2 кг
Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:
0,2 кг × 3 = 0,6 кг никеля
Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:
0,2 кг × 4 = 0,8 кг цинка
Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:
0,2 кг × 13 = 2,6 кг меди
Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.
Пример 3. Латунь — это сплав меди и цинка, массы которых относятся как 3 : 2. Для изготовления куска латуни требуется 120 г меди. Сколько требуется цинка для изготовления этого куска латуни?
Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:
120 : 3 = 40 граммов на одну часть
Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:
40 г × 2 = 80 граммов цинка
Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?
Решение
15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом
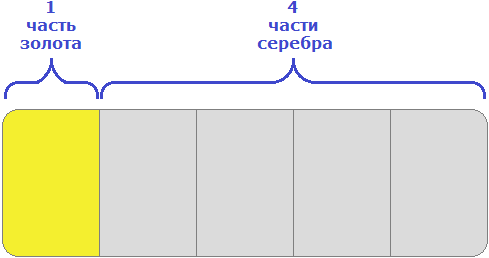
Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей
1 + 4 = 5
15 кг : 5 = 3 кг
Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.
Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.
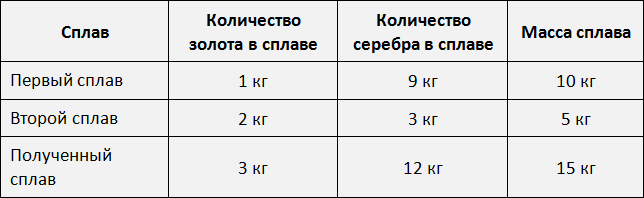
Теперь ответим на вопрос задачи — «Сколько нужно взять каждого сплава?»
Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.
Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Как найти отношение большего числа к меньшему
Найдите правильный ответ на вопрос ✅ «Как найти отношение большего числа к меньшему …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
