Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
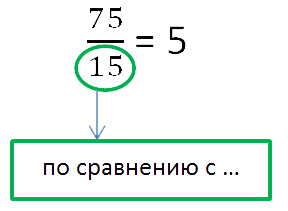
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
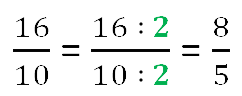
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Содержание
- Как найти отношение двух чисел примеры
- Примеры нахождения отношения двух чисел
- Формула для нахождения отношения двух чисел
- Заключение
- Как найти отношение двух чисел примеры
- Пример 1: Нахождение отношения двух чисел
- Пример 2: Нахождение отношения процентных значений
- Пример 3: Нахождение отношения валютных курсов
- Пример 4: Нахождение отношения дистанции к времени
- Пример 5: Нахождение отношения производительности
- Итог
- Как найти отношение двух чисел: примеры и объяснение
- Примеры расчетов отношения двух чисел
- Понимание математических принципов чтения формул отношения
- Расчеты отношения чисел на практике
- Итог
Как найти отношение двух чисел примеры
Отношение двух чисел — это результат деления одного числа на другое. Найти отношение двух чисел может потребоваться при решении математических задач, в финансовой деятельности, при анализе данных и других случаях.
Примеры нахождения отношения двух чисел
Чтобы найти отношение двух чисел, необходимо одно число разделить на другое. Например, если нужно найти отношение 10 к 5, необходимо разделить первое число на второе:
Отношение 10 к 5 = 10 / 5 = 2
В результате получается число 2. Это и есть отношение первого числа ко второму.
В другом примере, если необходимо найти отношение 15 к 3, необходимо сделать следующее:
Отношение 15 к 3 = 15 / 3 = 5
Результатом будет число 5 — это и есть отношение первого числа ко второму.
Формула для нахождения отношения двух чисел
Формула для нахождения отношения двух чисел следующая:
Отношение a к b = a / b
Здесь a и b — это числа, из которых нужно найти отношение. Применение этой формулы позволяет вычислять отношение любых чисел:
Например, если нужно найти отношение 24 к 8:
Отношение 24 к 8 = 24 / 8 = 3
Результатом будет число 3 — это и есть отношение первого числа ко второму.
Заключение
Найти отношение двух чисел довольно просто — нужно одно число разделить на другое. Формула для нахождения отношения двух чисел позволяет вычислять отношение любых чисел. На практике это может пригодиться при решении математических задач, в финансовой деятельности и в других областях.
Как найти отношение двух чисел примеры
Отношение двух чисел представляет собой дробь, в которой числитель — это первое число, а знаменатель — второе число. Отношение двух чисел может быть использовано в различных областях, начиная от математики и физики и заканчивая бизнесом и финансами. В этой статье мы рассмотрим, как находить отношение двух чисел с помощью простых примеров.
Пример 1: Нахождение отношения двух чисел
Предположим, что у нас есть два числа: 10 и 5. Чтобы найти отношение двух чисел, нужно разделить первое число на второе. В данном случае:
Отношение двух чисел = 10 / 5 = 2
Поэтому отношение чисел 10 и 5 равно 2.
Пример 2: Нахождение отношения процентных значений
Отношение процентных значений может быть найдено, когда мы имеем процент и целое число. Например, если мы хотим найти отношение 25% к 100, нужно сначала перевести процент в десятичное число, разделив его на 100. В данном случае:
25% = 0.25
Затем нужно умножить полученное число на целое число, чтобы найти значение:
Отношение процентных значений = 0.25 x 100 = 25
Поэтому отношение 25% к 100 равно 25.
Пример 3: Нахождение отношения валютных курсов
Отношение валютных курсов представляет собой отношение цены одной валюты к другой. Например, если мы хотим найти отношение курса доллара к евро, нужно разделить цену доллара на цену евро. В данном случае:
Отношение валютных курсов = Цена доллара / Цена евро
Например, если цена доллара равна 1,5 евро, а цена евро = 1, то:
Отношение валютных курсов = 1,5 / 1 = 1,5
Поэтому отношение курса доллара к евро равно 1,5.
Пример 4: Нахождение отношения дистанции к времени
Отношение дистанции к времени представляет собой отношение пройденной дистанции к затраченному времени. Например, если мы хотим найти скорость, двигаясь со скоростью 50 км/ч в течение 2 часов, нужно разделить пройденное расстояние на время:
Отношение дистанции к времени = Пройденная дистанция / Время
В данном примере, если скорость = 50 км/ч и время = 2 часа, то:
Отношение дистанции к времени = 50 x 2 = 100 км/ч
Поэтому скорость движения равна 100 км/ч.
Пример 5: Нахождение отношения производительности
Отношение производительности может быть найдено, когда мы имеем количество произведенной продукции и количество затраченного времени. Например, если мы хотим найти производительность рабочего, который произвел 500 единиц продукции за 4 часа, нужно разделить количество продукции на время:
Отношение производительности = Количество продукции / Время
В данном примере, если количество продукции = 500 единиц и время = 4 часа, то:
Отношение производительности = 500 / 4 = 125 единиц/час
Поэтому производительность рабочего равна 125 единиц/час.
Итог
Отношение двух чисел — это очень важный концепт в различных областях, включая математику, физику, бизнес и финансы. В этой статье мы рассмотрели несколько примеров, как находить отношение двух чисел в различных ситуациях. Надеемся, что этот материал был полезен и помог разобраться в данной теме.
Как найти отношение двух чисел: примеры и объяснение
Отношение двух чисел является одной из основных математических операций, которая используется на практике во многих областях, включая финансы, экономику, науку и технологии. Оно определяется как результат деления одного числа на другое и обозначается обычно символом «/», «:», «÷», или «|». Найти отношение двух чисел несложно, но требует понимания математических принципов и правильного применения формул.
Примеры расчетов отношения двух чисел
- Допустим, у вас есть 20 яблок и вы хотите узнать, какую долю от этого составляют 5 яблок. В этом случае отношение 5 к 20 будет выглядеть так:
- Если вы хотите распределить 300 долларов на трех людей, чтобы узнать, сколько денег будет доставаться каждому, вы можете использовать следующее уравнение:
- Если вы пытаетесь вычислить скорость объекта, измеренную в метрах в секунду (м/с), то вы можете использовать формулу:
- Если вы хотите узнать, какой процент людей на языковых курсах — это иностранцы, то вы можете использовать формулу:
5 / 20 = 0.25
Таким образом, 5 яблок составляют 25% от общего количества.
300 / 3 = 100
Следовательно, каждый человек получает по 100 долларов.
скорость = расстояние / время
Допустим, расстояние, пройденное объектом, равно 100 метров, а время, за которое он преодолел это расстояние, равно 10 секундам. Тогда отношение расстояния к времени будет равняться:
100 / 10 = 10
Следовательно, скорость объекта будет равна 10 м/с.
% иностранцев на курсе = (количество иностранцев / общее количество студентов) x 100%
Допустим, на языковом курсе из 40 студентов 10 иностранцев. Тогда:
(10 / 40) x 100% = 25%
Следовательно, 25% студентов языкового курса — иностранцы.
Понимание математических принципов чтения формул отношения
Как мы видим из примеров выше, отношение двух чисел является результатом деления одного числа на другое. При чтении формулы отношения, мы должны читать ее слева направо и понимать, что означает каждый символ в формуле. Символ на левой стороне формулы является числителем и числом, которое делится. Символ на правой стороне является знаменателем и числом, на которое делится.
Например, в формуле 5 / 20, число 5 в числителе является числом, которое делится на число 20 в знаменателе. Числитель может быть меньше, равен или больше знаменателя. В следующей формуле 20 / 5, число 20 в знаменателе делится на число 5 в числителе.
Формула отношения также может быть прочитана как дробь, в которой числитель представляет собой часть дроби, а знаменатель — целую дробь. Например, в формуле 5 / 20, мы можем прочитать ее как «пятая часть от двадцати».
Расчеты отношения чисел на практике
Расчеты отношения чисел имеют множество практических применений. В экономике и финансах, отношение может использоваться для вычисления стоимости акций, показателей рентабельности, финансового анализа и т.д.
В науке и технологиях, отношение может использоваться для вычисления скорости, производительности, эффективности машин и механизмов, анализа данных и т.д.
Итог
Отношение двух чисел — это одна из простейших математических операций, которая используется в различных областях. Она является результатом деления числа на другое и обозначается знаками «/», «:», «÷», или «|». Расчет отношения может быть применен к множеству задач и позволяет вычислить коэффициент, долю, процент и другие числовые параметры. При расчете отношения чисел важно понимать математические принципы и использовать формулы в соответствии с задачей. Примеры расчетов показывают, как применять формулы в практических задачах.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 
и 
– члены отношения; число – предыдущий член отношения; – последующий член отношения.
Например:
14 : 7 – отношение числа 14 к числу 7;
6 : 25 – отношение числа 6 к числу 25;
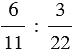– отношение числа 
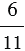к числу 
;
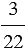1,15 : 0,36 – отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и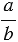 
.
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
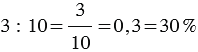
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел – это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
.
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
.
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб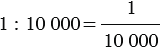 
, то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 
длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : = 1 : 10 000;
Решаем данное уравнение:
= 5
10 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 613,
Мерзляк, Полонский, Якир, Учебник
Номер 617,
Мерзляк, Полонский, Якир, Учебник
Номер 619,
Мерзляк, Полонский, Якир, Учебник
Номер 652,
Мерзляк, Полонский, Якир, Учебник
Номер 693,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Задание 732,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 752,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 805,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 998,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 149,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 230,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 303,
Мерзляк, Полонский, Якир, Учебник
Процентное отношение двух чисел
Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.
Процентное отношение двух чисел можно записать следующей формулой: 
Пример процентного отношения
Например есть два числа: 750 и 1100.
Процентное отношение 750 к 1100 равно 
Число 750 составляет 68.18% от 1100.
Процентное отношение 1100 к 750 равно 
Число 1100 составляет 146.67% от 750.
Пример-задача 1
Норма завода по производству автомобилей составляет 250 машин в месяц. Завод собрал за месяц 315 машин. Вопрос: на сколько процентов завод перевыполнил план?
Процентное отношение 315 к 250 = 315:250*100 = 126%.
План выполнен на 126%. План перевыполнен на 126% — 100% = 26%.
Пример-задача 2
Прибыль компании за 2011 год составила 126 млн $, в 2012 году прибыль составила 89 млн $. Вопрос: на сколько процентов упала прибыль в 2012 году?
Процентное отношение 89 млн к 126 млн = 89:126*100 = 70.63%
Прибыль упала на 100% — 70.63% = 29.37%
9 оценок
Категории
НаукаМатематика
Читайте также
- ГНОМ ГНОМ СКАЛА
- ДОМ ВОДА ДАЧА
- Спряжение глагола “to relate” (Английский язык)
Комментарии
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Эта информация доступна зарегистрированным пользователям
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf{a div b}) или же через дробную черту: (mathbf{frac{a}{b}})
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
(mathbf{256div8=32})
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
(mathbf{15div12=frac{15}{12}=frac{5cdot3}{4cdot3}=frac{5}{4}=1frac{1}{4}})
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf{1frac{1}{4}}) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
(mathbf{16div24=frac{16}{24}=frac{8cdot2}{8cdot3}=frac{2}{3}})
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf{frac{2}{3}}) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf{frac{2}{3}}) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
(mathbf{14div28=frac{14}{28}=frac{14cdot1}{14cdot2}=frac{1}{2}})
И посчитаем отношение 28 к 14
(mathbf{28div14=2})
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf{frac{2}{5}}), найдем отношение b к a
Для этого надо найти обратное число к (mathbf{frac{2}{5}})
(mathbf{1divfrac{2}{5}=frac{5}{2}=2frac{1}{2}})
Значит, отношение b к a равняется (mathbf{2frac{1}{2}})
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf{frac{1}{3}})
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf{frac{1}{3}})
Эта информация доступна зарегистрированным пользователям
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf{frac{3}{8}})
Перемножив, мы получим:
(mathbf{4cdotfrac{3}{8}=frac{4cdot3}{8}=frac{4cdot3}{4cdot2}=frac{3}{2}=1frac{1}{2}})
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
(mathbf{1frac{1}{2}div4=frac{3}{2}div4=frac{3}{2cdot4}=frac{3}{8}})
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf{2frac{1}{2}})
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
(mathbf{2frac{1}{2}div10=frac{2cdot2+1}{2}div10=frac{5}{2}div10=frac{5}{2cdot10}=frac{1}{2cdot2}=frac{1}{4}})
Ответ: дробь, взяв которую от 10 получили (mathbf{2frac{1}{2}}), равняется (mathbf{frac{1}{4}})
Пример 2
Отношение первого числа ко второму равно (mathbf{1frac{1}{5}}), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf{1frac{1}{5}})
(mathbf{1div1frac{1}{5}=1divfrac{6}{5}=1cdotfrac{5}{6}=frac{5}{6}})
Теперь можно найти второе число, домножим первое на эту дробь:
(mathbf{6cdotfrac{5}{6}=frac{6cdot5}{6}=5})
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
(mathbf{6div5=frac{6}{5}=1frac{1}{5}})
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf{1frac{1}{2}})
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
(mathbf{1div1frac{1}{2}=1divfrac{3}{2}=frac{2}{3}})
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
(mathbf{8divfrac{2}{3}=8cdotfrac{3}{2}=frac{8cdot3}{2}=4cdot3=12})
Ответ: число a равняется 12
Эта информация доступна зарегистрированным пользователям
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Эта информация доступна зарегистрированным пользователям
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
(mathbf{15div25=frac{15}{25}=frac{3cdot5}{5cdot5}=frac{3}{5}})
Значит, длина освещенного участка составляет (mathbf{frac{3}{5}}) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» – это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
(mathbf{25div15=frac{25}{15}=frac{5cdot5}{3cdot5}=frac{5}{3}=1frac{2}{3}})
Что отвечает на вопрос второго пункта.
Ответ: a) (mathbf{frac{3}{5}}), б) (mathbf{1frac{2}{3}})
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Эта информация доступна зарегистрированным пользователям
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
(mathbf{frac{350}{2000}=frac{35}{200}=frac{7cdot5}{5cdot40}=frac{7}{40}})
Ответ: (mathbf{frac{7}{40}}).
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 – получится трехзначное или четырехзначное число, где первые одна или две цифры – это день рождения, а последние две – месяц.
