Условие
B17. Две материальные точки движутся по окружностям радиусами R1 = 0,2 м и R2 = 0,4 м с одинаковыми периодами. Найдите отношение их центростремительных ускорений.
Решение
| R1 = 0,2 м; |
| R2 = 0,4 м; |
|
T1 = T2;
|
| ac2/ac1 – ? |
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и угловая скорость связаны соотношением (~a_c = omega^2 R), а угловая скорость и период – (~omega = frac{2 pi}{T}) . Тогда (~a_c = left( frac{2 pi}{T} right)^2 R) (1). Для тела 1 уравнение (1) примет вид (~a_{c1} = left( frac{2 pi}{T_1} right)^2 R_1) ; для тела 2 – (~a_{c2} = left( frac{2 pi}{T_2} right)^2 R_2) . Получаем
(~frac{a_{c2}}{a_{c1}} = frac{(2 pi)^2 cdot R_2}{T^2_2} cdot frac{T^2_1}{(2 pi)^2 cdot R_1} = frac{R_2}{R_1} = 2) .
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Движение по окружности
Криволинейное движение — механическое движение, траектория которого — кривые линии с произвольным ускорением и произвольной скоростью.
Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. [omega=dfracvarphi t=dfrac{2pi}{t}]
Период обращения — это время одного полного оборота.
Частота обращения — величина, обратная периоду. Частота показывает, сколько полных оборотов совершает материальная точка за секунду. [nu=dfrac1T]
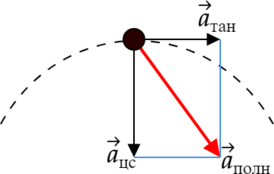
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения.
Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное к центру кривизны траектории. [a_text{цс}=dfrac{v^2}{r}]
Полное ускорение тела, движущегося по окружности равно векторной сумме тангенциального и нормального ускорений. [overrightarrow a_text{полн}=overrightarrow a_text{тан}+overrightarrow a_text{цс}]
Шарик движется по окружности радиусом (R_1 = 2) м со скоростью ( upsilon_1 = 3) м/с. Во сколько раз изменится его центростремительное ускорение, если радиус его окружности уменьшить в (n = 3) раза, а скорость увеличить в (k = 5) раз?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon_1^2}{R_1} qquad (1)] [a_{text{ц2}} = frac{upsilon_2^2}{R_2} qquad (2)]
По условию задачи: [upsilon_2=kupsilon_1 qquad (3)] [R_2 = frac{R_1}{n} qquad (4)]
Подставляя (3), (4) и (1) в (2) получаем: [a_{text{ц2}} = dfrac{(kupsilon_1)^2}{dfrac{R_1}{n}} = nk^2frac{upsilon_1^2}{R_1} = nk^2a_{text{ц1}}] [frac{a_{text{ц2}}}{a_{text{ц1}}} = nk^2 = 3cdot5^2 = 75]
Ответ: 75
Тело движется по окружности радиусом (R=4) м. В какой момент времени центростремительное ускорение (a_text{цс} = 1 text{ м/с$^2$})?
При движении по окужности центростремительное ускорение можно найти по следующей формуле: [a_text{цс} = frac{upsilon^2}{R}] где (v) – скорость тела
Отсюда: [upsilon = sqrt{a_text{цс} cdot R} = sqrt{1 cdot 4} = 2text{ м/с }] По графику видно, что (upsilon = 2) м/с в момент времени (t=5) с.
Ответ: 5
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Центростремительное ускорение (нормальное): (displaystyle a_{text{цс}}=frac{upsilon^2}R=frac{(20 text{ м/с})^2}{100 text{ м}}=4) м/с(^2)
Ответ: 4
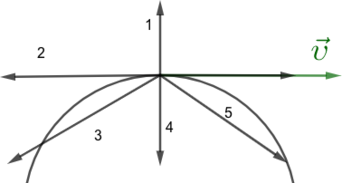
Велосипедист едет по круговому треку и замедляется. На рисунке указано направление скорости велосипедиста. Под каким номером верно указано направление центростремительного ускорения? Тангенциального ускорения? Куда направлено полное ускорение? (В ответе укажите последовательность цифр, например: 153)
Нормальная составляющая ускорения (центростремительное ускорение) характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело.
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости:
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным
Полное ускорение – это сумма нормального и тангенциального: [vec{a}_{text{полн}}=vec{a}_{text{норм}}+vec{a}_{text{танг}}]
Центростремительное ускорение направлено к центру (4). Так как велосепидист замедляется, то тангенциальное направлено против скорости (2). Полное ускорение является суммой 2 и 4, следовательно полное ускорение под номером 3.
Ответ: 423
Тело равномерно движется по окружности. Угловая скорость тела равна (w=6,5) рад/с. За какое время (t) тело совершит 5,5 оборотов? Принять (pi=3,14). Ответ округлить до десятых.
Cпособ 1:
Найдем длину дуги окружности: [l=2pi r,] где (r) — радиус окружности.
Т.к. тело прошло эту длину 5,5 раз, оно прошло путь: [S=5,5l=11pi rquad(1)] Выразим формульно линейную скорость (v) и угловую скорость тела:
[begin{cases}
v=2pi rnu\
w=2pinu
end{cases}
Rightarrow
v=wrquad(2)]
Т.к. тело движется равномерно, (v=const). По закону равномерного движения: [S=vt] Подставим ((1)) и ((2)): [11pi r=wrt] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Cпособ 2 :
Выразим формульно (w): [w=dfrac{Deltavarphi}{t},quad(1)] где (Deltavarphi) — угол поворота тела. [Deltavarphi=dfrac{S}{r},] где (S=5,5l=5,5cdot2pi r=11pi r) — путь, пройденный телом. [Deltavarphi=dfrac{11pi r}{r}=11piquad(2)] Подставим (2) в (1): [w=dfrac{11pi}{t}] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Ответ: 5,3
Две материальные точки движутся по окружностям радиусами (R_1) и (R_2), причем (R_2 = 3R_1). Скорости тел равны. Чему равно отношение их центростремительных ускорений?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon^2}{R_1}] [a_{text{ц2}} = frac{upsilon^2}{R_2}]
Тогда искомое отношение равно: [frac{a_{text{ц1}}}{a_{text{ц2}}} = frac{dfrac{upsilon^2}{R_1}}{dfrac{upsilon^2}{R_2}} = frac{R_2}{R_1} = frac{3R_1}{R_1} = 3]
Ответ: 3
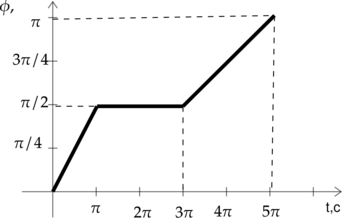
Точечное тело равномерно движется по окужности радиусом (R=2) м. На рисунке изображён график зависимости угла поворота (varphi) от времени (t). Найдите значение линейной скорости тела в интервале времени (3pi<t<5pi).
Линейная скорость тела, движущегося по окружности: [upsilon = omega cdot R qquad (1)] где (omega) – угловая скорость.
Угловая скорость: [omega = frac{Deltavarphi}{Delta t} qquad (2)] Подставив (2) в (1), получим: [upsilon = frac{Deltavarphi}{Delta t} cdot R] [upsilon = frac{dfrac{pi}{2}}{2pi} cdot 2 =0,5 text{ м/с}]
Ответ: 0,5

УСТАЛ? Просто отдохни
Задача 1
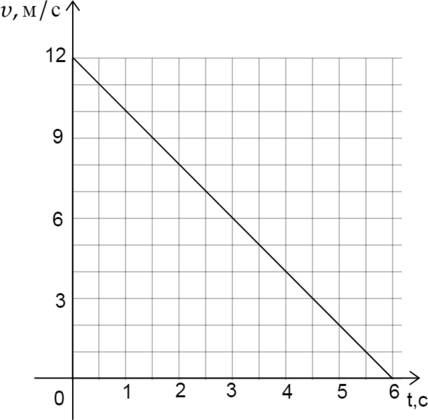
Материальная точка движется по окружности радиусом 4 м. На графике показана зависимость модуля её скорости v от времени t. Чему равен модуль центростремительного ускорения точки в момент t = 3 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Центростремительное ускорение вычисляется по формуле
Из графика находим, что скорость в момент времени t=3 c равна 6 м/c. Следовательно, модуль центростремительного ускорения точки в момент t=3 c равен
Ответ: 9.
Задача 2
Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?
Решение.
Центростремительное ускорение равно
Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:
Ответ: 2.
Равномерное движение тела по окружности
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ( T ) — время, в течение которого тело совершает один полный оборот. Единица периода — ( [,T,] ) = 1 с.
Частота обращения ( (n) ) — число полных оборотов тела за одну секунду: ( n=N/t ) . Единица частоты обращения — ( [,n,] ) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: ( n=1/T ) .
Пусть некоторое тело, движущееся по окружности, за время ( t ) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ( varphi ) .
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость ( omega ) — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ( omega=varphi/t ) . Единица угловой скорости — радиан в секунду, т.е. ( [,omega,] ) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ( 2pi ) . Поэтому ( omega=2pi/T ) .
Линейная скорость тела ( v ) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ( vec=l/t ) . За один оборот точка проходит путь, равный длине окружности. Поэтому ( vec=2pi!R/T ) . Связь между линейной и угловой скоростью выражается формулой: ( v=omega R ) .
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ( vec=frac<Deltavec> ) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ( a=frac ) . Так как ( v=omega R ) , то ( a=omega^2R ) .
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии ( R_1 ) от центра вращающегося колеса, равна ( v_1 ) . Чему равна скорость ( v_2 ) точки 2, находящейся от центра на расстоянии ( R_2=4R_1 ) ?
1) ( v_2=v_1 )
2) ( v_2=2v_1 )
3) ( v_2=0,25v_1 )
4) ( v_2=4v_1 )
3. Период обращения точки по окружности можно вычислить по формуле:
1) ( T=2pi!Rv )
2) ( T=2pi!R/v )
3) ( T=2pi v )
4) ( T=2pi/v )
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) ( omega=a^2R )
2) ( omega=vR^2 )
3) ( omega=vR )
4) ( omega=v/R )
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения
ФОРМУЛА
1) ( 1/T )
2) ( v^2/R )
3) ( v/R )
4) ( omega R )
5) ( 1/n )
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
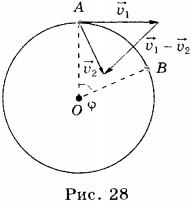
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное. С прямолинейным движением мы научились работать на предыдущих уроках, а именно решать главную задачу механики для такого вида движения.
Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.
Вопросу о том, как решается главная задача механики в случае криволинейного движения, и будет посвящен этот урок.
[spoiler title=”источники:”]
http://fizmat.by/kursy/kinematika/okruzhnost
http://interneturok.ru/lesson/physics/10-klass/mehanikakinematika/dvizhenie-tela-po-krivolineynoy-traektorii-dvizhenie-po-okruzhnosti-harakteristiki-vraschatelnogo-dvizheniya-tsentrostremitelnoe-uskorenie
[/spoiler]
Дан 1 ответ
Дано:
R = 6400 км = 6,4·106 м;
Т = 24 ч = 8,64·104 с;
υ – ?ацс – ?
Решение: Точки земной поверхности на экваторе движутся по окружности радиуса R, поэтому модуль их скорости:
υ=2пr/T=2*3.14*6.4*10^6/8.64*10^4=465м/с
Центростремительное ускорение:
ацс=υ^2/R=4.65*10^2/6.4*10^6=0.034м/с
Ответ: υ = 465 м/с, ацс = 0,034 м /с2.
эйнштейн777_zn
13 Март, 18