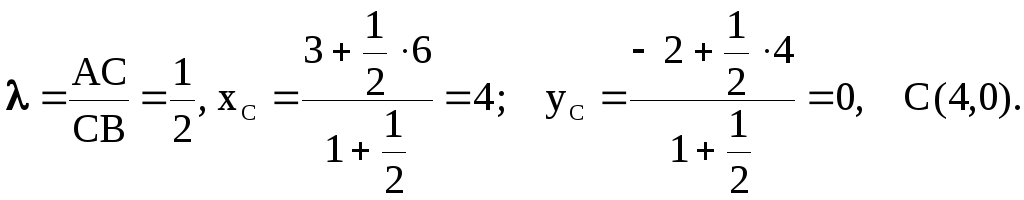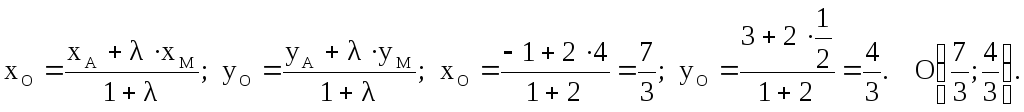Как найти отношение деления отрезка

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

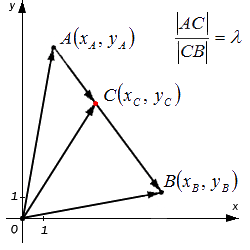
Исходные данные: задана прямоугольная система координат Oxy и две лежащие на ней, несовпадающие точки с заданными координатами A(xA,yA) и B(xB,yB) . А также задана точка С, делящая отрезок АВ в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С: xC и yC .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С, делящая отрезок АВ в отношении λ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке АВ (т.е. между точками А и В). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков АС и СВ равно λ. Т.е. верно равенство:

ACCB=λ .

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок ВА, тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1, то точка С является серединой отрезка АВ.

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А, В и точку С на отрезке АВ. Построим радиус-векторы указанных точек, а также векторы AC→ и CB→ . Согласно условиям задачи, точка С делит отрезок АВ в отношении λ.

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA) и OB→= (xB , yB) .

Определим координаты вектора : они будут равны координатам точки С, которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: OC→=OA→+AC→    OB→=OC→+CB→⇔CB→=OB→-OC→

По условию задачи точка С делит отрезок АВ в отношении λ, т.е. верно равенство AC=λ·CB .

Векторы AC→ и CB→ лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: AC →=λ·CB→ .

Преобразуем выражение, подставив в него : CB→=OB→-OC→ .

AC→=λ·(OB→-OC→) .

Равенство OC→=OA→+AC→ перепишем как OC→=OA→+λ·(OB→-OC→) .

Используя свойства операций над векторами, из последнего равенства следует: OC→=11+λ·(OA→+λ·OB→) .

Теперь нам остается непосредственно вычислить координаты вектора OC→=11+λ·OA→+λ·OB→ .

Выполним необходимые действия над векторами OA→ и OB→ .

OA →=(xA , yA) и OB→ = (xB , yB) , тогда OA→+λ·OB→ = (xA+λ·xB, yA+λ·yB) .

Таким образом, OC→=11+λ·(OA→+λ·OB→) = (xA+λ·xB1+λ , yA+λ·yB1+λ) .

Резюмируя: координаты точки С, делящей отрезок АВ в заданном отношении λ определяются по формулам : xC = xA+λ·xB1+λ и  yC=уA+λ·yB1+λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве 

Исходные данные: прямоугольная система координат Oxyz, точки с заданными координатами A (xA , yA , zA) и B (xB , yB , zB) .

Точка С делит отрезок АВ в отношении λ. Необходимо определить координаты точки С.

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

OC →=11+λ·(OA→+λ·OB→)

Векторы и являются радиус-векторами точек А и В, а значит:

OA→= (xA , yA , zA) и OB→=(xB , yB , zB), следовательно

OC→=11+λ·(OA→+λ·OB→) = (xA +λ·xB1+λ , yA +λ ·yB1+λ , zA + λ·zB1+λ)

Таким образом, точка С, делящая отрезок АВ в пространстве в заданном отношении λ, имеет координаты: (xA+λ·xB1+λ , yA+λ·yB1+λ , zA + λ·zB1+λ)

Рассмотрим теорию на конкретных примерах.

Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:

хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),

где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).

Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:

хС = (хА + хВ)/2, уС = (уА + уВ)/2.

Нужно иметь ввиду, что в задачах λ – это отношение длин отрезков, а поэтому числа, входящие в данное отношение не есть длины самих отрезков в заданной единице измерения. Например, АС = 12 см, СВ = 16 см: λ = АС/СВ = 12 см / 16 см = 3/4.

1. Поиск координат середины некоторого отрезка, по заданным координатам его концов

Пример 1.

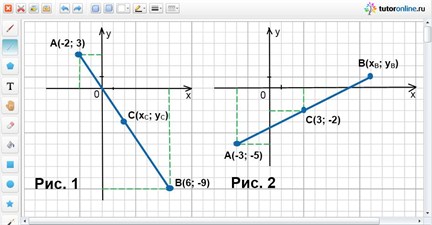
Точки А(-2; 3) и В(6; -9) – концы отрезка АВ. Найти точку С, являющиеся серединой отрезка АВ.

Решение.

В условии задачи задано, что хА = -2; хВ = 6; уА = 3 и уВ = -9. Требуется найти С(хС ; уС).

Применяя формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:

хС = (-2 + 6)/2 = 2, уС = (3 + (-9))/2 = -3.

Таким образом, точка С, являющаяся серединой отрезка АВ, имеет координаты (-2; 3) (рис. 1).
2. Вычисление координат конца некоторого отрезка, зная координаты его середины и другого конца

Пример 2.

Одним концом отрезка АВ является точка А, с координатами (-3; -5), а его серединой точка С(3; -2). Вычислите координаты второго конца отрезка – точки В.

Решение.

По условию задачи становится ясно, что хА = -3; уА = -5; хС = 3 и уС = -2.

Подставив эти значения в формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:

3 = (-3 + хВ)/2 и

-2 = (-5 + уВ)/2.

Решив первое уравнение относительно хВ и второе относительно уВ, найдем: хВ = 9 и уВ = 1, получается, что нужная точка В будет задаваться координатами (9; 1) (рис. 2).

3. Вычисление координат вершин некоторого треугольника по заданным координатам середин его сторон

Пример 3.

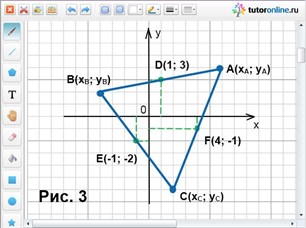
Серединами сторон треугольника АВС являются  точки D(1; 3), E(-1; -2) и F(4; -1). Найти координаты вершин А, В и С данного треугольника.

Решение.

Пусть точка D и есть середина стороны АВ, точка Е – середина ВС и точка F – середина сторона АС (рис. 3). Необходимо найти точки А, В и С.

Обозначаем вершины треугольника через А(хА; уА), В(хВ; уВ) и С(хС; уС) и зная координаты точек D, Е и F, по формулам  хС = (хА + хВ)/2, уС = (уА + уВ)/2 получим:

{1 = (хА + хВ)/2,
{-1 = (хВ + хС)/2,
{4 = (хА + хС)/2,

и

{3 = (уА + уВ)/2,
{-2 = (уВ + уС)/2,
{-1 = (уА + уС)/2.

Приведем уравнения к целому виду:

{хА + хВ = 2,
{хВ + хС = -2,
{хА + хС = 8,

и

{уА + уВ = 6,
{уВ + уС = -4,
{уА + уС = -2.

Решив системы, получим:
хА = 6; хВ = -4; хС = 2.
уА = 4; уВ = 2; уС = -6.

Точки А(6; 4), В(-4; 2) и С(2; -6) и есть необходимые вершины треугольника.

4. Вычисление координат точек, которые делят отрезок в определенном отношении, по заданным координатам концов этого отрезка

Пример 4.

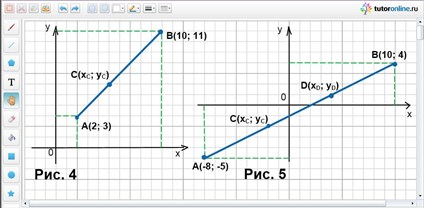
Отрезок АВ поделен точкой С в отношении 3 : 5 (считая от точки А к точке В). Концы отрезка АВ – точки А(2; 3) и В(10; 11). Найти точку С.

Решение.

В условии задачи сказано, что хА = 2; хВ = 10; уА = 3; уВ = 11; λ = АС/СВ = 3/5. Найти С(хС; уС) (рис. 4).

по формулам  хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:

хС = (2 + 3/5 · 10) / (1 + 3/5) = 5 и уС = (3 + 3/5 · 11) / (1 + 3/5) = 6. Таким образом, имеем С(5; 6).

Выполним проверку: АС = 3√2, СВ = 5√2, λ = АС/СВ = 3√2/5√2 = 3/5.

Замечание. В условии задачи указано, что деление отрезка производится в заданном отношении от точки А к точке В. Если бы это не уточнялось, то задача имела бы два решения. Второе решение: деление отрезка от точки В к точке А.
Пример 5.

Некоторый отрезок АВ разделен в отношении 2 : 3 : 5 (считая от точки А к точке В), его концы – есть точки с координатами А(-11; 1) и В(9; 11). Найти точки деления данного отрезка.

Решение.

Обозначим точки деления отрезка от А к В через С и D. В условии задачи дано, что
хА = -11; хВ = 9; уА = 1; уВ = 11. Найти С(хС; уС) и D(хD; уD), если АС : СD : DB = 2 : 3 : 5.

Точка С делит отрезок АВ в отношении  λ = АС/СВ = 2/(3 + 5) = 2/8 = 1/4.

По формулам  хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:

хС = (-11 + ¼ · 9) / (1 + 1/4) = -7 и уС = (1 + ¼ · 11) / (1 + 1/4) = 3.

Таким образом, С(-7; 3).

Точка D – есть середина отрезка АВ. Применив формулы хD = (хА + хВ)/2, уD = (уА + уВ)/2, найдем:

хD = (-11 + 9)/2 = -1, уD = (1 + 11)/2 = 6. Значит, D имеет координаты (-1; 6).

5. Вычисление координат точек, которые делят отрезок, если заданы координаты концов этого отрезка и число частей, на которые этот отрезок разделен

Пример 6.

Концы отрезка – точки А(-8; -5) и В(10; 4). Найти точки С и D, которые делят этот отрезок на три равные части.

Решение.

Из условия задачи известно, что хА = -8; хВ = 10; уА = -5; уВ = 4 и n = 3. Найдем С(хС; уС) и D(хD; уD) (рис. 5).

Найдем точку С. Она делит отрезок АВ в отношении λ = 1/2. Деление производим от точки А к точке В. По формулам  хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) имеем:

хС = (-8 + ½ · 10) / (1 + 1/2) = -2 и уС = (-5 + ½ · 4) / (1 + 1/2) = -2. Таким образом, С(-2; -2).

Деление отрезка СВ выполняется в отношении 1 : 1, поэтому используем формулы

хD = (хА + хВ)/2, уD = (уА + уВ)/2:

хD = (-2 + 10)/2 = 4, уD = (-2 + 4)/2 = 1. Таким образом, D(4; 1).

Точки деления С(-2; -2) и D(4; 1).

Замечание: Точку D можно найти, производя деление отрезок АВ в отношении 2 : 1. В таком случае надо будет снова применить формулы хD = (хА + λхВ) / (1 + λ), уD = (уА + λуВ) / (1 + λ).

Пример 7.

Точки А(5; -6) и В(-5; 9) – концами отрезка. Найти точки, которые поделят данный отрезок на пять равных частей.

Решение.

Пусть последовательные точки деления от А к В будут С(хС; уС), D(хD; уD), Е(хE; уE) и F(хF; уF). В условия задачи сказано, что хА = 5; хВ = -5; уА = -6; уВ = 9 и n = 5.

Найдем по формулам  хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) точку С. Она делит отрезок АВ в отношении λ = 1/4:

хС = (5 + 1/4 · (-5)) / (1 + 1/4) = 3 и уС = (-6 + 1/4 · 9) / (1 + 1/4) = -3, получаем, что точка С имеет координаты (3; -3).

Деление отрезка АВ точкой D производится в отношении 2 : 3 (т.е. λ = 2/3), поэтому:

xD = (5 + 2/3 · (-5)) / (1 + 2/3) = 1 и уD = (-6 + 2/3 · 9) / (1 + 2/3) = 0, значит D(1; 0).

Найдем точку Е. Она делит отрезок АВ в отношении λ = 2/3:

XЕ = (5 + 3/2 · (-5)) / (1 + 3/2) = -1 и уЕ = (-6 + 3/2 · 9) / (1 + 3/2) = 3. Таким образом, Е(-1; 3).

Точка F делит отрезок АВ в отношении λ = 4/1, поэтому:

XF = (5 + 4 · (-5)) / (1 + 4) = -3 и уF = (-6 + 4 · 9) / (1 + 4) = 6, F(-3; 6).

Точки деления С(-2; -2); D(4; 1); Е(-1; 3) и F(-3; 6).

 Остались вопросы? Не знаете, как решить задачу на деление отрезка?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Давно о геометрии не говорили, а о теореме ФАлеса (или ФалЕса?) вообще мало говорят. Хотя она весьма полезна. Начнем с формулировки, которая весьма не вразумительна, чем и объясняется не популярность данной теоремы.

Мутно, долго, не понятно. Мне больше нравится другая формулировка.

Тоже не понятно, но элегантно и коротко.

Задачи, которые решаются с помощью данной теоремы, довольно специфичны. Но есть одна задача на построение, которую можно встретить в реальной жизни. Это задача о делении отрезка в заданном отношении.

Суть вопроса: Дан отрезок. Его нужно поделить на два куска, чтобы их длины относились, как 2 : 5. Кусков может быть сколько угодно и отношение, может быть каким угодно. Алгебраически задача решается крайне легко: находим общее количество частей (2 + 5 = 7), делим длину отрезка на общее количество частей, находим длину каждого куска.

Но алгебраическое решение не всегда прокатывает. Например, мы не можем найти длину отрезка, или при делении получаются не целые числа. Тогда можно воспользоваться геометрическим способом.

Во-первых, проводим луч из конца отрезка. Любой, в любую сторону.

Дальше, на этом луче от точки А откладываем 7 (общее количество частей) равных отрезков.

Последнюю получившуюся точку – J соединяем с точкой В, а затем через каждую точку луча проводим прямую параллельную JB.

Таким образом, мы разделили отрезок АВ на 7 равных частей (по теореме Фалеса). Отсчитываем две части и ставим точку. Получаем: AK : KB = 2 : 5.

Вот таким простым образом, вы можете поделить свою комнату с соседом в любом отношении. Если вам кажется, что построение такого количества параллельных прямых дело сложное, то подумайте о перпендикулярах.

Даны точки
Требуется найти координаты точкиK(x,y),
делящей
отрезокMN
в отношении
Рассмотрим векторыЭти векторы коллинеарныИз векторной алгебры известно, что если
векторы коллинеарны, то соответствующие
координаты пропорциональны. Имеем:

(по условию).

Из этих уравнений
легко найти x
и y

(2.1.1)

Если
то точкаK
является серединой отрезка MN.
Формулы (2.1) примут вид:

(2.1.2)

Это формулы
координат середины отрезка.

Пример 1.
Найти
координаты
точки K,
делящей отрезок MN,
где M(-1,4)
и N(2,1),
в отношении 2 : 1.

Решение.
По условию
Подставим координаты точкиM
и N
в формулы (2.1.1). Имеем:

Точка K
имеет координаты: x=1,
y=2.

Ответ: K(1,2).

Пример 2.
Отрезок АВ разделен на три равные части.
Определить координаты точек деления,
если А(3,-2), В(6,4).

Решение.
Обозначим точки деления С и D.
Точка D
делит отрезок АВ в отно-

шении АD:DB
= 2. Координаты точки D
найдем по формулам (2.1.1).

Итак, D(5,2).

Координаты точки
С можно найти аналогично, взяв

Существует другой
способ нахождения координат точки С.
Точка С является серединой отрезка АD.
По формулам (2.1.2) имеем

Ответ:
D(5,2)
; C(4,0).

Пример 3.
Найти точку пересечения медиан
треугольника АВС, где А(-1,3) ;

B(3,-2);
C(5,3).

Решение:
Пусть точка О – точка пересечения медиан
AM
и BN
треугольника ABC.
Точка М является серединой отрезка ВС.
По формулам (2.1.2) получим координаты
точки М:

Из школьного курса
планиметрии известно, что точка О делит
медиану АМ в отношении АО:ОМ = 2:1.
По формулам (2.1.1) получим

Ответ:
Точка пересечения медиан

Замечание: Точка
пересечения медиан треугольника является
его центром тяжести.

3. Прямая на плоскости.

3.1. Простейшей из
линий является прямая. Всякую прямую,
не параллельную оси ординат, можно
представить уравнением вида

,
(3.1.1)

где к есть тангенс
угла
образованного прямой с положительным
направлением оси абсцисс (ox).

Величину к называют
угловым
коэффициентом.
Величину b
– начальной
ординатой.

Если прямая
параллельна оси ox,
то
Уравнение прямой примет вид:y
= b
(3.1.2)

Если прямая
параллельна оси oy,
то
не существует. В этом случае уравнение
прямой будет иметь вид:x
= a
(3.1.3),
где а – абсцисса точки, через которую
проходит данная прямая ( точки пересечения
прямой с осью ox).

Пример 1.
Какую прямую представляет уравнение

Решение. Данное
уравнение задает прямую, у которой
Так какПоэтому данное уравнение представляет
прямую, проходящую через начало координат
(b
= 0) и образующую с осью ox
угол

Пример 2.
Написать
уравнение прямой, параллельной оси ox
и имеющей на-

чальную
ординату b
=
.

Решение: По
формуле (3.1.2) имеем y
=где

Итак, искомая
прямая задается уравнением

Ответ:

Пример 3.
Написать уравнение прямой, параллельной
оси oy
и проходящей

через точку
M(3,1).

Решение:
По формуле (3.1.3) уравнение прямой имеет
вид x
= a
, где а – абсцисса точки М. а = 3. Уравнение
прямой x
= 3.

Ответ:
x
= 3.

3.2. Уравнение
прямой по точке и угловому коэффициенту.

Пусть прямая
проходит через точку
и имеет угловой коэффициент к. Уравнение
такой прямой можно записать в виде
(3.1.1)гдеb
– неизвестная
величина. Так как прямая проходит через
точку,
то координаты точки удовлетворяют
уравнению (3.1.1). ИмеемОтсюда

Подставим значение
“b”
в уравнение (3.1.1), получим
–или

(3.2.1)

Полученное уравнение
называется уравнением прямой по точке
и угловому коэффициенту.

Пример 1.
Составить уравнение прямой, проходящей
через точку

и образующей с
положительным направлением оси ox
угол

Решение:
Так как
тоПрименив формулу (3.2.1), получимy-(-2)=-1(x-1)
y+2
= -x+1

y=-x-1.

Ответ:
y=-x-1.

Пример 2.
Составить
уравнение прямой, проходящей через
точку А(-3,4) и имеющей угловой коэффициент
к = 2.

Решение:
Применяем
формулу (3.2.1) y
– 4 = 2 (x+3)
y
– 4 = 2x
+ 6

y
= 2x
+
10.

Ответ:
y
= 2x
+ 10.

Пример 3.
Составить
уравнение прямой, проходящей через
точку М(-1, 2) параллельно оси ox.

Решение:
Если прямая параллельна оси ox,
то угол между прямой и положительным
направлением оси ox
равен нулю. Следовательно,
По формуле (3.2.1) получимy
– 2 = 0 (x
+ 1)

y
– 2 = 0

Ответ:
y
= 2.

3.3.Уравнение
прямой по точке и нормальному вектору.

Пусть прямая
проходит через точку
Поднормальным
вектором
понимают вектор, который перпендикулярен
данной прямой. Обозначим его
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
Используя векторную алгебру, найдем
координаты вектораВекторперпендикулярен вектору.Из векторной
алгебры известно, что скалярное
произведение этих векторов равно нулю.
Следовательно,

(3.3.1)

Полученное уравнение
называется уравнением
прямой по точке и нормальному вектору.
Преобразуем полученное уравнение:

Ax + By –
A– B=
0.Пусть
C = -A-B,тогда
получим:

Ax
+ By + C = 0 (3.3.2)

Уравнение (3.3.2)
называется общим
уравнением прямой.
Напомним, что коэффициенты А и В в
уравнении определяют координаты
нормального вектора

Рассмотрим общее
уравнение прямой подробнее.

1). Если А = 0, то
уравнение примет вид

By
+ C
= 0 ; y
= –Прямая параллельна осиox.
(3.1.2)

2). Если В = 0, то
уравнение примет вид:

Ax
+ C
= 0, x
= –
Прямая параллельна оси oy.
(3.1.3.)

3). Если С = 0, то
уравнение примет вид: Ax
+ By
= 0. y
= –

Прямая проходит через начало координат
и имеет угловой коэффициент k
= –
См. пример 1 пункт 3.1.

Из общего
уравнения прямой, если
можно найти угловой коэффициент к. Для
этого выразимy
из этого уравнения : Ax
+ By
+ C
= 0.

By = – Ax –
C ; y = ––Отсюда,

k
= –
(3.3.3)

Пример 1.
Прямая задана уравнением 3x
– 4y
+5 = 0. Найти координаты нормального
вектора.

Решение:
Координатами
нормального вектора
являются коэффициенты приx
и y
данного уравнения прямой. Имеем А = 3;
В = – 4.

Ответ:

Пример 2.
Составить уравнение прямой, проходящей
через точку М(2,-1) и имеющей нормальный
вектор

Решение:
Применяем
формулу (3.3.1). Имеем 0(x
– 2) + 2(y
+ 1) = 0

2y
+ 2 = 0

y
+ 1 = 0.

Ответ:
y
+ 1 = 0.

Пример 3.
Составить уравнение прямой, проходящей
через точку М(0; 1) перпендикулярно вектору

где А(-1; 2), В(1; -1).

Решение:
Найдем координаты вектора
–
(-1); -1-2);
(2;
-3).

Вектор является нормальным
векторомискомой
прямой. По формуле (3.3.1) имеем 2(x
– 0) -3(y
-1) = 0

2x
– 3y
+ 3 = 0.

Ответ:
2x
– 3y
+ 3 = 0.

3.4. Уравнение
прямой по точке и направляющему вектору.

Пусть прямая
проходит через точку
Направляющим векторомданной прямой называется вектор,
параллельный этой прямой. Пусть дан
векторВозьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
Векторы
иколлинеарны,следовательно, их
соответствующие координаты пропорциональны.

(3.4.1)

Полученное уравнение
является уравнением прямой по
точке и направляющему вектору.

Пример 1.
Прямая задана
уравнением:

Написать координаты
направляющего вектора; найти координаты
точки, лежащей на прямой; составить
общее уравнение прямой.

Решение:
Направляющий
вектор
= (−1; 2). Точкумы получим, приравняв нулю числители
данного уравнения:x
+ 2 = 0

x
=−2; y
– 3 = 0

y
= 3.

Итак,
(−2; 3).

Общее уравнение
прямой получим по свойству пропорций:
(x+2)∙2
= (y−3)∙(−
1)

2x
+ 4 = −y
+ 3

2x
+ y
+ 1 = 0.

Ответ:
(−1;
2),
(−2;
3), 2x
+ y
+ 1 = 0.

Пример 2.
Составить
уравнение прямой по точке М(2,-5) и
направляющему вектору
(-2,4).

Решение:
Применяем
формулу
(3.4.1). Имеем:

4(x-2)
= -2(y+5)
4x
– 8 = – 2y
– 10

4x
+ 2y
+ 2 = 0

2x
+ y
+ 1 =0.

Ответ: 2x
+ y
+ 1 = 0.

Пример 3.
Через точку
С(- 2, 1) провести прямую, параллельную
вектору
где А(2,-1), В(3,4).

Решение:
Вектор можно взять за
направляющий вектор данной прямой. (3-2; 4-(-1)) = (1;
5). Применяем
формулу (3.4.1). Имеем:

5(x
+ 2) = y
– 1

5x
+ 10 = y
– 1

5x
– y
+ 11 = 0.

Ответ:
5x
– y
+11 = 0.

3.5. Уравнение
прямой, проходящей через две заданные
точки.

Известно, что
через две данные точки можно провести
единственную прямую. Пусть
прямая проходит через точкиЗа направляющий векторданной прямой можно взять вектор.

Составим уравнение
прямой по точке и направляющему
вектору

По формуле (3.4.1)
имеем:

(3.5.1)

Если
то прямая параллельна осиoy.
Ее уравнение имеет вид:

(3.5.2)

Если
то прямая параллельна осиox.
Ее уравнение :

y
=

(3.5.3)

Пример 1.
Составить уравнение прямой АВ, если
А(2,-1); В(1,3).

Решение:
Применяем
формулу (3.5.1):

4(x
– 2) = -(y
+ 1)
4x
+ y
– 7 = 0.

Ответ:
4x
+ y
– 7 = 0.

Пример 2.
Составить уравнение прямой, проходящей
через точки М(4,-2) и N(4,5).

Решение:
Так как

то по формуле (3.5.2) уравнение прямой
имеет вид:

x = 4.
Прямая
параллельна оси oy.

Пример 3. Дан
треугольник АВС, у которого А(1,2), В(4,3),
С(1,3). Составить уравнения его сторон.

Решение: 1)
Найдем уравнение стороны АВ. ПО формуле
(3.5.1) имеем:
x
– 1 = 3(y
– 2)
x
– 3y
+ 5 = 0.

2) Сторона ВС
находится по формуле (3.5.3), так как
y
= 3.

3) Уравнение стороны
АС выпишем по формуле (3.5.2), так как
x
= 1.

Ответ:
AB:
x
– 3y
+ 5 = 0; BC:
y
= 3; AC:
x
= 1.

Пример 4.
Даны вершины треугольника АВС А(- 1, 3),
В(3,-2), С(5,3). Составить уравнение медианы,
проведенной из вершины В.

Решение: Пусть
ВМ – медиана, тогда точка М является
серединой отрезка АС. По формулам (2.1.2)
имеем:

M(2,3).

Уравнение медианы
ВМ получим по формуле (3.5.1):

5(x-
3) = -(y
+2)

5x
+ y
– 13 = 0.

Ответ:
BM:
5x
+ y
– 13 = 0.

3.6. Уравнение
прямой в отрезках.

Если прямая отсекает
на осях отрезки а и b,
не равные нулю, то ее уравнение можно
записать в виде:
.
(3.6.1)

Такое уравнение
называется уравнением
в отрезках.
Рассмотрим это уравнение. Пусть x
= 0, тогда

Пусть y
= 0, тогда

Прямая проходит
через точки А(а,0) и B(0,b).

Пример.
Записать
уравнение прямой в отрезках. Построить
эту прямую.

3x
– 2y + 12 = 0.

Решение:
3x
– 2y
= – 12. Разделим обе части этого уравнения
на – 12. Получим:

a = – 4, b = 6.

Построим полученную
прямую. Для этого отложим на оси ox
a
= – 4, на оси oy

b
= 6 и соединим полученные точки.

3.7. Расстояние
от точки до прямой.

Пусть прямая
задана уравнением Ax
+ By
+ C
= 0. Найдем расстояние от точки
до этой прямой. Подрасстоянием
от точки до прямой понимают длину отрезкагде М – основание перпендикуляра,
опущенного из точкина данную прямую. Расстояниенаходим по формуле:

(3.7.1)

Пример. Найти
расстояние от точки
до прямой 3x
+ 4y
– 22 =0.

Решение: По
формуле (3.7.1) получим:

Ответ:
d
= 4.

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.20154.96 Кб8Содержание OneNote.onetoc2

• #

Пусть дан направленный отрезок АВ прямой; говорят, что точка

М этой прямой делит отрезок АВ в отношении, равном X, где произвольное вещественное число, если

Когда точка М лежит между точками А и В (т. е. внутри отрезка

АВ), то векторы АМ и МВ направлены в одну сторону (рис. 2) и отношение (1) положительно.

Рис. 2.

Когда точка М лежит вне отрезка

АВ, то векторы АМ и МВ направлены в противоположные стороны (рис. 3) и отношение (1) отрицательно.

Посмотрим, как изменяется отношение (1), когда точка М пробегает всю прямую. Когда точка М совпадает с точкой А, то отношение (1) равно нулю; если затем точка М пробегает отрезок АВ в направлении от А к В, то отношение (1) непрерывно возрастает, делаясь при приближении точки М к В сколь угодно большим. Когда , то дробь (1) теряет смысл, так как ее знаменатель обращается в нулевой вектор. При дальнейшем движении точки по прямой в том же направлении (на рис. 3, а направо от В) отношение (1) становится отрицательным, причем если Ж находится достаточно близко от В, то это отношение имеет сколь угодно большую абсолютную величину.

Так как , то (в силу предложения 8 § 4) имеем

Когда точка М, двигаясь все время в том же направлении (на нашем рис. 3, а слева направо), уходит но прямой в бесконечность, то дробь – стремится к нулю (так как ее числитель остается постоянным, а знаменатель неограниченно возрастает), следовательно, отношение , – стремится к -1.

Пусть теперь М переходит на «левую» из двух полупрямых, на которые точка А разбивает прямую (т. е. на ту полупрямую, которая не содержит отрезка АВ). Если при этом точка М находится достаточно далеко от точки А, то , снова сколь угодно мало и, значит, но формуле отношение сколь угодно мало отличается от —1. При приближении точки М слева к точке А (рис. 3, б) отношение (I), оставаясь отрицательным, непрерывно уменьшается по модулю и наконец делается равным нулю, когда точка М возвращается в точку А.

Рис. 3.

Заметим, что ни при каком положении точки М на прямой отношение не равно —1. В самом деле, отношение отрицательно, лишь когда точка М лежит вне отрезка АВ. Но в этом случае отрезки AM и MB никогда не бывают равны, т. е.

Пусть теперь на прямой установлена система координат и О — начало этой системы. Обозначим координату точки А через точки В — через , а переменной точки М — через . Тогда и

т. е.

Эти формулы позволяют для каждой точки найти отношение, в котором она делит отрезок АВ, и обратно, по заданному отношению к найти ту единственную точку , которая делит отрезок АВ в этом отношении. Установленное таким образом соответствие между точками М нашей прямой и числами К, выражающими отношение, в котором точка М делит отрезок АВ, было бы взаимно однозначным, если бы оно не нарушалось в двух случаях: во-первых, точке не соответствует никакое X, во-вторых, число не соответствует никакой точке М.

Но математика (в отличие от грамматики) не любит исключений! Поэтому постараемся и в нашем случае их устранить.