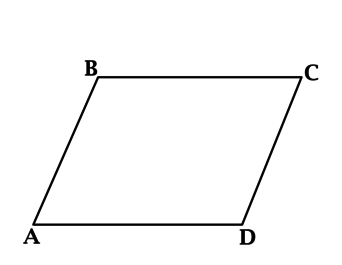
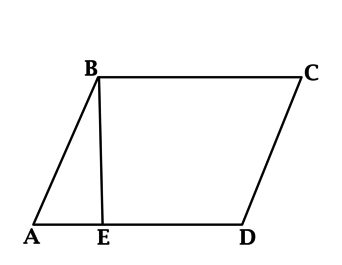
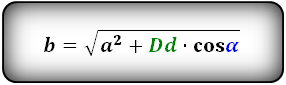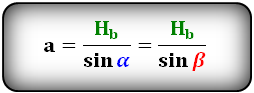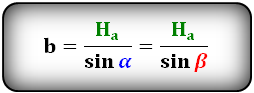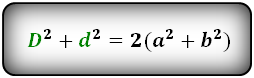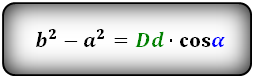Задача. Дан параллелограмм с острым углом, равным 60º. Квадраты длин диагоналей d и D параллелограмма относятся как 1:3. Необходимо найти отношение длин сторон а и b параллелограмма. Решение: Опустим из вершин В и С параллелограмма высоты на сторону АД и на её продолжение ДЕ. Получим два прямоугольных треугольника ДВК и АСЕ. Поскольку у этих треугольников равные высоты ВК и СЕ, то применим для их решения теорему Пифагора. В треугольнике АВК примем АВ за а, тогда, поскольку угол А равен 60º по условию, угол В в этом треугольнике будет равен 30º.
А мы знаем, что катет, лежащий против угла в 30º, равен половине гипотенузы. Т.е. АК=а/2. По этой же причине ДЕ = а/2. Так как АД=b, то КД = b — a/2. ВД = d, AC = D d²/D² = 1/3 3d² = D² Решаем уравнение: D² — (b + a/2)² = d² — (b — a/2)² D² — (b² + ab + a²/4) = d² — (b² — ab + a²/4) D² — b² — ab — a²/4 = d² — b² + ab — a²/4 D² — d² = 2ab 3d² — d² = 2ab d² = ab Из треугольника АВК ВК = а√3/2. Теперь решим треугольник ВКД по теореме Пифагора. d² = (а√3/2)² + (b — a/2)² ab = 3a²/4 + b² — ab + a²/4 b² — 2ab + a² = 0 (b — a)² = 0 b — a = 0 b = a Ответ: отношение длин сторон a и b равно 1.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 – 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
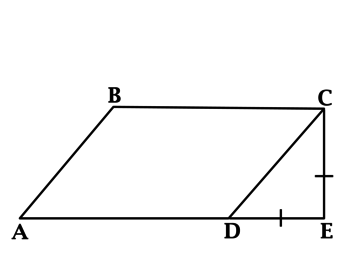
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} – 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 – BD^2 = 25 – 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 8), (P_{triangle AOD} = 9), а сумма смежных сторон равна (7). Найдите произведение этих сторон параллелограмма (ABCD).
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} – P_{triangle AOB} = AD – AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.
УСТАЛ? Просто отдохни
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
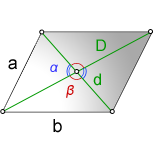
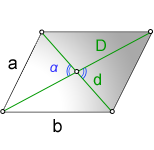
1. Формулы длины сторон через диагонали и угол между ними.
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
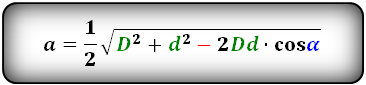
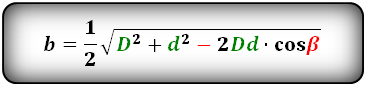
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
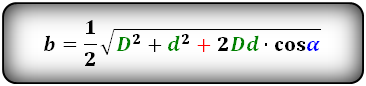
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
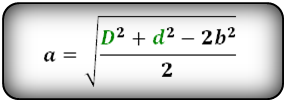
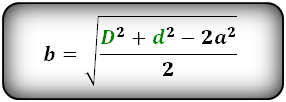
Формулы сторон параллелограмма , (a, b):
2. Формулы длины сторон параллелограмма через высоту.
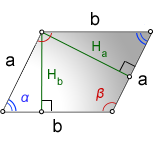
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
α, β – углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
3. Дополнительные, интересные формулы параллелограмма:
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
Формула суммы квадратов диагоналей:
Формула разности квадратов сторон:
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 31 октября 2011
-
Обновлено: 13 августа 2021
Содержание
- Как найти отношение двух сторон параллелограмма
- Формула для расчета отношения сторон параллелограмма
- Отношение диагоналей параллелограмма
- Общий итог:
- Как найти отношение двух сторон параллелограмма
- Что такое отношение двух сторон параллелограмма
- Формула для нахождения отношения двух сторон параллелограмма
- Пример решения задачи на нахождение отношения двух сторон параллелограмма
- Итоги
- Как найти отношение двух сторон параллелограмма
- Отношения сторон
- Пример
- Заключение
Как найти отношение двух сторон параллелограмма
Параллелограмм — это фигура, которая имеет две пары параллельных сторон. Это геометрическая фигура, которая находится во многих математических примерах и практических задачах. В этой статье мы расскажем, как найти отношение двух сторон параллелограмма.
Формула для расчета отношения сторон параллелограмма
Отношение сторон параллелограмма можно рассчитать с помощью формулы:
отношение AB к BC = отношение AD к DC
где:
- AB — одна из сторон параллелограмма
- BC — другая сторона параллелограмма
- AD — высота параллелограмма, проведенная к стороне AB
- DC — высота параллелограмма, проведенная к стороне BC
Это отношение сторон параллелограмма называется тангенсом угла между сторонами AB и BC.
Применим формулу на примере:
AB = 6, BC = 10, AD = 4, DC = 2.
Отношение AB к BC = отношение AD к DC:
6/10 = 4/2
0,6 = 2
Таким образом, тангенс угла между сторонами AB и BC в этом параллелограмме равен 0,6.
Отношение диагоналей параллелограмма
Также можно найти отношение диагоналей параллелограмма с помощью формулы:
отношение AC к BD = отношение AB к CD
где:
- AC — диагональ параллелограмма, соединяющая противоположные вершины A и C
- BD — диагональ параллелограмма, соединяющая противоположные вершины B и D
- AB — одна из сторон параллелограмма
- CD — другая сторона параллелограмма
Это отношение называется тангенсом угла между диагоналями параллелограмма.
Рассмотрим пример:
AC = 8, BD = 6, AB = 5, CD = 9.
Отношение AC к BD = отношение AB к CD:
8/6 = 5/9
1,33 = 0,56
Тангенс угла между диагоналями параллелограмма в этом примере равен 1,33/0,56 ≈ 2,38.
Общий итог:
Отношение сторон и диагоналей параллелограмма можно использовать для решения различных метрических задач.
- Для нахождения площади параллелограмма:
- Для нахождения высоты параллелограмма:
- Для нахождения углов:
Площадь параллелограмма = AB * AD
Высота = AD (если известны AB и AD) или высота = DC (если известны AB и DC)
Тангенс угла между сторонами параллелограмма = отношение AB к BC
Тангенс угла между диагоналями параллелограмма = отношение AC к BD
Таким образом, отношение сторон и диагоналей параллелограмма — это важные концепции в геометрии, которые могут использоваться для решения многих практических задач.
Как найти отношение двух сторон параллелограмма
Параллелограмм — это фигура, которая имеет две пары параллельных сторон. Для решения любой задачи, связанной с параллелограммом, вам необходимо знать свойства данной фигуры. В данной статье мы раскроем одно из свойств этой геометрической фигуры — отношение двух сторон параллелограмма.
Что такое отношение двух сторон параллелограмма
Отношение двух сторон параллелограмма — это отношение длин одной стороны параллелограмма к длине другой стороны параллелограмма. Кроме того, отношение может быть представлено в десятичном или процентном виде. Для нахождения отношения двух сторон параллелограмма необходимо знать длину данных сторон.
Формула для нахождения отношения двух сторон параллелограмма
Для нахождения отношения двух сторон параллелограмма необходимо разделить длину одной стороны на длину другой стороны:
Отношение сторон параллелограмма = Длина одной стороны параллелограмма / Длина другой стороны параллелограмма
Пример решения задачи на нахождение отношения двух сторон параллелограмма
Для лучшего понимания решения задачи на нахождение отношения двух сторон параллелограмма рассмотрим пример.
Дан параллелограмм ABCD, длина стороны AB = 5 см, а длина стороны BC = 10 см. Найдите отношение сторон параллелограмма.
Для решения этой задачи мы воспользуемся формулой:
Отношение сторон параллелограмма = Длина одной стороны параллелограмма / Длина другой стороны параллелограмма
Подставим данные из условия задачи в эту формулу:
Отношение сторон параллелограмма = 5 см / 10 см
Решим данное уравнение и получим:
Отношение сторон параллелограмма = 0,5
Ответ: Отношение сторон параллелограмма равно 0,5.
Итоги
Таким образом, для нахождения отношения двух сторон параллелограмма необходимо знать длину данных сторон и применить формулу отношения сторон. Отношение может быть представлено в виде десятичной дроби или процента. Это свойство параллелограмма является одним из базовых в геометрии, поэтому необходимо знать его для решения задач на эту тему.
Как найти отношение двух сторон параллелограмма
Параллелограмм – это четырехугольник с противоположными сторонами, которые параллельны друг другу. Это довольно простая геометрическая фигура, но при ее изучении возникают интересные математические вопросы, такие как: «Как найти отношение двух сторон параллелограмма?»
Отношения сторон
Отношение двух чисел – это результат деления одного числа на другое. Если, например, мы хотим найти отношение сторон параллелограмма, мы должны поделить длину одной стороны на длину другой.
Отношение сторон AB и BC параллелограмма ABCD:
AB / BC
Это даст вам конечное число, которое вы можете использовать, чтобы проверить соотношение сторон параллелограмма. Если отношение сторон равно единице, то это означает, что стороны параллельграмма находятся в пропорции.
Пример
Давайте рассмотрим конкретный пример. Предположим, что у вас есть параллелограмм ABCD, где сторона AB равна 8 см, а сторона BC равна 5 см. Чтобы найти отношение сторон, мы просто делим длину стороны AB на длину стороны BC:
AB / BC = 8 / 5 = 1,6
Отношение сторон параллелограмма ABCD – 1,6. Это означает, что сторона AB находится в 1,6 раза больше, чем сторона BC.
Заключение
Найти отношение двух сторон параллелограмма – это очень просто. Просто поделите длину одной стороны на длину другой, и вы получите ответ. Это важно знать, когда вы занимаетесь геометрией, так как это поможет вам лучше понимать форму и размеры фигур.
- параллелограмм
- отношение сторон
- длина сторон
- геометрия
Инфоурок
›
Геометрия
›Презентации›Признаки и свойства параллелограмма. Решение задач
Признаки и свойства параллелограмма. Решение задач
Скачать материал
Скачать материал
- Сейчас обучается 43 человека из 30 регионов
- Сейчас обучается 960 человек из 80 регионов
- Сейчас обучается 143 человека из 49 регионов
Описание презентации по отдельным слайдам:
-
1 слайд
Презентация к уроку по учебному предмету «Геометрия» в 8 классе на тему: «Признаки и свойства параллелограмма. Решение задач»
-
2 слайд
Параллелограмм
ABCD – параллелограмм
𝑨𝑩∥𝑪𝑫 и 𝑩𝑪∥𝑨𝑫 -
3 слайд
Существенные признаки понятия «Параллелограмм»
1.Противоположные стороны попарно равны2. Противоположные стороны попарно параллельны
3.Имеет центр симметрии
4. Диагонали в точке пересечения делятся пополам
-
4 слайд
Свойства параллелограмма
A
B
C
D
O
2
1
3
4 -
5 слайд
Найдите характеристические свойства параллелограмма
Четырехугольник
Выпуклый четырехугольник
Плоская фигура
Имеет площадь, имеет центр
Существует такая точка, через которую можно провести отрезок, которая поделит фигуру на две равные фигуры
Противоположные стороны попарно равны
Противоположные углы попарно равны
Две противоположные стороны равны и параллельны
Диагонали точкой пересечения делятся по палам -
6 слайд
Признаки параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм
Если в четырехугольнике противоположные стороны равны и параллельны, то этот четырехугольник – параллелограмм
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм -
-
8 слайд
Решение задач
Задача1: В параллелограмме ABCD проведена диагональ AC. ∠BCA = 30°, ∠BAC = 40°.
Найдите все углы параллелограмма.Решение:
Рассмотрим ΔBAC.
1) У него ∠BCA = 30°, ∠BAC = 40°,
значит ∠B = 180°−(𝟑𝟎°+𝟒𝟎°)=𝟏𝟏𝟎°.
2) ∠B = ∠D = 110°
(по свойству противоположных углов)
3) ∠A+∠B=180° (по свойству углов параллелограмма), ⇒
∠A=180°-110°=70°, ∠C=∠A=70°
(по свойству противоположных
углов параллелограмма)
Ответ: ∠C=∠A=70°, ∠B = ∠D = 110° -
9 слайд
Решение задач
Задача 2: ABCD – параллелограмм. Высота BK равна 2 см, ∠A=30°, сторона BC=13 см.
Найти периметр параллелограмма.Решение.
ΔABK – прямоугольный, ∠A=30°, ⇒
BK = ½ AB, ⇒ AB=2 BK, AB=4см
P=2·(AB+BC), Р=2·(4+13)=34(см).
Ответ: 34 см
А
В
С
D
К
30° -
10 слайд
Решение задач
Задача 375 (учебник Л.С. Атанасян):
Дано: ABCD – параллелограмм,
АК –биссектриса,
ВК= 7 см, КС=14 см
Найти: РРешение.
1) ABСD – Параллелограмм =>ВС || AD , ∠KAD= ∠ВKА – накрест лежащие
∠ВAК= ∠КАD , т.к. АК – биссектриса
=> ∠ВAК= ∠ВKА => ΔABK – равнобедренный => АВ=ВК=7 см
А
В
К
С
D
7
14
2) ВС= 7 см +14 см = 21 см
Р= (7 + 21)· 2 =56 (см)
Ответ : Р = 56 см -
11 слайд
Задача: ABCD – параллелограмм. Найти периметр
ΔCOD.Задача для самостоятельного решения
Ответ: Р=28 см
-
12 слайд
Решение задач по готовым чертежам с последующей самопроверкой
-
13 слайд
Задача: в параллелограмме ABCD проведена биссектриса угла А. Она разбивает сторону ВС на отрезки BH =6 см и HC =4 см. Найдите периметр параллелограмма.
Решение:
∠3=∠2, т.к. АH – биссектриса,
∠1=∠3 (накрест лежащие
при BC∥AD и секущей AH), ⇒ ∠1=∠2,
ΔABH – равнобедренный ( по признаку),
⇒ AB = BH = 6cм.
BC = AD = 10 cм, AB = CD = 6 cм.
Р = 2·(10+6) = 32 см.
Ответ: P=32 см. -
14 слайд
Задача: Найдите стороны параллелограмма, если две его стороны относятся как 4:5, а периметр равен 72 см.
Решение :
Т. к. отношение сторон равно 4: 5, то речь в условии задачи идет о соседних сторонах параллелограмма.
4+5 = 9 – частей на сумму
сторон AB и BC.
AB + BC = Р : 2 =72: 2 = 36 (см),
36 : 9 = 4 (см) – одна часть,
AB = 4·4=16 (см), BC = 4·5=20 (см).
CD = AB = 16 см, AD = BC = 20 см
(по свойству сторон параллелограмма)
Ответ: CD = AB = 16 см,
AD = BC = 20 смА
В
С
D -
15 слайд
Задача: ABCD – параллелограмм, . Найти AD и DC.
Ответ: DC=10 см, AD=4 см.
Рассмотрим Δ ВСЕ –прямоугольный, ∠СВЕ= 60°С => ∠С=30° => ВС=2ВЕ=4 см
АD=ВС=4 см (как противоположные стороны параллелограмма)
DС=АВ=10 см (как противоположные стороны параллелограмма)Решение:
-
16 слайд
Самостоятельная работа
1Вариант
Задача: ABCD – параллелограмм Найти AD.2Вариант
Задача: ABCD – параллелограмм Найти периметр AВСD. -
17 слайд
Домашняя работа
Учебник с. 100-102 , выучить признаки и свойства параллелограмма.
№ 374, 376 (в), 377 с. 103
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 261 240 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Тест Тетраэдр и Параллелепипед
- Учебник: «Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
- Тема: § 4. Тетраэдр и параллелепипед
- 12.09.2022
- 227
- 11
- 12.09.2022
- 59
- 2
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»
-
Настоящий материал опубликован пользователем Степаненко Лариса Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 3 года и 4 месяца
- Подписчики: 0
- Всего просмотров: 2707
-
Всего материалов:
7
