Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
тела
совершающего гармонические колебания
Выражение для
потенциальной энергии тела при
гармонических колебаниях следует из
определения потенциальной энергии
![]()
или
![]() .
.
В рассматриваемом случае имеем:
![]() ,
,
а
![]() .
.
Поэтому
![]() .
.
Полагая, что в
состоянии равновесия (![]() )
)
потенциальная энергия тела, совершающего
колебания, равна нулю, имеем:
![]() .
.
Кинетическая
энергия тела при гармонических колебаниях
определяется скоростью его движения
(![]()
) и определяется величиной:
![]() .
.
Полная энергия
тела, совершающего гармонические
колебания, равна сумме полученных
выражений для потенциальной и кинетической
энергий:
![]() .
.
Выражения
представленные выше показывают, что
при колебательном движении кинетическая
энергия преобразуется в потенциальную
и наоборот. При этом полная энергия
колебаний, не зависит от времени
(замкнутая система) и пропорциональна
квадрату амплитуды и квадрату частоты.
3.3. Пружинный, математический, физический и крутильный маятники
Пружинный
маятник
Пружинный
маятник представляет собой систему,
состоящую из пружины и тела, подвешенного
на этой пружине, систему, способную
совершать колебательное движение в
поле действия гравитационных сил или
сил инерции.
Уравнение,
описывающее движение пружинного маятника
в поле тяжести Земли имеет вид (см. рис.
3.1):
![]()
Преобразуем
это уравнение к виду:
![]()
и,
сделав замену переменных:
![]() ,
,
получим:
![]() .
.
Как
было показано выше, решением этого
уравнения являются гармонические
колебания
![]()
Возвращаясь
к переменной
![]() ,
,
получаем:
![]()
или,
с учетом собственной длины пружины
![]() ,
,
имеем:
![]() .
.
На
рисунке, представленном ниже,
![]() .
.

Следует отметить,
что в колебательном процессе участвует
не только тело массой![]() ,
,
подвешенное на пружине, но и сама пружина.
Таким образом, возникает вопрос о влиянии
массы пружины (![]() )
)
на частоту колебаний пружинного маятника.
Заметим, что если тело массой
![]()
в полной мере участвует в колебательном
движении, то различные части пружины
имеют различную амплитуду колебаний.
Таким образом, следует ожидать, что в
выражении для частоты колебаний войдет
не вся
![]() ,
,
а только ее часть. Расчеты показывают,
что это действительно так, и в этом
случае выражение для частоты колебаний
пружинного маятника имеет вид:

Математический
маятник
Математический
маятник состоит из подвешенной на
невесомой нерастяжимой нити материальной
точки, которая может совершать
колебательное движение в поле действия
гравитационных сил или в поле действия
сил инерции.

Для того, что бы
реализовать эту модель на практике
должны выполняться следующие условия:
-
размер
тела должен быть много меньше длины
нити
 ,
, -
масса
тела должна быть много больше массы
нити
 ,
, -
происходящее
во время колебаний изменение длины
нити должно быть много меньше длины
самой нити
 .
.
Остановимся на последнем более подробно.
При максимальном
отклонении маятника от состояния
равновесия сила натяжения нити
![]() ,
,
где
![]()
– угол максимального отклонения. При
прохождении телом положения равновесия
сила натяжения нити определяется как
силой тяжести, так и центробежной силой
![]() ,
,
где величина центробежной силы может
быть найдена следующим образом. Согласно
закону сохранения энергии запишем
![]() ,
,
![]()
откуда
следует:
![]() .
.
Итак, величина
![]() определяет
определяет
значение
![]() ,
,
которое должно быть много меньше
![]() .
.
Расчет показывает, что это условие
выполняется, когда
![]() .
.
Из полученного
выражения следует, что подбором амплитуды
колебаний (угла максимального отклонения)
это условие может быть всегда выполнено.
Теперь
рассмотрим движение самого маятника.
Возвращающая сила, действующая вдоль
оси «х» определяется силой натяжения
нити
![]() ,
,
где
![]() ,
,
а
![]()
-угол отклонения
![]() .
.
Воспользуемся законом сохранения
энергии и получим выражение для
центростремительной силы
![]() ,
,
где
![]()
соответствует отклонению маятника на
максимальный угол
![]() ,
,
а
![]() .
.
После
подстановки соответствующих величин
в выражение для
![]() получим:
получим:
![]()
Если угол отклонения
маятника настолько мал, что
![]() ,
,
то
![]()
Сравнивая
это выражение с выражением для силы,
определяющей гармонические колебания,
видим, что частота колебаний математического
маятника
![]() ,
,
а
период колебаний составляет величину:
![]() .
.
Период
колебаний математического маятника
зависит от его длины и от характеристики
поля, в котором он находится.
Физический
маятник
Физическим
маятником называется твердое тело,
способное совершать колебательное
движение в поле действия гравитационных
сил или сил инерции (см. рис. 3.3).
Ранее было показано,
что законы вращательного движения тела
формально не отличаются от законов
движения материальной точки, с той
разницей, что производится замена
величин
![]() ,
,
![]() ,
,
![]() .
.

В данном случае
(см. рисунок) момент силы действующий
на физический маятник равен:
![]() .
.
Если
амплитуда колебаний мала, то и углы
отклонения маятника от состояния
равновесия (![]() )
)
малы, поэтому
![]() .
.
В этом случае можем записать:
![]() .
.
Видим, что
![]() ~
~![]()
и что в рассматриваемом случае роль
коэффициента жесткости играет величина
![]() .
.
По
аналогии с выражением
![]()
можно написать выражение для частоты
колебаний физического маятника в виде:
 .
.
Замечание.
Если в полученное выражение для частоты
колебания физического маятника подставить
значение момента инерции, соответствующее
материальной точке находящейся на
расстоянии
![]()
от точки подвеса (![]() ),
),
то полученное выражение будет
соответствовать частоте колебаний
математического маятника, длиной
![]() .
.
Сравнивая
формулу для частоты колебаний физического
маятника, с соответствующей формулой
для математического маятника
![]() ,
,
мы видим, что частота колебаний физического
маятника будет равна частоте колебаний
математического, если его длина будет
составлять величину
![]() .
.
Это,
так называемая, приведенная
длина физического маятника.
Так как
![]() ,
,
где
![]()
– момент инерции тела относительно оси,
проходящей через центр инерции
![]() ,
,
выражение для приведенной длины мы
можем записать в виде:
![]() .
.
Из
этого выражения следует, что периоды
колебаний физического маятника,
подвешенного на параллельных осях,
отстоящих друг от друга на расстояние
![]()
равны. В самом деле, отложим на прямой
ОС отрезок
![]() .
.
Подвесим маятник на ось, проходящую
через точку
![]() .
.
Тогда приведенная длина будет
![]() ,
,
где
![]() .
.
Но
![]() .
.
Подставим это в выражение для
![]() и
и
получим:
 .
.
Итак:
приведенные длины, а значит и периоды
(частоты) колебаний физических маятников,
подвешенных на параллельных осях,
отстоящих друг от друга на величину
равную приведенной длине равны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примем за ноль точку, когда маятник просто висит, т. е самую нижнюю точку траектории. Здесь его потенциальная энергия равна нулю. Пусть маятник отклонился на угол фи и остановился (на мгновение) , здесь его кинетическая энергия равна нулю, т. е. она перешла полностью в потенциальную. Поэтому в этом положении потенциальная энергия равна численно полной энергии маяника. П = mgx = mgl(1-cosфи) . Т. к. массы и углы одинаковы, то у маятника, у которого нить длиннее в 2 раза будет и энергия больше в 2 раза.
Ну а вообще, задача поставлена немного некорректно, т. к. пот. энергия определяется с точностью до константы, если не принять условия, что в нижней точке П = 0, то ответ вообще говоря другой. Пусть в нижней точке у первого маятника пот. энергия П1, а у второго П2, тогда mgl(1-cosфи) – это изменения пот энергии по сравнению с начальным положением у первого маятника, а 2mgl(1-cosфи) – у второго. В положении, когда угол равен фи всё равно полная энергия равна потенциальной. Тогда отношение энергий маятников с длиной подвеса 2l и l равно: ( 2mgl(1-cosфи) + П2 )/( mgl(1-cosфи) + П1 ).
Как видите, при П1=П2=0 ответ совпадает с предыдущим. А вообще, задачи корректней нужно ставить. Допустим, П1=П2 = П и мы будем бесконечно удалять наши маятники от нулевого значения П, т. е. П стремится к бесконечности, тогда в пределе получим (при фиксированных m и l), что отношение энергий равно 1! Т. е. изменение за счёт угла весомой роли не играет.
Содержание:
Пружинные и математические маятники:
Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.
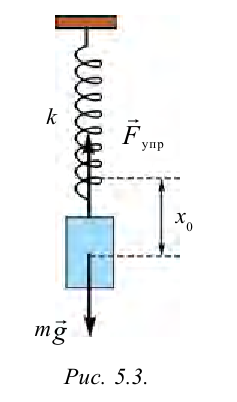
Система, состоящая из груза массой 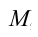

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:
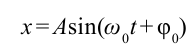
Если учесть, что ускорение тела, совершающего гармонические колебания 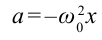 , то уравнение (5.10) примет вид:
, то уравнение (5.10) примет вид:
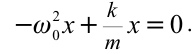
Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника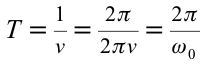 .
.
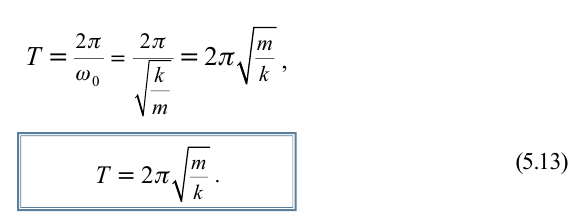
Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, 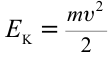 . В предыдущих темах было показано, что скорость можно выразить формулой
. В предыдущих темах было показано, что скорость можно выразить формулой 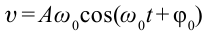 . В таком случае кинетическая энергия маятника равна
. В таком случае кинетическая энергия маятника равна
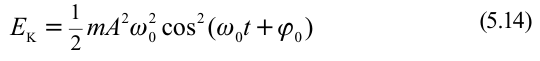
Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:
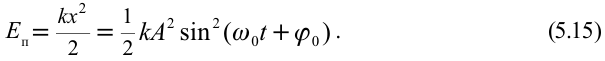
В большинстве случаев важно знать полную энергию системы:
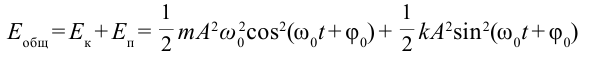
Если учесть, что 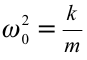 ,
,
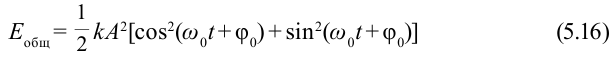

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки 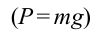 уравновешивает силу натяжения
уравновешивает силу натяжения  (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол
(рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол 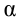 , силы
, силы 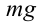 и
и  не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.
не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.
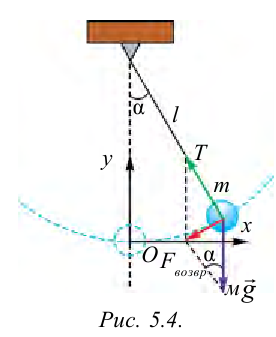
Из рис. 5.4. видим, что:
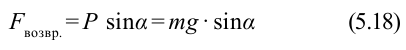
Согласно второму закону Ньютона, сила 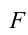 придает материальной точке ускорение
придает материальной точке ускорение 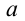 , поэтому
, поэтому
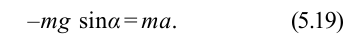
Из-за того, что угол наклона очень маленький 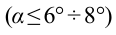 , а сила
, а сила 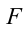 направлена противоположно смещению, формулу (5.19) можно записать в виде
направлена противоположно смещению, формулу (5.19) можно записать в виде

Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой 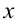 и учитывать соотношение
и учитывать соотношение 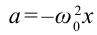 , получим
, получим 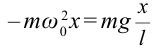
Следовательно 
Исходя из смысла периода колебания и учитывая, что 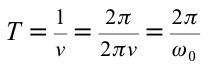 получаем
получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:
- при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
- период колебания математического маятника также не зависит от массы подвешенного на него груза;
- период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.
Отсюда колебание математического маятника записывается следующим выражением:
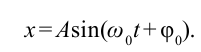
Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 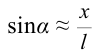 и для решения уравнения движения не применяется закон синусов или косинусов.
и для решения уравнения движения не применяется закон синусов или косинусов.
Пример:
Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.
Дано:
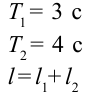
Найти:
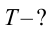
Формула:
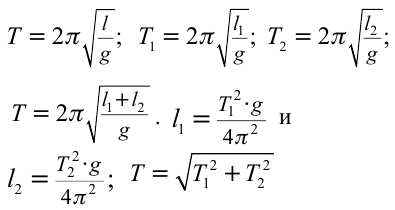
Решение:
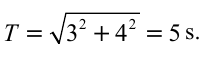
Ответ: 5 cек.
Пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
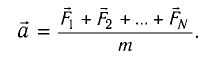
Закон Гука: модуль силы упругости 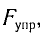 , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию)
, возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) 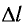 :
:
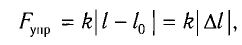
где k — жесткость тела, 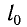 — длина недеформированного тела, l — длина деформированного тела.
— длина недеформированного тела, l — длина деформированного тела.
Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).
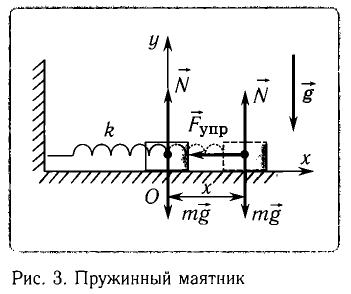
Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 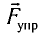 направленная влево.
направленная влево.
Запишем второй закон Ньютона для движения груза:
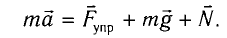
В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем
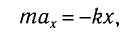 или
или 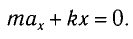
Следовательно,
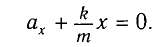
Это уравнение аналогично уравнению гармонических колебаний
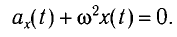
Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:
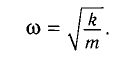
Тогда период колебаний пружинного маятника можно найти по формуле
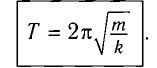
Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов 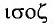 , — равный и
, — равный и 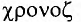 — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.
— время). Таким образом, колебания пружинного маятника обладают свойством изохронности.
Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).
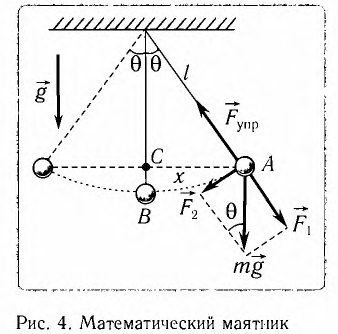
Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.
Галилео Галилей экспериментально определил, что период малых колебаний (9 < 10°) математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения  ). Он установил также, что период этих колебаний прямо пропорционален
). Он установил также, что период этих колебаний прямо пропорционален 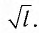 .
.
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
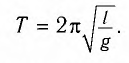
При углах отклонения математического маятника 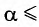 20° погрешность расчета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
20° погрешность расчета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
Отклонение маятника от положения равновесия будем характеризовать углом  (см. рис. 4), который нить образует с вертикалью.
(см. рис. 4), который нить образует с вертикалью.
Согласно второму закону Ньютона для движения шарика можем записать:
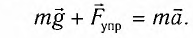
Смещение маятника вдоль дуги х = l , где угол
, где угол  выражен в радианах. Возвращающей силой в данном случае является проекция
выражен в радианах. Возвращающей силой в данном случае является проекция 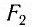 силы тяжести на касательную к дуге (см. рис. 4), которая определяется по формуле:
силы тяжести на касательную к дуге (см. рис. 4), которая определяется по формуле:
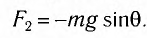
Заметим, что при малых углах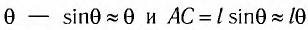 и длина дуги
и длина дуги
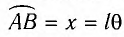 очень мало отличается от длины хорды
очень мало отличается от длины хорды 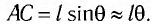 Для небольших углов (до 10°) значения
Для небольших углов (до 10°) значения  и sin
и sin различаются меньше чем на I %. Поэтому для таких углов равенство
различаются меньше чем на I %. Поэтому для таких углов равенство
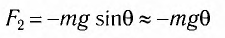 (1)
(1)
является очень хорошим приближением.
Подставляя в выражение (1) значение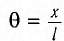 , получим
, получим
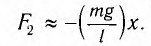
Таким образом, уравнение движения маятника запишется в виде
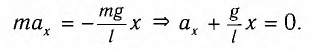
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 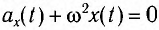 , то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
, то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
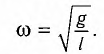
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 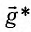 , характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
, характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
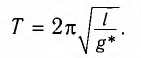
Пример:
Определите амплитуду А, циклическую частоту 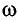 , период Т и начальную фазу
, период Т и начальную фазу 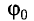 колебаний тела массой m = 0,50 кг, подвешенного к вертикальной пружине (рис. 5). Известно, что в состоянии покоя тело растягивает пружину на
колебаний тела массой m = 0,50 кг, подвешенного к вертикальной пружине (рис. 5). Известно, что в состоянии покоя тело растягивает пружину на 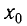 = 10 мм и для возбуждения колебаний его смещают вниз на x = 30 мм и отпускают.
= 10 мм и для возбуждения колебаний его смещают вниз на x = 30 мм и отпускают.
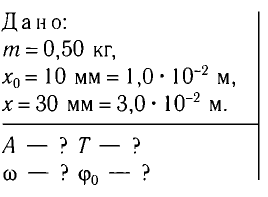
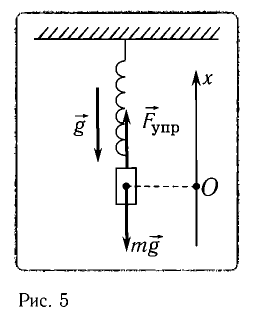
Решение
Циклическая частота колебаний «вертикального» пружинного маятника также определяется по формуле
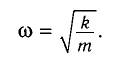
Найдем жесткость k пружины. Из условия равновесия тела следует
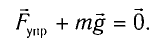
По закону Гука
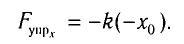
В проекции на ось Ох условие равновесия запишется в виде:
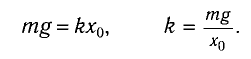
Отсюда для циклической частоты 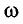 получаем
получаем
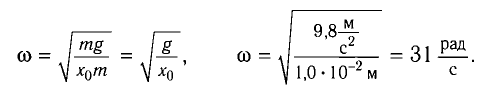
Так как по условию задачи тело сместили на расстояние х = 30 мм от положения равновесия, то амплитуда его колебаний
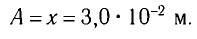
Период колебаний находим из соотношения
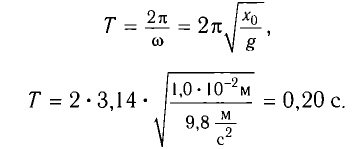
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний 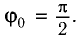
Ответ: 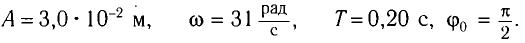
Пример:
Металлический шарик, подвешенный на длинной легкой нерастяжимой нити, поднимают по вертикали до точки подвеса и отпускают. Затем нить маятника отклоняют на небольшой угол от вертикали и также отпускают. В каком из этих случаев шарик быстрее возвратится в начальное положение?
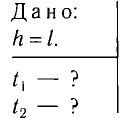
Решение
В первом случае шарик свободно падает без начальной скорости с высоты h = l, следовательно,
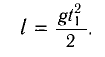
Отсюда находим промежуток времени 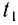 , необходимый для возвращения шарика в начальное положение:
, необходимый для возвращения шарика в начальное положение:
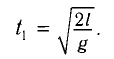
Во втором случае промежуток времени 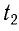 , необходимый шарику для возвращения из отклоненного положения в положение равновесия, найдем из уравнения гармонических колебаний
, необходимый шарику для возвращения из отклоненного положения в положение равновесия, найдем из уравнения гармонических колебаний
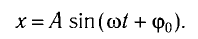
Поскольку в начальный момент времени t = 0 маятник имеет максимальное
отклонение от положения равновесия, то начальная фаза колебаний 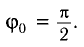 Так как в положении равновесия x = 0, то
Так как в положении равновесия x = 0, то
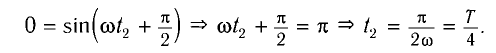
Используя формулу для периода колебаний математического маятника
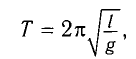 находим
находим 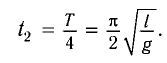
Разделив почленно уравнения для промежутков времени 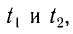 получим
получим
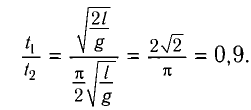
Ответ: шарик быстрее возвратится в начальное положение в случае, когда он движется вертикально вниз.
Пример:
Найдите периоды колебаний математического маятника длиной l= 1,0 м при перемещении его точки подвеса с ускорением, модуль которого а = 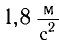 , направленным: а) вертикально вверх; б) вертикально вниз.
, направленным: а) вертикально вверх; б) вертикально вниз.
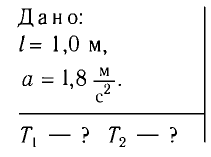
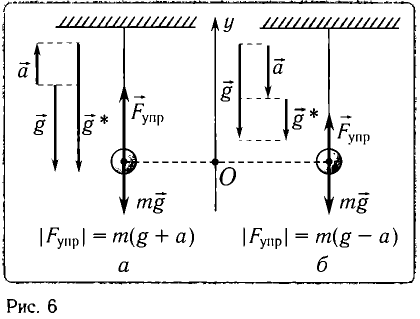
Решение
Период колебаний математического маятника в поле силы тяжести Земли
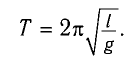
а) При движении маятника с ускорением 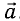 , направленным вверх (рис. 6, а), уравнение движения вдоль оси Оу
, направленным вверх (рис. 6, а), уравнение движения вдоль оси Оу
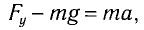
где Fy — проекция силы упругости нити.
Откуда находим
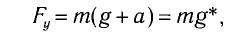
где g* = g + а — «эффективное ускорение».
Период колебаний определяется по формуле
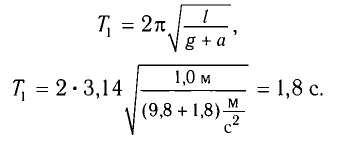
б) При движении точки подвеса маятника с ускорением 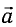 , направленным вниз (рис. 6, б), уравнение движения вдоль оси Оу
, направленным вниз (рис. 6, б), уравнение движения вдоль оси Оу
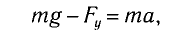
где Fy — проекция силы упругости нити. Откуда находим
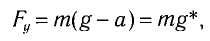
где g*=g-a — «эффективное ускорение». Период колебаний
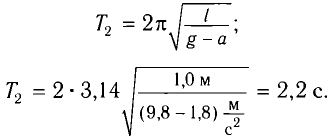
Ответ: 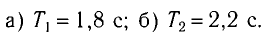
Что такое пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение тела прямо пропорционально результирующей силе и обратно пропорционально массе тела:
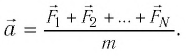
Закон Гука: при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
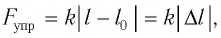
где 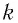 — жесткость тела,
— жесткость тела, 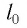 — длина недеформированного тела,
— длина недеформированного тела, 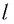 -длина деформированного тела.
-длина деформированного тела.
Колебательная система, состоящая из тела с прикрепленной к нему пружиной, называется пружинным маятником. Пружина может располагаться как вертикально (вертикальный пружинный маятник), так и горизонтально (горизонтальный пружинный маятник).
Рассмотрим колебания горизонтального пружинного маятника. Пусть груз массой 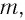 лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу легкой (невесомой) пружины жесткостью
лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу легкой (невесомой) пружины жесткостью 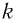 (рис. 6). Второй конец пружины неподвижен относительно данной инерциальной системы отсчета (ИСО).
(рис. 6). Второй конец пружины неподвижен относительно данной инерциальной системы отсчета (ИСО).
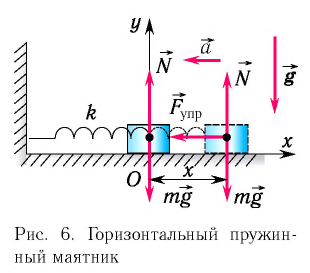
Выведем груз из положения равновесия, сместив его на расстояние 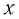 вправо (см. рис. 6). Тогда в пружине возникнет сила упругости
вправо (см. рис. 6). Тогда в пружине возникнет сила упругости 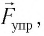 действующая на груз и направленная влево.
действующая на груз и направленная влево.
Согласно второму закону Ньютона для движения груза
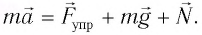
В проекции на ось 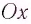 действующих на груз сил (см. рис. 6) с учетом закона Гука получаем:
действующих на груз сил (см. рис. 6) с учетом закона Гука получаем:
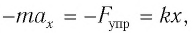
или
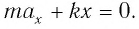
Перепишем полученное соотношение в виде:
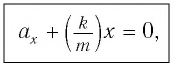
которое является уравнением гармонических колебаний пружинного маятника.
Сравнивая (1) с уравнением гармонических колебаний 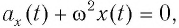 находим циклическую частоту колебаний горизонтального пружинного маятника
находим циклическую частоту колебаний горизонтального пружинного маятника
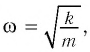
которая определяется массой 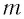 груза и жесткостью
груза и жесткостью 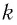 пружины.
пружины.
Для нахождения периода колебаний пружинного маятника воспользуемся формулой 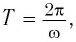 подставив в нее выражение (2):
подставив в нее выражение (2):
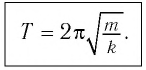
Как следует из формул (2) и (3), период и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греч. 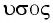 (изос) — равный и
(изос) — равный и 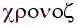 (хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности.
(хронос) — время). Следовательно, колебания пружинного маятника обладают свойством изохронности.
Изохронность колебаний маятника была открыта Гали-лео Галилеем в 1583 г. при изучении движения груза, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Колебательная система, состоящая из находящегося в поле силы тяжести тела, подвешенного на легкой нерастяжимой нити, размеры которого малы по сравнению с длиной нити, а его масса значительно больше массы нити, называется математическим маятником. При таких условиях тело можно считать материальной точкой, а нить — легкой нерастяжимой (рис. 7).
Рассмотрим колебания математического маятника.
Отклонение маятника от положения равновесия будем характеризовать углом 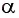 (см. рис. 7), который нить образует с вертикалью.
(см. рис. 7), который нить образует с вертикалью.
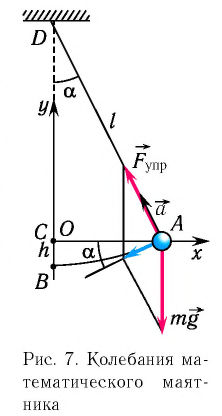
После отклонения маятника на него действуют две силы: направленная вертикально вниз сила тяжести 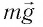 и направленная вдоль нити сила упругости
и направленная вдоль нити сила упругости 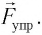 Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия.
Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия.
Согласно второму закону Ньютона для движения маятника можем записать:
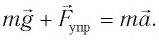
В проекциях на выбранные оси координат 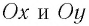 (см. рис. 7) получаем:
(см. рис. 7) получаем:
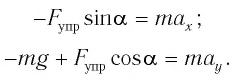
Для углов отклонения 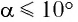 значения
значения 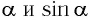 различаются меньше чем на 1 %. Поэтому при малых углах отклонения
различаются меньше чем на 1 %. Поэтому при малых углах отклонения 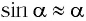 и длина дуги
и длина дуги 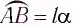 очень мало отличается от длины хорды
очень мало отличается от длины хорды 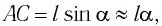 где угол
где угол 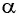 выражен в радианах. Тогда смещение маятника вдоль дуги
выражен в радианах. Тогда смещение маятника вдоль дуги 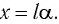 Но практически маятник движется вдоль оси
Но практически маятник движется вдоль оси 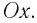 Из
Из 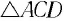 находим
находим 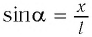 и, подставив это выражение в (5), получим:
и, подставив это выражение в (5), получим:
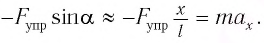
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия, является сила упругости его нити.
При малых углах отклонения маятника проекция вектора ускорения 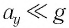 и ею можно пренебречь, а
и ею можно пренебречь, а 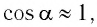 тогда из уравнения (6) следует, что
тогда из уравнения (6) следует, что 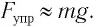
Следовательно, уравнение движения маятника вдоль оси 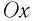 запишется в виде:
запишется в виде:
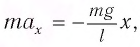
где 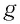 — ускорение, сообщаемое грузу маятника силой упругости нити.
— ускорение, сообщаемое грузу маятника силой упругости нити.
Отсюда получаем уравнение гармонических колебаний математического маятника:
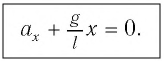
При сравнении уравнения (8) с уравнением гармонических колебаний 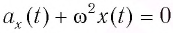 можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой
можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой
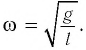
Тогда период малых колебаний математического маятника в поле тяжести Земли определяется по формуле Гюйгенса:
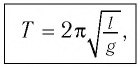
которую впервые получил ученик И. Ньютона Христиан Гюйгенс.
При углах отклонения математического маятника 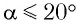 погрешность рас-чета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
погрешность рас-чета периода колебаний математического маятника по формуле Гюйгенса не превышает 1 %.
Как видно из формул (9) и (10), циклическая частота и период математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной 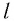 и модулем ускорения свободного падения
и модулем ускорения свободного падения 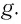
Галилео Галилей первый экспериментально определил, что период малых колебаний 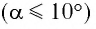 математического маятника длиной
математического маятника длиной 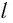 в поле силы тяжести не зависит от его массы
в поле силы тяжести не зависит от его массы 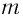 и амплитуды колебаний (угла начального отклонения
и амплитуды колебаний (угла начального отклонения 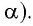 Он установил также, что период этих колебаний прямо пропорционален
Он установил также, что период этих колебаний прямо пропорционален 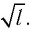
Если маятник приобретает дополнительное ускорение 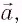 обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле:
обусловленное, например, ускоренным движением точки подвеса, то при этом будет изменяться сила упругости нити. В таком случае период колебаний маятника будет определяться по формуле:
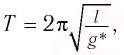
где 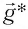 — «эффективное ускорение», равное векторной разности
— «эффективное ускорение», равное векторной разности 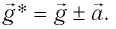
- Заказать решение задач по физике
Пример:
Выведите формулу для периода колебаний вертикального пружинного маятника, если масса груза 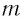 и жесткость пружины
и жесткость пружины 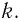
Решение
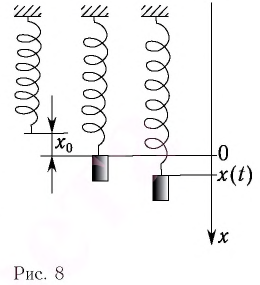
Рассмотрим вертикальное движение груза, происходящее под действием силы упругости пружины и силы тяжести груза после толчка. Начало координат поместим в точку, соответствующую равновесному положению тела (рис. 8). В этом положении пружина растянута на величину 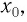 определяемую соотношением:
определяемую соотношением:
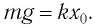
При смещении груза на величину 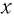 из положения равновесия сила, действующая со стороны пружины на груз, равна
из положения равновесия сила, действующая со стороны пружины на груз, равна 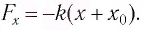
Тогда по второму закону Ньютона
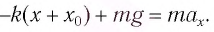
С учетом соотношения (1) это уравнение перепишем в виде:
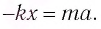
Если ввести обозначение 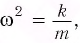 то уравнение движения груза запишется в виде:
то уравнение движения груза запишется в виде:
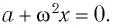
Оно описывает гармонические колебания вертикального пружинного маятника с частотой такой же, как у горизонтального пружинного маятника. Следовательно, период колебаний вертикального пружинного маятника такой же, как и горизонтального:
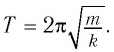
Ответ: 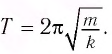
Таким образом, действующая в колебательной системе постоянная сила только смещает положения равновесия, но не изменяет частоту колебаний.
Пример:
Определите амплитуду 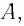 циклическую частоту
циклическую частоту 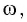 период
период 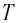 и начальную фазу
и начальную фазу 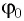 колебаний тела массой
колебаний тела массой 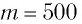 г подвешенного к вертикальной пружине (рис. 9). Известно, что в состоянии покоя тело растягивает пружину на расстояние
г подвешенного к вертикальной пружине (рис. 9). Известно, что в состоянии покоя тело растягивает пружину на расстояние 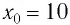 мм и для возбуждения колебаний его смещают вниз на расстояние
мм и для возбуждения колебаний его смещают вниз на расстояние 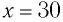 мм от положения равновесия и отпускают.
мм от положения равновесия и отпускают.
Дано:
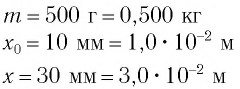
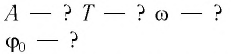
Решение
Циклическая частота колебаний вертикального пружинного маятника так же, как и горизонтального, определяется по формуле (см. пример 1):
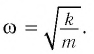
Для нахождения жесткости к пружины запишем условие равновесия тела:
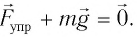
По закону Гука
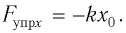
В проекции на ось 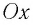 условие равновесия запишется:
условие равновесия запишется:
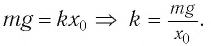
Отсюда для циклической частоты 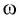 получаем:
получаем:
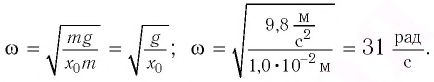
Амплитуда колебаний маятника определяется начальным смешением:
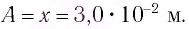
Период колебаний находим из соотношения:
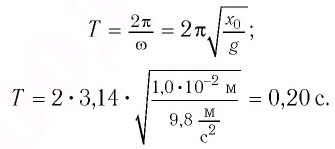
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний 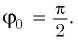
Ответ: 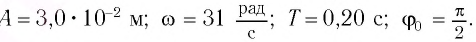
Подробное объяснение пружинного и математического маятника
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
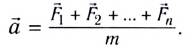
Закон Гука: модуль силы упругости 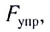 возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию)
возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) 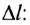
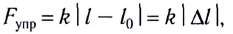
где k — жесткость тела, 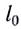 — длина недеформированного тела, l — длина деформированного тела.
— длина недеформированного тела, l — длина деформированного тела.
Простейшая колебательная система может быть получена с использованием груза и пружины.
Прикрепим груз массой m, лежащий на гладкой горизонтальной поверхности, к невесомой упругой пружине жесткостью k, второй конец которой зафиксирован (рис. 181). Такая система называется пружинным маятником.
Запишем второй закон Ньютона для этой системы
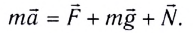
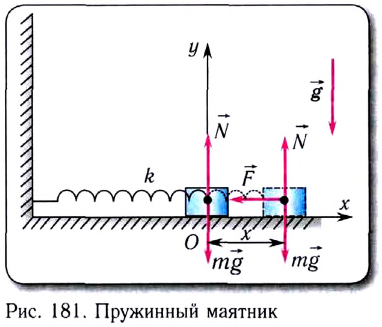
В проекции на ось Ох с учетом закона Гука получаем
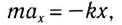 или
или
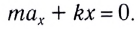
Запишем это уравнение в форме, аналогичной уравнению движения гармонического осциллятора:
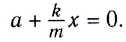
Сравнивая полученное выражение с уравнением гармонических колебаний
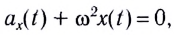
находим циклическую частоту колебаний пружинного маятника
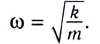
Тогда период колебаний пружинного маятника можно найти по формуле
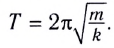
Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов 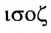 — равный и
— равный и 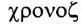 — время).
— время).
Как видим, пружинный маятник обладает свойством изохронности, поскольку период его колебаний не зависит от амплитуды.
Одной из наиболее распространенных колебательных систем является математический маятник.
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 182).
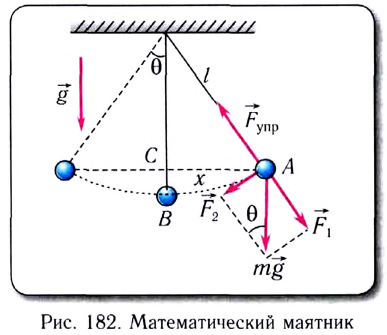
Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален 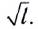
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
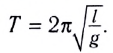
При углах отклонения математического маятника 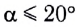 погрешность формулы Гюйгенса не превышает 1 %.
погрешность формулы Гюйгенса не превышает 1 %.
Отклонение маятника от положения равновесия будем характеризовать углом 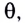 который нить образует с вертикалью.
который нить образует с вертикалью.
Из второго закона Ньютона следует (см. рис. 182):
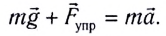
Смещение маятника вдоль дуги 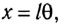 где угол
где угол 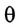 выражен в радианах.
выражен в радианах.
Возвращающей силой в данном случае является проекция на касательную к дуге силы тяжести 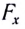 (см. рис. 182), которая определяется по формуле
(см. рис. 182), которая определяется по формуле
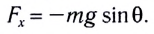
Заметим, что при малых углах 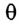 длина дуги АВ = х =
длина дуги АВ = х = 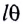 очень мало отличается от длины хорды
очень мало отличается от длины хорды 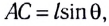 так как при малых
так как при малых 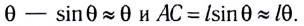
Для небольших углов (до 10°) значения 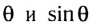 различаются меньше чем на 1 %. Поэтому для таких углов равенство
различаются меньше чем на 1 %. Поэтому для таких углов равенство
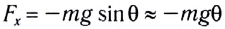 является очень хорошим приближением.
является очень хорошим приближением.
Используя полученное соотношение между координатой х и углом 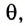 находим
находим 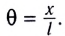 Подставляем его в выражение для проекции силы:
Подставляем его в выражение для проекции силы:
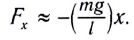
Таким образом, уравнение движения маятника запишется в виде 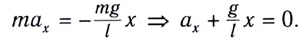
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 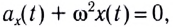 то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
то можно сделать вывод, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
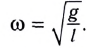
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 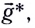 характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
характеризующее результирующее действие этих полей, и период колебаний маятника будет определяться по формуле
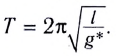
Математический и пружинный маятники и энергия колебаний
Колебательные движения очень разнообразны. При этом существует «классика» колебательных движений — они описаны сотни лет назад, их изучением занимались Галилео Галилей (1564– 1642) и Христиан Гюйгенс (1629–1695). Это колебания пружинного и математического маятников.
Колебания пружинного маятника
Пружинный маятник — это колебательная система, представляющая собой закрепленное на пружине тело.
Рассмотрим колебания горизонтального пружинного маятника — тележки массой m, закрепленной на пружине жесткостью k. Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот.
Колебания пружинного маятника:


Обратите внимание! В течение всего времени колебания сила упругости направлена в сторону, противоположную смещению тележки, — сила упругости все время «толкает» тележку к положению равновесия.
Итак, причины свободных колебаний пружинного маятника: 1) действующая на тело сила всегда направлена к положению равновесия; 2) колеблющееся тело инертно, поэтому оно не останавливается в положении равновесия (когда равнодействующая сил становится равной нулю), а продолжает движение в том же направлении.
Как вычислить период колебаний пружинного маятника
Рассмотрим колебания тележки, закрепленной на горизонтальной пружине, с точки зрения второго закона Ньютона (рис. 20.1). Запишем уравнение второго закона Ньютона в векторном виде: 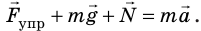
Сила тяжести и сила нормальной реакции опоры уравновешивают друг друга, поэтому 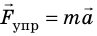 . Спроецировав это уравнение на ось ОХ
. Спроецировав это уравнение на ось ОХ 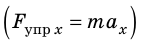 и воспользовавшись законом Гука
и воспользовавшись законом Гука 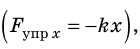 получим:
получим: 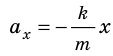 .
.
Последнее уравнение можно записать в виде 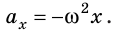 Таким образом, колебания тележки на пружине являются гармоническими колебаниями, а циклическая частота этих колебаний равна:
Таким образом, колебания тележки на пружине являются гармоническими колебаниями, а циклическая частота этих колебаний равна: 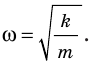
Приняв во внимание, что 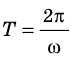 , получим формулу для вычисления периода колебаний пружинного маятника:
, получим формулу для вычисления периода колебаний пружинного маятника:
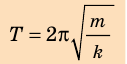
Обратите внимание! Период колебаний пружинного маятника не зависит ни от амплитуды колебаний, ни от места расположения маятника (на поверхности Земли или Луны, в космическом корабле и т. д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость k пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
Что называют математическим маятником
Любое твердое тело, которое совершает или может совершать колебания относительно оси, проходящей через точку подвеса, называют физическим маятником. Примером может быть игрушка, подвешенная на нити в салоне автомобиля. Если игрушку вывести из положения равновесия, она начнет колебаться. Однако изучать такие колебания сложно: их характер определяется размерами и формой игрушки, свойствами нити и другими факторами.
Чтобы размеры тела не влияли на характер его колебаний, следует взять нить, длина которой намного больше размеров тела, а масса незначительна по сравнению с его массой. В таком случае тело можно считать материальной точкой. А чтобы во время колебаний тело все время находилось на одинаковом расстоянии от точки подвеса, нить должна быть нерастяжимой. Таким образом будет получена физическая модель — математический маятник.
Математический маятник — это физическая модель колебательной системы, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити, и гравитационного поля.
Колебания математического маятника
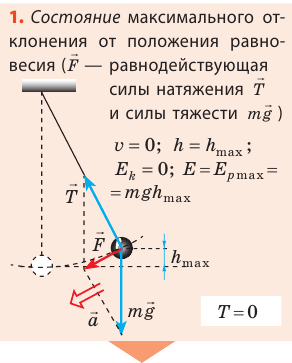
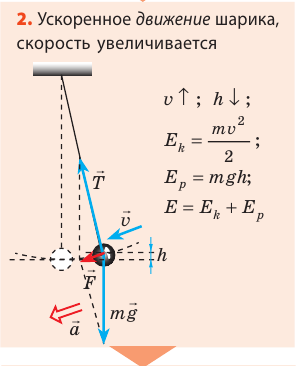
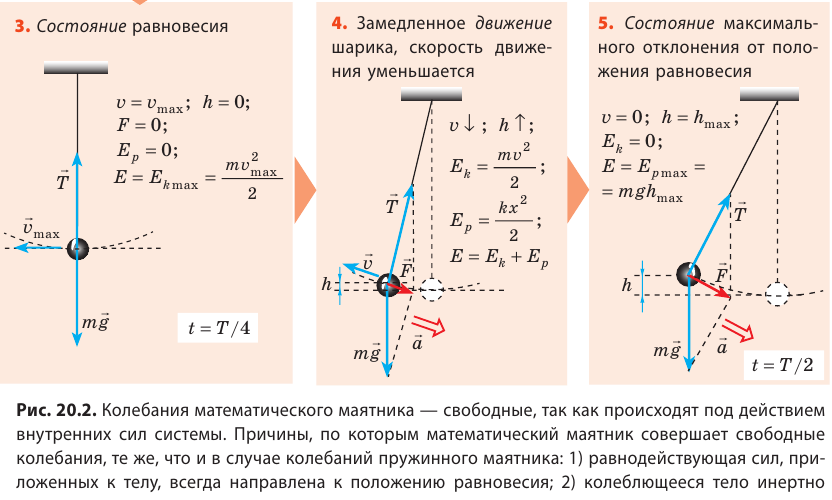
Возьмем небольшой, но достаточно тяжелый шарик и подвесим его на длинной нерастяжимой нити — такой маятник можно считать математическим. Если отклонить шарик от положения равновесия и отпустить, то в результате действия гравитационного поля Земли (силы тяжести) и силы натяжения нити шарик начнет колебаться около положения равновесия. Поскольку сопротивление воздуха пренебрежимо мало, а силы, действующие в системе, являются консервативными, полная механическая энергия шарика будет сохраняться: потенциальная энергия шарика будет превращаться в его кинетическую энергию, и наоборот.
Рассмотрите колебательное движение шарика (рис. 20.2). Объясните причины его движения. Какие происходят превращения энергии?
Как вычислить период колебаний математического маятника
Математический маятник, отклоненный от положения равновесия на небольшой угол (3–5°), будет совершать гармонические колебания, то есть ускорение его движения все время будет прямо пропорционально смещению и направлено в сторону, противоположную смещению: 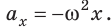
Для математического маятника: 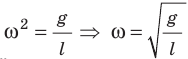 . Поскольку
. Поскольку 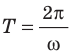 , имеем формулу для периода колебаний математического маятника:
, имеем формулу для периода колебаний математического маятника:
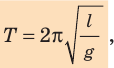
где l — длина маятника; g — ускорение свободного падения.
Данную формулу впервые получил в XVII в. голландский ученый Христиан Гюйгенс, поэтому ее называют формулой Гюйгенса.
Период колебаний математического маятника не зависит от массы маятника, а определяется только длиной нити и ускорением свободного падения в том месте, где расположен маятник. Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности.
Пример:
Уравнение колебаний груза массой 1 кг на пружине имеет вид: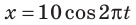 (cм). Найдите полную механическую энергию колебаний; наибольшую скорость груза; кинетическую и потенциальную энергии системы через
(cм). Найдите полную механическую энергию колебаний; наибольшую скорость груза; кинетическую и потенциальную энергии системы через 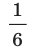 с после начала отсчета времени. Трением пренебречь.
с после начала отсчета времени. Трением пренебречь.
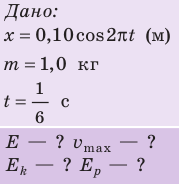
Решение:
Трение отсутствует, поэтому полная механическая энергия сохраняется:
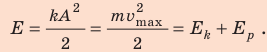
Сравним уравнение колебаний в общем виде с уравнением, приведенным в задаче:
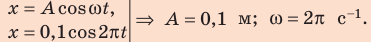
Поскольку
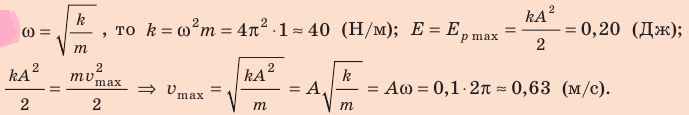
Определив удлинение пружины через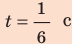 , вычислим потенциальную и кинетическую энергии пружины:
, вычислим потенциальную и кинетическую энергии пружины: 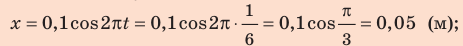
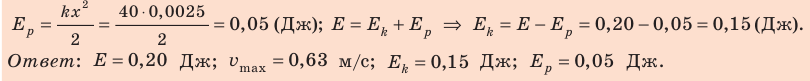
Выводы:
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
Преобразование энергии при механических колебаниях
План урока
- Преобразования энергии при механических колебаниях
- Период колебаний пружинного и математического маятников
Цели урока
- Знать: формулы для расчета механической энергии пружинного маятника; формулы периода пружинного и математического маятников
- Уметь объяснять, какие превращения энергии происходят в процессе механических колебаний
Разминка
- В какой момент времени скорость груза пружинного маятника максимальна?
- Чему равна потенциальная энергия пружины, когда груз находится в положении равновесия?
- Как вычисляется механическая энергия пружинного маятника?
Преобразования энергии при механических колебаниях
Рассмотрим превращения энергии, происходящие в процессе движения пружинного маятника (рис. 1).
Нам уже известно, что механическая энергия системы Eмех изменится только при совершении работы внутренними силами трения или в случае совершения работы над телами системы внешними силами.
Пусть в колебательной системе сумма работ сил трения и внешних сил равна нулю: Aтр + Aex=0. Тогда, согласно закону сохранения механической энергии, механическая энергия системы остается неизменной с течением времени:
Eмех=Eмех0 или Eкин0+Eпот0=Eкин+Eпот.
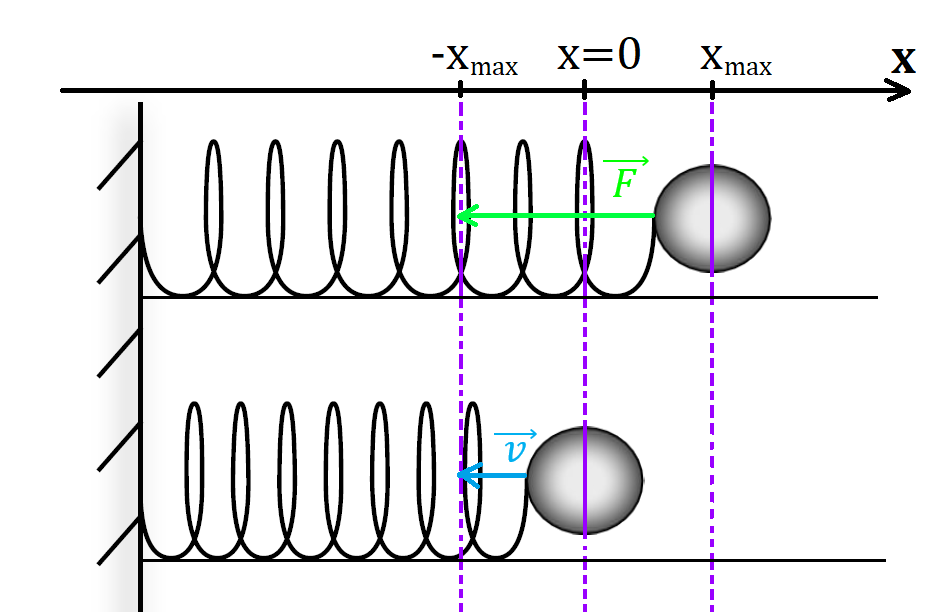
Рис. 1. Превращения энергии в пружинном маятнике
Пусть маятник начинает движение из крайнего правого положения, соответствующего координате х = хmax.
В данной точке пружина максимально растянута, потенциальная энергия пружины равна:
Eпот0=k·xmax22.
Скорость тела в данной точке равна нулю, а значит и кинетическая энергия тоже равна нулю:
Eкин0=0.
Тогда механическая энергия системы равна:
Eмех0=Eпот0=k·xmax22.
Двигаясь к положению равновесия, смещение тела уменьшается, а скорость растет. В некоторый момент времени, когда маятник находится между точками с координатами х = хmax и х = 0, координата тела равна х, а скорость – v.
Тогда потенциальная энергия маятника в данный момент времени равна:
Eпот1=k·x22.
Кинетическая энергия в рассматриваемый момент времени равна:
Eкин1=m·v22.
Механическая энергия равна сумме кинетической и потенциальной энергии системы:
Eмех1=Eпот1+Eкин1=k·x22+m·v22.
Оказавшись в точке с координатой х = 0, система пришла в положение равновесия. Пружина находится в недеформированном состоянии, смещение тела равно нулю, следовательно, потенциальная энергия пружины также равна нулю:
Eпот2=0.
С другой стороны, в данной точке шарик достиг максимального значения своей скорости vmax, тогда кинетическая энергия тела в данной точке равна:
Eкин2=m·vmax22.
Тогда механическая энергия системы равна:
Eмех2=Eкин2=m·vmax22.
Учтем, что по закону сохранения энергии механическая энергия во всех рассмотренных моментах времени одинакова:
Eмех=Eмех0=Eмех1=Eмех2.
В соответствии с уравнениями выше получаем:
Eмех=k·xmax22=k·x22+m·v22=m·vmax22.
Проанализируем полученное выражение.
Прежде всего, отметим, что в процессе колебательного движения сумма кинетической и потенциальной энергий k·x22+m·v22 остается постоянной. Если пружина растягивается, то есть увеличивается первое слагаемое, то скорость тела уменьшается – уменьшается второе слагаемое. Если увеличивается потенциальная энергия колебательной системы, одновременно уменьшается кинетическая энергия.
Во-вторых, из равенства выше следует, что максимальная потенциальная энергия колебательной системы равна максимальной кинетической энергии.
Наконец, используем это соотношение, чтобы вывести формулы максимальной скорости и максимального смещения маятника:
vmax=xmax·km2;
xmax=vmax·mk2.
Таким образом, чем больше амплитуда колебаний пружинного маятника, тем большую скорость он разовьет при прохождении положения равновесия. Чем больше скорость маятника, тем больше величина его смещения относительно положения равновесия.
Соотношение выше также позволяет найти скорость маятника, если известна амплитуда колебаний и текущее положение:
v=km·(xmax2-x2)2,
а также найти координату маятника в любой момент времени, если известна максимальная скорость в положении равновесия и скорость в рассматриваемый момент времени:
x=mk·(vmax2-v2)2.
Полученные закономерности справедливы и для математического маятника: если механическая энергия в процессе колебательного движения остается неизменной, то при прохождении положения равновесия маятник имеет максимальную скорость и максимальную кинетическую энергию, при удалении от положения равновесия кинетическая энергия маятника уменьшается, а потенциальная энергия увеличивается до некоторого максимального значения. При движении к положению устойчивого равновесия, напротив, кинетическая энергия маятника увеличивается, а потенциальная уменьшается.
Период колебаний пружинного и математического маятников
Выражение vmax=xmax·km2 показывает, что модуль максимальной скорости грузика увеличится при увеличении жесткости пружины и уменьшении массы груза. Чем быстрее движется маятник, тем меньше период его колебаний.
Понятно, что возвращающая сила упругости в колебательной системе будет тем больше, чем больше коэффициент жесткости пружины k. С другой стороны, чем легче грузик, тем он менее инертен, тем больше будет его скорость. С точки зрения динамики, также получается, что скорость маятника будет тем больше, чем больше коэффициент жесткости и чем меньше масса груза.
Зависимость между периодом колебаний пружинного маятника, жесткостью пружины и массой груза установлена экспериментально:
T=2·π·mk2,
где T [с] – период колебаний пружинного маятника;
m [кг] – масса колеблющегося груза;
k [Н/м] – коэффициент жесткости.
Период свободных гармонических колебаний
пружинного маятника
, состоящего из груза массой m и легкой пружины жесткостью k, равен:
T=2·π·mk2.
Формула выше показывает, что при увеличении массы груза в 9 раз период колебаний маятника увеличится в 3 раза; при увеличении жесткости пружины в 16 раз период колебаний уменьшится в 4 раза.
Период колебаний математического маятника не зависит от массы колеблющегося груза. Это связано с тем, что и кинетическая энергия груза, и его потенциальная энергия прямо пропорциональны массе груза. Период колебаний математического маятника зависит только от длины нити:
T=2·π·lg2,
где T [с] – период колебаний математического маятника;
l [м] – длина нити;
g = 10 м/с2 – модуль ускорения свободного падения.
Период свободных гармонических колебаний
математического маятника
, длина нити которого равна l, рассчитывается по следующей формуле:
T=2·π·lg2.
Таким образом, при уменьшении длины нити маятника в 4 раза период колебаний математического маятника уменьшится в 2 раза.
Эту формулу можно объяснить с точки зрения динамики движения груза: чем больше ускорение свободного падения, тем больше возвращающая сила тяжести, действующая на груз, тем больше его скорость и тем меньше период колебаний маятника.
Пример 1
Шарик массой 80 г, прикреплённый к одному из концов лёгкой пружины жесткостью 250 Н/м, совершает свободные гармонические колебания в горизонтальном направлении. Определите максимальное отклонение шарика от положения равновесия, если в некоторый момент времени его скорость равна 3 м/с, а отклонение от положения равновесия в этот же момент было 4 см. Трением пренебречь.
Решение
1. Перечислим исходные данные:
m=80 г=0,08 кг;v=3мс;k=250Нм;∆x=4 см=0,04 м.∆xmax-?
2. В крайних точках от положения равновесия тело обладает максимальной потенциальной энергией, а кинетическая энергия равна нулю, тогда механическая энергию будет:
Eмех=Eпотmax=k∆xmax22.
3. Запишем, чему равна механическая энергия в некоторый момент времени, когда шарик двигался со скоростью 3 м/с и отклонялся на 4 см:
Eмех’=mv22+k∆x22.
С другой стороны, в отсутствие трения, механическая энергия сохраняется, а значит Eмех=Eмех’.
⇒k∆xmax22=mv22+k∆x22
4. Из последнего равенства выразим ∆xmax:
∆xmax=mkv2+∆x2≈0,07 м.
Ответ: ∆xmax≈0,07 м.
Итоги
- Механическая энергия пружинного маятника при отсутствии потерь энергии в системе в любой момент времени постоянна и равна: Eмех=k·xmax22=k·x22+m·v22=m·vmax22;
- Период свободных гармонических колебаний
пружинного маятника
, состоящего из груза массой m и легкой пружины жесткостью k, равен: T=2·π·mk2; - Период свободных гармонических колебаний
математического маятника
, длина нити которого равна l, рассчитывается по следующей формуле: T=2·π·lg2.
Упражнение 1
1. Ученик проводил эксперименты с пружинным маятником. Сначала он определил, что амплитуда колебаний шарика массой 0,01 кг, прикрепленного к пружине, равна ∆xmax=20 см. Далее, ученик хотел узнать значение скорости в момент времени, когда отклонение шарика от положения равновесия составляло ∆x=10 см. Какое значение скорости было получено? Жёсткость пружины 300 Н/м.
2. Определите период колебаний пружинного маятника, состоящего из груза массой 0,3 кг и пружины жёсткостью 400 Н/м.
3. Чему равен период колебаний математического маятника, если груз подвешен на нити длинной 1,5 м?
Контрольные вопросы
1. Как рассчитать механическую энергию пружинного маятника?
2. От чего зависит период колебаний пружинного маятника?
3. Как рассчитывается период колебаний математического маятника?
Ответы
Упражнение 1
1. v=km∆xm2-∆x2=30 м/с.
2. ≈0,17 с.
3. ≈2,43 с.
