Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью
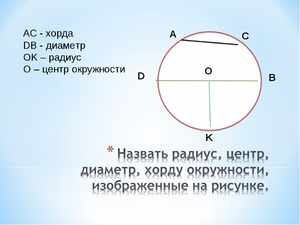
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Конечная часть плоскости, ограниченная окружностью
Отрезок, соединяющий центр окружности с любой точкой окружности
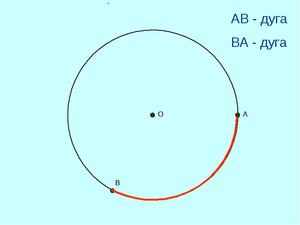
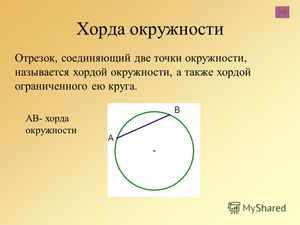
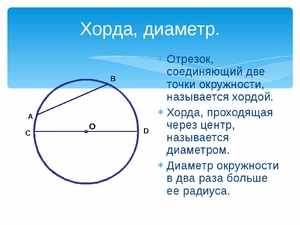
Отрезок, соединяющий две любые точки окружности
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Прямая, пересекающая окружность в двух точках
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
|
| Круг |  |
|
| Радиус |  |
|
| Хорда |  |
|
| Диаметр |  |
|
| Касательная |  |
|
| Секущая |  |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда

Отрезок, соединяющий две любые точки окружности
Диаметр

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Касательная

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Секущая

Прямая, пересекающая окружность в двух точках
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  |
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  |
Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  |
У равных дуг равны и хорды. |
| Параллельные хорды |  |
Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.
Равные дуги

У равных дуг равны и хорды.
Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.
Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.


| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
|
| Касательные, проведённые к окружности из одной точки |  |
|
| Касательная и секущая, проведённые к окружности из одной точки |  |
|
| Секущие, проведённые из одной точки вне круга |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.


| Пересекающиеся хорды |
 |
| Касательные, проведённые к окружности из одной точки |
 |
| Касательная и секущая, проведённые к окружности из одной точки |
 |
| Секущие, проведённые из одной точки вне круга |
 |
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки


Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Касательная и секущая, проведённые к окружности из одной точки



Секущие, проведённые из одной точки вне круга



Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).


Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).


Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).


Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).


Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.


Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:


Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим


Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим


Воспользовавшись теоремой 1, получим


Воспользовавшись равенствами (1) и (2), получим





Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Что такое хорда окружности в геометрии, её определение и свойства
 Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.
Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
 Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
 Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Хорда и радиус
Между этими понятиями существуют следующие связи:
 Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
 Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
 Две равные между собой хорды стягивают равные дуги.
Две равные между собой хорды стягивают равные дуги.- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
Окружность
Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.
Часть плоскости, ограниченная окружностью называется кругом.
Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.
Основные термины
Касательная
Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойства касательной
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Хорда
Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд
- Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Дуги, заключенные между параллельными хордами, равны.
Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Свойства окружности
- Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки ( секущая ).
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Точка касания двух окружностей лежит на линии, соединяющей их центры.
Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB .
Теорема о секущих
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Свойства углов, связанных с окружностью
- Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на диаметр, равен 90°.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Длины и площади
- Длина окружности C радиуса R вычисляется по формуле:
Площадь S круга радиуса R вычисляется по формуле:
Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле:
Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле:
Вписанные и описанные окружности
Окружность и треугольник
- центр вписанной окружности — точка пересечения биссектристреугольника, ее радиус r вычисляется по формуле:
где S — площадь треугольника, а — полупериметр;
центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле:
здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника;
Окружность и четырехугольники
- около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:
в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:
- около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
- около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
- в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
[spoiler title=”источники:”]
http://tarologiay.ru/nauka/chto-takoe-horda-okruzhnosti-v-geometrii-eyo-opredelenie-i-svoystva.html
http://www.univer.omsk.su/omsk/Edu/Rusanova/circles.htm
[/spoiler]
Нарисуем рисунок для понимания решения

Пусть K – точка пересечения хорд. Так как CK:KD = 2:3. То есть CK – 2 части, а KD – 3 части. А вместе 5 частей, но и весь отрезок CD = 5, тогда 1 часть – это 1 единица измерения. И CK = 2, KD = 3
Есть свойство пересекающихся хорд CK • KD = AK • KB
Если это свойство не помним, то оно быстро выводится из подобия ∆CAK и ∆BDK (подобны по 2 углам ∠K – вертикальные и ∠A = ∠D – вписанные опираются на одну дугу)
Итак получили: AK • KB = 2•3 = 6
Но так же по условию AK+KB = AB = 7
откуда KB = 7-AK и подставим в первое уравнение
AK•(7-AK) = 6, (можно сразу подобрать корни 1 и 6 или 6 и 1)
Но давайте аккуратно раскроем скобки и получим квадратное уравнение
AK² – 7AK + 6 = 0
D = 49 – 24 = 25
(AK)₁ = (7-5)/2 = 1 в этом случае (KB)₁ = 7-1 = 6
(AK)₂ = (7+5)/2 = 6 в этом случае (KB)₂ = 7-6 = 1
То есть в обоих случаях хорда AB точкой пересечения разбивает на два отрезка: 1 и 6
Отношение меньшего к большему 1:6
Ответ: 1:6
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 августа 2022 года; проверки требует 1 правка.



Теорема о произведении отрезков хорд описывает соотношения отрезков, образованных двумя пересекающимися хордами окружности. В теореме утверждается, что произведения длин отрезков каждой из хорд равны.
Формулировка теоремы[править | править код]
Для двух хорд AC и BD, пересекающихся в точке S, выполняется следующее равенство:
Обратное также верно, т. е. если для двух отрезков AC и BD, пересекающихся в точке S, вышеприведённое равенство выполняется, то их концы A, B, C и D лежат на одной окружности. Другими словами, если диагонали четырёхугольника ABCD пересекаются в точке S и выполняется вышеупомянутое равенство, то этот четырёхугольник является вписанным.
Степень точки[править | править код]
Значения двух произведений в теореме о хордах зависит от расстояния точки пересечения S от центра окружности и называется абсолютным значением степени точки S. Более точно это можно выразить следующим образом:
где r является радиусом окружности, а d является расстоянием между центром окружности и точкой пересечения S. Это свойство следует непосредственно из применения теоремы о хордах к третьей хорде, проведённой через точку S и центр окружности M (см. рисунок).
Наряду с теоремой о секущей и касательной и теоремой о двух секущих, теорема о пересекающихся хордах является одним из трёх основных случаев более общей теоремы о двух пересекающихся прямых и окружности — теоремы о степени точки.
Доказательство теоремы[править | править код]
Теорему можно доказать с помощью подобных треугольников (через теорему о вписанном угле). Рассмотрим углы треугольников ASD и BSC:
(углы, опирающиеся на хорду AB)
(углы, опирающиеся на хорду CD)
(вертикальные углы)
Это означает, что треугольники ASD и BSC подобны, а потому:
Вы можете посмотреть интерактивную иллюстрацию к теореме и её доказательству[1][2].
Примечания[править | править код]
- ↑ Amit Quackenbush. Intersecting Chords Theorem (англ.). GeoGebra. Дата обращения: 30 апреля 2021. Архивировано 21 января 2021 года.
- ↑ Josiah Fan Ern Wei. Intersecting chord theorem (англ.). GeoGebra. Дата обращения: 30 апреля 2021. Архивировано 21 января 2021 года.
Литература[править | править код]
- Glaister P. Intersecting Chords Theorem: 30 Years on // Mathematics in School. — 2007. — vol. 36. — № 1. — P. 22.
- Shawyer B. Explorations in Geometry. — World scientific, 2010. — P. 14. — ISBN 9789813100947.
- Schupp H. Elementargeometrie. — Schöningh, Paderborn, 1977. — P. 149. — ISBN 3-506-99189-2.
- Schülerduden — Mathematik I. — Bibliographisches Institut & F.A. Brockhaus, 2008. — S. 415—417. — ISBN 978-3-411-04208-1.
Рассмотрим свойство, которое проходят в 8 классе сразу после пропорциональных отрезков или после подобия треугольников. Такого свойства в оглавлении нет (скорее всего), эту теорему обычно дают внутри других тем (у Л.С. Атанасян , «73 Теорема о вписанном угле» ) ну или в виде задач (с доказательством). Свойство встречается и на экзамене ОГЭ. Несколько таких заданий собраны по ссылке в конце заметки.
Теорема
Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.
Доказательство
Рассмотрим такие хорды AB и CD, которые пересекаются в произвольной точке O:
Задача доказать, что OC • OD = OB • OA.
Соединим попарно точки A и C, B и D:
Получим два треугольника: ∆ACO и ∆OBD. Данные треугольники подобны по первому признаку подобия треугольников:
- Углы ∠ACD и ∠ABD, как опирающиеся на дугу AD – равны;
- Углы ∠AOC и ∠BOD, как вертикальные – равны.
А значит, верно отношение соответственных сторон в подобных треугольниках ∆ACO ~ ∆OBD:
Теорема доказана.
Применение
Свойство пересекающих хорд встречается и в первой части экзамена по математике ОГЭ: список заданий из первой части в которых ответ можно получить через данное свойство.
Окружность есть такая плоская кривая, у которой все точки находятся на равном расстоянии от одной точки, лежащей внутри ее и называемой центром.
Круг. Кругом называется часть плоскости, ограниченная окружностью.
Радиус. Радиусом называется отрезок, соединяющий центр с какой-нибудь точкой окружности. Радиус есть расстояние точки окружности от центра.
Из самого определения окружности следует, что все ее радиусы равны.
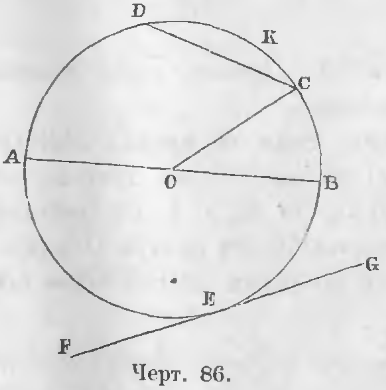
На чертеже 86 кривая линия BCDAEB есть окружность, O ее центр, отрезки OA, OB, OC — радиусы. Эти отрезки равны
OA = OB = OC.
Диаметр. Отрезок, проходящий через центр от одной точки окружности до другой, называется диаметром.
Всякий диаметр состоит из двух радиусов, а так как все радиусы равны, то следовательно и все диаметры равны.
Дуга есть часть окружности.
Слово дуга иногда обозначают знаком ◡, так что дугу BC изображают письменно: ◡BC.
Хорда. Отрезок, соединяющий две какие-нибудь точки окружности, называется хордой. Хорда есть прямая, стягивающая две точки дуги.
На чертеже 86 линия AB есть диаметр, часть окружности BC есть дуга, прямая CD есть хорда.
Сегмент есть часть плоскости, содержащийся между дугой и хордой.
Сектор есть часть плоскости, содержащийся между двумя радиусами и дугой круга.
На чертеже 86 площадь COB есть сектор, а CKD сегмент.
Касательная есть прямая, имеющая с окружностью только одну общую точку, которая называется точкой касания.
Углом при центре называется угол, имеющий вершину в центре. На чертеже 86 прямая FG есть касательная, а E точка касания.
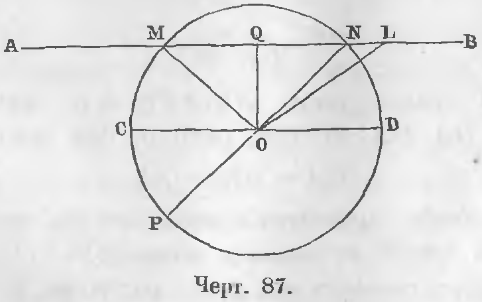
Теорема 55. Прямая может пересечь окружность только в двух точках.
Доказательство. Если бы прямая AB кроме двух точек M и N (черт. 87) имела бы еще третью точку пересечения L, то три точки окружности M, N, L, по свойству окружности, были бы на равном расстоянии от центра O, следовательно, три отрезка MO, NO, LO были бы равны: MO = NO = LO.
Если же NO = LO, то вышло бы, что равные наклонные находятся на неравных расстояниях от перпендикуляра OQ, что противоречит свойству косвенных, следовательно, третьей точки пересечения быть не может (ЧТД).
Теорема 56. Диаметр делит окружность и круг на две равные части.
Доказательство. Перегнем верхнюю часть круга около диаметра CD (черт. 87) до совпадения ее с нижней частью, тогда все точки верхней совпадут с точками нижней части окружности, ибо в противном случае не все точки окружности находились бы на равном расстоянии от центра.
Зависимость между углами, дугами и хордами
Теорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги.
Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны:
∠AOB = ∠A’O’B’.
Требуется доказать, что ◡AB = ◡A’B’.
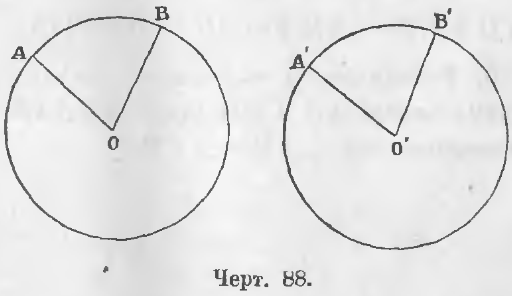
Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами.
Теорема 58 (обратная 57). Равным дугам соответствуют равные углы.
Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88).
Требуется доказать, что ∠AOB = ∠A’O’B’.
Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно,
∠AOB = ∠A’O’B’ (ЧТД).
Теорема 59. Диаметр больше всякой хорды.
Даны диаметр CD и хорда MN (черт. 87).
Требуется доказать, что CD > MN.
Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN
MON > MN или MO + ON > MN
Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства:
CO + OD > MN или CD > MN (ЧТД).
Теорема 60. Равные хорды стягивают равные дуги.
Даны равные хорды AB и CD (черт. 89) (AB = CD).
Требуется доказать, что ◡AB = ◡CD.
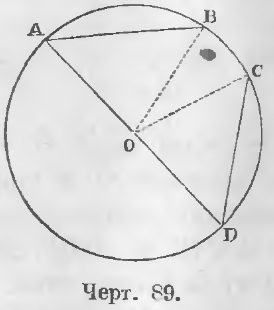
Доказательство. Соединив точки A, B, C, D с центром, имеем
∆AOB = ∆COD, ибо
OA = OC и OB = OD как радиусы, AB = CD по условию.
Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД).
Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами.
Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD).
Требуется доказать, что AB = CD.
Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД).
Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда.
Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC).
Требуется доказать, что BD > AC.
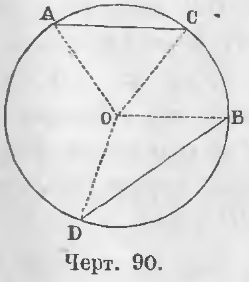
Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД).
Теорема 63 (обратная 62). Против большей хорды лежит большая дуга.
Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC).
Требуется доказать, что ◡BD > ◡AC.
Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД).
Взаимное отношение хорд и их расстояний от центров
Теорема 64. Радиус, перпендикулярный к хорде, делит как хорду так и дугу пополам.
Радиус OC перпендикулярен к хорде AB (черт. 91).
CO ⊥ AB.
Требуется доказать, что AD = BD и ◡AC = ◡CB.
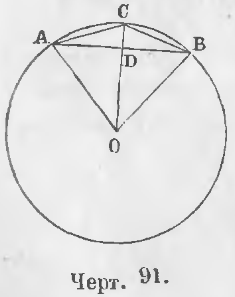
Доказательство. Соединим точки A и B с центром O. Равные наклонны OA и OB находятся на равных расстояниях от перпендикуляра OC, следовательно, AD = DB.
Если же перпендикуляр CD восставлен из середины отрезка AB, то его точка C находится на равном расстоянии от концов перпендикуляра, поэтому хорды AC и CB равны, а следовательно,
◡AC = ◡CB
т. е. дуга AB делится перпендикуляром OC пополам (ЧТД).
Следствие. Перпендикуляр, восставленный из середины хорды, проходит через центр.
Доказательство. Так как центр находится на равном расстоянии от концов хорды, то он находится на перпендикуляре, восставленном из середины хорды.
Теорема 65. Равные хорды находятся на равном расстоянии от центра.
Дано. Хорды AB и CD равны: AB = CD (черт. 92).
Требуется доказать, что их расстояния от центра равны, т. е.
OE = OF
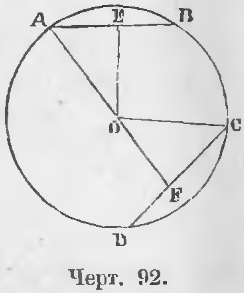
Доказательство. Соединив точки A и C с центром O, имеем два равных прямоугольных треугольника AEO и COF, ибо OA = OC как радиусы, AE = CF как половины равных хорд (теорема 64). Следовательно,
OE = OF (ЧТД).
Теорема 66 (обратная 65). На равных расстояниях от центра находятся равные хорды.
Дано. Расстояния хорд AB и CD от центра равны, т. е.
OE = OF (черт. 92).
Требуется доказать, что AB = CD.
Доказательство. Два прямоугольных треугольника AEO и COF равны, ибо имеют по равной гипотенузе и равному катету. Действительно, OE = OF по условию, OA = OC как радиусы, следовательно, AE = CF или ½AB = ½CD, откуда
AB = CD (ЧТД).
Теорема 67. Большая хорда к центру ближе меньшей.
Дано. Хорда AB больше хорды AC (черт. 93), т. е. AB > AC.
Требуется доказать, что OD < OE.
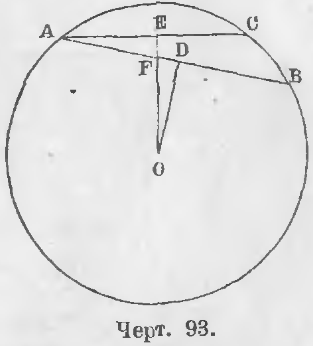
Доказательство. Линия OD перпендикулярна к AB, а линия OF наклонна, следовательно, OD < OF. Так как OF < OE, то и подавно OD < OE (ЧТД).
Свойства касательной
Прямая называется секущей, если она пересекает окружность в двух точках, и касательной, если она имеет с окружностью только одну общую точку. Эта точка называется точкой касания.
Теорема 68. Прямая, проведенная через в конец радиуса, перпендикулярно к нему, будет касательной к окружности.
Дано. Прямая AF перпендикулярно к радиусу AO в конце радиуса (черт. 94)
AF ⊥ AO.
Требуется доказать, что AF касательная к окружности.
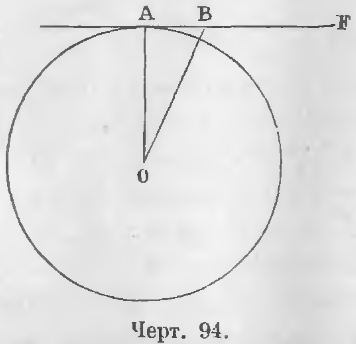
Доказательство. Всякая другая точка B перпендикуляра AB находится на расстоянии BO большем AO, ибо наклонная больше перпендикуляра, следовательно точка B находится вне окружности. Таким образом прямая AB имеет с окружностью только одну общую точку A, следовательно, она будет касательной (ЧТД).
Теорема 69 (обратная 68). Касательная к окружности, проведенная в конец радиуса, перпендикулярна к радиусу.
Дано. Прямая AF касается окружности в точке A (черт. 94).
Требуется доказать, что AF ⊥ OA.
Доказательство. Прямая AB как касательная имеет с окружностью только одну общую точку A. Всякая другая точка B лежит вне окружности, следовательно, всякий отрезок OB больше OA. Таким образом, отрезок OA есть кратчайшее расстояние точки O от AB, следовательно, OA ⊥ AB (ЧТД).
Теорема 70. Между параллельными хордами находятся равные дуги.
Дано. Хорды AB и CD параллельны: AB || CD (черт. 95).
Требуется доказать, что ◡AC = ◡BD.
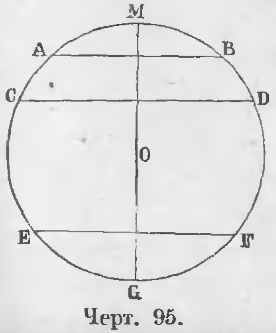
Доказательство. a) Из центра окружности O опустим перпендикуляр OM на хорду AB, тогла отрезок OM перпендикулярен и к хорде CD.
По теореме 64
◡CM = ◡MD
◡AM = ◡MB
Вычитая второе равенство из первого, получим:
◡CM – ◡AM = ◡MD – ◡MB или
◡AC = ◡BD.
b) Если параллельные хорды AB и EF (черт. 95) лежат по обе стороны центра, то, продолжив прямую OM до пересечения с окружностью в точке G, имеем:
◡MA = ◡MB, ◡GE = ◡GF.
Так как полуокружности MAG и MBG равны
MAG = MBG, то следовательно,
MAG – ◡MA – ◡GE = MBG – ◡MB – ◡GF
или ◡AE = ◡BF (ЧТД).
Относительное положение двух окружностей
Концентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают.
На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические.
Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга.
На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние.
Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку.
Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения.
Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101).
Линия центров есть отрезок, соединяющий центры двух кругов.
Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут.
Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102).
Требуется доказать, что другой общей точки у них нет.
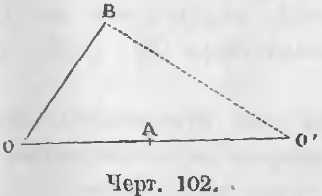
Доказательство. Положим, существует другая общая точка B, следовательно,
OB = OA и O’B = O’A.
Складывая эти равенства, мы имели бы
OB + O’B = OA + O’A или
OB + O’B = OO’
равенство несообразное, ибо ломаная не может равняться прямой.
Итак, другой общей точки быть не может (ЧТД).
Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров.
Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры.
Требуется доказать, что существует и другая общая точка по другую сторону центров.
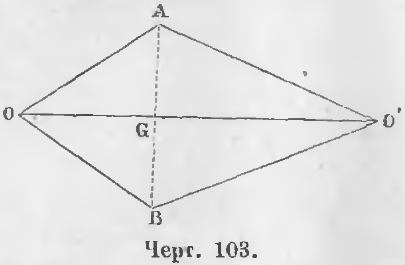
Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG.
Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД).
Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения.
Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей.
Требуется доказать, что AG = BG и AB ⊥ OO’.
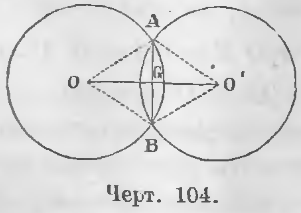
Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая.
OA = OB как радиусы окружности O.
O’A = O’B как радиусы окружности O’.
Следовательно,
∠AOO’ = ∠BOO’
Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров).
Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД).
Расстояние между центрами окружностей
1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов.
Действительно, с одной стороны (черт. 104)
OO’ < AO + AO’
с другой
AO + OO’ > AO’
следовательно,
OO’ > AO’ – AO
2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее.
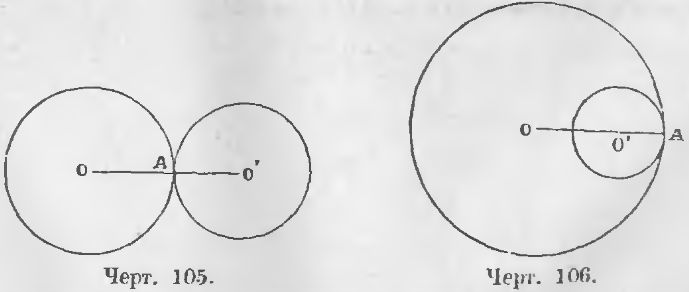
Из чертежа 105 видно, что
OO’ = AO + AO’
а из чертежа 106
OO’ = AO – AO’.
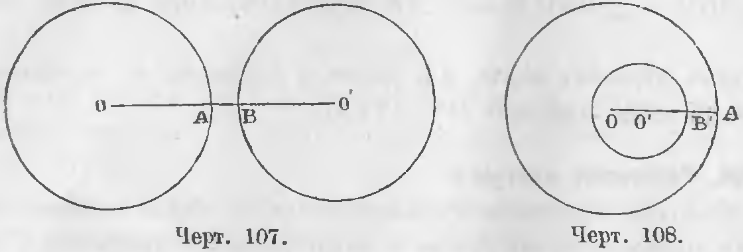
3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов.
Из чертежа 107 видно, что
OO’ > AO + BO’
4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов.
Действительно, из чертежа 108 видно, что
OO’ < AO – BO’.
Измерение углов
Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.
Относительно этих углов имеют место следующие теоремы.
Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.
Дано. Углы AOB и COD равны (черт. 109).
Требуется доказать, что ◡AB = ◡CD.
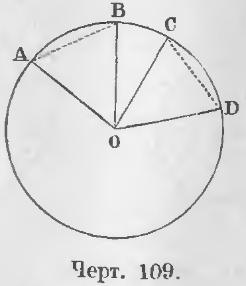
Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.
Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).
Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.
Дано. Дуги AB и CD равны (черт. 109).
Требуется доказать, что ∠AOB = ∠COD.
Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).
Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).
Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.
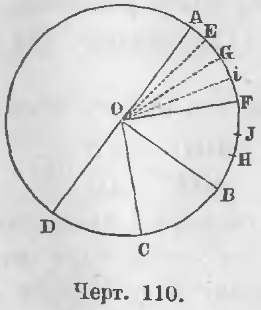
Даны два центральные угла AOB и COD (черт. 110).
Требуется доказать, что
AOB/COD = AB/CD.
Доказательство. Здесь имеют место два случая:
1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.
1-й случай. Дуги AB и CD соизмеримы.
Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.
Из равенств
AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE
получаем
AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).
2-й случай. Дуги AB и CD несоизмеримы.
Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.
Требуется доказать, что
AOB/AOF = AB/AF
Доказательство. A) Положим
AOB/AOF > AB/AF (1).
Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.
Положим, мы нашли, что имеет место равенство
AOB/AOF = AB/AG (a)
Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,
AOB/AOi = AB/Ai (b).
Разделив равенства (b) на (a), находим
AOF/AOi = AG/Ai
равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.
B) Допустим, что
AOB/AOF < AB/AF (2)
Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство
AOB/AOF = AB/AH (c)
Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,
AOB/AOJ = AB/AJ (d)
Разделив равенство (d) на (c) найдем
AOF/AOJ = AH/AJ
Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).
Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)
AOB/COD = AB/CD
можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.
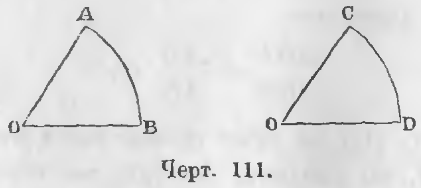
Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство
AOB/1 = AB/1
или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда
∠AOB = ◡AB.
Это равенство означает, что
числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.
Мера углов и дуг
За единицу угла обыкновенно принимают прямой угол.
Углы и дуги измеряют также частями окружности.
Для этого делят окружность на 360 равных частей, называемых градусами, градус на 60 минут, минуту на 60 секунд.
Таким образом, окружность имеет 360 градусов или 360°. Градус имеет 60 минут или 60′. Минута включает 60 секунд или 360”.
Выражение 12°7’16” означает дугу круга, имеющую 12 градусов 7 минут и 16 секунд. Угол, опирающийся на эту дугу, называется также углом в 12°7’16”.
Прямой угол имеет 90°.
Теорема 77. Углы, имеющие вершину на окружности, измеряются половиной дуги, содержащейся между его сторонами.
Здесь может быть несколько случаев (черт. 112).
Первый случай. Угол BAC образуется диаметром AC и хордой AB.
Соединим центр O с точкой B; тогда
∠BOC = ∠ABO + ∠BAO
Так как ∠ABO = ∠BAO как углы равнобедренного треугольника AOB, то
BOC = 2BAO и
BAO = ½ BOC.
Угол BOC измеряется дугой BC, следовательно, угол BAO измеряется дугой ½ BC.
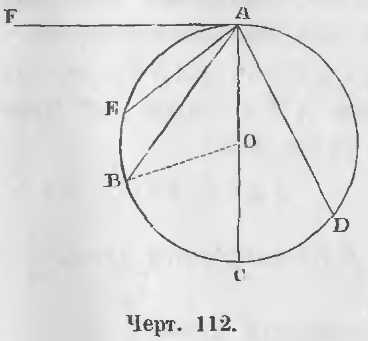
Второй случай. Угол BAD образуется двумя хордами, лежащими по обе стороны диаметра.
BAD = BAC + CAD
уг. BAD измеряется дугой ½ BC
уг. CAD измеряется дугой ½ CD.
Следовательно, угол BAD измеряется дугой
½ BC + ½ CD = ½ (BC + CD) = ½ BD.
Т. е. угол BAD измеряется половиной дуги, заключающейся между его сторонами (ЧТД).
Третий случай. Угол EAB образуется двумя хордами, лежащими по дну сторону диаметра.
EAB = EAC – BAC
EAC измеряется дугой ½ EC
BAC измеряется дугой ½ BC
следовательно, EAB измеряется дугой
½ EC – ½ BC = ½ (EC – BC) = ½ EB.
Правило остается то же.
Теорема 78. Угол, образуемый касательной и хордой, измеряется половиной дуги, стягиваемой хордой.
Доказательство. Угол FAE (черт. 112) есть угол, образуемой касательной AF и хордой AE. Проведя диаметр AC, мы получим прямой угол FAC.
FAE = FAC – EAC
Прямой угол FAC измеряется дугой ½AC.
Угол EAC измеряется дугой ½EC.
Угол FAE измеряется
½AC – ½EC = ½(AC – EC) = ½AE (ЧТД).
Теорема 79. Угол, имеющий вершину внутри окружности, измеряется полусуммой дуг, заключающихся между его основаниями.
Дан угол ACB, имеющий вершину C внутри окружности (черт. 113).
Требуется доказать, что он измеряется дугой ½(AB + DE).
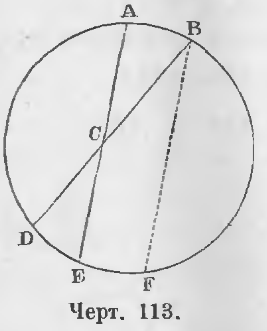
Доказательство. Из точки B проведем прямую BF параллельную AE, тогда
∠ACB = ∠DBF
Угол DBF измеряется дугой ½DF или
∠DBF = ½ DEF = ½ (DE + EF)
◡AB = ◡EF как дуги, содержащиеся между параллельными сторонами, следовательно,
ACB = ½ (DE + AB) (ЧТД).
Теорема 80. Угол, имеющий вершину вне окружности, измеряется полуразностью дуг, заключающихся между его сторонами.
Дано. Угол ACB имеет вершину вне окружности (черт. 114).
Требуется доказать, что он измеряется дугой ½ (AB – EF).
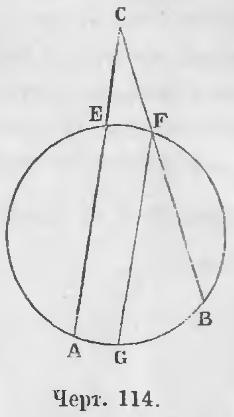
Доказательство. Проведем из точки F прямую FG параллельную AC, тогда
∠C = ∠GFB
Мера угла C равна мере угла GFB = ½ GB
GB = AB – AG
Так как AG = EF, то GB = AB – EF, следовательно, ∠C = ½ (AB – EF) (ЧТД).
Из предложенных теорем вытекают заключения:
1) Все углы, имеющие вершину на окружности и опирающиеся на диаметр, являются прямыми, ибо все они измеряются половиной полуокружности.
2) Все вписанные углы, опирающиеся на одну и туже дугу, равны.
Обратно:
3) Все прямые углы, имеющие вершину на окружности, опираются на концы диаметра.
4) Угол при центре вдвое больше угла вписанного и опирающегося на одну и ту же дугу.
Свойства углов и сторон описанного и вписанного четырехугольника
Теорема 81. Во всяком четырехугольнике, вписанном в окружность, сумма противоположных углов равна двум прямым.
Дано. Вписан четырехугольник ABCD (черт. 115).
Требуется доказать, что A + C = 2d, B + D = 2d.
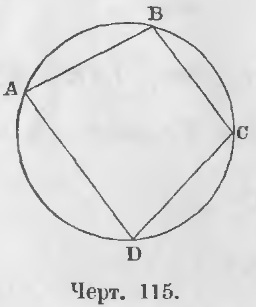
Доказательство. Угол B измеряется половиной дуги ADC, угол D измеряется половиной дуги ABC, следовательно сумма углов B + D измеряется ½ (ADC + ABC), т. е. полуокружностью.
Полуокружность есть мера двух прямых, следовательно,
B + D = 2d.
Это же заключение справедливо и для суммы углов A и C
A + C = 2d (ЧТД).
Теорема 82. Суммы противоположных сторон описанного четырехугольника равны.
Дан описанный четырехугольник ABCD (черт. 116); a, b, c, d четыре точки прикосновения его сторон с окружностью.
Требуется доказать, что AB + CD = BC + AD.
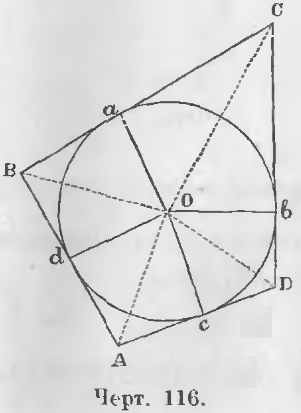
Доказательство. Соединим вершины и точки прикосновения a, b, c, d описанного четырехугольника с центром O.
Из чертежа 116 видно, что
∆OaC = ∆ObC
∆ObD = ∆OcD
∆OcA = ∆OdA
∆OdB = ∆OaB
ибо они, будучи прямоугольными, имеют по равной гипотенузе OC, OD, OA, OB и равным катетам, следовательно,
aC = bC
aB = dB
cA = dA
cD = bD
Сложив эти равенства, получаем:
aC + aB + cA + cD = bC + dB +dA + bD
или
BC + AD = CD + AB (ЧТД).





