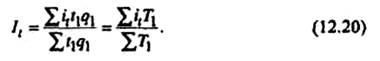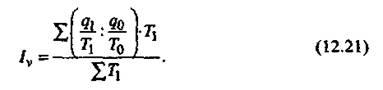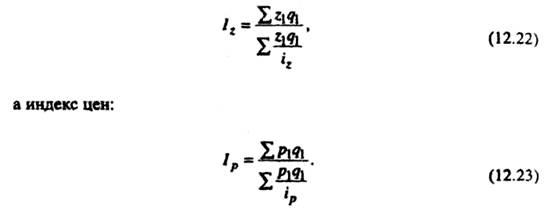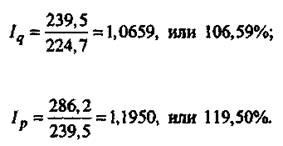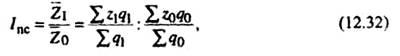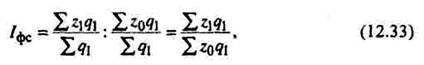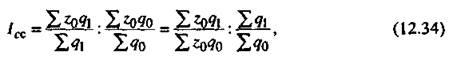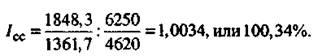Как найти отношение индексов - Сайт, где вы сможете решить свои вопросы

Содержание курса лекций «Статистика»

«Индекс» в переводе с латинского – указатель, показатель.

В статистике под индексом понимается относительная величина, характеризующая соотношение значений определенного показателя во времени, пространстве, а также сравнение фактических данных с планом или другим нормативом.

С помощью индексов можно определить количественные изменения самых различных показателей функционирования народного хозяйства, развития социально-экономических процессов и т.п.

В экономической работе с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, состоянии себестоимости и цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменения в цене акций на фондовых рынках (индекс Доу Джонса), сравнительную характеристику изменения погоды за определенный период времени (температуры, влажности, давления) и т.д. и т.п.

Индексы в своей основе представляют разновидность относительных величин, характеризующих средние показатели исследуемых процессов или явлений в социально-экономических и других областях деятельности общества. Однако от средних величин, рассмотрению которых посвящены были предыдущие темы, индексы отличаются тем, что они воплощают в себе, как правило, сводные, обобщающие показатели, т.е. выражают собой некоторое содержание, свойственное всем рассматриваемым явлениям и процессам.

Индексный метод имеет свою терминологию и символы.

Обозначения индексируемых величин:

i – индивидуальный индекс, его вычисляют для одной единицы совокупности;

I – общий (сводный) индекс (он определяется для всех единиц совокупности);

q – количество (объем) какого-либо товара в натуральном выражении;

p – цена единицы товара;

z – себестоимость единицы продукции;

t – затраты времени на производство единицы продукции, трудоемкость;

T – общие затраты времени на производство (tq) или численность рабочих;

pq – стоимость продукции или товарооборот;

zq – издержки производства.

Знак внизу справа означает период, например:

q₀ – базисный, q₁ – отчетный и т.п.

Экономический индекс – это относительная величина, которая характеризует изменение исследуемого явления во времени, в пространстве или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.п.).

Если в качестве базы сравнения используется уровень за какой-либо предшествующий период – получают динамический индекс; если же базой является уровень того же явления по другой территории – территориальный индекс.

Индексируемая величина – показатель, изменение которого характеризуется индексом, она содержится в названии самого индекса, например: индекс цен, индекс заработной платы, индекс физического объема продукции и т.д.

Вес индекса – величина, служащая для целей соизмерения индексируемых величин.

Классификация индексов:

по степени охвата явления индексы бывают индивидуальные и сводные;
по виду весов – с постоянными и переменными весами;
в зависимости от формы построения – агрегатные и сводные;
по базе сравнения – динамические и территориальные;
по характеру объема исследования – общие индексы подразделяются на количественные и качественные;
по составу явления – постоянного (фиксированного) состава и переменного состава,
по периоду исчисления – годовые, квартальные, месячные, недельные и т.д.

В экономическом анализе индексы используются не только для сопоставления уровней изучаемого явления, но главным образом для определения экономической значимости причин, объясняющих абсолютное различие сравниваемых уровней.

Экономические индексы позволяют: 1) измерить динамику социально-экономического явления за два и более периодов времени; 2) измерить динамику среднего экономического показателя; 3) измерить соотношение показателей по разным регионам; 4) определить степень влияния изменений значений одних показателей на динамику других; 5) пересчитать значения макроэкономических показателей из фактических цен в сопоставимые.

Методика построения агрегатного индекса предусматривает решение трех вопросов: 1) какая величина будет индексируемой; 2) по какому составу разнородных элементов явления необходимо исчислить индекс; 3) что будет служить весом при расчете индекса.

Правило при выборе индекса

При выборе веса индекса принято руководствоваться следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период, при построении индекса качественного показателя используются веса отчетного периода.

Расчет индивидуальных индексов

Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту, например:

– индекс цены определенного продукта (товара), где и цена товара, соответственно в текущем и в базисном периоде

(14.1);

‑ индекс объема одного определенного продукта (товара)

(14.2)

‑ индекс себестоимости единицы отдельного продукта

(14.3)

‑ индекс численности работников и т.д.

(14.4)

Все индивидуальные индексы показывают, каково соотношение между отчетным (со знаком «1») и базисным (со знаком «0») показателями или во сколько раз увеличилась (уменьшилась) индексируемая величина.

Все индивидуальные индексы по сути являются относительными величинами динамики или коэффициентами (темпами) роста (снижения).

Индивидуальные индексы характеризуют изменение отдельных единиц статистической совокупности. Характерной чертой индексов является то, что все они образуют системы взаимосвязанных показателей.

Расчеты индивидуальных индексов просты по своей сущности и выполняются путем вычисления отношения двух индексируемых величин. Индивидуальные индексы могут исчисляться в виде индексного ряда за несколько периодов.

Существуют два способа расчета индивидуальных индексов: цепной и базисный.

При цепном способе расчета за базу отношения принимается индексируемая величина соседнего прошлого периода, в этом случае база расчета в ряду постоянно меняется.

При базисном способе расчета за базу принимается индексируемая величина какого-либо отдельного периода.

Расчет общих индексов

В области экономических явлений наряду с индивидуальными индексами, характеризующими изменения единичных элементов, возникает необходимость расчета сводных относительных величин, обобщающих изменения определенного показателя в сложной совокупности, отдельные элементы которой несопоставимы (в физических единицах) и не могут суммироваться.

Например, нельзя тонны нефти и тонны стали, а также цены на разные товары (мясо, молоко, обувь, одежду и т.п.).

Для обобщения относительного изменения определенного показателя в сложной совокупности рассчитываются общие (сводные ) индексы.

Общий (сводный) индекс – показатель, измеряющий динамику сложного явления, составные части которого непосредственно несоизмеримы в физических единицах.

Например, по данным органов статистики, цены на продовольственные товары в декабре 2018 г. составили 116,1% по отношению к предыдущему месяцу (ноябрю) и 175 % по отношению к декабрю 2017 г.

С помощью общих индексов характеризуется изменение цен на товары, изменение уровня жизни, развитие производства отдельных отраслей и экономики в целом и многое другое.

Индексы могут иметь разный характер.

Одни являются объемными (количественными); другие условно можно назвать качественными: они представляют собой показатели, определяемые на какую-то единицу (цена единицы товара, себестоимость единицы продукции, урожайность с 1 га и т.д.).

В соответствии с этим и индексы можно подразделить на индексы количественных показателей (индекс физического объема производства, индекс продаж акций и т.п.) и качественных (индекс цен, индекс себестоимости, индекс заработной платы и пр.)

Каждый из этих индексов имеет свои особенности, но любой общий индекс может быть исчислен двумя способами: как агрегатный и как средний из индивидуальных.

Рассмотрим оба способа построения (исчисления) общих индексов.

Общий индекс, полученный путем сопоставления итоговых показателей, количественно выражающих сложное явление в отчетном и базисном периодах с помощью соизмерителей, называют агрегатным.

Соизмерители необходимы для перехода от натуральных измерителей, разнородных единиц статистической совокупности к однородным показателям.

При этом в числителе и знаменателе общего индекса изменяется только значение индексируемой величины, а их соизмерители являются постоянными величинами и фиксируются на одном уровне ‑ это необходимо для того, чтобы на величине индекса сказывалось лишь влияние фактора, который определяет изменения индексируемой величины.

Пример. В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цена, количество, себестоимость единицы продукции или затраты на единицу продукции и др.

При сравнении числителя и знаменателя данной формулы в разности определяется показатель абсолютного прироста.

При сравнении разности числителя и знаменателя индексного отношения получаем показатель, характеризующий прирост суммы в текущем периоде по сравнению с базисным периодом.

Обозначая объем продукции (товаров через q, а цены – через p, можно представить стоимость продукции в базисном периоде как , а в отчетном как . Сопоставляя эти два показателя, получим индекс стоимости (товарооборота).

(14.5)

Который показывает относительное изменение стоимости продукции как за счет изменения цен, так и за счет изменения объема отдельных товаров.

Если же продукцию двух сравниваемых периодов оценить в одних и тех же неизменных ценах, то очевидно, что стоимость продукции двух периодов будет отличаться лишь за счет изменения объема продукции. Поэтому общий индекс, исчисленный как отношение стоимости продукции двух периодов в одних и тех же ценах, называют агрегатный индекс физического объема .

В агрегатном индексе физического объема в качестве соизмерителя различных товаров принимаются цены базисного периода или цены, неизменные в течении ряда лет (такие цены называют также сопоставимыми).

(14.6)

где и ‑ объем продукции различных видов соответственно в базисном и отчетном периодах.

Отметим, что суммы в числителе и знаменателе имеют вполне реальный смысл:

‑ стоимость продукции базисного периода;

‑ стоимость продукции отчетного периода в базисных ценах.

Разность между числителем и знаменателем агрегатного индекса характеризует изменение в абсолютном выражении результативного показателя за счет изменения индексируемой величины.

Пример. Предположим, предприятие выпускает три вида неоднородной продукции. Данные о производстве и цены за два периода приведем в (табл. 14.1).

Таблица 14.1. – Данные о производстве продукции за 2 периода

Товар	Выработано тыс. единиц	Цена за единицу товара, руб.	Стоимость продукции в базисных ценах, тыс. руб.
Базисный период q₀	Отчетный период q₁	Базисный период р₀	Отчетный период р₁	Базисный период q₀p₀	Отчетный период q₁p₀
А	80	60	13	16	1040	780
Б	50	30	18	20	900	540
В	40	35	6	8	240	210
ИТОГО	–	–	–	–	2180	1530

Следовательно, общий объем (выпуск) продукции в отчетном периоде по сравнению с базисным составил 70,2% (или снизился на 29,8%).

А в абсолютном выражении за счет уменьшения выпуска стоимость продукции в отчетном периоде снизилась на 650 тыс. руб., вычитаем из числителя знаменатель

Как уже отмечалось, при построении агрегатного индекса физического объема могут использоваться и другие соизмерители. Так, например, если принять в качестве соизмерителей себестоимость единицы продукции в базисном периоде z₀, то агрегатный индекс физического объема можно записать как:

(14.7)

Разность между числителем и знаменателем покажет, как изменились общие затраты (издержки) на производство в связи с изменением выпуска продукции:ли в качестве соизмерителей принять затраты времени на единицу продукции в базисном периоде, то формула агрегатного индекса физического объема будет иметь вид:

(14.8)

разность будет характеризовать изменение общих затрат времени на производство продукции за счет изменения объема выпуска.

Агрегатный индекс цен. По аналогии с индексом физического объема для определенного набора товаров (продуктов) может быть построен и агрегатный индекс цен (индекс качественного показателя). При этом рассуждения остаются теми же: если нельзя суммировать цены на различные товары, то можно суммировать и сопоставлять стоимости этих товаров.

Однако, сопоставляя два значения стоимости рq, мы должны показать изменение последней лишь за счет изменения цен р, т.е. необходимо устранить влияние изменения количества производимой (или реализуемой) в разные периоды продукции q на стоимостный показатель продукции. Для этого один и тот же количественный набор продуктов надо оценить в ценах отчетного и базисного периодов и затем сопоставить первую величину со второй. Таким образом, в агрегатном индексе цен индексируемой величиной является, естественно, цена р, а соизмерителем (весами) ‑ количество произведенных (реализованных) товаров q, принятое на уровне базисного или отчётного периода.

Агрегатная формула общего индекса цен была впервые предложена в 1864 г. немецким ученым Э. Ласпейресом. Он предлагал строить агрегатный индекс цен, приняв в качестве весов продукцию базисного периода q₀:

(14.9)

В 1874 г. другой немецкий учёный, Г. Пааше, предложил строить агрегатный индекс цен по продукции текущего периода q₁:

(14.10)

Каждый из этих индексов имеет свои особенности, которым отдается предпочтение в конкретных условиях, использования.

Так, например, индекс Цен Ласпейреса удобен для оперативной (недельной, месячной, квартальной) информации об изменении цен на определенный фиксированный набор товаров, когда пересчет каждый раз на текущий набор (количество) товаров сопряжен с большими затратами, труда и времени.

По формуле Ласпейреса рассчитывают индекс потребительских цен (ИПЦ).

В то же время формуле Пааше отдается предпочтение, когда индекс цен рассматривается в системе с индексом стоимости и индексом физического объема. В этом случае, чтобы обеспечивать взаимосвязь между индексом стоимости и индексом физического объема.

Кроме того, при расчете индекса цен; по формуле Пааше, вычитая из числителя знаменатель, легко определить в абсолютном выражении сумму потерь (или прибыли) за счет изменения цен на продукцию отчетного (текущего) периода.

Рассмотрим расчет агрегатных индексов цен на примере.

Таблица 14.2. – Данные о реализации продукции за 2 периода (цифры условные)

Продукт	Ед. изм	Базисный период	Отчетный период	Стоимость базисного периода, руб	Стоимость отчетного периода, руб
Про-дано ед. q₀	Цена руб p₀	Про-дано ед. q₁	Цена руб p₁	q₀p₀	q₀p₁	q₁p₀	q₁p₁
Говядина	Кг	1000	25	900	30	25000	30000	22500	27000
Картофель	Кг	3000	2	4000	2,5	6000	7500	8000	10000
Молоко	л	5000	3	6000	3,2	15000	16000	18000	19200
Всего						46000	53500	48500	56200

Чтобы определить, как в среднем изменились цены на все продукты (или какова средняя величина изменения цен), рассчитаем сводный (общий) индекс цен в форме агрегатного индекса:

Пример вычисление по формуле Лайспереса

Пример вычисление по формуле Пааше

Вывод: т.е. по формуле Ласпейреса цены по всем продуктам выросли в среднем на 16,3%, а по формуле Пааше ‑ на 15,9% .

Расхождение не очень большое (на 0,4), но все же есть. Какому же индексу отдать предпочтение? На таком уровне исследования (по отдельному хозяйству и совокупности хозяйств) предпочтение следует отдать индексу Пааше, поскольку он показывает реальное изменение стоимости продукции, реализованной в отчетном периоде, за счет изменения цен. В этом индексе числитель ‑ реальная величина, фактическая выручка, полученная от реализации продукции в отчетном периоде, а знаменатель ‑ условная величина, показывающая, какой была бы выручка, если бы продукция отчетною периода продавалась по базисным ценам.

Разность между ними, (56200 ‑ 48500 = 7700 руб.), показывает в данном случае, какую прибыль дополнительно получило хозяйство при реализации продукции в отчетном периоде за счет роста цен.

В формуле же индекса цен Ласпейреса в знаменателе содержится реальная выручка (стоимость) от реализации в базисном периоде, а в числителе ‑ условная величина, характеризующая, какой была бы выручка от реализации продукции базисного периода по ценам отчетного периода. Разность практически не представляет интереса, так как эта величина слишком отвлеченная: она показывает, насколько изменилась бы выручка (стоимость) в прошлом (базисном) периоде, если бы базисная продукция была реализована по текущим (отчетным) ценам.

Кроме того, при расчете индекса цен по формуле Пааше, легко увязываются изменения трех взаимосвязанных показателей: стоимости (выручки), объема реализации и цен. Так, по данным табл. 14.2 индекс стоимости продукции

(или 122,2%), т.е. стоимость продукции (выручка от продажи) в отчетном периоде увеличилась на 22,2%, что составило в абсолютном выражении 10200 руб. (56200 – 46000).

Индекс физического объема реализаций по данным табл. 14.2

В абсолютном выражении увеличение стоимости за счет изменения объема реализации составило 2500 руб. (48500 – 46000)

Таким образом, имеет место увязка индексов (относительного изменения показателей):

(14.11)

А также абсолютных изменений: в нашем примере 10200 = 7700 + 2500,т.е. общее изменение стоимости продукции равно сумме приростов за счет изменения цен и за счет изменения объема.

В начале XX в. американский экономист И. Фишер предложил вместо формул индексов цен Ласпейреса и Пааше использовать среднюю геометрическую из них, т.е. корень квадратный из произведения индексов иен Ласпейреса и Пааше:

(14.12)

(Этот индекс назван им идеальным, поскольку в нем не отдается предпочтение ни продукция базисного периода, ни продукции текущего периода.

Кроме того, этот индекс «обратим» во времени, т.е. если рассчитывать индекс базисного периода к отчетному, он будет равен обратной величине первоначального индекса (т.е. отчетного периода к базисному). Другими словами, перемножение таких, «обратных» индексов дает единицу.

Однако индекс Фишера из-за его формальности и трудности экономической интерпретации используется редко, в основном при территориальных сопоставлениях.

Мы рассмотрели расчет агрегатных индексов физического объема и цен как наиболее типичных представителей агрегатных индексов соответственно для количественных и качественных индексируемых показателей.

По аналогии можно записать агрегатные индексы для многих других показателей.

Контрольные задания

Понятие о статистических индексах, их классификация.
Индивидуальные и общие индексы.
Агрегатный индекс как исходная форма индекса.
Назовите способы определения сумм экономического эффекта от изменения цен и количества проданных товаров.
По данным статистических сборников, СМИ и т.п. исчислите индивидуальные и общие индексы.

Содержание курса лекций «Статистика»

Источник

Основные формулы исчисления сводных, или общих, индексов

Наименование	Формула расчета	Что показывает индекс	Что показывает значение индекса, уменьшенное на 100%, т.е. 1-100	Что показывает разность числителя и знаменателя
Индекс физического объема продукции		Во сколько раз изменилась стоимость продукции в результате изменения ее объема, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема	На сколько процентов изменилась стоимость продукции в результате изменения ее объема	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема
Индекс цен		Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен	На сколько процентов изменилась стоимость продукции в результате изменения цен	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен
Индекс стоимости продукции (товарооборота)		Во сколько раз возросла (уменьшилась) стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным	На сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным
Индекс физического объема		Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения физического объема ее производства	На сколько процентов изменились издержки производства продукции в результате изменения объема ее производства	На сколько рублей изменились издержки производства продукции в результате роста (уменьшения) объема ее производства
Индекс себестоимости продукции		Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения ее себестоимости	На сколько процентов изменились издержки производства продукции в результате изменения ее себестоимости	На сколько рублей изменились издержки производства в результате роста (уменьшения) себестоимости продукции
Индекс издержек производства		Во сколько раз возросли (уменьшились) издержки производства продукции, или сколько процентов составил рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным	На сколько процентов возросли (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным	На сколько рублей увеличились (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции		Во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения физического объема ее производства	На сколько процентов изменились затраты времени на производство продукции в результате изменения объема ее производства	На сколько человеко-часов возросли (уменьшились) затраты времени на производство продукции в результате роста (уменьшения) объема производства продукции
Индекс производительности труда по трудовым затратам		Во сколько раз увеличилась (уменьшилась) производительность груда, или сколько процентов составило снижение (рост) производительности труда в текущем периоде по сравнению с базисным	На сколько процентов изменилась производительность труда в текущем периоде по сравнению с базисным	Абсолютный размер экономии (перерасхода) затрат живого труда в связи с ростом (уменьшением) его производительности
Индекс затрат времени на производство продукции		Во сколько раз изменились затраты времени на производство продукции, или сколько процентов составил рост (снижение) затрат времени на производство продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным	На сколько человеко-часов увеличились (уменьшились) затраты на производство продукции в текущем периоде по сравнению с базисным

Средний
арифметический индекс физического
объема продукции вычисляется по формуле:

Так
как i_q ∙ q₀ = q₁, то
формула этого индекса легко преобразуется
в формулу (12.14). Весами в формуле (12.19)
является стоимость продукции базисного
периода.

Средний
арифметический индекс производительности
труда определяется следующим образом:

Так
как i_t ∙ t₁ = t₀, то
формула этого индекса может быть
преобразована в агрегатный индекс
трудоемкости продукции. Весами являются
общие затраты времени на производство
продукции в текущем периоде.

В
статистике широко известен и другой
средний арифметический индекс, который
используется при анализе производительности
труда. Он носит название индекса
Струмилина и
определяется следующим образом:

Индекс
показывает, во сколько раз возросла
(уменьшилась) производительность труда,
или сколько процентов составил рост
(снижение) производительности труда в
среднем по всем единицам исследуемой
совокупности.

Средние
арифметические индексы чаще всего
применяются на практике для расчета
сводных индексов количественных
показателей. При анализе качественных
показателей данная форма индекса
применяется для исчисления приведенных
выше индексов (формулы (12.20) – (12.21)).

Индексы
других качественных показателей (цен,
себестоимости и т.д.) определяются по
формуле средней гармонической взвешенной
величины.

Средний
гармонический индекс тождествен
агрегатному, если индивидуальные индексы
взвешены с помощью слагаемых числителя
агрегатного индекса.

Например,
индекс себестоимости можно исчислить
так:

Таким
образом, при определении среднего
гармонического индекса себестоимости
весами являются издержки производства
текущего периода, а при вычислении
индекса цен веса – стоимость продукции
этого периода.

Рассчитаем
средние индексы цен и физического объема
продукции по данным табл. 12.1 (графы
11-12):

Этот
же результат получился при расчете
агрегатных индексов. Средние индексы
широко используются для анализа рынка
ценных бумаг. Наиболее известными
являются индексы Доу-Джонса, Стэндарда
и Пура.

Индекс
Доу-Джонса (Dow
Jones Industrial Average Index) определяется как
средний арифметический индекс значений
курсов акций, котирующихся на Нью-Йоркской
фондовой бирже. Один сводный и три
групповых индекса рассчитываются каждые
полчаса, и ежедневно публикуется их
значение на момент закрытия биржи.
Групповые индексы определяются по ценам
акций 30 промышленных, 20 транспортных и
15 компаний сферы услуг. Общий индекс
рассчитывается по всем 65 компаниям. Их
перечень был составлен в 1928 г. В качестве
базисного выбран 1920 г. Первоначальная
методика исчисления индекса была
разработана основателем и редактором
крупнейшей в США газеты «Уолл-стрит
джорнел» Чарлзом Доу.

Индекс
Стэндарда и Пура (Standard
and Poor’s 500 Stock Index) -индекс, рассчитываемый
по курсам акций 500 крупнейших компаний
Нью-Йоркской фондовой биржи как средний
взвешенный показатель, учитывающий
общее число выпущенных компанией акций.
В число компаний, акции которых включены
в индекс, входят 400 промышленных
корпораций, 40 – финансовых, 20 –
транспортных и 40 – сферы услуг.

31.Агрегатные и индивидуальные индексы
их сущность и расчет.

Индекс —
это обобщающий относительный показатель,
характеризующий изменение уровня
общественного явления во времени, по
сравнению с программой развития, планом,
прогнозом или его соотношение в
пространстве.

Наиболее
распространена сравнительная
характеристика во времени. В этом случае
индексы выступают как относительные
величины динамики.
Индексный
метод является
также важнейшим аналитическим средством
выявления связей между явлениями. При
этом применяются уже не отдельные
индексы, а их системы.
В статистической
практике индексы применяются при анализе
развития всех отраслей экономики, на
всех этапах экономической работы. В
условиях рыночной экономики особенно
возросла роль индексов
цен,
доходов населения, фондового рынка и
территориальных индексов.

Статистика
осуществляет классификацию индексов
по следующим признакам:

1.
В зависимости от объекта исследования:

индексы
объемных (количественных) показателей
(индексы физического объема: товарооборота,
продукции, потребления)
индексы
качественных показателей (индексы
цен, себестоимости, заработной
плата)

К
индексам объемных показателей относятся
индексы физического объема: товарооборота,
продукции, потребления материальных
благ и услуг; а также других показателей,
имеющих количественный характер:
численности работников, посевных
площадей и т.п. К индексам качественных
показателей относятся индексы: цен,
себестоимости продукции, заработной
платы, производительности труда,
урожайности и т.п.;

2.
По степени охвата элементов совокупности:

индивидуальные
индексы (дают
сравнительную характеристику отдельных
элементов явления)
общие
индексы (характеризуют
изменение совокупности элементов или
всего явления в целом)

3.
В зависимости от методологии исчисления
общие индексы подразделяются на:

агрегатные
(агрегатные индексы являются основной
формой индексов и строятся как агрегаты
путем взвешивания индексируемого
показателя с помощью неизменной величины
другого, взаимосвязанного с ним
показателя).
средние
(являются производными от агрегатных)

4.
В зависимости от базы сравнения различают:

базисные
(если при исчислении индексов за
несколько периодов времени база
сравнения остается постоянной)
цепные
(если база сравнения постоянно меняется)

Индексный
метод

Элиминирование,
то есть расчет влияния отдельных факторов
на обобщающий показатель, может
осуществляться такжеиндексным
методом.
Этот метод применяется для
расчленения экономических
показателей.
Индексы являются разновидностью
относительных величин. Индексы применяются
в анализе
хозяйственной деятельности с
целью характеристики экономических
явлений, состоящих из элементов, которые
не следует суммировать.

Технически
любой индекс представляет собой
показатель, определяемый как соотношение
двух каких-либо величин. Последние
являются, по существу, определенными
состояниями известного признака. С
помощью индексов осуществляются
сравнения фактических показателей с
базисными, то есть, как правило, с
плановыми и с показателями предшествующих
периодов.

Различают
два основных вида индексов:

простые
(частные, индивидуальные);
аналитические
(общие, агрегатные).

В
первом случае исследуемый признак
принимается без учета связи этого
признака с остальными признаками
исследуемых экономических явлений.
Такие индексы могут быть представлены
следующей формулой:

и —
соответственно сравниваемые состояния
какого-либо признака

Во
втором случае изучаемый признак
используется не изолированно, а в его
взаимосвязи с другими признаками.

Поэтому
любой аналитический индекс состоит из
двух элементов:

индексируемый
признак ,
то есть тот признак, изменение которого
подвергается изучению;
весовой
признак .

С
помощью весовых признаков исследуются
изменения экономических явлений,
составляющие элементы которых являются
несоизмеримыми. Следует иметь в виду,
что простые и аналитические индексы
взаимно дополняют друг друга.

Аналитические
индексы могут быть представлены следующим
образом:

или

где и—
весовые признаки

Использование
индексов в экономическом анализе
преследует следующие цели:

с
их помощью дается оценка относительного
изменения какого-либо экономического
явления или показателя;
применение
индексов дает возможность определить
влияние отдельных факторов на изменение
обобщающего (результативного) показателя
(признака).
дается
оценка влияния изменения структуры
какого-либо экономического явления на
величину динамики этого явления.

Рассмотрим
сущность индексного метода на конкретном
примере. Если анализируемая организация
выпускает разнородную продукцию, то
рассчитывается общий индекс объема
продукции.

Информация
об объеме и стоимости выпускаемой
продукции.

Виды продукции	Количество (штук)	Цена за 1 штуку (рублей)	Стоимость продукции (рублей)

А	10	13	5	5	50	65	65
Б	15	12	3	2	45	36	24
В	20	22	1	2	20	22	44
Итого:	–	–	–	–	115	123	133

В
рассматриваемом примере мы
исчислим аналитические
индексы,
где в качестве индексируемого
признака беретсяобъем
выпускаемой продукции,
а в качестве весового признака — цена
за единицу продукции. На основе данных,
приведенных в таблице, рассчитаем общий
индекс объема продукции:

На
полученный нами результат оказали
влияние два фактора:

изменение
количества продукции;
изменение
цен на продукцию.

Следует
отдельно определить:

индекс
изменения количества (объема) продукции
при условии ее оценки в одинаковых
ценах;
индекс
изменения цен на продукцию при условии
ее одинакового объема.

Вначале
найдем индекс изменения количества
продукции:

Затем
определим индекс изменения цен на
продукцию:

В
рассматриваемом примере индекс изменения
количества показывает увеличение объема
продукции на или
на 8 рублей, то есть (123 — 115). Индекс
изменения цен свидетельствует о повышении
цен на продукцию на,
что составляет 10 рублей, то есть (133 —
123).

Если
сложить влияние индексов получим общий
индекс объема продукции — 18 рублей.

С
помощью индексов можно сравнивать
данные за ряд лет, например, путем
расчетов темпов
роста продукции
в сопоставимых ценах.

В
условиях анализа динамики показателей
следует различать понятия цепного и
базисного индексов. Базисным называется
индекс, рассчитанный по отношению к
базисному периоду. Цепным называется
индекс, рассчитанный по отношению к
предыдущему периоду.

Индивидуальные
индексы

Способы
построения индексов зависят от содержания
изучаемого явления, методологии расчета
исходных статистических показателей
и целей исследования. В каждом индексе
выделяют 3 элемента:

В
каждом индексе выделяют 3 элемента:

индексируемый
показатель —
это показатель, соотношение уровней
которого характеризует индекс
сравниваемый
уровень —
это тот уровень, который сравнивают с
другим.
базисный
уровень —
это тот уровень, с которым производится
сравнение.

Для
расчета индекса необходимо найти
отношение сравниваемого уровня к
базисному и выразить его в виде
коэффициента, если база сравнения
приравнивается к единице, или в процентах,
если база сравнения принимается за
100%. Обычно расчеты индексов производятся
в форме коэффициентов с точностью до
третьего знака после запятой, т. е. до
0,001, в форме процентов — до десятых долей
процента, т.е. до 0,1%.

Для
удобства построения индексов используется
специальная символика:

i
— символ индексируемого показателя —
индекс, характеризующий изменение
уровня элемента явления.
I
— с подстрочным индексируемым показателем
— для группы элементов или всей
совокупности в целом.
q
— количество проданных товаров или
произведенной продукции в натуральном
выражении
p
— цена за единицу товара
z
— себестоимость единицы продукции
w
— производительность труда
T
— отработанное время или численность
работников
l
— средняя заработная плата одного
работника

0
— базисный период
1
— отчетный период

Исходные данные	Расчетные данные
Товары	Базисный период	Отчетный период	Товарооборот млн.руб	Индивидуальные индексы
Про-дано т.шт	Цена за 1 шт. т.руб	Про-дано т.шт	Цена за 1 шт. т.руб	Базисный период	Отчетный период	Отчетный период по ценам базисного периода	Физ. объема т-ооборота	Цен	Товаро-оборота
А	1	2	3	4	5=1*2	6=3*4	7=3*2	8=3:1	9=4:2	10=6:5
	q₀	p₀	q₁	p₁	q_0 *p₀	q_1 *p₁	q_1 *p₀
Телевизоры	400	3	360	3,3	1200	1188	1080	0,9	1,1	0,99
Видео-магнито-фоны	200	2	250	1,8	400	450	500	1,250	0,9	1,125
Итого	х	х	х	х	1600	1638	1580	0,9875	1,037	1,024

Индивидуальные
индексы характеризуют
изменение отдельного элемента явления.

Индивидуальный
индекс физического объема товарооборота

Так,
для изучения изменения количества
проданных товаров (физического объема
продаж) следует построить индивидуальный
индекс физического объема товарооборота
как отношение количества товара одного
вида, проданного в отчетном периоде, к
количеству того же товара, проданного
в базисном периоде (i_q =
q₁ /
q₀ ).
Поскольку базисный уровень индексируемого
показателя приравнивается к 1 или 100%,
то разность между полученным индексом
и 1 или 100% характерзиует относительную
величину изменения количества проданного
товара. По этому индексу можно определить
и абсолютное изменение количества
проданного товара в натуральном выражении
как разность между числителем и
знаменателем индекса .

Произведем
расчет индивидуальных индексов
физического объема товарооборота.

По
телевизорам: или90% и
рассчитываем тыс.шт,
то есть в отчетном периоде по сравнению
с базисным было продано телевизоров на
40 тыс.штук, или на 10% меньше, чем в базисном
году.

По
видеомагнитофонам: ,
и рассчитываемтыс.шт,
то есть количество проданных
видеомагнитофонов возрасло на 50 тыс.
штук или на25%.

Индивидуальный
индекс цен

Индивидуальный
индекс цен определяется
как отношение цены отдельного товара
в отчетном периоде к цене его в базисном
периоде, то есть по формуле: .
Разность между числителем и знаменателем
его покажет абсолютное изменение цены
за единицу товара в рублях.

Рассчитаем
индивидуальные индексы цен (9):

По
телевизорам: или
110% итыс.руб,
т.е. цена телевизора увеличилась на 0,3
тыс.руб., или на10% (110-100).

По
видеомагнитофомам: или90% и тыс.руб
т.е. цена видеомагнитофона снизилась
на 0,2 тыс.руб или на 10%.

Индивидуальный
индекс товарооборота

Индивидуальный
индекс товарооборота характеризует
изменение товарооборота по одному
товару и строится как отношение
товарооборота отчетного периода к
товарообороту базисного периода,
то есть по формуле:

Разница
между числителем и знаменателем его
покажет абсолютное изменение товарооборота
в рублях за счет двух фактров: изменения
количества проданного товара и изменения
цены этого товара, то есть

Рассчитаем
индивидуальные индексы товарооборота
(10):

По
телевизорам: или99% и млн.руб,
то есть товарооборот по телевизорам
стал меньше на 12 млн.руб, или на 1%
(99-100%).

По
видеомагнитофонам: или112.5% и млн.руб,
то есть товарооборот по видеомагнитофонам
увеличился на 50 млн.руб. или на 12,5%
(12,5-100%).

Рассмотренные
нами индивидуальные
индексы взаимосвязаны между собой так
же, как сами индексируемые показатели:
индекс товарооборота равен произведению
индекса физического объема товарооборота
на идекс цен, то есть

Проверим
взаимосвязь исчисленных индивидуальных
индексов:

По
телевизорам: 0,99 = 0,9*1,1
По
видеомагнитофонам: 1,125 = 1,25*0,9

Кроме
того, полученные данные позволяют
рассчитать абсолютные
показатели изменения товарооборота по
отдельным товарам за счет отдельных
факторов.

Так,
по телевизорам общее изменение
товарооборота составило: млн.руб,
то есть товарооборот по телевизорам в
отчетном периоде по сравнению с базисным
стал меньше на 12 млн.руб. Эта величина
может быть разложена на две:

1.
за счет изменения количества проданных
товаров: млн.руб,
то есть за счет уменьшения количества
проданных телевизоров на 40 тыс.штук
товарооборот стал меньше на 120 млн.руб.

2.
за счет изменения цен: млн.руб,
то есть за счет роста цены одного
телевизора на 0,3 тыс.руб товарооборот
возрос на 108 млн.руб.

Проверим
взаимосвязь исчисленных показателей: млн.руб.

По
видеомагнитофонам имеем изменение
товарооборота на 50 млн.руб.

1.
за счет изменения количества проданных
товаров:

2.
за счет изменения цен:

Товарооборот
по видеомагнитофонам увеличился на 50
млн.руб. За счет увеличения количества
проданных видеомагнитофонов на 50
тыс.штук товарооборот возрос на 100
млн.руб, а за счет снижения цен на
видеомагнитофоны на 0,2 тыс.руб за штуку
стал меньше на 50 млн.руб.

Общие
индексы

Все
рассмотренные нами индексы характеризуют
относительное изменение уровней
отдельных элементов явления и называются
индивидуальными индексами.

Однако
большинство изучаемых статистикой
общественных явлений и процессов состоят
из многих элементов, которые могут быть
как однородными, так и неоднородными. Однородные
явления можно непосредственно суммировать
и исчислять индексы, характеризующие
изменение не одного элемента, а группы
элементов или всей совокупности в целом.
Такие индексы называются общими
индексами. Так,
можно суммировать количество
проданныходнородных
товаров по
группе фирм и исчислить общий
индекс физического объема товарооборота по
формуле:

,
где знак означает
суммирование данных о количестве одного
товара по нескольким фирмам. Можно
суммировать товарооборот по нескольким
товарам и исчислять общий индекс
товарооборота по формуле,
где знакозначает
суммирование товарооборота по группе
товаров.

Если
же отдельные элементы явления неоднородны,
то непосредственное суммирование их
невозможно или бессмысленно и тогда
необходимо привести их к сопоставимому
виду. Все товары имеют стоимость, а
стоимости товаров можно суммировать.
Переход от натуральных показателей к
стоимостным позволяет преодолеть
несуммарность натурально-вещественных
элементов совокупности. Но изменение
стоимости товаров обусловлено совместным
изменением двух факторов — количества
товаров и цен на них, а нам необходимо
определить изменение каждого из этих
факторов в отдельности. Для изучения
изменения одного фактора необходимо
абстрагироваться от изменения второго,
взаимосвязанного с ним фактора и
построить общий индекс в агрегатной
форме.

Так, агрегатный
индекс физического объема товарооборота должен
показать изменение количества
проданныхразнородных
товаров,
поэтому в числителе его берется отчетное
количество товаров (q₁),
а в знаменателе — базисное (q₀),
т.е. индексируемый показатель изменяется,
а взвешивание производится в одних и
тех же ценах базисного период (p₀):

В
числителе этого индекса — условная
величина товарооборота отчетного
периода в ценах базисного периода, в
знаменателе — реальная величина
товарооборота базисного периода.
Разность между числителем и знаменателем
индекса покажет абсолютное изменение
товарооборота за счет изменения
физического объема товарооборота:

Рассчитаем агрегатный
индекс физического объема товарооборота по
данным нашего примера:

или 98,75% и млн.руб.,
то есть количество проданных магазином
товаров в среднем стало меньше на 1,25%
(98,75 — 100%), что привело к уменьшению
товарооборота на 20 млн.руб.

Агрегатные
индексы качественных показателей
строятся при весах — объемных показателях
отчетного периода. Так, агрегатный
индекс цен по формуле немецкого экономиста
Э.Пааше:

В
числителе индекса — товарооборот
отчетного периода, в знаменателе —
товарооборот отчетного периода в ценах
базисного периода, а разность между
ними характеризует: с позиции продавца
— абсолютное изменение товарооборота
за счет изменения цен, с позиции покупателя
— экономию (перерасход) населения от
изменения цен на товары: .

Рассчитаем
агрегатный индекс цен по данным нашего
примера:

или 103.7% и млн.руб,
то есть в среднем цены на товары возрасли
на 3,7%, что привело к росту товарооборота
на 58 млн.руб.

В
качестве весов в индексах качественных
показателей могут быть использованы
не только абсолютные объемные показатели,
но и показатели их структуры, то есть
доли.

В
статистической практике используется
также индекс цен, построенный с базисными
весами по формуле Э.Ласпейреса:

Агрегатный
индекс товарооборота исчисляется по
формуле:

или 102.4%.
Разность между числителем и знаменателем
этого индекса характеризует абсолютное
изменение товарооборота за счет двух
фактров: изменения количества проданных
товаров и цен на них: млн.руб,
то есть товарообот в отчетном периоде
по сравнению с базисным увеличился на
38 млн.руб. или на 2,4%.

Агрегатные
индексы объемных и качественных
показателей, построенные с различными
весами, взаимосвязаны между собой так
же, как индивидуальные индексы:
произведение агрегатного индекса
физического объема товарообора на
агрегатный индекс цен, дает агрегатный
индекс товарооборота:

Мы
получили систему взаимосвязанных
агрегатных индексов, каждый из которых
позволяет определить изменение
индексируемого показателя в относительном
выражении (%). Кроме того, по этим индексам
можно определить изменение обобщающего
показателя — товарооборота за счет
отдельных факторов в абсолютном выражении
как разность между числителем и
знаменателем соответствующего индекса.
Абсолютные показатели изменения
товарооборота за счет отдельных факторов
взаимосвязаны следующим образом.

Проверим
взаимосвязь показателей, исчисленных
по данным нашего примера:

1.
аграгатных индексов: 1,024 = 0,975*1,037

2.
абсолютных изменений: +38 млн.руб = — 20 +
58 млн.руб.

Аналогичным
образом строятся системы агрегатных
индексов других экономических
показателей.

32.Индексы структурных сдвигов и их
определение.

При
изучении динамики качественных
показателей приходится определять
изменение средней величины индексируемого
показателя, которое обусловлено
взаимодействием двух факторов –
изменением значения индексируемого
показателя у отдельных групп единиц и
изменением структуры явления.
Под изменением
структуры явления понимается
изменение доли отдельных групп единиц
совокупности в общей их численности.
Так, средняя заработная плата на
предприятии может вырасти в результате
роста оплаты труда работников или
увеличения доли высокооплачиваемых
сотрудников. Снижение трудоемкости
производства единицы продукции по
совокупности предприятий отрасли может
быть обусловлено повышением
производительности труда на предприятиях
или концентрацией производства продукции
на заводах с низкой трудоемкостью. Так
как на изменение среднего значения
показателя оказывают воздействие два
фактора, возникает задача определить
степень влияния каждого из факторов на
общую динамику средней.

Эта
задача решается с помощью индексного
метода, т.е. путем построения системы
взаимосвязанных индексов, в которую
включаются три индекса: переменного
состава, постоянного состава и структурных
сдвигов.

Индексом
переменного состава называется
индекс, выражающий соотношение средних
уровней изучаемого явления, относящихся
к разным периодам времени. Например,
индекс переменного состава себестоимости
продукции одного и того же вида
рассчитывается по формуле:

где I_пс – индекс
переменного состава.

Индекс
переменного состава отражает изменение
не только индексируемой величины (в
данном случае себестоимости), но и
структуры совокупности (весов).

Индекс
постоянного (фиксированного) состава
– это
индекс, исчисленный с весами,
зафиксированными на уровне одного
какого-либо периода, и показывающий
изменение только индексируемой величины.
Индекс фиксированного состава определяется
как агрегатный индекс. Так, индекс
фиксированного состава себестоимости
продукции рассчитывают по формуле:

где
/_фс –
индекс фиксированного состава.

Под индексом
структурных сдвигов понимают
индекс, характеризующий влияние изменения
структуры изучаемого явления на динамику
среднего уровня этого явления. Индекс
определяется по формуле (при изучении
изменения среднего уровня себестоимости):

где
/_сс –
индекс структурных сдвигов.

Система
взаимосвязанных индексов при анализе
динамики средней себестоимости имеет
следующий вид:

Рассмотрим
применение такой системы.

Пример. Пусть
имеются данные об объеме строительства
коттеджей и себестоимости 1 кв. м жилья
двух строительных фирм в мае-июне 2002 г.
(табл. 12.4).

В
июне по сравнению с маем 2002 г. себестоимость
1 кв. м коттеджного жилья в двух строительных
фирмах возросла: в ООО «Скат» она
увеличилась на 5,26%, а в ООО «Стройинвест»
– на 16,67%. При этом изменилась структура
рынка участников строительства:
уменьшилась доля первой строительной
фирмы (ООО «Скат») в общем объеме
строительства коттеджей (с 35,1 до 28,5%) и
возросла доля второй фирмы (ООО
«Стройинвест») – с 64,9 до 71,5%).

Таблица
12.4

Построено
коттеджного жилья и себестоимость 1 кв.
м по двум строительным фирмам в
мае-июне 2002
г. (Цифры
условные.)

Строительная фирма	Построено коттеджного жилья	Себестоимость единицы продукции, долл. США	Индивидуальные индексы себестоимости, % i_z = z₁ : z₀	Общие затраты на производство жилья, тыс. долл. США
Всего, кв. м	% к итогу	базисный период (май) z₀	текущий период (июнь) z₁		Базисный период (май) z₀q₀	текущий период (июнь) z₁q₁	z₀q₀
базисный период (май) q₀	текущий период (июнь)q₁	базисный период (май)	текущий период (июнь)
А	1	2	3	4	5	6	7 = 6 : 5	8 = 5 ∙ 1	9 = 6 ∙ 2	10 = 5 ∙ 2
ООО «Скат»	1620	1780	35,1	28,5	285	300	105,26	461,7	534,0	507,3
ООО «Строй-инвест»	3000	4470	64,9	71,5	300	350	116,67	900,0	1564,5	1341.0
Итого	4620	6250	100,0	100,0	–	–	–	1361,7	2098,5	1848,3

Рассчитаем
индекс переменного состава. Для этого
сначала определим среднюю себестоимость
единицы продукции в текущем и базисном
периодах:

Тогда

I_п.с =
335,8 : 294,7 = 1,1395, или 113,95%.

Следовательно,
средняя себестоимость по двум фирмам
возросла в текущем периоде по сравнению
с базисным на 13,95%, и в каждом из них в
отдельности она возрастала. Это результат
того, что исчисленный индекс учитывает
влияние еще и структурного фактора.

Определим
индекс себестоимости фиксированного
состава:

Таким
образом, себестоимость в текущем периоде
по сравнению с базисным возросла в
среднем на 13,5%.

Вычислим
влияние изменения структуры на динамику
средней себестоимости:

Изменение
доли строительных фирм в общем объеме
построенного коттеджного жилья привело
к увеличению себестоимости на 0,34%.

Аналогично
строятся системы индексов для других
показателей. Так, для показателя
производительности труда можно построить
систему индексов, в которой:

33.Отраслевые классификаторы и их виды.

Классифика́тор,
или (отлат.classis—разрядиfacere—делать) —
систематизированный перечень наименованных
объектов, каждому из которых в соответствие
дан уникальныйкод.
Классификация объектов производится
согласно правилам распределения
заданногомножестваобъектов
на подмножества (классификационные
группировки) в соответствии с
установленными признаками их различия
или сходства. Применяется вАвтоматизированных
системах управленияи обработке
информации. Классификатор является
стандартным кодовым языком документов,
финансовых отчётов и автоматизированных
систем.

Классификаторы
разрабатываются как на уровне отдельных
предприятий (организаций), так и на
уровне государств.
Существуют следующие уровни классификаторов:

международные —
стандартные классификаторы, используемые
по всему миру;
межгосударственные —
классификаторы, используемые в
рамках экономических
союзови других межгосударственных
объединений: например, классификаторы
используемые вЕС,СНГи т. д.
национальные,
или межотраслевые — классификаторы,
используемые в пределах государства.
Не должны противоречить международным
классификаторам;
отраслевые —
классификаторы, используемые в рамках
одной отрасли;
региональные
– классификаторы действующие на
территории региона. Например:
общемосковские классификаторы,
общегородские классификаторы
Санкт-Петербурга и т.п.
системные —
классификаторы, принятые отдельным
предприятием (организацией) для
применения в рамках своей автоматизированной
системы. Они содержат информацию,
необходимую для решения задач в
конкретной АС и отсутствующую в
национальном или отраслевом классификаторе.

34.Функциональные и стохастические
связи, их модели.

Связь
называется функциональной (или жестко
детерминированной), если любому значению
факторного признака соответствует
вполне определенное неслучайное значение
признака результативного. Система
называется жестко детерминированной,
если при данных начальных условиях она
переходит в единственно возможное
(совершенно определенное) состояние.
Анализ жестко детерминированных систем
часто называют факторным анализом.
Подробно он будет рассмотрен в разделе
2.6.2.

Связь
называется стохастической (вероятностной),
если любому значению факторного признака
соответствует множество значений
признака результатного (т.е. определенное
статистическое распределение). При этом
для каждого конкретного значения
признака х значения у образуют
распределение, называемое условным.
Поэтому изменение величины х приводит
к изменению величины у лишь в среднем.
Система называется вероятностной, если
при одних и тех же начальных условиях
она может переходить в различные
состояния, имеющие разные вероятности.
Анализ стохастических связей в
вероятностных системах будет рассмотрен
в разделе 2.8.

Типы
экономических моделей

Многие
аналитические методы используются в
совокупности с различными типами
моделей, которые позволяют структурировать
и идентифицировать связи между основными
показателями.

Можно
выделить три основных типа моделей,
используемых в экономическом анализе:
дескриптивные, предикативные и
нормативные.

Дескриптивные
модели. Эти модели, известные также как
модели описательного характера, являются
основными для оценки финансового
состояния предприятия. К ним относятся:
построение системы отчетных балансов,
представление финансовой отчетности
в различных аналитических разрезах,
вертикальный и горизонтальный анализ
отчетности, система аналитических
коэффициентов, аналитические записки
к отчетности. Все эти модели основаны
на использовании информации бухгалтерской
отчетности.

В основе
вертикального анализа лежит иное
представление бухгалтерской отчетности
– в виде относительных величин,
характеризующих структуру обобщающих
итоговых показателей. Обязательным
элементом анализа служат динамические
ряды этих величин, что позволяет
отслеживать и прогнозировать структурные
сдвиги в составе хозяйственных средств
и источников их покрытия.

Горизонтальный
анализ позволяет выявить тенденции
изменения отдельных статей или их групп,
входящих в состав бухгалтерской
отчетности. В основе этого анализа лежит
исчисление базисных темпов роста
балансовых статей или статей отчета о
прибылях и убытках.

Система
аналитических коэффициентов – ведущий
элемент анализа финансового состояния,
применяемый различными группами
пользователей: менеджерами, аналитиками,
акционерами, инвесторами, кредиторами
и др. Известны десятки этих показателей,
поэтому для удобства они подразделяются
на несколько групп. Чаще всего выделяют
пять групп показателей по следующим
направлениям финансового анализа.

1. Анализ
ликвидности. Показатели этой группы
позволяют описать и проанализировать
способность предприятия отвечать по
своим текущим обязательствам. В основу
алгоритма расчета этих показателей
заложена идея сопоставления текущих
активов (оборотных средств) с краткосрочной
кредиторской задолженностью. В результате
расчета устанавливается, в достаточной
ли степени предприятие обеспечено
оборотными средствами, необходимыми
для расчетов с кредиторами по текущим
операциям. Поскольку различные виды
оборотных средств обладают различной
степенью ликвидности (конвертации в
абсолютно ликвидные средства – денежные
средства), рассчитывают несколько
коэффициентов ликвидности (см. раздел
4.5).

2. Анализ
финансовой устойчивости. С помощью этих
показателей оценивается состав источников
финансирования и динамика соотношения
между ними. Анализ основывается на том,
что источники средств различаются
уровнем себестоимости, степенью
доступности, уровнем надежности, степенью
риска и др. (см. раздел 4.6).

3. Анализ
текущей деятельности. С позиции
кругооборота средств текущая деятельность
любого предприятия представляет собой
процесс непрерывной трансформации
одних видов оборотных активов в другие:

где ДС –
денежные средства;

СС – сырье
на складе;

НП –
незавершенное производство;

ГП – готовая
продукция;

СР – средства
в расчетах (дебиторы).

Эффективность
текущей финансово-хозяйственной
деятельности может быть оценена
протяженностью операционного цикла,
зависящей от оборачиваемости средств
в различных видах активов. При прочих
равных условиях ускорение оборачиваемости
свидетельствует о повышении эффективности.
Поэтому основными показателями этой
группы являются показатели эффективности
использования материальных, трудовых
и финансовых ресурсов: выработка,
фондоотдача, коэффициенты оборачиваемости
средств в запасах и расчетах (см. раздел
4.7).

4. Анализ
рентабельности. Показатели этой группы
предназначены для оценки общей
эффективности вложения средств в данное
предприятие. В отличие от показателей
второй группы здесь абстрагируются от
конкретных видов активов, рентабельность
капитала анализируют в целом. Основными
показателями поэтому являются
рентабельность авансированного капитала
и рентабельность собственного капитала
(см. раздел 4.8).

5. Анализ
положения и деятельности на рынке
капитала, В рамках этого анализа
выполняются пространственно-временные
сопоставления показателей, характеризующих
положение предприятия на рынке ценных
бумаг: дивидендный выход, доход на акцию,
ценность акции и др. Этот фрагмент
анализа выполняется главным образом в
компаниях, зарегистрированных на биржах
ценных бумаг и котирующих там свои
акции. Любое предприятие, имеющее
временно свободные денежные средства
и желающее вложить их в ценные бумаги,
также ориентируется на показатели
данной группы (см. раздел 4.9).

Предикативные
модели – это модели предсказательного,
прогностического характера, которые
используются для прогнозирования
доходов предприятия и его будущего
финансового состояния. Наиболее
распространенными из них являются
расчет точки критического объема продаж
(см. раздел 3.5), построение прогностических
финансовых отчетов (см. раздел 2.5.6),
модели динамического анализа (жестко
детерминированные факторные модели и
регрессионные модели – см. разделы 2.6.2
и 2.8.2), модели ситуационного анализа
(см. раздел 2.5.8). В указанных разделах
нашего пособия будут рассмотрены
некоторые теоретические и практические
аспекты применения подобных моделей.

Нормативные
модели. Модели этого типа позволяют
сравнить фактические результаты
деятельности предприятий с ожидаемыми,
рассчитанными по бюджету. Эти модели
используются в основном во внутреннем
финансовом анализе, а также в управленческом
учете, в частности в управлении затратами.
Их сущность сводится к установлению
нормативов по каждой статье расходов
по технологическим процессам, видам
изделий, центрам ответственности и т.п.
и к анализу отклонений фактических
данных от этих нормативов (см. раздел
3.4.2). Анализ в значительной степени
базируется на применении системы жестко
детерминированных факторных моделей.

35.Двухмерная (однофакторная) линейная
модель линейной корреляционной связи.

корреляционный
анализ

Задачей
описательной статистики является не
только систематизация эмпирических
данных в виде распределения частот и
расчеты типовых показателей МЦТ и
вариаций признаков ММ, но и выявление
связи между переменными, оцинюва Ання
его направления и интенсивности Сравнивая
различные виды связей, можно выделить
три типа зависимостей между переменными
X и Y:

функциональная зависимость
определяет значение переменной Y от X
однозначно;

корреляционная зависимость
определяет среднее значение переменной
Y от X;

стохастическая зависимость
определяет распределение переменной
Y от X

Итак,
наиболее общей считается стохастическая
зависимость Корреляционная зависимость
является зависимостью стохастической,
функциональная – рассматривается как
частный случай корреляционной зависимости

Сущность
корреляции

Корреляция (от
лат correlatio – соотношение) – это статистическая
зависимость между случайными величинами,
носит вероятностный характер

Корреляционные
связи можно изучать на качественном
уровне из диаграмм рассеяния эмпирических
значений переменных X и Y (рис 251) и
соответствующим образом их интерпретировать
Так, например, если повышение уровня
одной изм минной сопровождается
повышением уровня другой, то речь идет
оро положительнуюкорреляцию
или прямая связь (рис 251, б) Если же рост
одной переменной сопровождается
снижением значений другой, то имеем
дело с отрицательной корреляцией или
обратной связью (рис 251 г, г) Ноль ьовою
называется корреляция при отсутствии
связи переменных (рис 251 в) Однако нулевая
общая корреляция может свидетельствовать
лишь об отсутствиисутність линейной зависимости,
а не вообще об отсутствии
любогостатистического связи

Рис
251 Диаграммы рассеяния эмпирических
значений переменныхX и
В:

а)
строгая положительная корреляция б)
сильная положительная корреляция в)
нулевая корреляция г) умеренная
отрицательная корреляция г) строгая
отрицательная корреляция д) нелинейная
корреляция

В
психолого-педагогических исследованиях
основном наблюдаются связи нелинейные (см.
рис 251 д) Например, рост мотивации сначала
повышает эффективность научения, а
затем наступает снижение производительности
(эффект “перемотивации” – закон
Иеркса-Додсона) Количественная мера
корреляций ийного связи оценивается
по значениям коэффициентами корреляции
в пределах от -1 до 1 Отрицательные
значения коэффициентов указывают на
обратную связь, положительные – на прямую
Нулевое значение может свидетельствовать
пр в отсутствие связи Интенсивность
связи (слабая связь – умеренный –
существенный – сильный) оценивается по
абсолютным значениям коэффициентов
корреляцийіцієнтів кореляції.

Методы
расчета степени корреляционных связей
тесно связаны с применяемыми измерительными
шкалами (табл. 24)

Таблица
24

Коэффициенты
корреляции зависимости от типов
измерительных шкал

Шкалы признаки В	Шкалы признаки X
Интервальная (отношений)	Ранговая	Номинальная
Интервальная (отношений)	Коэффициент Пирсона г_х в; Дихотомическое коэффициент корреляции р; Тетрахоричний коэффициент корреляции т_ш
Ранговая	Коэффициент Спирмена г “(при условии, если длях шкалу интервалов или отношений превратить в ранговую шкалу)	Коэффициенты корреляции Спирмена т Кендалла; Коэффициент конкордации В
Номинальная	Точечно-бисериальный коэффициент корреляции мая ^_; бисериальный коэффициент корреляции гьии	рангов-бисериальный коэффициент корреляции	Коэффициент ассоциации Ф; Коэффициент контингенции Юла 6; Коэффициенты сопряженности Чупрова К и Пирсона С

Изучение
связи между признаками, которые принимают
случайные значения, начинается с оценки
его линейности

Линейная
корреляция

Линейный
корреляционная связь для эмпирических
данных, измеренных по шкале интервалов
или отношений, оценивается с помощью
коэффициента корреляции Пирсонаг_ху

где Хи и
в и – значения переменных X и Y; х и у –
средние X и Y; п – объем выборки

⁸ Указанные
методы расчета с использованием
компьютерной техники можно найти в
учебнике [56]

Формула
(222) может быть преобразована, если
заменить значение переменныхХ и
и в
и нормированными
значениями 2_х и
г_у,
и выглядеть так:

Пример
27 Оценить
связь между переменнымиX иУ по
эмпирическим данным таблицы рис 252 двумя
способами с использованием формул (222)
и (223) Способ 1

Последовательность
решения:

o
оценить характер линейности связи между
признакамиX и
В с помощью диаграммы рассеяния (рис
252);

Рис
252 Диаграмма рассеяния признаков

o
убедиться, что корреляция линейная и
продолжить расчеты коэффициента
корреляции Пирсона г_ху (рис
253 и 254);

o
в ячейках В16 и С16 рассчитать средние
значения х и у

х =
и х_і =
112,00; У =¹ ул
= 18,17;

o
в ячейках и В15 рассчитать суммы квадратов
разностей:

X (х,
– X)² =
386,00; у,
– у)² =
311,67;

Рис
253 Результаты расчета коэффициента
корреляцииг_ху

o
в ячейке Н18 рассчитать сумму произведений
разниц:

X
(х_і – X)
o (у_і –
у) = 242,00;

o
в ячейке В17 рассчитать коэффициент
корреляции г_ху по
формуле:

гху =
–^242,00 –
0,70 л/386, 00 o 311,67

Рис
254 Расчетные формулы Значение г_ху ~
0,70 свидетельствует о существенном
прямая связь между признаками

Способ
2

Последовательность
решения:

o
Результаты расчета г_ху за
нормируемыми данным показано на рис
255, расчетные формулы рис 256

Рис
255 Результаты расчета г_ху за
нормируемыми данным

o
в ячейках В16 и С16 рассчитать средние
значения х и у;

o
в ячейках В17 и С17 рассчитать стандартные
отклонения у_х и
у_у;

Рис
256 Формулы расчета г_ху за
нормируемыми данным o в столбцах Б и Е
рассчитать нормированные данные 2_х и
2_у (обратите
внимание

что
среднее нормированных данных равен 0,
а стандартное отклонение – 1,00);

o
в ячейке В18 рассчитать коэффициент
корреляцииr_xy по
формуле (223);

Выводы Одно
и то же значение r_xy ~
0,70 рассчитан двумя способами Методы
расчета за нормируемыми данным выглядят
более лаконично Значение парного коэффициента
корреляции Пирсона r_xy можно
получить с помощью специальной функции
MS Excel = Пирсон ()

36.Проверка адекватности однофакторной
регрессионной модели.

Для
практического использования моделей
регрессии большое значение имеет их
адекватность, т. е. соответствие
фактическим статистическим данным.

Адекватность
регрессионной модели при малой выборе
можно оценить F критерием Фишера:

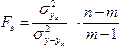
где
m – число параметров модели;

n
– число единиц наблюдения;

–
факторная дисперсия, которая характеризует
вариацию результативного признака под
влиянием признака фактора, включенного
в модель;

–
остаточная дисперсия, характеризующая
вариацию результативного признака под
влиянием прочих, неучтенных факторов;

–
общая дисперсия, показывающая вариацию
результативного признака под влиянием
всех факторов, вызывающих эту вариацию:

Эмпирическое
значение критерия сравнивается
с критическим (табличным)с
уровнем значимости 0,01 или 0,05 и числом
степеней свободы (m-1), (n-m).

Если >,
то уравнение регрессии признается
значимым.

Проведем
оценку адекватности регрессионной
модели ,
выражающей зависимость среднего объема
привлеченных средств банков от собственных
средств, с помощью F критерия Фишера:

;

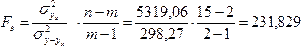
Табличное
значение F_т с
уровнем значимости 0,05 и числом степеней
свободы (2-1), (15-2) равно 4,68. (См. Приложение
7). Так как >,
то уравнение регрессии можно признать
адекватным.

При
численности объектов анализа до 30 единиц
(при малой выборе) возникает необходимость
испытания параметров уравнения на их
типичность (значимость). При этом
осуществляется проверка, насколько
вычисленные параметры характерны для
отображаемого комплекса условий, не
являются ли полученные значения
параметров результатами действия
случайных причин.

Для
проверки значимости параметров уравнения
регрессии используется t – критерий
Стьюдента. Вычисляются фактические
значения t критерия:

Для
параметра :

;

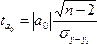
для
параметра :

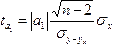
где –
среднее квадратическое отклонение
результативного признака от выравненных
значений;

–
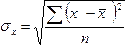
среднее квадратическое отклонение
факторного признака хот общей средней .

Полученные
фактические значения исравниваются
с критическим,
который получают по таблице Стьюдента
с учетом принятого уровня значимостиа (а=0,01
или а=0,05)
и числа степеней свободы k=n-2.

Параметр
признается значимым (типичным), если
эмпирическое значение больше
критического табличного:

> <.

Оценим
значимость параметров уравнения
регрессии с
помощью t – критерия Стьюдента:

;

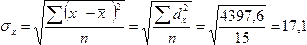
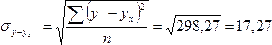
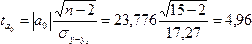
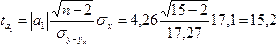
Табличное
значение t – критерия с уровнем значимости
0,05 и числом степеней свободы k=n-2=15-2=13
равно 2,161 (Приложение 6).

Сравним
фактические значения ис
критическим (=2,161),
получаем:

=
4,96 > =
2,161<=15,2.

Следовательно,
вычисленные по уравнению регрессии
параметры ипризнаются
значимыми.

Измерение
тесноты корреляционной связи.

Проверка
адекватности регрессионной модели
может быть дополнена корреляционным
анализом. Для этого необходимо определить
тесноту корреляционной связи между
переменными х и у.

Теснота
связи между двумя признаками может
измеряться линейным коэффициентов
корреляции (r), корреляционным отношением
( )
и индексом корреляции (R).

Линейный
коэффициент корреляции определяется
по формулам:

или .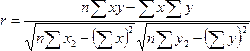

Линейный
коэффициент корреляции характеризует
степень тесноты только при прямолинейной
корреляционной зависимости. С коэффициентом
регрессии связан
таким соотношением:.

Величина принимает
значения в интервале:.
Отрицательные значения указывают на
обратную связь, положительные – на
прямую. При=0
линейная связь отсутствует. Чем ближепо
абсолютной величине к единице, тем
теснее связь между признаками. И, наконец,
при,
связь функциональная.

Квадрат
линейного коэффициента корреляции называется
линейным коэффициентом детерминации,
показывает удельный вес влияния данного
фактора в общей сумме всех факторов,
определяющих уровень результативного
признака.

Линейный
коэффициент корреляции предложили в
конце XIX века английские ученые Ф. Гальтон
и К. Пирсон.

При
наличии криволинейной корреляционной
связи недооценивает
тесноту связи и в некоторых случаях
может дать неверное представление о
степени тесноты связи.

Теоретическое
корреляционное отношение ( )
и индекс корреляции ()
служат для измерения тесноты связи как
при прямолинейной, так и при криволинейной
корреляционной связи.

Теоретическое
корреляционное отношение определяется
по формулам:

или .

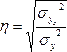
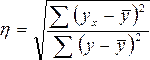
Корреляционное
отношение в квадрате показывает,
какую часть всей вариации результативного
признака составляет вариация, вызванная
факторным признаком.

Для
упрощения расчетов степени тесноты
связи часто применяется индекс корреляции.
Индекс корреляции определяется по
следующим формулам:

или .

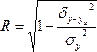
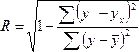
Абсолютные
размеры линейного коэффициента
корреляции, корреляционного отношения,
индекса корреляции колеблются от 0 до
1. Направление связи (знак перед и)
определяется непосредственно по исходным
данным.

Для
качественной оценки тесноты связи можно
воспользоваться также шкалой Чеддока:

Величина показателя тесноты связи	Характеристика тесноты
0,1- 0,3 0,3 – 0,5 0,5 – 0,7 0,7 – 0,9 0,9 – 0,99	Слабая Умеренная Заметная Высокая Весьма высокая

Показатели ипри
прямолинейной связи совпадают. Поэтому
вычисленные по одним и тем же данным
величиныичасто
используют для того, чтобы судить о том,
насколько для данного случая правильно
предположение о наличии именно
прямолинейной формы корреляционной
связи. Английский статистик Блекман
предложил следующий критерий: если
разностьне
превышает 0,1, предположение о прямолинейной
форме корреляционной связи можно считать
оправданным.

При
выборе вида уравнения можно воспользоваться
еще критерием криволинейности ,
если k> 2,5, то предположение о данном
виде криволинейной связи можно считать
оправданным.

Используем
данные табл. 7.7 и рассчитаем линейный
коэффициент корреляции, теоретическое
корреляционное отношение и индекс
корреляции:

;

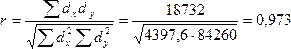
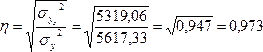
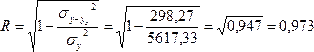
Все
показатели тесноты корреляционной
связи показывают весьма высокую связь
между объемами привлеченных и собственных
средств.

Коэффициент
детерминации 0,947 означает, что вариация
привлеченных средств банков на 94,7%
объясняется вариацией собственных
средств и на 5,7% – прочими факторами.

Так
как ,
то можно седлать заключение, что гипотеза
о линейной форме связи подтверждена.

37.Трехмерная (двухфакторная) линейная
модель линейной корреляционной связи.

38.Парные и частные коэффициенты
корреляции, совокупный коэффициент
множественной корреляции и детерминации.

Если
факторные признаки различны по своей
сущности и/или имеют различные единицы
измерения, то коэффициенты
регрессии при
разных факторах являются несопоставимыми.
Поэтому уравнение регрессии дополняют
соизмеримыми показателями тесноты
связи фактора с результатом,
позволяющими ранжировать факторы. К
ним относят: частные коэффициенты
эластичности, β-коэффициенты,
частные коэффициенты корреляции.

Парные
коэффициенты корреляции. Для
измерения тесноты связи между двумя из
рассматриваемых переменных (без учета
их взаимодействия с другими переменными)
применяются парные коэффициенты
корреляции. Методика расчета таких
коэффициентов и их интерпретации
аналогичны линейному коэффициенту
корреляции в случае однофакторной
связи.

где –
среднее квадратическое отклонение
факторного признака;

–
среднее квадратическое отклонение
результативного признака.

Коэффициент
частной корреляции измеряет
тесноту линейной связи между отдельным
фактором и результатом при устранении
воздействия прочих факторов модели.

Для
качественной оценки тесноты связи можно
использовать следующую классификацию:

0.1-
0.3- слабая связь

0.3-0.5
– умеренная связь

0.5-0.7-
заметная связь

0.7-0.9-
тесная связь

0.9-0.99-
весьма тесная

Для
расчета частных коэффициентов корреляции
могут быть использованы парные
коэффициенты корреляции.

Для
случая зависимости Y от
двух факторов можно вычислить 2
коэффициента частной корреляции:

(2-ой
фактор фиксирован);

(1-ый
фактор фиксирован).

Это
коэффициенты частной корреляции 1-ого
порядка (порядок определяется числом
факторов, влияние которых на результат
устраняется).

Частные
коэффициенты корреляции, рассчитанные
по таким формулам изменяются от -1 до
+1. Они используются не только для
ранжирования факторов модели по степени
влияния на результат, но и также для
отсева факторов. При малых значениях нет
смысла вводить в уравнение m-ый
фактор, т.к. качество уравнения регрессии
при его введении возрастет незначительно
(т.е. теоретический коэффициент
детерминации увеличится незначительно).

Совокупный
коэффициент множественной
корреляции или индекс
множественной корреляции определяет
тесноту совместного влияния факторов
на результат:

где остаточная
дисперсия;

или

.
Он принимает значения от 0 до 1 (в отличие
от парного коэффициента корреляции,
который может принимать отрицательные
значения, Rиспользуется
без учета направления связи). Чем
плотнее фактические значения располагаются
относительно линии регрессии, тем меньше
остаточная дисперсия и, следовательно,
больше величина. Таким
образом, при значенииR близком
к 1, уравнение регрессии лучше описывает
фактические данные и факторы сильнее
влияют на результат; при значении R близком
к 0 уравнение регрессии плохо описывает
фактические данные и факторы оказывают
слабое воздействие на результат.

При
трех переменных для двух факторного
уравнения регрессии данная формула
совокупного коэффициента множественной
корреляции легко приводится к следующему
виду:

Чем
R ближе к единице, тем совокупное влияние
изучаемых показателей x1 и x2 на
результативный фактор y больше
(корреляционная связь более интенсивная).

Множественный
(совокупный) коэффициент детерминации определим
как квадрат множественного коэффициента
корреляции. Показывает, какая доля
вариации изучаемого показателя
объясняется влиянием факторов, включенных
в уравнение множественной регрессии.
Его значение – в пределах от нуля до
единицы. Чем ближе множественный
коэффициент детерминации к единице,
тем вариация изучаемого показателя в
большей мере характеризуется влиянием
отобранных факторов.

Связь: Частный
коэффициент корреляции в отличие от
коэффициента (полного) парной корреляции
между явлениями показывает тесноту
связи после устранения изменений,
обусловленных влиянием третьего явления
на оба коррелируемых признака (из
значений корреляционных признаков
вычитаются линейные оценки в связи с
третьим признаком).

Также
из приведенных ранее формул частных
коэффициентов корреляции видна связь
этих показателей с совокупным коэффициентом
корреляции. Зная частные коэффициенты
корреляции (последовательно первого,
второго и более высокого порядка), можно
определить совокупный коэффициент
корреляции по формуле:

При
полной зависимости результативного
признака от исследуемых факторов
коэффициент совокупного их влияния
равен единице. Из единицы вычитается
доля остаточной дисперсии результативного
признака , обусловленная
последовательно включенными в анализ
факторами. В результате подкоренное
выражение характеризует совокупное
действие всех исследуемых факторов.

39.Непараметрические методы установления
связи между качественными признаками.

Методы
корреляционного и регрессионного
анализа не универсальны: их можно
применять, если все изучаемые признаки
являются количественными. Между тем в
статистике приходиться сталкиваться
с задачами измерения связи между
качественными признаками. Такие методы
измерения связи называются непараметрические.

Для
исследования степени тесноты связи
между качественными признаками, каждый
из которых представлен в виде альтернативных
признаков, может быть использован
коэффициент ассоциации Д. Юла или
коэффициент контингенции К. Пирсона.
Расчетная таблица в этом случае состоит
из четырех ячеек (таблица «четырех
полей») и имеет следующий вид:

Признаки	А (да)	(нет)	Итого
B (да)	a	b	а + b
(нет)	c	d	c + d
Итого	a + c	b + d	n

Коэффициент
ассоциации вычисляется по формуле:

Коэффициент
контингенции:

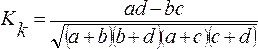
Если
по каждому из взаимосвязанных признаков
выделяется число групп более двух то
для подобного таблиц теснота связи
между качественными признаками может
быть измерена с помощью коэффициентов
взаимной сопряженности К. Пирсона и А.
А. Чупрова.

Коэффициент
взаимной сопряженности Пирсона
вычисляется по формуле:

,
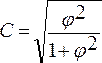
где j² –
показатель средней квадратической
сопряженности, который вычисляется по
формуле:

,
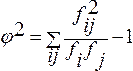
где ,.

Коэффициент
Чупрова:

,
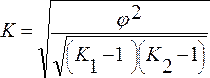
где К₁,
К₂ –
число групп по каждому из признаков.

Для
определения тесноты связи как между
количественными, так и между качественными
признаками, при условии, что значение
этих признаков могут быть проранжированы
по степени убывания или возрастания,
используется коэффициент корреляции
рангов Спирмена:

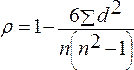
где d –
разность рангов признаков x и y ;

n –
число наблюдаемых единиц.

В
случае отсутствия связи r = 0. При прямой
связи коэффициент r – положительная
правильная дробь, при обратной –
отрицательная.

Если
объём исходной информации небольшой,
то необходимо выполнить проверку
существенности рангового коэффициента,
т. е. сверить с таблицей предельных
значений. Расчетное значение r должно
быть больше предельного.

Для
определения тесноты связи между
произвольным числом ранжированных
признаков применяется коэффициент
конкордации:

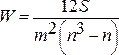
где m –
количество факторов;

n –
число наблюдений;

S –
отклонение суммы квадратов рангов от
средней квадратов рангов.

Рассмотрим
пример:

В
результате обследования студентов
факультета получены следующие данные:

Успеваемость	Количество студентов	Всего
Посещающих спортивные секции	Не посещающих спортивные секции
Удовлетворительная
Неудовлетворительная
Итого

Определите
коэффициент ассоциации и контингенции
между успеваемостью и посещаемостью
спортивных секций.

Коэффициент
ассоциации:

Коэффициент
контингенции:

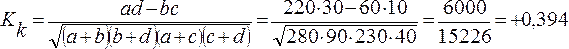
Полученные
коэффициенты подтверждают наличие
существенной связи между исследуемыми
признаками. Однако коэффициент
контингенции всегда меньше коэффициента
ассоциации и дает более корректную
оценку тесноту связи.

Источник

«Высшая ловкость состоит в том, чтобы всему знать истинную цену», — французский писатель XVII века Франсуа де Ларошфуко знал ценность цены — простите за тавтологию.

Всем нам не раз приходилось и оценивать, и сравнивать цены различных товаров или продуктов, как говорится, «на глазок».

Но такой подход не всегда дает объективный результат. Кроме того, как быть в ситуации, когда нужно сравнить цены большого количества совершенно разных вещей да еще за разные периоды времени?

Поэтому давайте разбираться с индексами цен, коих немало предусмотрено наукой эконометрикой специально для конкретных целей оценивания и анализа хозяйственной деятельности.

Понятие об индексах. Индексный метод

Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве. Наиболее распространена сравнительная характеристика во времени. В этом случае индексы выступают как относительные величины динамики.

Индекс цен общий: формула

Индексный метод является также важнейшим аналитическим средством выявления связей между явлениями. При этом применяются уже не отдельные индексы, а их системы. В статистической практике индексы применяются при анализе развития всех отраслей экономики, на всех этапах экономической работы. В условиях рыночной экономики особенно возросла роль индексов цен, доходов населения, фондового рынка и территориальных индексов.

Индексы являются разновидностью относительных величин. Индексы применяются в анализе хозяйственной деятельности с целью характеристики экономических явлений, состоящих из элементов, которые не следует суммировать.

Технически любой индекс представляет собой показатель, определяемый как соотношение двух каких-либо величин. Последние являются, по существу, определенными состояниями известного признака. С помощью индексов осуществляются сравнения фактических показателей с базисными, то есть, как правило, с плановыми и с показателями предшествующих периодов.

Индивидуальный индекс цен

В индексе выделяют 3 элемента:

индексируемый показатель — это показатель, соотношение уровней которого характеризует индекс;
сравниваемый уровень — это тот уровень, который сравнивают с другим;
базисный уровень — это тот уровень, с которым производится сравнение.

Для расчета индекса необходимо найти отношение сравниваемого уровня к базисному и выразить его в виде коэффициента, если база сравнения приравнивается к единице, или в процентах, если база сравнения принимается за 100%. Обычно расчеты индексов производятся в форме коэффициентов с точностью до третьего знака после запятой, т. е. до 0,001, в форме процентов — до десятых долей процента, т.е. до 0,1%.

Для удобства построения индексов используется специальная символика:

i — символ индексируемого показателя — индекс, характеризующий изменение уровня элемента явления;
I — с подстрочным индексируемым показателем — для группы элементов или всей совокупности в целом;
q — количество проданных товаров или произведенной продукции в натуральном выражении;
p — цена за единицу товара;
0 — базисный период;
1 — отчетный период.

Таблица 1. Пример расчета индивидуальных индексов

Индивидуальные индексы характеризуют изменение отдельного элемента явления. Индивидуальный индекс цен определяется как отношение цены отдельного товара в отчетном периоде к цене его в базисном периоде, то есть по формуле:

Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях:

Рассчитаем индивидуальные индексы цен:

Индекс цен общий: формула расчета

Все рассмотренные нами индексы характеризуют относительное изменение уровней отдельных элементов явления и называются индивидуальными индексами. Однако большинство изучаемых статистикой общественных явлений и процессов состоят из многих элементов, которые могут быть как однородными, так и неоднородными.

Однородные явления можно непосредственно суммировать и исчислять индексы, характеризующие изменение не одного элемента, а группы элементов или всей совокупности в целом. Такие индексы называются общими индексами.

Переход от натуральных показателей к стоимостным позволяет преодолеть несуммарность натурально-вещественных элементов совокупности. Но изменение стоимости товаров обусловлено совместным изменением двух факторов — количества товаров и цен на них, а нам необходимо определить изменение каждого из этих факторов в отдельности.

Для изучения изменения одного фактора необходимо абстрагироваться от изменения второго, взаимосвязанного с ним фактора и построить общий индекс в агрегатной форме.

Агрегатные индексы качественных показателей строятся при весах — объемных показателях отчетного периода. Так, агрегатный индекс цен по формуле немецкого экономиста Э.Пааше:

В числителе индекса — товарооборот отчетного периода, в знаменателе — товарооборот отчетного периода в ценах базисного периода, а разность между ними характеризует: с позиции продавца — абсолютное изменение товарооборота за счет изменения цен, с позиции покупателя — экономию (перерасход) населения от изменения цен на товары:

Рассчитаем агрегатный индекс цен по данным нашего примера:

В качестве весов в индексах качественных показателей могут быть использованы не только абсолютные объемные показатели, но и показатели их структуры, то есть доли.

В статистической практике используется также индекс цен, построенный с базисными весами по формуле Э.Ласпейреса:

Общий индекс цен показывает, во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен. Значение индекса, уменьшенное на 100%, показывает, на сколько процентов изменилась стоимость продукции в результате изменения цен.

Разность числителя и знаменателя показывает, на сколько денежных единиц изменилась стоимость продукции в результате роста (уменьшения) цен.

Источник: "grandars.ru"

Кто и как впервые рассчитал индекс потребительских цен

Как считать инфляцию? Сегодня анализ экономики немыслим без расчета индексов цен. С их помощью мы сегодня определяем, насколько подорожала жизнь в нашей стране, под какой процент нужно положить деньги в банк, чтобы не потерять. Формула расчета индекса цен выкристаллизовывалась постепенно на основе трудов разных экономистов.

И все же основным автором принято считать выходца из семьи гугенотов Этьена Ласпейреса, преподававшего в основных немецких университетах XIX века, в том числе в Риге и Тарту.

Эрнст Луи Этьен Ласпейрес родился 28 ноября 1834 года в саксонском городе Галле в семье профессора юриспруденции. Французское звучание имени будущего экономиста объясняется тем, что это была семья кальвинистов (или гугенотов), предки которых в конце XVII века иммигрировали из Французского королевства в более веротерпимую на тот момент Священную Римскую империю. Сначала они поселились в Берлине, а позднее оказались в Саксонии.

По достижении 19 лет Этьен Ласпейрес отправился изучать юриспруденцию и общественные финансы. К тому времени университет Галле объединился с университетом города Виттенберг. Молодой человек также учился в университетах Тюбингена, Геттингена и Берлина. В 1859 году Ласпейрес получил степень доктора философии в области политических наук и общественных финансов в университете города Гейдельберга.

Всю дальнейшую жизнь Ласпейрес посвятил карьере ученого. Он занимал различные посты в высших учебных заведениях Гейдельберга, Базеля, политехническом институте Риги, университете Дерпта (Тарту). Два последних города к тому времени уже входили в состав Российской империи, но говорили там, а тем более преподавали научные дисциплины на немецком.

Затем он преподавал в Карлсруэ, а в возрасте 40 лет осел в университете Гессена, где возглавлял кафедру политологии вплоть до выхода на пенсию в 1900 году. В процессе своей деятельности Ласпейрес основал семинар по политической научной статистике, активно участвовал в работе Международного статистического института и регулярно принимал участие в его конференциях.

В 1893 году он съездил в Чикаго, где за его командировочные расходы пришлось доплатить дополнительно три тысячи марок. Ласпейрес умер 4 августа 1913 года, не дожив года до начала Первой мировой войны. Похоронен профессор в Гессене, на старинном кладбище Альте Фридхоф, на котором погребены и другие деятели науки, в том числе Вильгельм Конрад Рентген, открывший икс-излучение.

Как считать цены

Как уже сказано выше, Ласпейрес не был первым в его поколении экономистов, посчитавшим индекс цен. Первым, скорее, следует считать Шарля Дюто, описавшего модель ценовых индексов в 1738 году. Почти параллельно с ним индекс цен построил в 1764 году итальянский экономист Карли, — по среднеарифметической формуле, без применения какой-либо системы взвешивания.

Индексы, построенные Дюто и Карли по принципу невзвешенной средней, применялись в теории и на практике того времени, однако порядок осреднения цен вызывал сомнения. В 1850-х годах в Калифорнии и Австралии началась «золотая лихорадка» — открыли новые месторождения золота. В экономике того времени это вызвало обесценение денег и рост цен. Исследованием этой проблемы занялся современник Ласпейреса английский экономист Стэнли Джевонс.

Он предложил считать общий индекс цен по формуле средней геометрической из отношений цен на отдельные товары. Средняя арифметическая и геометрическая довольно долго конкурировали в построении индексов. Недостатком данной модели было то, что все товары считались равнозначимыми.

Тут и оказалась эффективной формула Ласпейреса, который предложил использовать для расчета индекса среднюю арифметическую взвешенную.

При этом в качестве веса он использовал удельный вес выручки от продажи данного первого товара в базисном периоде в общей величине базовой выручки. Такой порядок взвешивания привел к формуле агрегатного индекса цен с базисными весами.

В разработке формулы индекса цен большой вклад принадлежит другому немецкому экономисту — Герману Пааше, который предложил усреднять относительные изменения цен на отдельные товары по формуле средней гармонической взвешенной.

И хотя аналогичный индекс был построен английским экономистом Томасом Маном на две с половиной сотни лет раньше, в экономической литературе его принято называть индексом Пааше. Формулы Ласпейреса и Пааше учитывают изменения цен при предположении, что количество товаров неизменно.

Отличие формул двух экономистов в том, что Ласпейрес берет количество товара в базисном периоде, а Пааше — в текущем. Недостаток формулы Пааше в том, что она не учитывает упавший спрос на товары, поэтому при исчислении индекса цен по Пааше необходимо делать поправки для формировании правильной системы весов.

Но этот недостаток не брался в расчет советской экономической наукой, которая не обращала внимания на такой показатель как колебания спроса. Поэтому в советской статистике при расчете индекса цен ориентировались на формулу Пааше. Только с 1991 года, когда страна перешла к рыночной экономике, начали считать по формуле Ласпейреса, принятой в международной практике.

Преимущества этой формулы в том, что сам расчет индекса и его последующие перерасчеты проводить с ее помощью значительно легче. Проще установить веса, поскольку достаточно иметь данные о стоимости продаж указанных товаров в базисный период. Именно поэтому в большинстве стран индексы инфляции строятся по формуле средней арифметической взвешенной.

Правда и ложь индекса цен

Впрочем, говорить о том, что формула расчета инфляции, предложенная Этьеном Ласпейресом более века назад, является универсальной, тоже нельзя. Об изъянах этой математической функции не говорит сегодня только ленивый. Ведь как ни крути она построена не на сплошном исследовании цен, а на выборочном.

Можно взять стоимость картофеля в магазине на окраине Краснодара, а можно — в супермаркете в центре Москвы. Результаты окажутся разными. Есть и другая составляющая формулы Ласпейреса, игра с которой позволяет статистическим органам манипулировать с показателями инфляции. Речь идет о тех самых весах.

Ведь продуктов в потребительской корзине много, каждый из них человек потребляет в разных количествах. Соответственно, и влияние их на общий уровень цен в корзине различно.

Но в том-то и дело, что определить точно, сколько россияне ежедневно потребляют мяса, а сколько помидоров, невозможно. Один — вегетарианец, второй предпочитает яичнице огурцы, поэтому и инфляция у каждого из нас своя, не совпадающая с теми цифрами, которые выдают статистические исследования.

Зато последние, путем пересмотра доли каждого продукта в потребительской корзине, имеют возможность как занижать свой показатель, так и завышать, — как больше нравится считающему. Что интересно, в России «весовые коэффициенты» каждого продукта в общей «корзине» Росстат начал публиковать всего несколько лет назад. До этого людям, знавшим правила эконометрии, ознакомиться с ними было практически невозможно.

А сами «веса», как признаются государственные статистики, меняются каждый год «в зависимости от изменения потребительских предпочтений россиян». Поди проверь… Наконец, при расчете инфляции важен не только учет стоимости каждого товара, но и определение доли населения, которое покупает их именно по таким ценам. Особенно в России, где разрыв между самыми бедными и самыми богатыми — один из самых больших в мире.

И формула Ласпейреса не позволяет это сделать. Хотя, возможно, со временем появится другая, более совершенная. Возможно, ее создаст кто-то из отечественных математиков. Но пока приходится пользоваться тем, что придумали немцы.

Источник: "lenta.ru"

Индексы цен

В макроэкономическом анализе важным показателем (кроме перечисленных в предыдущем параграфе) считается общий уровень цен. В реальной жизни цены меняются непрерывно, одни товары дешевеют, другие дорожают. Для того чтобы определить, на какую величину возросли или снизились цены, используют индексы цеп. Индекс цен — относительный показатель, характеризующий соотношение цен во времени.

При исчислении индексов цен обычно цены базового года принимают за 100 %, а цены других лет оценивают по отношению к этим 100 %. В общем виде индекс цен можно определить по формуле:

Индекс цен текущего года = (Цены текущего года / Цены базового года) х 100%.

Существует несколько видов индексов. Широкое применение получили индексы оптовых цен, индексы розничных (потребительских) цен, индексы цен — дефляторы ВНП, индексы импортных и экспортных цен и др.

Индекс оптовых цен (индекс цен производителей) включает три группы товаров, а именно:

конечные товары, готовые для использования;
промежуточные товары;
сырье, подготовленное для дальнейшей переработки.

Этот индекс показывает изменение среднего уровня продажных цен промышленных и строительных предприятий и компаний, сельскохозяйственных предприятий. Индекс потребительских (розничных) цен рассчитывается для группы товаров и услуг, входящих в потребительскую корзину среднего городского жителя:

ИПЦ = (Потребительская корзина в текущих ценах / Потребительская корзина в ценах базового года) х 100.

Важное место среди индексов цен занимает дефлятор ВНП, в котором «корзина» включает все конечные товары и услуги.

Этот индекс отражает изменение в ценах не только на товары широкого потребления, но и на все товары. Он позволяет сравнивать реальный и номинальный ВНП. Величина дефлятора определяется по формуле:

Дефлятор ВНП = (Реальный ВНП / Номинальный ВНП) х 100%.

Индексы цен используются также для исчисления уровня инфляции. Уровень инфляции определяется как процентное изменение цен:

Уровень инфляции = (цены текущего периода — цены прошлого периода) х 100 %.

Источник: "studme.org"

Статистические индексы

Само слово «индекс» (index) означает «показатель». Обычно этот термин используется для некоторой обобщающей характеристики изменений. Например, индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т.д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ.

В практике статистики индексы, наряду со средними величинами, являются наиболее распространенными статистическими показателями. Но индексы имеют три принципиальных отличия:

Во-первых, индексы позволяют измерить изменение сложных явлений (неоднородных статистических совокупностей).
Например, нужно определить, как изменились за год расходы жителей г. Луганска на городской транспорт. Для ответа на этот вопрос необходимо знать численность пассажиров, перевезенных за год каждым видом транспорта.

Нужно рассчитать среднемесячную численность пассажиров или взять точные данные из отчетов по месяцам, умножить численность на тариф перевозки (и число месяцев его действия – в случае использования среднемесячной численности) и полученные величины просуммировать.

То же нужно сделать по данным за прошлый год. Затем сопоставить сумму расходов за последний год с суммой за прошлый год. То есть это не просто средние двух чисел, как при расчете, например, темпов динамики или приростов, а получение и сравнение некоторых агрегатированных величин.
Во-вторых, индексы позволяют проанализировать изменения – выявить роль отдельных факторов. Например, можно определить, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров, изменения тарифов, наконец, за счет соотношения в объеме перевозок разными видами транспорта.
В-третьих, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами. Например, интересно знать, не только как изменилось среднедушевое потребление мяса в Украине в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого потребления мяса в Украине и в развитых странах Запада, Востока.
А также провести сравнение с нормативной величиной, отвечающей нормам рационального питания. Очевидно, что каждое направление сравнения вносит что-то новое.

Индексы для измерения динамики экономических изменений

Индекс – это показатель сравнений двух состояний одного и того же социально-экономического явления и представляет собой относительную величину, получаемую в результате сопоставления уровней сложных явлений во времени, в пространстве или с планом.

Индекс – это показатель, который сочетает в себе качества средних и относительных величин одновременно. Обычно индексы применяют для характеристики сложных совокупностей единиц наблюдения, то есть состоящих из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости.

Для определения общего объема реализации продуктов суммировать данные разнородные товары в натуральных единицах их учета, просто, нельзя, так как результат будет бессмысленным. Для получения обобщающих показателей в сложных статистических совокупностях необходимо применять индексный метод.

Например, в магазине ассортимент товаров состоит из разновидностей, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, консервы – в банках, торты – в штуках, макароны – в пачках и т.д.

Индексный метод представляет собой совокупность приемов, которая исторически возникла для измерения динамики социально-экономических явлений. Это сравнительно молодой метод в статистике. В простейшей форме его стали применять более 100 лет тому назад, но по-настоящему этот метод начал развиваться значительно позднее, когда появились большие теоретические работы и практические исследования в этой области.

Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям.

Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство. В зависимости от степени охвата и характера подвергнутых обобщению единиц изучаемой совокупности все индексы, употребляемые в статистике, делятся на два класса:

Индивидуальные (элементарные) индексы – это относительные числа, характеризующие изменения во времени показателей, относящихся к однородному объекту (к одной статистической совокупности), или изменения во времени показатели одновременно существующих однородных объектов (изменения уровней однотипных явлений).
Индивидуальные индексы вычисляются просто. Если, например, требуется показать динамику цены или производительности труда, урожайности пшеницы или любой другой культуры с помощью индивидуальных индексов, то берут величину текущего периода и делят ее на величину сравниваемого периода.
Общие (сложные) индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц сложной статистической совокупности или изменение сложных общественных явлений во времени.

Общие индексы подразделяются на:

индексы объемных показателей;
индексы качественных показателей.

К объемным показателям относятся:

физический объем продукции (обозначается буквой q). Выражается в натуральных единицах объема: кг, литры, метры, мешки, банки, ящики;
объем продукции или услуг (товарооборот), выраженный в стоимостной форме (обозначается буквами qp). Выражается в денежной форме: грн., доллар.

К качественным показателям относятся:

цена продукции или услуг (обозначается буквой p). Выражается в денежной форме: грн., доллар;
себестоимость продукции или услуг (обозначается буквой z). Выражается в денежной форме: грн., доллар;
затраты на производство продукции (обозначается буквами qz). Выражается в денежной форме: грн., доллар.

При вычислении индексов различают:

сравниваемый уровень (отчетный период);
уровень, с которым производится сравнение, называемый базисным.

Если показатель относится к сравниваемому (отчетному) уровню, то индексируемой величине присваивается символ «1» (например, p1 – цена товара за отчетный период), а если показатель относится к базисному периоду, то индексируемой величине присваивается символ «0» (например, q0 — объем продукции за базисный период).

Выбор базы сравнения определяется целью исследований. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком-либо периоде, предшествующем отношению. При этом возможны два способа расчета индексов – цепной и базисный:

Цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
Базисные индексы получают сопоставлением текущих уровней с уровнем периода, принятого за базу сравнения, т.е. база сравнения остается неизменной.

При использовании индексов как показателей выполнения плана, за базу сравнения принимаются плановые показатели. В статистике индивидуальные индексы принято обозначать буквой «i», а общие индексы – буквой «I». Рассмотрим порядок вычисления индивидуальных индексов.

Как уже отмечалось, индивидуальные индексы определяются как отношение уровня исследуемого показателя за отчетный период к уровню того же показателя за базисный период. При этом основным элементом индексного отношения является индексируемая величина, под которой понимается значение показателя за отчетный период.

Ее всегда записывают в числителе индексного отношения. Индивидуальные индексы цены продукции или услуг определяются по формуле:

где в числителе — цена продукции в текущем (отчетном) периоде; в знаменателе — цена продукции в базисном периоде.

Индивидуальные индексы для статистических исследований вычисляются крайне редко, так однородных совокупностей практически не бывает.

Основной формой общих индексов являются агрегатные индексы («aggrega» (лат.) – присоединять). В числителе и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых сложных статистических совокупностей.

Для достижения сопоставимости разнородных единиц в сложных статистических совокупностях в индексные соотношения вводят специальные сомножители – так называемые, соизмерители.

Они необходимы для перехода от натуральных измерений разнородных единиц к однородным показателям. При этом в числителе и знаменателе общего индекса изменяются лишь значения индексируемой величины, а их соизмерители остаются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода).

Это необходимо для того, чтобы на величине индекса называлось лишь влияние фактора, который определяет изменения индексируемой величины. Общий индекс цены:

Цена является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема q1 и отношение цены в отчетном периоде p1 к базисному p0).

Рассмотрим индексный метод изучения динамики сложных статистических совокупностей на примерах. Пусть имеются сведения о ценах и реализации товаров за два периода. Эти данные приведены в таблице 2:

Таблица 2. Сведения о ценах и реализации товаров

Как видно из таблицы, совокупность товаров разнородная (единицы измерения). Определим агрегатный индекс цен:

т.е. цены возросли в целом на 13,9%. В данном примере цена – индексируемый показатель, а объем — вес, взятый за отчётный период.

Можно в качестве весов взять объем и за базисный период. Тогда агрегатный индекс цен будет иметь вид:

т.е. цены возросли на 14,4 % (114,4-100 = 14,4%).

Используя два варианта расчета, получаем разное значение индекса цен. Какой из них ближе к реальному и принимать за действительный — зависит от цели исследований.

Правила построения общих индексов:

в исходные данные вводят необходимые буквенные обозначения;
записывают формулу общего индекса;
числитель и знаменатель формулы общего индекса расписывают в табличном виде;
производят промежуточные расчеты;
результаты вычислений подставляют в формулу общего индекса;
вычисляют общий индекс и делают выводы.

При анализе хозяйственной деятельности предприятий и организаций использование общих индексов в ряде случаев затруднено из-за отсутствия отдельных отчетных данных, особенно при вычислении планируемых показателей. Поэтому на практике часто используют формулы расчета общих индексов как величин, средних из соответствующих индивидуальных индексов.

В этом смысле общий индекс изучаемого явления рассматривается как результат изменения уровня данного явления у отдельных единиц совокупности. В процессе осреднения индивидуальных индексов веса подбираются такими, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме.

И наоборот, агрегатная форма общего индекса позволяет выбрать взвешивающий показатель при расчете общего индекса в виде средней величины. При изучении коммерческой деятельности предприятий приходится осуществлять индексные сопоставления более чем за два периода.

Поэтому индексные величины могут вычисляться как с постоянной, так и с переменной базами сравнения. При этом, если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляются базисные индексы. Но если требуется охарактеризовать последовательное изменение изучаемого явления из периода в период, то вычисляются цепные индексы.

В зависимости от задачи исследований и характера исходной информации, базисные и цепные индексы исчисляются как индивидуальные (однотоварные), так и общие. Способы расчета индивидуальных базисных и цепных индексов аналогичны расчету относительных величин динамики. Общие индексы, в зависимости от их вида (экономического содержания), вычисляются с переменными и постоянными весами – соизмерителями.

Источник: "ekonomstat.ru"

Система индексов цен

Индекс цен исторически является одним из первых экономических индексов. Практически задачи индекса цен в основном сводятся к оценке изменений цен во времени (индексы динамики) или в пространстве (территориальные индексы). Построение системы индексов цен базируется на общеметодологических принципах, согласно которым в ней выделяются индивидуальные, сводные индексы и индексы средних цен (тарифов).

Индивидуальный индекс динамики определяется как отношение цены конкретного i-го товара текущего периода к цене предыдущего периода или к цене одного из периодов динамического ряда, принятого за базу сравнения (0):

Для индивидуальных индексов цен не представляет труда переход от цепных к базисным индексам (свойство круговой сходимости индексов). Обозначим последовательные периоды ряда динамики цен от 0 до n. Исходя из свойства круговой сходимости индексов величину базисного индекса цен можно определить как произведение цепных.

Индивидуальные индексы цен позволяют решать многие практические задачи, но основной задачей является изучение динамики цен разнородной совокупности товаров и услуг. Эта задача решается с помощью сводных индексов, характеризующих среднее изменение цен изучаемой совокупности товаров и услуг.

Сводный (общий) индекс цен относится к числу классических показателей, разработкой которого исследователи занимаются с XVII в. Наиболее широкое применение в статистической практике получили агрегатные формулы сводных индексов цен, разработанные в середине XVIII в. немецкими учеными Э. Ласпейресом и Г. Пааше.

Индекс Ласпейреса:

Индекс Пааше:

Числитель и знаменатель в приведенных индексах состоят из агрегатов, включающих индексируемую величину р и вес q. Различие между индексами Ласпейреса и Пааше заключается в выборе периодов весов. В индексе Ласпейреса берутся веса базисного или предшествующего периода, а в индексе Пааше — текущего периода.

При использовании в индексе Ласпейреса весов одного и того же базисного периода в течение длительного времени получают систему сводных индексов цен с постоянными весами, что позволяет учитывать свойство круговой сходимости индексов:

Таблица 4. Динамика цен по двум товарам-представителям одной из групп продукции дробильно-размольного оборудования

В статистической практике при расчете сводных индексов цен широко применяются различные модификации агрегатных формул, в частности в виде формул среднеарифметических и среднегармонических с использованием индивидуальных индексов (ip).

Индекс Пааше (средняя гармоническая формула):

Индекс Ласпейреса (средняя арифметическая формула):

Выражение сводного индекса через индивидуальные (ip) позволяет наглядно представить как динамику цен по отдельным товарам, так и их роль в формировании сводного индекса. Необходимо отметить, что в индексе Пааше используются переменные веса, поэтому свойством транзитивности, или круговой сходимости, этот индекс не обладает. В индексе Ласпейреса могут применяться как переменные, так и постоянные веса.

В статистической практике при исчислении цепных и базисных индексов цен широко используется средняя арифметическая формула Ласпейреса с постоянными весами. При этом применяется рекурсивный принцип построения модифицированной формулы Ласпейреса. Пример расчета приведен выше в таблице 4.

При широком использовании в экономической практике индивидуальных и сводных индексов цен определенный интерес представляет исчисление индекса динамики средних цен.

Средние цены, а следовательно, и индекс средних цен определяются по достаточно однородным группам товаров и при условии, что все товары, входящие в группу, измеряются одинаковыми количественными единицами (тоннами, литрами и т.д.).

Средние цены определяются путем деления стоимости (Σpiqi) на общее количество изучаемых единиц в группе (Σqi). Индексы средних цен (тарифов) правомерно исчислять не только по достаточно однородным группам товаров (услуг), но и по одному виду товаров, произведенному или реализованному по совокупности территориальных единиц (районов, области и т.д.) или в разрезе временных периодов (месяцев, кварталов и т.д.).

Средние цены и индексы средних цен, исчисленные по отдельным товарным группам, можно агрегировать в более укрупненные группы и в целом по изучаемой совокупности, используя те же формулы сводных индексов цен, что и при агрегировании цен конкретных товаров, но в этом случае сводный индекс будет характеризовать среднее изменение средних цен, что важно иметь в виду при интерпретации и использовании таких индексов.

Источник: "bibliotekar.ru"

Индивидуальный и общий индексы цен

Индексы являются важнейшим видом обобщающих статистических показателей. Они используются для характеристики динамики явлений, сравнений по различным территориям, при контроле и разработке плановых заданий. Наравне со средними величинами они представляют собой один из самых распространенных видов статистических показателей.

Слово «индекс» (index) в переводе с латыни означает указатель, показатель. В статистике этот термин имеет специфическое значение.

Индекс – это относительная величина, характеризующая изменение сложных общественных явлений во времени, пространстве или по сравнению с планом. Индекс является результатом сравнения двух одноименных величин, поэтому необходимо различать величину сравнения (числителя индексного отношения) и базу сравнения (знаменатель).

Выбор базы сравнения определяется целью исследования; при изучении динамики в качестве базы используются данные какого-либо предыдущего периода; при контроле за выполнением плана – плановые данные; при территориальных сравнениях – данные другой территории. Величину сравнения обычно называют показателем отчетного периода, базу сравнения называют показателем базисного периода.

Если базисный уровень при исчислении индекса принимается за единицу, то индексы вычисляются в виде коэффициентов, а если базисный уровень принимается за 100, то индекс вычисляют в виде процентов. На основании вычисления можно определить, во сколько раз отчетная величина больше или меньше базисной или на сколько процентов она больше или меньше базисной.

Статистика изучает в основном сложные экономические явления, которые состоят из элементов непосредственно несоизмеримых.

Так, если электромеханический завод производит несколько видов продукции, то данные о выпуске продукции в натуральном выражении суммировать нельзя. Для того, чтобы показать общее изменение выпуска по нескольким видам продукции и вычисляются индексы. С их помощью можно дать обобщенную характеристику изменения себестоимости, цен, выпуска по нескольким видам продукции.

При всем их разнообразии экономические индексы подразделяются на индивидуальные и общие индексы. Индивидуальным называется индекс, характеризующий изменение объема производства, объема продажи, уровня производительности труда и т.д. в отношении какого-нибудь одного продукта. Индивидуальный индекс цен характеризует изменение цены по каждому виду продукции:

где в числителе — цена отчетного периода, в знаменателе — цена базисного периода.

Общим (агрегатным) называется индекс, характеризующий общее (среднее) изменение объема производства, объема продаж, уровней цен и т.д. в отношении совокупности рядов товаров. Например, индексы, показывающие изменение общего объема производства различных видов продукции или изменение уровня цен различных видов товаров в целом. При расчете общих индексов возникает проблемы соизмерения показателей по отдельным товарам.

Соизмеримость отдельных показателей достигается путем взвешивания, суть которого состоит в том, что при вычислении абстрагируются от влияния изменения одной из сторон изучаемого явления, принимая ее за неизменную величину.

Так, при расчете индекса объема проданной продукции неизменными величинами будут цены, а при расчете индекса цен – количество проданной продукции. Та сторона изучаемого явления, от влияния изменения которой абстрагируются, принимая ее за неизменную, называется весами индекса.

Перед общим (агрегатным) индексом качественного показателя ставится задача измерить не только относительное изменение уровня но и абсолютную величину того экономического эффекта, который получен в текущем периоде в результате этого изменения. В данном случае сумму экономии покупателей за счет снижения цен, или сумму их дополнительных расходов, если цены повысились.

Для получения общего индекса цен нужно построить его так, чтобы отразилось влияние только фактора изменения цен, и было бы исключено влияние изменения количества проданных товаров. Это возможно в том случае, если для обоих сравниваемых периодов количество проданных товаров будет взято одинаковое.

Количество проданных товаров следует брать в текущем периоде, так как только на приобретении этого количества потребитель может экономить в результате снижения цен или перерасходовать в результате их повышения.

Общий индекс цен Пааше:

где p – индексируемая величина; q – веса.

В числителе индекса дана суммарная стоимость проданных в текущем периоде товаров по ценам текущего периода, а в знаменателе – стоимость того же количества товаров, но рассчитанная по ценам базисного периода.

Экономия (перерасход) от изменения цен:

В статистике используются и другие формы представления общих индексов цен – Ласпейреса и Фишера.

Общий индекс цен Ласпейреса:

Общий индекс цен Фишера:

Источник: "life-prog.ru"

Общий индекс цен. Индекс Пааше

В условиях современной экономики и эконометрики важное место среди индексов качественных показателей отводится индексу цен, который представляет собой показатели динамики уровня цен. При помощи индекса потребительских цен (ИПЦ) проводится оценка динамики цен на товары производственного и непроизводственного потребления.

ИПЦ отражает динамику цен конечного потребления, измеряет общее изменение стоимости фиксированного набора потребительских товаров и услуг («потребительская корзина»), а также является одним из основных показателей, характеризующих уровень инфляции. ИПЦ используется при корректировке минимального размера труда, расчета ставок налогов и т.д.

В 1874 г. немецкий экономист Г. Пааше предложил агрегатный индекс цен с отчетными весами. Формула агрегатного индекса цен Пааше определяется так:

где в числителе — фактическая стоимость продукции отчетного периода;
в знаменателе — условная стоимость товаров, которые реализованы в отчетном периоде, по базисным ценам.

Индекс цен Пааше показывает, во сколько раз возрос или уменьшился в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом, т. е. он показывает, на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.

В 1864 г. немецкий экономист Э. Ласпейрес предложил индекс, отражающий изменение цен, который строится по продукции базисного периода. Формула агрегатного индекса цен Ласпейреса рассчитывается как отношение:

Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по продукции, которая была реализована в базисном периоде, и экономию (перерасход), который можно было бы получить от изменения цен. Индекс цен Ласпейреса также показывает, во сколько раз товары базисного периода подорожали (подешевели) в результате изменения цен на них в отчетном периоде.

Американский экономист И. Фишер предложил «идеальный» индекс цен, который назвали его именем, представляющий собой среднюю геометрическую произведения двух агрегатных индексов цен Ласпейреса и Пааше:

Идеальность данной формулы заключается в том, что индекс является обратимым во времени, т. е. при перестановке базисного и отчетного периодов полученный обратный индекс представляет собой величину, обратную величине первоначального индекса.

Недостаток формулы состоит в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен).

Средний гармонический индекс цен

Средний гармонический индекс цен применяется тогда, когда неизвестны значения p1, q1 но дано их произведение и индивидуальные индексы цен ip = p1/p0 а сводный индекс должен быть исчислен с отчетными весами.

Индивидуальные индексы определены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Выражая из формулы индивидуальных индексов цен неизвестное значение р0 = p1/ip, подставляем его в знаменатель агрегатной формулы и получим средний гармонический индекс цен, который равен формуле Пааше:

Весами индивидуальных индексов iр в индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода p1q1.

Средний арифметический индекс цен

Средний арифметический индекс цен получают в том случае, если из индивидуального индекса цен ip = p1/p0 выразить цену отчетного периода p1 = i0p0, а затем подставить ее в числитель агрегатного индекса цен. Данный индекс аналогичен агрегатному индексу Ласпейреса и имеет формулу:

В этом индексе весами осредненных индивидуальных индексов служит объем товарооборота в базисном периоде.

Источник: "univer-nn.ru"

Общий индекс цен. Индекс Ласпейреса

В большинстве экономически развитых стран общие индексы цен на потребительские товары, рассчитанные по отношению к одному из периодов, выбранному в качестве базисного, ежегодно публикуются и используются для характеристики процесса инфляции.

Таблица 3. Агрегатные, арифметические и гармонические формы индексов цен

Применяется индекс Ласпейреса, отличающийся от индекса Пааше тем, что в формуле в качестве весовых коэффициентов берутся q0, т. е. объемы реализации в базисном периоде. Индекс Ласпейреса обладает рядом весьма серьезных преимуществ перед индексом Пааше.

В частности, имея данные о значениях индекса Ласпейреса в двух произвольно выбранных годах, легко исчислить, как изменились цены в период между этими годами индекс Пааше сделать этого не позволяет из-за различия в весовых коэффициентах. Эта особенность имеет особое значение в ретроспективном анализе, когда приходится принимать во внимание балансовые оценки долгосрочных активов, приобретения.

С помощью индексов Ласпейреса легко построить аналитический баланс, в котором ценовые различия элиминированы. Общий индекс цен по формуле Этьена Ласпейреса:

В отечественной статистике до 1992 г. общий индекс цен рассчитывался по формуле Пааше, используя гармоническую его форму. Связано это было с простотой получения данных о текущем товарообороте (P,Qj) в связи со сплошной ежемесячной статистической отчетностью и незначительным изменением цен.

Однако после 1992 г., когда был осуществлен переход к рыночным отношениям и принята новая методика расчета индекса потребительских цен, он стал рассчитываться так же, как и в большинстве стран, по формуле Ласпейреса.

Контроль за изменением цен на отдельные виды товаров, а также на потребительские товары в целом осуществляется с помощью индексов цен. Существует два основных вида индекса цен частный, или индивидуальный, (ip) и общий, или агрегатный, (Iр). Именно последний используется для характеристики инфляции.

В статистике разработано несколько алгоритмов расчета агрегатного индекса цен, различающихся системой весовых коэффициентов в формуле расчета. Наибольшую известность получили индексы Карли, Маршалла, Пааше, Ласпейреса, Фишера. В нашей стране традиционно используется индекс Пааше, предусматривающий взвешивание цен по весам отчетного периода, в качестве которых выступают объемы реализованных товаров в натуральных измерителях.

Источник: "economy-ru.info"

Содержание:

1 Понятие об индексах. Индексный метод
- 1.1 Индивидуальный индекс цен
- 1.2 Индекс цен общий: формула расчета
2 Кто и как впервые рассчитал индекс потребительских цен
- 2.1 Как считать цены
- 2.2 Правда и ложь индекса цен
3 Индексы цен
4 Статистические индексы
- 4.1 Индексы для измерения динамики экономических изменений
5 Система индексов цен
6 Индивидуальный и общий индексы цен
7 Общий индекс цен. Индекс Пааше
- 7.1 Средний гармонический индекс цен
- 7.2 Средний арифметический индекс цен
8 Общий индекс цен. Индекс Ласпейреса

Источник

Обозначения индексируемых величин:

Классификация индексов:

Основные формулы исчисления сводных, или общих, индексов

Понятие об индексах. Индексный метод

Индивидуальный индекс цен

Индекс цен общий: формула расчета

Кто и как впервые рассчитал индекс потребительских цен

Как считать цены

Правда и ложь индекса цен

Индексы цен

Статистические индексы

Индексы для измерения динамики экономических изменений

Система индексов цен

Индивидуальный и общий индексы цен

Общий индекс цен. Индекс Пааше

Средний гармонический индекс цен

Средний арифметический индекс цен

Общий индекс цен. Индекс Ласпейреса

Вам также может понравиться

Как найти диагонали прямоугольника если даны диагонали

Как найти шестую производную

Как найти группы в mail

Добавить комментарий Отменить ответ