Как найти отношение кинетической энергии тела

Энергия – важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.

Что такое энергия?

Энергия в физике – это способность тела совершать работу. 

Кинетическая энергия

Что такое кинетическая энергия?

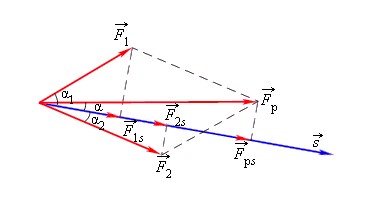
Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A. 

Работа всех сил, действующих на тело, равна работе равнодействующей силы. 

Fр→=F1→+F2→

A=F1·s·cosα1+F2·s·cosα2=Fрcosα.

Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины. 

Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:

A=Fs=F·v22-v122a=ma·v22-v122a

A=mv22-mv122=mv222-mv122.

Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела. 

Теорема о кинетической энергии

Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.

Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.

A=mv22=EK.

Чтобы остановить тело, нужно совершить работу 

A=-mv22=-EK

Потенциальная энергия

Что будет означать или обозначать кинетическая энергия?

Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.

Формула потенциальной энергии:

E пот = m * g * h

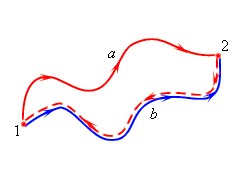
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу. 

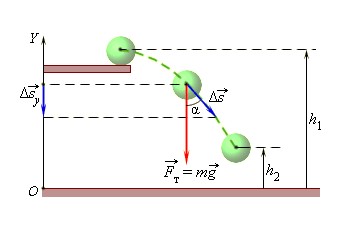
Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2. 

При этом сила тяжести совершила работу, равную 

A=-mg(h2-h1)=-(mgh2-mgh1).

Эта работа равна изменению величины mgh, взятому с противоположным знаком. 

Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A=-(EП2-EП1).

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

EП=-GmMr.

Здесь G – гравитационная постоянная, M – масса Земли.

Потенциальная энергия пружины

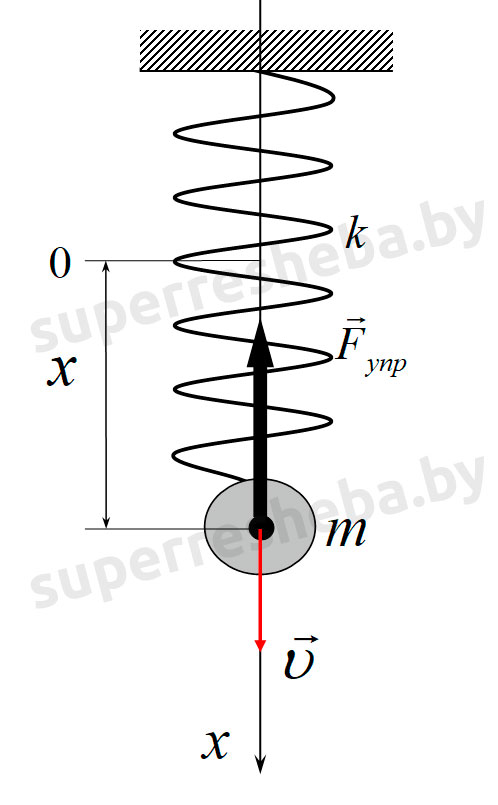
Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами. 

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Aупр=-A=-kx22.

Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.

Дано:

а) x=A2;а), x=dfrac{A}{2};

б) x=3A4;б), x=dfrac{3A}{4};

в) x=A.в), x=A.

Найти:

WкWп−?dfrac{W_к}{W_п}-?

Решение:

Вычислим потенциальную энергию по формуле:

Wп=kx22,W_п=dfrac{kx^2}{2},

где kk — коэффициент упругости пружинного маятника, xx — коэффициент упругости пружинного маятника.

Полная энергия колебаний вычисляется по формуле:

Wмех=kA22.W_{мех}=dfrac{kA^2}{2}.

Кинетическая энергия для момента времени, в который определяется потенциальная энергия, вычисляется по формуле:

Wк=Wмех−Wп;W_к=W_{мех}-W_п;

Wк=kA22−kx22;W_к=dfrac{kA^2}{2}-dfrac{kx^2}{2};

Wк=k(A2−x2)2.W_к=dfrac{k(A^2-x^2)}{2}.

Найдём отношение кинетической энергии к потенциальной:

WкWп=k(A2−x2)2:kx22;dfrac{W_к}{W_п}=dfrac{k(A^2-x^2)}{2}:dfrac{kx^2}{2};

WкWп=k(A2−x2)2⋅2kx2;dfrac{W_к}{W_п}=dfrac{k(A^2-x^2)}{2}cdot dfrac{2}{kx^2};

WкWп=k(A2−x2)kx2;dfrac{W_к}{W_п}=dfrac{k(A^2-x^2)}{kx^2};

WкWп=A2−x2x2;dfrac{W_к}{W_п}=dfrac{A^2-x^2}{x^2};

WкWп=(Ax)2−1.dfrac{W_к}{W_п}=left(dfrac{A}{x}right)^2-1.

а) при x=A2x=dfrac{A}{2} получим:

WкWп=(AA2)2−1=22−1=3.dfrac{W_к}{W_п}=left(dfrac{A}{dfrac{A}{2}}right)^2-1=2^2-1=3.

б) при x=3A2x=dfrac{3A}{2} получим:

WкWп=(A3A4)2−1=(43)2−1=79≈0.78.dfrac{W_к}{W_п}=left(dfrac{A}{dfrac{3A}{4}}right)^2-1=left(dfrac{4}{3}right)^2-1=dfrac{7}{9}approx0.78.

в) при x=Ax=A получим:

WкWп=(AA)2−1=12−1=0.dfrac{W_к}{W_п}=left(dfrac{A}{A}right)^2-1=1^2-1=0.

Ответ: а) 3;б) 0.78;в) 0.а), 3; б), 0.78; в), 0.

Решение: Для написания уравнения координаты от времени используем функцию сos. Напишем уравнение координаты:

x = X_m∙соsω∙t,

где: х – координата тела, Х_m – амплитуда, ω – угловая скорость, ω = 2∙π/Т, Т – период колебаний.   
Для нахождения скорости возьмем первую производную по времени от х:     

υ = – ω∙Х_m∙sinω∙t.

Запишем формулу для нахождения кинетической энергии:

[ {{E}_{K}}=frac{mcdot {{upsilon }^{2}}}{2}, {{E}_{K}}=frac{mcdot {{(-omega )}^{2}}cdot X_{m}^{2}cdot {{sin }^{2}}frac{2cdot pi }{T}cdot t}{2}. ]

Запишем формулу для нахождения потенциальной энергии:

[ {{E}_{p}}=frac{kcdot {{x}^{2}}}{2}, {{E}_{p}}=frac{kcdot X_{m}^{2}cdot {{cos }^{2}}frac{2cdot pi }{T}cdot t}{2}. ]

Учитываем что:

[ {{omega }^{2}}=frac{k}{m}. ]

Найдем отношение кинетической энергии точки, к ее потенциальной энергии:

[ frac{{{E}_{K}}}{{{E}_{p}}}=frac{2cdot mcdot {{(-omega )}^{2}}cdot X_{m}^{2}cdot {{sin }^{2}}frac{2cdot pi }{T}cdot t}{2cdot kcdot X_{m}^{2}cdot {{cos }^{2}}frac{2cdot pi }{T}cdot t}=t{{g}^{2}}frac{2cdot pi }{T}cdot tcdot  ]

[ t=frac{T}{12}, frac{{{E}_{K}}}{{{E}_{p}}}=t{{g}^{2}}frac{2cdot pi }{T}cdot frac{T}{12}=frac{1}{3,} ]

[ t=frac{T}{8}, frac{{{E}_{K}}}{{{E}_{p}}}=t{{g}^{2}}frac{2cdot pi }{T}cdot frac{T}{8}=1, ]

[  t=frac{T}{6}, frac{{{E}_{K}}}{{{E}_{p}}}=t{{g}^{2}}frac{2cdot pi }{T}cdot frac{T}{6}=3. ]

Ответ: 1/3, 1, 3.

2018-10-06   

Определите отношение кинетической и потенциальной энергии точки совершающей гармонические колебания к ее потенциальной энергии если известна фаза колебаний.

Решение:

Уравнение гармонических колебаний

$x = A cos ( omega_{0}t + phi )$,

Возьмем первую и вторую производную

$v = 4 omega_{0} sin ( omega_{0}t + phi )$,

$a = – A omega_{0}^{2} cos ( omega_{0}t + phi ) – omega_{0}^{2}x$.

Следовательно кинетическая и потенциальная энергия точки

$T = frac{mv^{2} }{2} = frac{mA^{2} omega_{0}^{2} }{2} sin^{2} ( omega_{0}t + phi )$,

$Pi = – int_{0}^{x} Fdx = int_{0}^{x} m omega_{0}^{2} x dx = frac{m omega_{0}^{2}x }{2} = frac{mA^{2} omega_{0}^{2} }{2} cos^{2} ( omega_{0}t + phi )$,

Отношение энергией

$frac{T}{ Pi} = frac{ sin^{2} ( omega_{0}t + phi ) }{ cos^{2} ( omega_{0} t + phi ) } = tg^{2} ( omega_{0}t + phi )$

Нашли ошибку? Сообщите в комментариях (внизу страницы)