|
v=(1/2pi)(k/m).^0.5 v1=(1/2pi)(k/m1).^0.5=15/t v2=(1/2pi)(k/m2).^0.5=30/t v2/v1=(m1/m2).^0.5=30/15=2 m1/m2=4 |
Получи верный ответ на вопрос 🏆 «Два пружинных маятника имеют пружины с соотношением коэффициентов упругости (k1/k2 = 4). Отношение масс грузов (m1/m2 = 1). Каково будет …» по предмету 📕 Физика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Физика » Два пружинных маятника имеют пружины с соотношением коэффициентов упругости (k1/k2 = 4). Отношение масс грузов (m1/m2 = 1). Каково будет соотношение периодов колебаний?
Михайленко А., Хаджи П. Маятник с несколькими грузиками //Квант. — 1998. — № 3. — С. 34-35.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Логическим и простейшим обобщением традиционного математического маятника является маятник с двумя или более грузиками. Такой маятник можно назвать частным случаем физического маятника.
Рис. 1
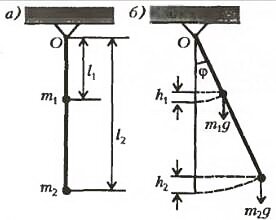
Рассмотрим сначала более простой случай. Пусть к жесткому невесомому стержню прикреплены два точечных тела с массами m1 и m2 на расстояниях l1 и l2 соответственно от точки подвеса (рис.1,а). Найдем частоту колебаний такого маятника.
В положении равновесия стержень маятника располагается вертикально. Выведем маятник из положения равновесия, отклонив стержень с грузами на небольшой угол φ (рис. 1,6). Каждый из грузов при этом поднимется на определенную высоту относительно своего положения равновесия. Первый поднимется на высоту (~h_1 = l_1 (1 – cos varphi)), a второй – на (~h_2 = l_2 (1 – cos varphi)). Запасенная системой грузов потенциальная энергия относительно положения равновесия будет равна
(~Delta E_p = m_1gh_1 + m_2gh_2 = (m_1l_1 + m_2l_2)g(1 – cos varphi)) .
Предоставим теперь маятник самому себе. Благодаря касательным составляющим сил тяжести грузов (которые играют роль «возвращающих» сил), маятник начнет двигаться к положению равновесия. Линейные скорости грузов по мере приближения к положению равновесия будут возрастать. В положении равновесия полная кинетическая энергия грузов станет равной
(~E_k = frac{m_1 upsilon^2_1}{2} + frac{m_2 upsilon^2_2}{2}) ,
где υ1 и υ2 — линейные скорости движения грузов. Выражая υ1 и υ2 через угловую скорость вращения стержня Ω и длины l1 и l2:
(~begin{matrix} upsilon_1 = Omega l_1 \ upsilon_2 = Omega l_2 end{matrix}) ,
кинетическую энергию системы можно представить в виде
(~E_k = frac 12 Omega^2 (m_1l^2_1 + m_2l^2_2)) .
Предполагая, что в системе отсутствуют потери энергии из-за трения в оси и сопротивления воздуха, и используя закон сохранения энергии, можно приравнять потенциальную энергию кинетической. В результате для угловой скорости вращения стержня получаем выражение
(~Omega^2 = 2g frac{m_1l_1 + m_2l_2}{m_1l^2_1 + m_2l^2_2}(1 – cos varphi)) .
Сравним наш маятник с некоторым математическим маятником, имеющим такую длину L, что при одном и том же начальном отклонении φ от положения равновесия угловые скорости Ω и периоды колебаний Т обоих маятников оказываются одинаковыми. Для математического маятника можно записать
(~begin{matrix} Delta E_p = mgL(1 – cos varphi) \ E_k = frac 12 m upsilon^2 \ upsilon = Omega L end{matrix}) .
Используя закон сохранения энергии, для угловой скорости Ω получаем выражение
(~Omega^2 = 2 frac{g}{L}(1 – cos varphi)) .
Так как при одном и том же угловом отклонении φ угловые скорости Ω обоих маятников равны, приравнивая правые части соответствующих равенств, находим длину L математического маятника, эквивалентного исходному маятнику с двумя грузами:
(~L = frac{m_1l^2_1 + m_2l^2_2}{m_1l_1 + m_2l_2}) ,
а значит, и частоту колебаний нашего физического маятника:
(~omega = sqrt{frac gL} = sqrt{g frac{m_1l_1 + m_2l_2}{m_1l^2_1 + m_2l^2_2}}) ,
и его период:
(~T = 2pi sqrt{frac 1g frac{m_1l^2_1 + m_2l^2_2}{m_1l_1 + m_2l_2}}) .
Если m1 либо m2 равны нулю (т.е. один из грузов отсутствует), то из последнего выражения получаем формулу для периода колебаний математического маятника. Если же, например, m1 = m2 (т.е. массы обоих грузов одинаковы), то
(~T = 2pi sqrt{frac 1g frac{l^2_1 + l^2_2}{l_1 + l_2}}) .
Таким образом, частота и период колебаний нашего маятника определяются как массами грузов, так и их расстояниями от оси вращения.
Сравним полученное выражение для частоты колебаний исследуемого маятника ω с частотами колебаний двух независимых математических маятников с длинами нитей l1 и l2 соответственно, которые выражаются формулами
(~omega_1 = sqrt{frac{g}{l_1}}) и (~omega_2 = sqrt{frac{g}{l_2}}).
Если положить l1 > l2, то получаем неравенство
(~omega_1 < omega < omega_2).
Таким образом, частота колебаний маятника с двумя грузами, расположенными на расстояниях l1 и l2 от оси вращения, меньше большей и больше меньшей из собственных частот колебаний двух независимых математических маятников с длинами нитей l1 и l2 соответственно.
Исследуем теперь более детально выражение для ω. Предположим, что один из грузов, например груз с массой m1, расположен на фиксированном расстоянии l1 от оси вращения маятника, а расстояние l2 второго груза с массой m2 меняется. Найдем отношение частоты колебаний нашего маятника к частоте колебаний математического маятника с длиной нити l1:
(~y = frac{omega}{omega_1} = sqrt{frac{l_1(m_1l_1 + m_2l_2)}{m_1l^2_1 + m_2l^2_2}}) .
Введем безразмерные переменные (~x = frac{l_2}{l_1}) и (~a = frac{m_2}{m_1}) . Тогда
(~y = sqrt{frac{1 + ax}{1 + ax^2}}) .
Исследуем зависимость y от x, т.е. зависимость отношения частот (~frac{omega}{omega_1}), от отношения длин (~frac{l_2}{l_1}) . Поступим следующим образом. Обозначим z = 1 + ax и запишем
(~y = sqrt{frac{az}{z^2 – 2z + a + 1}} = sqrt{frac{a}{z + frac{a + 1}{z} – 2}} = sqrt{frac{a}{left(sqrt z – sqrt{frac{a + 1}{z}}right)^2 + 2 (sqrt{a + 1} – 1)}}) .
Отсюда видно, что функция y{z) изменяется немонотонно: с ростом z (начиная с z = 1) функция сначала растет, достигает максимума при (~z = sqrt{a + 1}) (это следует из условия обращения в ноль первого слагаемого в знаменателе), после чего монотонно убывает. Максимальное значение при этом равно
(~y_{max} = sqrt{frac{a}{2 (sqrt{a + 1} – 1)}} = sqrt{frac 12 (sqrt{a + 1} – 1)}) .
Возвращаясь снова к переменной х, находим значение х = x0, при котором функция у(х) достигает максимума:
(~x = x_0 = frac{sqrt{a + 1} – 1}{a} = frac{sqrt{m_1(m_1 + m_2)} – m_1}{m_2}) .
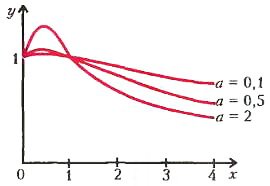
На рисунке 2 представлен график зависимости функции y = у{х). Видно, что y > 1 в области 0 < х < 1, т.е. при l1 > l2 получаем ω > ω1. Наоборот, y < 1 в области х > 1, т.е. при l1 < l2 получаем ω < ω1. Отметим, что чем больше параметр a, тем выше максимум.
Рис. 2
Нетрудно обобщить полученные результаты на случай n тел с массами m1, m2, …, mn, закрепленных на невесомом стержне на расстояниях l1, l2, …, ln соответственно от точки подвеса:
(~T = 2pi sqrt{frac 1g frac{m_1l^2_1 + m_2l^2_2 + ldots + m_nl^2_n}{m_1l_1 + m_2l_2 + ldots + m_nl_n}}) .
Если массы всех грузов одинаковы, то
(~T = 2pi sqrt{frac 1g frac{l^2_1 + l^2_2 + ldots + l^2_n}{l_1 + l_2 + ldots + l_n}}) ,
т.е. период колебаний определяется только расстояниями, на которых располагаются грузики.
Период колебания пружинного маятника, теория и онлайн калькуляторы
Период колебания пружинного маятника
Рассмотрим простейшую систему, в которой возможна реализация механических колебаний. Допустим, что на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$. Груз движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. Массу пружины считаем малой в сравнении с массой груза.
Уравнение движения груза при таких колебаниях имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${omega }^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=B{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
Частота и период колебаний пружинного маятника
Косинус (синус) – периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют
периодом колебаний. Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(3right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(4right).]
Зная, что для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, период колебаний его определим как:
[T=2pi sqrt{frac{m}{k}} left(5right).]
Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:
[left[Tright]=с.]
Примеры задач на период колебания пружинного маятника
Пример 1
Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?
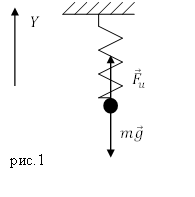
Решение. Сделаем рисунок.
Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:
[moverline{g}+{overline{F}}_u=0 left(1.1right).]
Запишем проекцию уравнения (1.1) на ось Y:
[mg=F_uleft(1.2right).]
Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:
[F_u=kDelta x left(1.3right).]
Используя выражения (1.2) и (1.3) найдем отношение $frac{m}{k}$:
[mg=kDelta xto frac{m}{k}=frac{Delta x }{g}left(1.4right).]
Период колебаний пружинного маятника при малых колебаниях можно найти, используя выражение:
[T=2pi sqrt{frac{m}{k}} left(1.5right).]
Заменяя отношение массы груза к жесткости пружины на правую часть выражения (1.4), получим:
[T=2pi sqrt{frac{Delta x }{g}.}]
Вычислим период колебаний нашего маятника, если $g=9,8 frac{м}{с^2}$:
[T=2pi sqrt{frac{0,09 }{9,8} approx 0,6 (с)}]
Ответ. $T$=0,6 с
Пример 2
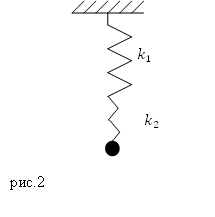
Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.
Решение.Период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(2.1right).]
Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}to k=frac{k_1k_2}{k_1{+k}_2}left(2.2right).]
Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{m(k_1{+k}_2)}{k_1k_2}}.]
Ответ. $T=2pi sqrt{frac{m(k_1{+k}_2)}{k_1k_2}}$
Читать дальше: плечо силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Два, подвешенных на нитях груза 1 и 2 различной массы могут двигаться в системе, состоящей из неподвижного блока Н и подвижного блока П (см. рис.).
1) Найти отношение сил натяжения нитей, на которых подвешены грузы 1 и 2.
2) Найти отношение масс грузов 1 и 2, если груз 2 движется с ускорением направленным вверх.
Массами нитей, блоков, а также трением в осях блоков можно пренебречь
Спрятать решение
Решение.
1. Так как блоки невесомые, то
2. Уравнения движения грузов (T — сила натяжения нити):
Из (1), (2):
Так как нить нерастяжима, то
Из (3), (4):
Ответ: 1) 2)
Спрятать критерии
Критерии проверки:
| № | Критерий | Максимальный балл |
|---|---|---|
| 1 | Ответ на первый вопрос — 3 балла | 3 |
| 2 | Есть связь ускорений — 2 балла, есть все уравнения движения — 2 балла, ответ на второй вопрос — 3 балла | 7 |
Классификатор: Механика. Движение связанных тел