Как найти отношение масс шаров

2019-12-17   

Рисунок сделан со стробоскопической фотографии движения двух сталкивающихся шариков одинаковых диаметров, но разных масс. Стрелкой на рисунке показано направление движения одного из шариков до столкновения.

1) Определить отношение масс шариков.

2) Указать, в каком направлении двигался до столкновения второй шар.

Решение:

Пусть $m_{1}$ – масса первого шарика, $vec{v}_{1}$ и $vec{v}_{1}^{ prime}$ – его скорости соответственно до и после столкновении, $m_{2}$ – масса второго

шарика, а $vec{v}_{2}$ и $vec{v}_{2}^{ prime}$ – его скорости до и после столкновения. Согласно закону сохранения импульса

$m_{1} Delta vec{v}_{1} + m_{2} Delta vec{v}_{2} = 0$, или $m_{1} Delta vec{v}_{1} = – m_{2} Delta vec{v}_{2}$. (1)

где $Delta vec{v}_{1} = vec{v}_{1}^{ prime} – vec{v}_{1}$ – изменение скорости первого шарика, $Delta vec{v}_{2} = vec{v}_{2}^{ prime} – vec{v}_{2}$ – изменение скорости второго шарика при столкновении. Из (1) получаем

$frac{m_{1} }{m_{2} } = frac{| Delta vec{v}_{2} |}{| Delta vec{v}_{1} |}$. (2)

Следовательно, для того чтобы найти отношение масс шаров, нужно построить векторы $Delta vec{v}_{1}$ и $Delta vec{v}_{2}$ и затем взять обратное отношение их модулей.

Скорости шариков равны перемещениям шариков за время $tau$ между последовательными вспышками лампы, деленным на $tau$. Так как значение $tau$ одинаково для обоих шариков как до, так и после столкновения, то в масштабе $1: frac{1}{ tau}$ – векторы, изображающие скорости шариков, просто равны векторам перемещений шариков за время между последовательными вспышками лампы. Воспользуемся этим для того, чтобы найти $Delta vec{v}_{1}$ и $Delta vec{v}_{2}$.

Мы знаем, как двигался один из шариков до столкновения. Для того чтобы построить вектор $Delta v_{1}^{ prime}$, необходимо также знать, как двигается этот шарик после столкновения по ветви II, III или IV? Для того чтобы выяснить это, нам придется перебрать все возможные варианты (их всего три). При правильном выборе траекторий движения шариков векторы $Delta vec{v}_{1}$ и $Delta vec{v}_{2}$ согласно равенству (1) должны быть направлены в прямо противоположные стороны.

Прежде чем приступить к построению, заметим, что $Delta vec{v}$ не меняется при “обращении” движения шарика, то есть если до столкновения шарик 1 двигался по ветви I, а после столкновения – по ветви II, то $Delta vec{v}$ такое же, как и в том случае, если до столкновения он двигался но ветви II, а после столкновения – по ветви I.

Теперь мы можем приступить к построению. Предположим, что к шарику I относятся ветви I и II, а к шарику 2 – ветви III и IV. Построив в этом случае векторы изменении скоростей шариков (рис.), получим, что они не направлены вдоль одной прямой (на рисунке для удобства векторы $vec{v}$ построены в масштабе $1 : frac{1}{3 tau}$). Следовательно, наше предположение не верно. Проверяя так же другие возможные варианты, убеждаемся, что к шарику I относятся ветви I и IV, а к шарику 2 – ветви II и III (рис.). Измерив длины векторов, изображающих $Delta vec{v}_{1}$ и $Delta vec{v}_{2}$ найдем:

$frac{m_{1} }{m_{2} } = frac{ | Delta vec{v}_{2} | }{ | Delta vec{v}_{1} | } = frac{1}{3}$.

Теперь ответим на второй вопрос. Обозначим $tau_{1}$ время между моментом столкновения шариков и последней до столкновении вспышкой лампы. Тогда ясно, что перемещение шарика за это время должно составлять $tau_{1}/ tau$ часть перемещения шарика за время $tau$ между вспышками. Померив соответствующие перемещения первого шарика, найдем, что $tau_{1}/ tau$ равно $11/19$. Таким же оно должно быть и для второго шарика. Непосредственным измерением убеждаемся, что этому условию удовлетворяет ветвь III. Следовательно, шарик 2 до столкновения двигался по ветви III.

1. Упругие столкновения

Столкновение
называется
абсолютно
упругим,
если по
завершении его тела полностью
восстанавливают свою первоначальную
форму и в их внутреннем состоянии не
происходит каких-

Столкновение
обычных либо изменений, если сохраняется
суммарная механическая энергия
тел.макроскопических тел в реальных
условиях всегда бывают в той или иной
степени неупругими, ибо они сопровождаются
нагреванием тел, возникновением
акустических волн и т.д., то есть
превращением части механической энергии
тел в другие виды энергии. Однако в
некоторых случаях столкновение
макроскопических тел можно с достаточной
степенью точности считать абсолютно
упругими (например, столкновение шаров
из слоновой кости или закаленной стали).
Особо важную роль упругие столкновения
играют в физике атомных явлений. Так
столкновение молекул газа друг с другом
и со стенками сосуда, в который газ
заключен, можно уподобить соударениям
абсолютно упругих шаров. Упруго
рассеиваются

– частицы при прохождении через тонкие
пленки вещества (опыт Резерфорда),
рентгеновские кванты при взаимодействии
с электронами и т.д.

Рассмотрим
абсолютно
упругое центральное столкновение
двух шаров с массами

и
.
Пусть шары движутся один за другим,
(первый шар догоняет второй) и перед
столкновением имеют скорости

и

соответственно. Во время столкновения
шары деформируются, силы упругой
деформации изменяют скорости шаров.
Обозначим скорости шаров после
столкновения

и
.
Полагая, что шары образуют замкнутую
систему, применим к ним закон сохранения
импульса:

(2.1)

Пусть массы шаров
таковы, что и после соударения они
продолжают двигаться в том же направлении,
в каком двигались до столкновения. Тогда
соотношение (2.1) в проекциях запишется
так:

(2.1,а)

Детальный анализ
деформации шаров в процессе упругого
столкновения весьма сложен. Но этот
анализ, в принципе, и не нужен. Так как
шары полностью восстанавливают свою
первоначальную форму, и в их внутреннем
состоянии не происходит изменений, то
закон сохранения энергии сводится к
сохранению кинетической энергии:

(2.2)

Решая уравнения
(2.1а) и (2.2) совместно (это следует проделать
самостоятельно), получаем:

(2.3)

(2.4)

Рассмотрим
некоторые частные случаи:

а)
Массы шаров равны:

Тогда

и
.
Шары просто обмениваются своими
скоростями. Если до столкновения второй
шар покоился
,
то после столкновения он начинает
двигаться со скоростью первого шара
(),
а первый шар останавливается

б)
Масса второго шара значительно больше
массы первого
.
Разделим числитель и знаменатель в
выражениях (2.3) и (2.4) на
:

;

.

В этих формулах
отношением

в силу его малости можно пренебречь.
Тогда

и

Вывод: при упругом
центральном столкновении шара малой
массы с шаром большой массы скорость
шара большей массы практически не
изменяется. Если до удара массивный шар
покоился (=
0), то шар малой массы отскакивает от
массивного неподвижного шара со
скоростью, почти равной по величине и
противоположной по направлению той
скорости, с которой он двигался до
соударения
.
При этом легкий шар практически не
передает свою кинетическую энергию
массивному шару.

Полученный вывод
можно применить к упругому удару шара
о неподвижную стенку, перпендикулярную
направлению движения шара (с этим случаем
мы сталкиваемся, например, при расчете
давления, оказываемого молекулами газа
на стенки сосуда). Найдем приращение
импульса шара при таком упругом
столкновении:

.

Такой же по величине,
но противоположный по знаку импульс,
получит стенка.

в)
,
но
.
Шары двигаются в одном направлении.
Тогда:

.

В этом случае малый
шар отскакивает от большого со скоростью,
меньшей первоначальной на величину

.

Нечто подобное
происходит в цилиндре с газом при
расширении газа. Молекулы, ударяющиеся
о удаляющийся поршень, теряют свою
скорость и, следовательно, кинетическую
энергию. Эти «потери» проявляются в
охлаждении газа.

г)
,
но
.
Шары двигаются
навстречу друг другу. Тогда:

,

т.е. проекция
скорости

на положительно выбранное направление
отрицательна. В рассматриваемом случае
малый шар отскакивает от большого со
скоростью, превышающей ту, с которой он
ударяется о большой шар на величину
.

Нечто подобное
происходит в цилиндре с газом при сжатии
газа. Молекулы, ударяющиеся в надвигающийся
поршень, увеличивают свою скорость и
кинетическую энергию, что проявляется
в нагревании газа.

Мы убедились, что,
используя законы сохранения импульса
и энергии, можно довольно просто
определить скорости шаров после удара
при известных величинах масс шаров и
их скоростей до удара. Наоборот, зная
массы шаров и их скорости до и после
столкновения, легко проверить основные
законы сохранения.

Рассмотрим случай,
когда один из шаров (пусть это будет шар
с массой
)
до столкновения покоился, а другой с
массой

обладает скоростью
.
Начальные скорости шаров после
столкновения обозначим соответственно

и
.
В силу законов сохранения импульса и
энергии приходим к уравнениям:

(3.1)

. (3.2)

При центральном
ударе движение столкнувшихся шаров
после удара будет происходить вдоль
той же прямой и в уравнении (3.1) векторные
значки можно снять

(3.3)

(3.4)

или

(3.5)

. (3.6)

Разделив последнее
из этих уравнений на предыдущее, находим

,

и, подставляя
значение

в уравнение (3.5), определим скорость
налетающей частицы после столкновения
через ее скорость до столкновения:

(3.7)

Теперь нетрудно
найти отношение кинетических энергий
шаров после и до столкновения:

, (3.8)

где через

обозначено
отношение масс шаров
.

Отсюда следует,
что шар ‑ снаряд при столкновении с
другим шаром замедляется тем сильнее,
чем ближе между собой массы шаров. Из
условия (3.3)
также следует, что при
,

0, то есть после столкновения с более
тяжелым шаром, шар-снаряд приобретает
скорость, направление которой
противоположно первоначальной.

МЕТОДИКА ЭКСПЕРИМЕНТА
И ОПИСАНИЕ УСТАНОВКИ

Лабораторная
установка по изучению столкновений
шаров представляет собой «бильярдный»
стол, снабженный наклонной плоскостью.
Для проверки основных закономерностей
упругого столкновения необходимо знать
скорости шаров до и после столкновения.
Их можно определить следующим образом.

1. Пусть шар массой
М
скатывается по наклонной плоскости с
высоты h
и в точке пересечения наклонной плоскости
с горизонтальной поверхностью стола,
отстоящей на расстоянии

от исходной, обладает скоростью .
Тогда, используя закон сохранения
энергии, имеем

,

где первое и второе
слагаемые справа выражают кинетическую
энергию поступательного и вращательного
движения шара соответственно, а третье
‑ работу шара против сил трения.
Последнюю можно выразить через коэффициент
трения
,
вес шара

(ввиду малости наклона считаем силу
давления на наклонную плоскость со
стороны шара равной его весу) и путь
:

.

Момент инерции
шара радиуса r
,
а угловая скорость
,
поэтому

,

откуда скорость
шара, скатившегося по наклонной плоскости,
определяется выражением

. (3.9)

2. Пусть в результате
абсолютно упругого центрального
столкновения шаров массой

и

они приобретают скорости

и

и от точки соударения проходят по столу
до полной остановки расстояния

и

соответственно. В силу закона сохранения
энергии имеем для первого шара

или

,

откуда начальная
скорость первого шара после соударения

(3.10)

Аналогично для
второго шара

(3.11)

3. Коэффициент
трения

можно определить следующим образом.
Если шар, скатываясь с высоты
,
пробегает
по горизонтальной поверхности стола
до полной остановки расстояние

,
то из равенства

находим

, (3.12)

ПОРЯДОК ВЫПОЛНЕНИЯ
РАБОТЫ

1. Установить с
   помощью уровня поверхность стола строго
   горизонтально.

2. Определить на
   весах массы шаров с точностью до 0,1 г.

3. Определить
   коэффициент трения
   .
   Для этого по наклонной плоскости,
   расположенной под малым углом к
   горизонтальной поверхности стола, с
   определенной высоты
   
   cкатить
   поочередно исследуемые шары и замерить
   пробегаемые ими расстояния
   
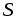
   от точки начала движения по горизонтальной
   поверхности стола до полной остановки
   шара. Значения
   
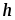
   и
   
   занести в таблицу. Расчет
   
   произвести,
   используя соотношение (3.12).

4. Проверить законы
   сохранения импульсов и энергии при
   столкновении. Для этого установить
   один из шаров в начале системы координат,
   нанесенной на столе и, скатывая с
   определенной высоты стальной шар,
   измерить расстояния
   
   и
   ,
   пробегаемые шарами после столкновения,
   а также углы
   
   и
   ,
   образуемые направлениями
   
   и
   
   с осью 0_x.
   Слегка смещая неподвижный шар по оси
   0_y,
   повторить опыт трижды, после чего
   сменить неподвижный шар и проделать
   то же с остальными шарами. При этом
   высота скатывания стального шара должна
   оставаться неизменной. Для каждого
   шара одно из столкновений должно быть
   центральным. Для проверки закона
   сохранения импульса уравнение следует
   записать через проекции импульсов на
   координатную ось 0_x:

.

Скорости
,

и


вычислить по формулам (3.9), (3.10), (3.11).
Результаты измерений и вычислений
занести в таблицу.

1. Исследовать
   распределение энергии шаров после
   центрального столкновения. С этой целью
   из предыдущих опытов выбрать случаи
   центрального столкновения и проверить
   формулу (3.8).

2. Исследовать
   нецентральные столкновения шаров
   равных масс. Для этого выбрать два шара
   равных масс и, скатывая один из них с

наклонной плоскости,
замерить углы

и
,
образуемые направлениями движения
шаров с осью

после их столкновения. Опыт повторить
пять раз.

0

1

кг

кг

м

м

м

м

м/с

кгм/с

м

м

м/с

м/с