План урока:
Отношение двух чисел
Определение пропорции
Масштаб
Отношение двух чисел
На уроке математики ребята выполняли самостоятельную работу. На решение самостоятельных заданий Наталья Ивановна выделила 15 минут, после чего попросила сдать тетради на проверку. Подумайте, какую часть урока заняла самостоятельная работа?
Чтобы дать ответ на данное задание, давайте вспомним, какую продолжительность имеет обычный урок? Всем известно, что стандартный урок длится 45 минут. Получается, из 45 минут только 15 дети решали самостоятельную работу. Следовательно, нужно выяснить, какая часть целого урока потрачена на самостоятельную работу. В арифметике для вычисления части от числа или определения во сколько раз одно число больше другого существует специальное понятие «Отношение чисел»:
Исходя из рассмотренного определения, необходимо составить отношение длительности самостоятельной работы к длительности целого урока. Таким образом, ответим на главный вопрос задачи. Запишем отношение (частное) двух чисел:
15/45 – данную дробь можно сократить, разделив числитель и знаменатель на 15.
15/45 = 1/3.
Выходит, что на самостоятельную работу класс потратил 1/3 всего урока.
Важно помнить, что числовое значение отношения чисел останется прежним, если каждый компонент отношения умножить или разделить на одно и то же число.
Например:
Давайте, составляющие отношения 6/7 умножим на 2, то есть на дробь 2/2.
6/7 × 2/2 (числитель умножаем на числитель, знаменатель на знаменатель);
Получаем:
6×2/7×2 = 12/14 – при сокращении на 2, получим исходную дробь.
Следовательно, числовое значение дроби не изменилось – 6/7 = 12/14.
При составлении отношений с использованием различных чисел и величин, важно помнить, что отношение будет верным, если все компоненты отношения выражены в одинаковых единицах измерения.
Разберем на примере.
В вазочке находился один килограмм конфет. Бабушка отсыпала 300 граммов сладостей в пакет. Определите, какую часть всех конфет отсыпала бабушка?
Чтобы ответить на главный вопрос задачи нужно составить отношение массы отсыпанных конфет к общей массе сладостей: 300 граммов/1 килограмм. Сразу определить числовое значение отношения не можем, составляющие имеют разные единицы измерения массы – грамм и килограмм. Выразим один килограмм в граммах:
1кг = 1000 грамм
Теперь определим, какую часть составили отсыпанные сладости:
Бабушка отсыпала 3/10 всех сладостей в пакет.
Запомни!
Если a и b числовые значения или значения, выраженные в одной и той же величине, тогда:
- отношение a/b, будет равно частному a и b;
- при условии, что a>b, отношение a/b говорит, во сколько раз a больше, чем b;
- при условии, что a<b, отношение a/b говорит, какую часть a составляет от b.
Определение пропорции
Руководитель детского хореографического кружка, для пошива костюмов своим воспитанникам, приобрел в магазине тканей 10 метров шелка, на сумму 420 рублей. Но купленной ткани не хватило. Какую сумму нужно потратить, чтобы купить еще 5 метров такого же материала?
Данную задачу можно решить двумя способами. Рассмотрим каждый из них подробно.
1 способ.
По условию нам известно, что 10 метров материала, стоит 420 рублей. Отсюда можно узнать цену одного метра. Для этого, общую сумму(420) необходимо разделить на количество приобретенной ткани(10):
420 : 10 = 42 рубля стоит один метр ткани.
Зная цену одного метра ткани, можно узнать стоимость пяти метров. Для этого стоимость одного метра (42), умножаем на количество таких метров (5):
42 × 5 = 210 рублей необходимо, для покупки 5 метров материала.
Этот способ известен еще из начальной школы. Но далеко не все задачи такого вида можно решить первым способом.
В этом случае используют второй способ решения задач такого вида.
2 способ.
Вначале, запишем краткое условие.
10м. – 420 р.
5м. – ? р.
Теперь нужно подумать. В нашем случае, количество материала уменьшается, следовательно,уменьшается стоимость покупки. Обозначим цену пяти метров материала – х.
Имеем,
10 – 420.
5 – х.
Для решения задач такого вида в математике существует специальное определение – «Пропорция»
Используя рассмотренное определение, подумаем, как составить пропорцию из чисел? Формировать пропорцию будем, опираясь на краткую запись условия задачи – десять относится к пяти как четыреста двадцать к иксу:
10/5 = 420/х.
Пропорция составлена и возникает вопрос, как вычислить неизвестный компонент?
Для вычисления неизвестной составляющей пропорции существует правило, которое называется «Основное свойство пропорции»:
Определим крайние и средние члены в составленном равенстве:
Крайними членами пропорции будут числа 10, х.
Средними членами пропорции будут числа 5, 420.
Запишем равенство произведений крайних и средних членов в составленной пропорции:
10/5 = 420/х;
10х = 5 × 420 – высчитываем произведение;
10х = 2100 – решаем как обычное уравнение;
х = 2100 : 10;
х = 210.
Выходит, 210 рублей необходимо для приобретения пяти метров материала.
Вот так на примере решения задачи мы разобрали новое определение. Запомните, пожалуйста, все правила и поиск неизвестного компонента в любых отношениях и пропорциях будет для вас только развлечением!
Продолжаем дальше знакомиться с пропорцией.
Прямая и обратная пропорциональная зависимость.
Рассмотрим ситуацию, в которой оказывается каждый, попадая в магазин.
Витя пришел в магазин за покупками. В кошельке ребенка лежало 300 рублей. Витя купил хлеб, молоко, масло, заплатил за товар. Денег у мальчика стало меньше. После посещения кондитерского отдела, где он купил карамель, пирожные, рулет денег стало совсем мало. Делаем вывод: чем больше покупок делает мальчик, тем меньше денег у него остается.
Значит, количество денег в нашем кошельке и количество покупок имеют обратно пропорциональную зависимость и являются обратно пропорциональными величинами.
А если взять ситуацию с оплатой за пользование водой и электроэнергией
Чем больше воды/электроэнергии мы используем, тем больше должны заплатить. В таком случае величины кубы воды/киловатты электроэнергии и денежные единицы называются прямо пропорциональными и имеют прямую пропорциональную зависимость.
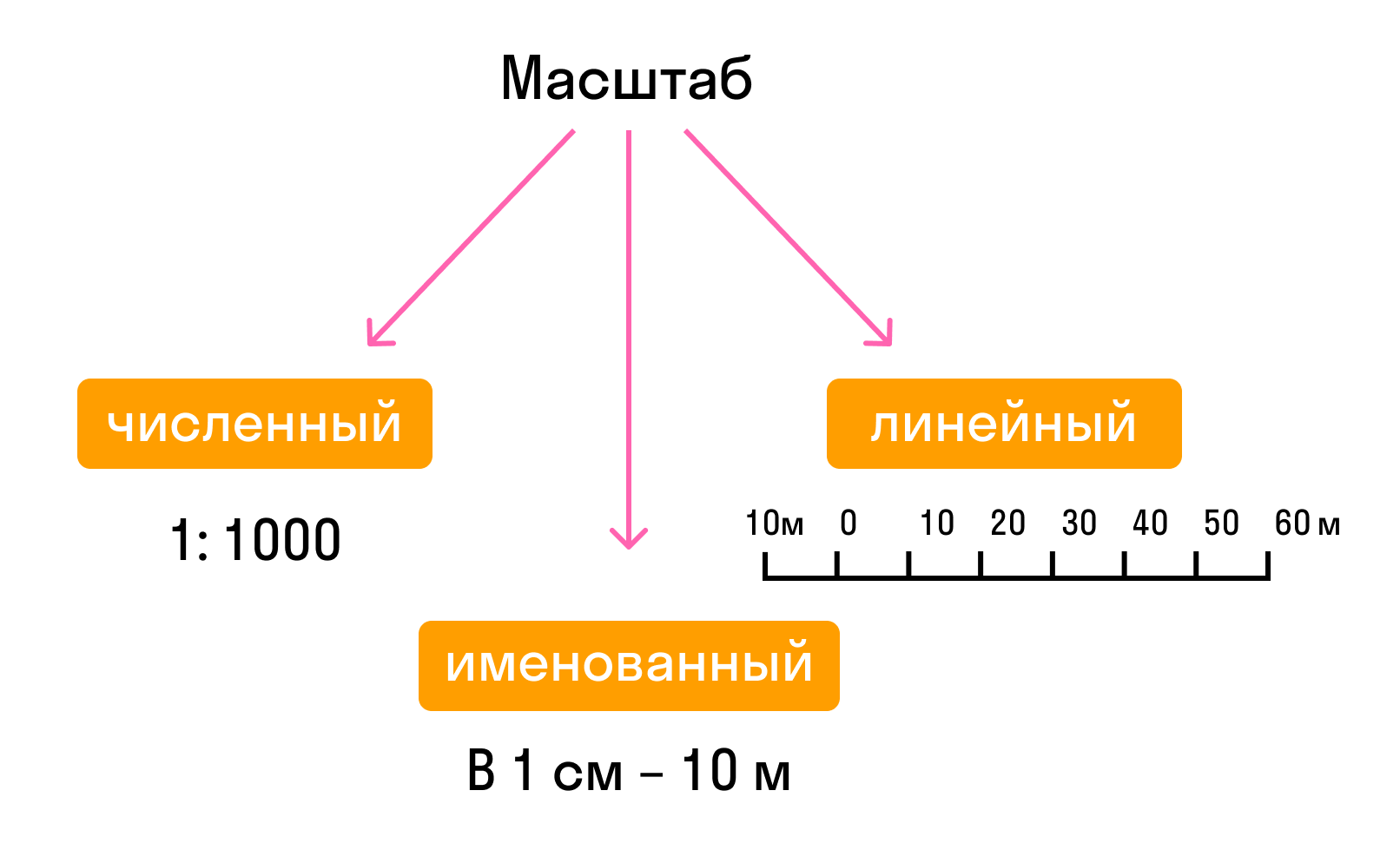
Масштаб
Мама с Арсением решили нарисовать путь, который проходит мальчик, идя из дома в школу. Ребенок заволновался: «Как можно на листке бумаги нарисовать 450 метров пути?». Мама успокоила сына и рассказала, что именно для таких случаев и используется определение масштаба карты.
Рассмотрим решение задачи с использованием масштаба.
Расстояние на карте от Москвы до Киева составляет пять сантиметров. Вычислите, сколько километров от Москвы до Киева, если масштаб карты 1:15 000 000.
В первую очередь, нужно понимать, что масштаб 1:15 000 000 показывает, что 1 см карты содержит 15 000 000 сантиметров или 150 километров на местности.
Чтобы ответить на главный вопрос задачи,составим пропорцию. Для этого, расстояние на местности от Москвы до Киева примем за х:
1 : 150 = 5 : х.
Помним, произведение крайних членов пропорции равно произведению средних. Имеем:
х= 150 × 5;
х = 750.
Выходит, 750 километров – расстояние от Москвы до Киева.
Расчеты оказались верными. Вся справочная литература говорит о том, что расстояние Москва – Киев составляет примерно 755 км!
Теперь вы совершенно самостоятельно можете рассчитать абсолютно любое расстояние, имея под рукой линейку и карту!
Интересно!
С пропорциями мы сталкиваемся, ежедневно, ежеминутно. Все в нашем мире пропорционально. Любая вещь, предмет, техника, животные, растения – все имеет свои пропорции! Мы можем любоваться красивой архитектурой – благодаря пропорциям, наслаждаться цветками роз или ромашек – тоже не без участия пропорций. Природа создает все в строгой пропорциональности. В случае, когда пропорции отсутствуют, вещь или предмет нам кажутся неправильными. Ведь даже в нашем теле все имеет свои пропорции:
- длина ладони равна длине четырех пальцев, длина четырех ладошек(без учета пальцев) равна длине стопы, шесть ладоней – длина локтя, а четыре локтя в точности укажут на рост хозяина;
- длина человеческой ладони с пальцами составляет 1/10 роста человека;
- длина расставленных в стороны рук совпадает с длиной человеческого тела;
- стопа составляет 1/7 часть роста;
- длина от корней волос до кончика подбородка равна 1/10 роста.
Математика
6 класс
Урок № 3
Масштаб
Перечень рассматриваемых вопросов:
- Понятие масштаба.
- Находить масштаб по заданному расстоянию на местности и расстоянию на карте (плане).
- При заданном масштабе и расстоянии на местности определять расстояние на карте (плане).
- При заданном масштабе и расстоянии на карте (плане) определять расстояние на местности.
Тезаурус
Частное двух не равных нулю чисел a и b называется отношением чисел a и b.
Числа a и b называются членами отношения.
Отношения 2 к 3 и 3 к 2 называются взаимно обратными.
Отношение величин одного наименования (длины, скорости, стоимости и т. д., выраженных одинаковыми единицами измерения) есть число.
Отношение величин различных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма и т. д.) есть новая величина.
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Масштаб, выраженный отношением чисел, называется численным.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.
Теоретический материал для самостоятельного изучения
Сегодня мы с вами разберём, что означает масштаб.
Давайте сначала вспомним, что отношение величин одного наименования – это число.
Составим отношения:
Все мы хорошо знаем, что участки земной поверхности, детали машин и многое другое изображается на бумаге в уменьшенном виде.
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Рассмотрим пример:
Длина отрезка на карте равна 8 см.
Ответ: 800 м.
Ещё один пример:
Длина отрезка на местности равна 130 километров.

Ответ: 13 см.
Что же означает данный масштаб:

Говорят: карта сделана в масштабе одна двухтысячная. Объект на карте уменьшен в 2000 раз.
Что будет означать такой масштаб:

Рассмотрим ещё несколько примеров.
Огород имеет вид прямоугольника, длина которого 60 м, а ширина 10 м.

Ответ: Огород на плане будет иметь размеры: ширина 20 см, длина 12 см.

Разбор заданий тренировочного модуля
№ 1. Тип задания: Установление соответствий между элементами двух множеств.
Расстояние между двумя городами равно 150 км. Определите расстояние между изображениями этих городов на карте при трёх разных масштабах карты.

№ 2. Тип задания: Выбор элемента из выпадающего списка.
Значит, выбираем ответ 15 км.
Отправляясь в увлекательное путешествие, выясняя адрес места встречи, определяя маршрут, открывая карту или навигатор, каждый человек сталкивается с таким понятием как масштаб.
Эта информация доступна зарегистрированным пользователям
Сегодня на уроке мы определим, что такое масштаб, рассмотрим, какие существуют виды масштаба и где им находят применение.
Научимся определять масштаб и решать задачи, связанные с ним.
С давних пор люди использовали изображения (рисунки) как средство общения и передачи информации друг другу.
Сначала это были простейшие изображения, но с течением времени они совершенствовались.
Создание рисунков и изображений все больше стали находить применение в жизни человека. Например, при строительстве сооружений.
Эта информация доступна зарегистрированным пользователям
Желание уменьшать размеры реальных объектов и переносить их изображения на плоскую поверхность возникало не только в области строительства, но и в других сферах деятельности человека.
Эта информация доступна зарегистрированным пользователям
Попробуем разобраться, что такое масштаб, для чего он необходим и что он показывает.
Масштаб – слово немецкого происхождения (Maßstab), переводится как мерило, мера, размер.
Масштаб – это отношение длины отрезка на карте (плане, чертеже) к длине соответствующего отрезка в действительности на местности.
Условно можно обозначить так:
Эта информация доступна зарегистрированным пользователям
Масштаб записывается в виде дроби (отношения двух чисел).
Обычно числитель этой дроби равен единице, а знаменатель показывает во сколько раз на карте (плане, чертеже) уменьшены размеры объекта относительно его размеров в действительности.
Пример:
Масштаб 1:100000 означает, что 1 сантиметру на карте соответствует 100 000 сантиметров (1 километр) реального расстояния на местности, т.е. можно говорить, что на карте все расстояния и размеры уменьшены в 100 000 раз по сравнению с действительными размерами.
При масштабе 1:100 000 на карте расстояние, равное 100 000 сантиметров (1 километр), будет изображаться отрезком в 1 сантиметр.
Масштаб обозначают целым словом «Масштаб» или заглавной буквой М.
Эта информация доступна зарегистрированным пользователям
Различают три вида масштаба:
- численный
- именованный
- графический
Графический, в свою очередь, делится на линейный и поперечный.
Эта информация доступна зарегистрированным пользователям
Численный масштаб представляют в виде дроби, где числитель – это единица, а знаменатель показывает степень уменьшения размеров изображения объектов относительно их реальных размеров.
Численный масштаб – это дробь, поэтому числитель и знаменатель выражены в одинаковых единицах измерения.
При обозначении численного масштаба не указывают единицы измерения, указывают только числа (1:2 000, 1:200 000, 1:100 и т.п.).
Пример 1
Численный масштаб карты 1:15 000 000, что он показывает?
Данный масштаб показывает, что 1 см на карте соответствует 15 000 000 см в действительности.
Нужно помнить, что чем меньше значение знаменателя в масштабе, тем крупнее масштаб.
Пример 2
Масштаб 1:1 000 крупнее, чем 1:15 000, так как знаменатель первого масштаба равен 1 000, а знаменатель второго масштаба 15 000.
1 000 меньше 15 000, следовательно, масштаб 1:1 000 крупнее.
Чем крупнее масштаб, тем больше можно изобразить объектов действительности, карта (план) получается подробней и содержательней.
При большем масштабе хорошо изображать небольшие по площади территории.
Применяется в топографических картах и планах.
На чертежах могут изображаться как уменьшенные изображения реальных объектов, так и увеличенные, если размеры изображаемого объекта слишком малы.
Эта информация доступна зарегистрированным пользователям
Именованный масштаб– это, по сути, словесное обозначение численного масштаба.
Такой масштаб показывает, сколько одному сантиметру на карте (плане) соответствует метров (километров) на местности.
Расстояние на местности, соответствующее 1 сантиметру на карте (плане), называют величиной масштаба.
Пример 3
Дан именованный масштаб: в 1 см – 250 м (в 1 сантиметре 250 метров).
Такой масштаб означает, что 250 м на местности соответствуют 1 см на карте (плане).
Величина этого масштаба равна 250 м.
Эта информация доступна зарегистрированным пользователям
Графический масштаб подразделяют на линейный и поперечный.
Линейный масштаб дает возможность определить расстояние и размеры без расчетов и переводов длин из масштабных в реальные, позволяя тем самым ускорить работу с картой.
Линейный масштаб представляет собой отрезок прямой, разделенный на деления (подобно линейке со шкалой).
Эти деления равной длины, но с разным номинальным значением, называют основанием линейного масштаба.
Каждое деление подписано значениями, указывающими размеры соответствующих им отрезков в действительности.
Основание откладывается по всей длине масштабного отрезка (чаще всего с шагом 2 см).
Крайнее левое от нуля основание делят на более мелкие деления – это наименьшее деление линейного масштаба.
Расстояние в действительности, соответствующее номинальному делению масштаба, называют точностью масштаба (т.е. это отрезок на местности, который соответствует одному минимальному значению масштаба).
Эта информация доступна зарегистрированным пользователям
Поперечный масштаб
Поперечный масштаб это улучшенный вариант линейного масштаба, позволяющий делать максимально точные измерения расстояний и размеров.
Выглядит поперечный масштаб, как сетка, состоящая из горизонтальных линий, пересеченных вертикалями и наклонными линиями (трансверсали).
Используют поперечный масштаб подобно линейному, но измерения откладываются по трем основаниям (горизонталям, вертикалям и трансверсалям).
Для фиксирования длины отрезка на карте также используют циркуль.
Чаще всего поперечный масштаб применяют на специализированных картах.
Этот вид масштаба удобен для определения длинны рек, дорог, горных хребтов и других кривых на карте.
Нередко для удобства на картах приводятся все три вида масштабов: численный, именованный, графический (линейный).
Эта информация доступна зарегистрированным пользователям
Задачи, связанные с масштабом, бывают трех типов:
- Задачи на определение расстояния (размеров) на карте
- Задачи на определение расстояния на местности (размеров реального объекта)
- Задачи на определение масштаба
Алгоритм решения задач первого и второго типа можно представить так:
- Привести единицы измерения величин к общему виду
- Обозначить неизвестную величину (чаще всего обозначают буквой х)
- Составить пропорцию с неизвестным членом
- Составить уравнение
- Решить уравнение (найти неизвестный член пропорции)
- Записать ответ
Задача 1
Длина отрезка на местности – 4 км.
Найдите длину этого отрезка на карте, если масштаб карты 1:200 000.
Решение:
В 1 см на карте- 200 000 см
1 км = 100 000 см
4 км = 400 000 см
Пусть х (см)- длина отрезка на карте.
Составим краткую запись задачи в виде таблицы
Эта информация доступна зарегистрированным пользователям
Составим пропорцию:
(mathbf{frac{x}{400000} = frac{1}{200000}})
Составим уравнение, используя основное свойство пропорции:
(mathbf{{x}cdot{200000} = {1}cdot{400000}})
(mathbf{{x}= frac{400000}{200000}})
(mathbf{x = 2})(см)
Ответ: (mathbf{x = 2}) (см) длина отрезка на карте.
Задача 2
Длина отрезка на карте 6 см.
Найдите длину соответствующего отрезка на местности, если масштаб карты 1:1000000.
Решение:
В 1 см на карте- 1 000 000 см
1 км = 100 000 см
Пусть х (см)- длина отрезка на местности.
Составим краткую запись задачи в виде таблицы
Эта информация доступна зарегистрированным пользователям
Составим пропорцию:
(mathbf{frac{6}{x} = frac{1}{100000}})
Составим уравнение, используя основное свойство пропорции:
(mathbf{{x}cdot{1} = {6}cdot{1000000}})
(mathbf{x = 6000000})(см)
(mathbf{x = 60})(км)
Ответ: (mathbf{x = 60}) (км) длина отрезка на местности.
Задача 3
Расстояние между населенными пунктами А и В составляет 400 км.
Расстояние между населенными пунктами А и В на карте равно 10 см.
Определите масштаб карты.
Эта информация доступна зарегистрированным пользователям
Решение:
Так как масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности
(mathbf{M = frac{L_{карта}}{L_{местность}}})
где М– масштаб карты
Lкарта– расстояние между населенными пунктами на карте
Lместность– расстояние между населенными пунктами на местности
Запишем, как относятся расстояние на карте и на местности для нашей задачи.
Приведем величины к единой единице измерения:
400 км = 400 000 м= 40 000 000 см
(mathbf{M = frac{10}{40000000}})
(mathbf{M = frac{1}{4000000}})
Ответ: Масштаб карты 1:4 000 000
Задача 4 (практика)
Выясним как пользоваться масштабом на карте
По карте нужно узнать реальное расстояние от пункта А до пункта В. Задан масштаб карты 1:500 000 (или в 1 см- 5 км).
Решение:
Необходимо взять линейку и измерить расстояние от пункта А до пункта В на карте. Полученную величину (допустим, измеренный отрезок получился равным 6 см) умножим на величину масштаба (для нашей задачи величина масштаба равна 5 км = 500 000 см)
(mathbf{6 см cdot 500 000 см = 3 000 000см = 30км})
Ответ: Расстояние между пунктами А и В равно 30 километров
Масштаб используют не только в картографии и геодезии, но и в других областях деятельности человека:
- на производстве при создании чертежей крупногабаритных или мелких деталей
- в проектировании и архитектуре при создании чертежей зданий, сооружений, коммуникаций
- в фото и видео технике есть возможность масштабирования картинки (увеличивая или уменьшая ее)
- в конструировании и моделировании (при создании макетов, моделей, выкроек)
Эта информация доступна зарегистрированным пользователям
Вчера мы с вами рассмотрели что такое отношения. Сегодня предлагаем вам узнать, а для чего еще можно использовать отношения на практике.
Человек очень часто использует не сами предметы, а их изображения – на карте, чертеже, фотографии.
Отношение длины отрезка на карте к его реальной длине на местности называют масштабом.
Как видим из определения, масштаб – это число. Для географических карт оно меньше единицы, ведь на местности расстояния намного больше, чем мы можем изобразить графически. 1:10 000, 1:100 000 000 и так далее.
Но для технических чертежей масштаб может быть большим единицы, если необходимо изобразить какие-либо детали маленького размера, тогда масштаб может быть 2:1, 10:1 и т.д.
Задачи на масштаб условно можно разделить на три группы:
- Определение расстояния на местности.
- Вычисление отрезка на карте.
- Нахождение масштаба.
Рассмотрим первую задачу.
Как видим, ничего страшного в этом нет. Решим задачу второго типа.
Третья задачка немного сложнее, но надеемся, вам станет понятнее.
Надеемся, эта статья была вам полезна. Задавайте вопросы в комментариях.
Содержание
- Масштаб в математике
- Понятие масштаба
- Определение масштаба на карте
- Решение задач на масштаб
- Как определить масштаб
- Пошаговая инструкция, как определить масштаб
- Понятие и виды масштабов
- Параметры точности масштаба
- Способ определения масштаба
- Правила оформления
- Порядок определения масштаба на готовом чертеже
- Советы бывалых
- Как определить масштаб
Масштаб в математике
Масштаб — интересная тема, которую можно применить в разных областях: математике, географии, черчении и даже в физике. В этом материале узнаем больше про масштаб, чтобы решать задачки и не растеряться, если в руках окажется карта сокровищ.
29 декабря 2020
· Обновлено 28 октября 2022
Понятие масштаба
Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.
Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.
Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.
- Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
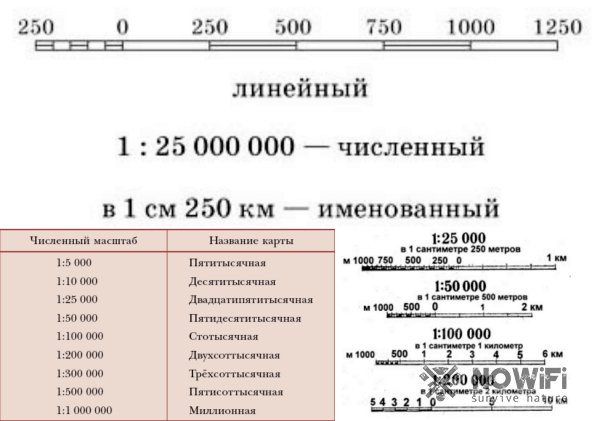
Масштаб бывает трех видов:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
- линейный, зная величину масштаба, можно определить расстояния.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Определение масштаба на карте
На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.
Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.
Масштаб — это отношение размера изображения к размеру изображаемого объекта.
Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.
На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.
Численные масштабы карт и соответствующие им масштабы на местности:
Масштаб 1 : 100 000
- 1 мм на карте — 100 м (0,1 км) на местности
- 1 см на карте — 1000 м (1 км) на местности
- 10 см на карте — 10000 м (10 км) на местности
Масштаб 1 : 10000
- 1 мм на карте — 10 м (0,01 км) на местности
- 1 см на карте — 100 м (0,1 км) на местности
- 10 см на карте — 1000 м (1 км) на местности
Масштаб 1 : 5000
- 1 мм на карте — 5 м (0,005 км) на местности
- 1 см на карте — 50 м (0,05 км) на местности
- 10 см на карте — 500 м (0,5 км) на местности
Масштаб 1 : 2000
- 1 мм на карте — 2 м (0,002 км) на местности
- 1 см на карте — 20 м (0,02 км) на местности
- 10 см на карте — 200 м (0,2 км) на местности
Масштаб 1 : 1000
- 1 мм на карте — 100 см (1 м) на местности
- 1 см на карте — 1000 см (10 м) на местности
- 10 см на карте — 100 м на местности
- 1 мм на карте — 50 см (0,5 метра) на местности
- 1 см на карте — 5 м на местности
- 10 см на карте — 50 м на местности
- 1 мм на карте — 0,2 м (20 см) на местности
- 1 см на карте — 2 м (200 см) на местности
- 10 см на карте — 20 м (0,2 км) на местности
- 1 мм на карте — 0,1 м (10 см) на местности
- 1 см на карте — 1 м (100 см) на местности
- 10 см на карте — 10м (0,01 км) на местности
Решение задач на масштаб
Для закрепления темы решим несколько математических задач на масштаб за 6 класс.
Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.
8 см — это 1 часть
8 * 10 000 = 80 000 (см) — это 10 000 частей
80 000 см = 800 м
Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.
400 км = 400 000 м = 40 000 000 см
40000000 : 5000000 = 40 : 5 = 8
Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?
Источник
Как определить масштаб
Отравляясь в лес или поход, мы всегда берем с собой карту. Именно с ее помощью туристы определяют свое местоположение на местности и прокладывают маршрут. Естественно, расстояния на картах показаны не в реальных показателях, а в определенном масштабе.
Соответственно, чтобы научиться читать карту, нужно знать, как определить масштаб в каждом конкретном случае. Именно этому вопросу и будет посвящена сегодняшняя статья.
Пошаговая инструкция, как определить масштаб
Обычно составитель указывает линейный или численный масштаб чертежа или карты, с помощью которого и определяется расстояние между объектами на местности. Но иногда топографическая карта не содержит этой информации, и определять масштаб приходится самостоятельно. В этом пригодятся некоторые знания в географии (рисунок 1).
Самый простой способ определить масштаб – использовать километровую сетку. Она проставлена на любой карте, а стороны каждого квадрата соответствуют определенному количеству километров.
Узнать это расстояние можно по подписям у выхода линий сетки к краям карты. Например, на подписи указано, что расстояние между двумя линиями сетки составляет 1 км. Теперь измерьте это расстояние линейкой. Предположим, вы получили показатель в 2 см. Соответственно, каждый сантиметр карты соответствует 500 метрам на местности, а сам масштаб чертежа составляет 1:50000.
Понятие и виды масштабов
Чтобы научиться правильно вычислять масштаб, будет нелишним ознакомиться с самыми определением этого понятия. Итак, с научной точки зрения масштаб – это определенный показатель, по которому длина отрезка на карте, плане или схеме топосъемки соответствует действительной длине этого же отрезка на местности (рисунок 2).
Существует несколько видов масштаба:
- Численный: масштаб, выполненный в виде дроби. В нем числитель – это всегда единица, а знаменатель – число, отображающее, во сколько раз уменьшено расстояние на карте.
- Линейный: масштаб, облегчающий ориентирование. Он представляет собой специальную мерную линейку, которую наносят на карты для облегчения вычисления расстояний на местности.
- Поперечный масштаб: используется для максимально точных измерений. Обычно его гравируют на металлических линейках, которые так и называют масштабными.
Самым простым считается именнованный или словесный масштаб. В данном случае на изображении карты просто указано, какому расстоянию соответствует 1 см плана (например, в 1 см 5 км).
Параметры точности масштаба
Точность масштаба на чертеже ограничена расстоянием в 0,01 см. Количество метров, соответствующее этому показателю на местности, и называется определением «графическая точность».
Чтобы узнать этот показатель, нужно воспользоваться градусной сеткой и провести некоторые вычисления. Лучше всего использовать численный масштаб. Берем его знаменатель и делим на 10 000, поскольку 1 см плана содержит 10 тысяч отрезков по 0,01 см. Полученное число и будет соответствовать размеру точности.
Например, если карта имеет масштаб 1:25 000, его точность на местности будет составлять 2,5 метра, а для схемы 1:100 000 – 10 метров и так далее.
Способ определения масштаба
В начале статьи мы уже описывали, как можно определить масштаб изображения с помощью километровой сетки и линейки. Но есть и другие способы установить степень уменьшения и масштабирование на конкретном плане местности (рисунок 3).
Туристы обычно пользуются такими методами:
- Номенклатура карты: чтобы воспользоваться данным способом, нужно внимательно рассмотреть реквизиты карты. Фактически, номенклатура – это буквенно-числовое название листа. У каждого масштабного ряда есть свое обозначение. Например, М-35 соответствует масштабу 1:1000000, а М-35-18-А-6-1 – 1:10000. Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения.
- Известные расстояния: в данном случае на карте нужно найти изображения километровых столбов, которые обычно устанавливают на шоссе. Прямо на карте нужно измерить расстояние между ними. В данном случае количество сантиметров на карте будет соответствовать одному километру на местности.
- Дуга меридиана: одна минута по меридиану соответствует 1,85 км, хотя обычно эту цифру округляют до 2 км. На боковой рамке любой карты есть подписи минут и градусов, а для выделения каждой минуты используется шашечка. Если длина одной минуты равна 3,7 см, то масштаб будет составлять 1:5000, то есть одному сантиметру на карте будет соответствовать 0,5 км на местности.
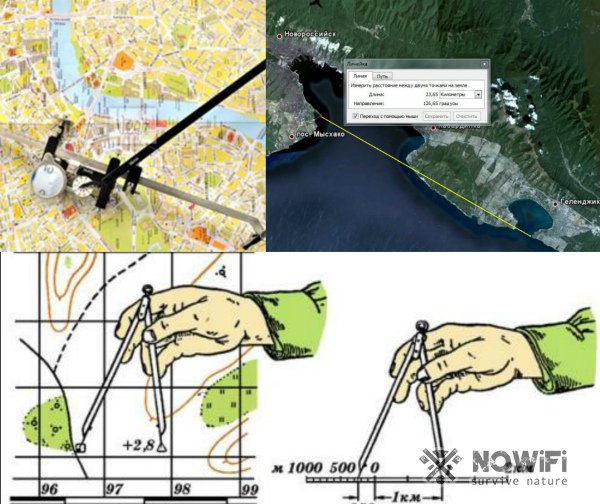
На картах с масштабом 1:2000000 обычно указывается расстояние между определенными населенными пунктами в километрах. В данном случае, для определения масштаба нужно измерить расстояние на карте линейкой. Потом расстояние, указанное в километрах, следует разделить на полученное число в сантиметрах. В результате у вас получится число, которое будет соответствовать количеству километров в одном сантиметре.
Правила оформления
Если топографическая карта местности была изготовлена правильно, на ней должен обязательно быть указан масштаб. Исключение могут быть только самодельные карты или планы местности, нарисованные вручную. Во всех остальных случаях масштаб должен быть оформлен согласно ГОСТу.
Если карта была составлена правильно, находить даже уменьшенные объекты не составит труда, ведь все измерения точно соответствуют расположению на местности.
Порядок определения масштаба на готовом чертеже
Масштаб нужно не только для того, чтобы определить расстояние на карте. Он также используется при составлении чертежей (рисунок 4).
Узнать масштаб чертежа несложно, так как он определяется примерно так же, как и географический. В первую очередь нужно внимательно изучить чертеж. Согласно ГОСТу, масштаб должен быть указан в правом нижнем углу. При этом в машиностроении и приборостроении обычно используют увеличение, а на строительных чертежах – уменьшение.
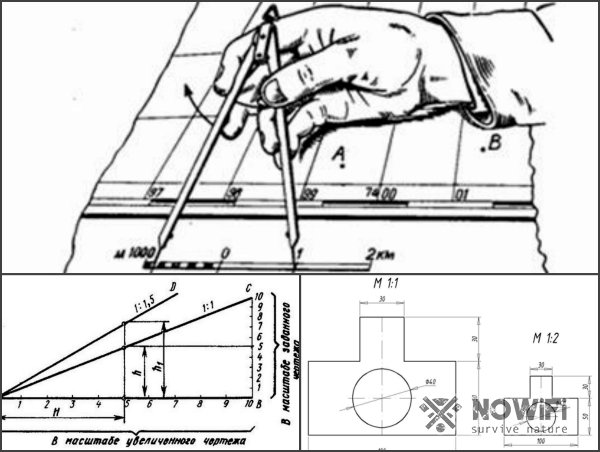
Если по каким-то причинам вы не можете найти масштаб на готовом чертеже невозможно, можно попытаться определить его. Если под рукой есть деталь, можно просто измерить ее штангенциркулем. Также можно определить масштаб по габаритным размерам детали, указанным на чертежах.
Советы бывалых
В целом, масштаб карты и топосъемки можно смело назвать весьма полезным понятием. На первый взгляд может показаться, что определять масштаб и ориентироваться с его помощью на местности сложно.
На самом деле, если научиться высчитывать расстояние, отображенное на карте, и соотносить его с объектами на местности, то отклонение будет составлять всего несколько метров.
Детальную информацию по определению масштаба вы найдете в видео.
Источник
Как определить масштаб
Обычно на каждой карте изображен линейный или численный масштаб. Но как быть, если по той или иной причине масштаб отсутствует? Опытный специалист по внешнему виду может сразу назвать масштаб рассматриваемой карты. Если же вы этого сделать не можете, то следует прибегнуть к следующим способам.
По километровой сетке. На всех топографических картах печатается километровая сетка. Стороны квадратов сетки соответствуют определенному количеству километров. Это легко узнать по подписям на выходах линий сетки у рамки карты. Допустим, что расстояние между двумя соседними линиями сетки равно 1 км. Измеряем это расстояние линейкой; у нас получается 2 см. Значит, масштаб карты в 1см 500 м (1000:2) или 1 :50 000.
По номенклатуре листа. Номенклатура — это буквенно-числовое название листа карты. Каждый масштабный ряд имеет свое обозначение, по которому нетрудно определить масштаб карты. Например:
По известным расстояниям. На картах крупного масштаба особым условным знаком изображаются километровые столбы на шоссейных дорогах. Стоит в таком^ме-сте измерить расстояние от одного столба до другого, и мы сразу узнаем масштаб карты (число сантиметров карты, соответствующее одному километру местности).
На других картах, например, масштаба 1 : 200 000, на дорогах поставлены расстояния в километрах между населенными пунктами. В этом случае надо измерить по карте линейкой расстояние в сантиметрах от одного населенного пункта до другого и подписанное количество километров разделить на расстояние в сантиметрах. Полученное число будет означать величину масштаба карты (число километров в одном сантиметре).
По измеренным расстояниям. В том случае, если мы находимся на местности, которая изображена на карте, масштаб ее можно определить непосредственным измерением расстояния между предметами, нанесенными на карту (а на карте даже детские городки отмечают).
По длине дуги меридиана. Чтобы пользоваться этим способом, нужно твердо помнить, что одна минута по меридиану равна примерно 2 км (точнее 1,85). Подписи градусов и минут всегда даются на боковых сторонах рамки карты и, кроме того, каждая минута выделена шашечкой. На рис. 24 длина одной минуты равна 3,7 см. Значит, масштаб карты будет 1 : 50 000, т. е. один см на карте соответствует 0,5 км на местности. Для уяснения сущности масштаба решим несколько задач.
Задача 1. Масштаб карты 1 : 50 000. На какое число надо разделить знаменатель дроби, чтобы узнать длину линии местности, соответствующей 1 см карты?
Обычно расстояния на местности даются в метрах, а метр, как известно, содержит 100 см. Значит, знаменатель надо делить на 100 (50 000 : 100 = 500 м).
Для решения таких задач полезно запомнить правило: если в знаменателе масштаба зачеркнуть два последних нуля, то оставшееся число покажет, сколько метров местности содержится в 1 см на карте.
Задача 2. Какая карта крупнее, если масштаб одной 1 : 50 000, а другой 1 : 100 000 и во сколько?
Как уже нам известно, масштаб выражается в виде дроби, числитель которой равен единице, а знаменатель число, показывающее, во сколько раз все линии на карте меньше соответствующих линий на местности. А дробь при одинаковом числителе будет больше та, у которой меньше знаменатель. Значит, карта масштаба 1 : 50 000 будет крупнее карты масштаба 1 : 100 000 ровно в два раза.
А если вам встретится такое выражение: «Масштаб карты более 1 км в 1 см», что же это будет за карта? Крупнее или мельче, чем карта масштаба 1 : 100 000, у которой 1 см точно соответствует 1 км? Оказывается, мельче, потому что величина 1 км помещается в знаменателе, а чем больше знаменатель, тем мельче масштаб карты.
Источник