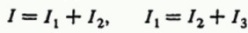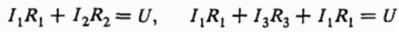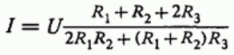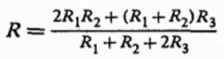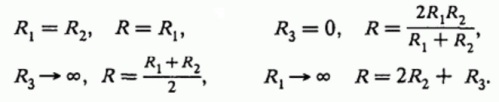Как найти отношение напряжений - Сайт, где вы сможете решить свои вопросы

Ток и напряжение при параллельном, последовательном и смешанном соединении проводников

Реальные электрические цепи чаще всего включают в себя не один проводник, а несколько проводников, как-то соединенных друг с другом. В самом простом виде электрическая цепь имеет только «вход» и «выход», то есть два вывода для соединения с другими проводниками, через которые заряд (ток) имеет возможность втекать в цепь и из цепи вытекать. При установившемся токе в цепи, значения величин токов на входе и на выходе будут одинаковы.

Если взглянуть на электрическую цепь, включающую в себя несколько разных проводников, и рассмотреть на ней пару точек (вход и выход), то в принципе остальная часть цепи может быть рассмотрена как одиночный резистор (по ее эквивалентному сопротивлению).

При таком подходе говорят, что если ток I – это ток в цепи, а напряжение U – напряжение на выводах, то есть разность электрических потенциалов между точками «входа» и «выхода», то тогда отношение U/I можно рассмотреть как величину эквивалентного сопротивления R цепи целиком.

Если закон Ома выполняется, то эквивалентное сопротивление можно вычислить довольно легко.

Ток и напряжение при последовательном соединении проводников

В простейшем случае, когда два и более проводников объединены друг с другом в последовательную цепь, ток в каждом проводнике окажется одним и тем же, а напряжение между «выходом» и «входом», то есть на выводах всей цепи, будет равным сумме напряжений на составляющих цепь резисторах. И поскольку закон Ома справедлив для любого из резисторов, то можно записать:

Итак, для последовательного соединения проводников характерны следующие закономерности:

Для нахождения общего сопротивления цепи, сопротивления составляющих цепь проводников складываются;

Ток через цепь равен току через любой из проводников, образующих цепь;

Напряжение на выводах цепи равно сумме напряжений на каждом из проводников, образующих цепь.

Ток и напряжение при параллельном соединении проводников

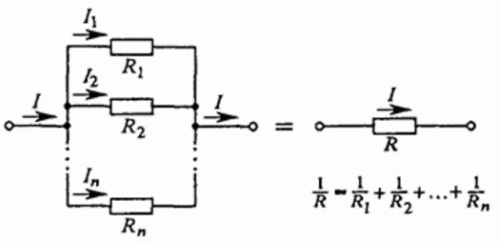
При параллельном соединении нескольких проводников друг с другом, напряжение на выводах такой цепи — это напряжение на каждом из проводников, составляющих цепь.

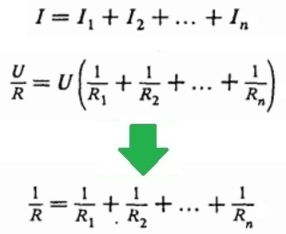
Напряжения на всех проводниках равны между собой и равны напряжению приложенному (U). Ток через всю цепь — на «входе» и «выходе» — равен сумме токов в каждой из ветвей цепи, параллельно объединенных и составляющих данную цепь. Зная, что I = U/R, получаем, что:

Итак, для параллельного соединения проводников характерны следующие закономерности:

Для нахождения общего сопротивления цепи — складываются обратные величины сопротивлений составляющих цепь проводников;

Ток через цепь равен сумме токов через каждый из проводников, образующих цепь;

Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.

Эквивалентные схемы простых и сложных (комбинированных) цепей

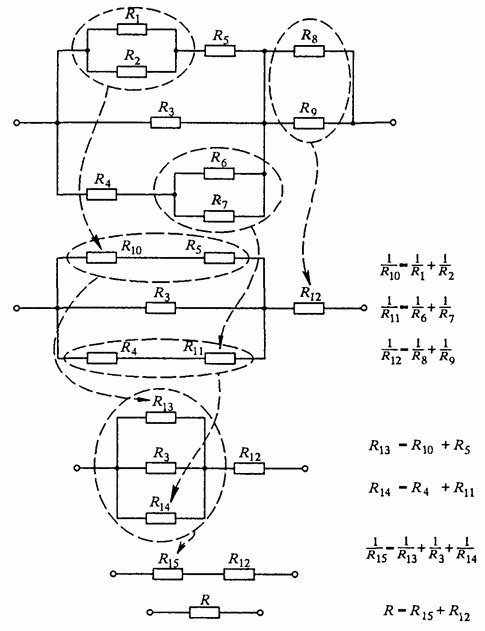
В большинстве случаев схемы цепей, являясь комбинированным соединением проводников, поддаются пошаговому упрощению.

Группы соединенных последовательно и параллельно частей цепи, заменяют эквивалентными сопротивлениями по приведенному выше принципу, шаг за шагом вычисляя эквивалентные сопротивления кусочков, затем приводя их к одному эквивалентному значению сопротивления всей цепи.

И если сначала схема выглядит довольно запутанной, то будучи упрощенной шаг за шагом, она может быть разбита на меньшие цепочки из последовательно и параллельно соединенных проводников, и так в конце концов сильно упрощена.

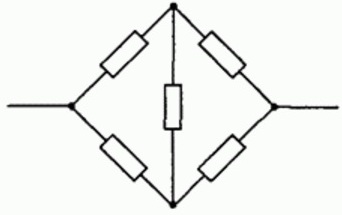
Между тем, не все схемы подаются упрощению таким простым путем. Простая с виду схема «моста» из проводников не может быть исследована таким образом. Здесь нужно применять уже несколько правил:

Для каждого резистора выполняется закон Ома;

В любом узле, то есть в точке схождения двух и более токов, алгебраическая сумма токов равна нулю: сумма токов втекающих в узел, равна сумме токов вытекающих из узла (первое правило Кирхгофа);

Сумма напряжений на участках цепи при обходе по любому пути от «входа» до «выхода» равна приложенному к цепи напряжению (второе правило Кирхгофа).

Мостовое соединение проводников

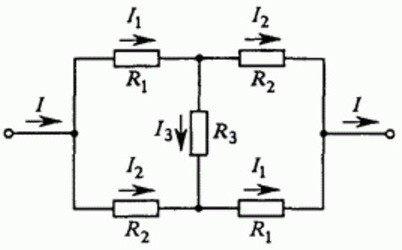
Дабы рассмотреть пример использования приведенных выше правил, рассчитаем цепь, собранную из проводников, объединенных в схему моста. Чтобы вычисления получились не слишком сложными, примем, что некоторые из сопротивлений проводников равны между собой.

Обозначим направления токов I, I1, I2, I3 на пути от «входа» в цепь — к «выходу» из цепи. Видно, что схема симметрична, поэтому токи через одинаковые резисторы одинаковы, поэтому обозначим их одинаковыми символами. В самом деле, если поменять у цепи местами «вход» и «выход», то схема будет неотличима от исходной.

Для каждого узла можно записать уравнения токов, исходя из того, что сумма токов втекающих в узел равна сумме токов вытекающих из узла (закон сохранения электрического заряда), получится два уравнения:

Следующим шагом записывают уравнения сумм напряжений для отдельных участков цепи при обходе цепи от входя к выходу различными путями. Так как схема является в данном примере симметричной, то достаточно двух уравнений:

В процессе решения системы линейных уравнений, получается формула для нахождения величины тока I между зажимами «входным» и «выходным», исходя из заданного приложенного к цепи напряжения U и сопротивлений проводников:

А для общего эквивалентного сопротивления цепи, исходя из того, что R = U/I, следует формула:

Можно даже проверить правильность решения, например приведя к предельным и к частным случаям величины сопротивлений:

Теперь вы знаете, как находить ток и напряжение при параллельном, последовательном, смешанном, и даже при мостовом соединении проводников, применяя закон Ома и правила Кирхгофа. Эти принципы очень просты, и даже самая сложная электрическая цепь с их помощью в конце концов приводится к элементарному виду путем нескольких несложных математических операций.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Последовательное и параллельное соединение сопротивлений

Последовательное соединение сопротивлений

Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).

Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.

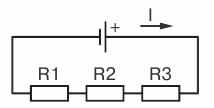
Рис 1 . Последовательное соединение сопротивлений

Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:

U1 = IR1 U2 = IR2 и U3 = IR3

Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .

Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3

Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).

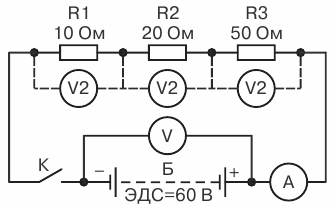
Рис. 2. Пример последовательного соединения трех сопротивлений

Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А

Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75 х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.

Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.

Параллельное соединение сопротивлений

Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.

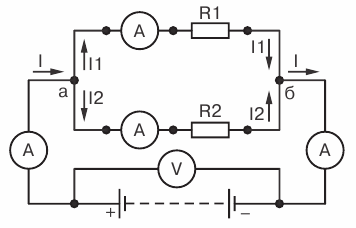
Рис 3. Параллельное соединение сопротивлений

Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.

Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.

Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.

Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).

Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).

Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим

Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .

Рассмотрим теперь, каково будет соотношение между токами в ветвях.

Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R 1 и R2, так как он соединен с началом и концом каждого сопротивления.

Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2 ,

где U — напряжение на зажимах источника тока; U 1 — падение напряжения на сопротивлении R 1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .

Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U 1 = U2, то и I1R1 = I2R2 .

Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.

Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.

Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:

I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА

I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1 + I2 = 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.

Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть ( I1 = 300 мА) пошла через меньшее сопротивление ( R1 = 10 Ом), а меньшая часть ( R2 = 150 мА) — через большее сопротивление ( R 2 = 20 Ом).

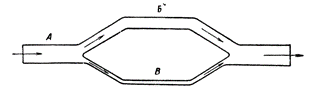
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.

Рис. 4 . Через тонкую трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую

Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.

Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.

Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.

Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U 1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )

Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2

Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.

На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.

Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.

Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?

Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.

Чтобы убедиться в этом, рассмотрим следующий пример.

Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).

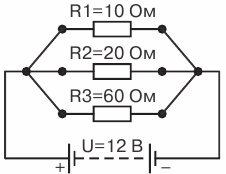
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями

Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60

Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.

Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.

Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.

Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0, 2 А

Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.

Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.

На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.

Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / ( R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Онлайн калькулятор закона Ома позволяет определять связь между силой тока, электрическим напряжением и сопротивлением проводника в электрических цепях.

Для расчета, вам понадобится воспользоваться отдельными графами:
– сила тока вычисляется в Ампер, исходя из данных напряжения (Вольт) и сопротивления (Ом);
– напряжение вычисляется в Вольт, исходя из данных силы тока (Ампер) и электрического сопротивления (Ом);
– электрическое сопротивление вычисляется в Ом, исходя из данных силы тока (Ампер) и напряжения (Вольт);
– мощность вычисляется в Ватт, исходя из данных силы тока (Ампер) и напряжения (Вольт).

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.

В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.

Закон Ома

Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:

U = I × R

или

I = V/R

или

R = V/I

Где:

V – напряжение в вольтах (В);
I – сила тока в амперах (А);
R – сопротивление в омах (Ом);

Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.

Видоизменения закона Ома.

Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».

Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .

Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

I – ток, протекающий по участку цепи.
R – сопротивление этого участка.
φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

U1=I*R1
U2=I*R2
Un=I*Rn
U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Все о законе Ома: простыми словами с примерами для “чайников”

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Следствия закона Ома.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
В сверхпроводниках;
Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
В вакуумных и газовых радиолампах;
В диодах и транзисторах.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

I = I1= I2 ;
U = U1+ U2 ;
R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

I = I1+ I2 … ;
U = U1= U2 … ;
1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

Источник

Главная
→
Примеры решения задач ТОЭ
→
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Основные положения и соотношения

1. Источники электрической энергии

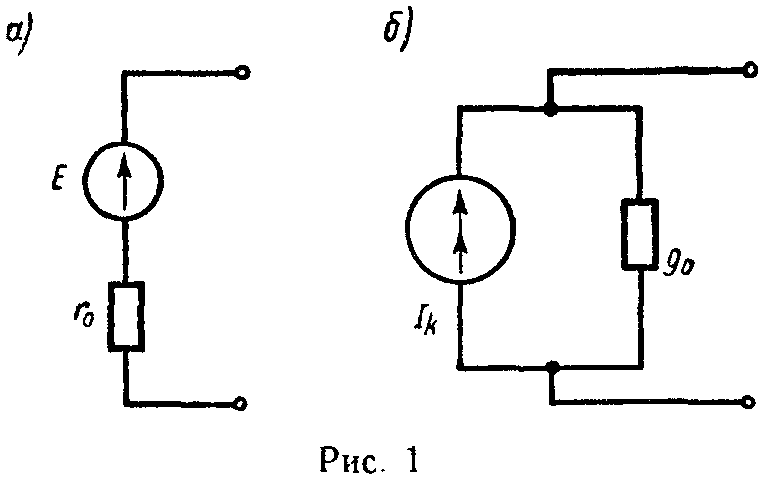
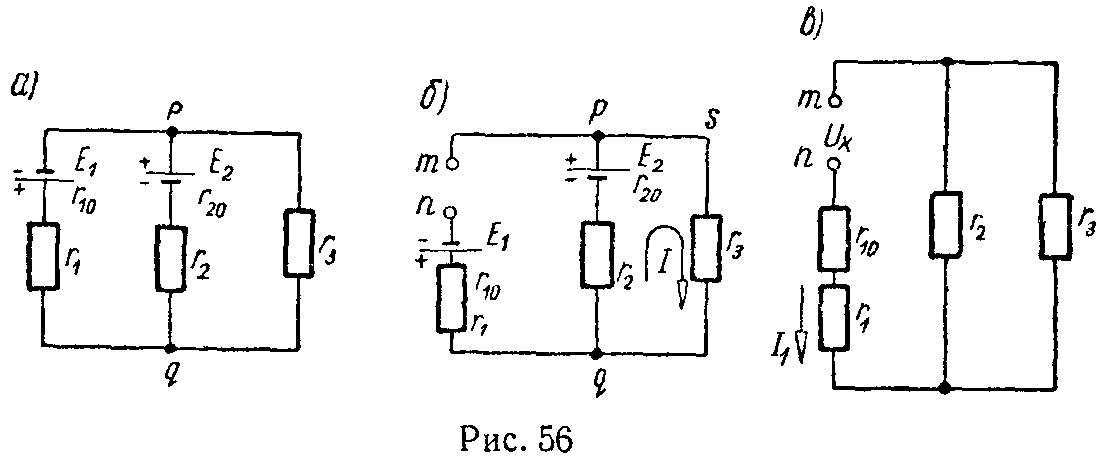
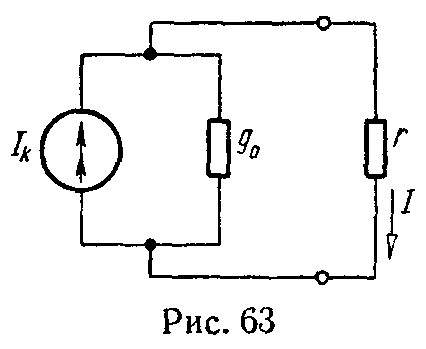
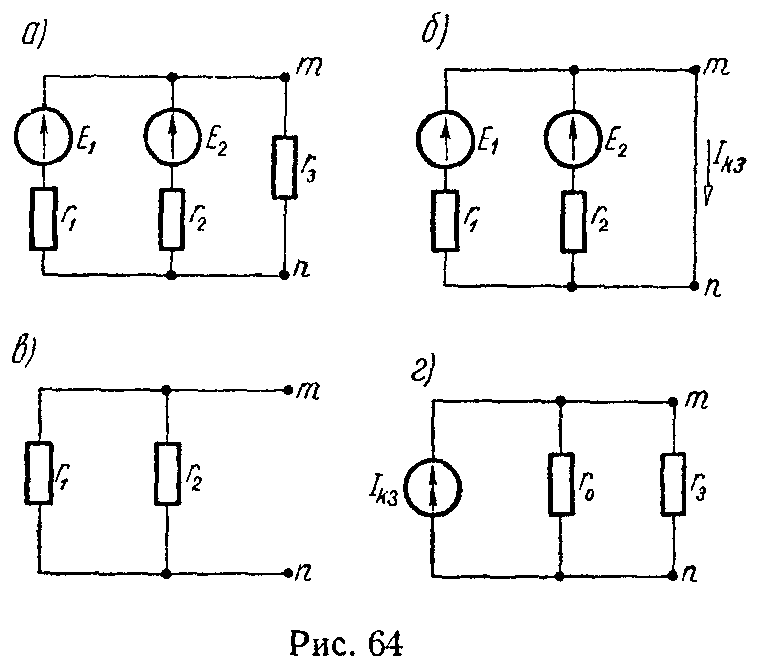
Реальный источник электрической энергии можно изобразить двояко: а) в виде генератора напряжения, который характеризуется э.д.с. Е, численно равной напряжению холостого хода источника, и включенной последовательно с сопротивлением r₀ (рис. 1, а), б) в виде генератора тока, который характеризуется током I_к, численно равным току короткого замыкания реального источника, и параллельно соединенной проводимостью g₀ (рис. 1, б).

Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам

I к = E r 0 , g 0 = 1 r 0 , (1)

а обратный переход от генератора тока к эквивалентному генератору напряжения по следующим формулам

E= I к g 0 , r 0 = 1 g 0 . (2)

У идеального генератора напряжения внутреннее сопротивление равно нулю, тогда как у идеального генератора тока внутренняя проводимость равна нулю.

2. Закон Ома

Закон Ома применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).

Для написания закона Ома следует прежде всего выбрать произвольно некоторое положительное направление для тока.

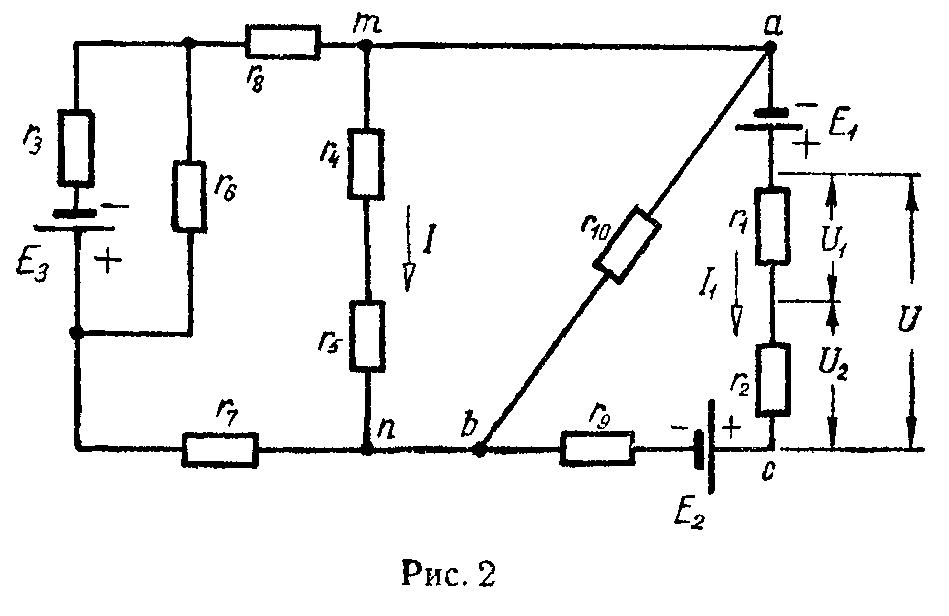
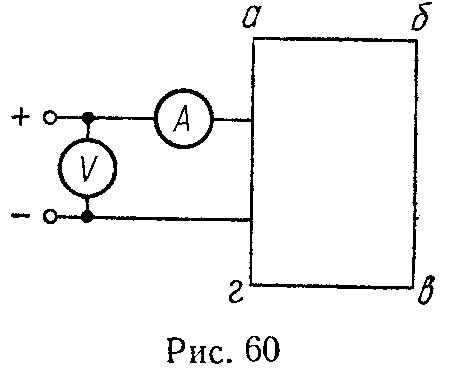
а) Для ветви, состоящей только из сопротивлений и не содержащей э.д.с. (например, для ветви mn на рис. 2), при положительном направлении для тока от точки m к точке n ток равен

I= φ m − φ n r mn = U mn r mn . (3)

Здесь φ_m и φ_n — потенциалы точек m и n, U_mn = φ_m — φ_n — разность потенциалов или напряжение между точками m и n, r_mn = r₄ + r₅ — полное сопротивление ветви между точками m и n.

Пример — в задаче 17.

б) Для замкнутой одноконтурной цепи

I= ΣE Σr , (4)

где Σr — арифметическая сумма всех внешних и внутренних сопротивлений цепи, ΣE — алгебраическая сумма ее электродвижущих сил.

Со знаком плюс берут те э.д.с., направления которых совпадают с выбранным положительным направлением для тока, и со знаком минус — э.д.с. с противоположными направлениями.

Примеры — в задачах 15 и 17.

в) Для ветви, содержащей э.д.с. и сопротивления (например, для ветви acb на рис. 2),

I 1 = φ a − φ b +ΣE Σ r ab = U ab + E 1 − E 2 r 1 + r 2 + r 9 , (5)

где U_ab = φ_a — φ_b — напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока, ΣE — алгебраическая сумма э.д.с., находящихся в этой ветви, а Σr — арифметическая сумма ее сопротивлений.

Формулу (5) называют обобщенным законом Ома.

Примеры — в задачах 15 и 17.

3. Законы Кирхгофа

Для написания законов Кирхгофа следует прежде всего задаться положительными направлениями для токов в каждой ветви.

Первый закон Кирхгофа

∑ k=1 n I k =0, (6)

Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, притекающие к узлу, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот).

Второй закон Кирхгофа

∑ k=1 n I k ⋅ r k = ∑ k=1 n E k . (7)

Алгебраическая сумма падений напряжений любого замкнутого контура равна алгебраической сумме э.д.с. в нем.

Направление обхода контура выбирается произвольно. При записи левой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода (независимо от направления э.д.с. в этих ветвях), и со знаком минус — падения напряжения в тех ветвях, в которых положительное направление, тока противоположно направлению обхода. При записи правой части равенства э.д.с., направления которых совпадают с выбранным направлением обхода (независимо от направления тока, протекающего через них), принимаются положительными, а э.д.с., направленные против выбранного направления обхода, принимаются отрицательными.

Пример — в задаче 29.

Распределение напряжений при последовательном соединении двух сопротивлений (см. рис. 2)

I 1 = U 1 r 1 = U 2 r 2 = U r 1 + r 2 ,

U 1 =U⋅ r 1 r 1 + r 2 , U 2 =U⋅ r 2 r 1 + r 2 . (8)

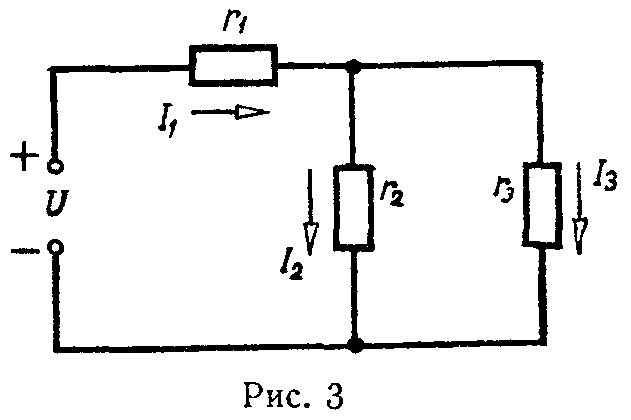
Распределение токов в двух параллельных ветвях — формула разброса токов или формула делителя токов (рис. 3)

U 2 = U 3 = U 2,3 , I 2 ⋅ r 2 = I 3 ⋅ r 3 = I 1 ⋅ r 2,3 = I 1 ⋅ r 2 ⋅ r 3 r 2 + r 3 ,

I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 . (9)

Распределение напряжений при последовательном соединении n сопротивлений

U k =U⋅ r k ∑ k=1 n r k .

Распределение токов в n параллельных ветвях

I k =I⋅ g k ∑ k=1 n g k .

4. Методы расчета сложных цепей постоянного тока

Пусть электрическая цепь состоит из p ветвей и имеет q узлов.

Применение законов Кирхгофа

Прежде всего, устанавливается число неизвестных токов, которое равно числу ветвей (p). Для каждой ветви задаются положительным направлением для тока.

Число n₁ независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы

n₁ = q – 1.

Число n₂ независимых уравнений, составляемых по второму закону Кирхгофа, равно числу ячеек (контуров)

n₂ = p — q + 1.

Общее число уравнений n, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов

n = n₁ + n₂ = p.

Решение этой системы уравнений дает значения искомых токов.

Пример — в задаче 29.

Метод контурных токов (МКТ, Максвелла).

Число n независимых контуров цепи равно числу уравнений по второму закону Кирхгофа

n = n₂ = p — q + 1.

Расчет цепи методом контурных токов, состоящей из n независимых контуров, сводится к решению системы из n уравнений, составляемых для контурных токов I₁₁, I₂₂, …, I_nn; ток в каждой ветви находится как алгебраическая сумма контурных токов, обтекающих эту ветвь.

Выбор направлений контурных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один контур.

Система уравнений МКТ для n контурных токов имеет вид

{ r 11 ⋅ I 11 + r 12 ⋅ I 22 +…+ r 1n ⋅ I nn = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 +…+ r 2n ⋅ I nn = E 22 ; ………………………………………………. r n1 ⋅ I 11 + r n2 ⋅ I 22 +…+ r nn ⋅ I nn = E nn . (10)

Здесь r_kk — собственное сопротивление контура k (сумма сопротивлений всех ветвей, входящих в контур k), r_kl — общее сопротивление контуров k и l, причем r_kl = r_lk; если направления контурных токов в ветви, общей для контуров k и l, совпадают, то r_kl положительно (r_kl > 0), в противном случае r_kl — отрицательно (r_kl < 0); E_kk — алгебраическая сумма э.д.с., включенных в ветви, образующие контур k.

Пример — в задаче 41.

Метод узловых потенциалов (МУП)

Число n независимых узлов цепи равно числу уравнений по первому закону Кирхгофа

n = n₁ = q — 1.

Для определения потенциалов всех узлов электрической схемы, имеющей q узлов, следует принять потенциал одного из узлов равным нулю, а для определения потенциалов остальных n = q — 1 узлов составляется следующая система уравнений

{ φ 1 ⋅ g 11 + φ 2 ⋅ g 12 +…+ φ n ⋅ g 1n = ∑ 1 Eg ; φ 1 ⋅ g 21 + φ 2 ⋅ g 22 +…+ φ n ⋅ g 2n = ∑ 2 Eg ; ……………………………………………….. φ 1 ⋅ g n1 + φ 2 ⋅ g n2 +…+ φ n ⋅ g nn = ∑ n Eg . (11)

Здесь g_ss — сумма проводимостей ветвей, присоединенных к узлу s; g_sq — сумма проводимостей, соединяющих узел s с узлом q; – алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу s, на их проводимости (т.е. токов короткого замыкания этих ветвей); при этом со знаком плюс берутся те из произведений Eg, в ветвях которых э.д.с. действуют в направлении узла s, и со знаком минус — в направлении от узла.

Определив потенциалы узлов, находят токи в ветвях посредством закона Ома.

Этим методом рекомендуется пользоваться в тех случаях, когда число уравнений здесь будет меньше числа уравнений, составленных по методу контурных токов.

Примеры — в задачах 44 и 45.

Метод наложения

Ток в любой ветви может быть рассчитан как алгебраическая сумма токов, вызываемых в ней каждой э.д.с. в отдельности. При этом надо иметь в виду, что когда ведется расчет для какой-либо одной действующей э.д.с., то вместо остальных источников должны быть включены сопротивления, равные внутренним сопротивлениям этих источников.

Примеры — в задачах 47 и 49.

Метод эквивалентных преобразований

Во всех случаях применения метода эквивалентных преобразований замена одних схем другими, им эквивалентными, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.

1) Замена последовательных сопротивлений одним эквивалентным. Сопротивления последовательны, если они обтекаются одним и тем же током. Например, на схеме цепи, изображенной на рис. 2, сопротивления r₁, r₂ и r₉ соединены последовательно; так же последовательны сопротивления r₇ и r₈.

Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных участков, равно сумме этих сопротивлений этих участков

r э = r 1 + r 2 +…+ r n = ∑ k=1 n r k . (12)

2) Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Например (рис. 2), сопротивления r₄₅ = r₄ + r₅ и r₁₀ параллельны.

Эквивалентная проводимость цепи, состоящей из n параллельно соединенных ветвей равна сумме этих проводимостей этих ветвей. Эквивалентное сопротивление такой цепи находится как величина обратная эквивалентной проводимости этой цепи

1 r э = 1 r 1 + 1 r 2 +…+ 1 r n = ∑ k=1 n 1 r k . (13)

В частном случае параллельного соединения двух сопротивлений r₁ и r₂ эквивалентное сопротивление

r э = r 1 ⋅ r 2 r 1 + r 2 . (14)

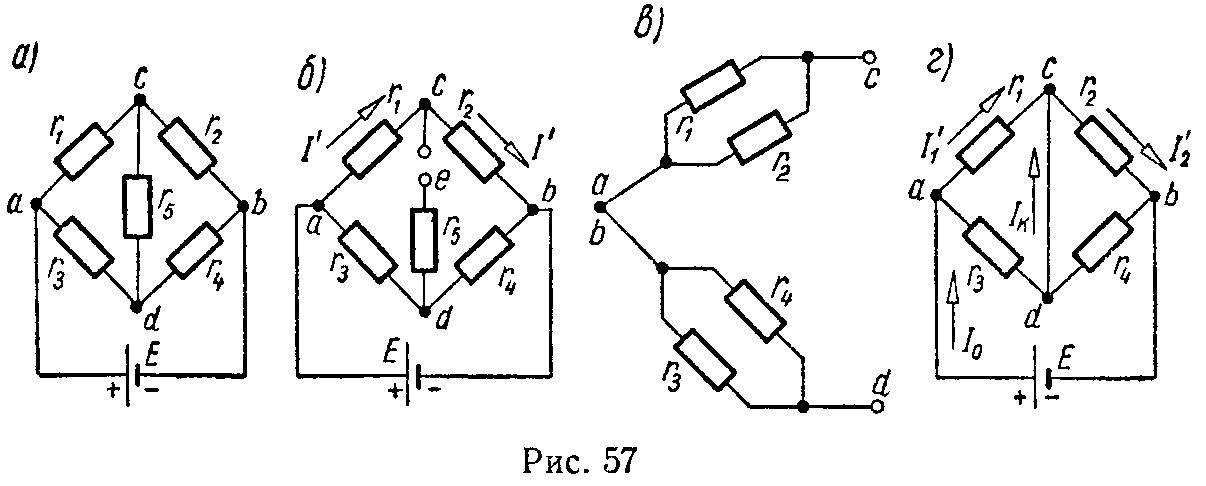
3) Замена смешанного соединения сопротивлений одним эквивалентным. Смешанное соединение — это сочетание последовательного и параллельного соединения сопротивлений. Например, сопротивления r₁, r₂ и r₃ (рис. 3) находятся в смешанном соединении. Их эквивалентное сопротивление равно

r э = r 1 + r 2,3 = r 1 + r 2 ⋅ r 3 r 2 + r 3 . (15)

При смешанном соединении сопротивлений токи ветвей цепи (рис. 3):

по закону Ома

I 1 = U r э , (16)

по формуле разброса токов (делителя токов)

I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 .

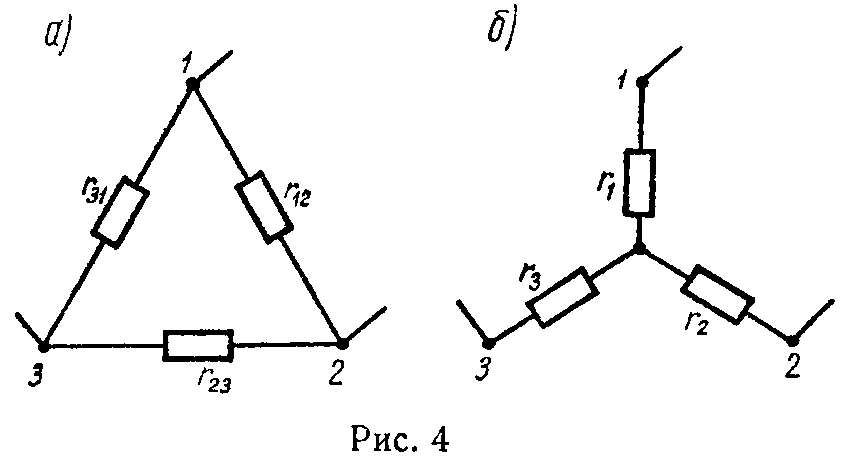
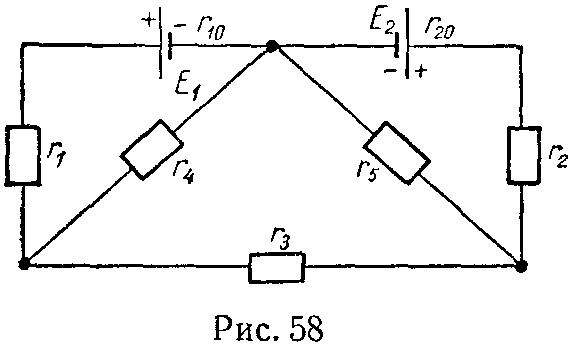
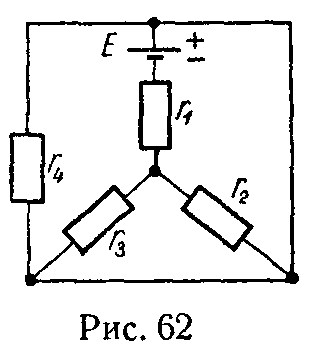
4) Формулы преобразования треугольника сопротивлений (рис. 4, а) в эквивалентную звезду сопротивлений (рис. 4, б) и наоборот имеют вид

{ r 1 = r 12 ⋅ r 31 r 12 + r 23 + r 31 ; r 2 = r 23 ⋅ r 12 r 12 + r 23 + r 31 ; r 3 = r 31 ⋅ r 23 r 12 + r 23 + r 31 , (17)

{ g 12 = g 1 ⋅ g 2 g 1 + g 2 + g 3 ; g 23 = g 2 ⋅ g 3 g 1 + g 2 + g 3 ; g 31 = g 3 ⋅ g 1 g 1 + g 2 + g 3 , (18)

где g — проводимость соответствующей ветви.

Формулы (18) можно записать через сопротивления так

r 12 = r 1 + r 2 + r 1 ⋅ r 2 r 3 ; r 23 = r 2 + r 3 + r 2 ⋅ r 3 r 1 ; r 31 = r 3 + r 1 + r 3 ⋅ r 1 r 2 . (19)

Пример — в задаче 51.

Метод эквивалентного генератора напряжения (метод холостого хода и короткого замыкания или метод активного двухполюсника)

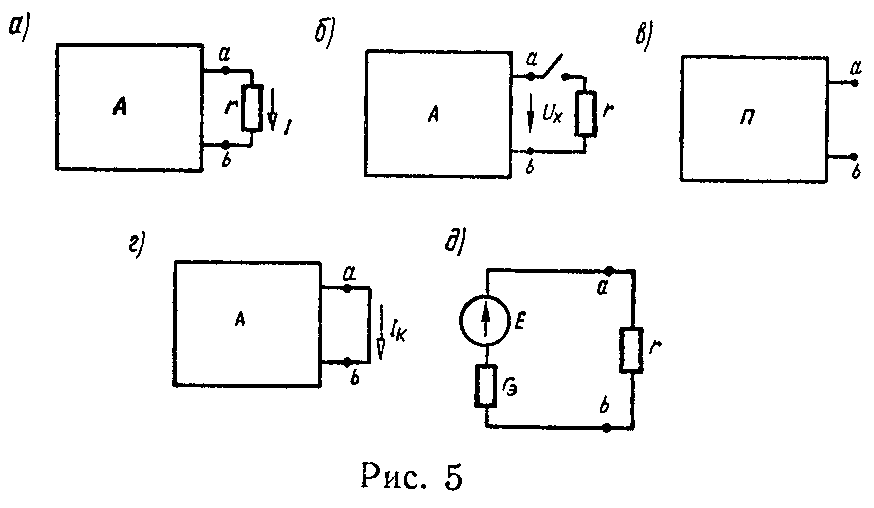
Для нахождения тока I в ветви ab, сопротивление которой r (рис. 5, а, буква А на рисунке обозначает активный двухполюсник), надо разомкнуть эту ветвь и при этом найти (любым способом) разность потенциалов на зажимах разомкнутой ветви — U_х (рис. 5, б). Затем надо вычислить сопротивление короткого замыкания r_к, равное эквивалентному сопротивлению всей остальной цепи, вычисленному в предположении, что в ней отсутствуют э.д.с. (при этом внутренние сопротивления источников сохраняются) и что она питается от постороннего источника, присоединенного непосредственно к зажимам a и b (рис. 5, в; буква П на рисунке обозначает пассивный двухполюсник).

Сопротивление r_к может быть вычислено либо непосредственно по схеме рис. 5, в, либо из соотношения

r к = U х I к , (20)

где I_к — ток короткого замыкания, протекающий по ветви ab, если ее сопротивление r сделать равным нулю (рис. 5, г).

Заданная схема (рис. 5, а) может быть заменена эквивалентным генератором напряжения с э.д.с. E = U_х и внутренним сопротивлением r_э = r_к, присоединенным к зажимам ab сопротивления r (рис. 5, д).

Ток в искомой ветви, имеющей сопротивление r, определяется из формулы закона Ома

I= U х r+ r к . (21)

Примеры — в задачах 55 и 56.

Метод эквивалентного генератора тока

В предыдущем пункте показано, как в любой сложной цепи можно получить эквивалентный генератор напряжения с э.д.с. E и внутренним сопротивлением r_к. Этот генератор напряжения (рис. 5, д) на основании формул (1) может быть заменен эквивалентным генератором тока (рис. 1, б) по формулам

I к = U х r к , g 0 = 1 r к . (22)

где I_к — ток эквивалентного генератора тока, равный току короткого замыкания в той ветви, по отношению к которой производится эквивалентное преобразование всей остальной части цепи, g₀ — внутренняя проводимость, равная эквивалентной проводимости всей остальной цепи между зажимами ab, к которым присоединен приемник энергии, в предположении, что э.д.с. всех генераторов равны нулю.

Пример — в задаче 65.

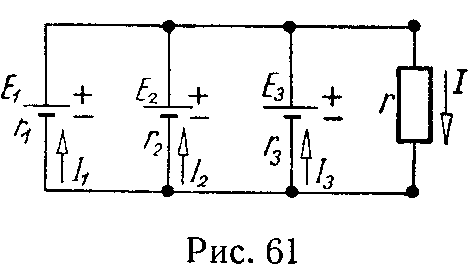
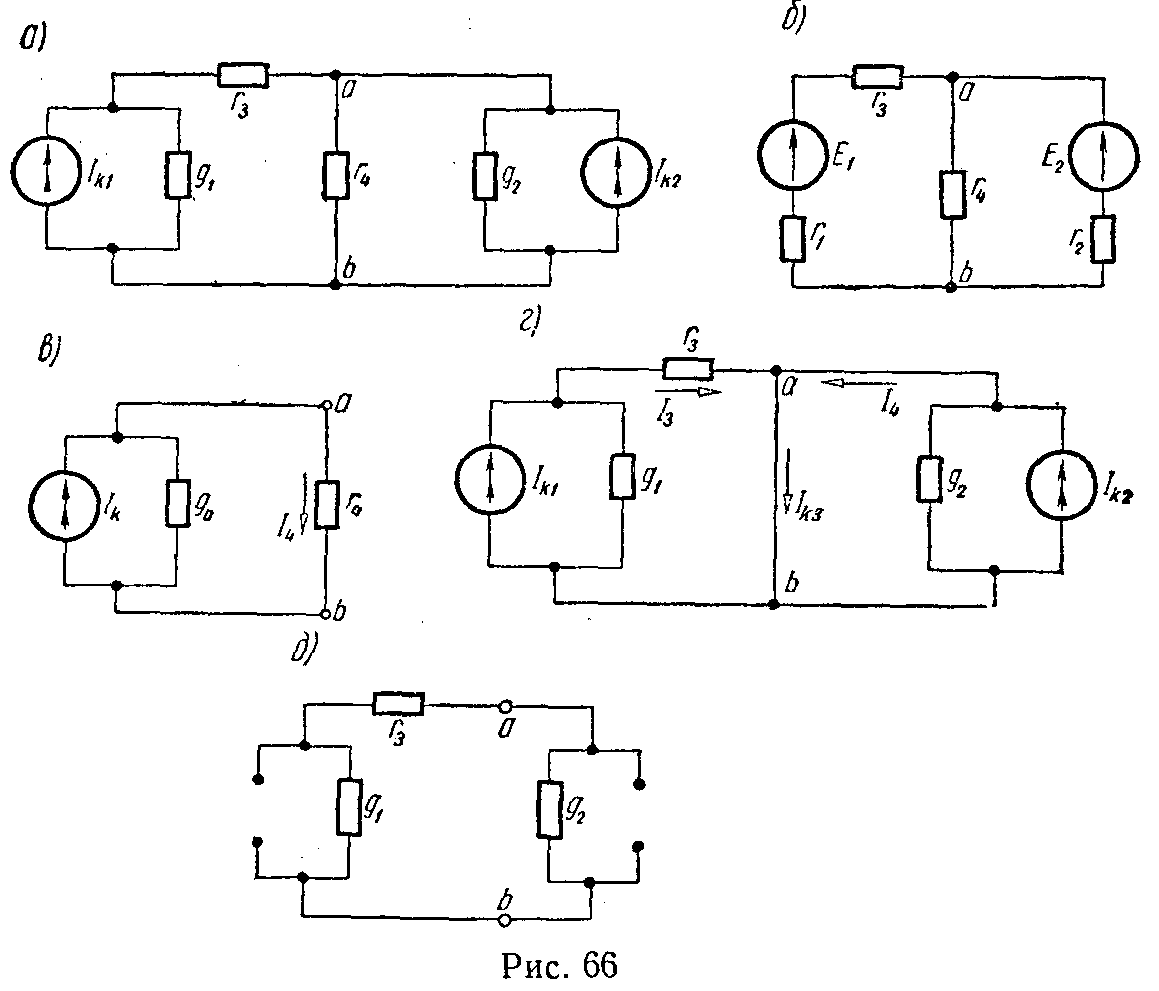
Метод замены нескольких параллельных генераторов напряжения одним эквивалентным

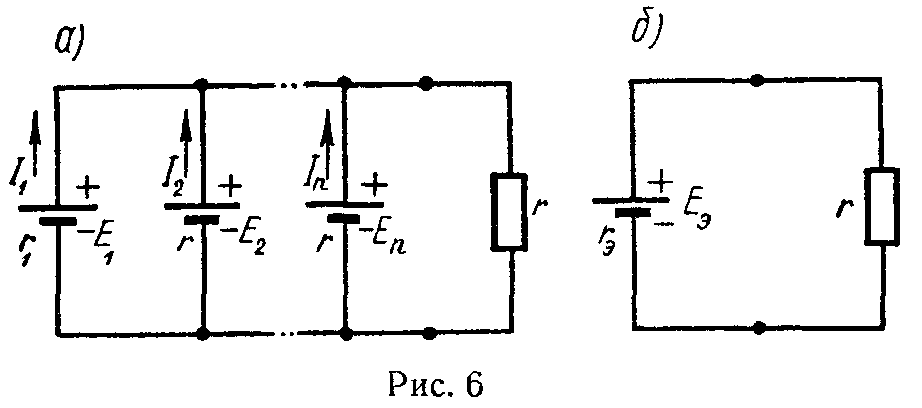
Если имеется несколько генераторов напряжения с э.д.с. E₁, E₂, …, E_n и внутренними сопротивлениями r₁, r₂, …, r_n, работающие параллельно на общее сопротивление нагрузки r (рис. 6, а), то они могут быть заменены одним эквивалентным генератором напряжений, э.д.с. которого E_э, а внутреннее сопротивление r_э (рис. 6, б),

при этом

{ E э = ∑ k=1 n E k g k ∑ k=1 n g k ; 1 r э = 1 r 1 + 1 r 2 +…+ 1 r n ; g k = 1 r k . (23)

Ток в сопротивлении r определится по формуле

I= E э r+ r э . (24)

Ток в каждой из ветвей находится по формуле

I k = E k −U r k , (25)

где U = I·r.

Пример — в задаче 60.

Метод замены параллельно соединенных генераторов тока одним эквивалентным

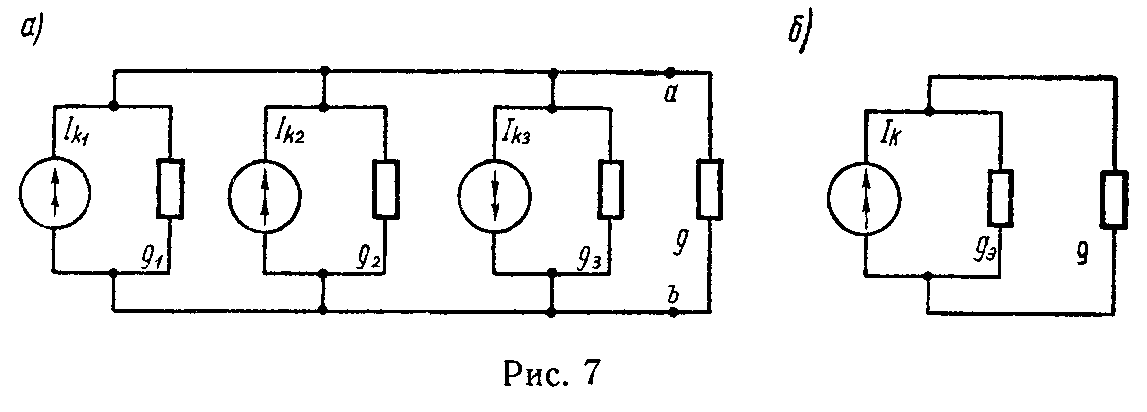
Если несколько генераторов тока с токами I_k₁, I_k₂, …, I_kn и внутренними проводимостями g₁, g₂, …, g_n соединены параллельно (рис. 7, а) и работают на общий приемник энергии с проводимостью g то они могут быть заменены одним эквивалентным генератором тока (рис. 7, б), ток которого I_k равен алгебраической сумме токов, а его внутренняя проводимость равна сумме внутренних проводимостей отдельных генераторов

I k = I k1 + I k2 − I k3 +…= ∑ m=1 n I km , (26)

g э = g 1 + g 2 + g 3 +…= ∑ m=1 n g m . (27)

5. Принцип взаимности

Принцип взаимности гласит: если э.д.с. E, находящаяся в ветви ab сколь угодно сложной цепи, вызывает ток в другой ветви cd этой же цепи, то при переносе этой э.д.с. в ветвь cd она вызовет в ветви ab такой же ток I.

6. Принцип компенсации

Принцип компенсации: любое сопротивление в электрической цепи может без изменения распределения токов в ее ветвях быть заменено э.д.с., численно равной падению напряжения в заменяемом сопротивлении и направленной навстречу току.

7. Входное сопротивление цепи относительно ветви

Входное сопротивление цепи относительно ветви k определяется как отношение э.д.с. E_k, действующей в этой ветви, к току I_k в этой же ветви при э.д.с. в остальных ветвях равных нулю

r kk = E k I k . (28)

Входная проводимость ветви k — величина обратная входному сопротивлению этой ветви

g kk = 1 r kk . (29)

Взаимное сопротивление (передаточное сопротивление) ветвей k и l — отношение э.д.с. E_k, действующей в ветви k, к току I_l, проходящему по ветви l при э.д.с. в остальных ветвях равных нулю

r kl = E k I l . (30)

Взаимная проводимость ветвей k и l — величина обратная взаимному сопротивлению тех же ветвей

g kl = 1 r kl . (31)

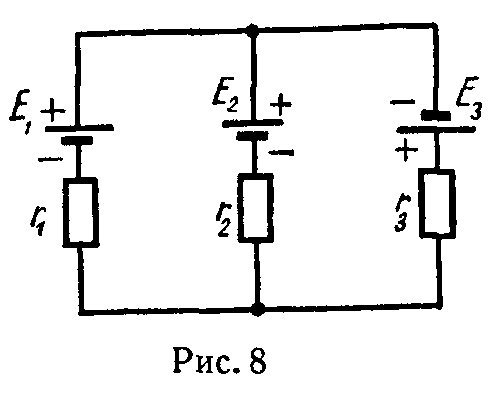
Пример. Для схемы рис. 8 входные сопротивления цепи относительно ветвей 1, 2 и 3 соответственно равны

r 11 = D r 2 + r 3 , r 22 = D r 1 + r 3 , r 33 = D r 1 + r 2 ,

а взаимные сопротивления ветвей 1 и 2, 2 и 3, 3 и 1 соответственно равны

r 12 = r 21 = D r 3 , r 23 = r 32 = D r 1 , r 13 = r 31 = D r 2 ,

где D = r₁·r₂ + r₁·r₃ + r₂·r₃.

8. Баланс мощностей

Для любой замкнутой электрической цепи сумма мощностей, развиваемых источниками электрической энергии, равна сумме мощностей, расходуемых в приемниках энергии

ΣP_ист = ΣP_потреб, или ΣEI = ΣI²r (32)

где ΣEI — алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. E и соответствующего тока I совпадают, в противном случае слагаемое отрицательно (при выборе положительных направлений токов в ветвях с э.д.с. выбираем направление тока совпадающим с действием соответствующей э.д.с.); ΣI²r — арифметическая сумма; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.

Упражнения и задачи

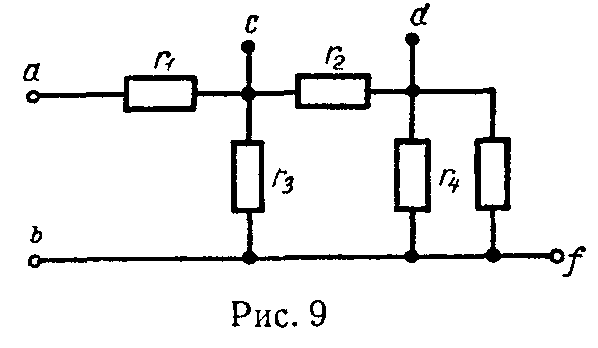
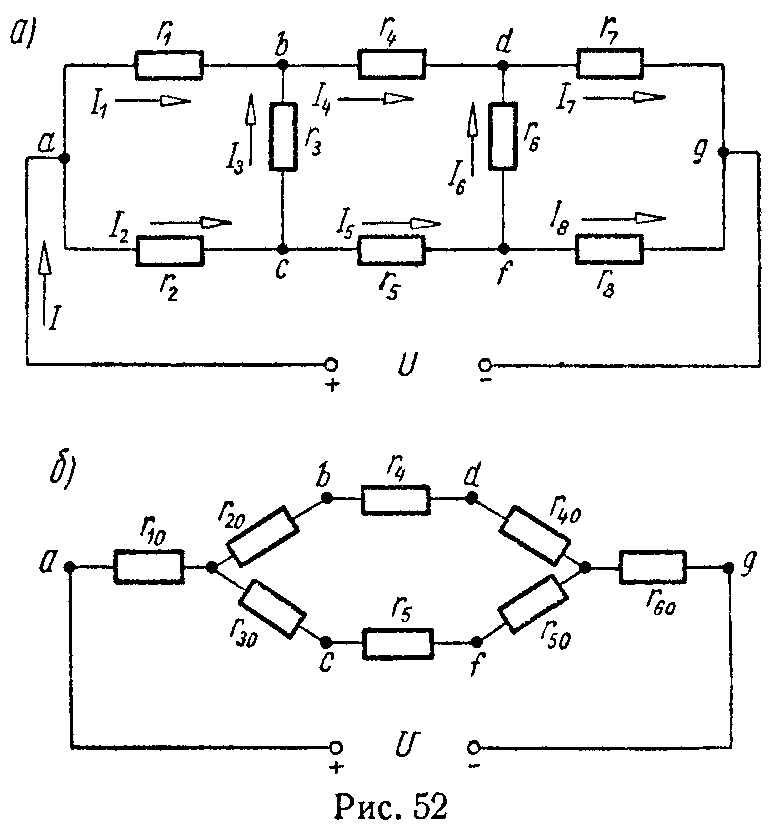
Задача 1. Для цепи (рис. 9) найти эквивалентные сопротивления между зажимами a и b, c и d, d и f, если r₁ = 6 Ом, r₂ = 5 Ом. r₃ = 15 Ом, r₄ = 30 Ом, r₅ = 6 Ом.

Решение

Расчет сопротивления r_ab.

Эквивалентное сопротивление соединенных параллельно сопротивлений r₄ и r₅ найдем по формуле (14)

r 45 = r 4 ⋅ r 5 r 4 + r 5 = 30⋅6 30+6 =5 Ом;

оно соединено последовательно с r₂; их общее сопротивление

r’ = r₂ + r₄₅ = 5 + 5 = 10 Ом.

Сопротивление цепи состоит из сопротивления r₁, последовательно с которым соединены два параллельных сопротивления r’ и r₃

r ab = r 1 + r ′ ⋅ r 3 r ′ + r 3 =6+ 10⋅15 10+15 =12 Ом.

Расчет сопротивления r_cd.

Сопротивления r₄ и r₅ теперь соединены параллельно друг другу; сопротивление r₃ к ним включено последовательно

r ″ = r 3 + r 4 ⋅ r 5 r 4 + r 5 =15+ 30⋅6 30+6 =20 Ом.

Сопротивление r_cd состоит из двух параллельно соединенных сопротивлений r₂ и r» и равно

r cd = r 2 ⋅ r ″ r 2 + r ″ = 5⋅20 5+20 =4 Ом.

Расчет сопротивления r_df.

Эквивалентное сопротивление цепи между точками d и f состоит из трех параллельно соединенных сопротивлений: r₅, r₄ и r₂ + r₃ и может быть определено по формуле (13)

1 r df = 1 r 5 + 1 r 4 + 1 r 2 + r 3 = 1 6 + 1 30 + 1 20 = 1 4 ,

откуда r_df. = 4 ом.

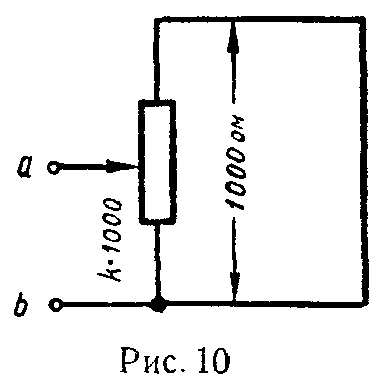
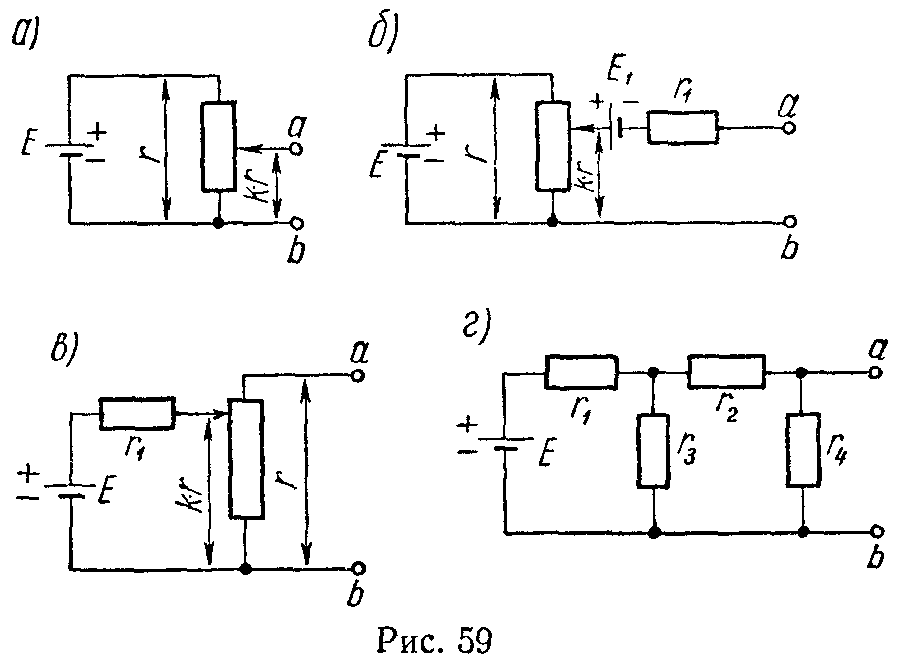
Задача 2. Для цепи (рис. 10) начертить кривую зависимости эквивалентного сопротивления между точками a и b как функцию от k (0 ≤ k ≤ 10).

Ответ: при k = 0 и k = 1 r_ab = 0; при k = 0,5 r_ab_макс = 250 Ом.

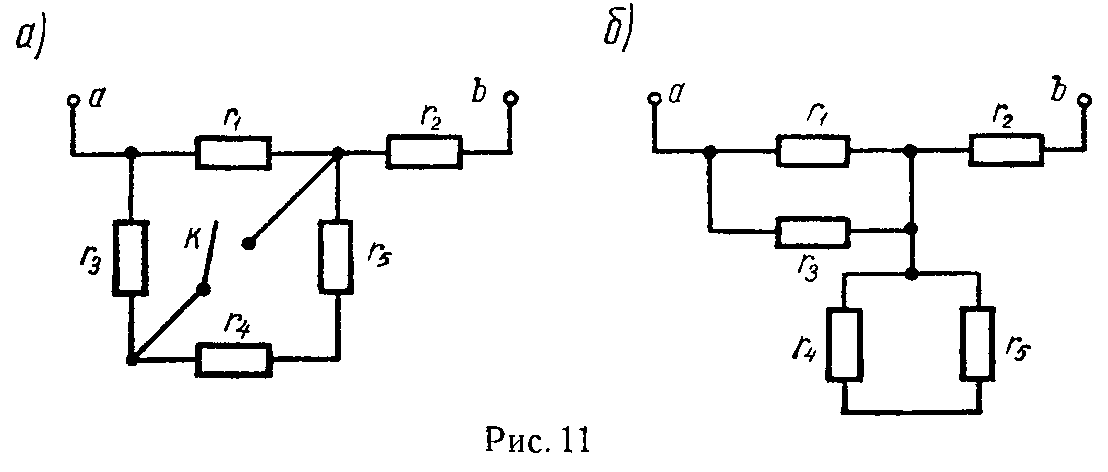
Задача 3. Цепь, схема которой изображена на рис. 11, а, состоит из пяти одинаковых сопротивлений r₁ = r₂ = r₃ = r₄ = r₅ = 10 кОм.

Чему равно сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К?

Решение

Ключ разомкнут.

Сопротивления r₃, r₄ и r₅ соединены между собой последовательно; заменяющее их эквивалентное сопротивление является параллельным к сопротивлению r₁; величина сопротивления, заменяющего r₃, r₄, r₅ и r₁, равна

r ′ = r 1 ⋅ ( r 3 + r 4 + r 5 ) r 1 + ( r 3 + r 4 + r 5 ) = 10⋅30 40 =7,5 кОм.

Искомое сопротивление цепи

r_ab = r’ + r₂ = 7,5 + 10 = 17,5 кОм.

Ключ замкнут.

В этом случае сопротивления r₁ и r₃ соединены параллельно друг другу, а сопротивления r₄ и r₅ закорочены (рис. 11, б). Искомое сопротивление цепи будет

r ab = r 1 ⋅ r 3 r 1 + r 3 + r 2 = 10⋅10 20 +10=15 кОм.

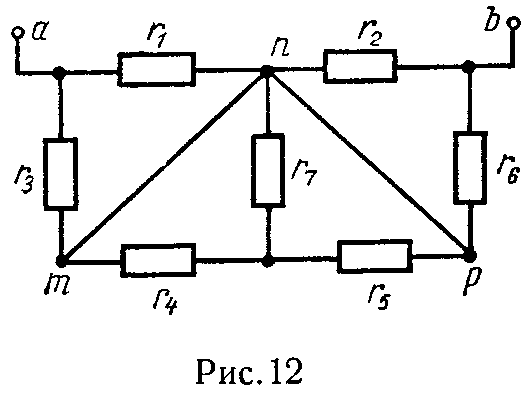
Задача 4. Вычислить эквивалентное сопротивление цепи (рис. 12) между зажимами a и b, если все семь ее сопротивлений одинаковы:

Указание. Обратить внимание на закорачивающие проводники mn и np.

Ответ: 10 Ом.

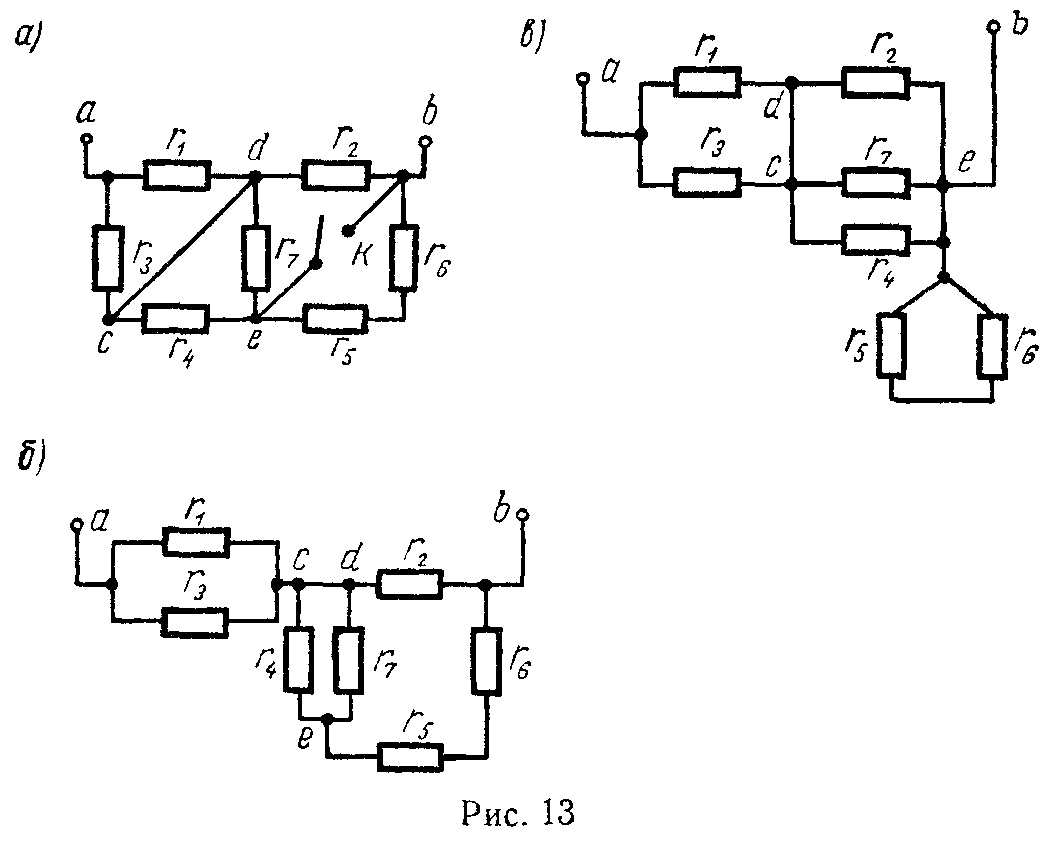
Задача 5. Определить эквивалентное сопротивление цепи между точками a и b при разомкнутом и замкнутом ключе К (рис. 13, а): r₁ = r₂ = r₃ = r₄ = r₅ = r₆ = r₇ = 10 Ом.

Решение

При разомкнутом ключе заданная схема может быть изображена согласно рис. 13, б.

Искомое сопротивление

r ab = r 1 ⋅ r 3 r 1 + r 3 = ( r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 )⋅ r 2 r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 + r 2 =5+ 25⋅10 35 =12,1 Ом.

При замкнутом ключе заданная схема имеет вид, изображенный на рис. 13, в.

Сопротивление цепи равно сумме двух сопротивлений

r ′ = r 1 ⋅ r 3 r 1 + r 3 10⋅10 20 =5 Ом,

и r”, определяемого из формулы

1 r ″ = 1 r 4 + 1 r 7 + 1 r 2 ,

откуда r’ = 3,33 Ом. Таким образом,

r ab = r ′ + r ″ =5+3,33=8,33 Ом.

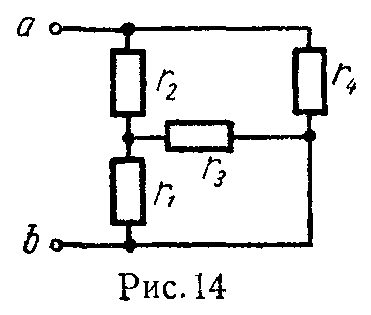
Задача 6. Найти эквивалентное сопротивление между зажимами a и b для схемы рис. 14. Даны: r₁ = 600 Ом, r₂ = 360 Ом, r₃ = 400 Ом, r₄ = 300 Ом.

Ответ: 200 Ом.

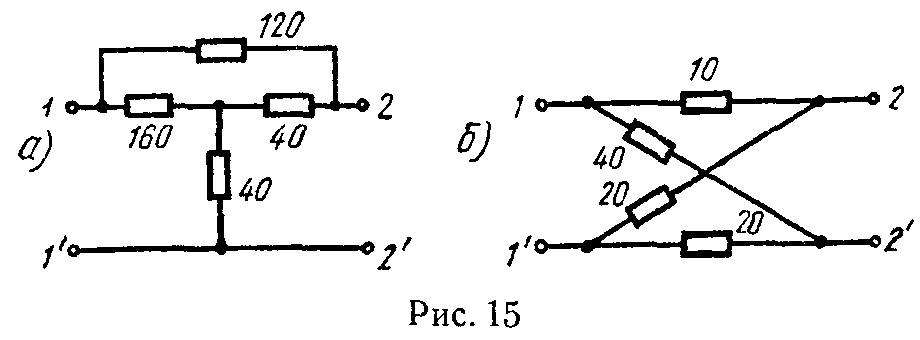
Задача 7. Определить сопротивление каждой из цепей (рис. 15, а и б) между зажимами 1–1′ при холостом ходе (точки 2 и 2′ разомкнуты) и при коротком замыкании (точки 2 и 2′ закорочены). Сопротивления в омах даны на схеме.

Ответ: а) r_1х = 120 Ом, r_1к = 72 Ом; б) r_1х = 20 Ом, r_1к = 18 Ом.

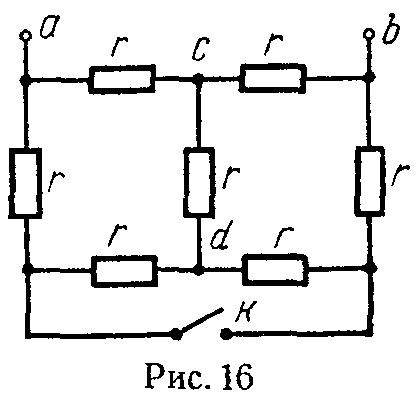
Задача 8. Вычислить сопротивление между зажимами a и b для схемы рис. 16 при разомкнутом и замкнутом ключе К. Все семь сопротивлений одинаковы и каждое равно r = 30 Ом.

Указание. Учесть, что точки c и d равнопотенциальны.

Ответ: При разомкнутом ключе r_ab = 40 Ом; при замкнутом — r_ab = 30 Ом.

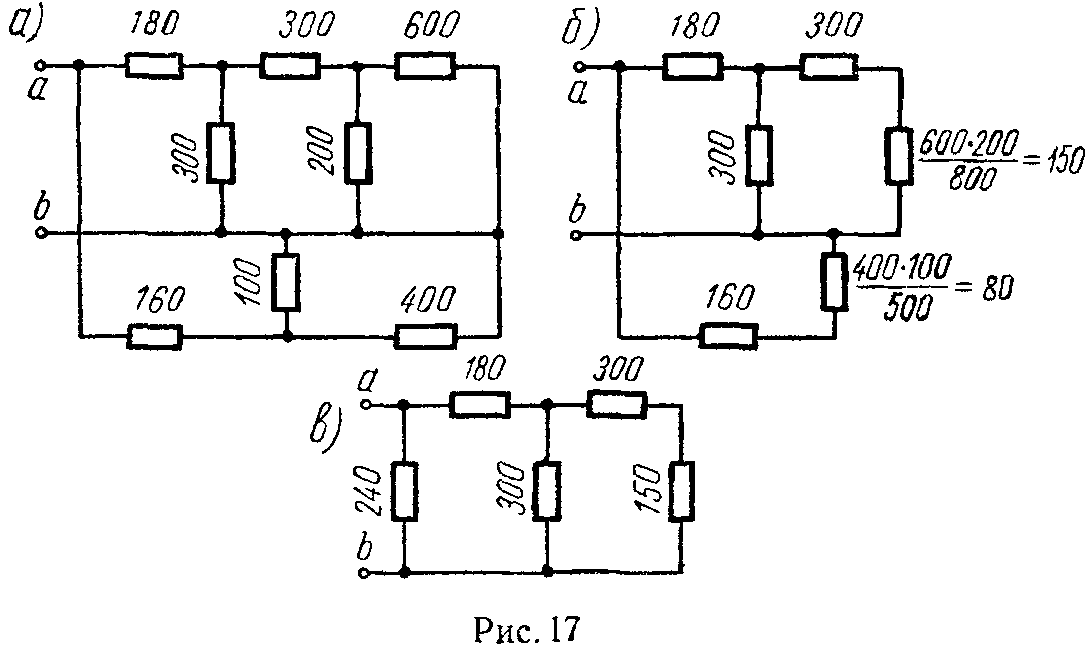
Задача 9. Найти сопротивление между зажимами a и b для схемы рис. 17, а. Значения сопротивлений в омах даны на схеме.

Решение

От данной схемы можно перейти к более простым схемам, изображенным на рис. 17, б и в. Искомое сопротивление

r ab = 240⋅ ( 180+ 300⋅450 750 ) 240+180+ 300⋅450 750 =144 Ом.

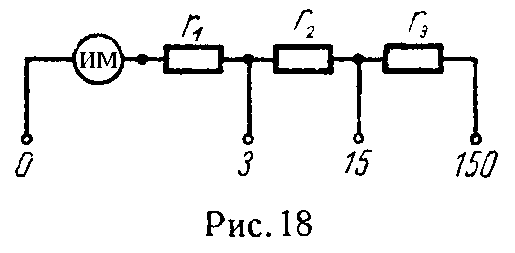
Задача 10. Имеется вольтметр, который может быть включен па три предела измерения: 3; 15 и 150 В (рис. 18). Максимально допустимый ток в измерительном механизме 30 мА.

Найти сопротивления r₁, r₂ и r₃.

Решение

Полагаем внутреннее сопротивление измерительного механизма (ИМ) равным нулю.

На пределе измерения 3 В: ток 30 мА, сопротивление r₁ = 3/0,030 = 100 Ом.

На пределе измерения 15 В: ток 30 мА, сопротивление r₁ + r₂ = 15/0,030 = 500 Ом, а сопротивление r₂ = 500 — 100 = 400 Ом.

Аналогично находится r₃ = 4500 Ом.

Задача 11. Два вольтметра, пределы измерения которых равны 150 и 100 В и внутренние сопротивления — 15000 и 7500 Ом, соединенные последовательно друг с другом и с добавочным сопротивлением 2500 Ом, подключены к сети 220 В. Чему равно показание каждого вольтметра?

Ответ: 132 и 66 В.

Задача 12. Батарея, э.д.с. которой E = 6,4 В и внутреннее сопротивление r₀ = 0,1 Ом, присоединена к сопротивлению r = 3,1 Ом. Найти ток батареи и напряжение на ее зажимах.

Решение

Применяя формулу закона Ома для замкнутой цепи (формула 4), находим ток

I= E r+ r 0 = 6,1 3,1+0,1 =2 А.

Напряжение на зажимах батареи может быть найдено двумя путями: или

U = E — I·r₀ = 6,4 — 2·0,1 = 6,2 В,

или

U = I·r = 2·3,1 = 6,2 В.

Задача 13. Напряжение холостого хода батареи равно 16,4 В. Чему равно внутреннее сопротивление батареи, если при токе во внешней цепи, равном 8 А, напряжение на ее зажимах равно 15,2 В?

Ответ: 0,15 Ом.

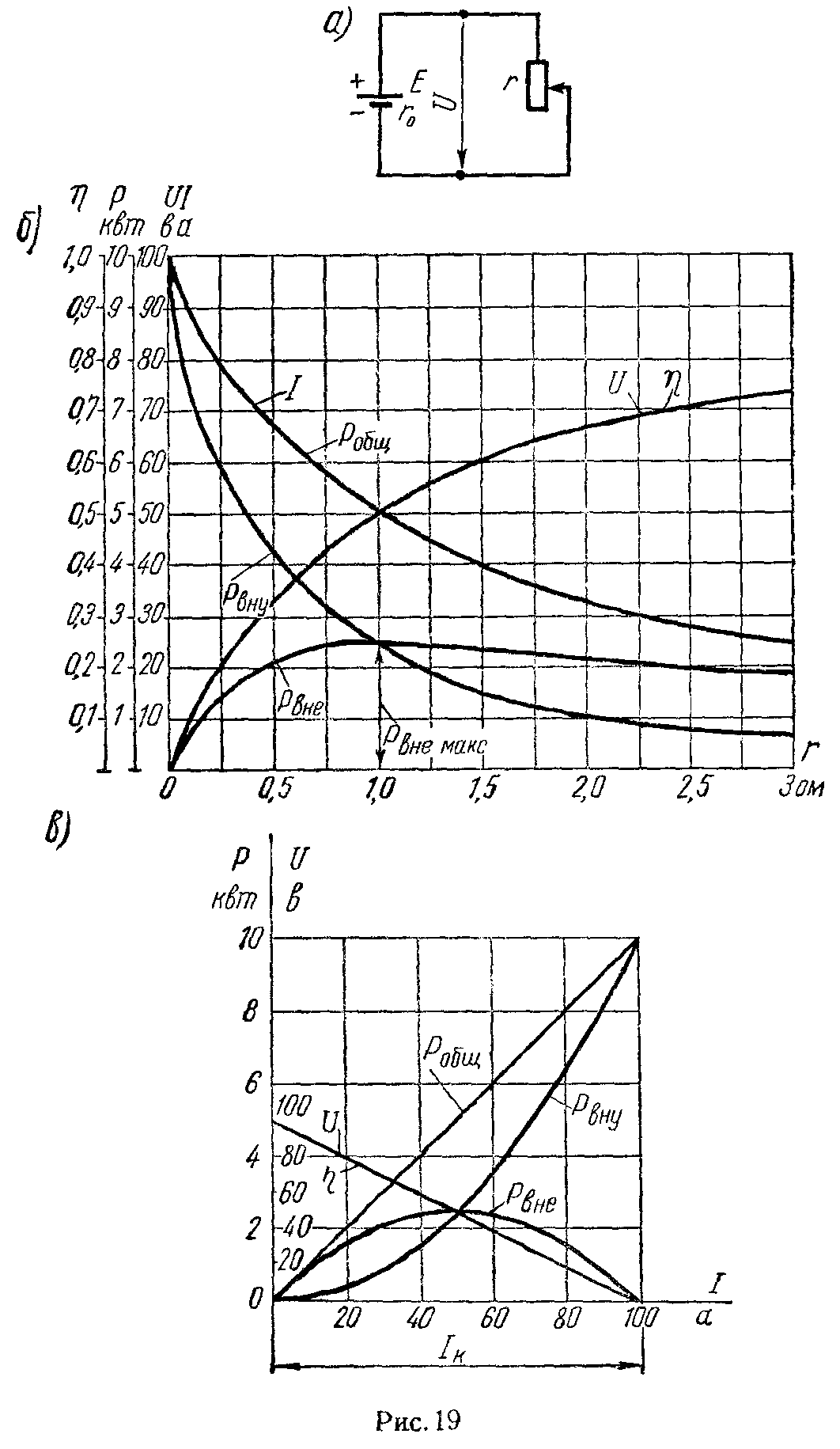
Задача 14. Источник с э.д.с. E = 100 В, внутренним сопротивлением r₀ = 1 Ом замкнут на внешнее сопротивление r, которое меняется от нуля до бесконечности (рис. 19, а). Определить в функции этого сопротивления: 1) ток I; 2) напряжение на зажимах источника U; 3) мощность, отдаваемую источником во внешнюю цепь P_внеш; 4) мощность, затрачиваемую в самом источнике P_внутр; 5) общую мощность P_общ; 6) коэффициент полезного действия η. При каком внешнем сопротивлении P_внеш будет максимальным? Чему оно равно?

Построить кривые I = F₁ (r), U = F₂ (r), P_внеш = F₃ (r), P_внутр = F₄ (r), P_общ = F₅ (r), η = F₆ (r).

Написать уравнения и построить кривые зависимостей U, P_внеш, P_внутр, P_общ и η в функции тока I.

Решение

I= E r+ r 0 = 100 r+1 ;

I=I⋅r= E⋅r r+ r 0 = 100⋅r r+1 ;

P внеш = I 2 ⋅r= E 2 ⋅r ( r+ r 0 ) 2 = 10000⋅r ( r+1 ) 2 ;

P внутр = I 2 ⋅ r 0 = E 2 ⋅ r 0 ( r+ r 0 ) 2 = 10000 ( r+1 ) 2 ;

P общ = I 2 ⋅ ( r+ r 0 )= E 2 ( r+ r 0 ) = 10000 r+1 ;

η= P внеш P общ = r r+ r 0 = r r+1 .

Определим r, при котором P_внеш будет максимально. Для этого вычислим производную от P_внеш по r и приравняем ее нулю

d P внеш dr = E 2 d dr r ( r+ r 0 ) 2 = E 2 d dr r⋅ ( r+ r 0 ) 2 −r⋅ d dr ( r+ r 0 ) 2 ( r+ r 0 ) 4 = = E 2 ( r+ r 0 ) 2 −r⋅2 ( r+ r 0 ) ( r+ r 0 ) 4 = E 2 r 0 −r ( r+ r 0 ) 3 =0.

Взяв вторую производную, можно убедиться, что она отрицательна. Это соответствует условию максимума.

Отсюда найдем, что r = r₀, т.е. при внешнем сопротивлении равном внутреннему сопротивлению, мощность, поступающая во внешнюю цепь, будет максимальна. При этом, по уравнению (6), коэффициент полезного действия равен 0,5. Величина максимальной мощности, поступающей во внешнюю цепь при r = r₀, по уравнению (3) равна

P внеш.макс = [ E 2 ⋅r ( r+ r 0 ) 2 ] r= r 0 = E 2 4r =2500 Вт.

По написанным выше уравнениям на рис. 19, б построены кривые.

Искомые уравнения зависимостей в функции тока имеют вид

U=E−I⋅ r 0 ; P внеш =E⋅I− I 2 ⋅ r 0 ; P внутр = I 2 ⋅ r 0 ; P общ =E⋅I; η=1− I⋅ r 0 E .

По этим уравнениям на рис. 19, в построены кривые.

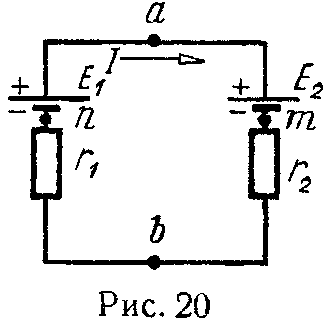
Задача 15. В схеме (рис. 20) э.д.с. E₁ = 120 В, E₂ = 40 В, а сопротивления r₁ = 12 Ом, r₂ = 8 Ом. Внутренние сопротивления источников энергии равны нулю. Определить напряжение между точками a и b.

Решение

Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) имеем

I= E 1 − E 2 r 1 + r 2 = 120−40 12+8 =4 А.

Так как результат оказался положительным, то, следовательно, фактическое направление тока совпадает с выбранным. Напряжение между точками a и b можно найти по закону Ома (формула 5), примененному к участку amb

I= U ab − E 2 r 2 ,

откуда

U ab = E 2 +I⋅ r 2 =40+4⋅8=72 В.

Такой же результат можно получить, если применить ту же формулу к участку bna

I= U ba + E 1 r 1 ,

откуда

U ba =I⋅ r 1 − E 1 =4⋅12−120=−72 В,

а, следовательно, U_ab = 72 В.

Замечание. Следует запомнить, что если на участке цепи, содержащем э.д.с. и сопротивление, ток и э.д.с. совпадают по направлению, то напряжение на зажимах участка меньше э.д.с. на величину падения напряжения в сопротивлении участка, а если направление тока противоположно направлению э.д.с., то напряжение на зажимах участка больше э.д.с. на величину падения напряжения в рассматриваемом участке.

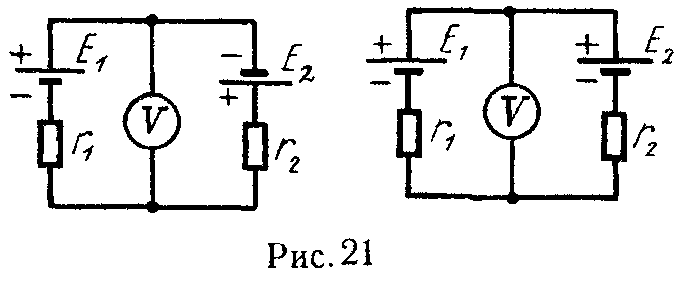
Задача 16. Определить показание вольтметра (рис. 21), сопротивление которого весьма велико по сравнению с r₁ и r₂.

Для обоих случаев даны: E₁ = 40 В, E₂ = 10 В, r₁ = r₂ = 5 Ом. Внутренними сопротивлениями источников энергии пренебречь.

Ответ: а) 15 В, б) 25 В.

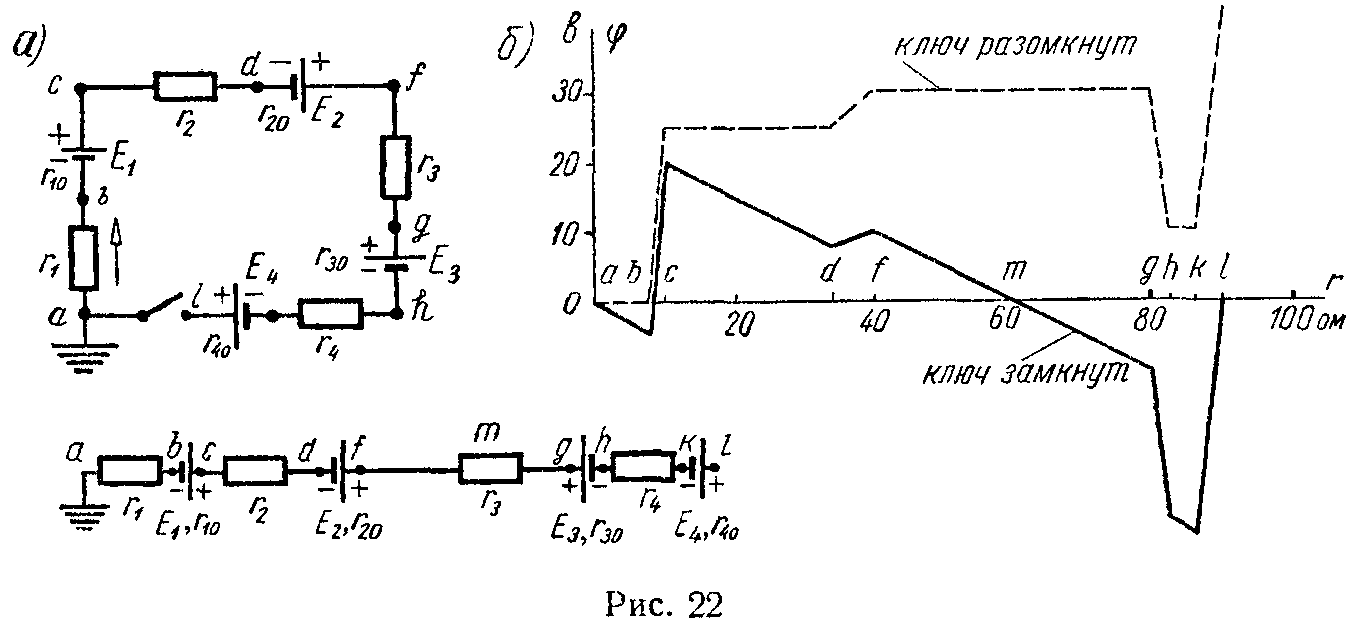
Задача 17. Построить график изменения потенциала вдоль цепи, изображенной на рис. 22, а, при замкнутом ключе и при разомкнутом ключе, предполагая в обоих случаях, что точка a заземлена (φ_a = 0).

В схеме найти точку, равнопотенцнальную точке a. Определить, потенциал какой точки следует принять равным нулю, чтобы потенциалы всех остальных точек были положительны (при замкнутом ключе).

Электродвижущие силы равны: E₁ = 25 В, E₂ = 5 В, E₃ = 20 В, E₄ = 35 В.

Внешние сопротивления имеют следующие значения: r₁ = 8 Ом, r₂ = 24 Ом, r₃ = 40 Ом, r₄ = 4 Ом. Внутренние сопротивления источников электрической энергии равны: r₁₀ = 2 Ом, r₂₀ = 6 Ом, r₃₀ = 2 Ом, r₄₀ = 4 Ом.

Решение

Ключ замкнут. Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) найдем ток

I= E 1 + E 2 − E 3 + E 4 r 1 + r 10 + r 2 + r 20 + r 3 + r 30 + r 4 + r 40 = 45 90 =0,5 А.

Пользуясь формулами (3) и (5), вычислим потенциалы всех точек, обходя контур тока по часовой стрелке

φ a =0; φ b = φ a −I⋅ r 1 =0−0,5⋅8=−4 B; φ c = φ b + E 1 −I⋅ r 10 = ( −4 )+25−0,5⋅2=20 B; φ d = φ c −I⋅ r 2 =20−0,5⋅24=8 B; φ f = φ d + E 2 −I⋅ r 20 =8+5−0,5⋅6=10 B; φ g = φ f −I⋅ r 3 =10−0,5⋅40=−10 B; φ h = φ g − E 3 −I⋅ r 30 = ( −10 )−20−0,5⋅2=−31 B; φ k = φ h −I⋅ r 4 = ( −31 )−0,5⋅4=−33 B; φ a = φ k + E 4 −I⋅ r 40 = ( −33 )+35−0,5⋅4=0.

На рис. 22, б начерчен потенциальный график. По оси абсцисс отложены величины сопротивлений отдельных участков цепи, а по оси ординат — значения потенциалов в отдельных точках цепи.

Найдем точку, равнопотенциальную точке a. Из графика видно, что искомая точка m находится на участке сопротивления fg, так как в этой точке прямая падения потенциалов пересекает ось абсцисс, потенциал которой равен φ_a = 0. Обозначая участок сопротивления между точками f и m через r_fm и применяя к участку abcdfm формулу закона Ома (5) и учитывая, что φ_a = φ_m, найдем

I= φ a − φ m + E 1 + E 2 r 1 + r 10 + r 2 + r 20 + r fm ,

или

0,5= 30 40+ r fm ,

откуда r_fm = 20 Ом, т.е. точка m находится на середине сопротивления r₃.

Для нахождения точки, потенциал которой следует принять равным нулю при условии, чтобы потенциалы всех остальных точек были положительны, следует обратиться к потенциальному графику, из которого видно, что такой точкой является точка k.

Ключ разомкнут. Тока в цепи нет, поэтому точки a и b равнопотенциальны, т. е. φ_a = φ_b = 0. Потенциал точки c превышает потенциал точки b на величину э.д.с. E₁ и φ_c = E₁ = 25 В; рассуждая аналогично, найдем

φ d = φ c =25 B; φ f = φ d + E 2 =25+5=30 B; φ g = φ f =30 B; φ h = φ g − E 3 =30−20=10 B; φ k = φ h =10 B; φ l = φ k + E 4 =10+35=45 B.

На основе полученных результатов на рис. 22, б начерчен график изменения потенциала при разомкнутом ключе.

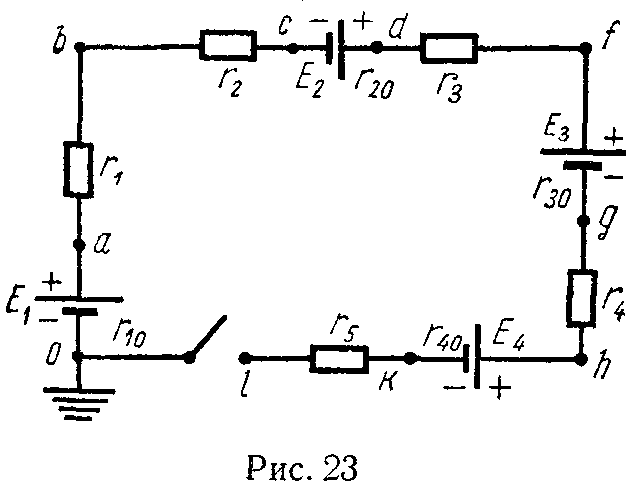
Задача 18. Для схемы рис. 23 построить потенциальные графики 0abcdfghkl при разомкнутом и замкнутом ключе, если E₁ = 60 В, E₂ = 40 В, E₃ = 25 В, E₄ = 15 В, r₁₀ = 6 Ом, r₂₀ = 4 Ом, r₃₀ = 3 Ом, r₄₀ = 2 Ом, r₁ = 24 Ом, r₂ = 16 Ом, r₃ = 25 Ом, r₄ = 22 Ом, r₅ = 18 Ом.

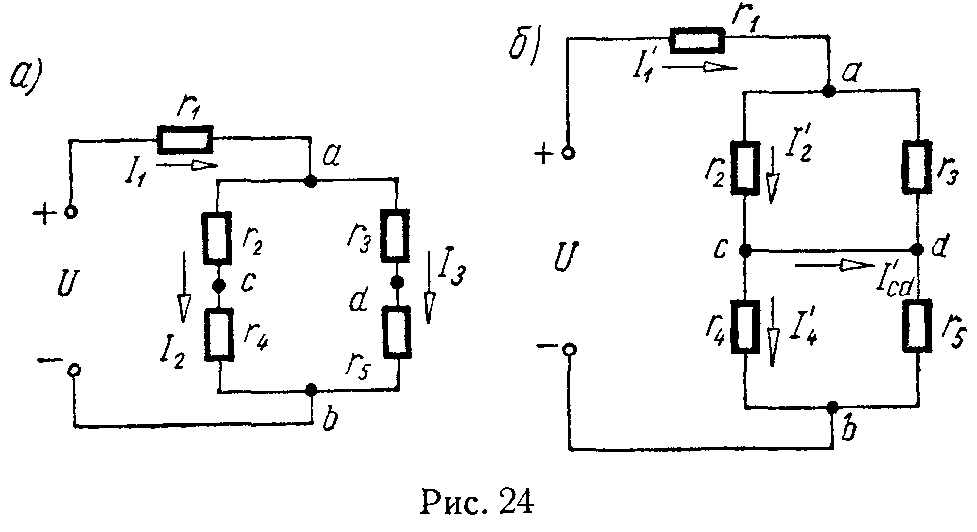
Задача 19. Определить токи в ветвях цепи (рис. 24, а) и напряжение между точками c и d и показание амперметра, включенного между точками c и d. Сопротивление амперметра считать равным нулю. Сопротивления элементов цепи r₁ = 10 Ом, r₂ = r₃ = r₅ = 25 Ом, r₄ = 50 Ом, а приложенное к ней напряжение U = 120 В.

Решение

Эквивалентное сопротивление всей цепи (рис. 24, а) равно

r= r 1 + ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =10+ 75⋅50 125 =40 Ом.

В неразветвленной части цепи протекает ток

I= U r = 120 40 =30 А.

Токи, протекающие через сопротивления r₂ + r₄ и r₃ + r₅, можно найти различными способами.

1) В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формулы 9)

I 2 = I 1 ⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 50 125 =1,2 А, I 3 = I 1 ⋅ ( r 2 + r 4 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75 125 =1,8 А.

2) Найдем напряжение на зажимах параллельных ветвей

U ab = I 1 ⋅ ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75⋅50 125 =90 В.

Токи в ветвях с сопротивлениями r₂ + r₄ и r₃ + r₅ равны

I 2 = U ab r 2 + r 4 = 90 75 =1,2 А, I 3 = U ab r 3 + r 5 = 90 50 =1,8 А.

Напряжение на зажимах параллельных ветвей может быть найдена как разность между приложенным напряжением и падением напряжения на сопротивлении r₁

U ab =U− I 1 ⋅ r 1 =120−3⋅10=90 В.

Найдем напряжение между точками c и d

U cd =− I 2 ⋅ r 2 + I 3 ⋅ r 3 =−1,2⋅25+1,8⋅25=15 В.

Наконец, вычислим ток, проходящий через амперметр, он равен току короткого замыкания I’_cd (рис. 24, б). Для его нахождения вычислим токи

I ′ 1 = U r 1 + r 2 ⋅ r 3 r 2 + r 3 + r 4 ⋅ r 5 r 4 + r 5 = 144 47 А, I ′ 2 = I ′ 1 ⋅ r 3 r 2 + r 3 = 144 47 ⋅ 1 2 = 72 47 А, I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 = 144 47 ⋅ 25 75 = 48 47 А.

Искомый ток, проходящий через амперметр, равен

I A = I ′ cd = I ′ 2 − I ′ 4 = 72 47 − 48 47 = 24 47 =0.51 А.

Задача 20. Для измерения тока применены амперметры, пределы измерений которых равны 5 и 2,5 А, и шунт, сопротивление которого неизвестно. Первый амперметр, включенный с шунтом в некоторую цепь, показал 3,6 А, второй — с тем же шунтом показал в той же цепи ток 2 А. Сопротивления амперметров r₁ = 0,002 Ом и r₂ = 0,004 Ом. Чему равен ток в цепи?

Ответ: 18 А; r_ш = 0,0005 А.

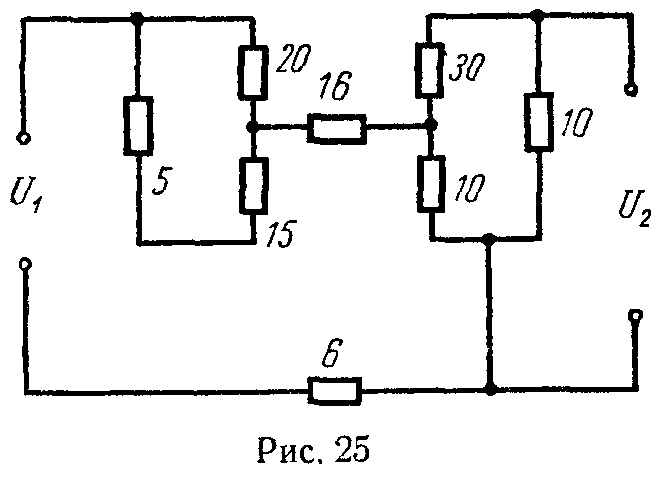
Задача 21. Для цепи рис. 25 определить отношение напряжения на выходе U₂ к напряжению на входе цепи U₁. Сопротивления отдельных ветвей цепи в омах указаны на схеме.

Ответ: U₂: U₁ = 0,05.

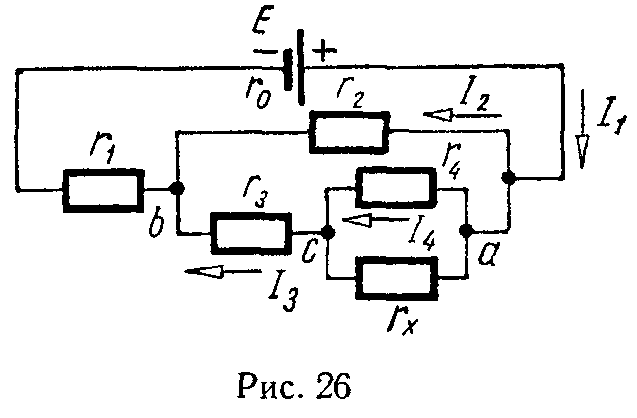
Задача 22. В схеме (рис. 26) найти сопротивление r_x, если I₁ = 2,6 А, I₃ = 0,6 А, r₁ = 0,5 Ом, r₂ =1,4 Ом, r₃ = 3 Ом, r₄ = 2,5 Ом. Найти э.д.с. батареи E, если ее внутреннее сопротивление r₀ = 0,1 Ом.

Решение

На основании первого закона Кирхгофа найдем

I₂ = I₁ — I₃ = 2,6 — 0,6 = 2 А.

По закону Ома, примененному к участку, содержащему сопротивление r₂, найдем

U_ab = I₂·r₂ = 2·1,4 = 2,8 В.

Применяя закон Ома к участку цепи ab, содержащему э.д.с. E и сопротивления r₁ и r₀, найдем искомую э.д.с.

E = U_ab + I₁· (r₁ + r₀) = 2,8 + 2,6·0,6 = 4,36 В.

Теперь найдем напряжение на параллельных ветвях с сопротивлениями r₄ и r_x и токи в них

U_ac = U_ab — I₃·r₃ = 2,8 — 0,6·3 = 1 В;

I₄ = U_ac/r₄ = 1/2,5 = 0,4 А;

I_x = I₃ — I₄ = 0,6 — 0,4 = 0,2 А.

Искомое сопротивление

r_x = U_ac/I_x = 1/0,2 = 5 Ом.

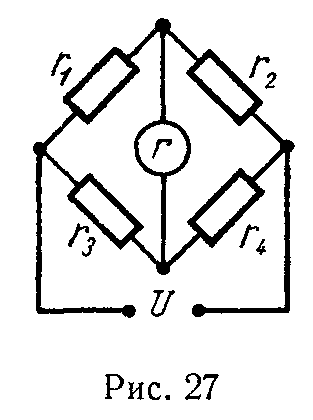
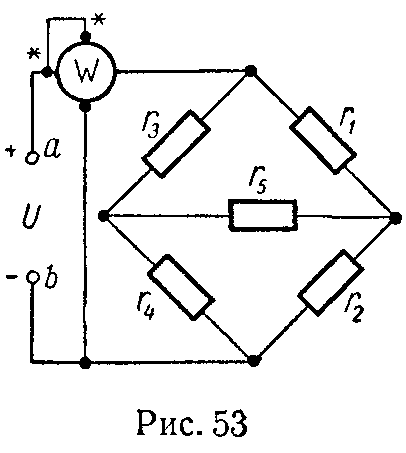
Задача 23. В схеме мостика (рис. 27) известны сопротивления r₁ = 1300 Ом, r₂ = 800 Ом, r₃ = 400 Ом. Сопротивление гальванометра r_г = 600 Ом. Через, сопротивление r₁ протекает ток I₁ = 1 мА. К мостику приложено напряжение U = 2,5 В.

Найти сопротивление r₄.

Ответ: 750 Ом.

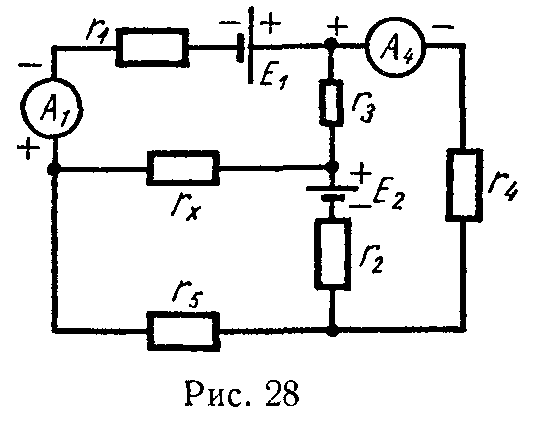
Задача 24. В цепи (рис. 28) найти E₁ и r_x, если E₂ = 3 В, r₁ = r₂ = 1 кОм, r₃ = 4 кОм, r₄ = 2 кОм, r₅ = 1 кОм. Внутренние сопротивления батарей принять равными нулю.

Амперметр А₁ показывает 4 мА, а А₄ — 3 мА; полярности приборов показаны на схеме, а их сопротивлениями можно пренебречь.

Ответ: E₁ = 12 В, r_x = 2 Ом.

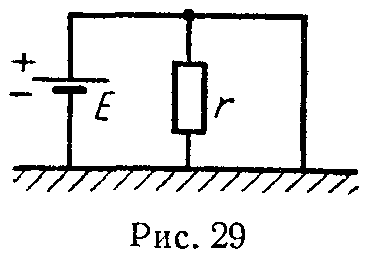
Задача 25. Однопроводная линия с сопротивлением r₀ на единицу длины, питаемая батареей с э.д.с., равной E, закорочена на приемном конце (рис. 29).

В каком месте линия должна иметь утечку с сопротивлением r, чтобы ток I на приемном конце был минимальным?

Ответ: по середине линии.

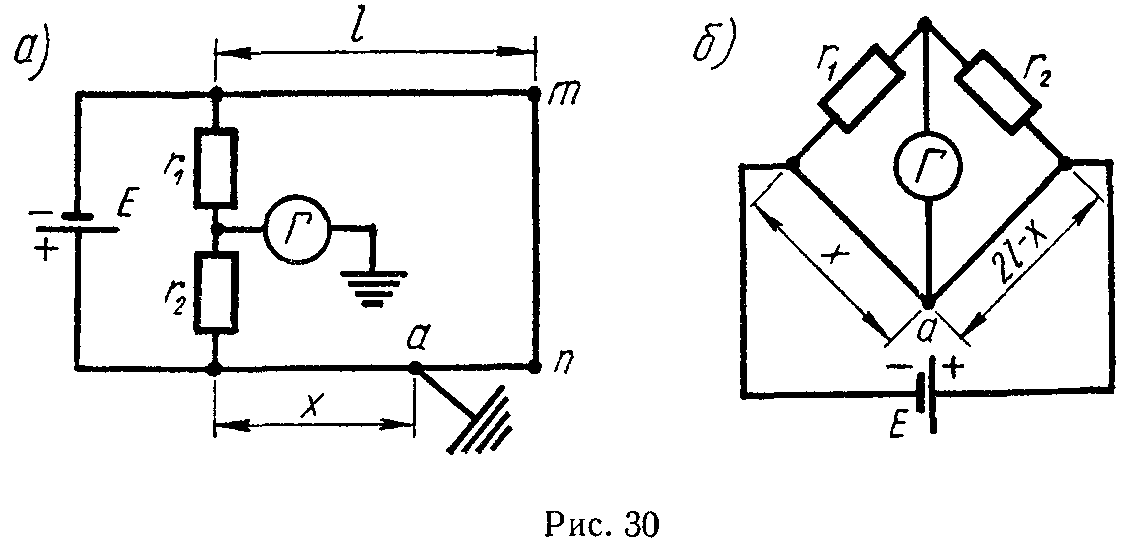
Задача 26. Для определения места повреждения изоляции линии применяется схема, изображенная на рис. 30, а; r₁ и r₂ — магазины сопротивлений.

Правый зажим гальванометра заземлен. Свободные концы тип линии соединены между собой накоротко. Подбором сопротивлений r₁ и r₂ добиваются отсутствия тока в гальванометре.

Показать, что если сечения обоих проводов одинаковы, то расстояние от места повреждения изоляции a до начала линии равно

2l⋅ r 2 r 1 + r 2 .

Указание. Заданная схема может быть заменена схемой рис. 30, б.

Задача 27. При проверке постоянной C счетчика оказалось, что при силе тока 10 А и напряжении 120 В якорь его в продолжение 30 сек сделал 37 оборотов. Определить ошибку в показаниях счетчика, если на счетчике указано, что 1 ГВт·ч соответствует 400 оборотам счетчика.

Примечание. Постоянной счетчика называется число ватт-часов, приходящихся на один оборот счетчика.

Ответ: 7,5%.

Задача 28. Каково должно быть сечение медных проводов линии для передачи потребителю мощности P = 16 кВт при условии, что потеря мощности не превысит p = 5%, если длина линии l = 180 м и напряжение в конце линии равно U = 220 В?

Ответ: точное значение 41,8 мм², по ГОСТ надо взять 50 мм².

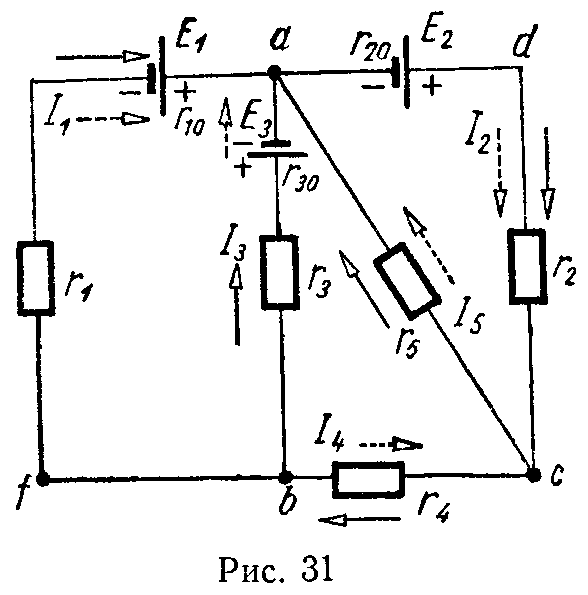
Задача 29. Для схемы (рис. 31), пользуясь законами Кирхгофа, найти токи и проверить баланс мощностей, если E₁ = 15 В, E₂ = 70 В, E₃ = 5 В, r₁₀ = r₂₀ = 1 Ом, r₃₀ = 2 Ом, r₁ = 5 Ом, r₁ = 5 Ом, r₂ = 4 Ом, r₃ = 8 Ом, r₄ = 2,5 Ом, r₅ = 15 Ом.

Решение

Всего узлов в схеме три (a, b, c), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. Число контуров равно трем, следовательно, по второму закону Кирхгофа можно составить три взаимно независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов в пяти ветвях схемы.

Выберем положительные направления для токов, которые обозначены пунктирными стрелками, и составим систему уравнений Кирхгофа:

для узла a

I₁ — I₂ + I₃ + I₅ = 0; (1)

для узла b

–I₁ — I₃ — I₄ = 0; (2)

для контура abfa

E₁ + E₃ = I₁· (r₁ + r₁₀) — I₃· (r₃ + r₃₀); (3)

для контура abca

E₃ = –I₃· (r₃ + r₃₀) + I₄·r₄ + I₅·r₅; (4)

для контура adca

E₂ = I₂· (r₂ + r₂₀) + I₅·r₅. (5)

Уравнения (1) — (5) после подстановки в них числовых значений будут иметь следующий вид

I₁ — I₂ + I₃ + I₅ = 0,

I₁ + I₃ + I₄ = 0,

6I₁ — 10I₃ = 20,

–10I₃ + 2,5I₄ + 15I₅ = 5,

5I₂ + 15I₅ = 70.

Решая эту систему уравнений, получим

I₁ = 5 А; I₂ = 8 А; I₃ = 1 А; I₄ = –6 А; I₅ = 2 А.

Отрицательный знак для тока I₄ означает, что истинное направление этого тока противоположно принятому. При проверке баланса мощностей надо иметь в виду, что в тех ветвях цепи, где истинное направление тока совпадает с направлением э.д.с., соответствующая э.д.с. будет являться источником энергии, а в тех участках, где направления э.д.с. и тока противоположны, э.д.с. будет являться потребителем энергии. Все сопротивления как внешние, так и самих источников, независимо от направления протекающего через них тока, будут являться потребителями энергии.

Баланс мощностей для рассматриваемой схемы будет

E₁·I₁ + E₂·I₂ + E₃· (–I₃) = I₁²· (r₁ + r₁₀) + I₂²· (r₂ + r₂₀) + I₃²· (r₃ + r₃₀) + I₄²·r₄ + I₅²·r₅,

или

15·5 + 70·8 — 5·1 = 5²·6 + 8²·5 + 1²·10 + 6²·2,5 + 2²·15,

получено тождество 630 Вт = 630 Вт.

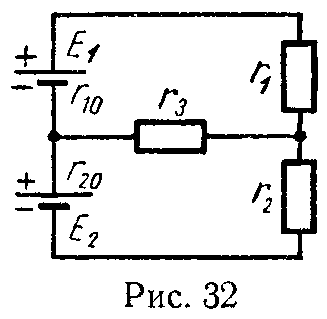
Задача 30. В схеме (рис. 32) найти все токи, если известны: E₁ = 20 В, E₂ = 1,1 В, r₁₀ = 0,2 Ом, r₂₀ = 0,4 Ом, r₁ = r₂ = 5 Ом, r₃ = 7 Ом.

Ответ: 2,5 А, 1,5 А, 1 А.

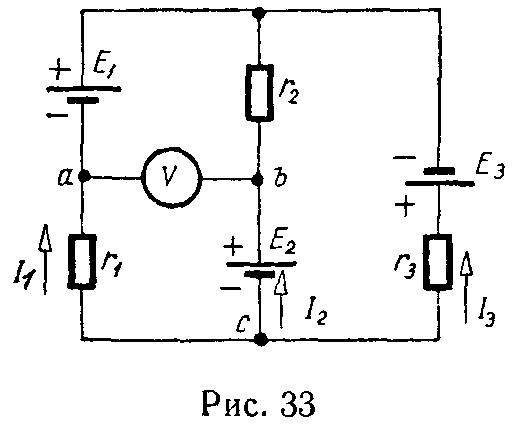
Задача 31. Для цепи, изображенной на рис. 33, рассчитать токи и определить показание вольтметра, если E₁ = 40 В, E₂ = 5 В, E₃ = 25 В, r₁ = 5 Ом, r₂ = r₃ = 10 Ом.

Внутренними сопротивлениями источников энергии и током, протекающим через вольтметр, можно пренебречь.

Ответ: I₁ = 5 А, I₂ = 1 А, I₃ = 4 А, U_ba = 30 В.

Задача 32. Аккумуляторная батарея из 20 последовательно соединенных элементов работает параллельно с генератором на сеть, имеющую нагрузку 30 А. Каждый аккумулятор имеет э.д.с. 1,82 В и сопротивление 0,001 Ом. Э.д.с. генератора 36,4 В и его сопротивление 0,04 Ом. Определить нагрузку генератора и батареи (т. е. отдаваемые ими токи) и напряжение на их зажимах.

Какую э.д.с. должен развивать генератор, чтобы нагрузка распределилась поровну между генератором и батареей?

Ответ: 20 А, 10 А, 36 В, 36,7 В.

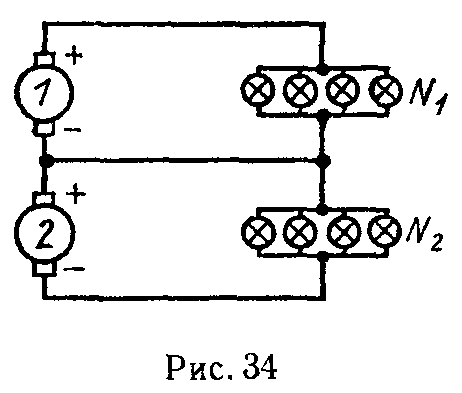
Задача 33. По трехпроводной линии длиной 0,5 км (рис. 34) от двух генераторов 1 и 2 питаются две группы ламп 50 Вт, 110 В.

В первой группе — N₁ = 200 ламп, а во второй — N₂ = 600 ламп. Сечение крайних проводов q = 35 мм², а сечение среднего (нулевого) провода q₀ = 16 мм². Каждый генератор имеет внутреннее сопротивление 0,01 Ом и развивает э.д.с. 120 В. Определить токи во всех проводах линии и напряжение на зажимах каждой группы ламп, сопротивления которых считать постоянным. Материал проводов линии — медь.

Ответ: I₁ = 98 А, I₂ = 144 А, I₀ = 46 А, U₁ = 102 В, U₂ = 71 В.

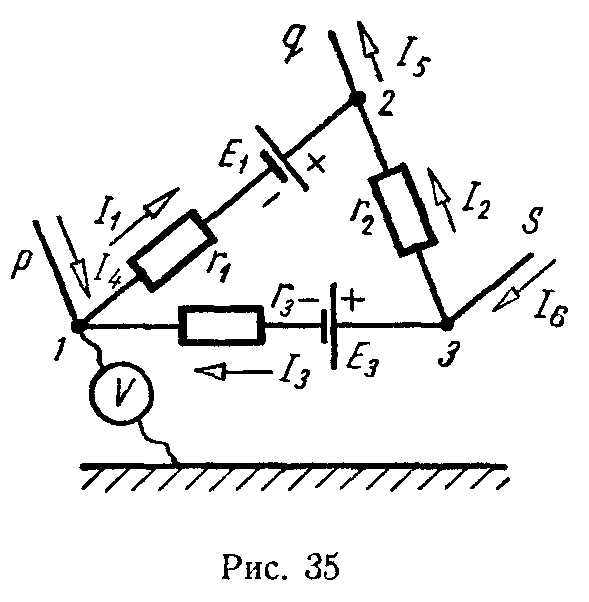
Задача 34. Напряжения, измеренные электростатическим вольтметром, между узловыми точками схемы и землей, равны: U₁₀ = –15 В, U₂₀ = 52 В, U₃₀ = 64 В (рис. 35).

Определить токи в ветвях и отходящих проводах при следующих данных: E₁ = 80 В, E₃ = 70 В, r₁ = 5 Ом, r₂ = 10 Ом, r₃ = 12 Ом.

Решение

Вычислим напряжения между точками 1 и 2, 2 и 3, 3 и 1

U₁₀ — U₂₀ = U₁₂ = (–15) — 52 = –67 В,

U₂₀ — U₃₀ = U₂₃ = 52 — 64 = –12 В,

U₃₀ — U₁₀ = U₃₁ = 64 — (–15) = 79 В.

Применяя к ветвям 1–2, 2–3, 3–1 закон Ома, найдем токи

I 1 = U 12 + E 1 r 1 = ( −67 )+80 5 =2,6 А, I 2 = U 32 r 2 = 12 10 =1,2 А, I 3 = U 31 − E 3 r 3 = 79−70 12 =0,75 А.

Так как все токи оказались положительными, то они имеют направления в соответствии с только что записанными уравнениями и нанесены на рис. 35.

Токи в ответвлениях от узловых точек 1–p, 2–q, 3–s находим по первому закону Кирхгофа

I₄ = I₁ — I₃ = 1,85 А, I₅ = I₁ + I₂ = 3,8 А, I₆ = I₂ + I₃ = 1,95 А.

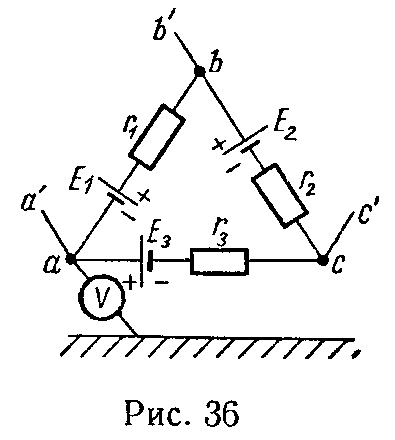
Задача 35. В цепи (рис. 36) известны э.д.с. E₁ = 120 В, E₂ = 40 В, E₃ = 70 В и сопротивления r₁ = 20 Ом, r₂ = 10 Ом, r₃ = 40 Ом.

Потенциалы точек a, b и c относительно земли соответственно равны (определены посредством вольтметра): U_a₀ =160 В, U_b₀ = 180 В, U_c₀ = 50 В. Определить токи в ветвях ab, bc, ca и в проводах aa’, bb’ и cc’, подходящих к точкам a, b и c.

Ответ: I₁ = 5 А, I₂ = 9 А, I₃ = 1 А.

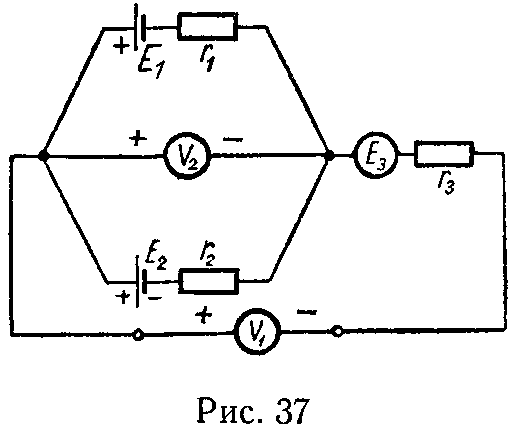
Задача 36. В цепи (рис. 37) известны э.д.с. E₁ = 40 В, E₂ = 30 В.

Сопротивления элементов схемы r₁ = 8 Ом, r₂ = 5 Ом, r₃ = 10 Ом. Показания вольтметров соответственно равны: U₁ = 125 В, U₂ = 60 В; полярность зажимов вольтметров показана на схеме. Пренебрегая внутренними сопротивлениями источников электрической энергии и считая потребляемые вольтметрами токи приближенно равными нулю, определить величину и полярность э.д.с. E₃. Найти все токи.

Ответ: E₃ = 20 В, I₁ = 2,5 А, I₂ = 6 А, I₃ = 8,5 А.

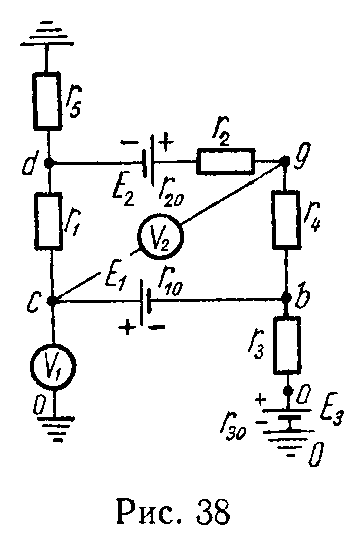
Задача 37. В цепи, изображенной на рис. 38, найти токи и показания вольтметров, включенных между точками 0 и c, c и g, если известно, что E₁ = 32 В, E₂ = 64 В, E₃ = 72 В, r₁ = 9 Ом, r₁₀ = 1 Ом, r₂ = 5 Ом, r₂₀ = 1 Ом, r₃ = 2 Ом, r₃₀ = 1 Ом, r₄ = 2 Ом, r₅ = 1 Ом. Сопротивления вольтметров весьма велики по сравнению с сопротивлениями элементов цепи.

Ответ: I₁ = 5 А, I₂ = 9 А, I₃ = 1 А.

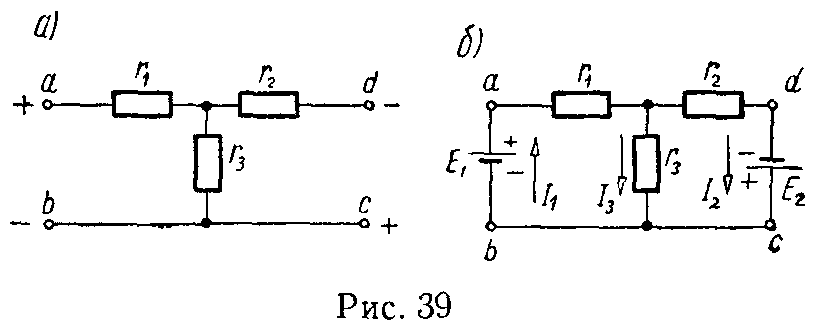
Задача 38. Для схемы (рис. 39, а) найти токи и проверить баланс мощностей, если U_ab = 12 В, U_cd = 5,6 В, r₁ = 4 Ом, r₂ = 5 Ом, r₃ = 3 Ом.

Решение

Данная схема может быть заменена эквивалентной, в которой между точками a и b, а также c и d включены э.д.с., численное значение которых E₁ = U_ab и E₂ = U_cd, а их внутренние сопротивления равны нулю (рис. 39, б). Обращаем внимание на то, что при включении э.д.с. следует соблюдать заданные полярности напряжений.

Задавшись направлениями для токов, составим систему уравнений Кирхгофа

I₁ — I₂ — I₃ = 0,

E₁ = I₁·r₁ + I₃·r₃,

E₂ = I₂·r₂ — I₃·r₃.

Подставляя сюда числовые значения и решая систему уравнений, найдем:

I₁ = 2,4 А, I₂ = 1,6 А, I₃ = 0,8 А.

Для проверки баланса мощностей составим уравнение

U_ab·I₁ + U_cd·I₂ = I₁²·r₁ + I₂²·r₂ + I₃²·r₃,

12·2,4 + 5,6·1,6 = 2,4²·4 + 1,6²·5 + 0,8²·3;

получено тождество 37,76 = 37,76.

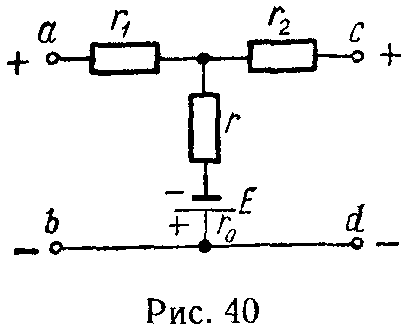
Задача 39. В цепи (рис. 40) найти токи и проверить баланс мощностей, если U_ab = 16 В, U_cd = 11,2 В, E = 5 В, r₀ = 0, r = 10 Ом, r₁ = 5 Ом, r₂ = 4 Ом.

Ответ: I₁ = 1,2 А, I₂ = 0,3 А, I = 1,5 А.

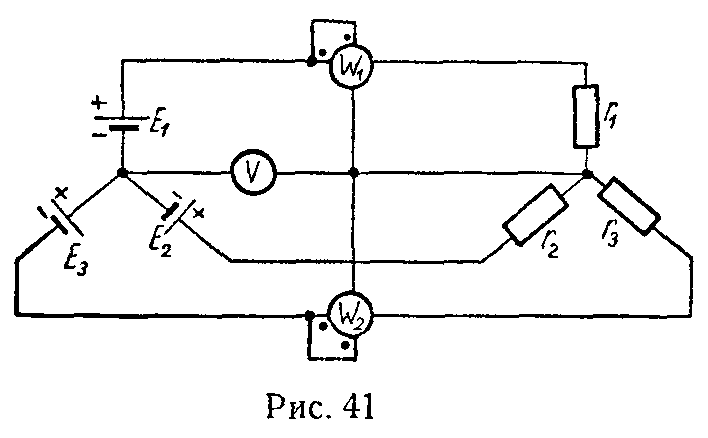
Задача 40. Чему равно показание вольтметра на рис. 41, если током вольтметра можно пренебречь по сравнению с токами в нагрузках? Внутренние сопротивления батарей принять равными нулю.

Определить показания ваттметров и убедиться в том, что их сумма равна сумме мощностей, расходуемых в сопротивлениях r₁, r₂ и r₃. Потерями в катушках ваттметров пренебречь.

Дано: E₁ = 30 В, E₂ = 21 В, E₃ = 5 В, r₁ = 5 Ом, r₂ = 10 Ом, r₃ = 50 Ом.

Ответ: 25 В, P₁ = 9 Вт, P₂ = 15,6 Вт.

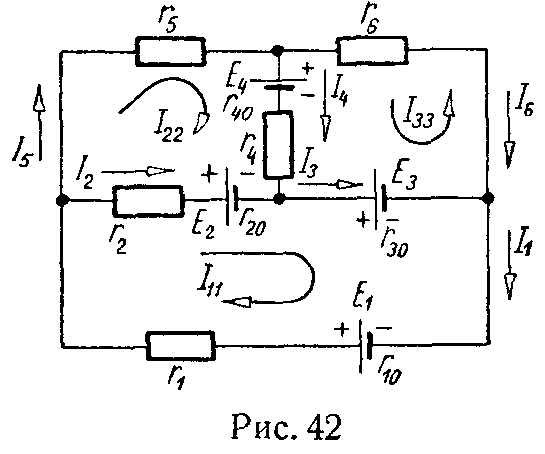
Задача 41. Методом контурных токов найти токи в цепи, схема которой изображена на рис. 42; даны: E₁ = 100 В, E₂ = 30 В, E₃ = 10 В, E₄ = 6 В, r₁ = 10 Ом, r₂ = 10 Ом, r₄ = 6 Ом, r₅ = 5 Ом, r₆ = 15 Ом, r₁₀ = r₂₀ = r₃₀ = 0, r₄₀ = 1 Ом.

Решение

Выберем направления контурных токов, которые обозначим через I₁₁, I₂₂, I₃₃.

Составим систему уравнений для контуров

E₁ — E₂ — E₃ = I₁₁· (r₁ + r₁₀ + r₂ + r₂₀ + r₃₀) — I₂₂· (r₂ + r₂₀) + I₃₃·r₃₀,

E₂ — E₄ = I₂₂· (r₂ + r₂₀ + r₅ + r₄ + r₄₀) + I₃₃· (r₄ + r₄₀) — I₁₁· (r₂ + r₂₀),

–E₃ — E₄ = I₃₃· (r₃₀ + r₆ + r₄ + r₄₀) + I₂₂· (r₄ + r₄₀) + I₁₁·r₃₀.

После подстановки числовых значений будем иметь

60 = 20·I₁₁ — 10·I₂₂ + 0·I₃₃,

24 = –10·I₁₁ + 22·I₂₂ + 7·I₃₃,

–16 = 0·I₁₁ + 7·I₂₂ + 22·I₃₃.

Решив эту систему уравнений, найдем контурные токи

I₁₁ = 5 А, I₂₂ = 4 А, I₃₃ = –2 А.

Теперь найдем истинные токи во всех ветвях.

В ветви, где действует э.д.с. E₁, истинный ток I₁ имеет направление контурного тока I₁₁ и равен

I₁ = I₁₁ = 5 А.

В ветви с сопротивлением r₅ истинный ток I₅ имеет направление контурного тока I₂₂ и равен

I₅ = I₂₂ = 4 А.

В ветви с сопротивлением r₆ истинный ток I₆ имеет направление, противоположное контурному току I₃₃, и равен

I₆ = –I₃₃ = — (–2) = 2 А.

В ветви с сопротивлением r₂ истинный ток I₂ получится от наложения контурных токов I₁₁ и I₂₂ и будет иметь направление большего контурного тока I₁₁;

I₂ = I₁₁ — I₂₂ = 5 — 4 = 1 А.

В ветви с сопротивлением r₄ истинный ток I₄ получится от наложения контурных токов I₂₂ и I₃₃ и будет иметь направление контурного тока I₂₂;

I₄ = I₂₂ + I₃₃ = 4 + (–2) = 2 А.

В ветви, где действует э.д.с. E₃, истинный ток I₃ получится от наложения контурных токов I₁₁ и I₃₃ и будет иметь направление тока I₁₁;

I₃ = I₁₁ + I₃₃ = 5 + (–2) = 3 А.

Эта же задача может быть решена методом определителей. Для этого уравнения для контурных токов следует записать в форме (10), а именно

{ r 11 ⋅ I 11 + r 12 ⋅ I 22 + r 13 ⋅ I 33 = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 + r 23 ⋅ I 33 = E 22 ; r 31 ⋅ I 11 + r 32 ⋅ I 22 + r 33 ⋅ I 33 = E 33 ,

где контурные сопротивления

r₁₁ = r₁ + r₁₀ + r₂ + r₂₀ + r₃₀ = 20 Ом;

r₂₂ = r₂ + r₂₀ + r₅ + r₄ + r₄₀ = 22 Ом;

r₃₃ = r₃₀ + r₆ + r₄ + r₄₀ = 22 Ом,

взаимные сопротивления контуров

r₁₂ = r₂₁ = — (r₂ + r₂₀) = –10 Ом;

r₁₃ = r₃₁ = r₃₀ = 0;

r₂₃ = r₃₂ = r₄ + r₄₀ = 7 Ом,

контурные э.д.с.

E₁₁ = E₁ — E₂ — E₃ = 60 В;

E₂₂ = E₂ — E₄ = 24 В;

E₃₃ = –E₃ — E₄ = –16 В.

Получим численную систему уравнений метода контурных токов

{ 20⋅ I 11 − 10⋅ I 22 + 0⋅ I 33 =60; −10⋅ I 11 +22⋅ I 22 + 7⋅ I 33 =24; 0⋅ I 11 + 7⋅ I 22 +22⋅ I 33 =−16,

или в матричной форме записи

( 20 −10 0 −10 22 7 0 7 22 )⋅ ( I 11 I 22 I 33 )= ( 60 24 −16 ).

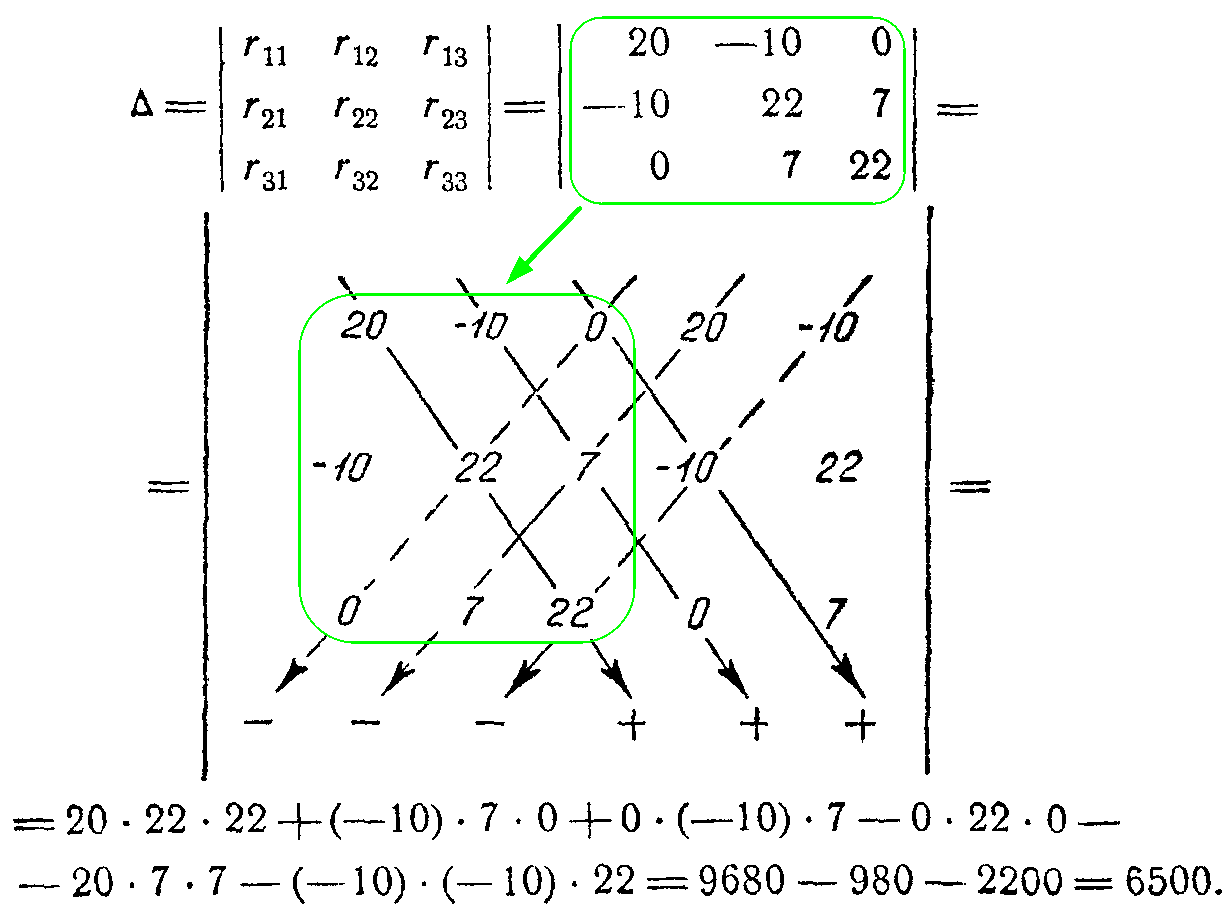
Составим главный определитель системы? и вычислим его значение

Вычислим значения вспомогательных определителей

Δ 11 =| E 11 r 12 r 13 E 22 r 22 r 23 E 33 r 32 r 33 |=| 60 −10 0 24 22 7 −16 7 22 |=32500; Δ 22 =| r 11 E 11 r 13 r 21 E 22 r 23 r 31 E 33 r 33 |=| 20 60 0 −10 24 7 0 −16 22 |=26000; Δ 33 =| r 11 r 12 E 11 r 21 r 22 E 22 r 31 r 32 E 33 |=| 20 −10 60 −10 22 24 0 7 −16 |=−13000.

Искомые контурные токи определяем по формулам

I 11 = Δ 11 Δ = 32500 6500 =5 А; I 22 = Δ 22 Δ = 26000 6500 =4 А; I 33 = Δ 33 Δ = −13000 6500 =−2 А.

Мы получили те же результаты, что и ранее.

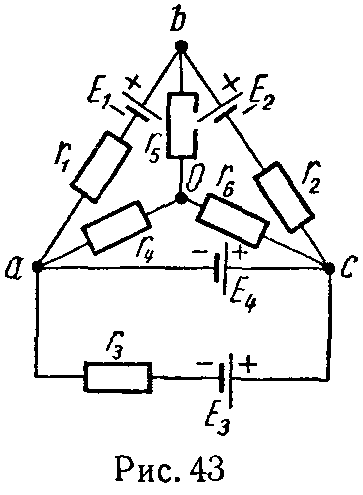
Задача 42. Найти все токи и определить потенциалы точек a, b, c и 0 относительно земли (рис. 43).

Задачу решить методом контурных токов, Внутренние сопротивления источников электрической энергии считать равными нулю: E₁ = 85 В, E₂ = 84 В, E₃ = 5 В, E₄ = 12 В, r₁ = 8 Ом, r₂ = 10 Ом, r₃ = 10 Ом, r₄ = 10 Ом, r₅ = 10 Ом, r₆ = 4 Ом.

Ответ: I₁ = 2 А, I₂ = 2,7 А, I₃ = 0,7 А, I₄ = 2,2 А, I₅ = 4,7 А, I₆ = 2,5 А.

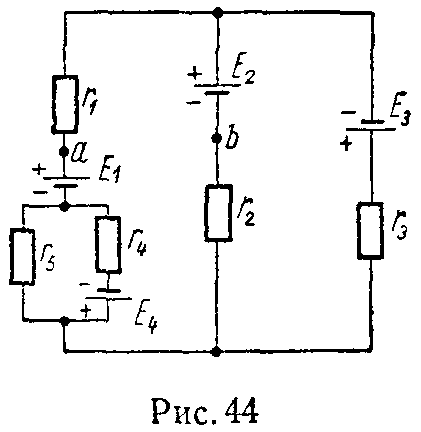
Задача 43. Для схемы (рис. 44) найти токи и U_ab, если E₁ = 70 В, E₂ = 5 В, E₃ = 15 В, E₄ = 10 В, r₁ = 5 Ом, r₂ = r₃ = 10 Ом, r₄ = 5 Ом, r₅ = 3 Ом.

Задачу решить методом контурных токов. Внутренние сопротивления источников энергии равны нулю.

Ответ: I₁ = 6 А, I₂ = 2 А, I₃ = 4 А, I₄ = 1 А, I₅ = 5 А.

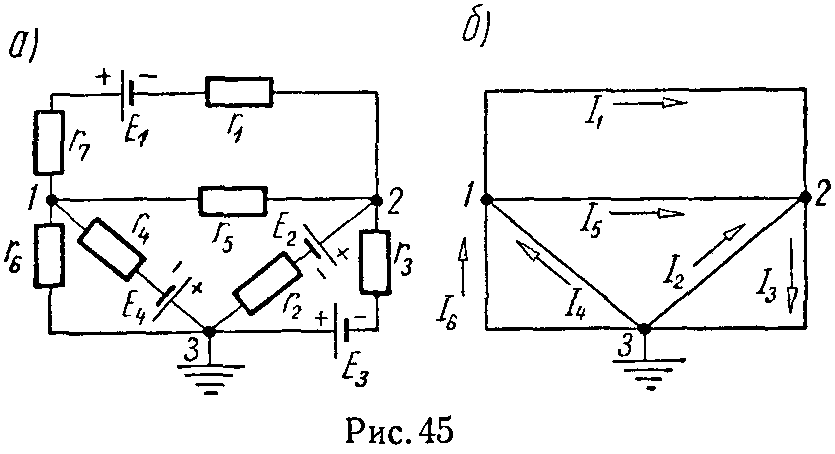
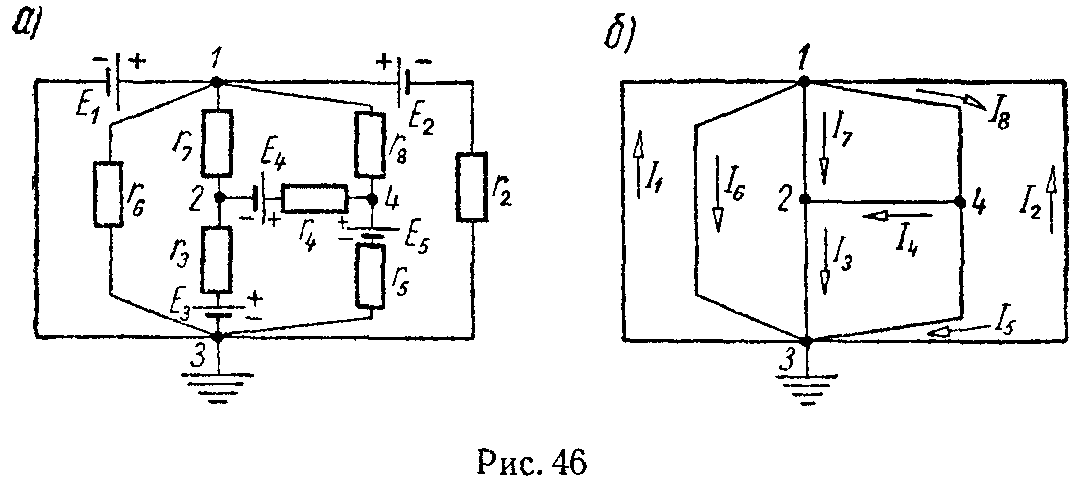
Задача 44. Для схемы, изображенной на рисунке 45, а, пользуясь методом узловых потенциалов, определить все токи. Данные схемы: E₁ = 30 В, E₂ = 10 В, E₃ = 200 В, E₄ = 56 В, r₁ = 20 Ом, r₂ = 30 Ом, r₃ = 6 Ом, r₄ = 8 Ом, r₅ = 15 Ом, r₆ = 40 Ом, r₇ = 10 Ом. Внутренние сопротивления источников напряжения равны нулю.

Решение

Примем потенциал точки 3 равным нулю. Тогда, на основании формулы (11), запишем систему уравнений для определения потенциалов точек 1 и 2

φ 1 ⋅ g 11 + φ 2 ⋅ g 12 = ∑ 1 E⋅g , (1) φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = ∑ 2 E⋅g . (2)

Подсчитаем g₁₁ — сумму проводимостей, присоединенных к узлу 1

g 11 = 1 r 1 + r 7 + 1 r 5 + 1 r 4 + 1 r 6 = 1 30 + 1 15 + 1 8 + 1 40 =0,25 1 Ом .

Аналогично g₂₂ — сумма проводимостей, присоединенных к узлу 2

g 22 = 1 r 1 + r 7 + 1 r 5 + 1 r 2 + 1 r 3 = 1 30 + 1 15 + 1 30 + 1 6 =0,3 1 Ом .

Взаимные проводимости первого и второго узлов

g 12 = g 21 =− ( 1 r 1 + r 7 + 1 r 5 )=− 1 30 − 1 15 =−0,1 1 Ом .

Подставим в уравнения (1) и (2) числовые значения

0,25⋅ φ 1 + ( −0,1 )⋅ φ 2 =30⋅ 1 30 −56⋅ 1 8 =−6, ( −0,1 )⋅ φ 1 +0,3⋅ φ 2 =−30⋅ 1 30 +10⋅ 1 30 −200⋅ 1 6 =−34.

Решив последние два уравнения, найдем потенциалы точек 1 и 2

φ₁ = –80 В; φ₂ = –140 В.

Наконец, применяя закон Ома для отдельных ветвей, определим искомые токи

I 1 = φ 1 − φ 2 − E 1 r 1 = ( −80 )− ( −140 )−30 30 =1 А; I 2 = φ 3 − φ 2 + E 2 r 2 = 0− ( −140 )+10 30 =5 А; I 3 = φ 2 − φ 3 + E 3 r 3 = ( −140 )−0+200 6 =5 А; I 4 = φ 3 − φ 1 − E 4 r 4 = 0− ( −80 )−56 8 =3 А; I 5 = φ 1 − φ 2 r 5 = ( −80 )− ( −140 ) 15 =4 А.

Направления найденных токов указаны на скелетной схеме (рис. 45, б).

Рекомендуем читателю решить ту же задачу, приняв за нуль потенциал узловой точки 1.

Задача 45. Методом узловых потенциалов определить токи во всех ветвях схемы, изображенной на рис. 46, а; заданы: E₁ = 20 В, E₂ = 30 В, E₃ = 2 В, E₄ = 1,2 В, E₅ = 5,6 В, r₂ = 50 Ом, r₃ = 10 Ом, r₄ = 20 Ом, r₅ = 10 Ом, r₆ = 100 Ом, r₇ = 50 Ом, r₈ = 20 Ом.

Внутренние сопротивления источников напряжения считать равными нулю.

Решение

В тех случаях, когда в цепи имеется ветвь с э.д.с., но не содержащая сопротивления, целесообразно принять равным нулю потенциал одной из узловых точек, к которой подходит указанная ветвь.

В нашем случае примем потенциал узла 3 равным нулю (φ₃ = 0). Тогда потенциал точки 1 имеет значение, равное E₁, т.е. φ₁ = 20 В. Общее число уравнений уменьшается и равняется числу узлов минус два. В нашей задаче достаточно составить всего два уравнения для узлов 2 и 4.

Определим сумму проводимостей, присоединенных к узлу 2

g 22 = 1 r 3 + 1 r 4 + 1 r 7 =0,17 1 Ом ,

и, соответственно, к узлу 4

g 44 = 1 r 4 + 1 r 5 + 1 r 8 =0,2 1 Ом .

Найдем взаимные проводимости узлов 2 и 1, 2 и 4, 4 и 1

g 12 = g 21 =− 1 r 7 =−0,02 1 Ом , g 24 = g 42 =− 1 r 4 =−0,05 1 Ом , g 14 = g 41 =− 1 r 8 =−0,05 1 Ом .

Вычислим суммы произведений э.д,с. на проводимости, присоединенные соответственно к узлам 2 и 4

∑ 2 E⋅g = E 3 ⋅ g 3 − E 4 ⋅ g 4 =0,14 В Ом , ∑ 4 E⋅g = E 4 ⋅ g 4 + E 5 ⋅ g 5 =0,62 В Ом .

Составим систему уравнений на основании формул (11) для узла 2:

φ 1 ⋅ g 21 + φ 2 ⋅ g 22 + φ 4 ⋅ g 24 = ∑ 2 E⋅g ,

для узла 4

φ 1 ⋅ g 41 + φ 2 ⋅ g 42 + φ 4 ⋅ g 44 = ∑ 4 E⋅g .

Подставляя сюда числовые значения, получим

0,17⋅ φ 2 + ( −0,05 )⋅ φ 4 =0,54, ( −0,05 )⋅ φ 2 +0,2⋅ φ 4 =1,62.

Решая эту систему уравнений, найдем

φ₂ = 6 В; φ₄ = 9,6 В.

Наконец, применяя к отдельным ветвям формулы закона Ома, получим значения всех токов, которые нанесены на скелетной схеме (46, б)

I₂ = 0,2 А, I₃ = 0,4 А, I₄ = 0,12 А, I₅ = 0,4 А, I₆ = 0,2 А, I₇ = 0,28 А, I₈ = 0,52 А.

Ток I₁ определяется на основании первого закона Кирхгофа

I₁ = I₃ + I₅ + I₆ – I₂ = 0,8 А.

Задача 46. Методом узловых потенциалов рассчитать токи в цепи (рис. 47). Даны: E₁ = 160 мВ, E₂ = 300 мВ, r₃ = r₄ = 100 Ом, r₅ = 150 Ом, r₆ = 40 Ом. Внутренние сопротивления генераторов напряжения равны нулю.

Указание. Для решения задачи достаточно составить всего одно уравнение, так как в схеме имеется две ветви с э.д.с., но не содержащие сопротивления, а узлов в схеме четыре.

Ответ: I₁ = 2,25 мА, I₂ = 1,4 мА, I₃ = 0,85 мА, I₄ = 0,75 мА, I₅ = 0,1 мА, I₆ = 1,5 мА.

Задача 47. Методом наложения рассчитать токи в схеме (рис. 48. а), если E₁ = 10 В, E₂ = 40 В, E₃ = 5 В, r₁₀ = 5 Ом, r₂₀ = r₃₀ = 2 Ом, r₁ = 30 Ом, r₂ = 3 Ом, r₃ = 8 Ом.

Решение

Сначала предполагаем, что действует только э.д.с. E₁, а э.д.с. E₂ и E₃ считаем недействующими (рис. 48, б), тогда

I ′ 1 = E 1 r 1Э ,

где

r 1Э = r 1 + r 10 + ( r 2 + r 20 )⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) =35+ 5⋅10 15 = 115 3 Ом.

Ток

I ′ 1 = E 1 r 1Э = 10 115/3 = 6 23 А.

Токи в параллельных ветвях найдем согласно формуле (9)

I ′ 2 = I ′ 1 ⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 10 15 = 4 23 А, I ′ 3 = I ′ 1 ⋅ ( r 2 + r 20 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 5 15 = 2 23 А.

Теперь проведем расчет, предполагая, что действует э.д.с. E₂, а э.д.с. E₁ и E₃ считаем недействующими (рис. 48, в)

I ″ 2 = E 2 r 2Э ; r 2Э = r 2 + r 20 + ( r 1 + r 10 )⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 115 9 Ом; I ″ 2 = E 2 r 2Э = 40 115/9 = 72 23 А; I ″ 1 = I ″ 2 ⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 10 45 = 16 23 А; I ″ 3 = I ″ 2 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 35 45 = 56 23 А.

Аналогично рассчитываем величины токов при действии только одной э.д.с. E₃ (рис. 48, г)

I ? 3 = E 3 r 3Э ; r 3Э = r 3 + r 30 + ( r 1 + r 10 )⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 115 8 Ом; I ? 3 = E 3 r 3Э = 5 115/8 = 8 23 А; I ? 1 = I ? 3 ⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 5 40 = 1 23 А; I ? 2 = I ? 3 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 35 40 = 7 23 А.

Истинное значение тока в каждой ветви найдется как алгебраическая сумма токов, определяемых каждой э.д.с. в отдельности.

Ток в первой ветви

I 1 = I ′ 1 + I ″ 1 + I ? 1 = 6 23 + 16 23 + 1 23 =1 А.

Ток во второй ветви

I 2 = I ′ 2 + I ″ 2 − I ? 2 = 4 23 + 72 23 − 7 23 =3 А.

Ток в третьей ветви

I 3 =− I ′ 3 + I ″ 3 − I ? 3 =− 2 23 + 56 23 − 8 23 =2 А.

Направления этих токов показаны на рис. 48, а.

Задача 48. Найти токи в ветвях цепи, изображенной на рис. 49, если известны E₁ = 125 мВ, E = 120 мВ, r₁ = 40 Ом, r₂ = 36 Ом, r₃ = r₄ = 60 Ом. Внутренними сопротивлениями источников пренебречь. Задачу решить методами наложения и контурных токов.

Ответ: I₁ = 0,8 А, I₂ = 0,75 А, I₃ = 2 А, I₄ = 1,55 А, I = 2,75 А.

Задача 49. В схеме (рис. 50, а) методом наложения найти все токи. Внутренние сопротивления источников э.д.с. принять равными нулю. Электродвижущие силы и сопротивления элементов цепи имеют следующие значения: E₁ = 96 В, E₂ = 75 В, r₃ = 3 Ом, r₄ = 15 Ом, r₅ = 10 Ом, r₆ = 6 Ом.

Решение

Положим, что действует только э.д.с. E₁, а э.д.с. E₂ не действует. В этом случае схема примет вид, изображенный на рис. 50, б. Так как внутреннее сопротивление э.д.с. E₂ равно нулю, то на его месте между точками b и d показано короткое замыкание. Для большей наглядности схему рис. 50, б можно начертить в виде, показанном на рис. 50, в.

Полное сопротивление этой схемы равно

r 1экв = r 3 ⋅ r 6 r 3 + r 6 + r 4 ⋅ r 5 r 4 + r 5 = 3⋅6 9 + 15⋅10 25 =8 Ом.

Определим все токи

I ′ 1 = E 1 r 1экв = 96 8 =12 А, I ′ 3 = I ′ 1 ⋅ r 6 r 3 + r 6 =12⋅ 6 9 =8 А; I ′ 6 = I ′ 1 − I ′ 3 =4 А; I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 =12⋅ 10 25 =4,8 А; I ′ 5 = I ′ 1 − I ′ 4 =7,2 А; I ′ 2 = I ′ 3 − I ′ 4 =8−4,8=3,2 А или I ′ 2 = I ′ 5 − I ′ 6 =3,2 А .

Теперь положим, что действует только э.д.с. E₂, а э.д.с. E₁ считаем недействующей (рис. 50, г).

Схему (рис. 50, г) для большей наглядности можно представить в виде, показанном на рис. 50, д. Ее полное сонротивление

r 2экв = r 3 ⋅ r 4 r 3 + r 4 + r 5 ⋅ r 6 r 5 + r 6 = 3⋅15 18 + 6⋅10 16 =6,25 Ом.

Вычислим все токи

I ″ 2 = E 2 r 2экв = 75 6,25 =12 А, I ″ 3 = I ″ 2 ⋅ r 4 r 3 + r 4 =12⋅ 15 18 =10 А; I ″ 4 = I ″ 2 − I ″ 3 =2 А; I ″ 6 = I ″ 2 ⋅ r 5 r 5 + r 6 =12⋅ 10 16 =7,5 А; I ″ 5 = I ″ 2 − I ″ 6 =4,5 А; I ″ 1 = I ″ 3 − I ″ 6 =10−7,5=2,5 А .

Складывая алгебраически токи, полученные от действия каждой э.д.с. в отдельности (рис. 50, б и 50, г), найдем истинные токи в каждой ветви (они нанесены на рис. 50, а)

I 1 = I ′ 1 + I ″ 1 =12+2,5=14,5 А, I 2 = I ′ 2 + I ″ 2 =3,2+12=15,2 А, I 3 = I ′ 3 + I ″ 3 =8+10=18 А, I 4 = I ′ 4 − I ″ 4 =4,8−2=2,8 А, I 5 = I ′ 5 + I ″ 5 =7,2+4,5=11,7 А, I 6 = I ′ 6 − I ″ 6 =7,5−4=3,5 А.

Задача 50. Для схемы (рис. 51) методами наложения, контурных токов и при помощи законов Кирхгофа найти все токи. Внутренние сопротивления источников электрической энергии считать равными нулю.

Дано: E₁ = 90 В, E₂ = 54 В, r₁ = 30 Ом, r₃ = 60 Ом, r₄ = 24 Ом, r₅ = 20 Ом.

Ответ: I₁ = 1,7 А, I₂ = 2,5 А, I₃ = 0,25 А, I₄ = 2,25 А, I₅ = 1,95 А.

Задача 51. Найти эквивалентное сопротивление цепи (рис. 52, а) и все токи, если U = 114 В, r₁ = 30 Ом, r₂ = r₃ = 10 Ом, r₄ = 26 Ом, r₅ = 11 Ом, r₆ = 10 Ом, r₇ = 40 Ом, r₈ = 50 Ом. Задачу решить методом преобразования треугольника сопротивлений в эквивалентную звезду.

Решение

Заменим треугольники сопротивлений abc и dfg эквивалентными звездами (рис. 52, б).

Подсчитаем сопротивления лучей звезды r₁₀, r₂₀ и r₃₀, эквивалентной треугольнику abc сопротивлений r₁, r₂ и r₃ (формулы 17)

r 10 = r 1 ⋅ r 2 r 1 + r 2 + r 3 =6 Ом, r 20 = r 1 ⋅ r 3 r 1 + r 2 + r 3 =6 Ом, r 30 = r 2 ⋅ r 3 r 1 + r 2 + r 3 =2 Ом.

Сопротивления лучей звезды r₄₀, r₅₀, r₆₀ эквивалентной треугольнику dfg сопротивлений r₆, r₇, r₈, равны

r 40 = r 6 ⋅ r 7 r 6 + r 7 + r 8 =4 Ом, r 50 = r 6 ⋅ r 8 r 6 + r 7 + r 8 =5 Ом, r 60 = r 7 ⋅ r 8 r 6 + r 7 + r 8 =20 Ом.

Эквивалентное сопротивление всей схемы

r Э = r 10 + r I ⋅ r II r I + r II + r 60 =38 Ом,

где

r I = r 20 + r 4 + r 40 =36 Ом, r II = r 3 + r 5 + r 50 =18 Ом.

Ток в неразветвленной части цепи

I= U r Э = 114 38 =3 А.

Токи в параллельных ветвях I’ (r₂₀r₄r₄₀) и I» (r₃₀r₅r₅₀)

I ′ =I⋅ r II r I + r II =3⋅ 18 36+18 =1 А; I ″ =I⋅ r I r I + r II =3⋅ 36 36+18 =2 А.

Теперь найдем токи в сопротивлениях заданной цепи. Для этого предварительно из схемы (рис. 52, б) найдем напряжения между точками a и b, a и c, b и c, d и g, f и g, d и f

U ab =I⋅ r 10 + I ′ ⋅ r 20 =3⋅6+1⋅6=24 В; U ac =I⋅ r 10 + I ″ ⋅ r 30 =3⋅6+2⋅2=22 В; U ab − U ac = ( φ a − φ b )− ( φ a − φ c )= φ c − φ b = U cb =24−22=2 В; U dg = I ′ ⋅ r 40 +I⋅ r 60 =1⋅4+3⋅20=64 В; U fg = I ″ ⋅ r 50 +I⋅ r 60 =2⋅5+3⋅20=70 В; U fg − U dg = ( φ f − φ g )− ( φ d − φ g )= φ f − φ d = U fd =70−64=6 В.

искомые токи будут

I 1 = U ab r 1 = 24 30 =0,8 А, I 2 = U ac r 2 = 22 10 =2,2 А, I 3 = U cb r 3 = 2 10 =0,2 А, I 4 = I ′ =1 А, I 5 = I ″ =2 А, I 6 = U fd r 8 = 6 10 =0,6 А, I 7 = U dg r 7 = 64 40 =1,6 А, I 8 = U fg r 8 = 70 50 =1,4 А.

Задача 52. В схеме (рис. 53) найти токи, применив преобразование треугольника в звезду. Определить эквивалентное сопротивление между точками a и b.

Приложенное напряжение U = 30 В; сопротивления: r₁ = 60 Ом, r₂ = 120 Ом, r₃ = 180 Ом, r₄ = 80 Ом, r₅ = 120 Ом.

Определить показание ваттметра и убедиться в том, что оно равно сумме мощностей, расходуемых во всех сопротивлениях.

Ответ: I = 0,3 А, I₁ = 0,2 А, I₂ = 0,15 А, I₃ = 0,1 А, I₄ = 0,15 А, I₅ = 0,05 А, r_ab = 100 Ом, P = 9 Вт.

Задача 53. Вычислить токи, проходящие во всех ветвях схемы (рис. 54), если E = 213 В, E₁ = 90 В, r₁ = 6 Ом, r₂ = 40 Ом, r₃ = 10 Ом, r₄ = 100 Ом, r₅ = 60 Ом.

Задачу решить преобразованием треугольника в эквивалентную звезду. Внутренними сопротивлениями источников напряжения пренебречь.

Определить входное сопротивление относительно ветви r₁ и взаимное сопротивление ветвей r₁ и r₂.

Ответ: I = 3,8 А, I₁ = 0,5 А, I₂ = 1,5 А, I₃ = 3,3 А, I₄ = 1,8 А, I₅ = 2 А, r₁₁ = 33 Ом, r₁₂ = 60 Ом.

Задача 54. Определить величины токов, проходящих по цепи, схема которой показана на рис. 55.

Данные цепи: E₁ = 100 В, E₂ = 140 В, r₁ = 15 Ом, r₂ = 5 Ом, r₃ = 10 Ом, r₄ = 4 Ом, r₅ = 50 Ом, r₁₀ = r₂₀ = 0.

Задачу решить методами контурных токов и узловых потенциалов.

Ответ: I₁ = 4 А, I₂ = 8 А, I₃ = 6 А, I₄ = 10 А, I₅ = 2 А.

Задача 55. Для схемы (рис. 56, а) найти методом эквивалентного генератора напряжения ток в ветви с сопротивлением r₁, если E₁ = 18 В, E₂ = 21 В, r₁₀ = 1 Ом, r₁ = 2 Ом, r₂₀ = 0, r₂ = 9 Ом, r₃ = 6 Ом.

Решение

Разомкнем цепь, содержащую сопротивление r₁, и найдем напряжение между точками m и n (рис. 56, б).

Очевидно, что в разомкнутой ветви тока нет, точки m и p равнопотенциальны (φ_m = φ_p), а потенциал точки q превышает потенциал точки n на величину φ_q — φ_n = E₁.

Имея это в виду, определим U_x = U_mn

φ_m = φ_p, φ_n = φ_q — E₁,

φ_m — φ_n = φ_p — φ_q + E₁, U_mn = U_pq + E₁.

Найдем напряжение U_pq. Для этого сначала определим ток в контуре psqp

I= E 2 r 2 + r 20 + r 3 = 21 15 =1,4 А.

По закону Ома

U_pq = I·r₃ = 1,4·6 = 8,4 В.

Окончательно

U_x = U_mn = U_pq + E₁ = 8,4 + 18 = 26,4 В.

Для нахождения тока в ветви r₁ сначала определим сопротивление короткого замыкания (рис. 56, в)

r k = r 2 ⋅ r 3 r 2 + r 3 = 9⋅6 15 =3,6 Ом.

Искомый ток

I 1 = U x r 1 + r 10 + r k = 26,4 1+2+3,6 =4 А.

Этот ток течет от точки m к точке n.

Задача 56. Методом эквивалентного генератора напряжения найти ток (рис. 57, а), проходящий через сопротивление r₅, если E = 120 В, r₁ = 60 Ом, r₂ = 15 Ом, r₃ = 90 Ом, r₄ = 60 Ом, r₅ = 12 Ом. Внутреннее сопротивление источника напряжения равно нулю.

Решение

Разомкнем сопротивление r₅ и. найдем напряжение между точками c и e (рис. 57, б).

Через сопротивления r₁ и r₂ протекает ток I’, а через r₃ и r₄ ток I»

I ′ = E r 1 + r 2 = 120 75 =1,6 А, I ″ = E r 3 + r 4 = 120 150 =0,8 А, φ a − φ c = U ac = I ′ ⋅ r 1 =1,6⋅60=96 В, φ a − φ d = U ad = I ″ ⋅ r 3 =0,8⋅90=72 В, ( φ a − φ c )− ( φ a − φ d )= φ d − φ c = U dc =24 В.

Но так как φ_d = φ_e, то U_dc = U_ec. Итак, напряжение холостого хода U_x = 24 В.

Теперь найдем сопротивление короткого замыкания. Определим его двумя способами.

1) Путем непосредственного подсчета по схеме.

В этом случае надо э.д.с. выключить, оставив ее внутреннее сопротивление, равное в данном случае нулю (рис. 57, в). Сопротивление короткого замыкания двухполюсника равно сопротивлению цепи между точками c и d

r k = r 1 ⋅ r 2 r 1 + r 2 + r 3 ⋅ r 4 r 3 + r 4 = 60⋅15 75 + 90⋅60 150 =48 Ом.

2) То же сопротивление можно найти и другим путем. Для этого надо замкнуть точки c и d накоротко, вычислить ток I_к, протекающий через короткозамкнутый участок (рис. 57, г), и сопротивление короткого замыкания определить по формуле (20).

Сопротивление схемы равно

r cx = r 1 ⋅ r 3 r 1 + r 3 + r 2 ⋅ r 4 r 2 + r 4 = 60⋅90 150 + 15⋅60 75 =48 Ом.

Найдем токи в ветвях

I 0 = E r cx = 120 48 =2,5 А, I ′ 1 = I 0 ⋅ r 3 r 1 + r 3 =2,5⋅ 90 150 =1,5 А, I ′ 2 = I 0 ⋅ r 4 r 2 + r 4 =2,5⋅ 60 75 =2 А.

Отсюда

I k = I ′ 2 − I ′ 1 =0,5 А.

Сопротивление короткого замыкания (формула 20) равно

r k = U x I k = 24 0,5 =48 Ом.

Искомый ток находим по формуле (21)

I 5 = U x r 5 + r k = 24 12+48 =0,4 А.

Задача 57. Для схемы (рис. 58) методом эквивалентного генератора напряжений найти ток в ветви с сопротивлением r₃, если E₁ = 5 В, E₂ = 7 В, r₁ = 7,5 Ом, r₂ = 2,5 Ом, r₃ = 5 Ом, r₄ = 2 Ом, r₅ = 25 Ом, r₁₀ = r₂₀ = 0.

Ответ: I₃ = 0,6 А.

Задача 58. Пользуясь методом эквивалентного генератора напряжений, найти э.д.с. и внутреннее сопротивление источников, эквивалентных каждой из схем (рис. 59 а, б, в и г; 0 < k < 1). Внутренние сопротивления источников энергий равны нулю.

Ответ: 1) U₀ = k·E, r_k = k· (1 — k)·r; 2) U₀ = k·E — E₁, r_k = r₁ + k· (1 — k)·r;

3) U 0 = k⋅E⋅r r 1 +k⋅r , r k = ( 1−k )⋅r+ k⋅r⋅ r 1 k⋅r+ r 1 ;

4) U 0 = E⋅ r 3 r 4 r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 , r k = r 4 ⋅ ( r 1 r 2 + r 1 r 3 + r 2 r 3 ) r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 .

Задача 59. По показаниям приборов, полученным из двух опытов, найти э.д.с. и внутреннее сопротивление источника электрической энергии, эквивалентного схеме (рис. 60), в случаях:

1)	U, B	I, A	2)	U, B	I, A	3)	U, B	I, A
	20	2		20	12		20	3
	30	3		30	14		30	5

Примечание. В части схемы, обведенной на рис. 60 четырехугольником абвг и называемой двухполюсником, в действительности может быть включено большое количество различных э.д.с. и сопротивлений так, что полный расчет занял бы слишком много времени. Поэтому решено ограничиться экспериментальным исследованием двухполюсника, результаты которого помещены в таблице данных.

Ответ: 1) сопротивление 10 Ом. 2) источник энергии с э.д.с. 40 В и внутренним сопротивлением 5 Ом. 3) источник энергии с э.д.с. 5 В и внутренним сопротивлением 5 Ом.

Задача 60. Три генератора напряжений, э.д.с. которых E₁ = 48 В, E₂ = 45 В, E₃ = 45 В, а внутренние сопротивления r₁ = 1,2 Ом, r₂ = 1 Ом, r₃ = 1,5 Ом, работают параллельно на общую нагрузку, сопротивление которой r = 4,2 Ом (рис. 61).

Произвести замену заданных генераторов напряжений одним эквивалентным, определив его э.д.с. и внутреннее сопротивление. Чему равны токи, протекающие через каждый генератор и нагрузку?

Решение

Значения э.д.с. и внутреннего сопротивления эквивалентного генератора напряжения могут быть определены по формулам (23)

E Э = E 1 ⋅ 1 r 1 + E 2 ⋅ 1 r 2 + E 3 ⋅ 1 r 3 1 r 1 + 1 r 2 + 1 r 3 = 115 2,5 =46 В, 1 r Э = 1 r 1 + 1 r 2 + 1 r 3 =2,5 1 Ом , r Э = 1 2,5 =0,4 Ом.

Ток в нагрузке

I= E Э r+ r Э = 46 4,2+0,4 =10 А.

Напряжение на нагрузке

U=I⋅r=10⋅4,2=42 В.

Таково же напряжение на каждой из параллельных ветвей. Ток в каждой из ветвей найдем по формуле (25)

I 1 = E 1 −U r 1 = 48−42 1,2 =5 А, I 2 = E 2 −U r 2 = 45−42 1 =3 А, I 3 = E 3 −U r 3 = 45−42 1,5 =2 А.

Проверка показывает, что ток в нагрузке I равен сумме трех токов: I₁, I₂ и I₃.

Задача 61. Для цепи, изображенной на рис. 62, проверить принцип взаимности, если э.д.с. E переместить в ветвь с сопротивлением r₃.

Даны: E = 80 В, r₁ = 8 Ом, r₂ = 20 Ом, r₃ = 30 Ом, r₄ = 12 Ом.

Задача 62. Определить ток, проходящий через сопротивление r = 5 Ом, подключенное к генератору тока (рис. 63), параметры которого имеют следующие величины: ток I_k = 6 мА, внутренняя проводимость g₀ = 0,04 1/Ом.

Решение

Внутреннее сопротивление генератора тока

r 0 = 1 g 0 = 1 0,04 =25 Ом.

Ток I_k распределяется по двум параллельным ветвям r и r₀ обратно пропорционально их сопротивлениям. Поэтому искомый ток

I= I k ⋅ r 0 r 0 +r =6⋅ 25 25+5 =5 мА.

Задача 63. Пользуясь теоремой об эквивалентном генераторе тока, определить ток I₃ в ветви r₃ = 12 Ом (рис. 64, а). Электродвижущие силы генераторов напряжения равны E₁ = 120 В, E₂ = 100 В, их внутренние сопротивления r₁ = 6 Ом, r₂ = 4 Ом.

Решение

Из теории известно, что ток эквивалентного генератора тока равен току короткого замыкания I_кз, проходящему между короткозамкнутыми зажимами m и n, к которым подключена данная ветвь (рис. 64, б)

I кз = E 1 r 1 + E 2 r 2 =45 А,

а внутренняя проводимость генератора тока равна проводимости пассивной цепи между зажимами m и n при разомкнутой ветви r₃ (рис. 64, в)

g 0 = 1 r 1 + 1 r 2 = 5 12 1 Ом , r 0 = 1 g 0 =2,4 Ом.

Схема эквивалентного генератора тока представлена на рис. 64 г.

Искомый ток

I 3 = I кз ⋅ r 0 r 0 + r 3 =45⋅ 2,4 2,4+12 =7,5 А.

Задача 64. Генератор тока создает в цепи ток I_k = 30 мА (рис. 65). Внутренней проводимостью генератора можно пренебречь.

Чему равны токи в ветвях, сопротивления которых равны r₁ =1,8 кОм, r₂ = 3 кОм, r₃ = 1,5 кОм, r₄ = 2 кОм.

Ответ: I₁ = 10 мА, I₂ = 4 мА, I₃ = 20 мА, I₄ = 6 мА.

Задача 65. Два генератора тока соединены в цепь, показанную на рис. 66, а. Ток первого генератора I_k₁ = 3 мА, его внутренняя проводимость g₁ = 0,05 1/Ом, второго — I_k₂ = 2 мА, g₂ = 0,01 1/Ом. Сопротивления равны: r₃ = 5 Ом, r₄ = 30 Ом.

Определить ток, проходящий через сопротивление r₄.

Решение

1-й способ. Преобразуем генераторы тока в эквивалентные генераторы напряжения, получим схему рис. 66, б. Э.д.с. и внутренние сопротивления генераторов напряжения находим по формулам (2)

E 1 = I k1 g 1 = 3 0,05 =60 мВ, r 1 = 1 g 1 = 1 0,05 =20 Ом, E 2 = I k2 g 2 = 2 0,01 =200 мВ, r 2 = 1 g 2 = 1 0,01 =100 Ом.

Далее, любым способом находим искомый ток. Обозначим

По методу узловых потенциалов находим

U ab = E 1 ⋅ 1 r 1 + r 3 + E 2 ⋅ 1 r 2 1 r 1 + r 3 + 1 r 2 + 1 r 4 = 60⋅ 1 20+5 +200⋅ 1 100 1 20+5 + 1 100 + 1 30 =52,8 мВ.

Искомый ток

I 4 = U ab r 4 = 52,8 30 =1,76 мА.

2-й способ. Решим задачу методом эквивалентного генератора тока. Для этого заменим всю цепь, за исключением ветви с r₄ эквивалентным генератором тока (рис. 66, в). Для определения его параметров I_k и g₀ сначала исключим ветвь с r₄, а точки a и b закоротим (рис. 66, г). Найдем ток короткого замыкания I_кз. Предварительно определим токи I₃ и I₄

I 3 = I k1 ⋅ 1 g 1 1 g 1 + r 3 =3⋅ 20 25 =2,4 мА, I 4 = I k2 =2 мА .

Следовательно, ток эквивалентного генератора тока

I_k = I₃ + I₄ = 2,4 + 2 = 4,4 А.

Теперь определим внутреннюю проводимость эквивалентного генератора тока g₀ между точками a и b. Для этого исключим генераторы токов и оставим лишь их внутренние сопротивления (рис. 66, д)

g 0 = g ab = 1 1 g 1 + r 3 + g 2 = 1 20+5 +0,01=0,05 См .

Ток в искомой ветви (рис. 66, в) равен

I 4 = I k ⋅ 1 g 0 1 g 0 + r 4 =4,4⋅ 20 20+30 =1,76 мА .

Задача 66. В схеме рис. 67 простейшим способом вычислить токи. Даны: E₁ = 100 В, E₂ = 80 В, E₃ = 40 В, r₁ = 10 Ом, r₂ = 10 Ом, r₃ = 20 Ом, r₄ = 30 Ом.

Внутренние сопротивления источников напряжения равны нулю.

Ответ: I₁ = 3,6 А, I₂ = 1,6 А, I₃ = 5,2 А, I₄ = 0.

В начало статьи Линейные электрические цепи постоянного тока

генератор тока,
Генератор напряжения,
закон Ома,
обобщенный закон Ома,
Законы Кирхгофа,
первый закон Кирхгофа,
второй закон Кирхгофа,
метод контурных токов,
метод узловых потенциалов,
метод наложения,
Метод эквивалентных преобразований,
метод эквивалентного генератора,
метод активного двухполюсника,
принцип взаимности,
принцип компенсации,
входная проводимость,
взаимная проводимость,
баланс мощностей

Источник

По сути дела, во втором случае проволоку разделили на два фрагмента, которые в свою очередь соединили параллельно друг другу. Так как по условию из проволоки свернули правильный пятиугольник, то и стороны этого пятиугольника равны, а значит сопротивления обоих фрагментов, как и их общее сопротивление можно выразить через сопротивление всей проволоки.

Если сопротивление длинной проволоки принять за R, то во втором случае эту же проволоку разделили на два участка, сопротивление которых составило R/5 и 4R/5, а так как эти участки соединены параллельно, то их общее сопротивление составит

( R/5 * 4R/5 )/( R/5 + 4R/5 ) =

= ( 4R²/25 ) / R = 4R/25

Так как напряжение питания в обоих случаях одинаково, то в обоих случаях ток в цепи можно вычислить по формуле

I = U/R

В каждом из описываемых случае ток в цепи будет равен, соответственно,

I(1) = U/R и

I(2) = U/(4R/25) = 25U/(4R) , а их отношение

I(1)/I(2) = (U/R)/(25U/(4R)) = (4RU)/(25RU) = 4/25 = 0,16 , что и будет ответом на эту задачу.

Источник

Ток и напряжение при параллельном, последовательном и смешанном соединении проводников

Последовательное и параллельное соединение сопротивлений

Смотрите также

Закон Ома

Закон Ома для цепи

Для ЭДС

Для полной цепи

Для переменного тока

Для замкнутой цепи

Сфера применения

Последовательное и параллельное включение элементов

Цепь последовательно включенных резистивных элементов

Цепь параллельно включенных резистивных элементов

Интегральная и дифференциальная формы закона

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Вам также может понравиться

Как правильно составить полное имя файла

Как найти скорость центра масс шара

Как найти партнеров яндекс такси

Добавить комментарий Отменить ответ