Как найти отношение объемов тетраэдров

Слайд 1

Задачи на сравнение объемов многогранников. Выполнил: Раздобарин Дмитрий, 11ИМ, лицей «Дубна». Учитель: Рычкова Татьяна Викторовна. 2009г. Дубна

Слайд 2

Оглавление. Введение. Теоретический материал. Ключевые задачи на сравнение объемов многогранников. Задачи из ЕГЭ части C4. Литература.

Слайд 3

Теоретический материал.

Слайд 4

2 . Объемы пирамид с общим основанием пропорциональны проведенным к нему высотам . 1 . Объемы пирамид с общей высотой пропорциональны площадям их оснований : B C D A K S H L A B C D S S 1 H 2 H 1

Слайд 5

3 . Если вершины S и T пирамид SA 1 …A n и TA 1 …A n лежат по одну сторону от плоскости A 1 …A n , то эти пирамиды равновелики тогда и только тогда, когда прямая ST параллельна плоскости A 1 …A n . S T T T A 1 A 4 A 3 A 2

Слайд 6

4 . Если тетраэдры SABC и SA 1 B 1 C 1 имеют общий трехгранный угол при вершине S, то 5 . Отношение объемов подобных многогранников равно кубу коэффициента подобия. S A B C C 1 B 1 A 1 A A 1 D C B D 1 C 1 B 1 A 2 C 2 B 2 B 3 C 3 D 3 A 3 D 2

Слайд 7

Ключевые задачи на сравнение объемов.

Слайд 8

Задача 1 . Дана правильная четырехугольная пирамида SABCD. Точка F – середина ребра BC. Найдите, в каком отношении делит объем пирамиды плоскость DSF. Решение . Поскольку пирамида и части, на которые она разбивается плоскостью сечения, имеют одинаковую высоту, то отношение объемов частей равно отношению площадей оснований: Диагональ квадрата ABCD делит его на два равных треугольника ABD и BDC, а прямая DF делит треугольник BDC на две равновеликие части (высоты треугольников равны CD, основания тоже равны). Следовательно, квадрат ABCD прямой DF делится на части, отношение которых равно 3:1. A B D C S F

Слайд 9

∆ COS подобен ∆ CMF Проведем FM ┴ AC. FM = h. Задача 2 . В правильной четырехугольной пирамиде SABCD через середину бокового ребра SC – точку F – и диагональ основания BD проведено сечение. Найдите отношение объемов фигур, на которые плоскость сечения делит пирамиду. Решение. Пусть AB = a, OS = H. B C D A F S O a H M

Слайд 10

В каком отношении делит объем пирамиды плоскость, параллельная основанию и пересекающая боковые ребра пирамиды? Решение. Исходная и отсекаемая пирамиды подобны с коэффициентом подобия Следовательно, отношение их объемов равно кубу коэффициента подобия. Две плоскости, параллельные основанию пирамиды, делят ее на три равновеликие части. В каком отношении эти плоскости делят высоту пирамиды? Два сечения делят фигуру на три подобных фигуры с объемами V, 2V, 3V.

Слайд 11

Олимпиадные задачи на сравнение объемов многогранников.

Слайд 12

C B A S L K M N Решение. Многогранники, на которые делит тетраэдр плоскость KMN, не поддаются стандартной классификации, поэтому хотя бы один из них, например, M KC NLB , разрежем на части: проведем L C и LM , тогда он окажется составленным из двух пирамид – LMNBC и LMKC . Будем сравнивать их объемы с объемом тетраэдра SABC . В треугольно пирамиде SABC проведена плоскость, параллельная ребрам SA и BC. Эта плоскость пересекает ребро AC в точке M так, что AM : MC = 1 : 2. В каком отношении эта плоскость делит объем пирамиды? 1 . LMNBC LABC (имеют общую высоту , ∆ANM подобен ∆АВС ) . 2 . LABC SАВС (имеют общий трехгранный угол при вершине В, основание АВС, высоту, проведенную из вершины С). 3 . LMKC LA SC SABC. Итак, Ответ: 20 /7 .

Слайд 13

P B L A C M N E T K В пирамиде TABC AB : BC = 3 : 5, точка K – середина ребра TA, точка M расположена на ребре AC, AM : MC = 3 : 1. Плоскость проходит через точки K и M параллельно биссектрисе BE треугольника ABC и делит пирамиду на две части. Вычислите отношение их объемов. A E C N B P 3b 5b 3a 2a 3a P B A T K L 1. Многогранник B LNAKM удобно рассматривать как часть тетраэдра PAKM с «отколотым куском» – тетраэдром PBLN. (Тетраэдры имеют общий трехгранный угол при вершине P, значит, надо найти отношения отрезков PL : PK, P B : PA и PN : PM ). 2 . Тетраэдры PAKM и TABC имеют общий трехгранный угол при вершине Р, поэтому нужно знать отношение АК:АТ, АМ:АС и АВ:АР. AE = 3a EC = 5a, AC = 8a. MC = 2a, EM = 3a. следовательно, Далее: тогда В итоге Ответ: 11 /9.

Слайд 14

S C B Y X A M L J D N K C X D B M A Y В основании четырехугольной пирамиды SABCD лежит параллелограмм ABCD. Через середину ребер AB, AD и SC проведена плоскость. Найдите отношение объемов частей, на которые эта плоскость делит пирамиду. 1 . Многогранник MNJKLBCD представляет собой часть тетраэдра с отколотыми кусками XJDN и YMBL в форме тетраэдров (Тетраэдры имеют с ним по общему трехгранному углу, нужно вычислить XJ : XK, XD : XC, XN : XY, YL : YK, YB : YC, YM, YX). 2 . Тетраэдр CXKY имеет общий трехгранный угол с тетраэдром CSBD, объем которого равен половину объема пирамиды SABCD ( Нужно вычислить CX : CD, CY : CB, CK : CS). XD : XC = 1:3, CX : CD = 3 : 2, YB : YC = 1 : 3, CY : CB = 3 : 2 Y B T K S L C a 2a YB = a, YC = 3a, BC = 2a, YL : YK = 1 : 2. Аналогично , XJ: XK = 1 : 2. BT = TC = a. Ответ: 1.

Слайд 15

Задачи из ЕГЭ части C4.

Слайд 16

В основании пирамиды DABC лежит треугольник ABC, в котором угол C = 60°, AC = 14, BC = 8. Боковые грани DAC и DAB перпендикулярны плоскости основания, а ребро AD = 4 √ 3 . Сечение пирамиды плоскостью, проходящей через середину ребра BD параллельно прямым BC и AD, является основанием второй пирамиды, вершина которой в точке C. Найдите объем второй пирамиды. В основании пирамиды DABC лежит треугольник ABC, в котором угол C = 30°, AC = 20, BC = 8/√ 3 . Боковое ребро AD равно 6 √ 3 и перпендикулярно плоскости ABC. Сечение пирамиды плоскостью, проходящей через середину ребра BD параллельно прямым BC и AD, является основанием второй пирамиды. Ее вершина T – основание высоты BT треугольника ABC. Найдите объем второй пирамиды. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 . На его боковых ребрах AA 1 и BB 1 лежат точки M и N соответственно так, что AM : MA 1 = 8 : 11, B 1 P : PB = 2 : 1. Во сколько раз объем данного параллелепипеда больше объема пирамиды с вершиной в точке P, основанием которой является сечение данного параллелепипеда плоскостью BMD 1

Слайд 17

Основанием пирамиды является треугольник АВС , в котором АВ = 4, АС =6 и угол АВС =90 ° Ребро AF перпендикулярно АВС и равно 12. Отрезок АL является биссектрисой треугольника FАВ, а отрезок АN является высотой треугольника FАС. Найдите объем пирамиды АLNC. A C B N L F 1 . Заметим, что пирамиды ALNC и ALNF имеют общую высоту из вершины L, поэтому отношение объемов этих пирамид равно отношению их граней ANC и ANF: Отношение площадей треугольников ANC и ANF равно отношению отрезков NC и NF ( высота треугольников из вершины A является общей): Таким образом: Аналогично: Перемножая (1) и (2) получаем: 2. Найдем отношения Так как AL – биссектриса треугольника AFB, то По условию AF = 12, AB = 4 FL = 3BL Так как AN – высота к гипотенузе прямоугольного треугольника AFC, то Воспользовавшись (3) получим: Ответ: 2 ,4√5.

Слайд 18

Литература. Туманов С. И. «Поиски решения задач». Зеленский А. С. «Сборник конкурсных задач по математике». Куланин Е. Д., Федин С. Н., Федяев О. И. «Геометрия 10-11 класс». Шарыгин И. Ф., Голубев В. И., «Решение задач. 11 класс». Готман Э. Г., Скопец З. А. «Задача одна – решения разные: Геометрические задачи. Книга для учащихся». Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев «Геометрия: Учебник для 10-11 классов общеобразовательных учреждений». Погорелов А. В. «Геометрия: учебник для 7-11 классов общеобразовательных учреждений». Потоскуев Е. В. Звавич Л. И. «Геометрия 11 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики». В. И. Мусатов «Сборник задач по геометрии. Стереометрия. Для 10 – 11-х классов ФМШ». Судаков Д. А. «Методическое пособие». Шарыгин И.Ф., Гордин Р. К. «Сборник задач по геометрии. 5000 задач с ответами. Учебное пособие для общеобразовательных учреждений.

“В задачах по элементарной геометрии
приходиться пользоваться очень остроумными,
подчас тонкими приемами, и тот, кто в своей
молодости вкусил их прелесть, никогда их не
забудет”.
Э. Борель

Цель урока: продолжить изучение
свойств многогранников, которые можно
использовать для решения задач на сравнение их
объемов; показать их применение в задачах;
развивать умение учащихся применять полученные
знания в конкретных ситуациях.

Оборудование: модели многогранников,
мультимедийная установка, компьютерный класс,
карточки для решения задач.

Ход урока

Организационный момент – постановка
цели урока, ознакомление с планом работы на
уроке.

Геометрическая разминка – решение
задач на готовых чертежах.

Вариант 1.

• Боковые ребра треугольной пирамиды взаимно
  перпендикулярны и каждое из них имеет длину 2 см.
  Вычислите объем пирамиды.
• Боковая грань АДС тетраэдра ДАВС
  перпендикулярна плоскости основания АВС. Ребра
  АВ=АС=BС=АД=ДС=2 см. Найдите объем тетраэдра.
• Двугранные углы треугольной пирамиды равны по 60⁰.
  Найдите высоту пирамиды, если площадь ее боковой
  поверхности 72 см², а объем 24 см³.

Вариант 2.

• Плоские углы при вершине тетраэдра прямые,
  боковые ребра равны 1 см; 2 см; 3 см. Найдите объем
  тетраэдра.
• В основании треугольной пирамиды ДАВС
  прямоугольный треугольник АВС, угол С равен 90⁰,
  АС=ВС. Боковая грань АДВ перпендикулярна
  плоскости основания. Угол АДВ равен 90, АД=ДВ, АВ=4
  см. Найдите объем пирамиды.
• Объем пирамиды 24 см³ . Найдите площадь
  боковой поверхности этой пирамиды, если все
  боковые грани образуют с основанием угол 60⁰,
  а высота пирамиды равна 2 см.

После решения данных задач проводим проверку
ответов, обсуждаем особенности задач.

Вопросы по задачам:

– В чем заключается прием, используемый при
решении задачи № 1?

– Какое свойство пирамиды, одна из боковых
граней которой перпендикулярна плоскости
основания, используется в решении задачи № 2?

– Какая формула связывает площадь основания и
площадь боковой поверхности пирамиды, у которой
все двугранные углы при ребрах основания равны?

3. Повторение материала, изученного на
прошлом уроке.

Среди стереометрических задач часто
рассматриваются не только задачи на вычисление
объемов, но и на сравнение объемов
многогранников, на нахождение отношения объемов
частей, на которые многогранник разбивается
секущей плоскостью.

В планиметрии мы изучали свойства площадей
треугольников, четырехугольников, например:

– отношение площадей треугольников с общим
основанием равно отношению их высот;

– медиана делит треугольник на два
равновеликих;

– отношение площадей треугольников, имеющих
равный угол, равно отношению произведений
сторон, заключающих равный угол;

– если в трапеции провести диагонали, то
треугольники, прилежащие к боковым сторонам
будут равновелики; а треугольники, прилежащие к
основаниям, подобны.

На прошлом уроке мы рассмотрели ряд
свойств многогранников, связанных с их объемами:

– объемы пирамид с равными высотами
пропорциональны площадям их оснований;

– объемы пирамид с общим основанием
пропорциональны проведенным к нему высотам;

– объемы тетраэдров, имеющих равные трехгранные
углы, относятся как произведения длин ребер,
образующих эти углы;

– отношение объемов подобных многогранников
равно кубу коэффициента подобия;

– плоскость, проходящая через ребро тетраэдра и
середину противоположного ребра тетраэдра,
делит его на две равновеликие части.

Доказательство данных свойств можно изучить в Приложении 1 (фрагмент реферата
ученицы 11 класса по теме “Сравнение объемов
многогранников”, раздел “Некоторые интересные
свойства объемов многогранников”).

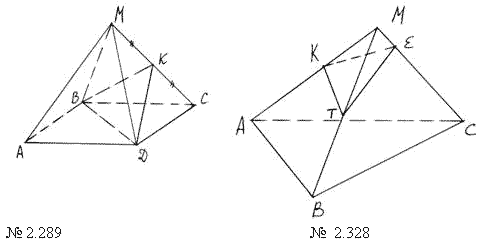
А) Какие из перечисленных свойств вы
использовали при выполнении домашнего задания
(2.289; 2.328, [2])? Чертежи заготовлены заранее, решение
задач обсуждаем.

Б) Работая в парах на компьютерах, примените
изученные свойства для решения задач № 4, 5, 6, 7, 8,
дополнительно задача № 9 (Диск ” Стереометрия”
1С, [7], тема “Сравнение объемов многогранников”).

После окончания работы на компьютере
фронтально проверяем решения задач, вынося
чертежи и условие данных задач на доску через
мультимедийную установку.

В) Используя каркасные модели, устно решаем
задачу: Как провести сечение тетраэдра и
параллелепипеда, чтобы объем отсеченного
многогранника был равен половине, четверти,
девятой, восьмой части исходного объема?

Г) На листах, где решали задачи на готовых
чертежах, постройте сечения так, чтобы объем
отсеченного многогранника был равен половине,
трети и двадцать седьмой части объема тетраэдра.

Листы сдаем (на листах решение задач
геометрической разминки и сечения – задание Г).

4. Изучение нового материала. При
определении объемов самых разных по форме
многогранников можно эффективно использовать
свойства ортогонального проектирования.

Выведем формулу для вычисления объема тела,
полученного при пересечении призматической
поверхности двумя плоскостями. Для этого
рассмотрим теорему и следствие из нее:

– Пусть ABCA₁B₁C₁ – тело, которое
получено при пересечении треугольной
призматической поверхности 2-мя плоскостями: (ABC),
перпендикулярной ребрам призматической
поверхности, и (A₁B₁C₁), при этом AA₁
BB₁ CC₁. Тогда объем этого тела
равен произведению площади основания, лежащего в
плоскости (ABC), и среднего арифметического длин
ребер AA₁, BB₁, CC₁.

– Пусть ABCA₁B₁C₁ – тело,
которое получено при пересечении треугольной
призматической поверхности 2-мя плоскостями (ABC) и
(A₁B₁C₁), при этом AA₁ BB₁ CC₁. (A₀B₀C₀) – сечение,
перпендикулярное ребрам призматической
поверхности. Тогда объем этого тела равен
произведению площади сечения, лежащего в
плоскости (A₀B₀C₀), и среднего
арифметического длин ребер AA₁, BB₁, CC₁
(Приложение 2).

Покажем применение данной формулы при решении
задачи:

Площадь основания АВС прямой треугольной
призмы АВСА₁В₁С₁ равна 10. Точки
К, Р, М лежат на ребрах АА₁, ВВ₁,СС₁,
причем АК=6. Определите объем треугольной
пирамиды MAKP.

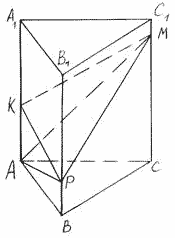
Решение:

Ортогональной проекцией сечений КРМ и АРМ на
плоскость АВС является треугольник АВС, площадь
которого равна 10. AK= a = 6, в = с = 0, тогда объем
пирамиды МАКР равен

V=^*10 = 20.

О т в е т: 20.

5. Подведение итогов урока.

6. Домашнее задание: 2.325; 2.330, [2]; выучить
свойства многогранников, которые используются
для сравнения их объемов.

Список использованных источников.

1. Геометрия.10 кл.:Учеб. для общеобразоват.
   учреждений с углубл. и профильным изучением
   математики/ Е.В. Потоскуев, Л.И. Звавич. – М. Дрофа,
   2003.
2. Геометрия.10 кл.: Задачник для общеобразоват.
   учреждений с углубл. и профильным изучением
   математики/ Е.В. Потоскуев, Л.И. Звавич. – М. Дрофа,
   2003.
3. Губин А.В., Крайко М.А. Задачи на сравнение
   объемов многогранников// Математика в школе. –
   2006- № 5.
4. Куланин Е.Д., Федин С.Н., Федяев О.И. Геометрия 10-11
   классы. – М.: Рольф, Айрис-пресс, 1997.
5. Куланин Е.Д., Федин С.Н. Сборник задач по
   геометрии для 10-11 классов.- М.: Рольф, Айрис-пресс,
   1997.
6. Пособие по математике для поступающих в ВУЗы /
   Под ред. Г.Н.Яковлева. – 3-е изд., перераб.- М.: Наука,
   1988.
7. Диск “Стереометрия” 1С, ООО “Кордис&Медиа”,
   1999, ЗАО “КУДИЦ”, 1999.

Как найти отношение объемов тетраэдров

Тетраэдр — это геометрическое тело, состоящее из четырех треугольных граней, которые сходятся в одной точке. Объем тетраэдра можно вычислить по формуле V=1/3*Sh, где S — площадь основания, h — высота. В этой статье мы рассмотрим как найти отношение объемов двух тетраэдров.

Шаг 1. Найдите площадь основания каждого тетраэдра

Первый шаг — определить площадь каждого основания тетраэдра. Площадь основания отличается в зависимости от формы тетраэдра. Например, у правильного тетраэдра (где все грани равносторонние треугольники) площадь основания можно вычислить по формуле S=(a^2*√3)/4, где а — длина стороны.

Шаг 2. Найдите высоту каждого тетраэдра

Для вычисления объема тетраэдра необходимо знать высоту h. Высоту можно найти различными способами, в зависимости от известных параметров тетраэдра. Например, для правильного тетраэдра высоту можно вычислить по формуле h=(√2/3)*a, где а — длина стороны.

Шаг 3. Вычислите объем каждого тетраэдра

Используя найденные значения площади основания и высоты, можно вычислить объем каждого тетраэдра. Подставляем значения в формулу V=1/3*Sh и получаем объем.

Шаг 4. Найдите отношение объемов

Наконец, чтобы найти отношение объемов двух тетраэдров, необходимо разделить объем первого тетраэдра на объем второго. То есть V1/V2, где V1 — объем первого тетраэдра, V2 — объем второго тетраэдра.

Пример: допустим, у нас есть два правильных тетраэдра со сторонами a1=5 и a2=7. Найдем их объемы:

• Площадь основания первого тетраэдра: S1=(5^2*√3)/4 ≈ 10.8
• Высота первого тетраэдра: h1=(√2/3)*5 ≈ 2.9
• Объем первого тетраэдра: V1=1/3*10.8*2.9 ≈ 10.4
• Площадь основания второго тетраэдра: S2=(7^2*√3)/4 ≈ 21.2
• Высота второго тетраэдра: h2=(√2/3)*7 ≈ 4.8
• Объем второго тетраэдра: V2=1/3*21.2*4.8 ≈ 40.3
• Отношение объемов: V1/V2 ≈ 0.26

Итог

Таким образом, теперь вы знаете, как найти отношение объемов двух тетраэдров. Для этого необходимо вычислить площадь основания и высоту каждого тетраэдра, и затем использовать формулу V=1/3*Sh для нахождения объема. Найдите отношение объемов двух тетраэдров, разделив объем первого на объем второго. Надеемся, что эта информация была полезной для вас.

Как найти отношение объемов тетраэдров

Тетраэдр — это геометрическая фигура, которая представляет собой пирамиду с четырьмя треугольниками в основании. Эта фигура является одной из основных в геометрии, и знание ее свойств может помочь в различных сферах, включая строительство, архитектуру и даже медицину. Один из ключевых вопросов при работе с тетраэдрами — это нахождение отношения их объемов.

Формула объема тетраэдра

Перед тем, как можно будет говорить об отношении объемов, нужно понимать, как получить объем каждого из тетраэдров. Формула для вычисления объема тетраэдра:

V = (a³ * √2) / 12

где а — длина ребра тетраэдра.

Отметим, что данная формула является относительно простой, и ее можно легко использовать для расчетов. Главное — правильно определить длину ребра.

Нахождение отношения объемов тетраэдров

Как уже было упомянуто, нахождение отношения объемов тетраэдров — это один из центральных вопросов при работе с данными фигурами. Допустим, у нас есть два тетраэдра, и мы хотим найти их отношение. Для этого нужно:

• Определить длину ребер каждого тетраэдра
• Вычислить объем каждого тетраэдра по формуле
• Поделить объем первого тетраэдра на объем второго. Результат и будет искомым отношением.

Если же у нас имеется третий тетраэдр, то отношение объемов нужно считать иначе:

• Вычислить объем первого тетраэдра
• Вычислить объем второго тетраэдра
• Вычислить объем третьего тетраэдра
• Поделить сумму объемов первых двух тетраэдров на объем третьего
• Результат и будет искомым отношением

Как можно заметить, нахождение отношения объемов тетраэдров не является сложным процессом. Однако его важность исходит из того, что данная информация может помочь в создании различных условий при работе с тетраэдрами.

Вывод

В данной статье мы рассмотрели, как найти отношение объемов тетраэдров. Описанные методы довольно просты, и с их помощью можно получить необходимую информацию для различных вопросов строительства, архитектуры или медицины. Помните, что хоть тетраэдры и могут иметь сложную структуру и вид, правильное определение их объема поможет сделать работу с ними проще и быстрее.

Как найти отношение объемов тетраэдров

Если вы задумались о том, как найти отношение объемов тетраэдров, то, вероятно, вы уже знакомы с понятием тетраэдр и его основными свойствами. Но даже если вы только начинаете учить геометрию, этот материал поможет вам разобраться в этой задаче.

Что такое тетраэдр

Тетраэдр – это геометрическое тело, ограниченное четырьмя треугольными гранями. Каждая грань соприкасается с другими тремя. Тетраэдр имеет четыре вершины.

Как найти объем тетраэдра

Объем тетраэдра можно найти по формуле:

V = (1/3) * S * h

где V – объем тетраэдра, S – площадь основания, h – высота тетраэдра.

Площадь основания можно найти, зная длины его сторон. Высоту можно найти по формуле:

h = (V * 3) / S

Следовательно, если известны объемы двух тетраэдров и площади их оснований, вы можете найти отношение их объемов, используя эти формулы.

Пример

Пусть есть два тетраэдра, первый с площадью основания S₁ и объемом V₁, а второй с площадью основания S₂ и объемом V₂. Мы хотим найти отношение их объемов.

Сначала найдем высоты тетраэдров: h₁ = (V₁ * 3) / S₁ и h₂ = (V₂ * 3) / S₂.

Затем найдем объемы:

V₁ = (1/3) * S₁ * h₁
V₂ = (1/3) * S₂ * h₂

Теперь мы можем выразить отношение объемов:

V₁ / V₂ = [(1/3) * S₁ * h₁] / [(1/3) * S₂ * h₂]
V₁ / V₂ = S₁ * h₁ / S₂ * h₂

Таким образом, мы можем найти отношение объемов двух тетраэдров, используя знание площадей их оснований и объемов.

Общий итог

Как видите, найти отношение объемов тетраэдров довольно просто, если известны площади их оснований и объемы. Вы можете использовать формулы для нахождения объема и высоты тетраэдра, а затем использовать их для вычисления отношения объемов. Это также поможет вам укрепить свои знания о тетраэдрах и их свойствах.

• Тетраэдр — геометрическое тело, ограниченное четырьмя треугольными гранями.
• Объем тетраэдра можно найти по формуле: V = (1/3) * S * h.
• Отношение объемов двух тетраэдров можно найти, зная площади их оснований и объемы.