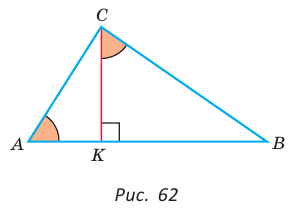
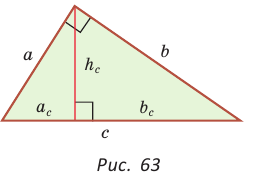
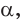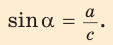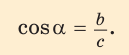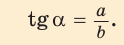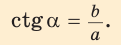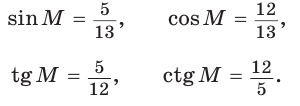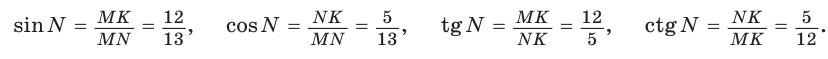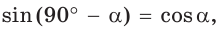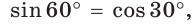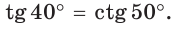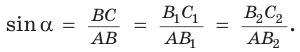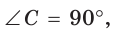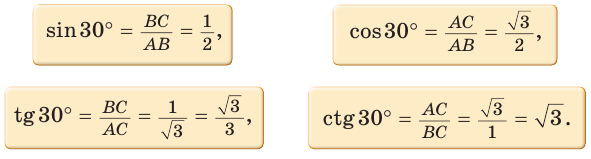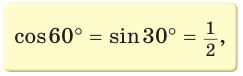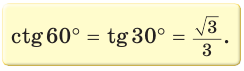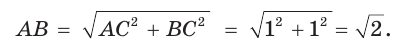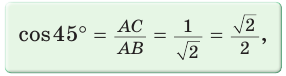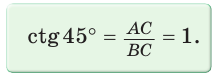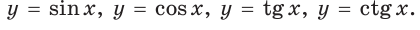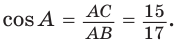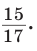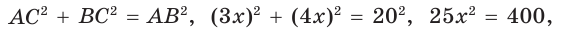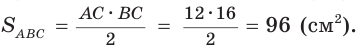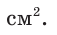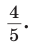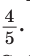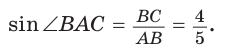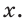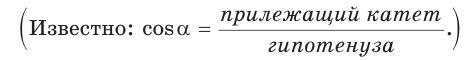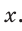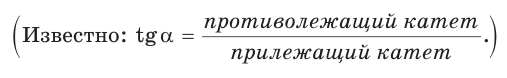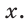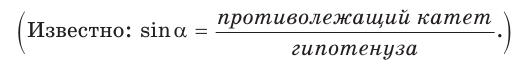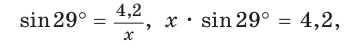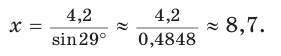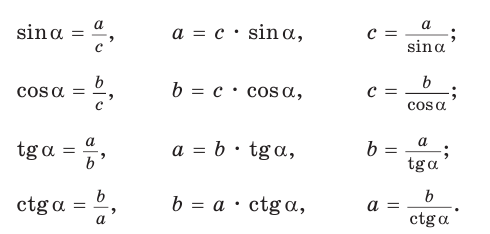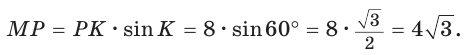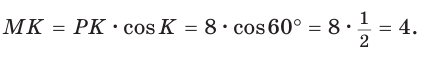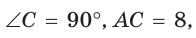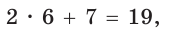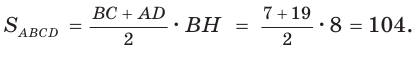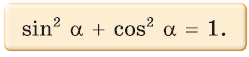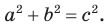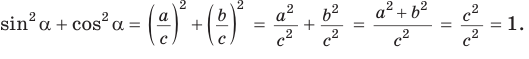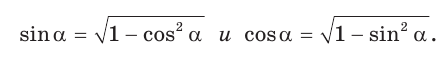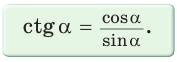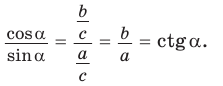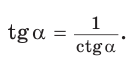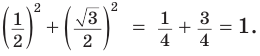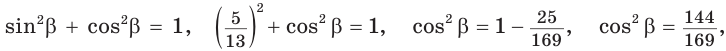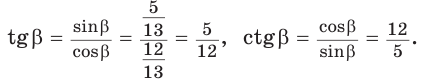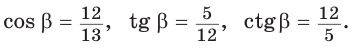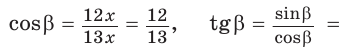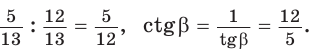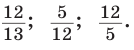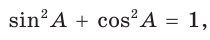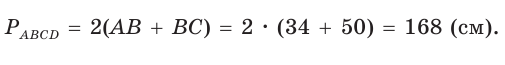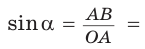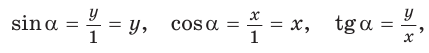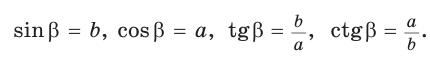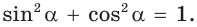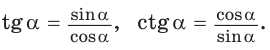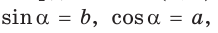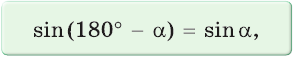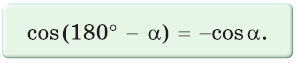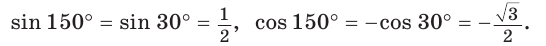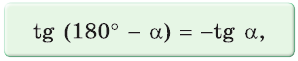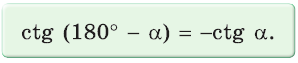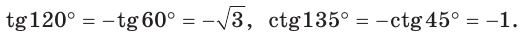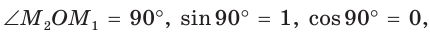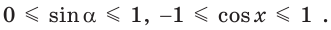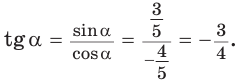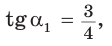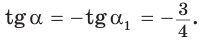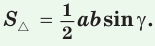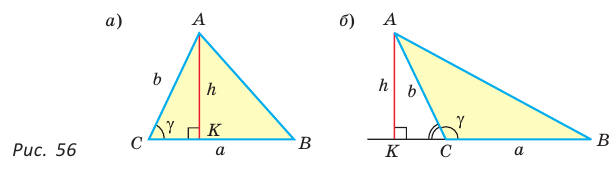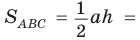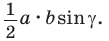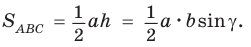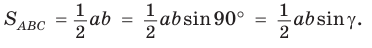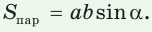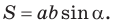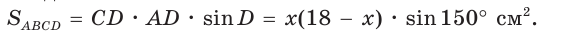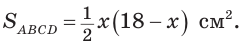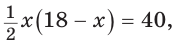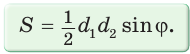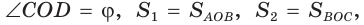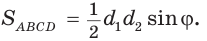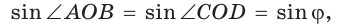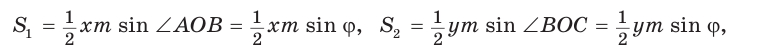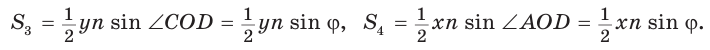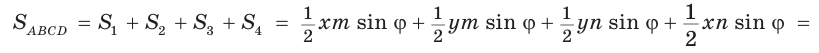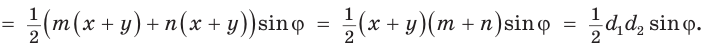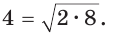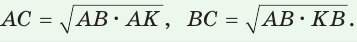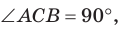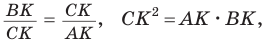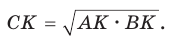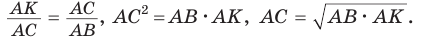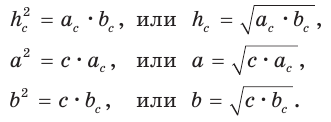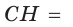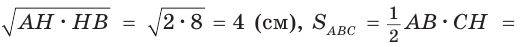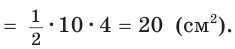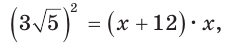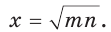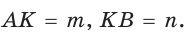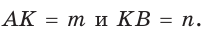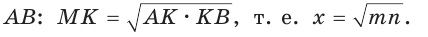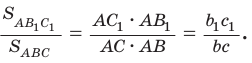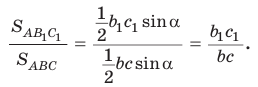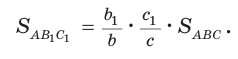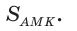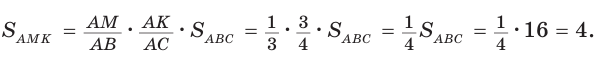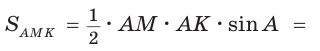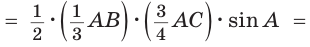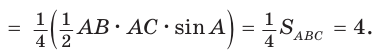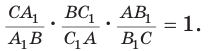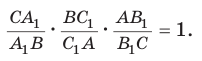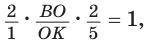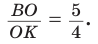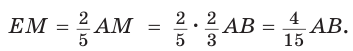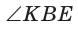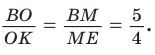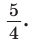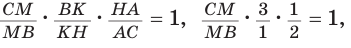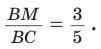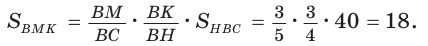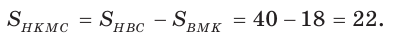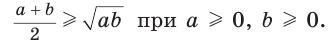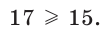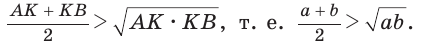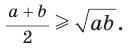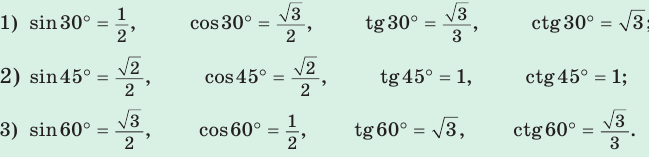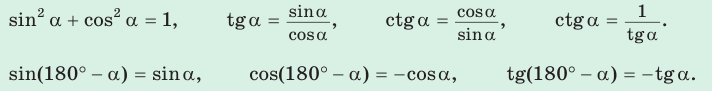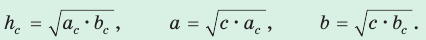Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
1) Свойство высоты, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
или
2) Свойства катетов прямоугольного треугольника.
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
или
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
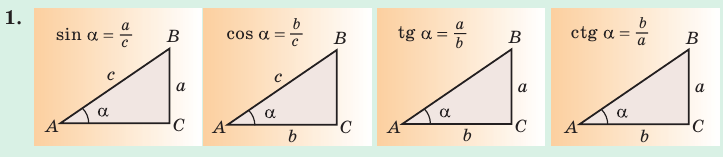
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`c` – гипотенуза `AB`;
`a` и `b` – катеты `BC` и `AC` (по-гречески “kathetos – катет” означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
Напомним, что если `alpha` – величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то
`sin alpha = a/c`, `cos alpha = b/c` и `”tg”alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
`a^2 = c * a_c`
`b^2 = c * b_c`
Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ – alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.
Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c`. Аналогично доказывается второе равенство.
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
`h^2 = a_c * b_c`
Из треугольника `ACD` (рис. 1) имеем `”tg”alpha = (CD)/(AD)`, а из треугольника `BCD` `”tg”alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
`a * b = c * h`
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
`m_c = 1/2 c`
Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`
.
Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
`R = m_c = 1/2 c`
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Пусть `O` – центр вписанной окружности и `F`, `N` и `S` – точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` – квадрат со стороной `r`, поэтому `BF = BC – FC`, `AN = AC – CN`, т. е. `BF = a – r` и `AN = b – r`.
Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` – общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b – r`.
Аналогично доказывается, что `BS = a – r`, поэтому из `AB = AS + BS` следует `c = (b – r) + (a – r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
`a = sqrt(c * a_c)`
`b = sqrt(c * b_c)`
`h = sqrt(a_c * b_c)`
и, соответственно, формулируются утверждения
Катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.
Высота, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Приведём примеры применения доказанных метрических соотношений в прямоугольном треугольнике.
Проекции катетов прямоугольного треугольника на гипотенузу равны `9` и `16` . Найти радиус вписанной окружности.
1. Пусть `a_c = 9`, `b_c = 16` (рис. 4), тогда `c = a_c + b_c = 25`.
2. По Свойству 1: `a = sqrt(c * a_c) = 15`, `b = sqrt(c * b_c) = 20`.
3. По Свойству 6: находим радиус `r = 1/2 (a + b – c) = 5`.
В прямоугольном треугольнике из вершины прямого угла проведены медиана и высота (рис. 5), расстояние между их основаниями равно `1`. Найти катеты, если известно, что один из них в два раза больше другого.
1. Заметим, что `a_c = c/2 – 1`, a `b_c = c/2 + 1` (рис. 5), откуда `a^2 = c * a_c = c(c/2 – 1)` и `b^2 = c * b_c = c(c/2 + 1)`.
2. По условию `b = 2a`, значит `b^2 = 4a^2`, т. е. `c(c/2 + 1) = 4c(c/2 – 1)`.
Находим `c = (10)/3`, и `a = sqrt(c(c/2 – 1)) = 2/3 sqrt5` и `b = 2a = 4/3 sqrt5`.
Как найти проекцию катета на гипотенузу
Две короткие стороны прямоугольного треугольника называют катетами, а длинную – гипотенузой. Проекции коротких сторон на длинную делят гипотенузу на два отрезка разной длины. Если возникает необходимость в вычислении величины одного из этих отрезков, то способы решения задачи целиком зависят от предлагаемого в условиях набора исходных данных.

Инструкция
Если в исходных условиях задачи приведены длины гипотенузы (С) и того катета (А), проекцию которого (Ас) требуется вычислить, то используйте одно из свойств треугольника. Воспользуйтесь тем, что среднее геометрическое длин гипотенузы и искомой проекции равно длине катета: А = √(С*Ас). Так как понятие «среднее геометрическое» эквивалентно «корню из произведения», то для нахождения проекции катета возводите в квадрат длину катета и делите полученное значение на длину гипотенузы: Ас = (А/√С)² = А²/С.
Если длина гипотенузы неизвестна, а даны лишь длины обоих катетов (А и В), то в вычислении длины нужной проекции (Ас) можно задействовать теорему Пифагора. Выразите в соответствии с ней длину гипотенузы через длины катетов √(А²+В²) и подставьте полученное выражение в формулу из предыдущего шага: Ас = А²/√(А²+В²).
Если известна длина проекции одного из катетов (Вс) и длина гипотенузы (С), то способ нахождения длины проекции другого катета (Ас) очевиден – просто отнимите от второй известной величины первую: Ас = С-Вс.
Если длины катетов неизвестны, но дано их соотношение (x/y), а также длина гипотенузы (C), то воспользуйтесь парой формул из первого и третьего шагов. Согласно выражению из первого шага, соотношение проекций катетов (Ас и Вс) будет равно соотношению квадратов их длин: Ас/Вс = x²/y². С другой стороны, согласно формуле из предыдущего шага, Ас+Вс = С. В первом равенстве выразите длину ненужной проекции через нужную и подставьте полученное значение во вторую формулу: Ас + Ас*x²/y² = Ас*(1 + x²/y²) = С. Из этого равенства выведите формулу нахождения нужной проекции катета: Ас = С/(1 + x²/y²).
Если известна длина проекции на гипотенузу одного катета (Вс), а длина самой гипотенузы не приведена в условиях, но дана высота (Н), проведенная из прямого угла треугольника, то этого тоже будет достаточно для вычисления длины проекции другого катета (Ас). Возведите высоту в квадрат и разделите на длину известной проекции: Ас = Н²/Вс.
Источники:
- формула катета
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
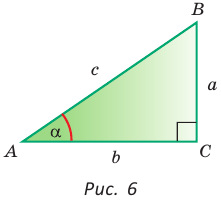
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен
Определения синуса, косинуса, тангенса и котангенса острого угла
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
Пример:
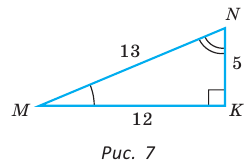
Угол К в 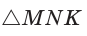
Тогда:
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
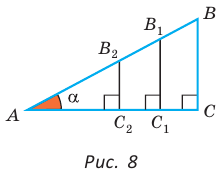
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 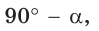
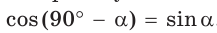
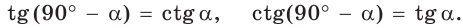
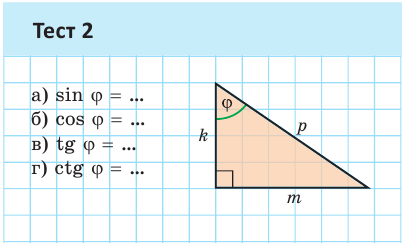
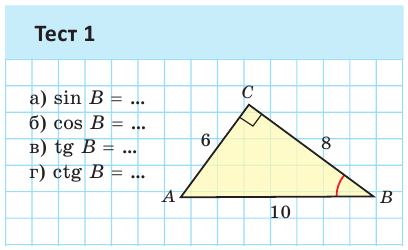
А теперь выполните Тест 1 и Тест 2.
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в 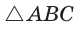
Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
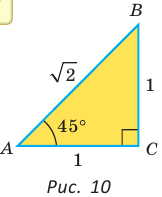
Рассмотрим прямоугольный треугольник АВС, у которого 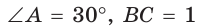
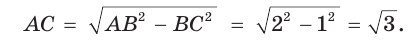
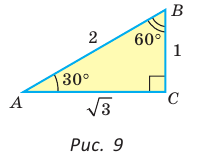
Так как 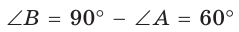

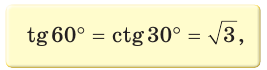
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 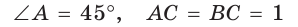
Тогда:
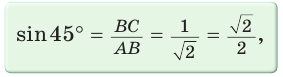
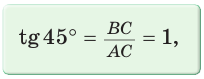
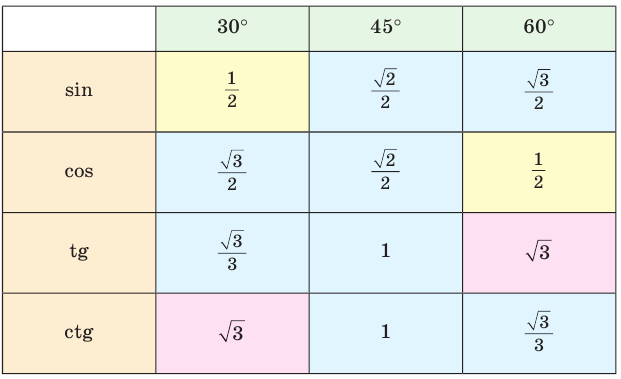
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 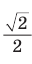
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно 
А теперь выполните Тест 3.
Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 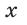
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 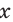
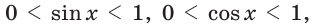
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
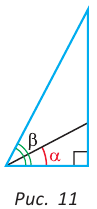
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 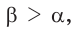
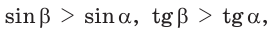
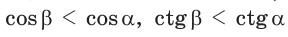
Пример №1
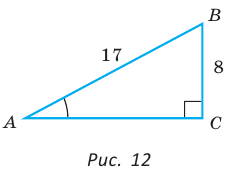
В прямоугольном треугольнике АВС, где 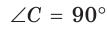
Решение:
По теореме Пифагора найдем катет 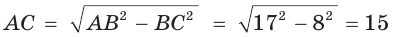
Ответ:
Пример №2
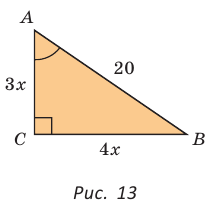
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 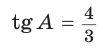
Решение:
Так как 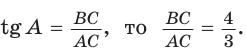
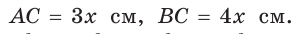
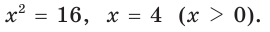
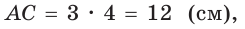
Ответ: 96
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен
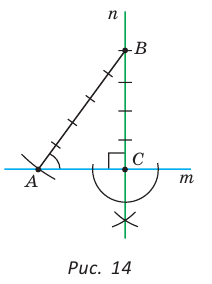
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую 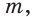
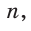
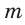
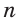
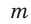
Угол ВАС — искомый.
Доказательство:
Из 
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
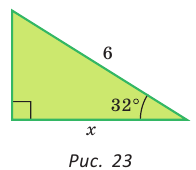
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
Решение:
Примем длину искомого катета за
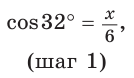

Ответ: 5,1.
Пример №5
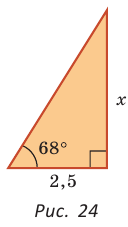
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за
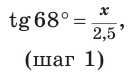
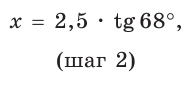
Ответ: 6,2.
Пример №6
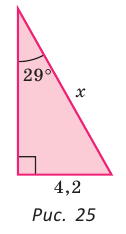
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за
Ответ: 8,7.
Правила решения прямоугольного треугольника
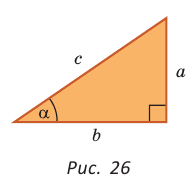
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
Удобно пользоваться следующими правилами:
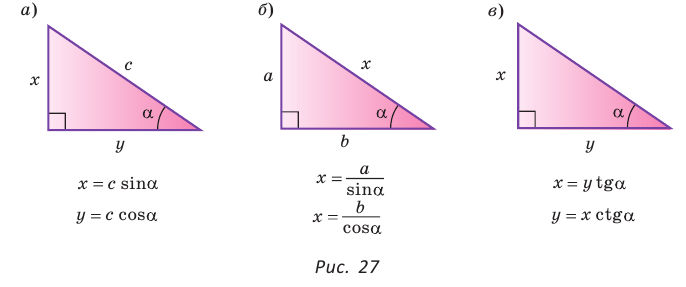
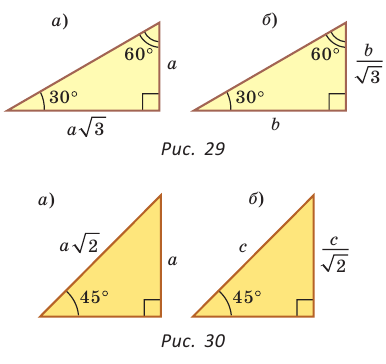
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 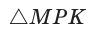
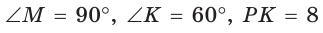
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 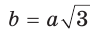
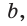
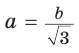
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 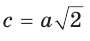
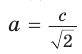
Пример №8
В прямоугольном треугольнике АВС известно: 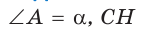
Решение:
Заметим, что 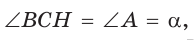
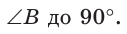
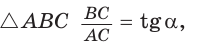
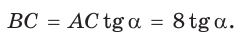
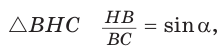
Ответ:
Пример №9
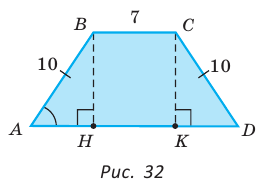
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 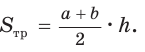
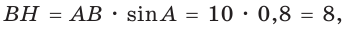
Ответ: 104.
Тригонометрические формулы
Используя формулы 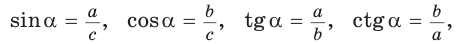
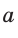
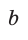
1. Основное тригонометрическое тождество
Доказательство:
По теореме Пифагора
Тогда
Следствие:
Так как синус и косинус острого угла а положительны, то
2. Выражение тангенса и котангенса через синус и косинус
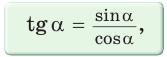
Доказательство:
a)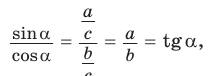
Следствие:
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 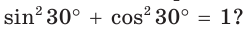
3. Основная задача
Дано: 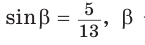
Найти:
Решение:
Способ 1. Используем основное тригонометрическое тождество: 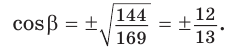
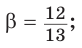
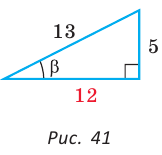
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 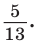
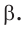
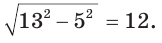
Способ 3. Пусть катет, противолежащий углу 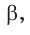
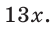
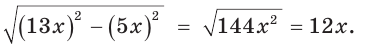
Ответ:
Пример №10
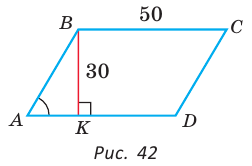
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 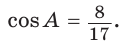
Решение:
Из треугольника АВК находим: 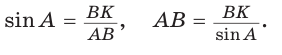
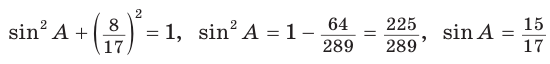
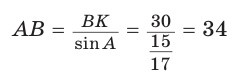
Ответ: 168 см.
Пример №11
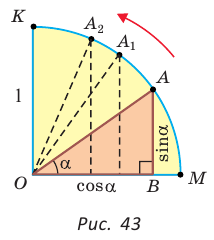
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
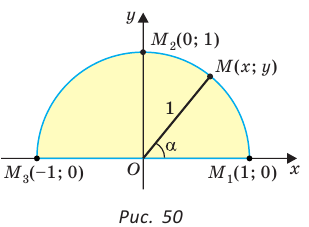
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 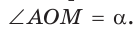
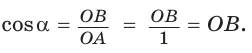
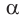
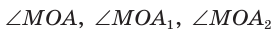
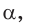
Из формулы 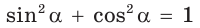
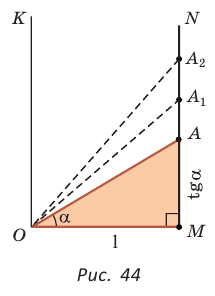
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 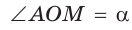
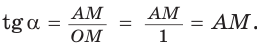
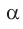
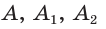
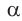
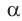
К такому же выводу можно прийти, рассматривая формулу 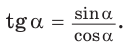
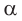
Пример №12
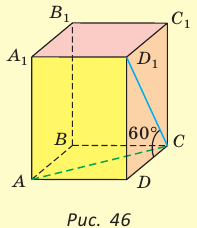
В основании прямоугольного параллелепипеда 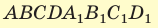
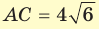
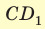
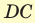

Решение:
Объем прямоугольного параллелепипеда находится по формуле 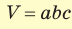
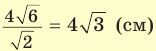
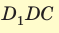
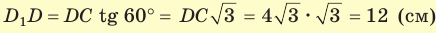
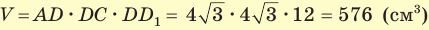
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 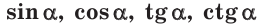
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
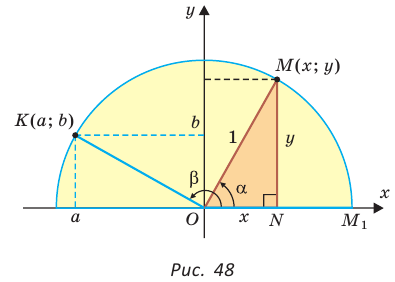
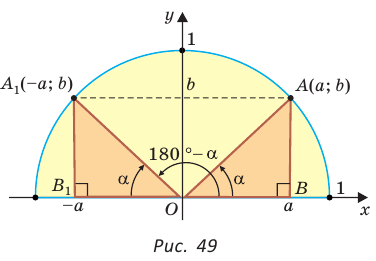
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси 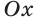
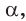
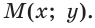
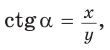
тангенс и котангенс острого угла а выражаются через координаты 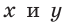
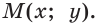
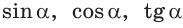
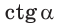
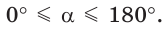
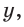
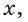
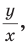
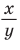
Например, для тупого 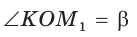
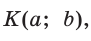
Для любого положения точки 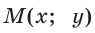
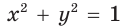
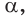

Также верны тождества:
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
Пусть 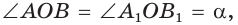
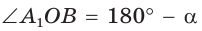
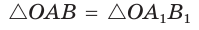
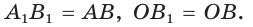
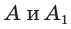
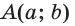
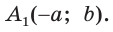
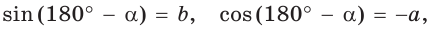
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1.
Разделив почленно равенство 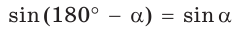
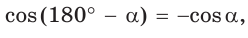
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2.
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
Если луч ОМ совпадет с лучом 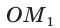
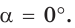
а) 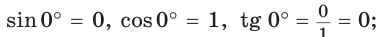
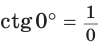
б) 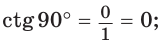
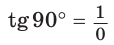
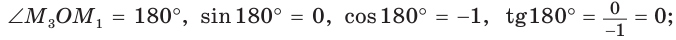
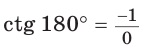
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 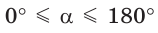
Пример №13
Найти 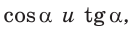
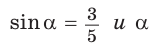
Решение:
Способ 1. Так как 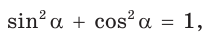
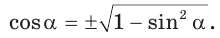
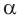
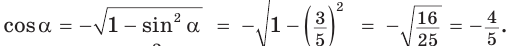
Способ 2. Синус острого угла 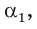
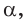
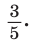
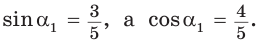
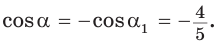
Ответ:
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е.
Доказательство:
Пусть в треугольнике 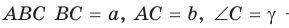
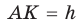
Из прямоугольного треугольника 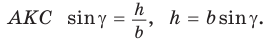
Если угол 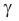
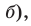
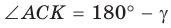
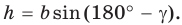
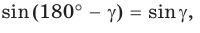
Если 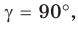
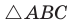
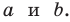

Теорема доказана.
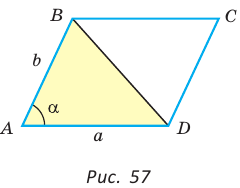
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е.
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 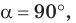
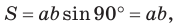

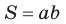
Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14
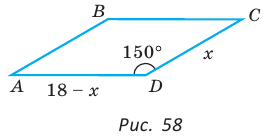
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
Решение:
Полупериметр параллелограмма равен 18 см. Если 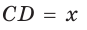
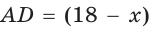
Тогда
Так как 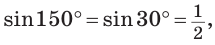
По условию 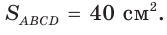
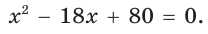
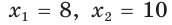
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
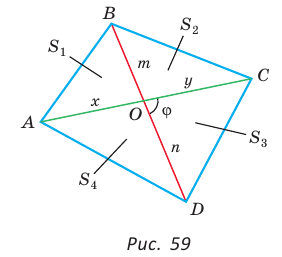
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е.
Доказательство:
Пусть диагонали 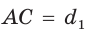
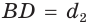
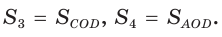
Обозначим 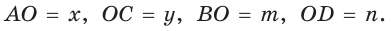
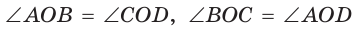
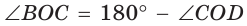
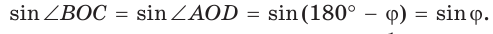
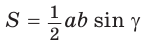
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 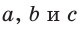
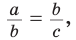
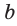
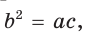
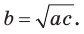
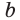
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 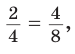
В прямоугольном треугольнике АВС, где 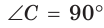
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 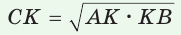
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е.
Доказательство:
а)3аметим, что если 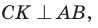
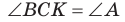
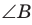
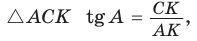
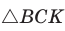
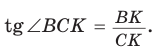
б) Из 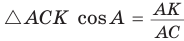
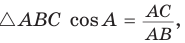
Аналогично доказывается, что 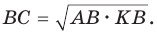
Обозначив катеты 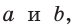
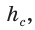
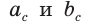
Пример №17
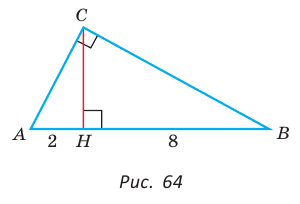
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
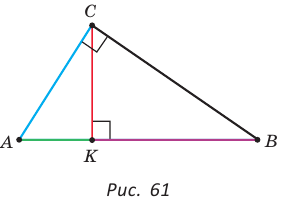
Пусть СН — высота прямоугольного треугольника АВС 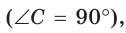
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то
Ответ: 20 см2.
Пример №18
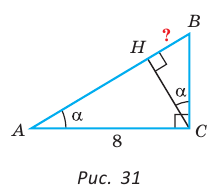
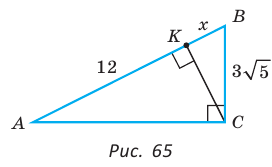
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 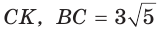
Решение:
Пусть 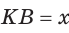
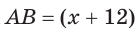
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 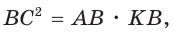
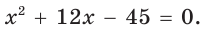
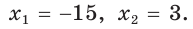
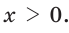
Ответ: 15 см.
Пример №19
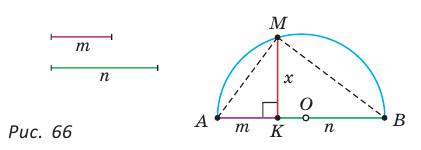
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок
Построение.
1) На произвольной прямой откладываем данные отрезки:
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 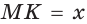
Доказательство:
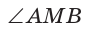
Повторение*
В 8-м классе мы доказали следующую теорему:
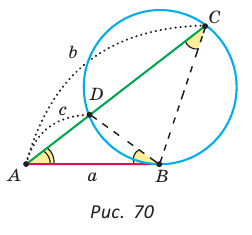
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 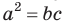
Как видим, отрезок 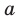
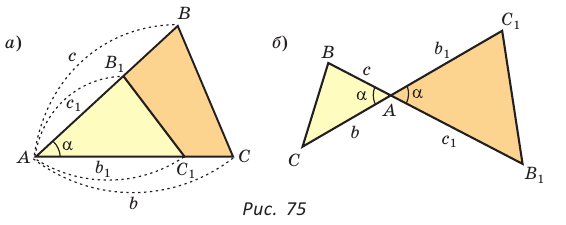
Теорема о площадях треугольников с общим (равным) углом
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е.
Доказательство:
Следствие: Верно:
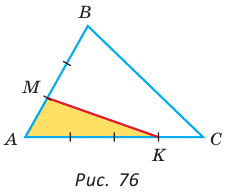
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
Способ 2.
Ответ: 4.
Теорема Менелая
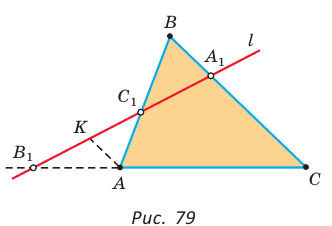
Если дан треугольник АВС и прямая 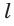
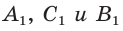
Доказательство:
Проведем отрезок 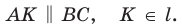
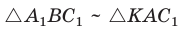

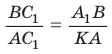
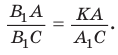
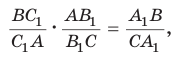
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой 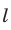
Пример №21
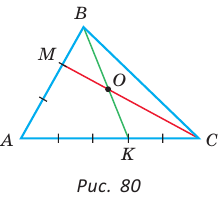
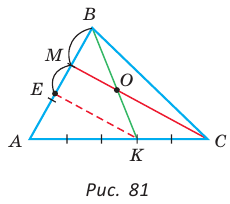
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
Решение:
Способ 1 (теорема Менелая). Рассмотрим 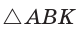
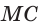
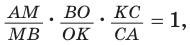
Способ 2 (теорема Фалеса обобщенная). Проведем 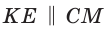
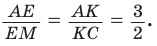
Но 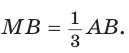
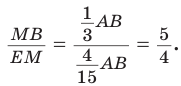
по теореме Фалеса
Ответ:
Пример №22
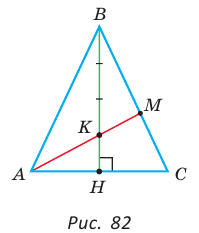
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) 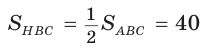
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке 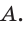
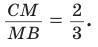
3)
4)
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
Например, 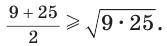
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 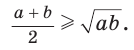
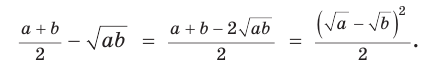
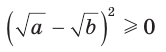
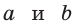
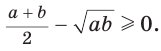
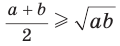
Неравенство 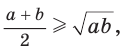
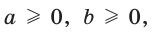
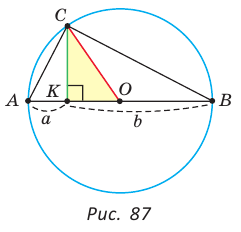
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 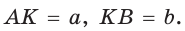

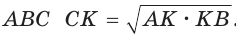
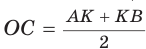
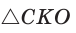
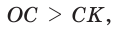
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 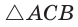
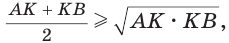
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
3. Тригонометрические формулы (тождества):
Примеры:
4. Формулы площади треугольника и параллелограмма:
5. Среднее пропорциональное в прямоугольном треугольнике:
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол – определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
Роман Тургенева «Накануне»: идейно-художественное своеобразие
Из каких слоев общества появятся «новые люди»? Что будет отличать их от поколения Рудиных и Лаврецких? Какую программу обновления России они примут и как приступят к освобождению народа от крепостного права? Эти вопросы волновали Тургенева давно. Еще в 1855 году, в момент работы над «Рудиным», задача, которую он поставил в «Накануне», уже начинала возникать перед ним: «Фигура главной героини, Елены, тогда еще нового типа в русской жизни, довольно ясно обрисовывалась в моем воображении,— вспоминал Тургенев,— но недоставало героя, такого лица, которому Елена, при ее еще смутном, хотя сильном стремлении к свободе, могла предаться» (XII, 306), Тогда же сосед Тургенева, отправляясь в Крым в качестве офицера дворянского ополчения, оставил писателю рукопись автобиографической повести, одним из главных героев которой был молодой болгарский революционер, студент Московского университета. Теперь мы знаем, что прототипом тургеневского Инсарова явился Николай Димитров Катранов, родившийся в 1829 году в болгарском городе Свиштов в небогатой купеческой семье. В 1848 году в составе большой группы болгарских юношей он приехал в Россию и поступил на историко-филологический факультет Московского университета.
Начавшаяся в 1853 году русско-турецкая война всколыхнула революционные настроения балканских славян, боровшихся за избавление от многовекового турецкого ига. В начале 1853 года Николай Катранов с русской женой Ларисой уехал на родину. Но внезапная вспышка туберкулеза спутала все планы. Пришлось вернуться в Россию, а затем ехать на лечение в Венецию, где Катранов простудился и скоропостижно скончался 5 мая 1853 года. Это был талантливый человек: он писал стихи, занимался переводами, горячо пропагандировал среди русских друзей идею освобождения родины.
Вплоть до 1859 года тетрадь с рукописью Каратеева — так звали тургеневского соседа — лежала без движения, хотя, познакомившись с ней, писатель воскликнул: «Вот герой, которого я искал! Между тогдашними русскими такого еще не было». Почему же Тургенев обратился к этой тетради в 1859 году, когда и в России подобного типа герои уже появились? Почему в качестве образца для русских «сознательно-героических натур» Тургенев предлагает болгарина Дмитрия Инсарова? Что не устроило, наконец, Тургенева в добролюбовской интерпретации романа «Накануне», опубликованного в январском номере журнала «Русский вестник» в 1860 году?
Н. А. Добролюбов, посвятивший разбору этого романа специальную статью «Когда же придет настоящий день?», дал классическое определение художественному дарованию Тургенева, увидев в нем писателя, чуткого к общественным проблемам. Очередной его роман «Накануне» еще раз блестяще оправдал эту репутацию. Добролюбов отметил четкую расстановку в нем главных действующих лиц. Центральная героиня Елена Стахова стоит перед выбором, на место ее избранника претендуют молодой ученый, историк Берсенев, будущий художник, человек искусства Шубин, успешно начинающий служебную деятельность чиновник Курнатовский и, наконец, человек гражданского подвига, болгарский революционер Инсаров. Социально-бытовой сюжет романа имеет символический подтекст: Елена Стахова олицетворяет молодую Россию «накануне» предстоящих перемен, Кто всего нужнее ей сейчас: люди науки или искусства, государственные чиновники или героические натуры, люди гражданского подвига? Выбор Еленой Инсарова дает недвусмысленный ответ на этот вопрос.
Добролюбов заметил, что в Елене Стаховой «сказалась та смутная тоска по чем-то, та почти бессознательная, но неотразимая потребность новой жизни, новых людей, которая охватывает теперь все русское общество, и даже не одно только так называемое образованное» (VI, 120).
В описании детских лет Елены Тургенев обращает внимание на глубокую близость ее к народу. С тайным уважением и страхом слушает она рассказы нищей девочки Кати о жизни «на всей божьей воле» и воображает себя странницей, покинувшей отчий дом и скитающейся по дорогам. Из народного источника пришла к Елене русская мечта о правде, которую надо искать далеко-далеко, со странническим посохом в руках. Из того же источника— готовность пожертвовать собой ради других, ради высокой цели спасения людей, попавших в беду, страдающих и несчастных. Не случайно в разговорах с Инсаровым Елена вспоминает буфетчика Василия, «который вытащил из горевшей избы безногого старика и сам чуть не погиб».
Даже внешний облик Елены напоминает птицу, готовую взлететь, и ходит героиня «быстро, почти стремительно, немного наклонясь вперед». Смутная тоска и неудовлетворенность Елены тоже связаны с темой полета: «Отчего я с завистью гляжу на пролетающих птиц? Кажется, полетела бы с ними, полетела — куда, не знаю, только далеко, далеко отсюда» (VIII, 79). Устремленность к полету проявляется и в безотчетных поступках героини: «Долго глядела она на темное, низко нависшее небо; потом она встала, движением головы откинула от лица волосы и, сама не зная зачем, протянула к нему, к этому небу, свои обнаженные, похолодевшие руки…» (VIII, 35—36). Проходит тревога — «опускаются невзлетевшие крылья». И в роковую минуту, у постели больного Инсарова, Елена видит высоко над водой белую чайку: «Вот если она полетит сюда,— подумала Елена,— это будет хороший знак…» Чайка закружилась на месте, сложила крылья — и, как подстреленная, с жалобным криком пала куда-то далеко за темный корабль» (VIII, 157).
Таким же окрыленным героем, достойным Елены, оказывается Дмитрий Инсаров. Что отличает его от русских Берсеневых и Шубиных? Прежде всего — цельность характера, полное отсутствие противоречий между словом и делом. Он занят не собой, все помыслы его сосредоточены на одной цели — освобождении родины, Болгарии. Тургенев верно уловил в характере Инсарова типические черты лучших людей эпохи болгарского Возрождения: широту и разносторонность умственных интересов, сфокусированных в одну точку, подчиненных одному делу — освобождению народа от векового рабства. Силы Инсарова питает и укрепляет живая связь с родной землей, чего так не хватает русским героям романа — Берсеневу, который пишет труд «О некоторых особенностях древнегерманского права в деле судебных наказаний», талантливому Шубину, который лепит вакханок и мечтает об Италии. И Берсенев, и Шубин — тоже деятельные люди, но их деятельность слишком далека от насущных потребностей народной жизни. Это люди без крепкого корня, отсутствие которого придает их характерам или внутреннюю вялость, как у Берсенева, или мотыльковое непостоянство, как у Шубина.
В то же время в характере Инсарова сказывается родовая ограниченность, типичная для Дон-Кихота. В поведении героя подчеркиваются упрямство и прямолинейность, некоторый педантизм. Художественную завершенность эта двойственная характеристика получает в ключевом эпизоде с двумя статуэтками героя, которые вылепил Шубин. В первой Инсаров представлен героем, а во второй — бараном, поднявшимся на задние ноги и склоняющим рога для удара. Не обходит Тургенев в своем романе и размышлений о трагичности судьбы людей донкихотского склада.
Рядом с сюжетом социальным, отчасти вырастая из него, отчасти возвышаясь над ним, развертывается в романе сюжет философский. «Накануне» открывается спором между Шубиным и Берсеневым о счастье и долге. «…Каждый из нас желает для себя счастья… Но такое ли это слово «счастье», которое соединило, воспламенило бы нас обоих, заставило бы нас подать друг другу руки? Не эгоистическое ли, я хочу сказать, не разъединяющее ли это слово?» (VIII, 14). Соединяют людей слова: «родина», «наука», «справедливость». И «любовь», но только если она — не «любовь-наслаждение», а «любовь-жертва».
Инсарову и Елене кажется, что их любовь соединяет личное с общественным, что она одухотворяется высшей целью. Но вот оказывается, что жизнь вступает в некоторое противоречие с желаниями и надеждами героев. На протяжении всего романа Инсаров и Елена не могут избавиться от ощущения непростительности своего счастья, от чувства виновности перед кем-то, от страха расплаты за свою любовь. Почему?
Жизнь ставит перед влюбленной Еленой роковой вопрос: совместимо ли великое дело, которому она отдалась, с горем бедной, одинокой матери, которое попутно этим делом вызывается? Елена смущается и не находит на этот вопрос возражения. Ведь любовь Елены к Инсарову приносит страдание не только матери: она оборачивается невольной нетерпимостью и по отношению к отцу, к русским друзьям — Берсеневу и Шубину, она ведет Елену к разрыву с Россией. «Ведь все-таки это мой дом,—думала она,— моя семья, моя родина…»
Елена безотчетно ощущает, что и в ее чувствах к Инсарову счастье близости с любимым человеком временами преобладает над любовью к тому делу, которому весь, без остатка, хочет отдаться герой. Отсюда — чувство вины перед Инсаровым: «Кто знает, может быть, я его убила».
В свою очередь, Инсаров задает Елене аналогичный вопрос: «Скажи мне, не приходило ли тебе в голову, что эта болезнь послана нам в наказание?» (VIII, 128). Любовь и общее дело оказываются не вполне совместимыми. В бреду, в период первой болезни, а потом в предсмертные мгновения коснеющим языком Инсаров произносит два роковых для него слова: «резеда» и «Рендич». Резеда — это тонкий запах духов, оставленный Еленой в комнате больного Инсарова; Рендич — соотечественник героя, один из организаторов готовящегося восстания балканских славян против турецких поработителей. Бред выдает глубокое внутреннее раздвоение цельного Инсарова, источником этого раздвоения является любовь.
В отличие от Чернышевского и Добролюбова с их оптимистической теорией «разумного эгоизма», утверждавшей единство личного и общего, счастья и долга, любви и революции в природе человека, Тургенев обращает внимание на скрытый драматизм человеческих чувств, на вечную борьбу центростремительных (эгоистических) и центробежных (альтруистических) начал в душе каждого человека. Человек, по Тургеневу, драматичен не только в своем внутреннем существе, но и в отношениях с окружающей его природой. Природа не считается с неповторимой ценностью человеческой личности: с равнодушным спокойствием она поглощает и простого смертного, и героя; все равны перед ее неразличающим взором. Этот мотив универсального трагизма жизни вторгается в роман неожиданной смертью Инсарова, исчезновением Елены на этой земле —«навсегда, безвозвратно». «Смерть, как рыбак,—с горечью говорит Тургенев,—который поймал рыбу в свою сеть и оставляет ее на время в воде: рыба еще плавает, но сеть на ней, и рыбак выхватит ее —когда захочет» (VIII, 166). С точки зрения «равнодушной природы» каждый из нас «виноват уже тем, что живет».
Однако мысль о трагизме человеческого существования не умаляет, а, напротив, укрупняет в романе Тургенева красоту и величие дерзновенных, освободительных порывов человеческого духа, оттеняет поэзию любви Елены к Инсарову, придает широкий общечеловеческий смысл социальному содержанию романа. Неудовлетворенность Елены современным состоянием жизни в России, ее тоска по иному, более совершенному социальному порядку в философском плане романа приобретает «продолжающийся» смысл, актуальный во все эпохи и все времена. «Накануне» — это роман о порыве России к новым общественным отношениям, пронизанный нетерпеливым ожиданием «сознательно-героических натур», которые двинут вперед дело освобождения крестьян.
И в то же время это роман о бесконечных исканиях человечества, о постоянном стремлении его к социальному совершенству, о вечном вызове, который бросает человеческая личность «равнодушной природе»:
«О, как тиха и ласкова была ночь, какою голубиною кротостию дышал лазурный воздух, как всякое страдание, всякое горе должно было замолкнуть и заснуть под этим ясным небом, под этими святыми, невинными лучами! «О боже! — думала Елена,— зачем смерть, зачем разлука, болезнь и слезы? или зачем эта красота, это сладостное чувство надежды, зачем успокоительное сознание прочного убежища, неизменной защиты, бессмертного покровительства? Что же значит это улыбающееся, благословляющее небо, эта счастливая, отдыхающая земля? Ужели это все только в нас, а вне нас вечный холод и безмолвие? Ужели мы одни… одни… а там, повсюду, во всех этих недосягаемых безднах и глубинах, — все, все нам чуждо? К чему же тогда эта жажда и радость молитвы?.. Неужели же нельзя умолить, отвратить, спасти… О боже! неужели нельзя верить чуду?» (VIII, 156).
Современников Тургенева из лагеря революционной демократии, для которых главнее был социальный смысл романа, не мог не смущать его финал: неопределенный ответ Увара Ивановича на вопрос Шубина, будут ли у нас,. в России, люди, подобные Инсарову. Какие могли быть загадки на этот счет в конце 1859 года, когда дело реформы стремительно подвигалось вперед, когда «новые люди» заняли ключевые посты в журнале «Современник»? Чтобы правильно ответить на этот вопрос, нужно выяснить, какую программу действий предлагал Тургенев «русским Инсаровым».
Автор «Записок охотника» вынашивал мысль о братском союзе всех антикрепостнических сил и надеялся на гармонический исход социальных конфликтов. Инсаров говорит: «Заметьте: последний мужик, последний нищий в Болгарии и я — мы желаем одного и того же. У всех у нас одна цель. Поймите, какую это дает уверенность и крепость!» (VIII, 68). Тургеневу хотелось, чтобы все прогрессивно настроенные люди России, без различия социальных положений и оттенков в политических убеждениях, протянули друг другу руки.
В жизни случилось другое. Добролюбов в статье «Когда же придет настоящий день?» решительно противопоставил задачи «русских Инсаровых» той программе общенационального единения, которую провозгласил в романе Тургенева болгарский революционер. «Русским Инсаровым» предстояла борьба с «внутренними турками», в число которых у Добролюбова попадали не только консерваторы, противники реформ, но и либеральные партии русского общества. Статья била в святая святых убеждений и верований Тургенева. Поэтому он буквально умолял Некрасова не печатать ее, а когда она была опубликована – покинул журнал «Современник» навсегда.
В романе «Накануне» (1860) смутные светлые предчувствия и надежды, которые пронизывали меланхоличное повествование «Дворянского гнезда», превращаются в определенные решения. Основной для Тургенева вопрос о соотношении мысли и деятельности, человека дела и теоретика в этом романе решается в пользу практически осуществляющего идею героя.
Само название романа «Накануне» — название «временное», в отличие от «локального» названия «Дворянское гнездо», — отражает то обстоятельство, что замкнутости, неподвижности патриархальной русской жизни приходит конец. Русский дворянский дом с вековым укладом его быта, с приживалками, соседями, карточными проигрышами оказывается на распутье мировых дорог. Русская девушка находит применение своим силам и самоотверженным стремлениям, участвуя в борьбе за независимость болгарского народа. Сразу после выхода в свет романа читатели и критики обратили внимание на то, что личностью, которую русское молодое поколение готово признать за образец, здесь представлен болгарин.
Название романа «Накануне» не только отражает прямое, сюжетное его содержание (Инсаров гибнет накануне войны за независимость его родины, в которой он страстно хочет принять участие), но и содержит оценку состояния русского общества накануне реформы и мысль о значении народно-освободительной борьбы в одной стране (Болгарии) как кануна общеевропейских политических перемен (в романе косвенно затрагивается и вопрос о значении сопротивления итальянского народа австрийскому владычеству).
Добролюбов считал образ Елены средоточием романа — воплощением молодой России. В этой героине, по мнению критика, воплощена «неотразимая потребность новой жизни, новых людей, которая охватывает теперь все русское общество, и даже не одно только так называемое «образованное» <.. .> «Желание деятельного добра» есть в нас, и силы есть; но боязнь, неуверенность в своих силах и, наконец, незнание: что делать? — постоянно нас останавливают <…> и мы всё ищем, жаждем, ждем… ждем, чтобы нам хоть кто-нибудь объяснил, что делать».
Таким образом, Елена, представлявшая, по его мнению, молодое поколение страны, ее свежие силы, характеризуется стихийностью протеста, она ищет «учителя» — черта, присущая деятельным героиням Тургенева.
Идея романа и структурное ее выражение, столь сложные и многозначные в «Дворянском гнезде», в «Накануне» предельно ясны, однозначны. Героиня, ищущая учителя-наставника, достойного любви, в «Накануне» выбирает из четырех претендентов на ее руку, из четырех идеальных вариантов, ибо каждый из героев — высшее выражение своего этико-идейного типа. Шубин и Берсенев представляют художественно-мыслительный тип (тип людей отвлеченно-теоретического или образно-художественного творчества), Инсаров и Курнатовский относятся к «деятельному» типу, т. е. к людям, призвание которых состоит в практическом «жизнетворчестве».
Говоря о значении в романе выбора своего пути и своего «героя», который делает Елена, Добролюбов рассматривает этот поиск-выбор как некий процесс, эволюцию, аналогичную развитию русского общества за последнее десятилетие. Шубин, а затем и Берсенев соответствуют по своим принципам и характерам более архаичным, отдаленным стадиям этого процесса. Вместе с тем оба они не настолько архаичны, чтобы быть «несовместимыми» с Курнатовским (деятелем эпохи реформ) и Инсаровым (особое значение которому придает складывающаяся революционная ситуация), Берсенев и Шубин — люди 50-х гг. Ни один из них не является чистым представителем гамлетовского типа. Таким образом, Тургенев в «Накануне» как бы распростился со своим излюбленным типом. И Берсенев, и Шубин генетически связаны с «лишними людьми», но в них нет многих главных черт героев этого рода. Оба они прежде всего не погружены в чистую мысль, анализ действительности не является их основным занятием. От рефлексии, самоанализа и бесконечного ухода в теорию их «спасает» профессионализация, призвание, живой интерес к определенной сфере деятельности и постоянный труд.
«Одарив» своего героя-художника Шубина фамилией великого русского скульптора, Тургенев придал его портрету привлекательные черты, напоминающие внешность Карла Брюллова, — он сильный, ловкий блондин.
Из первого же разговора героев — друзей и антиподов (наружность Берсенева рисуется как прямая противоположность внешности Шубина: он худой, черный, неловкий), разговора, который является как бы прологом романа, выясняется, что один из них «умница, философ, третий кандидат московского университета», начинающий ученый, другой — художник, «артист», скульптор. Но характерные черты «артиста» — черты человека 50-х гг. и идеала людей 50-х гг. — сильно рознятся от романтического представления о художнике. Тургенев нарочито дает это понять: в самом начале романа Берсенев указывает Шубину, каковы должны быть его — «артиста» — вкусы и склонности, и Шубин, шутливо «отбиваясь» от этой обязательной и неприемлемой для него позиции художника-романтика, защищает свою любовь к чувственной жизни и ее реальной красоте.
В самом подходе Шубина к своей профессии проявляется его связь с эпохой. Сознавая ограниченность возможностей скульптуры как художественного рода, он стремится передать в скульптурном портрете не только и не столько внешние формы, сколько духовную суть, психологию оригинала, не «линии лица», а взгляд глаз. Вместе с тем ему присуща особенная, заостренная способность оценивать людей и умение возводить их в типы. Меткость характеристик, которые он дает другим героям романа, превращает его выражения в крылатые слова; Эти характеристики в большинстве случаев и являются ключом к типам, изображенным в романе.
Если в уста Шубина автор романа вложил все социально-исторические приговоры, вплоть до приговора о правомерности «выбора Елены», Берсеневу он передал ряд этических деклараций. Берсенев — носитель высокого этического принципа самоотвержения и служения идее («идее науки»), как Шубин — воплощение идеального «высокого» эгоизма, эгоизма здоровой и цельной натуры.
Берсеневу придана нравственная черта, которой Тургенев отводил особенно высокое место на шкале душевных достоинств: доброта. Приписывая эту черту Дон-Кихоту, Тургенев на ней основывался в своем утверждении исключительного этического значения образа Дон-Кихота для человечества. «Все пройдет, все исчезнет, высочайший сан, власть, всеобъемлющий гений, всё рассыплется прахом <…> Но добрые дела не разлетятся дымом: они долговечнее самой сияющей красоты» (VIII, 191). У Берсенева эта доброта происходит от глубоко, органически усвоенной им гуманистической культуры и присущей ему «справедливости», объективности историка, способного встать выше личных, эгоистических интересов и пристрастий и оценить значение явлений действительности безотносительно к своей личности.
Отсюда и проистекает истолкованная Добролюбовым как признак нравственной слабости «скромность», понимание им второстепенного значения своих интересов в духовной жизни современного общества и своего «второго номера» в строго определенной иерархии типов современных деятелей.
Тип ученого как идеал оказывается исторически дезавуированным. Это «низведение» закреплено и сюжетной ситуацией (отношение Елены к Берсеневу), и прямыми оценками, данными герою в тексте романа, и самооценкой, вложенной в его уста. Такое отношение к профессиональной деятельности ученого могло родиться лишь в момент, когда жажда непосредственного жизнестроительства, исторического общественного творчества охватила лучших людей молодого поколения. Этот практицизм, это деятельное отношение к жизни не у всех молодых людей 60-х гг. носили характер революционного или даже просто бескорыстного служения. В «Накануне» Берсенев выступает как антипод не столько Инсарова (мы уже отмечали, что он более чем кто-либо другой способен оценить значение личности Инсарова), сколько обер-секретаря Сената — карьериста Курнатовского.
В характеристике Курнатовского, «приписанной» автором Елене, раскрывается мысль о принадлежности Курнатовского, как и Инсарова, к «действенному типу» и о взаимовраждебных позициях, занимаемых ими внутри этого — очень широкого — психологического типа. Вместе с тем в этой характеристике сказывается и то, как исторические задачи, необходимость решения которых ясна всему обществу (по словам Ленина, во время революционной ситуации обнаруживается невозможность «для господствующих классов сохранить в неизменном виде свое господство» и вместе с тем наблюдается «значительное повышение <…> активности масс», не желающих жить по-старому), заставляют людей самой разной политической ориентации надевать маску прогрессивного человека и культивировать в себе черты, которые приписываются обществом таким людям.
«Вера» Курнатовского — это вера в государство в приложении к реальной русской жизни эпохи, вера в сословно-бюрократическое, монархическое государство. Понимая, что реформы неизбежны, деятели типа Курнатовского связывали все возможные в жизни страны изменения с функционированием сильного государства, а себя считали носителями идеи государства и исполнителями его исторической миссии, отсюда — самоуверенность, вера в себя, по словам Елены.
В центре романа — болгарский патриот-демократ и революционер по духу — Инсаров. Он стремится опрокинуть деспотическое правление в родной стране, рабство, утвержденное веками, и систему попрания национального чувства, охраняемую кровавым, террористическим режимом. Душевный подъем, который он испытывает и сообщает Елене, связан с верой в дело, которому он служит, с чувством своего единства со всем страдающим народом Болгарии. Любовь в романе «Накануне» именно такова, какой ее рисует Тургенев в выше цитированных словах о любви как революции («Вешние воды»). Воодушевленные герои радостно летят на свет борьбы, готовые к жертве, гибели и победе.
В «Накануне» впервые любовь предстала как единство в убеждениях и участие в общем деле. Здесь была опоэтизирована ситуация, характерная для большого периода последующей жизни русского общества и имевшая огромное значение как выражение нового этического идеала. Прежде чем соединить свою жизнь с ее жизнью, Инсаров подвергает Елену своеобразному «экзамену», предвосхищающему символический «допрос», которому подвергает таинственный голос судьбы смелую девушку-революционерку в стихотворении в прозе Тургенева «Порог». При этом герой «Накануне» вводит любимую девушку в свои планы, свои интересы и заключает с ней своеобразный договор, предполагающий с ее стороны сознательную оценку их возможной будущности, — черта отношений, характерная для демократов-шестидесятников.
Любовь Елены и ее благородная решимость разрушают аскетическую замкнутость Инсарова, делают его счастливым. Добролюбов особенно ценил страницы романа, где изображалась светлая и счастливая любовь молодых людей. В уста Шубина Тургенев вложил лирическую апологию идеала героической молодости: «Да, молодое, славное, смелое дело. Смерть, жизнь, борьба, падение, торжество, любовь, свобода, родина… Хорошо, хорошо. Дай бог всякому! Это не то, что сидеть по горло в болоте да стараться показывать вид, что тебе всё равно, когда тебе действительно в сущности всё равно. А там — натянуты струны, звени на весь мир или порвись!» (VIII, 141).