Какая величина является отношением пути ко времени? В каких единицах она измеряется? Найдите отношение расстояния s (м), которое пробежал мальчик, ко времени t (мин), в течении которого он бежал, если s = 900, t = 5. Что выражает это отношение?
reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 6.1 Вопросы к параграфу. Номер №4
Решение
Получай решения и ответы с помощью нашего бота
v
=
s
t
− скорость является отношением пути ко времени.
при s = 900, t = 5:
v
=
900
5
=
180
(м/мин) − скорость мальчика.
Ответ: 180 м/мин
|
Есть такой способ решения задач, конечно более сложных, как решение по размерности. В данном случае он поможет не запутаться с решением этого примера. Мы просто заменяем в отношении слова Путь и Время единицами измерения. Путь измеряем в метрах, время в секундах, то есть их отношение дает нам размерность метр/секунду. В этих единицах измеряют скорость. Следовательно и отношение Пути ко Времени также равно Скорости. автор вопроса выбрал этот ответ лучшим worker2312 6 лет назад Не зря на спидометрах транспортных средств обозначается км/час. И говорят сколько километров в час ты едешь. Поэтому, путь будет преодолен за тот промежуток времени, с какой скоростью будет двигаться средство. Дистанция=Времени=Скорости. Знаете ответ? |
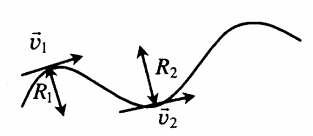
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22k
- Категория: ГДЗ Математика учебник 6 класс Дорофеев, Шарыгин
Ответы на вопросы к параграфу 6.1 Что такое отношение
1. Учитель проверил 45 контрольных работ, и ему осталось проверить еще 75.
а) Найдите отношение числа непроверенных работ к числу проверенных и обратное отношение. Объясните, что показывает каждое из них.
б) Используя данные задачи, найдите другие отношения и объясните, что они показывают.
Решение
а) 1) $frac{75}{45}=frac53=1frac23$ − отношение числа непроверенных работ к числу проверенных, которое показывает, что число непроверенных работ в $1frac23$ раза больше числа проверенных работ;
2) $frac{45}{75}=frac35$ − отношение числа проверенных работ к числу непроверенных, которое показывает, что число проверенных работ составляет 3/5 части от числа проверенных работ.б) 1) $frac{45}{45+75}=frac{45}{120}=frac38$ − отношение числа проверенных работ к общему числу работ, которое показывает, что число проверенных работ составляет 3/8 части от числа всех работ;
2) $frac{45+75}{45}=frac{120}{45}=frac83=2frac23$ − отношение числа всех работ к числу проверенных работ, которое показывает, что число всех работ в $2frac23$ раза больше, чем число проверенных работ;
3) $frac{75}{45+75}=frac{75}{120}=frac58$ − отношение числа не проверенных работ к общему числу работ, которое показывает, что число не проверенных работ составляет 5/8 части от числа всех работ;
4) $frac{45+75}{75}=frac{120}{75}=frac85=1frac35$ − отношение числа всех работ к числу не проверенных работ, которое показывает, что число всех работ в $1frac35$ раза больше, чем число не проверенных работ.
2. Замените отношение более простым:
а) 12 : 8;
б) 15 : 20;
в) 5/2 :3.
Решение
а) 12 : 8 = 3 : 2
б) 15 : 20 = 3 : 4
в) 5/2 : 3 = 5 : 6
3. Объясните, как найти отношение 3 км к 750 м, и найдите его.
Решение
Выразим 3 км в метрах:
3 км = 3000 м
Найдем отношение 3 км к 750 м:
3000/750 = 4
4. Какая величина является отношением пути ко времени? В каких единицах она измеряется? Найдите отношение расстояния s (м), которое пробежал мальчик, ко времени t (мин), в течении которого он бежал, если s = 900, t = 5. Что выражает это отношение?
Решение
v = s/t − скорость является отношением пути ко времени.
при s = 900, t = 5:
v = 900/5 = 180 (м/мин) − скорость мальчика.
Ответ: 180 м/мин.
5. Что называют масштабом? Масштаб карты 1 : 200000. Объясните, что показывает это отношение. Сколько километров на местности изображает отрезок в 1 см на этой карте? отрезок в 5 см? Каким будет на этой карте расстояние, равно 20 км на местности?
Решение
1) Масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.
2) Масштаб карты 1 : 200000 показывает, что 1 см на карте изображает 200000 см на местности.
3) 200000 (см) = 2000 (м) = 2 (км) − на местности изображает отрезок в 1 см на этой карте.
4) 2 км * 5 = 10 (км) − на местности изображает отрезок в 5 см на этой карте.
5) 20 км = 2000000 см
2000000 : 200000 = 10 (см) − расстояние на карте, которое изображает 20 км на местности.
Скорость равномерного движения тела

4.2
Средняя оценка: 4.2
Всего получено оценок: 286.
4.2
Средняя оценка: 4.2
Всего получено оценок: 286.
Важнейшим параметром движения в кинематике является скорость. Рассмотрим особенности этой характеристики для случая равномерного движения тела.
Равномерное движение тела
Если тело движется, то путь, пройденный им постоянно увеличивается. Однако, если мы будем отмечать путь, пройденный движущимся телом за каждую секунду или каждый час (или любой другой одинаковый промежуток времени), то этот путь не обязательно будет увеличиваться. Он может и уменьшаться, и оставаться без изменения, и даже может быть нулевым (ясно, что в этом случае тело покоится на месте).
Движение, при котором за равные промежутки времени тело проходит равный путь, называется равномерным.
Хотя, в природе равномерные движения достаточно редки, в жизни человека таких движений гораздо больше. Эталон равномерного движения – стрелки часов, которые каждый час проходят один и тот же путь по циферблату.
Скорость, как главная характеристика движения
На примере стрелок часов – часовой, минутной и секундной – можно видеть разницу в движении. Хотя все эти три стрелки проходят за равные промежутки времени равные пути, а значит, все три движутся равномерно, двигаются они совершенно по-разному.
Для характеристики этой разницы введено понятие скорости.
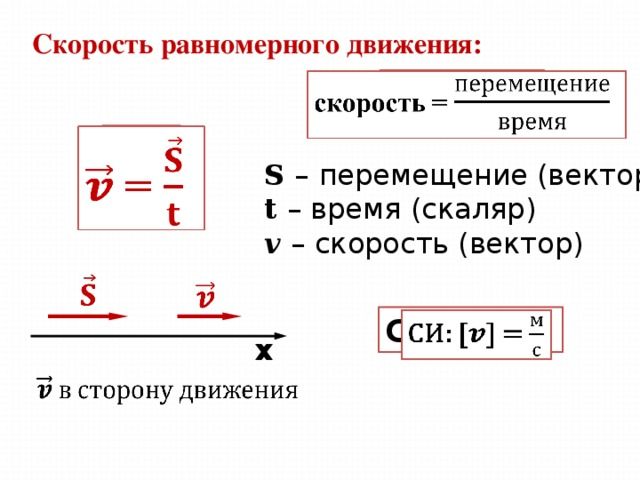
Скорость равномерного движения тела равна пути, проходимому телом за единицу времени.
То есть, для нахождения скорости надо найти отношение пройденного пути ко времени, за который этот путь был пройден. Поскольку при равномерном движении тело за любой равный промежуток времени проходит одно и то же время, то это отношение будет всегда одинаковым. Формула скорости равномерного движения:
$$v={s over t},$$
где:
- $v$ – скорость;
- $s$ – путь;
- $t$ – время;
Таким образом, физический смысл скорости – это путь, проходимый телом в единицу времени.
Из этой же формулы можно найти размерность скорости. Поскольку расстояние в системе СИ измеряется в метрах, а время в секундах, то единицей скорости является:
$$v={s over t}={м over сек}$$
то есть, метры в секунду.
Хотя математически скорость может принимать любое значение, в реальном мире скорость любого материального тела не может быть больше скорости света в вакууме. Она равна примерно $3×10^8$ м/с.
Скорость – векторная величина
Полученное значение говорит о величине скорости. Однако, эта характеристика не единственная.
Представим себе, что нам надо через 10 часов прибыть на северный полюс, до которого 10 тысяч километров, на самолете, движущемся со скоростью тысяча километров в час. Если самолет летит точно на север, он прибудет вовремя. А что будет, если самолет полетит на восток ? Мы не достигнем цели не только через 10 часов, но и вообще никогда.
Из этого примера можно видеть важнейшую особенность скорости – она имеет направление. Величины, не имеющие направления, называются скалярными. Величины, имеющие направление, называются векторными.
Скорость – одна из векторных величин. Для полного определения скорости необходимо указывать не только ее величину, но и направление.
Что мы узнали?
Скорость равномерного движения равна отношению пройденного пути ко времени, за который этот путь был пройден. Скорость измеряется в метрах в секунду и является векторной величиной.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 286.
А какая ваша оценка?