Как найти отношение скоростей физика

Поучительная задачка на предмет того, насколько мы зашорены и ограничены в мышлении предыдущим опытом решения подобных задач. А также на предмет того, что условие задачи должно должно быть достаточно полным, чтобы позволить однозначно решить задачу.

Давйте попробуем начертить план, на котором обозначим точками города А и В, а также положения автомобиля и мотоцикла в начальный момент времени А0 и М0, а моменты времени 1 час и 2 часа, соответственно точками А1 и А2 и М1 и М2.

Очевидно, что точка А0 совпадает сточкой А (обозначением города), а М0 – с точкой В.

Что нам задано однозначно? “Через час автомобиль был посередине между пунктом А и мотоциклом.”.

Т.е. мы можем произвольно поставить точки А0 и М1, соединить их отрезком и на его середине поставить точку А1. Условие “Через час автомобиль был посередине между пунктом А и мотоциклом.” – выполнено. И Всё. Больше нас ничто не ограничивает в наших фантазиях (к условию “Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.” вернёмся чуть позже.

Нигде в условии не сказано, что движение автомобиля и мотоцикла прямолинейное и с постоянными скоростями. Ну ладно, можно согласиться, что вопрос “Найти отношение скоростей мотоцикла и автомобиля” предполагает, что величины скоростей остаются постоянными. Но ведь движение может быть и не по прямой. Начертим на нашем плане ЛЮБУЮ кривую линию Любой длины от точки А0 к точке А1. Затем поставим на плане совершенно ПРОИЗВОЛЬНО точку А2 почти в любом месте с единственным ограничением, чтобы длина прямой А1А2 не превышала длины кривой А0А1 (можно измерить курвиметром. Далее, проведём окружность радиусом А0А2 с центром в точке А0 (т.е. в городе А). Теперь, АБСОЛЮТНО В ЛЮБОМ месте этой окружности поставим точку М2. Теперь условие “Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.” тоже выполнено. От точки М1 до точки М2 мы можем нарисовать любую кривую линию. Далее, от точки М1 мы можем нарисовать любую кривую линию той же длины, что и между М2 и М1, и там поставить точку М0 (город В).

Итак, все условия задачи выполнены, и количество решений у нас – насколько хватает фантазии.

В большинстве школьных задач на движение молчаливо предполагается (если особо не оговаривается, например при беге по кругу на стадионе), что движение происходит по прямой, хотя ЭТО УСЛОВИЕ ОБЯЗАТЕЛНО НУЖНО ОГОВАРИВАТЬ.

Ну ладно, предположим, что у нас в условии сказано, что движение прямолинейное и с постоянной скоростью. Тогда число вариантов значительно уменьшается, но ещё остаётся бесконечно большим.

Начертим план заново. Чертим отрезок А0М1. На середине его ставим точку А1. откладывая от точки А1 отрезок А1А2, равный отрезку А0А1 приходим к точке А2, в этой ситуации она совпадает с точкой М1. Чертим окружность радиуса А0А2 с центром в точке А0. Точку М2 можно поставить в ЛЮБОЙ точке этой окружности. Далее, через точки М2 и М1 провести прямую, и от точки М1 отложить отрезок М1М0, равный по длине отрезку М2М1. И в этом месте поставить точку В.

Итак, даже если бы было оговорено, что движение прямолинейное и всё время в одном направлении, т.е. векторы скоростей не меняются, всё равно получается бесконечное множество решений.

И ТОЛЬКО ЕСЛИ ВВЕСТИ ДОПОЛНИТЕЛЬНОЕ ОГРАНИЧЕНИЕ, ЧТО движение автомобиля и мотоцикла происходит только по прямой, проведённой через точки А и В, то только тогда условие задачи и решение становятся однозначными.

Продолжим радиус А0А2 за точку А0 до пересечения с окружностью. Если точку М2 поставить на этом пересечении, то получится, что за второй час мотоцикл проехал отрезок М1М2, равный диаметру окружности, а автомобиль – отрезок А1А2, равный половине радиуса окружности. Следовательно, скорость мотоцикла в 4 раза выше скорости автомобиля.

А если допустима скорость мотоцикла равная 0, то появляется ещё и второй вариант, когда точки в, А2 М0 М1 и М2 совпадают.

Ну, и напоследок, числовая иллюстрация. Скорость автомобиля 20 км/ч, мотоцикла 80 км/ч. Расстояние между городами равно 120 км. За первый час автомобиль проехал по направлению к городу В 20 км (точка А1). Мотоцикл проехал за это время 80 км по направлению к городу А и находился в 40 км от А (точка М1, она же впоследствии А2). За половину второго часа мотоцикл достиг города А, но не остановился и продолжил движение и к концу второго часа оказался на расстоянии 40 км от города А (точка М2) в противоположную от города В сторону. А автомобиль – в точке А2, она же М1 на линии между городами А и В в 40 км от города А и 80 км от города В.

Источник

Чтобы получить точное представление о движении двух объектов относительно друг друга относительная скорость является важным. Поэтому в этой статье мы подробно поговорим об относительной скорости между двумя объектами.

Относительная скорость — это, по сути, скорость одного объекта по отношению к другому. Рассмотрим следующие два объекта, А и В, которые движутся с разными скоростями. Скорость объекта А по отношению к объекту В или наоборот называется относительной скоростью. Он также известен как скорость изменения относительного положения одного объекта по отношению к другому с течением времени.

Как найти относительную скорость двух тел?

🠊 Техника определения скорости объекта требует определения скорости изменения положения объекта по отношению к неподвижному окружающему объекту.

Когда объекты A и B находятся в относительном движении, их соответствующие скорости также будут в относительном движении. Чтобы получить относительную скорость объекта A по отношению к B, нужно математически придать равную и противоположную скорость B как объекту A, так и объекту B, чтобы привести объект B в состояние покоя.

В результате равнодействующая обеих скоростей (скорости объекта А и Б) дает нам относительную скорость объекта А относительно объекта Б.

Уравнения относительной скорости следующие:

Скорость объекта А относительно объекта В можно рассчитать следующим образом:

V_abV =_a – V_b

Скорость объекта B относительно объекта A можно рассчитать следующим образом:

V_ba V =_b– V_a

Из двух выражений мы можем вывести следующее:

V_ab = – V_ba

Однако обе величины равны математически и могут быть представлены как:

|V_ab|= |В_ba|

Какова относительная скорость между двумя телами, когда они движутся с одинаковой скоростью в одном направлении?

🠊 Когда два тела А и В движутся в одном направлении с одинаковой скоростью, угол между ними равен 0°.

относительная скорость между двумя объектами

Предположим, что два транспортных средства A и B движутся в одном направлении, т. е. параллельно друг другу, с одинаковой скоростью или скоростью (поскольку они движутся в одном направлении), т. е. V_a V =_b.

В результате скорость автомобиля А относительно автомобиля В равна:

V_abV =_a– V_b = 0

Аналогичным образом, скорость транспортного средства B относительная к транспортному средству А:

V_ba V =_b – V_a= 0

Это означает, что если два объекта двигаться в одном направлении с одинаковой скоростью или скорость, их относительная скорость становится равной нулю. Это демонстрирует, что другой может казаться покоящимся для одного объекта.

Построение графика положение-время для двух объектов, движущихся в одном направлении с одинаковой скоростью, приводит к прямым параллельным линиям, как показано на графике ниже.

Какова относительная скорость между двумя телами, когда они движутся с разными скоростями в одном направлении?

🠊 Если два транспортных средства, A и B, движутся в одном направлении с разными скоростями, в первую очередь следует рассмотреть два сценария:

(1) Начальные точки одинаковы (V_a > V_b):

Если два транспортных средства движутся с разными скоростями в одном направлении с одной и той же начальной точкой и Va > Vb, человек в транспортном средстве B воспринимает транспортное средство A как удаляющееся от него со скоростью:

V_ab V =_a – V_b

Транспортное средство B движется назад к пассажиру в транспортном средстве A со скоростью:

V_ba V =_b – V_a = -( В_a – V_b) = -V_ab

В результате обе скорости имеют одинаковую величину, но противоположные знаки.

(2) Различные отправные точки:

Мы можем думать о двух сценариях здесь:

(i) Предположим, что транспортное средство A имеет более высокую скорость, чем транспортное средство B, т. е. V_a > V_b, и следует за автомобилем B.

В этой ситуации транспортное средство A в конечном итоге догонит транспортное средство B, как показано на их графике положение-время.

V_ab V =_a – V_b≠ 0

(ii) Рассмотрим ситуацию, когда V_a > V_b и автомобиль А движется впереди автомобиля В.

В этом случае транспортное средство B никогда не сможет обогнать транспортное средство A.. Графики положения и времени обоих транспортных средств не будут пересекаться по мере их удаления друг от друга.

V_ab V =_a – V_b ≠ 0

Какова будет относительная скорость двух тел, когда они движутся в противоположных направлениях?

🠊 Угол, образованный двумя телами, движущимися в противоположных направлениях по прямой, называется 180°.

Рассмотрим два автомобиля А и В, движущихся в противоположных направлениях по прямой.

В результате скорость автомобиля А относительно автомобиля В равна:

V_ab V =_a -(- В_b) = В_a +V_b

Скорость транспортного средства B по отношению к A аналогична:

V_ba V =_b-(- В_a) = В_a +V_b

В результате можем написать:

V_ab V =_ba

Это указывает на то, что если два объекта движутся в противоположных направлениях по прямой линии, кажется, что каждый объект движется очень быстро по сравнению с другим.

Какова относительная скорость, когда два тела движутся под углом?

🠊 Рассмотрим пример относительной скорости, который возникает, когда два объекта, A и B, движутся под углом со скоростями Va и Vb.

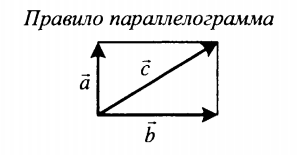
Диагональ даст нам относительную скорость, если мы построим параллелограмм, как показано на рисунке. В результате величина диагонального вектора параллелограмма или относительная скорость с использованием закона косинусов составляет:

Но Cos(180°-𝛳) = -Cos𝛳

Когда два объекта движутся под углом, приведенное выше уравнение дает нам их относительную скорость. Мы также можем вывести случай того же направления и случай противоположного направления из этого уравнения, изменив значение угла на 0° и 180° соответственно.

Однако, как показано на изображении, если вектор относительной скорости Vab образует угол ꞵ со скоростью объекта A, то

Но Sin(180°-𝛳) = Sin𝛳

Или,

Важность относительной скорости:

Важность относительной скорости резюмируется ниже:

Рассчитать скорость звезд и астероидов относительно Земли.
Для измерения расстояния между любыми двумя объектами в пространстве.
Чтобы запустить ракету.
Для определения скорости любого объекта.
Это помогает нам, когда объект движется через жидкость.

Проблемы, связанные с относительной скоростью:

1. Автомобиль, едущий по шоссе со скоростью 110 км/ч, проезжает мимо автобуса, идущего со скоростью 85 км/ч. Какова скорость автомобиля с точки зрения пассажира автобуса?

Данный:

Скорость автомобиля V_c = 110 км/ч

Скорость автобуса V_b = 85 км/ч

Найти:

Относительная скорость автомобиля относительно автобуса V_cb знак равно

Решение:

Поскольку автомобиль и автобус едут в одном направлении, относительная скорость автомобиля с точки зрения пассажира автобуса равна:

V_cb V =_c – V_b = (110 -85)км/ч = 25 км/ч

Таким образом, скорость автомобиля с точки зрения пассажира автобуса составляет 25 км/ч.

2. Две машины, находящиеся на некотором расстоянии друг от друга, начинают двигаться навстречу друг другу со скоростями 150 м/с и 200 м/с по прямой дороге. С какой скоростью они приближаются друг к другу?

Данный:

Скорость автомобиля 1 В₁ = 150 м / с

Скорость автомобиля 2 В₂= 200 м / с

Найти:

Относительная скорость вагона 1 относительно вагона 2 V₁₂ знак равно

Относительная скорость вагона 2 относительно вагона 1 V₂₁ знак равно

Решение:

Так как оба автомобиля едут в противоположном направлении, относительная скорость:

V₁₂ V =₁ + V₂ = (150 + 200) м/с = 350 м/с

Кроме того,

V₂₁ V =₁ + V₂ = (150 + 200) м/с = 350 м/с

В результате два автомобиля движутся навстречу друг другу с относительной скоростью 350 м/с.

Резюме:

Скорость одного объекта по отношению к другому объекту просто называется относительной скоростью этих двух объектов.
Рассмотрим два объекта, которые движутся в одном направлении. В этой ситуации величина относительной скорости одного объекта по отношению к другому будет равна разнице в величине их скоростей.
Если два объекта движутся в одном направлении и с одинаковыми скоростями, их относительная скорость будет ноль.
Предположим, что любые два объекта движутся в противоположном направлении. В этом случае величина относительной скорости одного объекта по отношению к другому окажется суммой величины их скоростей.

Источник

From Wikipedia, the free encyclopedia

The relative velocity ${displaystyle {vec {v}}_{Bmid A}}$ (also ${displaystyle {vec {v}}_{BA}}$ or ${displaystyle {vec {v}}_{Boperatorname {rel} A}}$ ) is the velocity of an object or observer B in the rest frame of another object or observer A.

Classical mechanics[edit]

In one dimension (non-relativistic)[edit]

Relative motion man on train

We begin with relative motion in the classical, (or non-relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and by train) for one hour. This, by definition, is 50 km/h, which suggests that the prescription for calculating relative velocity in this fashion is to add the two velocities.

The diagram displays clocks and rulers to remind the reader that while the logic behind this calculation seem flawless, it makes false assumptions about how clocks and rulers behave. (See The train-and-platform thought experiment.) To recognize that this classical model of relative motion violates special relativity, we generalize the example into an equation:

${displaystyle underbrace {{vec {v}}_{Mmid E}} _{text{50 km/h}}=underbrace {{vec {v}}_{Mmid T}} _{text{10 km/h}}+underbrace {{vec {v}}_{Tmid E}} _{text{40 km/h}},}$

where:

${displaystyle {vec {v}}_{Mmid E}}$

is the velocity of the Man relative to Earth,

${displaystyle {vec {v}}_{Mmid T}}$

is the velocity of the Man relative to the Train,

${displaystyle {vec {v}}_{Tmid E}}$

is the velocity of the Train relative to Earth.

Fully legitimate expressions for “the velocity of A relative to B” include “the velocity of A with respect to B” and “the velocity of A in the coordinate system where B is always at rest”. The violation of special relativity occurs because this equation for relative velocity falsely predicts that different observers will measure different speeds when observing the motion of light. ^{[note 1]}

In two dimensions (non-relativistic)[edit]

Relative velocities between two particles in classical mechanics

The figure shows two objects A and B moving at constant velocity. The equations of motion are:

${displaystyle {vec {r}}_{A}={vec {r}}_{Ai}+{vec {v}}_{A}t,}$

${displaystyle {vec {r}}_{B}={vec {r}}_{Bi}+{vec {v}}_{B}t,}$

where the subscript i refers to the initial displacement (at time t equal to zero). The difference between the two displacement vectors, ${vec r}_{B}-{vec r}_{A}$ , represents the location of B as seen from A.

${displaystyle {vec {r}}_{B}-{vec {r}}_{A}=underbrace {{vec {r}}_{Bi}-{vec {r}}_{Ai}} _{text{initial separation}}+underbrace {({vec {v}}_{B}-{vec {v}}_{A})t} _{text{relative velocity}}.}$

Hence:

${displaystyle {vec {v}}_{Bmid A}={vec {v}}_{B}-{vec {v}}_{A}.}$

After making the substitutions ${vec v}_{{A|C}}={vec v}_{A}$ and ${vec v}_{{B|C}}={vec v}_{B}$ , we have:

${displaystyle {vec {v}}_{Bmid A}={vec {v}}_{Bmid C}-{vec {v}}_{Amid C}Rightarrow }$

${displaystyle {vec {v}}_{Bmid C}={vec {v}}_{Bmid A}+{vec {v}}_{Amid C}.}$

Galilean transformation (non-relativistic)[edit]

To construct a theory of relative motion consistent with the theory of special relativity, we must adopt a different convention. Continuing to work in the (non-relativistic) Newtonian limit we begin with a Galilean transformation in one dimension:^{[note 2]}

where x’ is the position as seen by a reference frame that is moving at speed, v, in the “unprimed” (x) reference frame.^{[note 3]} Taking the differential of the first of the two equations above, we have, , and what may seem like the obvious^{[note 4]} statement that dt'=dt , we have:

${frac {dx'}{dt'}}={frac {dx}{dt}}-v$

To recover the previous expressions for relative velocity, we assume that particle A is following the path defined by dx/dt in the unprimed reference (and hence dx′/dt′ in the primed frame). Thus ${displaystyle dx/dt=v_{Amid O}}$ and ${displaystyle dx'/dt=v_{Amid O'}}$ , where and refer to motion of A as seen by an observer in the unprimed and primed frame, respectively. Recall that v is the motion of a stationary object in the primed frame, as seen from the unprimed frame. Thus we have ${displaystyle v=v_{O'mid O}}$ , and:

${displaystyle v_{Amid O'}=v_{Amid O}-v_{O'mid O}Rightarrow v_{Amid O}=v_{Amid O'}+v_{O'mid O},}$

where the latter form has the desired (easily learned) symmetry.

Special relativity[edit]

As in classical mechanics, in Special Relativity the relative velocity ${vec {v}}_{{mathrm {B|A}}}$ is the velocity of an object or observer B in the rest frame of another object or observer A. However, unlike the case of classical mechanics, in Special Relativity, it is generally not the case that

${vec {v}}_{{mathrm {B|A}}}=-{vec {v}}_{{mathrm {A|B}}}$

This peculiar lack of symmetry is related to Thomas precession and the fact that two successive Lorentz transformations rotate the coordinate system. This rotation has no effect on the magnitude of a vector, and hence relative speed is symmetrical.

$|{vec {v}}_{{mathrm {B|A}}}|=|{vec {v}}_{{mathrm {A|B}}}|=v_{{mathrm {B|A}}}=v_{{mathrm {A|B}}}$

Parallel velocities[edit]

In the case where two objects are traveling in parallel directions, the relativistic formula for relative velocity is similar in form to the formula for addition of relativistic velocities.

${vec {v}}_{{mathrm {B|A}}}={frac {{vec {v}}_{{mathrm {B}}}-{vec {v}}_{{mathrm {A}}}}{1-{frac {{vec {v}}_{{mathrm {A}}}{vec {v}}_{{mathrm {B}}}}{c^{2}}}}}$

The relative speed is given by the formula:

${displaystyle v_{mathrm {B|A} }={frac {left|{vec {v}}_{mathrm {B} }-{vec {v}}_{mathrm {A} }right|}{1-{frac {{vec {v}}_{mathrm {A} }{vec {v}}_{mathrm {B} }}{c^{2}}}}}}$

Perpendicular velocities[edit]

In the case where two objects are traveling in perpendicular directions, the relativistic relative velocity ${vec {v}}_{{mathrm {B|A}}}$ is given by the formula:

${vec {v}}_{{mathrm {B|A}}}={{frac {{vec {v}}_{{mathrm {B}}}}{gamma _{{mathrm {A}}}}}}-{vec {v}}_{{mathrm {A}}}$

where

${displaystyle gamma _{mathrm {A} }={frac {1}{sqrt {1-left({frac {v_{mathrm {A} }}{c}}right)^{2}}}}}$

The relative speed is given by the formula

${displaystyle v_{mathrm {B|A} }={frac {sqrt {c^{4}-left(c^{2}-v_{mathrm {A} }^{2}right)left(c^{2}-v_{mathrm {B} }^{2}right)}}{c}}}$

General case[edit]

The general formula for the relative velocity ${vec {v}}_{{mathrm {B|A}}}$ of an object or observer B in the rest frame of another object or observer A is given by the formula:^[1]

${displaystyle {vec {v}}_{mathrm {B|A} }={frac {1}{gamma _{mathrm {A} }left(1-{frac {{vec {v}}_{mathrm {A} }{vec {v}}_{mathrm {B} }}{c^{2}}}right)}}left[{vec {v}}_{mathrm {B} }-{vec {v}}_{mathrm {A} }+{vec {v}}_{mathrm {A} }(gamma _{mathrm {A} }-1)left({frac {{vec {v}}_{mathrm {A} }cdot {vec {v}}_{mathrm {B} }}{v_{mathrm {A} }^{2}}}-1right)right]}$

where

${displaystyle gamma _{mathrm {A} }={frac {1}{sqrt {1-left({frac {v_{mathrm {A} }}{c}}right)^{2}}}}}$

The relative speed is given by the formula

${displaystyle v_{mathrm {B|A} }={sqrt {1-{frac {left(c^{2}-v_{mathrm {A} }^{2}right)left(c^{2}-v_{mathrm {B} }^{2}right)}{left(c^{2}-{vec {v}}_{mathrm {A} }cdot {vec {v}}_{mathrm {B} }right)^{2}}}}}cdot c}$

Notes[edit]

^ For example, replace the “Man” by a photon traveling at the speed of light.
^ This result is valid if all motion is restricted to the x-axis, but can be easily generalized by replacing the first equation by
^ It is easy to be confused about the minus sign before v, or whether v is defined in the prime or unprimed reference frame. It might help to visualize the fact that if x = vt, then x′ = 0, meaning that a particle that is following the path x = vt is at rest in the primed reference frame.
^ Keep in mind that, due to time dilation, dt = dt′ is valid only in the approximation that the speed is much less than that of light.

References[edit]

^ Fock 1964 The theory of Space Time and Gravitation, retrieved from https://archive.org/details/TheTheoryOfSpaceTimeGravitation

External links[edit]

Relative Motion at HyperPhysics
A Java applet illustrating Relative Velocity, by Andrew Duffy
Relatív mozgás (1)…(3) Relative motion of two train (1)…(3). Videos on the portal FizKapu. (in Hungarian)
Sebességek összegzése Relative tranquility of trout in creek. Video on the portal FizKapu. (in Hungarian)

Источник

Чтобы разобраться в относительности механического движения, зададимся вопросом:

«Мы сейчас, в настоящий момент времени, движемся или находимся в состоянии покоя?»

Ты, конечно же, ответишь, что всё зависит от того, что мы делаем.

Просто сидим на месте или двигаемся куда-нибудь.

Однако это не совсем верно.

Дело в том, что даже когда ты сидишь, стоишь или лежишь на одном и том же месте —

ты всё равно движешься!

Как это понять? Да всё очень просто. Я предполагаю, что ты сейчас находишься на планете Земля, так вот знай: она движется вокруг Солнца, таким образом, и ты движешься вместе с Землёй вокруг Солнца.

Магазины и деревья на улице не стоят на месте? Стоя возле них, мы же видим, что они никуда не движутся. Так движутся или нет?

Со всем разобраться поможет слово «относительно».

Пример:

Если ты находишься в движущемся вагоне поезда, то относительно лампочки этого же поезда ты не движешься, а относительно автомобиля, стоящего возле дома, ты движешься.

Рис. (1). Транспорт

Давайте примем дом за неподвижное тело. Правильно оно называется тело отсчёта. Относительно него стоящие рядом деревья находятся на месте, то есть не движутся. А пролетающие рядом птицы и едущие по дороге автомобили находятся в движении.

Чтобы найти скорость движения одного тела относительно другого, необходимо сложить векторы этих скоростей.

Классический закон сложения скоростей гласит:

скорость тела относительно неподвижной системы отсчёта равна геометрической сумме двух скоростей — скорости тела относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.

Вспомним, как складываются векторы. Пусть это будут векторы скорости

V→1

V→2

Вот они направлены в одну сторону, например, так:

Рис. (2). Векторы скорости, расположенные на параллельных прямых

Для того чтобы их сложить, нужно выстроить их друг за другом.

Это называется сложением векторов по правилу треугольника.

Должно получиться так:

Рис. (3). Векторы скорости друг за другом

В результате сложения таких векторов должен получиться один результирующий.

Покажем его красным цветом. Это вектор

V→

Он получился, когда мы соединили начало первого вектора с концом последнего.

Рис. (4). Вектор, получившийся в результате сложения

Два вектора

V→1

V→2

сложились, и получился один вектор

V→

. Всё просто.

Бывает, что векторы могут быть направлены в разные стороны. Скажем, вот так:

Рис. (5). Векторы направлены в разные стороны, расположены на параллельных прямых

Будем пробовать их складывать по известному правилу — правилу треугольника.

Выстроим векторы друг за другом. Должно получиться примерно так:

Рис. (6). Выстроенные вместе векторы

Снова соединим начало первого вектора с концом последнего.

Чтобы было лучше видно, изобразим результирующий вектор красным цветом.

Рис. (7). Результирующий вектор

Два вектора

V→1

V→2

сложились, и получился один вектор

V→

Может случиться, что векторы лежат не так ровно, а, скажем, под углом (90°) друг к другу.

Например:

Рис. (8). Векторы, перпендикулярные друг другу

Перед нами два вектора —

V→1

V→2

. Как же их сложить?

Снова выстраиваем их друг за другом, чтобы получились стороны треугольника.

Или соединяем начала этих векторов — тогда получится правило параллелограмма.

Рис. (9). Соединённые векторы

Правило треугольника нам уже знакомо. Просто соединяем начало первого вектора с концом последнего.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Результат сложения не зависит от выбранного правила сложения — правила треугольника или правила параллелограмма.

Должен получиться один и тот же вектор

V→

. Изобразим его красным.

Рис. (10). Результирующий вектор по правилу параллелограмма

Теперь можно приступать к решению задач на относительное движение.

Источники:

Рис. (2). Векторы скорости, расположенные на параллельных прямых. © ЯКласс.

Рис. (3). Векторы скорости друг за другом. © ЯКласс.

Источник

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:

s′ = s₁ + s₂

s′ — перемещение МТ относительно НСО, s₁— перемещение МТ относительно ПСО, s₂ — перемещение ПСО относительно НСО.

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Полезные факты

Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ + s₂

Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ – s₂

Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = √(s₁² + s₂²)

Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s₁=0, перемещение s′ = s₂
Если тело движется относительно двух НСО, то его перемещение относительно НСО₁ равно перемещению движения относительно НСО₂. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s₂=0, перемещение s′ = s₁

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

s′=|s₁ – s₂|=|10 – 2|=8 (м).

Относительность скорости в ПСО и НСО

Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:

v′ = v + u

v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Полезные факты

Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v + u

Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v – u

Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = √(v² + u²)

Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u

Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

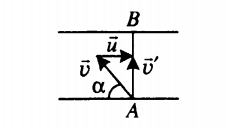
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v_отн= v₁– v₂

v_отн — относительная скорость, или скорость первого тела относительно второго, v₁и v₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

v₁₂ — скорость первого тела относительно второго. Ее проекция равна:

v_12x = v_1x – v_2x

v₂₁ — скорость второго тела относительно первого. Ее проекция равна v_21x = v_2x – v_1x

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Полезные факты

Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:

v_отн = |v₁ – v₂|

Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:

v_отн = |v₁ + v₂|

Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:

v_отн = √(v₁² + v₂²)

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .

Сложение двух сонаправленных векторов
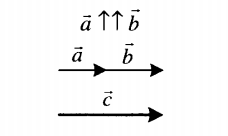	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
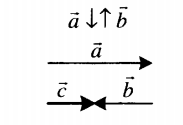	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = \|a – b\|.
Сложение двух векторов, расположенных друг к другу под углом
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
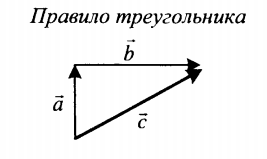	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .

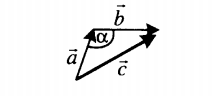	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .
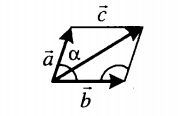	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .

Правила вычитания векторов

Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Вычитание двух сонаправленных векторов
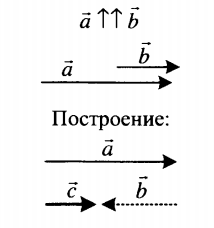	Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = \|a – b\|.
Вычитание двух противоположно направленных векторов
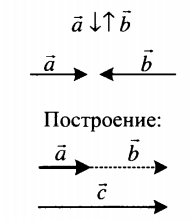	Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b.
Вычитание двух векторов, расположенных друг к другу под углом
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
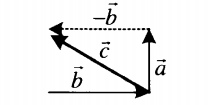	Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: .
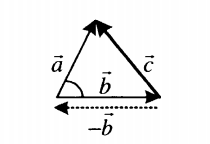	Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: .

Задание EF17727

Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.

Алгоритм решения

Записать данные в определенной системе отсчета.
Изобразить графическую модель ситуации задачи.
Записать классический закон сложения скоростей в векторном виде.
Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
Найти искомую величину.

Решение

Записываем данные относительно Земли:

Скорость первого автомобиля относительно оси ОХ: v₁ = v.
Скорость второго автомобиля относительно оси ОХ: v₂ = –4v.

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v′ = v + u

v′ — скорость второго автомобиля относительно оси ОХ (v₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

v₂ = v + v₁

Отсюда:

v = v₂ — v₁ = –4v – v = –5v

Ответ: -5v

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17518

Два автомобиля движутся в одном направлении. Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?

Алгоритм решения

Записать данные в определенной системе отсчета.
Изобразить графическую модель ситуации задачи.
Записать классический закон сложения скоростей в векторном виде.
Выбрать систему отсчета.
Записать классический закон сложения скоростей в скалярном виде.
Найти искомую величину.

Решение

Записываем данные относительно Земли:

Скорость первого автомобиля относительно неподвижной системы отсчета: v₁ = 110 км/ч;
Скорость второго автомобиля относительно Земли: v₂ = 60 км/ч.

Изображаем графическую модель ситуации:

Записываем закон сложения скоростей в векторном виде:

v′ = v + u

v′ — скорость автомобиля относительно земли (v₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v₂).

По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

v’ = v + u

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

v = v’ – u = v₁– v₂ = 110 – 60 = 50 (км/ч).

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.3k

Источник

Как найти относительную скорость двух тел?

Какова относительная скорость между двумя телами, когда они движутся с одинаковой скоростью в одном направлении?

Какова относительная скорость между двумя телами, когда они движутся с разными скоростями в одном направлении?

Какова будет относительная скорость двух тел, когда они движутся в противоположных направлениях?

Какова относительная скорость, когда два тела движутся под углом?

Важность относительной скорости:

Проблемы, связанные с относительной скоростью:

Резюме:

Classical mechanics[edit]

In one dimension (non-relativistic)[edit]

In two dimensions (non-relativistic)[edit]

Galilean transformation (non-relativistic)[edit]

Special relativity[edit]

Parallel velocities[edit]

Perpendicular velocities[edit]

General case[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

External links[edit]

Относительность перемещения

Относительность скорости в ПСО и НСО

Относительная скорость двух тел

Правила сложения векторов

Правила вычитания векторов

Добавить комментарий Отменить ответ

Как найти относительную скорость двух тел?

Какова относительная скорость между двумя телами, когда они движутся с одинаковой скоростью в одном направлении?

Какова относительная скорость между двумя телами, когда они движутся с разными скоростями в одном направлении?

Какова будет относительная скорость двух тел, когда они движутся в противоположных направлениях?

Какова относительная скорость, когда два тела движутся под углом?

Важность относительной скорости:

Проблемы, связанные с относительной скоростью:

Резюме:

Classical mechanics[edit]

In one dimension (non-relativistic)[edit]

In two dimensions (non-relativistic)[edit]

Galilean transformation (non-relativistic)[edit]

Special relativity[edit]

Parallel velocities[edit]

Perpendicular velocities[edit]

General case[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

External links[edit]

Относительность перемещения

Относительность скорости в ПСО и НСО

Относительная скорость двух тел

Правила сложения векторов

Правила вычитания векторов

Вам также может понравиться

Как найти человека если не помнишь фамилию

Как найти карту миграции на агропроме

Как найти груз на свой камаз

Добавить комментарий Отменить ответ