Как найти отношение скоростей формула

Поучительная задачка на предмет того, насколько мы зашорены и ограничены в мышлении предыдущим опытом решения подобных задач. А также на предмет того, что условие задачи должно должно быть достаточно полным, чтобы позволить однозначно решить задачу.

---

Давйте попробуем начертить план, на котором обозначим точками города А и В, а также положения автомобиля и мотоцикла в начальный момент времени А0 и М0, а моменты времени 1 час и 2 часа, соответственно точками А1 и А2 и М1 и М2.

Очевидно, что точка А0 совпадает сточкой А (обозначением города), а М0 – с точкой В.

Что нам задано однозначно? “Через час автомобиль был посередине между пунктом А и мотоциклом.”.

Т.е. мы можем произвольно поставить точки А0 и М1, соединить их отрезком и на его середине поставить точку А1. Условие “Через час автомобиль был посередине между пунктом А и мотоциклом.” – выполнено. И Всё. Больше нас ничто не ограничивает в наших фантазиях (к условию “Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.” вернёмся чуть позже.

---

Нигде в условии не сказано, что движение автомобиля и мотоцикла прямолинейное и с постоянными скоростями. Ну ладно, можно согласиться, что вопрос “Найти отношение скоростей мотоцикла и автомобиля” предполагает, что величины скоростей остаются постоянными. Но ведь движение может быть и не по прямой. Начертим на нашем плане ЛЮБУЮ кривую линию Любой длины от точки А0 к точке А1. Затем поставим на плане совершенно ПРОИЗВОЛЬНО точку А2 почти в любом месте с единственным ограничением, чтобы длина прямой А1А2 не превышала длины кривой А0А1 (можно измерить курвиметром. Далее, проведём окружность радиусом А0А2 с центром в точке А0 (т.е. в городе А). Теперь, АБСОЛЮТНО В ЛЮБОМ месте этой окружности поставим точку М2. Теперь условие “Еще через час автомобиль и мотоцикл находились на одинаковом расстоянии от пункта А.” тоже выполнено. От точки М1 до точки М2 мы можем нарисовать любую кривую линию. Далее, от точки М1 мы можем нарисовать любую кривую линию той же длины, что и между М2 и М1, и там поставить точку М0 (город В).

Итак, все условия задачи выполнены, и количество решений у нас – насколько хватает фантазии.

---

В большинстве школьных задач на движение молчаливо предполагается (если особо не оговаривается, например при беге по кругу на стадионе), что движение происходит по прямой, хотя ЭТО УСЛОВИЕ ОБЯЗАТЕЛНО НУЖНО ОГОВАРИВАТЬ.

Ну ладно, предположим, что у нас в условии сказано, что движение прямолинейное и с постоянной скоростью. Тогда число вариантов значительно уменьшается, но ещё остаётся бесконечно большим.

Начертим план заново. Чертим отрезок А0М1. На середине его ставим точку А1. откладывая от точки А1 отрезок А1А2, равный отрезку А0А1 приходим к точке А2, в этой ситуации она совпадает с точкой М1. Чертим окружность радиуса А0А2 с центром в точке А0. Точку М2 можно поставить в ЛЮБОЙ точке этой окружности. Далее, через точки М2 и М1 провести прямую, и от точки М1 отложить отрезок М1М0, равный по длине отрезку М2М1. И в этом месте поставить точку В.

---

Итак, даже если бы было оговорено, что движение прямолинейное и всё время в одном направлении, т.е. векторы скоростей не меняются, всё равно получается бесконечное множество решений.

И ТОЛЬКО ЕСЛИ ВВЕСТИ ДОПОЛНИТЕЛЬНОЕ ОГРАНИЧЕНИЕ, ЧТО движение автомобиля и мотоцикла происходит только по прямой, проведённой через точки А и В, то только тогда условие задачи и решение становятся однозначными.

Продолжим радиус А0А2 за точку А0 до пересечения с окружностью. Если точку М2 поставить на этом пересечении, то получится, что за второй час мотоцикл проехал отрезок М1М2, равный диаметру окружности, а автомобиль – отрезок А1А2, равный половине радиуса окружности. Следовательно, скорость мотоцикла в 4 раза выше скорости автомобиля.

А если допустима скорость мотоцикла равная 0, то появляется ещё и второй вариант, когда точки в, А2 М0 М1 и М2 совпадают.

---

Ну, и напоследок, числовая иллюстрация. Скорость автомобиля 20 км/ч, мотоцикла 80 км/ч. Расстояние между городами равно 120 км. За первый час автомобиль проехал по направлению к городу В 20 км (точка А1). Мотоцикл проехал за это время 80 км по направлению к городу А и находился в 40 км от А (точка М1, она же впоследствии А2). За половину второго часа мотоцикл достиг города А, но не остановился и продолжил движение и к концу второго часа оказался на расстоянии 40 км от города А (точка М2) в противоположную от города В сторону. А автомобиль – в точке А2, она же М1 на линии между городами А и В в 40 км от города А и 80 км от города В.

Соотношение скоростей Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Количество зубьев на ведомом: 15 –> Конверсия не требуется
Кол-во зубьев на драйвере: 20 –> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.75 –> Конверсия не требуется

13 Поезда передач Калькуляторы

10+ Коэффициент скорости Калькуляторы

Соотношение скоростей формула

Коэффициент скорости = Количество зубьев на ведомом/Кол-во зубьев на драйвере

i = T_driven/T_driver

Какое соотношение скорости id?

Передаточное число (или отношение скоростей) зубчатой передачи – это отношение скорости водителя к скорости ведомого или ведомого (или) отношение скоростей любой пары шестерен в зацеплении является обратной величине их числа зубьев.

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

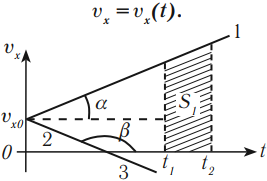
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

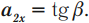
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»