1) Определим
λmax — наибольшее
собственное значение матрицы суждений
А по формуле λmax=
.
см табл.4.
2) Вычислим индекс
согласованности и отношение согласованности.
ИС = (λmax
-n)/(n-1),
где n
– число сравниваемых элементов. Для
обратносимметричной матрицы всегда
λmaxn.
Результаты для 2-го уровня приведены в
табл.4. Величину случайного
индекса (СИ)
для вычисления отношения
согласованности
ОС возьмем из табл.5.
ОС=ИС/СИ при n=8.
Результат в табл.4.
Промежуточная
интерпретация результатов.
Наличие
адекватного финансирования воспринимается
семьей как наиболее важный критерий
при выборе дома. Фактически он почти в
2 раза важнее размеров (0,333 против 0,173) и
намного более важен, чем время постройки,
который имеет низкий приоритет, равный
0,018.
Таблица 4
Покупка дома:
матрица попарных сравнений для уровня
2, решения и согласованность
|
Общее удовлетворение |
Размеры дома |
Удобство автобусных |
Окрестности |
Когда построен |
Двор |
Современное |
Общее состояние |
Финансовые |
Вектор приоритетов |
|
Размеры дома |
1 |
5 |
3 |
7 |
6 |
6 |
1/3 |
1/4 |
0,173 |
|
Удобство автобусных |
1/5 |
1 |
1/3 |
5 |
3 |
3 |
1/5 |
1/7 |
0,054 |
|
Окрестности |
1/3 |
3 |
1 |
6 |
3 |
4 |
6 |
1/5 |
0,188 |
|
Когда построен |
1/7 |
1/5 |
1/6 |
1 |
1/3 |
1/4 |
1/7 |
1/8 |
0,018 |
|
Двор |
1/6 |
1/3 |
1/3 |
3 |
1 |
1/2 |
1/5 |
1/6 |
0,031 |
|
Современное |
1/6 |
1/3 |
1/4 |
4 |
2 |
1 |
1/5 |
1/6 |
0,036 |
|
Общее состояние |
3 |
5 |
1/6 |
7 |
5 |
5 |
1 |
1/2 |
0,167 |
|
Финансовые |
4 |
7 |
5 |
8 |
6 |
6 |
2 |
1 λmax = ИС = ОС = |
0,333 -9,669 0,238 0,169 |
Таблица 5
Таблица средних значений СИ
|
Порядок матрицы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
СИ |
0,00 |
0,00 |
0,58 |
0,9 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
5 шаг. Проведение
синтеза приоритетов
для 3-го уровня иерархии:
получение парных
сравнений для третьего уровня иерархии,
иллюстрирующие сравнительную желательность
домов А, Б и В по отношению к критериям
второго уровня. Получим 8 матриц размером
3х3;
вычисление вектора
приоритетов при n=3;
определение λmax
n=3;
вычисление индекса
согласованности и отношения согласованности.
Результаты
вычислений приведены в табл.6.
7 шаг.
Использовать иерархический синтез для
взвешивания собственных векторов весами
критериев и вычислить сумму по всем
соответствующим взвешенным компонентам
собственных векторов уровня иерархии,
лежащего ниже
Для выявления
составных, или глобальных, приоритетов
домов в матрице локальные приоритеты
располагаются по отношению к каждому
критерию, каждый столбец векторов
умножается на приоритет соответствующего
критерия и результат складывается вдоль
каждой строки. Например, для дома А
имеем:
(0,754х0,173) +(0,233х0,054)+
… +(0,072х0.333)=0,396.
Результаты
представлены в табл.7.
Таблица 6
Покупка
дома: матрицы попарных сравнений для
уровня 3, решения
и
согласованность
|
Размеры дома |
А Б В |
Вектор приоритетов |
Двор |
А Б В |
Вектор приоритетов |
|
А Б В |
1 6 8 1/6 1/8 |
0,754 0,181 0,065 λmax ИС ОС |
А Б В |
1 5 4 1/5 1/4 |
0,674 0,101 0,226 λmax ИС ОС |
|
Удобство автобусных |
А Б В |
Век гор приоритетов |
Современное |
А Б В |
Вектор приоритетов |
|
А Б В |
1 7 1/5 1/7 5 |
0,233 0,005 0.713 λmax ИС= ОС |
А Б В |
1 8 6 1/8 1/6 |
0,747 0,060 0,193 λmax ИС ОС |
|
Окрестности |
А Б В |
Вектор приоритетов |
Общее состояние |
А Б В |
Вектор приоритетов |
|
А Б В |
1 8 6 1/8 1/6 |
0,745 0,065 0,181 λmax ИС ОС |
А Б В |
1 1/2 1/2 2 2 |
0,200 0,400 0,400 λmax ИС ОС |
|
Когда построен |
А Б В |
Вектор приоритетов |
Финансовые |
А Б В |
Вектор приоритетов |
|
А Б В |
1 1 1 1 1 |
0,333 0,333 0,333 λmax ИС ОС |
А Б В |
1 1/7 1/5 7 5 |
0,072 0,650 0,278 λmax ИС ОС |
Таблица 7
Глобальные
приоритеты
|
1 (0,173) |
2 (0,054) |
3 (0,188) |
4 (0,018) |
5 (0,031) |
6 (0,036) |
7 (0,167) |
8 (0,333) |
Обобщенные или |
|
|
А |
0,754 |
0,233 |
0,745 |
0,333 |
0,674 |
0,747 |
0,200 |
0,072 |
0,396 |
|
Б |
0,181 |
0,055 |
0,065 |
0,333 |
0,101 |
0,060 |
0,400 |
0,650 |
0,341 |
|
В |
0,065 |
0,713 |
0,181 |
0,333 |
0,226 |
0,193 |
0,400 |
0,278 |
0,263 |
Выводы:
Дом А, который был наименее желателен
с точки зрения финансовых условий
(критерии с наивысшим приоритетом),
вопреки ожиданию оказался победителем.
Этот дом и был куплен. Семья сделала
выбор безоговорочно.
При анализе можно
убедиться, что исход не был удивительным,
если принять во внимание тот факт, что
дом А превосходил остальные дома по
четырем из семи критериев, по которым
не было ничейных результатов. Пример
также показывает, что следует быть
осторожным, решив исключить из рассмотрения
какие-то критерии после первых вычислений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Общая характеристика метода анализа иерархий.
- Этапы применения метода анализа иерархий.
- Основные понятия метода анализа иерархий.
Общая характеристика метода анализа иерархий
Метод Анализа Иерархий (МАИ) – математический инструмент системного подхода к решению проблем принятия решений. МАИ не предписывает лицу, принимающему решение (ЛПР), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Этот метод разработан американским ученым Томасом Л. Саати в 1970 году, с тех пор он активно развивается и широко используется на практике. Метод анализа иерархий можно применять не только для сравнения объектов, но и для решения более сложных проблем управления, прогнозирования и др.
Основным достоинством метода анализа иерархий является высокая универсальность – метод может применяться для решения самых разнообразных задач: анализа возможных сценариев развития ситуации, распределения ресурсов, составления рейтинга клиентов, принятия кадровых решений и др.
Недостатком метода анализа иерархий является необходимость получения большого объема информации от экспертов. Метод в наибольшей мере подходит для тех случаев, когда основная часть данных основана на предпочтениях лица, принимающего решения, в процессе выбора наилучшего варианта решения из множества существующих альтернатив.
В типичной ситуации принятия решения:
- рассматриваются несколько вариантов решения,
- задан критерий, по которому определяется в какой мере то или иное решение является подходящим,
- известны условия, в которых решается проблема, и причины, влияющие на выбор того или иного решения.
Постановка задачи в процессе применения метода анализа иерархий: Пусть имеется множество альтернатив (вариантов решений): В1, В2, … Вk. Каждая из альтернатив оценивается списком критериев: К1, К2, … Кn. Требуется определить наилучшее решение.
Этапы применения метода анализа иерархий:
1. Предварительное ранжирование критериев, в результате которого они располагаются в порядке убывания важности (значимости).
2. Попарное сравнение критериев по важности по девятибалльной шкале с составлением соответствующей матрицы (таблицы) размера (n х n). Система парных сведений приводит к результату, который может быть представлен в виде обратно симметричной матрицы. Элементом матрицы a(i,j) является интенсивность проявления элемента иерархии i относительно элемента иерархии j, оцениваемая по шкале интенсивности от 1 до 9, где оценки имеют следующий смысл:
- равная важность – 1;
- умеренное превосходство – 3;
- значительное превосходство – 5;
- сильное превосходство – 7;
- очень сильное превосходство – 9;
- в промежуточных случаях ставятся четные оценки: 2, 4, 6, 8 (например, 4 – между умеренным и значительным превосходством).
При этом при проведении попарных сравнений в основном ставятся следующие вопросы при сравнении элементов А и Б:
- какой из них важнее или имеет большее воздействие ?
- какой из них более вероятен?
- какой из них предпочтительнее ?
Затем формируется матрица (схема представлена в Таблице 2). В процессе заполнения матрицы если элемент i важнее элемента j, то клетка (i, j), соответствующая строке i и столбцу j , заполняется целым числом, а клетка (j, i), соответствующая строке j и столбцу i, заполняется обратным числом (дробью).
Например, если К1 умеренно превосходит К4, то в клетку (1;4) (на пересечении первой строки и четвертого столбца) ставится число 3, а в клетку (4;1) (четвертая строка первый столбец) – обратная величина, равная 1/3. Если же элемент j более важен, чем элемент i, то целое число ставится в клетку (j, i), а обратная величина – в клетку (i, j). Если считается, что i, j одинаковы, то в обе клетки ставится единица.
Заполнение таблицы (см.примерная схема в табл.2) проводится построчно с наиболее важного критерия. Сначала проставляют целочисленные оценки, тогда соответствующие им дробные оценки получаются из них автоматически (как обратные к целым числам). Чем важнее критерий, тем больше целочисленных оценок будет в соответствующей ему строке матрицы, и сами оценки имеют большие значения. Так как каждый критерий равен себе по важности, то главная диагональ матрицы всегда будет состоять из единиц. Очевидно, что сумма компонентов равна единице. Каждый компонент НВП представляет собой оценку важности соответствующего критерия (например, 1-й компонент представляет собой оценку важности первого критерия). 

Таблица 1 – Значение показателя случайной согласованности (ПСС)*
| Размер матрицы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ПСС | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
*Примечание:
Показатель Случайной Согласованности (ПСС) Т.Л.Саати называет Случайный индекс (СИ).
Значения ПСС (СИ) см, например, на с.25 Саати Т.Л. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993, на с. 137 Романов В.Н. Системный анализ для инженеров. – СПб.: СЗГЗТУ, 2006.
Оценки в матрице считаются согласованными, если ОС≤10-15%, в противном случае их надо пересматривать.
5. Проводится попарное сравнение вариантов по каждому критерию аналогично тому, как это делалось для критериев, и заполняются соответствующие таблицы (см.ниже – схема представлена в Таблице 3). Для каждой таблицы проводится проверка согласованности локальных приоритетов путем расчета трех характеристик (см.описание 4-го этапа).
6. Определяется общий критерий (приоритет) для каждого варианта:
К(В1) = оценка В1 по первому критерию х 1й компонент НВП + оценка В1 по второму критерию х 2й компонент НВП + … + оценка В1 по nму критерию х nй компонент НВП (6)
Аналогично подсчитываются К(В2), К(В3) и т.д., при этом в выражении В1 заменяется на В2 , В3 и т.д. соответственно. Заполняется таблица (см.ниже – схема представлена в Таблице 4).
7. Определяется наилучшее решение, для которого значение К максимально.
8. Проверяется достоверность решения:
8.1. расчет обобщенного индекса согласования:
ОИС = ИС1 х 1й компонент НВП + ИС2 х 2й компонент НВП + … + ИСnх nй компонент НВП (7)
8.2. расчет обобщенного отношения согласованности:
ООС = ОИС/ ОПСС (8)
где ОПСС определяется по таблице 1 на уровне ПСС (показателя случайной согласованности) для матриц сравнения вариантов по критериям.
Решение считается достоверным, если ООС≤10-15%, в противном случае нужно корректировать матрицы сравнения вариантов по критериям.
Таблица 2 – Форма таблицы сравнения критериев
| К1 | К2 | …. | Кn | Средние геометрические | НВП(по фор-муле (2)) | |
| К1 | ||||||
| К2 | ||||||
| …. | ||||||
| Кn | ||||||
| ИТОГО | по формуле (1) | |||||
| λmax | по форм. (3) | |||||
| ИС | по форм. (4) | |||||
| ОС | по форм. (5) |
Таблица 3 – Форма таблицы сравнения вариантов по критериям (заполняется по каждому j-му критерию сравнения Kj j=1,n)
| Кj | В1 | В2 | …. | Вk | Средние геометрические | НВП(по фор-муле (2)) |
| В1 | ||||||
| В2 | ||||||
| …. | ||||||
| Вk | ||||||
| ИТОГО | по формуле (1) | |||||
| λmaxj | по форм. (3) | |||||
| ИСj | по форм. (4) | |||||
| ОСj | по форм. (5) |
Таблица 4 – Форма таблицы расчета итоговых значений приоритетов
| К1 | К2 | …. | Кn | Итоговые значения приоритетов (расчет по формуле (6)) | |
| приводятся значения 1-го компонента НВП из таблицы 2 | приводятся значения 2-го компонент НВП из таблицы 2 | приводятся значения n-го компонента НВП из таблицы 2 | |||
| В1 | К(В1)= | ||||
| В2 | К(В2)= | ||||
| …. | … | ||||
| Вk | К(В3)= | ||||
| ИС | приводится зна-чение ИС1 по К1 | приводится зна-чение ИС2 по К2 | … | приводится зна-чение ИСn по Кn | приводится сумма по столбцу |
| ОИС | расч. по форм. (7) | ||||
| ООС | расч. по форм. (8) |
Основные понятия метода анализа иерархий
В соответствии с формулировкой задачи принятия решения структура модели принятия решения в методе анализа иерархий представляет собой схему (граф), которая включает:
- набор альтернативных решений,
- главный критерий рейтингования решений,
- набор групп однотипных факторов, влияющих на рейтинг,
- множество направленных связей, указывающих на влияния решений, критерия и факторов друг на друга.
Структура модели отражает результат анализа ситуации принятия решения. Основные группы понятий метода анализа иерархий:
- Первая группа понятий связана с описанием возможных структур моделей принятия решения. Для вычисления приоритетов альтернативных решений к структуре необходимо добавить информацию о силе влияний решений, критерия и факторов друг на друга.
- Вторая группа понятий связана с описанием данных для моделей принятия решения. После того как сформирована структура и собраны все данные, модель принятия решения готова, т.е. в ней могут быть получены рейтинги приоритетов решений и факторов. Знание приоритетов используется для поддержки принятия решения.
- Третья группа понятий связана с описанием результатов, получаемых в моделях принятия решения. Четвертая группа понятий связана с пояснением того, как организованы вычисления. Знание этих понятий необходимо лишь для понимания математических обоснований метода. Для применения метода знание этих понятий необязательно.
1. Cтруктуры
1.1) Узел – общее название для всех возможных решений (альтернатив), главного критерия (главной цели) рейтингования решений, всех факторов, от которых, так или иначе, зависит рейтинг. Название узла совпадает с названием соответствующего решения, критерия или фактора. Заметим, что с математической точки зрения схема ситуации принятия решения (структура модели), которая строится в методе анализа иерархий, является графом. Таким образом, понятие «узел» вполне оправдано. Ясно также, что решения, критерий и факторы являются «узлами» проблемы принятия решения.
1.2) Уровень – группа всех однотипных (равноправных, однородных, гомогенных и т.п.) узлов. Название уровня отражает назначения, функцию группы узлов в ситуации принятия решения. Каждый узел определяется не только своим названием, но и названием уровня, которому он принадлежит. Ясно, что отдельный уровень образуют альтернативные решения (узлы этого уровня однотипны в том смысле, что они являются решениями; прочие узлы таковыми не являются). Главный критерий рейтингования, как правило, один – это отдельный уровень. На рейтинг оказывают влияние несколько групп факторов – это также уровни.
1.3) Вершина – узел, соответствующий главному критерию (главной цели) отбора альтернатив.
1.4) Связь – указание на наличие влияния одного узла (доминирующего) на другой (подчиненный). На схеме связь изображается стрелкой. Направление связи (и соответствующей стрелки) совпадает с направлением влияния. С точки зрения теории графов связь – дуга направленного графа. Связь от узла-фактора к узлу-решению означает, что предпочтительность (важность, оптимальность) решения оценивается с точки зрения воздействия данного фактора. Связь от вершины к узлу-фактору означает, что важность учета фактора оценивается с точки зрения главного критерия рейтингования альтернатив. Связь от узла-фактора к узлу-фактору означает, что важность учета второго фактора рассматривается с точки зрения первого фактора.
1.5) Кластер – группа узлов одного уровня, подчиненных некоторому узлу другого уровня –вершине кластера (доминирующему узлу). Кластеры образуются при расстановке связей между узлами, т.е. при расстановке связей происходит формирование кластерной структурыAdvice_KlasterStruct. Важность узлов кластера друг относительно друга оценивается в соответствие с тем, какой узел является вершиной кластера.
Кластер определяется: 1) своей вершиной, 2) названием уровня, 3) списком узлов. 1.6) Система (структура модели, схема ситуации принятия решения) – совокупность всех узлов, сгруппированных по уровням, и всех связей между узлами.
С математической точки зрения системы, которыми приходится оперировать в методе анализа иерархий, являются – направленными графами (сетями). Связи образуют пути, ведущие от одних узлов к другим. Все пути так или иначе являются частями основных путей, ведущих от главного критерия рейтингования через факторы к альтернативам, т.е. основные пути, по сути, являются логическими цепочками, ведущими к выбору одной из альтернатив.
Эта система является иерархической (но не является строгой иерархией). Попутно заметим, что даже для простых задач структуры моделей, строящихся с помощью метода анализа иерархий, представляют собой довольно сложные схемы. Однако это свидетельствует лишь о том, что метод позволяет вскрыть реальную сложность задач, которые человеку приходится решать мысленно. Название системы отражает ее назначение, принадлежность к сфере деятельности, в которой принимается решение.
1.7) Иерархия – система, в которой уровни расположены и пронумерованы так, что: 1) нижний уровень содержит рейтингуемые альтернативы, 2) узлы уровней с большими номерами могут доминировать только над узлами уровней с меньшими номерами. Таким образом, в иерархии связи определяют пути одной направленности — от вершины к альтернативам через промежуточные уровни, которые состоят из узлов-факторов. Система представляет собой строгую иерархию, если допустимы связи только между соседними уровнями от верхнего уровня к нижнему.
1.8) Система с обратными связями. Система имеет обратные связи, если при любом способе нумерации уровней в системе есть узлы, доминирующие и над узлами уровней с большими номерами, и над узлами уровней с меньшими номерами, т .е. система имеет обратные связи, если ни при каких перестановках уровней она не сводится к иерархии. Кроме того, понять различия в структуре иерархии и системы с обратными связями можно, рассматривая пути, образованные связями.
Если в системе нет ни одного такого уровня, что по путям, начинающимся в узлах этого уровня, можно попасть в узлы того же уровня, то система является иерархией, т.е. в иерархии любой путь может пересекаться с каждым уровнем лишь однажды. Если в системе имеются такие уровни, что по пути, начинающемуся в одном из узлов этого уровня, можно попасть в один из узлов того же уровня, то система имеет обратные связи. Т.е. в системе с обратными связями обязательно есть пути, пересекающие некоторые уровни хотя бы дважды. Формирование структуры без обратных связей (иерархии) и формирование структуры с обратными связями производятся по определенным правилам.
2. Данные
2.1) Приоритет узла в кластере – положительное число, служащее для количественного выражения важности (веса, значимости, предпочтительности и т.п.) данного узла в кластере относительно остальных узлов кластера в соответствие с критерием, заключенным в вершине кластера. Сумма всех приоритетов узлов кластера равна единице. Поэтому часто приоритеты можно трактовать как вероятности, доли общего ресурса и т.п. в зависимости от рассматриваемого случая.Часто трудно непосредственно определить набор приоритетов (вектор приоритетов) узлов кластера. Тогда используется процедура парных сравнений и метод собственного вектора
2.2) Пaрные сравнения узлов кластера – оценки (качественные или количественные) отношения приоритета одного узла к приоритету другого, т.е. результаты парных сравнений – это оценки важности (предпочтительности, вероятности и т.п.) каждого узла кластера относительно каждого из других по критерию, заключенному в вершине кластера. Результат парного сравнения – оценка отношения «весов» сравниваемых объектов («веса» объектов численно выражают их предпочтительность, оптимальность, значимость и т.п.). Цель парных сравнений – определение приоритетов узлов кластера. Для того, чтобы уточнить, в каком смысле название вершины кластера является критерием для проведения сравнений используется формулировка критерия для парных сравнений. Для проведения парных сравнений задаются параметры: шкала сравнений и способ сравнений. При проведении парного сравнения объектов и достаточно установить только один из результатов (оценка отношения «веса» объекта и весу объекта ) или , так как .
2.3) Шкала сравнений – упорядоченный набор градаций (терминов, чисел и т.п.) для выражения результатов парных сравнений. Шкала сравнений позволяет выражать оценки отношений значений приоритетов узлов, поэтому ее деления – безразмерные величины. Шкалы, использующиеся в методе анализа иерархий, являются шкалами отношений. Т.е. если результату сравнения пары объектов ставится в соответствие значение на шкале, то число — оценка отношения «весов» объектов («веса» объектов численно выражают их предпочтительность, оптимальность, значимость и т.п.)
Шкала является количественной, если результаты парных сравнений выражаются непосредственно с помощью чисел. Шкала является качественной, если результаты парных сравнений выражаются с помощью с градаций-предпочтений. Градациям качественных шкал, использующихся в методе анализа иерархий, соответствуют числа.Т.е. качественные шкалы предоставляют возможность опосредованного оценивания приоритетов через предпочтения.
Дискретная шкала имеет конечных набор градаций (при переходе от одной градации к другой значение парного сравнения изменяется скачком). Дискретной шкале соответствует конечный набор чисел. Дискретные шкалы отличаются по величине наибольшего значения (при количественных сравнениях) или по количеству основных градаций (при качественных сравнениях).
Если число — верхний предел шкалы, то — нижний предел шкалы, т.е. все результаты парных сравнений, выраженные в такой шкале, лежат в пределах от до . Если результату сравнения пары объектов соответствует единица, то значения «весов» объектов оцениваются как равные. Кроме того, для дискретной шкалы — количество градаций для выражения превосходства одного из сравниваемых объектов над другим. При этом дискретная шкала имеет градации . В качестве градаций непрерывной шкалы может использоваться любое из действительных чисел от до .
Непрерывная шкала имеет непрерывный набор градаций (между основными делениями шкалы есть всевозможные промежуточные). Градациям непрерывной шкалы соответствуют числа на отрезке числовой прямой. Непрерывные шкалы отличаются по величине наибольшего значения (при количественных сравнениях) или по количеству основных градаций (при качественных сравнениях). Если «вес» объекта оценивается как превышающий «вес» объекта , результату парного сравнения объектов и соответствует значение на шкале, большее единицы. В противном случае лежит на шкале слева от единицы. В соответствии с этим правилом осуществляется и перевод градаций качественных шкал в числовые значения.
2.4) Способ сравнений определяется набором парных сравнений, необходимых для определения приоритетов узлов кластера. При сравнениях с эталоном (по Стивенсу) выбирается один из узлов кластера, с которым сравниваются все остальные. При проведении классических сравнений (по Саати) каждый узел кластера сравнивается со всеми остальными узлами кластера.
2.5) Сравнения кластеров — процедура оценки важности (приоритетности, силы подчинения) кластеров, имеющих общую вершину.Кластеры сравниваются друг с другом по критерию, заданному названием их вершины. Для проведения сравнений используется та же методика, что и для сравнений узлов в кластере. Фактически при сравнении кластеров, подчиненных одному узлу, производится рейтингование уровней по критерию, определяемому этим узлом.
2.6) Матрица сравнений – таблица числовых значений парных сравнений (для узлов кластера или для кластеров, имеющих общую вершину).
2.7) Индекс согласованности – количественная оценка противоречивости результатов сравнений (для системы в целом, для узлов одного кластера или для кластеров, имеющих общую вершину). Следует иметь в виду, что между достоверностью и непротиворечивостью сравнений нет явной связи. Противоречия в сравнениях возникают из-за субъективных ошибок экспертов. Индекс согласованности не зависит от шкал сравнений, но зависит от количества парных сравнений. Индекс согласованности – положительное число. Чем меньше противоречий в сравнениях, тем меньше значение индекса согласованности. При использовании способа сравнений с эталоном значение индекса согласованности равно нулю.
2.8) Достоверность результата сравнения – количественной оценка, характеризующая степень неточности (размытости) результата сравнения, связанная с компетентностью эксперта, уровнем доверия к данным и т.п. Достоверность сравнения выражается долей единицы (или в процентах). Нулю соответствуют абсолютно недостоверные сравнения, единице (или 100%) – абсолютно достоверные сравнения. На основе значений достоверности сравнений для кластеров, имеющих общую вершину, и значений достоверности парных сравнений в кластерах определяется достоверность данных в масштабах всей системы.
2.9) Относительная согласованность матрицы сравнений– отношение индекса согласованности к среднестатистическому значению индекса согласованности при случайном выборе коэффициентов матрицы сравнений. Относительная согласованность для системы в целом характеризует взвешенное среднее значение относительной согласованности по всем матрицам сравнений. Данные можно считать практически непротиворечивыми (достаточно согласованными), если значение относительной согласованности меньше чем 0,1. Это заключение справедливо как для данных кластера, так и для данных в масштабе всей системы.
2.10) Идеальные сравнения – наиболее близкие к имеющимся непротиворечивые результаты сравнений. Идеальным сравнениям соответствуют нулевой индекс согласованности и, соответственно, нулевое значение относительной согласованности. Знание идеальных сравнений используется при проведении процедуры согласования для кластеров, позволяющей скорректировать сравнения для уменьшения их противоречивости.
2.11) Наиболее противоречивые сравнения – это результаты нескольких парных сравнений узлов одного кластера или кластеров, имеющих общую вершину, вносящие наибольший вклад в значение относительной согласованности.
3. Результаты
3.1) Итоговый вектор приоритетов – рейтинг альтернатив. Каждой альтернативе (каждому возможному решению) ставится в соответствие положительное число – приоритет. Приоритет количественно выражает важность (предпочтительность, вероятность, оптимальность и т.п.) альтернативы в соответствии с главным критерием. Сумма приоритетов всех альтернатив равна единице. Вследствие этого часто допустимо отождествление приоритетов с вероятностями. Для поддержки принятия решения в основном с помощью итогового вектора приоритетов производится интерпретация результатов применения метода. Например, принимается решение с наибольшим приоритетом, отвергается решение с наименьшим приоритетом и т.п.
3.2) Вектор приоритетов уровня – рейтинг узлов данного уровня. Вектор приоритетов уровня вычисляется в предположении, что узлы данного уровня являются альтернативами. Все уровни, кроме тех, что содержат альтернативы и главный критерий рейтингования альтернатив, состоят из факторов, влияющих на итоговый вектор приоритетов. Таким образом, приоритеты узлов-факторов количественно характеризуют важность учета каждого фактора относительно других факторов того же уровня. При вычислении вектора приоритетов уровня рассматриваются только такие пути, образованные связями, которые ведут от вершины к узлам данного уровня. Приоритет узла в системе – это соответствующая компонента вектора приоритетов уровня, которому принадлежит данный узел.
3.3) Вектор приоритетов кластера – рейтинг узлов кластера. Вектор приоритетов узлов кластера может задаваться напрямую (без проведения сравнений) или рассчитываться на основе матрицы сравнений.
3.4) Показатели согласованности и достоверности для системы в целом, характеризующие качество данных, использованных для вычисления векторов приоритетов, также являются результатами. Величины этих показателей позволяют оценить степень доверия к результатам, полученным с помощью метода анализа иерархий. Знание показателей согласованности позволяет решать промежуточную задачу выявления участков проблемы, по которым имеется наиболее противоречивая информация. Решение такой задачи позволяет сделать сбор и корректировку данных более целенаправленными.
3.5) Устойчивость вектора приоритетов – качественная характеристика чувствительности значений приоритетов к малым изменениям данных или структуры модели. Очевидно, данные, использующиеся для принятия решений, всегда более или менее неточны. Поэтому чем меньше чувствительность значений приоритетов, тем больше обоснованность использования этих приоритетов для поддержки принятия решения. В зависимости от решаемой задачи определяется понятие «существенное изменение рейтинга» (смена лидера, смена аутсайдера и т.п.). Если при малых изменениях данных или структуры рейтинг изменяется несущественно, то он считается устойчивым.
3.6) Существенные элементы структуры – это узлы или связи между узлами, удаление которых приводит к существенному изменению рейтинга. Очевидно, заранее бывает чрезвычайно сложно определить, какие факторы являются определяющими для принятия решения, а какими можно пренебречь. Часто при принятии решений происходит упрощение ситуации (отбрасывание ряда факторов) или делается попытка учесть максимально возможное количество факторов. Поэтому поиск существенных факторов является важной самостоятельной задачей в процессе подготовки принятия решения.
3.7) Приоритет узла в модели – соответствующая компонента вектора приоритетов уровня, которому принадлежит данный узел. Допустим, в решаемой задаче близость приоритета к единице (к нулю) ассоциируется с предпочтительностью оптимальностью и т.п. Тогда, как правило, узлы с малыми (с большими) приоритетами оказываются несущественными.
3.8) Приоритет кластера в модели. Если некоторый узел является вершиной только одного кластера, то приоритет кластера в модели совпадает с приоритетом его вершины. (В модели, структура которой является строгой иерархией, так определяется приоритет для каждого кластера.) Если некоторый узел является вершиной нескольких кластеров, то для них устанавливаются приоритеты относительно общей вершины. Приоритет каждого из таких кластеров определяется как произведение приоритета относительно вершины на приоритет узла-вершины в модели.
Источники по процедуре применения Метода анализа иерархий
- Саати Т.Л. Принятие решений. Метод анализа иерархий. – М.: Радио и связь, 1993.
- Саати Т.Л. Принятие решений при зависимостях и обратных свя-зях: аналитические сети. – М.: Либроком, 2009.
- Гудков П.А. Методы сравнительного анализа. Учеб. пособие. – Пенза: Изд-во Пенз. гос. ун-та, 2008.
- Романов В.Н. Системный анализ для инженеров. – СПб.: СЗГЗТУ, 2006.
Это 4-я статья цикла по разработке, управляемой моделями. В предыдущих статьях мы познакомились с OCL и метамоделями, Eclipse Modeling Framework и Sirius. Сегодня научимся описывать метамодели в текстовой нотации (а не в виде диаграмм как раньше) и познакомимся с табличным представлением моделей в Sirius. Сделаем это на примере кризиса среднего возраста и метода анализа иерархий. Возможно, это пригодится вам при разработке ИИ в играх, при принятии решений или в работе.
Введение
Вообще, я планировал статью про разработку DSL и преобразование моделей. Но мои планы внезапно нарушили мысли о смысле жизни, о том, тем ли я вообще занимаюсь.
Самое очевидное, что может при этом сделать специалист по разработке, управляемой моделями, это
- Выбрать метод, который позволит получить интересующие ответы (раздел 1)
- Создать метамодель под этот метод (раздел 2)
- Создать инструмент разработки моделей в соответствии с метамоделью (раздел 3)
- Создать модель (раздел 4)
- …
- Profit
Именно этим мы и займемся.
Прмечание
Если вам интересен метод анализа иерархий, но вы не хотите разбираться в метамоделях и т.п., то тут доступен Excel-калькулятор приоритетов.
1 Метод анализа иерархий
Меня интересовали следующие вопросы:
- Чем мне интересно заниматься?
- Достаточно ли времени я уделяю интересным вещам?
- Что можно изменить в жизни к лучшему?
- Не станет ли от этих изменений хуже?
- …
Когда я учился в вузе, для получения ответов на разные вопросы мы использовали метод анализа иерархий. Суть метода следующая.
- Вы определяете
- цель,
- критерии достижения цели и
- возможные альтернативы.
- Оцениваете значимость критериев.
- Оцениваете альтернативы по каждому из критериев.
- Рассчитываете приоритеты альтернатив.
- Принимаете решение.
Более подробно этот метод описан в книге Томаса Саати «Принятие решений. Метод анализа иерархий» (она легко гуглится). Кстати, в ней много примеров от психологии до мировой экономики.
1.1 Построение иерархии
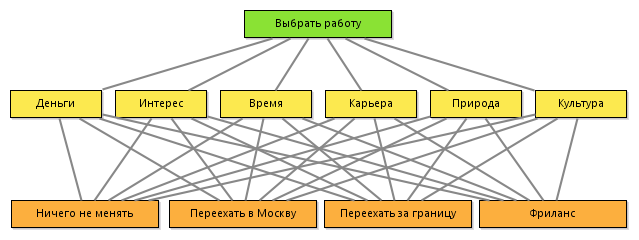
Итак, в простейшем случае иерархия должна содержать цель, критерии и альтернативы.
Если суммировать все мои вопросы, то, по большому счету, меня интересует стоит ли мне сменить работу. Поэтому цель: выбрать работу.
При выборе работы меня интересует
- сколько денег я буду зарабатывать,
- на сколько интересно мне будет этим заниматься,
- будет ли у меня время на жизнь,
- карьерные перспективы,
- смогу ли я бывать на природе или буду видеть солнце и деревья раз в год,
- на сколько близка мне культура коллег, соседей и остальных людей.
При этом возможны следующие альтернативы:
- ничего не менять,
- переехать в Москву,
- переехать за границу,
- заняться фрилансом или каким-нибудь предпринимательством.
В соответствии с методом анализа иерархий строится следующая иерархия:
1.2 Оценка критериев
У разных людей при принятии решений могут быть примерно одинаковые критерии. Однако, их значимость может сильно различаться. Кто-то работает в большей степени ради денег, кто-то ради интереса, кому-то просто нравится общаться с коллегами и т.д.
В соответствии со своими приоритетами один человек не раздумывая выберет более денежную работу, а другой – более интересную. Не существует работы, которая по всем критериям подходит абсолютно всем.
Наверное, при принятии решений большинство людей в явной или неявной форме ранжируют критерии от самого значимого до самого незначительного. Последние отбрасывают, а по первым сравнивают возможные альтернативы. На каждую возможную работу они навешивают ярлычок: вот, эта работа более денежная, но не интересная, а эта интересная и коллектив там хороший, но сомнительные карьерные перспективы и т.д.
Если сходу не получается сделать выбор, то человек начинает переоценивать критерии: может быть интерес пока не так важен и в пробке можно лишние два часа постоять, зато там больше зарплата, вот, выплачу ипотеку и займусь чем-то интересным.
Подобные рассуждения могут продолжаться долго, мучительно и без гарантии, что в итоге действительно будет принято оптимальное решение.
В методе анализа иерархий предлагается формальный алгоритм принятия подобных решений: все критерии попарно сравниваются друг с другом по шкале от 1 до 9.
Например, что для меня важнее: интерес или деньги? Интерес важнее, но не сказать, что очень сильно. Если максимальная оценка 9 к 1, то для себя я оцениваю приоритеты как 5 к 1.
Или, например, что важнее: деньги или наличие времени для жизни, хобби? Готов ли я ради дополнительных денег работать в выходные или стоять по два часа в пробках? Я для себя оцениваю значимость этих критериев как 1 к 7.
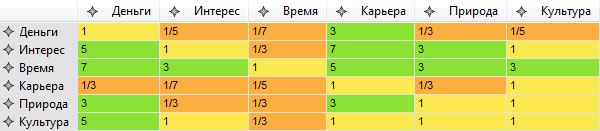
В итоге заполняется подобная таблица:
Очевидно, что по диагонали всегда будут единицы. Также очевидно, что все оценки будут обратно-симметричны относительно главной диагонали. Например, если я оцениваю значимость «интерес-деньги» как 5 к 1, то значимость «деньги-интерес» будет 1 к 5. Иногда такие матрицы называют обратно-симметричными.
В общем случае, если мы сравниваем N критериев, то необходимо сделать (N*(N-1))/2 сравнений. Казалось бы, всё только усложнилось. Если изначально было 6 критериев, то сейчас целая матрица каких-то чисел. Чтобы снова вернуться к критериям, рассчитаем собственный вектор матрицы. Элементы этого вектора и будут относительной значимостью каждого критерия.
В книге Томаса Саати предлагается несколько упрощенных методов расчета собственного вектора в уме или на бумаге. Мы воспользуемся более точным итеративным алгоритмом:
N = количество критериев
m = матрица оценок размерностью NxN
eigenvector = вектор размерностью N, заполненный значениями 1/N
Повторяем пока eigenvalue не начнет сходиться к определенному значению
или пока не сделаем максимально допустимое количество итераций
x = m * eigenvector
eigenvalue = sum(x)
eigenvector = x / eigenvalue
В итоге получаем следующий вектор:
[ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ]
Наиболее значимый критерий – время (0,3846), наименее значимый – карьера (0,0555).
При парных сравнениях некоторые оценки могут получиться несогласованными. Например, для меня интерес важнее денег, а деньги важнее карьеры. Очевидно, что интерес должен быть существенно важнее карьеры. В данной таблице так и есть. Но если бы оценка для «интерес-карьера» была меньшей или вообще обратной, то мои оценки были бы не согласованы между собой.
Оценить меру этой несогласованности поможет собственное значение матрицы сравнений. Оно равно 6,7048.
Очевидно, что собственное значение пропорционально количеству критериев. Чтобы оценка согласованности не зависела от количества критериев, рассчитывается так называемый индекс согласованности = (собственное значение — N) / (N — 1).
Наконец, чтобы оценка была совсем объективной необходимо разделить данный индекс на усредненный индекс согласованности для случайных матриц. Если полученная величина (отношение согласованности) меньше 0,1000, то парные сравнения можно считать более-менее согласованными. В нашем примере оно равно 0,1137, это значит, что рассчитанным приоритетам можно более-менее доверять.
1.3 Оценка альтернатив
Теперь необходимо сравнить все альтернативы по каждому из критериев.
Например, при переезде в Москву я существенно выиграю в зарплате. Но работа, скорее всего, будет менее интересная, а также будет оставаться меньше времени для жизни. Или при переезде за границу мне придется отказаться от своего языка, подстраиваться под чужие культурные ценности.
По каждому критерию рассчитывается собственный вектор и отношение согласованности.
Полученные собственные векторы записаны в столбцах:
Отношения согласованности по каждому критерию записаны в следующем векторе:
[ 0,0337; 0,0211; 0,1012; 0,1399; 0,1270; 0,9507 ]
Большинство значений меньше или незначительно превышают 0,1000. Однако для критерия «культура» отношение согласованности получилось очень большое. Это связано с тем, что я неправильно расставил часть оценок. Хотел поставить 7 для «ничего не менять – переехать за границу», потому что жить в родном городе гораздо комфортнее. Но по ошибке поставил 1/7.
1.4 Определение приоритетов альтернатив
Итак, мы оценили критерии, навесили на каждую альтернативу ярлычок: какой вариант более денежный, какой более интересный и т.д. Теперь необходимо оценить альтернативы по всем критериям в сумме. Для этого достаточно умножить матрицу
на вектор
[ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ]
В итоге мы получим следующий вектор:
[ 0,3184; 0,1227; 0,2049; 0,3540 ]
Это и есть значимости альтернатив относительно достижения цели.
1.5 Принятие решения
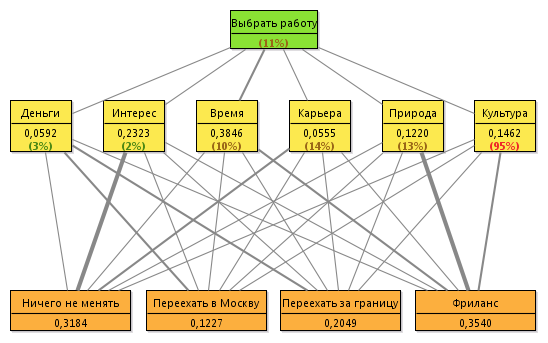
Теперь изобразим все рассчитанные значения на следующем рисунке:
В скобках указано отношение согласованности оценок.
Толщина линий пропорциональна приоритетам. Наиболее интересна и перспективна в плане карьеры текущая работа. Фриланс позволил бы больше бывать на природе и больше времени тратить на жизнь. Более денежная работа в Москве и заграницей.
Видно, что Москва совсем отпадает. Заграница чуть лучше, но тоже не очень. Ничего не менять и фриланс примерно на одном уровне.
2 Создание метамодели
Теперь опишем как всё это рисуется и считается.
Сначала необходимо описать метамодель: виды сущностей, которые используются в методе анализа иерархий. Причем, в отличие от предыдущей статьи мы не будем рисовать метамодель в виде диаграммы, а опишем её в текстовой нотации Xcore.
Как и раньше понадобится Eclipse Modeling Tools. Установите Xcore и Sirius.
Вы можете взять либо готовый проект, либо сделать всё самостоятельно. Если самостоятельно, то создайте Xcore-проект. В папке model создайте файл ahp.xcore со следующим содержимым:
@Ecore(nsURI="http://www.example.org/ahp")
@GenModel(
modelName="AHP",
prefix="AHP",
editDirectory="/xctest.edit/src-gen",
editorDirectory="/xctest.editor/src-gen",
testsDirectory="/xctest.tests/src-gen")
package ahp
class Hierarchy
{
contains Goal[1] goal
contains Criterion[+] criteria
contains Alternative[2..*] alternatives
}
interface Named
{
String[1] name
}
class Goal extends Named { }
class Criterion extends Named { }
class Alternative extends Named { }
Смысл должен быть интуитивно понятен. Мы описали иерархию, которая содержит одну цель, хотя бы один критерий, две или более альтернативы. У всех трёх сущностей есть имя.
После сохранения файла автоматически сформируется Java API для работы с иерархиями в папке src-gen. А также будут созданы 3 дополнительных проекта. Нечто подобное мы уже делали в статье про EMF. Только там было две модели (ecore и genmodel), и генерацию кода мы запускали вручную. Xcore делает это автоматически.
Думаю, что описывать всю метамодель в статье нет смысла, вы можете посмотреть её самостоятельно.
Остановимся только на самых интересных вещах. Xcore в отличие от Ecore позволяет описывать не только структуру модели, но и некоторую логику на Java-подобном языке. Опишем, например, тип данных для хранения оценок. Положительные оценки будем хранить в виде положительных целых чисел. А обратные оценки вида 1/n будем хранить как -n. Мы могли бы хранить оценки в виде строк или в виде действительных чисел, но, наверное, это плохая идея.
При этом нам нужны две функции для преобразования оценок из или в строковое представление. На Xcore это будет выглядеть так:
type Weight wraps int
create
{
if (it.matches("\d+")) {
Integer.parseInt(it)
}
else if (it.matches("1\s*/\s*\d+")) {
val result = Integer.parseInt(it.replaceFirst("1\s*/\s*", ""))
if (result <= 1) 1 else -result
}
else {
throw new NumberFormatException("The weight must be either n or 1/n")
}
}
convert
{
if (it >= 1) {
it.toString
}
else if (it >= -1) {
"1"
}
else {
"1/" + (-it).toString
}
}
Xcore позволяет описывать также и относительно сложную логику.
Вот, например, операция расчета приоритетов в иерархии.
class Hierarchy
{
op void updatePriorities()
{
priorities.clear
inconsistencies.clear
val mat = new JudgmentMatrix<Criterion>(criteria)
val criteriaJudgments = judgments.filter(typeof(CriterionJudgment)).filter(cj | cj.goal == goal)
for (judgment : criteriaJudgments) {
mat.set(judgment.first, judgment.second, judgment.weight)
}
for (criterion : criteria) {
val GoalCriterionPriority priority = AHPFactory.eINSTANCE.createGoalCriterionPriority
priority.goal = goal
priority.criterion = criterion
priority.value = mat.findEigenvectorElement(criterion)
priorities.add(priority)
}
val goalInconsistency = AHPFactory.eINSTANCE.createGoalInconsistency
goalInconsistency.goal = goal
goalInconsistency.value = mat.inconsistency
inconsistencies.add(goalInconsistency)
val mat2 = new Matrix(alternatives.size, criteria.size)
criteria.forEach[criterion, j|
val mat3 = new JudgmentMatrix<Alternative>(alternatives)
val alternativeJudgments = judgments.filter(typeof(AlternativeJudgment)).filter(aj | aj.criterion == criterion)
for (judgment : alternativeJudgments) {
mat3.set(judgment.first, judgment.second, judgment.weight)
}
val criterionInconsistency = AHPFactory.eINSTANCE.createCriterionInconsistency
criterionInconsistency.criterion = criterion
criterionInconsistency.value = mat3.inconsistency
inconsistencies.add(criterionInconsistency)
alternatives.forEach[alternative, i|
val CriterionAlternativePriority priority = AHPFactory.eINSTANCE.createCriterionAlternativePriority
priority.criterion = criterion
priority.alternative = alternative
priority.value = mat3.findEigenvectorElement(alternative)
priorities.add(priority)
mat2.set(i, j, priority.value)
]
]
val mat4 = mat2.multiply(mat.eigenvector)
alternatives.forEach[alternative, i|
val GoalAlternativePriority priority = AHPFactory.eINSTANCE.createGoalAlternativePriority
priority.goal = goal
priority.alternative = alternative
priority.value = mat4.get(i)
priorities.add(priority)
]
}
}
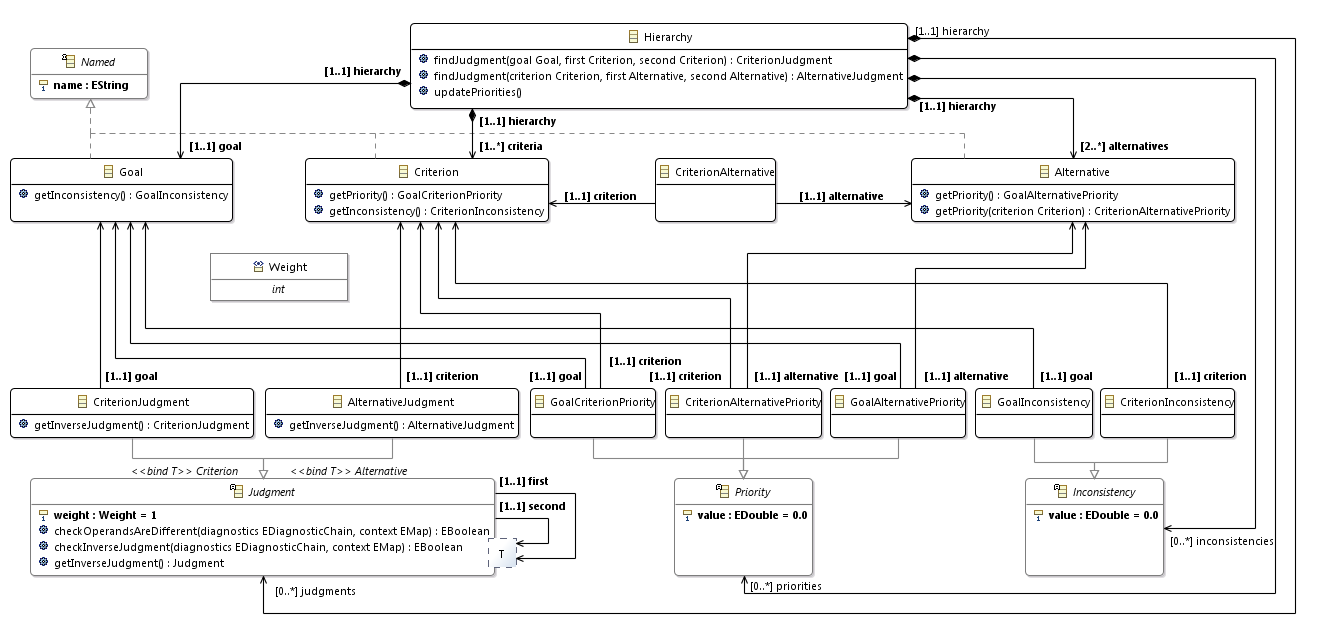
Наконец, для Xcore-модели (как и для Ecore-модели) вы можете создать диаграмму классов.
Так выглядит метамодель для метода анализа иерархий. Это максимально упрощенный вариант. А в общем случае, иерархия может содержать более трех уровней (например, у критериев могут быть подкритерии). Матрицы связей между уровнями могут быть разреженными. Оценки могут ставить несколько экспертов, а не один.
3 Разработка инструмента для работы с моделями
Метамодель готова, теперь нужен редактор иерархий и матриц. Наверное, нет смысла подробно описывать как всё это сделано. Если вам это интересно, то можете прочитать предыдущую статью про Sirius и посмотреть готовый проект.
Так выглядит спецификация редактора диаграмм и таблиц:
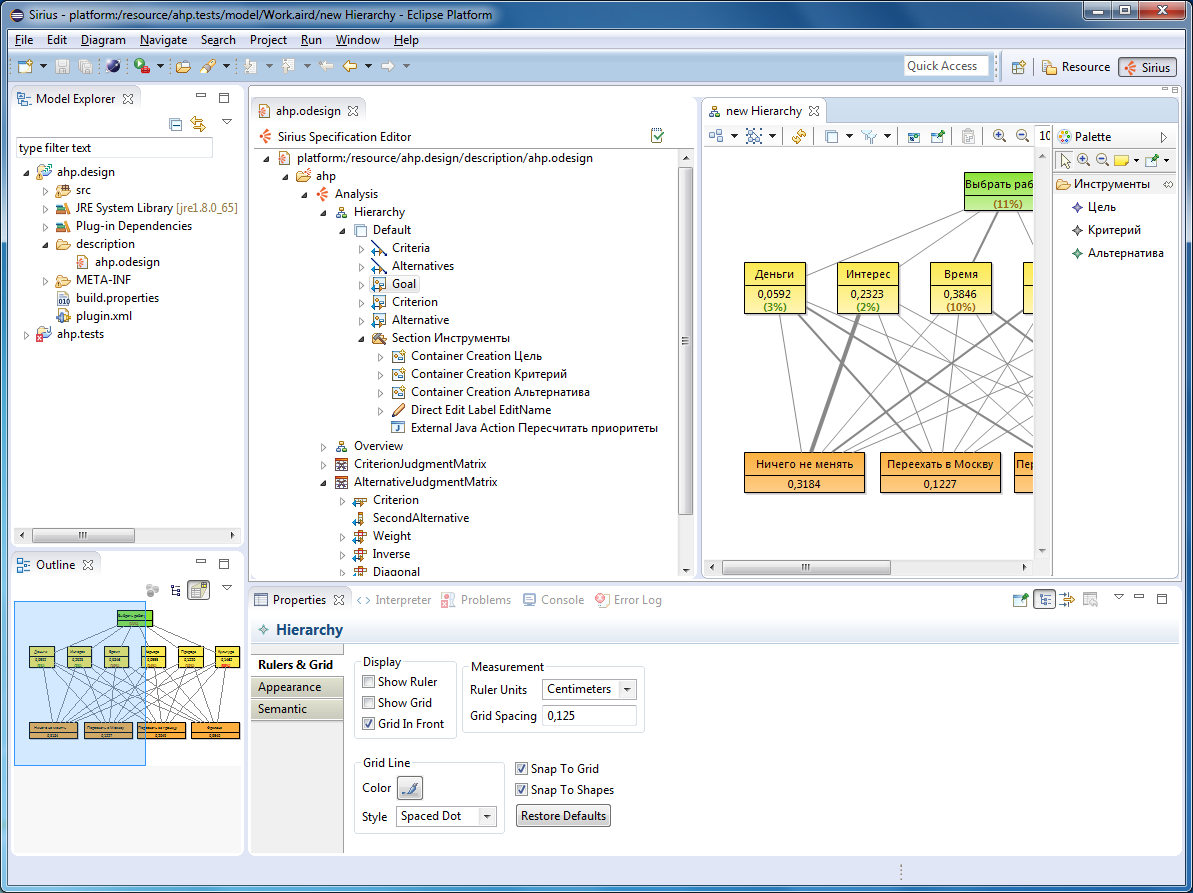
Так выглядит результирующий редактор:
Совсем декларативно описать редактор иерархий не получилось, пришлось писать расширения на Java. Думаю, стоит остановиться на этом немного подробней. В Sirius есть по крайней мере два варианта расширений: службы (service) и действия (action).
С помощью служб вы можете добавить классам из метамодели некоторые дополнительные операции. Например, следующие две операции соответственно форматируют приоритет и рассчитывают толщину связей между критериями и альтернативами.
public class Service {
public String toString(Priority priority) {
return String.format("%.4f", priority.getValue());
}
public int getEdgeWidth(Alternative alternative, EdgeTarget targetView) {
DSemanticDecorator targetNode = (DSemanticDecorator)targetView;
Criterion criterion = (Criterion)targetNode.getTarget();
Priority priority = alternative.getPriority(criterion);
return (int) (priority.getValue() * 7);
}
}
Удобно то, что эти операции вы можете использовать прямо в AQL-выражениях. Однако, вы не можете с их помощью изменять модель.
Для изменения модели нужно использовать Java-действия. Действия в отличие от служб уже не могут вызываться в AQL-выражениях. Их можно запускать, например, через контекстное меню или по нажатию кнопки. Действия можно откатывать с помощью команды Undo.
Пример действия, которое пересчитывает приоритеты в иерархии.
package ahp.design;
import java.util.Collection;
import java.util.Iterator;
import java.util.Map;
import org.eclipse.emf.ecore.EObject;
import org.eclipse.emf.transaction.RecordingCommand;
import org.eclipse.emf.transaction.TransactionalEditingDomain;
import org.eclipse.sirius.business.api.action.AbstractExternalJavaAction;
import org.eclipse.sirius.business.api.session.Session;
import org.eclipse.sirius.business.api.session.SessionManager;
import org.eclipse.sirius.diagram.DSemanticDiagram;
import ahp.Hierarchy;
public class UpdatePrioritiesAction extends AbstractExternalJavaAction {
public UpdatePrioritiesAction() {
}
@Override
public boolean canExecute(Collection<? extends EObject> arg0) {
return true;
}
@Override
public void execute(Collection<? extends EObject> selections, Map<String, Object> parameters) {
Iterator<? extends EObject> iter = selections.iterator();
if (!iter.hasNext()) {
System.out.println("Selections is empty");
return;
}
EObject obj = selections.iterator().next();
if (!(obj instanceof DSemanticDiagram)) {
System.out.println("DSemanticDiagram is expected");
}
DSemanticDiagram diagram = (DSemanticDiagram)obj;
EObject target = diagram.getTarget();
if (!(target instanceof Hierarchy)) {
System.out.println("Hierarchy is expected");
}
Hierarchy hierarchy = (Hierarchy)target;
Session session = SessionManager.INSTANCE.getSession(target);
TransactionalEditingDomain ted = session.getTransactionalEditingDomain();
RecordingCommand cmd = new RecordingCommand(ted) {
@Override
protected void doExecute() {
hierarchy.updatePriorities();
}
};
ted.getCommandStack().execute(cmd);
}
}
4 Создание модели
Ну, собственно, свою модель я уже создал и показал выше. Попробуйте взять этот проект и построить свою иерархию.
Profit
После прочтения данной статьи вы должны
- получить общее представление о методе анализа иерархий,
- научиться описывать метамодели на языке Xcore,
- научиться создавать сводные таблицы с помощью Sirius,
- научиться писать расширения для Sirius на Java.