поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Решение: для газов скорость звука рассчитывается по формуле:
[ upsilon =sqrt{frac{gamma cdot Rcdot T}{M}}, ]
где R = 8,31 Дж/(моль∙К) – универсальная газовая постоянная, T — абсолютная температура в кельвинах, M — молярная масса, γ — показатель адиабаты, который может быть выражен через количество степеней свободы (i) молекул газа:
[ gamma =frac{i+2}{i}. ]
Для одноатомного идеального газа i = 3 (три степени свободы). Средняя квадратичная скорость молекул газа
[ leftlangle upsilon rightrangle =sqrt{frac{3cdot Rcdot T}{M}}, ]
Таким образом, искомое отношение
[ frac{leftlangle upsilon rightrangle }{upsilon }=frac{sqrt{frac{3cdot Rcdot T}{M}}}{sqrt{frac{gamma cdot Rcdot T}{M}}}=sqrt{frac{3cdot Rcdot T}{M}cdot frac{M}{gamma cdot Rcdot T}}=sqrt{frac{3}{gamma }}=sqrt{frac{3cdot i}{i+2}}, ]
[ frac{leftlangle upsilon rightrangle }{upsilon }=sqrt{frac{3cdot 3}{3+2}}=sqrt{frac{9}{5}}=1,34. ]
Ответ: 1,34.
1.Основное уравнение молекулярно-кинетической
теории газов
где m0– масса
молекулы, <υ2>
– средняя квадратичная скорость
поступательного движения молекулы,
<εk> – средняя
кинетическая энергия поступательного
движения молекулы,n–
концентрация молекул, ρ – плотность.
2. Закон равномерного распределения
энергии по степеням свободы: на
каждую степень свободы поступательного
и вращательного движения
молекулы приходится средняя энергия
.
-
Средняя энергия молекулы газа
,
где i– число степеней
свободы молекулы.
-
Скорости молекул газа.

– средняя арифметическая скорость,
– наиболее вероятная скорость.
-
Функция распределения Максвелла
.
-
Распределение Больцмана
,
где EП–
потенциальная энергия молекулы
n– концентрация
молекул, имеющих энергиюEП,
n0–
концентрация молекул, имеющих энергиюEП=0.
Примеры решения задач.
Задача 1.При давленииP=0,1
МПа молекулы идеального газа с количеством
степеней
свободы молекулы i=5 имеют
среднюю энергию <ε>=Дж.
Определить концентрацию молекул газа.
Д
Решение
i=5
Воспользуемся основным уравнением
P=Па
молекулярно-кинетической
теории газов.
<
Дж

(1)
n- ?
Так как средняя кинетическая энергия
поступательного
движения
молекулы
,
а средняя энергия
молекулы, включая кинетическую энергию
вращательного движения,
,
то с учетом закона равномерного
распределения энергии по степеням
свободы
для <ε> получаем

(2)
Использую (1) – (2), находим:

Проверка размерности:
.
Вычисления:
Ответ:
.
Задача 2. Вычислить наиболее вероятную,
среднюю и тепловую скорости молекул
газа, у которого при нормальном атмосферном
давлении плотность равна.
Д
Решение
Для нахождения искомых
скоростей воспользуемся

При этом параметры
(температуру и массу молекулы,
входящие в эти формулы) выразим из
уравнения состояния идеального газа.
Таким образом, получаем:
– наиболее вероятная скорость;
– средняя арифметическая скорость;
– среднеквадратичная (тепловая) скорость.
Проверка размерности:
Вычисления:
;
;
.
Ответ:
,
,
.
Задача 3. Найти наиболее вероятную
скорость молекул газа, находящегося
в состоянии теплового равновесия, при
котором скоростям молекул
и
соответствуют одинаковые значения
функции распределения Максвелла.
Д
Решение
Распределение Максвелла
с точностью до постоянного
множителя имеет вид:
.
Учитывая выражения для определения
наиболее вероятной скорости
,
получаем функцию распределения
Максвелла в следующем виде:

Из условия задачи
находим:

Для υBполучим:
Соответствие размерности очевидно.
Вычисления:

Ответ:
.
Задача 4. При наблюдении в микроскоп
взвешенных частиц гуммигута обнаружено,
что среднее число их в слоях, расстояние
между которыми
,
отличается враза. Температура
.
Диаметр частиц,
а их плотность
на
больше плотности окружающей жидкости.
Определить по этим
данным число Авогадро.
Д
Решение
Распределение частиц, взвешенных
в жидкости,
подчиняется
закону Больцмана
, (1)
Поле тяжести Земли в пределах
рассматриваемых
изменений высоты можно считать
однородным. Если

что частицы гуммигута испытывают
действие
выталкивающей
силы Архимеда,
(2)
где V– объем частицы,
то для потенциальной энергии частицы
следует записать:
Число частиц на высоте h1равно,
а на высоте h2>h1:
.
Найдем отношение n1/n2:.
(3)
Учитывая, что
и
,
из (3) находим.
Проверка размерности:

Вычисления:
.
Ответ:
.
Задачи для самостоятельного решения.
2.1. Найти отношение средних квадратичных
скоростей молекул гелия и водорода при
одинаковых температурах.
2.2. Средняя квадратичная
скорость молекул некоторого газа
равна 500 м/с
при давление 4·105 Па.
Найти плотность газа.
2.3. Найти среднюю арифметическую
и среднюю квадратичную скорости молекул
газа, плотность которого при давлении
2·105 Пa
равна 0,8 г/м2
.
2.4. Во сколько раз средняя квадратичная
скорость пылинок, взвешенных в
воздухе, меньше средней квадратичной
скорости молекул воздуха?
Масса пылинки 10-8 г.
Воздух считать однородным газом с
молярной массой 29г/моль.
2.5. Два одинаковых сосуда содержат
одинаковое число молекул кисло-
рода. Сосуды соединены краном. В первом
сосуде средняя квадратичная скорость
молекул равна 400 м/с, во втором —
500 м/с. Какой будет эта скорость,
если открыть кран, соединяющий сосуды?
2.6. При какой температуре средняя
квадратичная скорость атомов гелия
станет равной второй космической
скорости на Земле?
2.7. При какой температуре
молекулы кислорода имеют такую же
среднюю квадратичную скорость, как
и молекулы водорода при температуре
100 K?
2.8. Колба объемом 4 л
содержит некоторый газ массой 0,6 г
под давлением 200 кПа. Определить
среднюю квадратичную скорость молекул
газа.
2.9. Смесь гелия и аргона находится при
температуре 1,2·10 К. Определить
среднюю квадратичную скорость и среднюю
кинетическую энергию атомов гелия и
аргона.
2.10. Определить среднюю арифметическую
скорость молекул газа, если их средняя
квадратичная скорость равна 1 км/с.
2.11. При 0°С вычислить среднюю квадратичную
скорость теплового движения молекулы:
1) водорода; 2) азота; 3) кислорода.
2.12. Найти средний квадратичный
импульс молекулы водорода Н2
при температуре 27°С.
2.13. При какой температуре средняя
квадратичная скорость молекул кислорода
равна средней квадратичной скорости
молекул азота при температуре 100°С?
2.14. На рис. 2.1 изображена молекула
кислорода. Найти значение средней
к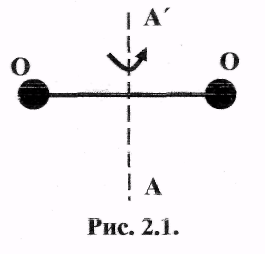
частоты вращения молекулы кислорода
при 27°С. Момент инерции молекулы кислорода
относительно оси АА’ равен 19,2·10-40 г·см3
2.15. Найти кинетическую
энергию теплового движения всех молекул
кислорода, занимающих объем 5,5 л
при давлении 2·105 Па.
Колебаниями атомов в молекулах пренебречь.
2.16. Газ, состоящий из жестких
двухатомных молекул, находится при
температуре 300 К. Вычислить среднюю
квадратичную угловую скорость молекулы,
если ее момент инерции 2,1·10-39 г·см
.
2.17. Считать, что воздух состоит из
молекул азота, кислорода, водорода
и углекислого газа. Молекулы какого из
газов обладают наибольшей средней
скоростью?
2.18. Сравнить средние
квадратичные скорости молекул двух
газов с параметрами: a)
p1=
600 кПа, р=1,2 кг/м3;
б) Р2=400 кПа,
ρ2=0,8 кг/м3.
2.19. При какой температуре средняя
кинетическая энергия теплового движения
атомов гелия будет достаточна для того,
чтобы атомы гелия преодолели земное
тяготение и навсегда покинули земную
атмосферу?
2.20. Частицы гуммигута
диаметром 10-6 м
участвуют в броуновском движении.
Плотность гуммигута 1.2·103 кг·м3.
Найти среднюю
квадратичную скорость частиц при 17°С.
2.21. В момент взрыва атомной
бомбы температура достигает 107°С.
Считать, что при этой температуре
молекулы полностью диссоциированы
на атомы, а атомы ионизированы. Найти
при этих условиях среднюю квадратичную
скорость иона водорода.
2.22. Пользуясь распределением
Максвелла и понятием относительной
скорости а как
отношения скорости молекулы υ
к наиболее вероятной скорости υв,
получить распределение в приведенном
виде:
2.23. Определить вероятность того, что
какая-нибудь молекула кислорода при
температуре 0°С имеет скорость, точно
равную наиболее вероятной скорости.
2.24. Перейти от распределения Максвелла
для молекул по интервалам скоростей
к распределению молекул по интервалам
энергий:
где ε
— кинетическая энергия молекулы, υB
– наиболее вероятная скорость.
2.25. Доказать, что максимум функции
распределения молекул по интервалам
энергий:
соответствует скорости
.
2.26. Сколько процентов молекул кислорода
обладает скоростями, отличающимися
от наиболее вероятной не более чем на
1%?
2.27. Сколько процентов молекул кислорода
обладает скоростями, отличающимися
от средней квадратичной скорости не
более чем на 1%?
2.28. Какая часть молекул азота при
нормальных условиях имеет скорости,
лежащие в интервале от 99 м/с до 101 м/с?
2.29. При какой температуре число молекул
азота, обладающих скоростями в
интервале от 299 м/с до 301 м/с, равно
числу молекул, обладающих скоростями
в интервале от 599 м/с до 601 м/с?
2.30. Сколько процентов
молекул азота при температуре 280 К
обладает скоростями в интервале от
500 м/с до 510 м/с?
2.31. Сколько процентов молекул кислорода
обладает скоростями, отличающимися
от наиболее вероятной не более чем на
10 м/с, при температуре 0°С.
2.32. Водород находится при температуре
273 К. Определить отношение числа
молекул водорода, обладающих скоростями
в интервале от 2000 м/с до 2001 м/с, к
числу молекул, обладающих скоростями
от 1000 м/с до 1001 м/с.
2.33. Определить температуру при которой
функция распределения молекул
кислорода по скоростям имеет максимум
при скорости 500 м/с.
2.34. Сколько процентов молекул кислорода
обладает скоростями, отличающимися
от наиболее вероятной скорости не более
чем на 10 м/с, при температуре 300°С?
2.35. Найти температуру кислорода, при
которой скоростям молекул 400 м/с и
600 м/с соответствуют одинаковые
значения функции распределения
Максвелла.
2.36. Определить высоту горы, если давление
на ее вершине равно половине давления
на уровне моря. Температуру считать
одинаковой и равной 273 К.
2.37. Определить показания барометра на
высоте Останкинской телевизионной
башни равной 540 м. Температуру считать
одинаковой и равной 280 К.
2.38. При подъеме аэростата
барометр изменил свое показание на
11 кПа.
На какой высоте находится аэростат,
если на поверхности Земли барометр
показывал 0,1 МПа?
Температуру воздуха считать одинаковой
и равной 290 К.
2.39. Чему равна концентрация
молекул воздуха на высоте 2км над уровнем
моря? Давление на уровне моря 101 кПа,
а температура 10°С. Изменением
температуры с высотой пренебречь.
2.40. Пылинки массой 10-10 г
взвешены в воздухе. Определить толщину
слоя воздуха, в пределах которого
концентрация пылинок различается не
более чем на 1%. Температуру воздуха во
всем объеме считать равной 27°С.
2.41. У поверхности Земли
концентрация молекул водорода почти в
106 раз
меньше, чем концентрация молекул азота.
На какой высоте при 0°С концентрация
молекул водорода и молекул азота будут
равны?
2.42. При наблюдении в микроскоп
взвешенных частиц гуммигута обнаружено,
что их среднее число в слоях, расстояние
между которыми 40 мкм,
отличается друг от друга в 2 раза. Диаметр
частиц 0,4 мкм,
а их плотность на 0,20 г/см
больше плотности окружающей жидкости.
Температура среды 290 К.
Определить по этим данным число Авогадро.
2.43. Найти массу водяного
пара, заключенного в столбе атмосферного
воздуха сечением 1,0 м2
и высотой 4,15 км.
Температура воздуха во всех слоях
постоянна и равна 15°С. Парциальное
давление паров воды на поверхности
Земли 103 Па.
2.44. Толщина слоя воздуха, в пределах
которого концентрация взвешенных в
воздухе пылинок различается не более
чем на 1%, равна 4,2 мм. Определить
массу пылинки. Температуру воздуха
считать одинаковой и равной 300 К.
2.45. На высоте 123 км
от поверхности Земли концентрация
молекул водорода и азота равны.
Вычислить отношение концентрации
молекул водорода и азота у поверхности
Земли.
2.46. При наблюдении в микроскоп
взвешенных в воде частиц гуммигута
оказалось, что среднее число их в слоях,
расстояние между которыми 40 мкм,
отличается друг от друга в 2 раза.
Плотность гуммигута 1,2 г/см3.
Температура среды 290 К.
Определить диаметр частиц.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Найдите отношение средних скоростей молекул O2 и H2 при одинаковой температуре.
Задача №4.1.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(T_1=T_2), (frac{upsilon_1}{upsilon_2}-?)
Решение задачи:
Вообще, среднюю квадратичную скорость молекул газа можно определить по формуле:
[{upsilon _{кв}} = sqrt {frac{{3RT}}{M}} ]
В этой формуле (R) – универсальная газовая постоянная, (T) – абсолютная температура газа, (M) – молярная масса газа. Из формулы видно, что скорость молекул газа тем больше, чем меньше его молярная масса.
Тогда отношение скоростей молекул водорода к молекулам кислорода равно:
[frac{{{upsilon _{кв1}}}}{{{upsilon _{кв2}}}} = sqrt {frac{{3R{T_1} cdot {M_2}}}{{{M_1} cdot 3R{T_2}}}} = sqrt {frac{{{M_2}{T_1}}}{{{M_1}{T_2}}}} ]
Так как по условию (T_1=T_2), то:
[frac{{{upsilon _{кв1}}}}{{{upsilon _{кв2}}}} = sqrt {frac{{{M_2}}}{{{M_1}}}} ]
Молярная масса водорода H2 (M_1) равна 0,002 кг/моль, кислорода O2 (M_2) равна 0,032 кг/моль. Посчитаем ответ:
[frac{{{upsilon _{кв1}}}}{{{upsilon _{кв2}}}} = sqrt {frac{{0,032}}{{0,002}}} = 4]
Ответ: 4.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.1.42 Под каким давлением находится кислород в баллоне, если при температуре 27 C
4.1.44 Найти среднюю квадратичную скорость молекул газа, имеющего плотность 1,8 кг/м3
4.1.45 В баллоне находится кислород при давлении 4 МПа и температуре 42 C. Определить
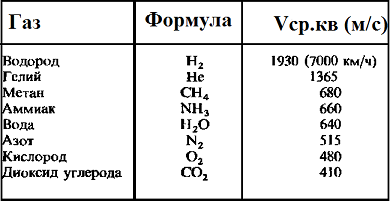
Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа
Таблица значений средней квадратичной скорости молекул некоторых газов
Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):
Где у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:
Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):
Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:
Но средняя кинетическая энергия, так же находится, как :
А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа:
А если расписать универсальную газовую постоянную, как , и за одно молярную массу
, то у нас получится?
В Формуле мы использовали :
— Средняя квадратичная скорость молекул
— Постоянная Больцмана
— Температура
— Масса одной молекулы
— Универсальная газовая постоянная
— Молярная масса
— Количество вещества
— Средняя кинетическая энергия молекул
— Число Авогадро