Как найти отношение средних плотностей

Как найти отношение объемов планет

Галактика, в которой мы живем, заполнена бесчисленным количеством планет. Есть большие и маленькие, каменные и газовые, и каждая из них имеет свой объем. Но как узнать отношение объемов двух или более планет?

Математические формулы

Первый шаг для нахождения отношения объемов планет — это знание математических формул. Объем сферы можно найти с помощью следующей формулы:

V=4/3πr³, где V — объем сферы, π — число Пи (3,14159), r — радиус сферы.

Представим, что у нас есть две планеты: Плутон и Земля. Путон имеет радиус 737,5 км, а Земля — 6 371 км. Чтобы найти отношение их объемов, мы должны сначала найти объем каждой из них:

• Объем Плутона = 4/3 * 3,14159 * (737.5)^3 = 6,39 * 10^9 км³
• Объем Земли = 4/3 * 3,14159 * (6371)^3 = 1,08 * 10^12 км³

Научные исследования

Есть несколько научных исследований, которые могут помочь определить отношение объемов планет. Одно из таких исследований — изучение гравитационного воздействия планет друг на друга. Если мы знаем массы планет и их расстояние друг от друга, можно использовать закон всемирного тяготения Ньютона для определения силы гравитации между ними. Отсюда следует, что есть определенный относительный объем между двумя планетами.

Еще один способ может использоваться для определения объемов планет — это изучение их радиуса и массы. Что нельзя увидеть на поверхности некоторых планет, так это их массу. Но с помощью спутников и технологии радара мы можем определить точное значение массы планеты. Зная массу и радиус планеты, можно использовать формулу для нахождения объема планеты.

Выводы

Есть несколько способов, которые могут помочь определить отношение между объемами разных планет. Самый распространенный способ — это использование математических формул для нахождения объема, затем просто сравнить их значения. Также научные исследования гравитационного поля и масс планет могут помочь определить относительный объем между планетами.

Какой бы способ мы не использовали, знание размеров и объемов планет может помочь нам лучше понять нашу галактику и понять, какие другие миры могут быть жизнеспособными.

Как найти отношение объемов планет: советы и рекомендации

Когда мы говорим о размерах планет, возникает естественный вопрос: как же определить их объемы и, главное, как сравнить их между собой? Существуют различные методы, которые можно использовать для этого. В этой статье мы расскажем о некоторых из них.

Методы определения объема планет

• Метод гравиметрического поля. Этот метод заключается в измерении изменения гравитационного поля планеты в зависимости от ее массы. Он может быть использован для определения объемов планет с низкой плотностью, таких как Юпитер или Нептун.
• Метод радиус-вектора. Этот метод основан на измерении расстояния от центра планеты до ее поверхности. Он может использоваться для определения объемов планет с более высокой плотностью, таких как Земля и Марс.
• Метод объемно-массовой модели. Этот метод заключается в разделении планеты на небольшие объемы и измерении их массы. Затем объем планеты может быть определен путем интегрирования этих масс. Этот метод часто используется для определения объемов планет средней плотности, таких как Венера и Сатурн.

Как сравнить объемы планет

Для сравнения объемов планет можно использовать различные подходы. Один из наиболее распространенных — это выражение объема планеты в единицах Земли. Например, если мы хотим сравнить объем Земли и Марса, то мы можем выразить объем Марса в процентах от объема Земли.

Объем Марса составляет около 15% объема Земли.

Это позволяет легко сравнить размеры планет и понять, насколько они отличаются друг от друга. Также можно сравнивать плотность планет, которая может намного лучше отражать их размеры и массы.

Выводы

Не существует одного универсального метода, который можно использовать для определения объемов всех планет. Вместо этого необходимо использовать различные методы в зависимости от конкретной планеты. Однако, сравнение объемов и плотностей планет может помочь нам лучше понять, как они отличаются друг от друга и каких выводов можно сделать из этих различий.

Как найти отношение объемов планет

Планеты Солнечной системы имеют различные размеры и объемы, и их отношение может быть интересным для ученых и любопытных людей. В этой статье мы рассмотрим несколько способов, которыми можно вычислить отношение объемов планет.

1. Использование радиуса и формулы объема

Один из самых простых способов вычисления объема планеты — использование ее радиуса и формулы объема. Формула объема для сферы:

V = (4/3) * π * r^3

где V — объем, π — число Пи (приблизительно равно 3,14), r — радиус.

Современные измерения радиусов планет получены благодаря миссиям космических аппаратов, включая Вояджер, Кассини и Новую Горизонты. Так что радиусы большинства планет известны с точностью до нескольких километров.

Таким образом, для вычисления объема планеты с известным радиусом необходимо ввести известные значения в формулу. Например, для Земли:

V = (4/3) * π * 6 371^3V ≈ 1.0832 * 10^12 км^3

Для Юпитера:

V = (4/3) * π * 69 911^3V ≈ 1.4313 * 10^15 км^3

Отношение объемов планет можно вычислить путем деления значений объемов:

отношение V(Земли)/V(Юпитера) ≈ 7.6 * 10^-4

2. Использование данных о массе и плотности

Еще один способ вычисления объемов планет заключается в использовании данных о плотности и массе. Плотность — это отношение массы к объему:

ρ = m/V

где ρ — плотность, m — масса, V — объем.

Массы планет измеряются в земных массах (М⊕). Плотности измеряются в г/см^3 или кг/м^3. Например, плотность Земли составляет примерно 5,5 г/см^3.

Используя известные значения масс планет и средних плотностей, можно выразить их объемы:

V = m/ρ

Например, для Земли:

V ≈ 5.9722 * 10^24 кг / 5.5 г/см^3V ≈ 1.0832 * 10^12 км^3

Для Юпитера:

V ≈ 1898 М⊕ / 1.33 г/см^3V ≈ 1.4313 * 10^15 км^3

Отношение объемов планет можно вычислить путем деления значений объемов:

отношение V(Земли)/V(Юпитера) ≈ 7.6 * 10^-4

3. Использование данных о средней плотности

Еще один способ вычисления объемов планет — использование данных о их средней плотности. В этом случае можно использовать формулу:

V = m/ρ * (4/3) * π * R^3

где V — объем, m — масса, ρ — плотность, R — радиус, π — число Пи.

Для этой формулы необходимо знать только среднюю плотность планеты, которая может быть получена из наблюдений ее гравитационного поля и других характеристик.

С помощью этой формулы можно оценить отношение объемов различных планет. Например, для Земли:

V ≈ 5.97 * 10^24 кг / 5.52 г/см^3 * (4/3) * π * 6,371 км^3V ≈ 1.086 * 10^12 км^3

Для Юпитера:

V ≈ 1.898 * М⊕ / 1.33 г/см^3 * (4/3) * π * 69,911 км^3V ≈ 1.431 * 10^15 км^3

Отношение объемов планет можно вычислить путем деления значений объемов:

отношение V(Земли)/V(Юпитера) ≈ 7.6 * 10^-4

Итог

Существует несколько способов вычисления отношения объемов планет, включая использование радиуса и формулы объема, данных о массе и плотности, а также данных о средней плотности. Выбор метода зависит от доступных данных и доступных инструментов вычисления. Однако в любом случае, вычисление отношения объемов планет — интересный способ познать нашу Вселенную и ее устройство.

• Отношение объемов планет можно вычислить, используя радиус и формулу объема
• Данные о массе и плотности планет также могут быть использованы для вычисления объемов
• Данные о средней плотности планет могут быть использованы для вычисления объемов, используя соответствующую формулу

Обновлено: 23.05.2023

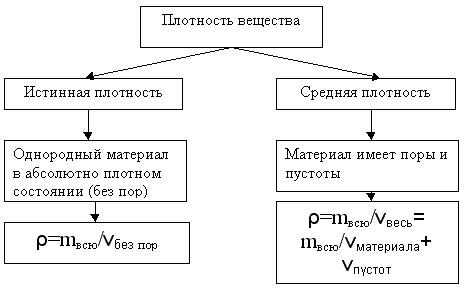
Плотностью называют физическую величину, определяемую для однородного вещества его массой в единице объема. Для неоднородного вещества, плотность r его в определенной точке есть предел отношения массы m к объему V при объеме, стремящимся к этой точке:

r = lim m ¤ V при V ® 0.

Для характеристики макроструктуры материала с учетом наличия газовой фазы используют термин “средняя плотность”, обозначаемый символом rm. Средняя плотность всегда меньше истинной, т.к. на одну и ту же единицу массы приходится больший объем (rm rам-кр.стр. > rам.структуры или rкристалла > rситалла > rстекла.

Если рассматривать различные агрегатные состояния одного и того же соединения, то можно заметить:

rтв.тела > rжидк. > rгаза,

что вполне отвечает вышеизложенному положению. Исключение составляют лишь чугун и вода, у которых плотность в жидком состоянии больше плотности твердого тела.

Истинная плотность (прежнее название – удельный вес) – масса единицы объема материала в абсолютно плотном состоянии, т. е. без пор и пустот. Определяют по формуле ? = m / V, где m – масса материала, кг; V – абсолютный объем, занимаемый материалом (без пор и пустот), м 3 . Истинная плотность жидкостей и материалов, полученных из расплавленных масс (металла, стекла, а также гранита, мрамора и других подобных горных пород), практически соответствует их плотности в естественном состоянии, а пористых материалов – приводится к абсолютно плотному состоянию искусственным путем.

Истинная плотность – свойство, которое контролируются только при геологической разведке с подземными сетями.

Для горных пород, служащих сырьем при производстве облицовочных материалов, не имеет решающего значения при их оценке. Однако этот показатель позволяет косвенно выявить другие свойства камня, например вычислить его пористость.

Плотность различных материалов

Истинную плотность р, кг/м 3 , вычисляют по формуле

где m – навеска порошка, высушенного до постоянной массы, г; m₁ – масса пикнометра с дистиллированной водой, г; m₂— то же, с навеской и дистиллированной водой после удаления пузырьков воздуха, г; р„ – истинная плотность воды: р_в = 1 г/см 3 .

Средняя плотность ? (прежнее название – объемная масса) – масса единицы объема материала в естественном состоянии, т. е. вместе с порами и пустотами. Определяется по формуле ? = m / V₁, где m – масса материала, кг; V₁ – объем материала в естественном состоянии, м 3 . Средняя плотность металла и стекла практически равна их истинной плотности, у большинства строительных материалов она, как правило, меньше (из-за наличия пор).

Для каждого материала стандарты устанавливают значение влажности, при котором вычисляют среднюю плотность, необходимую для расчета пористости, теплопроводности и теплоемкости материалов, определения стоимости их перевозок и расчета прочности конструкций с учетом их собственной массы.

Истинная и средняя плотности широко используемых материалов показаны в табл. 1.

Средняя плотность – физическое свойство облицовочного камня, используемое обычно при его общей характеристике. Этим показателем пользуются при вычислении массы изделий из камня по их объему или при определении объема, когда известна масса изделий. Кроме того, используя среднюю плотность, определяют пористость камня и некоторые другие показатели. Особенно важное значение имеет это свойство для горных пород, используемых при производстве стеновых материалов, где значение этого показателя не должно превышать 2100 кг/м 3 .

Для определения средней плотности берут пять образцов кубической формы с размером ребра 40—50 мм или цилиндры диаметром и высотой 40—50 мм. Каждый образец очищают щеткой от рыхлых частиц и высушивают до постоянной массы, после чего взвешивают на настольных (гирных) или циферблатных весах. Затем измеряют размеры кубов или цилиндров камня и вычисляют объемы образцов.

Среднюю плотность каждого образца вычисляют по формуле, приведенной в § 2. Средняя плотность горной породы будет средним арифметическим результатом определения этой характеристики для пяти образцов. Значения средней плотности у наиболее распространенных видов облицовочного камня СНГ даны в приложении.

Среднюю плотность сыпучих (рыхлых) материалов (цемента, извести, песка, гравия, щебня) называют насыпной средней плотностью (прежнее название – насыпная объемная масса). В объем сыпучих материалов включают не только объем пор в самом материале, но и пустот между зернами или кусками материала.

Таблица 1. Плотность материалов в воздушно-сухом состоянии

Примечание. Для сыпучих (рыхлых) материалов: песка, цемента, гравия приведена насыпная средняя плотность.

Истинная плотность ρ– это масса единицы объема материала в абсолютно плотном состоянии, т.е. без пор и пустот.

ρ =m/V_a г/см 3 (кг/м 3 )

m – масса материала, г

V_a – абсолютный объем, см 3

Определение истинной пористости производится с помощью объемометров или стеклянного мерного цилиндра.

Истинная плотность большинства стройматериалов >1 (за единицу условно принимают массу 1 г/см 3 воды при температуре 4 °С); исключение составляют лаки, олифы, некоторые пластмассы.

ρ= 2,2— 3,3 г/см 3 для каменных материалов (горных пород)

ρ = 0,9—1,6 г/см 3 для органических материалов (дерево, битумы, дегти, пеки, оли‑­

фа, лаки, пластмассы)

ρ = 7,25—7,85г/см 3 для черных металлов (чугун сталь)

^ Средняя плотность – масса единицы объема материала в естественном состоянии (с порами и пустотами)

ρ₀ = m/V_е г/см 3 (кг/м 3 )

m – масса материала, г

V_е – объем материала в естественном состоянии (с порами и пустотами), см 3

Среднюю плотность рыхлых материалов (песка, щебня) определяют без вычета пустот между их частицами и называют насыпной плотностью ρ_н.

Плотность материала по отношению к плотности воды – относительная плотность d
ρ₀ 3 .

ρ₀ = ρ для абсолют‑­

но плотных материалов (стекло, сталь, битум, Ме и жидкие материалы) Среднюю плотность необходима при расчетах прочности (устойчивости) строительных конструкций, для подсчетов при перевозках материалов. В отличие от истинной плот‑­

ности средняя плотность различных строительных материалов колеблет‑­

ся в очень широких пределах: от 20 кг/м 3 у некоторых легчайших теплоизоляционных материалов до 7850 кг/м 3 у сталей. Увеличение влажности материала повышает его среднюю плотность. Кирпич глиняный 1800-2400 кг/м 3 Дуб 700-900 кг/м 3 Бетон обычный 1800-2400 кг/м 3

2. Насыпная плотность и плотность зёрен сыпучих материалов.

Насыпная плотность, это отношение массы к занимаемому объему. Учитывается и пространство между зёрнами заполнителя. Эта характеристика достаточно важна при расчёте состава бетона. Как же определить насыпную плотность? Для этого заполнитель с высоты в сто миллиметров насыпают в мерный сосуд. Перед выполнением этой операции сосуд взвешивается. Засыпается заполнитель до образования конуса над сосудом. После чего конус необходимо срезать, при помощи линейки, и сосуд взвешивается. Насыпная плотность заполнителя высчитывается по простой формуле: Pн = (m2 – m1)/V, где m2 – масса сосуда с заполнителем, m1 – масса этого же сосуда без заполнителя, V – вместимость мерного сосуда.

Насыпную плотность, когда масса материала в единице объема находится в насыпном состоянии (в насыпной объем включены межзерновые пустоты);

r_н – насыпная плотность, г/см 3 ;

m_н – насыпная масса материала, г;

V_н – насыпной объем, см 3 .

Насыпную плотность определяют как в рыхлонасыпном состоянии, так и в уплотненном. В первом случае материал засыпается в сосуд с определенной высоты, во втором – уплотняется на виброплощадке (30-60 сек).

Насыпная плотность – это плотность в не уплотненном состоянии. При уплотнении (трамбовки) сыпучего материала, его плотность увеличивается и перестает быть насыпной. Отвал щебня, или двадцать кубов песка в кузове самосвала – все они находятся в не уплотненном состоянии и обладают свою насыпную плотность. Она учитывает как объем самих частиц материала (песчинок или отдельных камней гравия), так и пространство между ними, так что насыпная плотность меньше, чем плотность обычная.

Насыпная плотность сыпучих материалов р_п опреде­ляется отношением массы m_d к единице объема просушенного, свободно насыпанного материала V_н.
Насыпную плотность определяют по формуле (г/см 3 , кг/м 3 , т/м 3 )

где: m_d—масса просушенного материала в мерном сосуде, г, кг, т; V_d – объем мерного сосуда, см 3 , м 3 .
Для определения насыпной плотности материал на­сыпают в тару с помощью специальной воронки, наклон­ного лотка или совка. Расстояние от насыпающего приспособления до верхней кромки сосуда должно быть 50-100 мм. Насыпную плотность сыпучих (рыхлых) ма­териалов (песок, цемент, гравий) определяют вместе с пустотами между их частицами. Показатель средней на­сыпной плотности увеличивается с повышением влажно­сти материала.

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму. Более строгое определение плотности требует уточнение формулировки:

• Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
• Плотность вещества — это плотность тел, состоящих из этого вещества. Отсюда вытекает и короткая формулировка определения плотности вещества: плотность вещества — это масса его единичного объёма.
• Плотность тела в точке — это предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда этот объём стремится к нулю [1] , или, записывая кратко, ” width=”” height=”” />
  . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.

Содержание

Виды плотности и единицы измерения

Исходя из определения плотности, её размерность кг/м³ в системе СИ и в г/см³ в системе СГС.

Для сыпучих и пористых тел различают:

• истинную плотность, определяемую без учёта пустот; , рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.

Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.

Формула нахождения плотности

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

Плотность тела в точке записывается как ,” width=”” height=”” />
тогда масса неоднородного тела (тела с плотностью, зависящей от места) рассчитывается как

Зависимость плотности от температуры

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого числа.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается.

Диапазон плотностей в природе

Для различных природных объектов плотность меняется в очень широком диапазоне.

• Самую низкую плотность имеет межгалактическая среда (2·10 −31 ÷5·10 −31 кг/м³) [2] .
• Плотность межзвёздной среды приблизительно равна 10 −23 ÷10 −21 кг/м³.
• Средняя плотность Солнца примерно в 1,5 раза выше плотности воды.
• Средняя плотность красных гигантов на много порядков меньше, чем у Солнца, из-за того, что их радиус в сотни раз больше.
• Средняя плотность Земли равна 5520 кг/м³. при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
• Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
• Плотность пресной воды составляет 1000 кг/м³. имеет плотность 2600 кг/м³.
• Плотность железа равна 7874 кг/м³.
• Наибольшую плотность среди металлов имеет осмий (22 587 кг/м³).
• Плотность атомных ядер приблизительно равна 2·10 17 кг/м³.
• Плотность белых карликов составляет 10 8 ÷10 12 кг/м³.
• Плотность нейтронных звёзд имеет порядок 10 17 ÷10 18 кг/м³.
• Теоретически верхнюю границу представляет планковская плотность (современная физика оценивает её в 5,1·10 96 кг/м³, хотя не исключено, что она очень сильно завышена).

Плотности астрономических объектов

Средние плотности планет Солнечной системы и Солнца:

• Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10 −21 ÷10 −20 кг/м³.
• Плотность межзвёздной среды ~10 −23 ÷10 −21 кг/м³.
• Плотность межгалактической среды от 2×10 −34 до 5×10 −34 кг/м³.
• Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
• Плотность белых карликов 10 8 ÷10 12 кг/м³
• Плотность нейтронных звёзд имеет порядок 10 17 ÷10 18 кг/м³.
• Средняя (по объёму под горизонтом событий) плотность чёрной дыры
  • у чёрной дыры с массой порядка солнечной превышает ядерную плотность,
  • у сверхмассивной чёрной дыры с массой в 10 9 солнечных масс (существование таких чёрных дыр подозревается в квазарах) оставляет около 20 кг/м³,
  • у сверхмассивной чёрной дыры в центре галактики может быть 0,2 кг/м³.

  Плотности некоторых газов

  Плотности некоторых жидкостей

  Плотность некоторых пород древесины

  Измерение плотности

  Для измерения плотности используются:

  — прибор для измерения истинной плотности (денсиметр, плотномер) — измеритель плотности жидкостей. и бур Зайдельмана — приборы для измерения плотности почвы. — прибор для измерения плотности жидкости и газа под давлением.

  См. также

  Примечания

  1. ↑ Подразумевается также, что область стягивается к точке, то есть, не только ее объем стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и ее диаметр (максимальный линейный размер).
  2. ↑Агекян Т. А. Расширение Вселенной. Модель Вселенной. // Звёзды, галактики, Метагалактика / Под ред. А. Б. Васильева. — 3-е изд. — М .: Наука, 1982. — С. 249. — 416 с.
  3. ↑ (англ.) Planetary Fact Sheet
  4. ↑ (англ.) Sun Fact Sheet

  Ссылки

  Источники

  • Физические величины по алфавиту
  • Плотность

  Wikimedia Foundation . 2010 .

  Полезное

  Смотреть что такое “Плотность” в других словарях:

  ПЛОТНОСТЬ — ПЛОТНОСТЬ, плотности, жен. 1. только ед. отвлеч. сущ. к плотный. Плотность населения. Плотность ткани. Плотность воздуха. Плотность огня (воен.). 2. Масса какого нибудь тела, заключенная в единице его объема (физ.). За единицу плотности… … Толковый словарь Ушакова

  ПЛОТНОСТЬ — (r), масса единицы объема вещества. В СИ единица плотности 1 кг/м3. Отношение плотностей двух веществ называется относительной плотностью (обычно плотность веществ определяют относительно плотности дистиллированной воды). Малой плотностью… … Современная энциклопедия

  ПЛОТНОСТЬ — (обозначение r) отношение массы к объему для данного вещества, обычно выражаемое в единицах СИ как килограммы на кубический метр (кг/м 1). Эта величина является показателем концентрации частиц в материале. Плотность твердого или жидкого вещества… … Научно-технический энциклопедический словарь

  плотность — густота, концентрация; массивность, тесность, коренастость, тучность, насыщенность, кряжистость, компактность, уплотненность, кучность Словарь русских синонимов. плотность компактность Словарь синонимов русского языка. Практический справочник. М … Словарь синонимов

  плотность — (density) – это отношение массы тела к его объему. Выражается в кг/дм3 или в кг/м3. Объем зависит от температуры (в большой степени) и давления (в небольшой степени), следовательно, вязкость тоже зависит от этих параметров. С ростом температуры и … Автомобильный словарь

  Плотность — (r), масса единицы объема вещества. В СИ единица плотности 1 кг/м3. Отношение плотностей двух веществ называется относительной плотностью (обычно плотность веществ определяют относительно плотности дистиллированной воды). Малой плотностью… … Иллюстрированный энциклопедический словарь

  Плотность — – характеристика вещества, определяемая отношением массы вещества, заключенной в некотором объеме, к величине этого объема. [Блюм Э. Э. Словарь основных металловедческих терминов. Екатеринбург 2002] Плотность – масса единичного объема … Энциклопедия терминов, определений и пояснений строительных материалов

  ПЛОТНОСТЬ — (1) вещества (объёмная) одна из основных физ. характеристик вещества, в нормальных условиях численно равная отношению массы т однородного тела к его объёму V, обозначается р. В СИ выражается в кг/м3. П. вещества растёт с увеличением давления и,… … Большая политехническая энциклопедия

  ПЛОТНОСТЬ — (?) масса единичного объема вещества. Величина, обратная удельному объему. Отношение плотности двух веществ называют относительной плотностью (обычно плотность веществ определяют относительно плотности дистиллированной воды) … Большой Энциклопедический словарь

  ПЛОТНОСТЬ — (r), величина, определяемая для однородного в ва его массой в единице объёма. П. неоднородного в ва в определённой точке предел отношения массы т тела к его объёму V, когда объём стягивается к этой точке. Средняя П. неоднородного тела также есть… … Физическая энциклопедия

  ПЛОТНОСТЬ — (Density) масса данного тела, заключенная в единице объема. За единицу плотности принимается плотность воды при 4° Цельсия. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь

  Читайте также:

    

  • К службе готовы кадетские классы есть в более чем 110 школах столицы

    

  • Почему лига наций не смогла предотвратить вторую мировую войну кратко

    

  • Отдел выездных проверок чем занимается кратко

    

  • Какие примеры борьбы с западным влиянием в ссср вам известны кратко

    

  • Как можно добиться понимания между родителями и детьми кратко

В курсе физики 7 класса мы при прохождении темы
“ Механическое движение” вводим понятие
средней скорости, и при определенном полученном
навыке решения задач большинство учащихся с
расчетами средней скорости справляются. (Только
жаль, что часто при решении ребята сталкиваются с
громоздким математическим решением, а они пока к
этому не готовы)

Через несколько уроков мы приступаем к
введению понятий массы и плотности.

На начальном уровне все основное по данному
вопросу в любом учебнике-7 ,в принципе, сказано, но
почему мы не оговариваем сразу такой важный
закон, как закон сохранения массы? Он нам
пригодится для введения понятия средней
плотности!

Если растворить сахар в воде, то масса раствора
строго равна массе сахара и воды.

При любом дроблении и при растворении масса
остается одной и той же.

Формулировка закона: При любых
изменениях изолированной системы тел или частиц
масса этой системы остается неизменной и равна
сумме масс составляющих ее частей.

Так как понятие изолированной системы мы пока
не вводим, то можно закон сформулировать проще;

Масса тел до взаимодействия равна массе тел
после взаимодействия,т. е. остается неизменной

Математическое выражение закона: m₁ + m₂
+ … + m_N =m ^/₁ + m ^/₂ + … + m ^/_N

Границы и условия применимости закона можно
пока не вводить

Приоритет в открытии закона сохранения массы
вещества принадлежит российскому ученому
Михаилу Васильевичу Ломоносову и французу
Антуану Лавуазье (Antoine Laurent Lavoisier).

Закон был открыт и сформулирован ими
независимо друг от друга на основе анализа
многочисленных опытных данных.

В 1756 г. М.В.Ломоносов самостоятельно
сформулировал философский принцип сохранения
материи и движения: “…все перемены, в натуре
случающиеся, такого суть состояния, что сколько
чего у одного тела отнимется, столько
присовокупится к другому…”.

Он считал этот закон одним из основных законов
природы!

Примеры проявления закона в природе

1. Явления диффузии
2. Процессы растворения веществ.
3. Дробление и разрушение тел.
4. Глобальный круговорот вещества в биосфере,
   перенос твердых, жидких и газообразных тел при
   различных давлениях и температурах, в течение
   веков и тысячелетий происходит в полном
   соответствии с законом сохранения массы. Эти же
   самые слова можно сказать об одном из самых
   грандиозных процессов – круговороте воды на
   поверхности земного шара.

Пример:

1) Если взять 1 кг манки, 2 кг гречки, 3 кг пшена и
все крупы смешать, то получим массу строго 6 кг

m_см = m_манки + m_гречки + m_пшена
= 1 кг + 2 кг +3 кг = 6 кг

2) В пассажирский самолет перед началом рейса
погрузили 300 кг продуктов. Изменилась ли масса
авиалайнера после того, как в полете все продукты
были съедены?

Так как заданий на закон сохранения массы в
задачниках нет, то можно предложить ребятам дома
самим поработать над их составлением. А из лучших
работ составить сборник и вклеить в задачник,
которым пользуемся на уроке. Я думаю, что многие
ребята захотят в этом поучаствовать.

А теперь о понятии плотность.

При введении этой величины в учебниках
почему-то не оговаривается, что речь идет о
сплошных телах! И хотя в олимпиадных задачах и
в некоторых сборниках предлагаются задачи на
нахождение средней плотности (или задачи,
связанные с этой величиной) на уроках мы о ней не
говорим. А ведь несколько уроков назад было
введено понятие средней скорости, так почему по
аналогии не ввести понятие средней плотности?

Истинная плотность – отношение массы к
объему в абсолютно плотном состоянии (без пор и
пустот)

Средняя плотность – физическая величина,
определяемая отношением массы материала ко
всему занимаемому им объему, включая поры и
пустоты.

Средняя плотность не является величиной
постоянной и изменяется в зависимости от
пористости материала.

Интересно, что средняя плотность играет очень
важное значение для человека. Его плавучесть
зависит от средней плотности тканей его тела,
плотности воды, вдоха и выдоха. Чем меньше
средняя плотность тканей тела, тем лучше его
плавучесть. При глубоком вдохе пловец, как
правило, обладает положительной плавучестью, при
полном выдохе – отрицательной, он тонет. Человек
способен изменять свою среднюю плотность,
регулируя количество воздуха в легких! При
полном вдохе средняя плотность человеческого
тела становится меньше плотности воды. При
выдохе, когда тело теряет плавучесть, человеку
приходится создавать подъемную силу движением
рук. Получается, что умение плавать – это умение
правильно дышать!

Когда вводится понятие выталкивающей силы,
может ребятам будет понятнее, почему такие
огромные, тяжелые корабли плавают, если
поговорить опять о средней плотности корабля и
воды! Или привести такой пример: Плотность
стекла, из которого сделана бутылка, равна 2200 кг/
м³; плотность воды – 1000 кг/ м³.
Следовательно, стекло пойдет ко дну. Но если
стеклянная бутылка, наполненная воздухом, плотно
закрыта пробкой, она будет плавать на
поверхности воды. Масса стеклянной литровой
бутылки примерно равна 0,5 кг; масса воздуха,
заключенного в ней, – около 0,001 кг, а средняя
плотность закупоренной бутылки с воздухом – 501 кг/
м³ (0,5001 кг / 0,001 м³), т.е. вдвое меньше
плотности воды!

На уроке можно решить следующие задачи:

Какова плотность смеси глицерина и спирта, если
объем спирта составляет половину объема смеси?

Как изменится ответ, если масса спирта
составляет половину массы смеси?

Ответ: (900 кг/ м³)

Сплав золота и серебра массой 400г имеет
плотность 1,4 · 10⁴ кг/ м³. Полагая объем
сплава равным сумме объемов его составных
частей, определите массу золота в сплаве.

Ответ: (0,2 кг)

(Примеры данных задач взяты из сборника
“Решение ключевых задач по физике для основной
школы. 7-9 классы. Гейндешптейн Л.Э., Кирик Л.А.,
Гельфгат И.М, там же представлены их подробные
решения)

Использованная литература:

1. Гейндешптейн Л.Э., Кирик Л.А., Гельфгат И.М.
   “Решение ключевых задач по физике для основной
   школы. 7-9 классы. – М.: Илекса, 2006.
2. Детская энциклопедия, том 3 , издательство
   “Просвещение”, 1966
3. С.Е.Каменецкий, В.П.Орехов “Методика решения
   задач по физике в средней школе” издательство
   “Просвещение”, 1986
4. Г.С.Ландсберг “Элементарный учебник физики”,
   том 3, издательство “Физматлит”, 2000

Плотность
Размерность	L−3 M
Единицы измерения
СИ	кг/м³
СГС	г/см³
Примечания
скалярная величина

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму^[1].

Для обозначения плотности обычно используется греческая буква ρ (ро) (происхождение обозначения подлежит уточнению), иногда используются также латинские буквы D и d (от лат. densitas — «плотность»).

Более точное определение плотности требует уточнение формулировки:

• Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
• Плотность вещества — это плотность однородного или равномерно неоднородного тела, состоящего из этого вещества.
• Плотность тела в точке — это предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда этот объём стремится к нулю^[2], или, записывая кратко, . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.

Поскольку масса в теле может быть распределена неравномерно, более адекватная модель определяет плотность в каждой точке тела как производную массы по объёму. Если учитывать точечные массы, то плотность можно определить как меру, либо как производную Радона—Никодима по отношению к некоторой опорной мере.

Виды плотности и единицы измерения

Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.

Для сыпучих и пористых тел различают:

• истинную плотность, определяемую без учёта пустот;
• удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму. Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме. Для сыпучих тел удельная плотность называется насыпно́й плотностью.

Формула нахождения плотности

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

где m — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.

• При вычислении плотности газов при нормальных условиях эта формула может быть записана и в виде:

где М — молярная масса газа,  — молярный объём (при нормальных условиях приближённо равен 22,4 л/моль).

Плотность тела в точке записывается как

тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как

Зависимость плотности от температуры

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.

Диапазон плотностей в природе

Для различных природных объектов плотность меняется в очень широком диапазоне.

• Самую низкую плотность имеет межгалактическая среда (2·10⁻³¹—5·10⁻³¹ кг/м³, без учёта тёмной материи)^[3].
• Плотность межзвёздной среды приблизительно равна 10⁻²³—10⁻²¹ кг/м³.
• Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
• Плотность газообразного водорода (самого лёгкого газа) при нормальных условиях равна 0,0899 кг/м³.
• Плотность сухого воздуха при нормальных условиях составляет 1,293 кг/м³.
• Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
• Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
• Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
• Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
• Плотность пресной воды при 4 °C 1000 кг/м³.
• Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
• Гранит имеет плотность 2600 кг/м³.
• Средняя плотность Земли равна 5520 кг/м³.
• Плотность железа равна 7874 кг/м³.
• Плотность металлического урана 19100 кг/м³.
• Плотность атомных ядер приблизительно 2·10¹⁷ кг/м³.
• Теоретически верхняя граница плотности по современным физическим представлениям это планковская плотность 5,1·10⁹⁶ кг/м³.

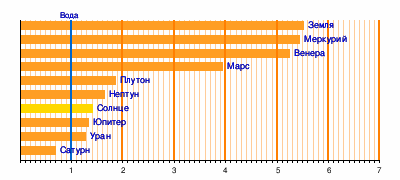
Плотности астрономических объектов

• Средние плотности небесных тел Солнечной системы см. на врезке.
• Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10⁻²¹÷10⁻²⁰ кг/м³.
• Плотность межзвёздной среды ~10⁻²³÷10⁻²¹ кг/м³.
• Плотность межгалактической среды 2×10⁻³⁴÷5×10⁻³⁴ кг/м³.
• Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
• Плотность белых карликов 10⁸÷10¹² кг/м³
• Плотность нейтронных звёзд имеет порядок 10¹⁷÷10¹⁸ кг/м³.
• Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:

Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M⁻²). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 10¹⁹ кг/м³, превышающей ядерную плотность (2×10¹⁷ кг/м³), то сверхмассивная чёрная дыра с массой в 10⁹ солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).

Плотности некоторых газов

Плотность газов, кг/м³ при НУ.

Азот	1,250	Кислород	1,429
Аммиак	0,771	Криптон	3,743
Аргон	1,784	Ксенон	5,851
Водород	0,090	Метан	0,717
Водяной пар (100 °C)	0,598	Неон	0,900
Воздух	1,293	Радон	9,81
Гексафторид вольфрама	12,9	Углекислый газ	1,977
Гелий	0,178	Хлор	3,164
Дициан	2,38	Этилен	1,260

Плотности некоторых жидкостей

Плотность жидкостей, кг/м³

Бензин	710	Молоко	1040
Вода (4 °C)	1000	Ртуть (0 °C)	13600
Керосин	820	Эфир	720
Глицерин	1260	Спирт	800
Морская вода	1030	Скипидар	860
Масло оливковое	920	Ацетон	792
Масло моторное	910	Серная кислота	1840
Нефть	550—1050	Жидкий водород (−253 °C)	70

Плотность некоторых пород древесины

Плотность древесины, г/см³

Бальса	0,15	Пихта сибирская	0,39
Секвойя вечнозелёная	0,41	Ель	0,45
Ива	0,46	Ольха	0,49
Осина	0,51	Сосна	0,52
Липа	0,53	Конский каштан	0,56
Каштан съедобный	0,59	Кипарис	0,60
Черёмуха	0,61	Лещина	0,63
Грецкий орех	0,64	Берёза	0,65
Вишня	0,66	Вяз гладкий	0,66
Лиственница	0,66	Клён полевой	0,67
Тиковое дерево	0,67	Бук	0,68
Груша	0,69	Дуб	0,69
Свитения (Махагони)	0,70	Платан	0,70
Жостер (крушина)	0,71	Тис	0,75
Ясень	0,75	Слива	0,80
Сирень	0,80	Боярышник	0,80
Пекан (кария)	0,83	Сандаловое дерево	0,90
Самшит	0,96	Эбеновое дерево	1,08
Квебрахо	1,21	Бакаут	1,28
Пробка	0,20

Плотность некоторых металлов

Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.

Плотность металлов, г/см³

Осмий	22,61[7]	Родий	12,41[8]	Хром	7,19[9]
Иридий	22,56[10]	Палладий	12,02[11]	Германий	5,32[12]
Плутоний	19,84[13]	Свинец	11,35[14]	Алюминий	2,70[15]
Платина	19,59[16]	Серебро	10,50[17]	Бериллий	1,85[18]
Тантал	19,30[19]	Медь	8,94[20]	Цезий	1,84[21]
Золото	19,30[14]	Никель	8,91[22]	Рубидий	1,53[23]
Уран	19,05[24]	Кобальт	8,86[25]	Натрий	0,97[26]
Ртуть	13,53[27]	Железо	7,87[28]	Калий	0,86[29]
Рутений	12,45[30]	Марганец	7,44[31]	Литий	0,53[32]

Измерение плотности

Для измерений плотности используются:

• Пикнометр — прибор для измерения истинной плотности
• Различные виды ареометров — измерители плотности жидкостей.
• Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
• Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.

См. также

• Список химических элементов с указанием их плотности
• Удельный вес
• Удельная плотность
• Относительная плотность
• Объёмная плотность
• Конденсация
• Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
• Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
• Концентрация частиц
• Концентрация растворов
• Плотность заряда
• Уравнение неразрывности

Примечания

Литература

• Плотность — статья из Большой советской энциклопедии.  — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
• Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
• Krebs R. E.  The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.

Ссылки

• Онлайн интерактивная таблица плотности веществ (рус.)
• Подробная таблица значений плотности распространенных жидкостей (рус.)

Как найти отношение средних плотностей

Отношение средних плотностей — это важный показатель, используемый в науке и инженерии. Оно позволяет определить соотношение массовых плотностей двух различных веществ. В этой статье мы рассмотрим, что такое отношение средних плотностей, зачем оно нужно и как его можно рассчитать.

Что такое отношение средних плотностей?

Отношение средних плотностей — это соотношение массовых плотностей двух различных веществ. Массовая плотность — это масса вещества, занимающего определенный объем пространства. Она измеряется в килограммах на кубический метр (кг/м3).

Отношение средних плотностей двух веществ может быть вычислено, если известны их массовые плотности. Это показатель часто используется в научных и инженерных расчетах, где необходимо знать соотношение масс двух различных веществ.

Зачем нужно отношение средних плотностей?

Отношение средних плотностей используется в различных областях науки и инженерии. Например, в строительстве и архитектуре оно используется для расчета нагрузки, которую может выдержать определенный материал или конструкция. В физике оно используется для анализа взаимодействия материалов или соединений. Также этот показатель может быть полезен в медицинских и биологических исследованиях для определения свойств тканей и организмов.

Как рассчитать отношение средних плотностей?

Для рассчета отношения средних плотностей двух веществ необходимо знать их массовые плотности. Формула для вычисления этого показателя выглядит следующим образом:

Отношение средних плотностей = массовая плотность первого вещества / массовая плотность второго вещества

Для примера, предположим, что массовая плотность первого вещества равна 2,5 кг/м3, а массовая плотность второго вещества — 1,5 кг/м3. Тогда отношение средних плотностей будет равно:

Отношение средних плотностей = 2,5 кг/м3 / 1,5 кг/м3 = 1,67

Это означает, что первое вещество имеет на 67% большую массовую плотность, чем второе вещество.

Вывод

Отношение средних плотностей — это важный показатель, используемый в науке и инженерии для определения соотношения масс двух различных веществ. Для его рассчета необходимо знать массовые плотности двух веществ. Он широко применяется в многих областях, включая строительство, физику, медицину и биологию.

• отношение средних плотностей
• средняя плотность
• массовая плотность
• вещество
• наука
• инженерия
• рассчет
• строительство
• физика
• медицина
• биология

Как найти отношение средних плотностей

Отношение средних плотностей — это важный параметр, который используется в различных областях науки и техники, включая физику, геологию и инженерное дело. Чтобы понять, как найти отношение средних плотностей, необходимо понимать, что это такое и как можно измерить плотность вещества.

Что такое плотность?

Плотность — это мера количества массы, содержащегося в единице объема вещества. Она определяется путем деления массы объекта на его объем.

Плотность = масса / объем

Плотность измеряется в стандартных единицах массы и объема, таких как килограмм на кубический метр (кг / м3) или грамм на кубический сантиметр (г / см3).

Как измерить плотность?

Существует несколько способов измерения плотности разных веществ, включая прямые и непрямые методы. Некоторые методы прямого измерения включают использование гравиметрических методов, анализа объемовых методов и пикнометровых методов.

Гравиметрические методы основаны на измерении массы материала и использовании его объема для вычисления плотности. Объемные методы используются для измерения объема вещества и вычисления его плотности на основе массы. Пикнометровые методы используют особое оборудование, называемое пикнометром, для измерения объема пробы посредством ее окунания в жидкость известной плотности.

Что такое средняя плотность и отношение средних плотностей?

Средняя плотность — это среднее значение плотности для некоторого количества материала, образцов или других объектов. Она вычисляется путем деления суммарной массы на суммарный объем объектов.

Отношение средних плотностей — это отношение средних плотностей двух разных веществ. Оно может быть полезным для сравнения различных материалов и определения их свойств.

Как найти отношение средних плотностей?

Отношение средних плотностей может быть найдено путем измерения плотности двух разных веществ и вычисления их средних значений для каждого вещества.

1. Выберите два разных вещества для измерения и подготовьте образцы.
2. Измерьте массу каждого образца, используя весы с высокой точностью.
3. Определите объем каждого образца с помощью пикнометра или другого способа измерения объема.
4. Вычислите плотность каждого образца, используя формулу плотности.
5. Найдите среднюю плотность каждого вещества, сложив плотности каждого образца и делением суммы на количество образцов.
6. Вычислите отношение средних плотностей путем деления средней плотности первого вещества на среднюю плотность второго вещества.

Отношение средних плотностей в различных науках и технике

Отношение средних плотностей играет важную роль в различных научных и технических областях, включая:

• Геология — отношение средних плотностей может использоваться для определения типа породы и ее состава.
• Авиация — отношение средних плотностей используется для определения оптимальной формы крыла самолета.
• Машиностроение — отношение средних плотностей может помочь инженерам выбрать оптимальный материал для производства запчастей и компонентов.
• Медицина — отношение средних плотностей может быть использовано для определения плотности тканей и диагностики заболеваний.

Вывод

Отношение средних плотностей — это важный параметр, который может помочь в понимании свойств материалов в различных научных и технических областях. Его можно вычислить путем измерения плотности каждого вещества и вычисления средних значений.

Измерение плотности требует использования специального оборудования и может быть сложным процессом, но понимание отношения средних плотностей может быть важным инструментом в решении научных и технических проблем.

Как найти отношение средних плотностей

Отношение средних плотностей может быть определено как соотношение плотностей двух материалов, которые находятся в смеси. Эта величина может быть использована для определения процента каждого материала в смеси. Однако, для этого нам нужно знать некоторые основные формулы математики и физики. В этой статье мы расскажем вам, как найти отношение средних плотностей без использования сложных формул и таблиц.

Определение понятий

Перед тем, как мы начнем, давайте рассмотрим некоторые основные понятия, которые будут использоваться в этой статье.

• Плотность — это масса в единицу объема. Обозначается символом «p» (ро).
• Смесь — это соединение двух или более веществ, которые находятся в одном и том же физическом состоянии.

Как найти отношение средних плотностей

Для определения отношения средних плотностей нам нужно знать плотности каждого из материалов, которые находятся в смеси, а также их процентное содержание в смеси.

Для удобства, давайте рассмотрим конкретный пример.

Представьте, что у вас есть смесь двух материалов. Первый материал имеет плотность 2,5 г/см³ и составляет 60% от всей смеси. Второй материал имеет плотность 3,5 г/см³ и составляет 40% от всей смеси. Каково отношение средних плотностей?

Для решения этой задачи нам необходимо выполнить следующие шаги:

1. Найдите вес каждого материала в смеси.
2. Найдите объем каждого материала в смеси.
3. Найдите среднюю плотность смеси.
4. Найдите отношение средней плотности к плотности каждого из материалов.

Шаг 1 – Найдите вес каждого материала в смеси

Первый шаг состоит в определении веса каждого материала в смеси. Для этого мы умножаем процентное содержание каждого материала на общий вес смеси.

Давайте найдем вес каждого материала в смеси:

• Первый материал: 0,6 x 1000 г = 600 г (масса первого материала в смеси).
• Второй материал: 0,4 x 1000 г = 400 г (масса второго материала в смеси).

Шаг 2 – Найдите объем каждого материала в смеси

После того, как мы нашли массу каждого материала в смеси, нам необходимо найти объем каждого материала в смеси. Для этого нам нужно знать плотности каждого из материалов.

Давайте найдем объем каждого материала в смеси:

• Первый материал: масса / плотность = 600 г / 2,5 г/см³ = 240 см³ (объем первого материала в смеси).
• Второй материал: масса / плотность = 400 г / 3,5 г/см³ = 114,3 см³ (объем второго материала в смеси).

Шаг 3 – Найдите среднюю плотность смеси

Теперь, когда мы знаем объем каждого материала в смеси, мы можем определить среднюю плотность смеси. Для этого мы суммируем объем каждого материала и делим на общий объем смеси.

Давайте найдем среднюю плотность смеси:

• Средний объем = объем первого материала + объем второго материала = 240 см³ + 114,3 см³ = 354,3 см³.
• Общий объем смеси = 1000 см³.
• Средняя плотность смеси = масса смеси / общий объем смеси = 1000 г / 1000 см³ = 1 г/см³.

Шаг 4 – Найдите отношение средней плотности к плотности каждого из материалов

Теперь мы можем найти отношение средней плотности к плотности каждого из материалов. Для этого мы делим среднюю плотность на плотность каждого материала.

Давайте найдем отношение средней плотности к плотности каждого из материалов:

• Первый материал: 1 г/см³ / 2,5 г/см³ = 0,4.
• Второй материал: 1 г/см³ / 3,5 г/см³ ≈ 0,29.

Вывод

Как мы видим, определение отношения средних плотностей не так уж и сложно, если есть необходимые формулы и калькуляторы. Для того чтобы справиться с этой задачей, нам нужно знать плотность каждого из материалов, их процентное содержание в смеси, а также следовать определенным шагам для расчета отношения средних плотностей. Это полезное умение, которое может пригодиться в различных областях, связанных с изучением материалов. Следуя нашим инструкциям, вы сможете легко определить отношение средних плотностей для любой смеси.