Опубликовано 3 года назад по предмету
Геометрия
от Настюша9518
-
Ответ
Ответ дан
Мавортий1)S1/S2=k^2=(2/3)^2=4/9
2)a1/a2=k=(9/2)=3/
(2)
3)a1/a2=P1/P2=90/60=1.5
S1/S2=k^2=(1.5)^2=2.25
4)k=15/10=1.5
S2=S1/k^2=45/2.25=20см^2
Самые новые вопросы
![]()
Математика – 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x – 5,21 = 9,54
![]()
Информатика – 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
![]()
География – 3 года назад
Почему япония – лидер по выплавке стали?
![]()
Математика – 3 года назад
Чему равно: 1*(умножить)х? 0*х?
![]()
Русский язык – 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
ГЛАВА VIII.
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ ФИГУР.
§ 92. ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ФИГУР.
1. Отношение площадей квадратов.
Рассмотрим отношение площадей двух квадратов. Если сторону одного квадрата обозначим через т, а сторону другого — через п, то площади будут соответственно равны
т2 и п2 (черт. 379).
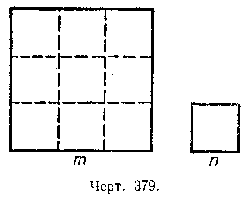
Обозначив площадь первого квадрата через S, а площадь второго через S’, получим: S/S’ = m2/n2 , т. е. площади квадратов относятся как квадраты их сторон.
Полученную формулу можно преобразовать так: S/S’ = ( m/n)2 .
Значит, можно сказать, что отношение площадей двух квадратов равно квадрату отношения их сторон.
На чертеже 379 отношение сторон квадратов равно 3, отношение их площадей равно
32 = 9.
2. Отношение площадей двух подобных треугольников.
Пусть / AВС ![]() / A’В’С’ (черт. 380). Из подобия треугольников следует, что
/ A’В’С’ (черт. 380). Из подобия треугольников следует, что
/
A = /
A’ , /
B = /
B’ и /
С = /
С’ . Кроме того, AB/A’B’ = BC/B’C’ = AC/A’C’.
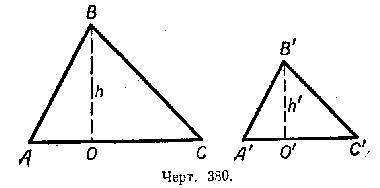
В этих треугольниках из вершин В и В’ проведём высоты и обозначим их через h и h‘. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника A’C’•h’/2.
Обозначив площадь первого треугольника через S, а площадь второго — через S’ получим: S/S’ = AC•h/A’C’•h’ или S/S’ = AC/A’C’ • h/h’
Из подобия треугольников АВО и А’В’О’ (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно /
A = /
A’ ) следует:
h/h’ = AB/A’B’ . Но AB/A’B’ = AC/A’C’ . Следовательно, h/h’ = AC/A’C’. Заменив в формуле S/S’ = AC/A’C’ • h/h’ отношение h/h’ равным ему отношением AC/A’C’ , получим:
S/S’ = AC/A’C’ • AC/A’C’ , или ![]() .
.
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S’ = (AC/A’C’ )2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
3. Отношение площадей подобных многоугольников.
Пусть ABCDE и A’B’C’D’E’ — подобные многоугольники (черт. 381).
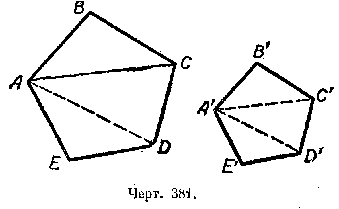
Известно, что / AВС ![]() / A’В’С’; / ACD
/ A’В’С’; / ACD ![]() / A’C’D’ и / ADE
/ A’C’D’ и / ADE ![]() / A’D’E’ (§90).
/ A’D’E’ (§90).
Кроме того,
![]() ;
; ![]()
Так как вторые отнoшения этих пропорций равны, что вытекает из подобия многоугольников, то ![]()
Используя свойство ряда равных отношений получим:
![]() , или
, или ![]()
где S и S’ — площади данных подобных многоугольников.
Следовательно, площади подобных многоугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать к такому виду: S/S’ = (AВ/A’В’ )2
Упражнения.
1. Сторона первого квадрата больше стороны второго квадрата в 2 раза (в 5 раз). Во сколько раз площадь первого квадрата больше площади второго квадрата?
2. Сторона первого квадрата составляет 1/3 (0,1) стороны второго квадрата. Какую часть площадь первого квадрата составляет от площади второго квадрата?
3. Коэффициент подобия в подобных многоугольниках равен 4 (1/5; 0,4; 2,5). Чему равно отношение их площадей?
4. Отношение площадей подобных многоугольников равно 36 (100; 0,09). Чему равно отношение сходственных сторон этих многоугольников?
1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно : 2 : 3 2.
Как относятся стороны двух квадратов, если отношение площадей этих квадратов равно : 4 : 9 Просьба с объяснением : 3.
Перед вами страница с вопросом 1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно : 2 : 3 2?, который относится к
категории Геометрия. Уровень сложности соответствует учебной программе для
учащихся 5 – 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
Найди верный ответ на вопрос ✅ «1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно: 2 : 3 2. Как относятся стороны двух квадратов, …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Геометрия » 1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно: 2 : 3 2. Как относятся стороны двух квадратов, если отношение площадей этих квадратов равно: 4:9 Просьба с объяснением: 3
Сторона одного квадрата равна 12 см, а сторона другого квадрата равна 2 см. Найдите отношение:
1) стороны большого квадрата к стороне малого квадрата;
2) периметра большого квадрата к площади малого квадрата;
3) площади большого квадрата к площади малого квадрата.
Какие из этих отношений равны? Равны ли отношения площадей и сторон квадратов?

reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 6.1 Что такое отношение. Номер №480
Решение 1
12 : 2 = 6 : 1 − отношение стороны большого квадрата к стороне малого квадрата.
Ответ: 6 : 1
Решение 2
1) 12 * 4 = 48 (см) − периметр большого квадрата;
2) 2 * 4 = 8 (см) − периметр малого квадрата;
3) 48 : 8 = 6 : 1 − отношение периметра большого квадрата к площади малого квадрата.
Ответ: 6 : 1
Решение 3
1) 12 * 12 = 144
(
с
м
2
)
− площадь большого квадрата;
2) 2 * 2 = 4
(
с
м
2
)
площадь малого квадрата;
3) 144 : 4 = 36 : 1 − отношение площади большого квадрата к площади малого квадрата.
Ответ: 36 : 1
Равны отношения стороны большого квадрата к стороне малого квадрата и отношение периметра большого квадрата к периметру малого квадрата. Отношения площадей и сторон квадратов не равны.
