ГЛАВА VIII.
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ ФИГУР.
§ 92. ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ФИГУР.
1. Отношение площадей квадратов.
Рассмотрим отношение площадей двух квадратов. Если сторону одного квадрата обозначим через т, а сторону другого — через п, то площади будут соответственно равны
т2 и п2 (черт. 379).
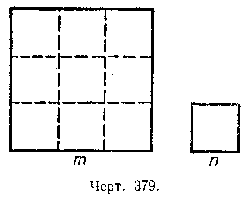
Обозначив площадь первого квадрата через S, а площадь второго через S’, получим: S/S’ = m2/n2 , т. е. площади квадратов относятся как квадраты их сторон.
Полученную формулу можно преобразовать так: S/S’ = ( m/n)2 .
Значит, можно сказать, что отношение площадей двух квадратов равно квадрату отношения их сторон.
На чертеже 379 отношение сторон квадратов равно 3, отношение их площадей равно
32 = 9.
2. Отношение площадей двух подобных треугольников.
Пусть / AВС ![]() / A’В’С’ (черт. 380). Из подобия треугольников следует, что
/ A’В’С’ (черт. 380). Из подобия треугольников следует, что
/
A = /
A’ , /
B = /
B’ и /
С = /
С’ . Кроме того, AB/A’B’ = BC/B’C’ = AC/A’C’.
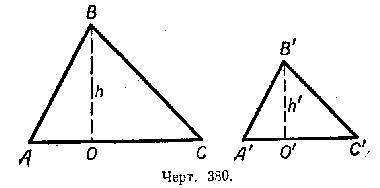
В этих треугольниках из вершин В и В’ проведём высоты и обозначим их через h и h‘. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника A’C’•h’/2.
Обозначив площадь первого треугольника через S, а площадь второго — через S’ получим: S/S’ = AC•h/A’C’•h’ или S/S’ = AC/A’C’ • h/h’
Из подобия треугольников АВО и А’В’О’ (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно /
A = /
A’ ) следует:
h/h’ = AB/A’B’ . Но AB/A’B’ = AC/A’C’ . Следовательно, h/h’ = AC/A’C’. Заменив в формуле S/S’ = AC/A’C’ • h/h’ отношение h/h’ равным ему отношением AC/A’C’ , получим:
S/S’ = AC/A’C’ • AC/A’C’ , или ![]() .
.
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S’ = (AC/A’C’ )2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
3. Отношение площадей подобных многоугольников.
Пусть ABCDE и A’B’C’D’E’ — подобные многоугольники (черт. 381).
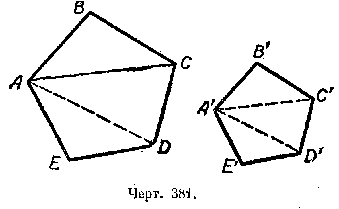
Известно, что / AВС ![]() / A’В’С’; / ACD
/ A’В’С’; / ACD ![]() / A’C’D’ и / ADE
/ A’C’D’ и / ADE ![]() / A’D’E’ (§90).
/ A’D’E’ (§90).
Кроме того,
![]() ;
; ![]()
Так как вторые отнoшения этих пропорций равны, что вытекает из подобия многоугольников, то ![]()
Используя свойство ряда равных отношений получим:
![]() , или
, или ![]()
где S и S’ — площади данных подобных многоугольников.
Следовательно, площади подобных многоугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать к такому виду: S/S’ = (AВ/A’В’ )2
Упражнения.
1. Сторона первого квадрата больше стороны второго квадрата в 2 раза (в 5 раз). Во сколько раз площадь первого квадрата больше площади второго квадрата?
2. Сторона первого квадрата составляет 1/3 (0,1) стороны второго квадрата. Какую часть площадь первого квадрата составляет от площади второго квадрата?
3. Коэффициент подобия в подобных многоугольниках равен 4 (1/5; 0,4; 2,5). Чему равно отношение их площадей?
4. Отношение площадей подобных многоугольников равно 36 (100; 0,09). Чему равно отношение сходственных сторон этих многоугольников?
1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно : 2 : 3 2.
Как относятся стороны двух квадратов, если отношение площадей этих квадратов равно : 4 : 9 Просьба с объяснением : 3.
Перед вами страница с вопросом 1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно : 2 : 3 2?, который относится к
категории Геометрия. Уровень сложности соответствует учебной программе для
учащихся 5 – 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
Канал видеоролика: Решение задач Математика и Физика

Смотреть видео:
#физика #егэфизика #огэфизика #термодинамика #ифтис #фтф #мифи #мфти #физтех
Свежая информация для ЕГЭ и ОГЭ по Физике (листай):
С этим видео ученики смотрят следующие ролики:

Геометрия Найдите отношение площадей двух квадратов, стороны которых относятся как: 1) 3:4; 2) 2:√5
Решение задач Математика и Физика

Геометрия Подобны ли два треугольника, если стороны одного относятся как 3:8:9, а стороны другого
Решение задач Математика и Физика

Геометрия доказательство теоремы косинусов Квадрат стороны треугольника равен сумме квадратов двух
Решение задач Математика и Физика

Геометрия Докажите что если квадрат стороны треугольника равен неполному квадрату суммы двух других
Решение задач Математика и Физика
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
16.11.2020
Найди верный ответ на вопрос ✅ «1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно: 2 : 3 2. Как относятся стороны двух квадратов, …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Геометрия » 1. Найдите отношение площадей двух квадратов, если отношение сторон этих квадратов равно: 2 : 3 2. Как относятся стороны двух квадратов, если отношение площадей этих квадратов равно: 4:9 Просьба с объяснением: 3
Утверждение
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия.
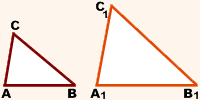 Дано:
Дано:
![]()
Доказать:
![]()
Площадь треугольника ABC может быть найдена, например, по двум сторонам и углу между ними:
![]()
Аналогично,
![]()
Так как углы подобных треугольников равны, а стороны — пропорциональны, то ∠A=∠A1,
![]()
то есть
![]()
Теперь можем найти, как относятся площади подобных треугольников:
![]()
![]()
Так как
![]()
то
![]()
то есть
![]()
![]()
Что и требовалось доказать.
Поскольку отношение любых линейных размеров (высот, медиан, биссектрис, периметров) подобных треугольников равно коэффициенту подобия, площади подобных треугольников относятся как квадраты их соответствующих линейных размеров.
