Как найти отношение заряда к массе электрона - Сайт, где вы сможете решить свои вопросы

Министерство
путей сообщения Российской
Федерации

Департамент
кадров и учебных заведений

Самарская государственная академия путей сообщения

Кафедра физики и экологической теплофизики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ по
дисциплине

«ФИЗИКА. ЭЛЕКТРИЧЕСТВО»

для
студентов всех специальностей

дневной
и заочной форм обучения

Составители: Жмур
Л.Е.

Рящиков А.С.

Стрыгин Ю.Ф.

САМАРА
2004

УДК
537

Методические
указанияк
выполнению лабораторных работ по
дисциплине «Физика. Электричество» для
студентов всех специальностей дневной
и заочной форм обучения / Составители:
Л.Е. Жмур, А.С. Рящиков, Ю.Ф. Стрыгин. –
Самара: СамГАПС, 2004- 31 c.

Утверждены
на заседании кафедры «Физика и ЭТ» 26
июня 2003 г, протокол № 10.

Печатается по
решению редакционно-издательского
совета академии.

Приведены
методические указания по выполнению
лабораторных работ для студентов по
рассматриваемой дисциплине.

В методических
указаниях приведены необходимые
теоретические сведения по разделу
«Электричество», даны схемы и описания
лабораторных установок, порядок
проведения исследований и контрольные
вопросы для самостоятельной подготовки
студентов.

Составители: Жмур
Леонид Емельянович,

Рящиков
Александр Сергеевич,

Стрыгин
Юрий Федорович

Рецензенты: к.т.н.,
профессор Гуменников Валерий Борисович,
СамГАПС;

д.ф.-м.н.,
профессор Кононенко Вадим Степанович
СамГТУ.

Редактор: И.М.
Егорова

Компьютерная
верстка: А.А. Егоров

Подписано в печать
29.09.04.Формат 6090 1/16.

Бумага писчая.
Печать оперативная. Усл. п. л. 2,0.

Тираж 700 экз. Заказ
№135.

©Самарская государственная академия
путей сообщения, 2004

ЛАБОРАТОРНАЯ
РАБОТА № 20

Определение отношения заряда электрона к его массе методом магнетрона

Цель
работы: изучение движения электронов
в электрических и магнитных полях;
ознакомление с методами измерения
параметров элементарных частиц.

ТЕОРЕТИЧЕСКОЕ
ВВЕДЕНИЕ

М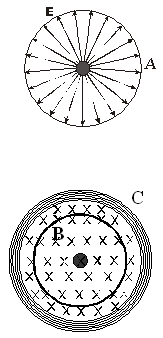асса
и заряд микрочастиц являются основными
величинами, определяющими
их свойства.
Эти величины можно определить, изучая
движение таких частиц в электрических
и магнитных полях.

Рис.
1

ля создания потока электронов
применяется электронная лампа, катод
которой расположен вдоль оси цилиндрического
анода А. На рис. 1 катод изображен черным
кружком в центре. Между анодом и катодом
создается разность потенциалов, которая
называется анодным напряжением
U_a.
Стрелками показаны силовые линии
напряженности Е электрического
поля между анодом и катодом.
Электроны, вылетающие из
раскаленного катода с различными
скоростями, под действием сил электрического
поля движутся к аноду. Поток этих
электронов создает анодный ток I_a
лампы.

Для создания внутри
электронной лампы однородного магнитного
поля ее помещают в достаточно длинный
соленоид С (рис. 2). Электронная лампа
вместе с соленоидом представляет собой
прибор, который называется магнетроном.

Рис.
2

При пропускании через
соленоид электрического тока силой I_св нем возникает магнитное поле.
Магнитная индукцияВэтого поля
направлена вдоль оси соленоида и
параллельна катоду.

Значение
индукции магнитного поля в соленоиде
вычисляется по формуле

(1)

где п
– число витков
на единицу длины соленоида,

 –
магнитная проницаемость среды внутри
соленоида (для воздуха считать 
= 1),

₀=
4·10^-7Гн/м –
магнитная постоянная.

На электроны,
движущиеся от катода к аноду, действуют
электрическое и магнитное поля.

Действие
электрического поля на электрон.
Рассмотрим только те электроны, которые
покидают катод со скоростями, близкими
к нулю. Тогда можно считать, что скорость
v,
приобретенная электроном под действием
сил электрического поля, направлена
вдоль радиуса цилиндрического анода
А. Скорость каждого электрона, движущегося
от катода к аноду, под действием сил
электрического поля увеличивается. Для
описанной электронной лампы расчет
показывает, что напряженность
электрического поля имеет заметную
величину только вблизи катода. Поэтому
можно считать, что электроны почти всю
свою скорость приобретают в области,
близкой к катоду. Дальнейшее их движение
к аноду происходит с почти постоянной
по величине скоростью.

Скорость электронов
можно определить из условия, что работа
сил электрического поля по
перемещению
электрона от катода к аноду, равная eU_a,идет на
приращение кинетической энергии
электрона. Для электронов, испускаемых
нагретым катодом с начальной скоростью
равной нулю, получаем:

. (2)

Здесь
е
–
заряд электрона, а m
– его масса.

Из
выражения (2) следует, что скорость, с
которой электрон подходит к аноду

. (3)

Опыт показывает,
что магнитное поле действует на отдельные
движущиеся электрические заряды. Сила,
действующая на электрический заряд Q,
движущийся в магнитном поле со скоростью
v,
называется силой Лоренца, которая
определяется выражением:

F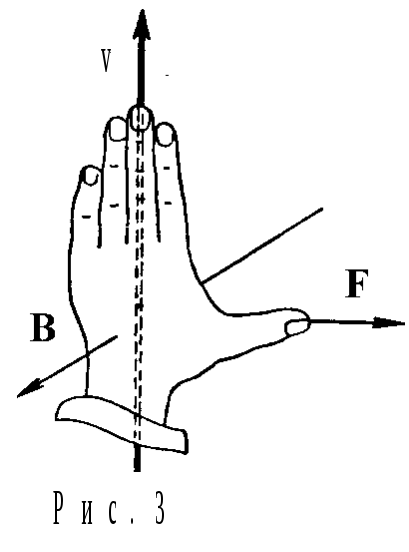_л
= QvB,

где
В
– вектор индукция
магнитного поля, в котором движется

заряд.

Величина
этой силы для электрона вычисляется по
формуле

, (4)

где B
– модуль
индукции магнитного поля внутри
соленоида,



Рис.
3

– угол между
вектором индукции магнитного поля и
вектором скорости заряженной частицы
(электрона). Для нашего случая 
= 90⁰.
Следовательно,

. (5).

Направление силы
Лоренца для положительного заряда
определяется с помощью правила левой
руки (рис. 3).

Если ладонь
левой руки расположить так, чтобы в нее
входил вектор
В,
а четыре вытянутых пальца направить
вдоль вектора скорости v
положительного заряда,
то отогнутый большой палец покажет
направление силы, действующей на заряд.

С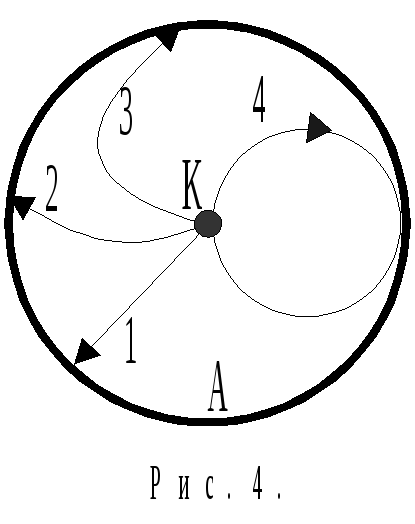ила
Лоренца, действующая на отрицательный
заряд, в частности на электрон, будет
направлена в противоположную сторону.

Рис.
4

сли на движущийся электрический
заряд кроме магнитного поля с индукциейВ действует
электрическое поле с напряженностью
Е, то
результирующая сила F,
приложенная к заряду, равна векторной
сумме сил, действующих со стороны
электрического поля и силы Лоренца:

F
= QE+QvB.

Иногда
эту силу также называют силой Лоренца,
но мы этого делать не будем.

Рис.
5

илаF_л
направлена перпендикулярно
к вектору скорости электрона. Поэтому
под действием силы Лоренца изменяется
только направление скорости электрона,
а ее модуль остается постоянным.
Вследствие этого траектория движения
электронов искривляется. На рис. 4
показаны траектории электронов в
магнетроне при одновременном действии
электрического и магнитного полей
(силовые линии этих полей не показаны).
При отсутствии магнитного поля (В
= 0) электрон движется по радиусу анода
(кривая 1). В слабых магнитных полях, т.е.
при 0<В<B₀
, траектория электронов в разной степени
искривляется, но они доходят до анода
(кривые 2-3). При достаточно сильном
магнитном поле (В = B₀)
траектория электрона становится
окружностью с радиусом r
= R/2,
и он не попадает на анод (R–радиус
анода). При В > B₀
радиус траектории электрона становится
еще меньше. Электроны, не достигающие
анода, не участвуют в создании анодного
тока. Поэтому при увеличении магнитного
поля в соленоиде анодный ток уменьшается.

Графически
зависимость силы анодного тока I_a
от силы тока в соленоиде I_c
представлена на рис. 5. Пока I_cизменяется
от нуля до I₀,траектория
электронов искривляется, но все они
достигают анода (рис. 4). Поэтому анодный
ток не изменяется. При силе тока в
соленоиде равном I₀,
который соответствует индукции магнитного
поля в соленоиде В₀,
анодный ток начинает уменьшаться за
счет электронов, которые покидают катод
со скоростью равной нулю и не доходят
до анода. При дальнейшем увеличении
силы тока в соленоиде до анода не доходят
электроны, имеющие различную начальную
скорость. Поэтому при увеличении
магнитного поля анодный ток продолжает
уменьшаться.

Под действием силы
Лоренца электрон получает нормальное
ускорение v²/r,
где r–
радиус кривизны траектории электрона.
По второму закону Ньютона связь между
массой электрона m,
его ускорением и силой F_л
для рассматриваемого случая выражается
равенством:

.
(6)

Из равенства (6)
имеем:

. (7)

Из формул (2) и (7)
получим выражение для отношения заряда
электрона к его массе:

. (8)

При силе тока в
соленоиде равном I₀
индукция магнитного поля в соленоиде

B
= В₀,
а r
= R/2.

Подставляя в
формулу (8) значения r
= R/2
и В =B₀₀nI₀,
получим

. (9)

Описание методики
измерений

Основой
лабораторной установки является модуль
ФПЭ–03, в котором находится магнетрон
(электронная лампа в соленоиде). На
передней панели модуля изображена
упрощенная принципиальная электрическая
схема и установлены гнезда РА для
подключения прибора, измеряющего анодный
ток лампы. Там же установлен амперметр
для измерения силы тока в соленоиде и
вольтметр для измерения анодного
напряжения. Источник питания подключается
к модулю ФПЭ–03 кабелем с соответствующими
разъемами. На задней панели установлены
разъем для подвода питания и клемма
заземления.

Принцип
работы модуля ФПЭ–03 заключается в
измерении анодного тока лампы, помещенной
в магнитное поле соленоида. Ток в
соленоиде изменяется ручкой с надписью
2,5…25 В. При этом переключатель,
расположенный рядом, нужно направить
в сторону этой ручки. Ток накала
устанавливается ручкой с надписью 2,5 –
4,5 В.

Параметры
лабораторной установки, необходимые
для выполнения работы:

1) Средний радиус
анода лампы магнетрона R,
мм 3.

2)Длина соленоида
l,
мм 120.

3)Число витков
соленоида
N 2800.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Фундаментальные физические постоянные

[универсальные] [электромагнитные] [атомные] [электрон] [мюон] [протон] [нейтрон] [физико-химические]

УНИВЕРСАЛЬНЫЕ ПОСТОЯННЫЕ

Скорость света в вакууме
c = 299 792 458 м*с^-1 =
2,997 924 58*10¹⁰ см / с (точно)

Магнитная постоянная
μ₀ = 4 π*10^-7 Гн / м = 12,566 370 614*10^-7 Гн / м (точно)

Электрическая постоянная
ε₀ = (μ₀ c²)^-1 = 8,854 187 817*10^-12 Ф / м (точно)

Гравитационная постоянная
G = 6,672 59(85)*10^-11 Н*м² / кг² =
6,672 59(85)*10^-8 дин*см² / г²

Постоянная Планка
h = 6,626 075 5(40)*10^-34 Дж с = 6,626 075(40)*10^-27 эрг с,
h = h / (2π) = 1,054 588 7(57)*10^-34 Дж с = 1,054 588 7(57)*10^-27 эрг с.
Планковская масса (h c / G)^1/2 = m_Pl = 2,176 71(14)*10^-8 кг
Планковская длина h / (m_Pl c) = l_Pl = 1,616 05(10)*10^-35 м
Планковское время l_Pl / c = t_Pl = 5,390 56(34)*10^-44 с

ЭЛЕКТРОМАГНИТЫЕ ПОСТОЯННЫЕ

Элементарный заряд
e = 1,602 177 33(49)*10^-19 Кл = 4,8032 СГС

Квант магнитного потока
Ф₀ = h / (2 e) = 2,067 834 61(61)*10^-15 Вб

Квант холловского сопротивления
R_H = h / e² = 25 812,805 6(12) Ом

Соотношение Джозефсона между частотой и напряжением
При приложении напряжения к двум сверхпроводникам, разделенным тонким (порядка одного нанометра) слоем диэлектрика, через образующийся при этом неплотный контакт идет переменный
сверхпроводящий ток, частота которого связана с напряжением соотношением

где 2 e / h = 4,835 976 7(14)*10¹⁴ Гц / В.

Бора магнетон
Электрон, обращающийся по круговой орбите, в “классической” теории Бора представляет собой
круговой ток, обладающий магнитным моментом. Для основной орбиты этот момент называется магнетоном Бора.

μ_B =e h / (2 m_e)
μ_B = 9,274 015 4(31)*10^-24 Дж / Тл =
9,274 015 4(31)*10^-11 эрг / Гс =
   = 5,788 382 63(52)*10^-5 эВ*Тл^-1

Ядерный магнетон
μ_N = e h / (2 m_p) = 5,050 786 6(17)*10^-27 Дж / Тл =
3,152 451 66(28)*10^-8 эВ / Тл

АТОМНЫЕ ПОСТОЯННЫЕ

Тонкой структуры постоянная.
Исследование спектральных линий водорода с помощью приборов высокой разрешающей способности показало, что эти линии обладают тонкой структурой, то есть состоят из нескольких линий,
весьма близко расположенных друк к другу. Тонкая структура объясняется при учете теории относительности и собственного магнитного момента электрона. Добавочная энергия, создающая расщепление линий, определяется выражением, в которое входит безразмерный множитель,
называемый постоянной тонкой структуры. Его выражение

α = μ₀ c e² / 2 h  (СИ),
α = e² / h c    (СГС)
и числовое значение:   α = 0,007 297 353 08(33).
Обратное значение постоянной тонкой структуры:   1 / α = 137,035 989 5(61).

Ридберга постоянная

Формула

ν = RZ² (1 / n₁² – 1 / n₂²),
(где ν – волновое число данной линии, n₁ и n₂ – квантовые числа энергетических уровней, переход между которыми сопровождается излучением
соответстующего кванта, R – так называемая постоянная Ридберга.)
определяет волновые числа спектральных линий водородоподобного атома. Входящая в эту формулу постоянная Ридберга определяется выражением

R = [ (m_ee⁴) / (4πh³e) ]*[λ + m_e / M ],
где M – масса ядра атома. Для ядра бесконечой массы
R_∞ = 10 973 731,534(13) м^-1 = 109 737,315 34(113) см^-1
R_∞ c = 3,289 841 949 9(39)*10¹⁵ Гц
R_∞ h c =13,605 698 1(40) эВ

Радиус Бора – радиус первой (основной) орбиты электрона в атоме водорода по “классической” теории Бора:
a₀ = α / (4πR_∞) = 0,529 177 249(24)*10^-10 м = 0,052 917 724 9(24) нм

Хартри энергия
E_H = 2 R_∞ h c =
   = 4,359 748 2(26)*10^-18 Дж = 27,211 396 1(81) эВ

ЭЛЕКТРОН

Масса покоя электрона
m_e = 9,109 389 7(54)*10^-31 кг = 9,109 389 7(54)*10^-28 г =
5,485 799 03(13)*10^-4 а.е.м.

Погрешность определения абсолютных значений масс электрона и атомных частиц (в килограммах или граммах) выше, чем погрешность определения относительных масс (в атомных единицах массы), так как ограничена погрешностью определения числа Авогадро.

Энергия, эквивалентная массе покоя электрона,
m_e c² = 8,187 24(5)*10^-14 Дж = 8,187 24(5)*10^-7 эрг = 0,510 999 06(15) МэВ.

Удельный заряд электрона (отношение заряда электрона к его массе)
e / m_e =- 1,758 819 62(53)*10¹¹ Кл / кг = 5,272 764(9)*10^-17 СГС / г.

Молярная масса электрона
M_e = 5,485 799 03(13)*10^-7 кг / моль

Комптоновская длина волны электрона
При рассеянии рентгеновских лучей на свободных электронах происходит изменение длины волны, обусловленное обменом энергией и импульсом между фотоном и электроном.
Это изменение определяется формулой

δλ = λ_C(1 + cos θ),
где θ – угол отклонения фотона от первоначального направления, а λ_C – комптоновская длина волны:
λ_C = h / (m_e c) = 2,426 310 58(22)*10^-12 м = 2,426 310 58(22)*10^-3 нм.
Иногда в уравнеия вводят величину, в 2π раз меньшую:
λ_C = λ_C / (2 π) = 0,386 159 0(6)*10^-12 м = 0,386 159 0(6)*10^-3 нм.

Классический радиус электрона
r_e = α² α₀ = 2,817 940 92(38)*10^-15 м

Томсоновское сечение рассеяния (электрона)
σ_e = (8 π / 3) r_e³ = 0,665 246 16(18)*10^-28 м²

Магнитный момент электрона
μ_e = 9,284 770 1(31)*10^-24 Дж / Тл = 928 477,01(31)*10^-21 эрг / Гс
μ_e / μ_B = 1,001 159 652 193(10)

Аномалия магнитного момента (электрона)
a_e = μ_e / μ_B – 1 = 1,159 652 193(9)*10^-3
g-фактор,
g_e = 2 (1 + a_e) = 2,002 319 304 386(20)

МЮОН

Масса мюона
m_μ = 1,883 532 7(11)*10^-28 кг = 0,113 428 913(17) а.е.м
Энергия, соответствующая массе покоя мюона,
m_μ c² =105,658 389(34) МэВ

Магнитный момент мюона
μ_μ = 4,490 451 4(15)*10^-26 Дж / Тл
μ_μ / μ_N = 8,890 598 1(13)

Аномалия магнитного момента мюона

a_μ = μ_μ – 1 = 1,165 923 0(84)*10^-3

e h / (2 m_μ)

g-фактор,
g_μ = 2 (1 + a_μ) = 2,002 331 846(17)

ПРОТОН

Масса покоя протона
m_p = 1,672 623 1(10)*10^-27 кг = 1,672 623 1(10)*10^-24 г = 1,007 276 470(12) а.е.м.
Энергия, эквивалентная массе покоя протона,
m_p c² = 1,503 301(9)*10^-10 Дж = 1,503 301(9)*10^-3 эрг = 938,272 31(28) МэВ.

Отношение массы протона к массе электрона
m_p / m_e = 1836,152 701(37)

Удельный заряд протона
e / m_p = 9,578 830 9(29)*10⁷ Кл / кг

Комптоновская длина волны протона
λ_C,p = 1,321 410 02(12)*10^-15 м

Магнитный момент протона
μ_p = 1,410 607 61(47)*10^-26 Дж / Тл
μ_p / μ_N = 2,792 847 386(63)

Поправка на диамагнитное экранирование для сферического образца H₂O при 25^oC
1 – μ_p / μ_p‘ = 25,689*10^-6

Магнитный момент протона без поправки на диамагнетизм
μ_p‘ = 1,410 541 38(47)*10^-26 Дж/ Тл

Гиромагнитное отношение (протона)
γ_p = 26 752 212 8(81)*10⁴ с^-1 Тл^-1

НЕЙТРОН

Масса покоя нейтрона
m_n = 1,674 928 6(10)*10^-27 кг = 1,674 928 6(10)*10^-24 г = 1,008 664 904(14) а.е.м.
Энергия, соответствующая массе покоя нейтрона,
m_n c² = 1,505 373(9)*10^-10 Дж = 1,505 373(9)*10^-3 эрг = 939,573(3) МэВ.

Отношение массы нейтрона к массе протона
m_n / m_p = 1,001 378 404(9)

Комптоновская длина волны (нейтрона)
λ_C,n = h / (m_n c) = 1,319 591 10(12)*10^-15 м

Магнитный момент нейтрона (скалярная величина момента) {Магниный момент н. антипараллелен механическому, и знак магнитого момента отрицательный}
μ_n = 0,966 237 07(40)*10^-26 Дж / Тл
μ_n / μ_N = 1,913 042 75(45)

ФИЗИКО-ХИМИЧЕСКИЕ ПОСТОЯННЫЕ

Авогадро постоянная (число Авогадро)
N_A = 6,022 136 7(36)*10²³ моль^-1

Атомная единица массы – одна двенадцатая часть массы изотопа углерода с массовым числом 12:
1 а.е.м. = (m_u) = m(¹²C) / 12 = 1,660 540 2(10)*10^-27 кг = 1,660 540 2(10)*10^-24 г
Энергия, эквивалентная атомной единице массы,
1 (а.е.м)*c² = 1,492441(9)*10^-10 Дж = 1,492441(9)*10^-10 = 931,494 32(98) МэВ.

Атмосфера стандартная
1 атм = 101 325 Па (точно)

Больцмана постоянная может быть определена как отношение универсальной газовой постоянной к постоянной Авогадро:
k = R / N_A = 1,380 658(12)*10^-23 Дж / K = 1,380 658(12)*10^-16 эрг / K

Вина постоянная
b = 2,897 8(1)*10^-3 м K = 0,289 78(1) см K

Постоянную в законе Стефана-Больцмана можно связать с постоянной Планка и скоростью света, если проинтегрировать формулу Планка по частотам или по длинам волн и определить коэффициет

Точно так же может быть определена постоянная в законе смещения Вина, если продифференцировать формулу Планка по длинам волн и найти положение максимума. Постоянная при этом имеет вид

Числа 1,0823 и 4,9651 получаются в процессе решения уравнений.

Излучения постоянная
первая   c₁ = 2 π h c² = 3,741 774 9(22)*10^-16 Вт м²
вторая   c₂ = h c / k = 0,014 387 69(12) м K

Лошмидта постоянная(число Лошмидта) – число молекул в единице объема вещества, находящегося в состоянии идеального газа при нормальных условиях
(T₀ = 273,15 K, p₀ = 1,013 25*10⁵ Па)
N_Л = 2,686 75*10²⁵ м^-3 = 2,686 75*10¹⁹ см^-3

Объем моля идеального газа при нормальных условиях
(Нормальный объем газа, T₀ = 273,16 K,  p₀ = 101 325 Па)
V₀ = 22,413 83(10)*10^-3 м³моль^-1.

Стефана-Больцмана постоянная
σ = π² k² / (60 h³ c²) =
    = 5,670 51(19)*10^-8 Вт / (м² K⁴) =
5,670 51(19)*10^-5 эрг / (с см² K⁴)

Ускорение силы тяжести (стандартное)
g_n = 9,806 65 м / с² (точно)

Универсальная газовая постоянная (молярная газовая постоянная).

Уравнение Менделеева-Клапейрона устанавливает связь между
температурой, давлением, объемом и количеством молей газа.

где R – универсальная (молярная) газовая постоянная. Строго говоря, уравнение Менделеева-Клапейрона
справедливо для идеального газа, но практически хорошо оправдывается при не слишком больших давлениях
и не слишком низких температурах. Из уравнения Менделеева-Клапейрона можно определить универсальную
газовую постоянную, если известен объем данного количества молей газа при заданных условиях. Этот объем
(нормальный объем) известен при нормальных условиях. Подставляя в уравнение

R = p₀ V₀ / T₀
соответствующие значения, найдем

R = 8,314 510(70) Дж / (моль K) = 8,314 510(70)*10⁷ эрг / (моль K)
Универсальная газовая постоянная численно равна работе расширения одного моля газя на один градус при постоянном давлении.

Фарадея постоянная (число Фарадея) – произведение постоянной Авогадро на элементарный электрическиий заряд:
F = e N_A = 96 485,309(29) Кл / моль = 2,892 53(1)*10¹⁴ СГС / моль

Электрон-вольт
1эВ = 1,602 177 33(49)*10^-19 Дж

Источник

Ответ:

-2*10¹¹ Кл/кг

Объяснение:

Кулоновская сила сообщает электрону центростремительное ускорение (силами гравитационного взаимодействия частиц пренебрегаем), запишем второй закон Ньютона: