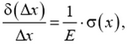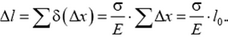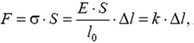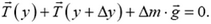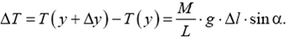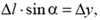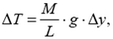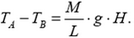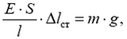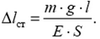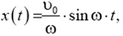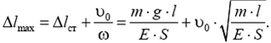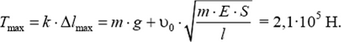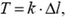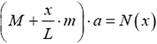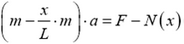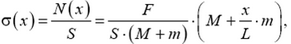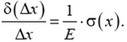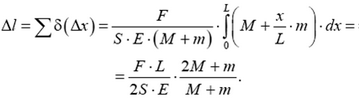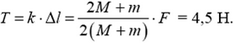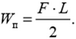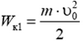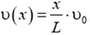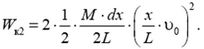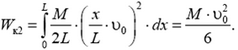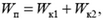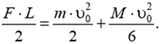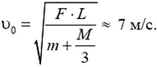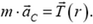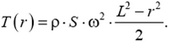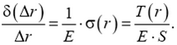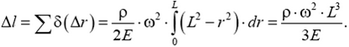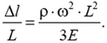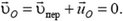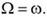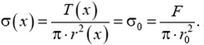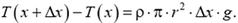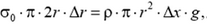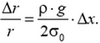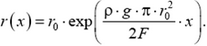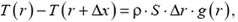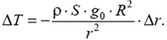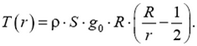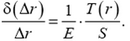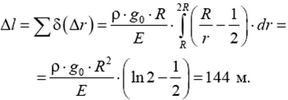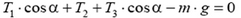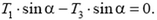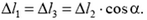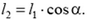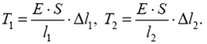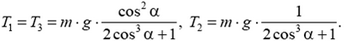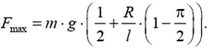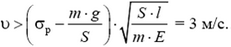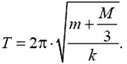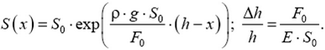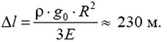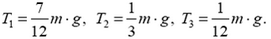Как найти относительное удлинение стержня

Как найти относительное удлинение стержня

Макеты страниц

Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна то после нагружения она станет равной (рис. 1.6). Величину называют абсолютным удлинением стержня.

Рис. 1.8

Будем считать, что абсолютное удлинение и деформации связаны только с напряжениями, возникающими в стержне. В действительности имеются и другие факторы, влияющие на деформации. Так, деформации зависят от температуры и времени действия нагрузки. Неупругие деформации зависят от “истории” нагружения, т.е. от порядка возрастания и убывания внешних сил. Пока, однако, этих вопросов мы касаться не будем.

Если стержень нагружен только силой Р, то напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях; деформация по оси стержня остается одной и той же, равной своему среднему значению по длине

Эта величина называется относительным удлинением стержня.

Если стержень нагружен сосредоточенной силой Р и распределенными силами (наиболее общий случай), то относительное удлинение не будет постоянным по длине стержня. Получим выражение для относительного удлинения стержня, рассматривая элемент стержня между плоскостями и

до и после нагружения (см. рис. 1.6). Если обозначить перемещение плоскости АА элемента стержня через и, то плоскость будет иметь перемещение, равное и где – дополнительное перемещение из-за растяжения элемента стержня. Тогда относительное удлинение элемента будет равно

Заметим, что вследствие равномерного распределения напряжений по сечению удлинения для всех элементарных отрезков (см. рис. 1.6), взятых на участке оказываются одинаковыми. Следовательно, если концы отрезков до нагружения образуют плоскость, то и после нагружения стержня они образуют плоскость, но смещенную вдоль оси стержня. Это положение может быть взято в основу толкования механизма растяжения и сжатия и трактуется как гипотеза плоских сечений (гипотеза Бернулли). Если эту гипотезу принять как основную, то тогда из нее, уже как следствие, вытекает высказанное ранее предположение о равномерности распределения напряжений в поперечном сечении.

В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:

Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода. Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и а, т.е. в мегапаскалях. Вместе с тем, поскольку модуль упругости может иметь довольно большие числовые значения, его предпочтительнее измерять не в мега-, а в гигапаскалях:

Для наиболее часто применяемых материалов модуль упругости Е имеет следующие значения,

Закон Гука представляет собой простейшую и очевидную аппроксимацию наблюдаемой в опытах зависимости удлинения от напряжения. Естественно, что точность этой аппроксимации определяется в первую очередь тем, сколь широкий диапазон изменения напряжения имеется в виду. Всегда можно подобрать достаточно малый интервал напряжений, чтобы в его пределах функцию можно было бы с заданной точностью рассматривать как линейную. И конечно, для разных материалов это выглядит по-разному. Для некоторых материалов, таких как, например, сталь, закон Гука соблюдается с высокой степенью точности в широких пределах изменения напряжений. Для отожженной меди, для чугуна этот интервал изменения напряжений существенно меньше. В тех случаях, когда закон Гука явно не соблюдается, деформацию задают в виде некоторой нелинейной функции от напряжения с таким расчетом, чтобы эта функция отвечала кривой, полученной при испытании материала.

Вернемся к выражению (1.4) и заменим в нем а на на Тогда получим

или

В результате получаем систему, состоящую из двух уравнений: первого уравнения системы (полагая ) и уравнения (1.5), которая позволяет определить напряженно-деформированное состояние прямолинейного стержня, нагруженного осевыми силами:

Из первого уравнения системы (1.6) находим осевое усилие а из второго – Получаемые выражения для и и будут содержать две произвольные постоянные, определяемые из двух краевых условий: при

Абсолютное удлинение стержня переменного сечения на длине будет равно

В том случае, когда стержень нагружен только по концам, нормальная сила не зависит от Если, кроме того, стержень имеет постоянные размеры поперечного сечения то из выражения (1.5) получаем

При решении многих практических задач возникает необходимость наряду с удлинениями, обусловленными напряжением учитывать также удлинения, связанные с температурным воздействием. В этом случае пользуются способом

наложения и деформацию с рассматривают как сумму силовой и чисто температурной деформации:

где а – коэффициент температурного расширения материала.

Для однородного стержня, нагруженного по концам и равномерно нагретого, получаем

Таким образом, силовая и температурная деформации рассматриваются как независимые. Основанием этому служит экспериментально установленный факт, что модуль упругости Е при умеренном нагреве слабо меняется с температурой, точно так же как и а практически не зависит от . Для стали это имеет место до температуры порядка . При более высоких температурах необходимо учитывать зависимость Е от

Рассмотрим примеры определения напряжений и перемещений в некоторых простейших случаях растяжения и сжатия.

Пример 1.1. Требуется выявить закон изменения нормальных сил, напряжений и перемещений по длине ступенчатого стержня, нагруженного на конце силой Р (рис. 1.7, а), определить числовые значения наибольшего напряжения и наибольшего перемещения, если Материал – сталь, Поскольку сила Р велкка, собственный вес стержня можно не учитывать.

Рис. 1.7

Из условий равновесия любой отсеченной части стержня вытекает, что нормальная сила в каждом сечении стержня равна внешней силе Р. Построим график изменения силы вдоль оси стержня. Графики подобного рода называются в сопротивлении материалов эпюрами. Они дают наглядное представление о законах изменения различных исследуемых величин. В данном случае эпюра нормальной силы представлена на рис. 1.7, б прямоугольником, поскольку На рисунке эпюра заштрихована линиями, которые проведены параллельно откладываемым на графике значениям . В данном случае значение силы откладывают вверх, поэтому штриховка проведена вертикально.

Для того чтобы получить эпюру напряжений а, надо ординаты эпюры изменить обратно пропорционально величине (рис. 1.7, в). Большее значение а равно

Определим перемещение и каждого сечения стержня по направлению силы Р. Перемещение сечения равно удлинению отрезка длиной . Следовательно, согласно формуле (1.6), . Таким образом, на участке изменения от нуля до I перемещение и пропорционально z (рис. 1.7, а). На втором участке стержня перемещение Зависимость и от также будет линейной. Наибольшее перемещение имеет торцевое сечение стержня: мм.

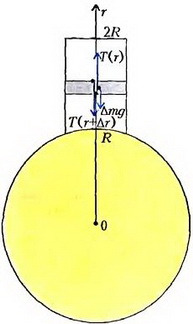
Пример 1.2. Построить эпюры нормальных сил, напряжений и перемещений для свободно подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 1.8, о). Длина стержня площадь поперечного сечения плотность материала у.

Рис. 1.8

Нормальная сила в сечении z равна весу нижележащей части стержня: Следовательно, нормальная сила пропорциональна г. Эпюру в данном случае штрихуют горизонтальными линиями, поскольку

значения откладывают в горизонтальном налравденхн (рис. 1.8, в). Наг пряжение в сечении равно (см. рис. 1.8, в).

Перемещение и в сечении z равно удлинению верхнего участка стержня. Согласно формуле (1.5),

Таким образом, закон изменения и изображается квадратичной функцией 2. Наибольшее перемещение «шах имеет нижнее торцевое сечение (рис. 1.8, г):

Пример 1.3. Колонна (рис. 1.9, а) нагружена силой Р и силами собственного веса. Требуется подобрать такой закон изменения площади поперечного сечения чтобы напряжения во всех сечениях были одинаковы и равны Построить эпюры нормальных сил, напряжений и перемещений.

Рис. 1.9

На расстоянии от торца нормальная сжимающая сила равна

По условию задачи

откуда

Дифференцируя обе части этого равенства по z, получим или После интегрирования находим

При следовательно, и тогда искомый закон изменения площади принимает вид

Построение эпюр удобнее всего начинать с эпюры напряжения которое вдоль оси колонны по условию не меняется (рис. 1.9, б). Поскольку напряжение постоянно, то постоянным будет и относительное удлинение е. Поэтому перемещение и возрастает пропорционально расстоянию от основания колонны (рис 1.9, в).

Нормальная сила в сечении z равна Эпюра показана на рис. 1.9, г.

Рассмотренная задача относится к числу часто встречающихся в сопротивлении материалов задач на отыскание условий равнопрочности. Если напряжение в некотором теле (в данном случае в колонне) будет постоянно для всех точек объема, такую конструкцию называют равнопрочной. В подобных конструкциях материал используется наиболее эффективно.

Пример 1.4. Кронштейн нагружен на конце силой Р (рис. 1.10, а). Требуете подобрать поперечное сечение стержней АВ и с таким расчетом, чтобы возникающие в них напряжения имели одинаковую заданную величину а. При этом угол а должен быть выбран из условия минимального веса конструкции при заданном вылете кронштейна

Из условий равновесия узла В (рис. 1.10, б) находим нормальные силы в стержнях: .

Далее определяем площади поперечного сечения стержней по величине заданного напряжения и:

Рис. 1.10

Вес конструкции кронштейна пропорционален объему: Подставляя длины и площади стержней, находим

Величина V имеет минимум при .

1

Оглавление

  • Предисловие
  • Введение
  • В2. Реальный объект и расчетная схема
  • В3. Силы внешние и внутренние. Уравнения равновесия стержня
  • В4. Напряжения
  • В5. Перемещения и деформации
  • В6. Закон Гука и принцип независимости действия сил
  • В7. Общие принципы расчета элементов конструкции
  • Глава 1. РАСТЯЖЕНИЕ И СЖАТИЕ
  • 1.1. Внутренние силы и напряжения, возникающие в поперечных сечениях стержня при растяжении – сжатии
  • 1.2. Удлинения стержня и закон Гука. Уравнения равновесия
  • 1.3. Потенциальная энергия деформации при растяжении – сжатии стержня
  • 1.4. Статически определимые и статически неопределимые стержневые системы
  • 1.5. Напряженное и деформированное состояния при растяжении — сжатии
  • 1.6. Испытание материалов на растяжение – сжатие
  • 1.7. Диаграмма растяжения
  • 1.8. Механизм образования деформации
  • 1.9. Основные механические характеристики материала
  • 1.10. Пластичность и хрупкость. Твердость
  • 1.11. Влияние температуры и фактора времени на механические характеристики материала
  • 1.12. Коэффициент запаса
  • Глава 2. КРУЧЕНИЕ
  • 2.1. Чистый сдвиг и его особенности
  • 2.2. Кручение стержня с круглым поперечным сечением. Уравнения равновесия
  • 2.3. Кручение стержня с некруглым поперечным сечением
  • 2.4. Краткие сведения о пленочной (мембранной) аналогии
  • 2.5. Кручение тонкостенного стержня
  • Глава 3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ СТЕРЖНЯ
  • 3.2. Моменты инерции сечения
  • 3.3. Главные оси и главные моменты инерции
  • Глава 4. ИЗГИБ СТЕРЖНЕЙ
  • 4.1. Внутренние силовые факторы, возникающие в поперечных сечениях стержня при изгибе
  • 4.2. Напряжения при чистом изгибе
  • 4.3. Напряжения при поперечном изгибе
  • 4.4. Касательные напряжения при поперечном изгибе тонкостенных стержней
  • 4.5. Центр изгиба
  • 4.6. Дифференциальные уравнения равновесия стержня. Перемещения при изгибе
  • 4.7. Стержень на упругом основании
  • 4.8. Косой изгиб
  • 4.9. Внецентренное растяжение – сжатие
  • 4.10. Изгиб бруса большой кривизны
  • Глава 5. ПЕРЕМЕЩЕНИЯ В СТЕРЖНЕВОЙ СИСТЕМЕ ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ
  • 5.2. Теорема Кастилиано
  • 5.3. Интеграл Мора
  • 5.4. Способ Верещагина
  • 5.5. Определение перемещений и напряжений в витых пружинах
  • 5.6. Теорема взаимности работ
  • Глава 6. РАСКРЫТИЕ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ СТЕРЖНЕВЫХ СИСТЕМ МЕТОДОМ СИЛ
  • 6.2. Метод сил. Выбор основной системы
  • 6.3. Канонические уравнения метода сил
  • 6.4. Использование свойств симметрии при раскрытии статической неопределимости
  • 6.5. Плоскопространственные и пространственные системы
  • 6.6. Определение перемещений в статически неопределимых системах
  • 6.7. О методе перемещений
  • Глава 7. ОСНОВЫ ТЕОРИИ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЙ
  • 7.2. Определение напряжений в произвольно ориентированной площадке
  • 7.3. Главные оси и главные напряжения
  • 7.4. Круговая диаграмма напряженного состояния
  • 7.5. Обзор различных типов напряженных состояний
  • 7.6. Деформированное состояние
  • 7.7. Обобщенный закон Гука и потенциальная энергия деформации в общем случае напряженного состояния
  • 7.8. Анизотропия
  • Глава 8. КРИТЕРИИ ПЛАСТИЧНОСТИ И РАЗРУШЕНИЯ
  • 8.2. Гипотезы (критерии) появления пластических деформаций
  • 8.3. Теория Мора и ее применение
  • 8.4. О хрупком разрушении и вязкости
  • 8.5. О новых материалах
  • Глава 9. ТОЛСТОСТЕННЫЕ ТРУБЫ
  • 9.2. Определение перемещений и напряжений в толстостенном цилиндре
  • 9.3. Определение напряжений в составных трубах
  • Глава 10. ПЛАСТИНЫ И ОБОЛОЧКИ
  • 10.1. Основные особенности пластин и оболочек
  • 10.2. Определение напряжений в симметричных оболочках по беэмоментной теории
  • 10.3. Изгиб круглых симметрично нагруженных пластин
  • 10.4. Определение напряжений и перемещений в круглых пластинах
  • 10.5. Изгиб прямоугольных пластин
  • 10.6. Изгиб цилиндрической оболочки при симметричном нагружении
  • Глава 11. ОСНОВЫ РАСЧЕТА ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, РАБОТАЮЩИХ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
  • 11.2. Напряжения и перемещения в простейших стержневых системах при наличии пластических деформаций
  • 11.3. Упругопластический изгиб стержня
  • 11.4. Кручение стержня круглого поперечного сечения при наличии пластических деформаций
  • 11.5. Основы расчета по предельным нагрузкам
  • 11.6. Основы теории пластичности
  • Глава 12. ПРОЧНОСТЬ ПРИ ЦИКЛИЧЕСКИ ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЯХ
  • 12.2. Основные характеристики цикла и предел выносливости
  • 12.3. Влияние концентрации напряжений на прочность при циклическом нагружении
  • 12.4. Масштабный эффект
  • 12.5. Влияние качества обработки поверхности
  • 12.6. Коэффициент запаса при циклическом нагружении и его определение
  • Глава 13. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ДЕФОРМИРУЕМЫХ СИСТЕМ
  • 13.2. Определение критических нагрузок
  • 13.3. Задача Эйлера
  • 13.4. Зависимость критической силы от условий закрепления стержня
  • 13.5. Устойчивость плоской формы изгиба прямолинейного стержня
  • 13.6. Энергетический метод определения критических нагрузок
  • 13.7. Продольно-поперечный изгиб
  • Глава 14. МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ДЕФОРМИРОВАННОГО И НАПРЯЖЕННОГО СОСТОЯНИЙ
  • 14.2. Определение деформаций при помощи механических тензометров
  • 14.3. Применение датчиков сопротивления
  • 14.4. Оптический метод определения напряжений при помощи прозрачных моделей
  • ПРИЛОЖЕНИЕ
Источник

Под растяжением
понимается такой вид нагружения, при
ко­тором в поперечных сечениях бруса
(стержня) возникают только нормальные
силы, а все прочие внутренние силовые
факторы (по­перечные силы, крутящий
и изгибающие моменты) равны нулю.
Сжатие отличается от растяжения только
знаком силы N:
при растяжении
нормальная сила N
направлена
от сечения (см. рис. 2.1), а
при сжатии – к сечению. Поэтому при
анализе внутренних сил сохраняется
единство подхода к вопросам растяжения
и сжатия. Исключение составят длинные
тонкие стержни, для которых сжа­тие
сопровождается изгибом (см. подразд.
2.7).

Закон Гука.
Многочисленные
наблюдения за поведением твер­дых
тел показывают, что в подавляющем
большинстве случаев перемещения в
определенных пределах пропорциональны
дейст­вующим силам. Впервые в 1676 г.
Гуком был сформулирован закон о том,
что «какова сила, такова и деформация».

В современной
трактовке закон Гука определяет линейную
за­висимость между напряжением и
деформацией:

(1.4)

Здесь коэффициент
пропорциональности Е
есть модуль
упругости первого рода, ε – деформация,
которую для однородного стержня можно
определить как

(1.5)

Величину
ε
иногда называют относительным
удлинением стержня
длиной l,
удлинение которого под действием
приложенной силы составило Δl.

Модуль упругости
первого рода
является физической констан­той
материала; он определяется экспериментально.
Для наиболее часто
встречающихся материалов его значения
приведены в табл. 2.1 (см.
подразд. 2.3).

Удлинение
стержня. Если
в закон Гука вместо напряжения под­ставить


=
N/S,
а вместо
деформации

, то для стержня, у которого на длине l
внутренняя
нормальная сила постоянная и поперечное
сечение не изменяется, получим выражение
для опре­деления удлинения стержня:

(1.5)

При решении многих
практических задач возникает необхо­димость
наряду с удлинением, обусловленным
напряжением а, учитывать также удлинения,
связанные с температурным воз­действием.

В этом случае
деформацию рассматривают как сумму
силовой и чисто температурной деформации:

(1.6)

где

– коэффициент
температурного расширения материала.
Для однородного стержня, нагруженного
по концам и равномерно нагретого, имеем

(1.7)

Построение эпюр.
График
изменения нормальной силы, напря­жений
и перемещений стержня вдоль его оси
называется эпюрой соответственно
нормальных сил, напряжений и перемещений.
Эпюры дают наглядное представление о
законах изменения раз­личных исследуемых
величин. Построение эпюр рассмотрим на
конкретном примере.

Пример 1

Для
бруса, изображенного на рис. 2.3, а,
построить
эпюры внутренних сил, напряжений
и перемещений по длине бруса.

Рис. 2.3

Решение.

1. Выбираем
начало отсчета в неподвижном сечении
(точка О);

положи­тельное
направление оси z
направим
по оси бруса, т.е. вниз.

2.
Определим
реакцию, составив одно уравнение
равновесия:

N0
–
3F
+ F
= 0.
Отсюда
N0
=2F.

3. Построим
эпюру внутренних сил N.
Для
этого на расстоянии z1
рассечем

брус
и рассмотрим равновесие нижней части
(рис. 2.3, б):

∑ Fiz
= 0; – N1
+ F
= 0

Отсюда
N1
=F
,
что справедливо для l
≤ z1
≤ 3l.
В этих пределах в брусе возни­кает
растяжение, так как продольная сила N1
направлена
от сечения.

Теперь
выберем второй участок бруса 0
≤ z2
≤ l
и рассмотрим равновесие верхней
части (рис. 2.3, в):

∑ Fiz
= 0; N0
– N2
= 0; 2F – N2
= 0

Отсюда
N2
= 2F. Поскольку
N2
направлена
к сечению, то брус под дейст­вием
сил N0
и N2
сжимается.

После
того как определили все внутренние
нормальные силы, переходим к
построению эпюры нормальных сил (рис.
2.3, г).
Вправо
будем отклады­вать положительные
значения, а влево – отрицательные значения
нормаль­ных
сил.

Анализируя
построенную эпюру (N)
,
заметим, что внутренние силы не за­висят
от размеров поперечного сечения, а
зависят только от приложенных внешних
сил. Поэтому длину бруса разбивают на
такое число участков, сколько
сил на его длине приложено. В данном
случае было два участка.

При
проверке правильности построения эпюры
следует обратить внимание
на то, что на эпюре внутренних сил в тех
сечениях, где были приложены
внешние силы, должны быть скачки, равные
приложенной внешней силе.

4.
Построим эпюру напряжений (σ).
Брус следует разбить на участки.
По­скольку
σ
= N/S,
то
участков на эпюре будет столько, сколько
раз меняется поперечное
сечение; при этом следует обращать
внимание, чтобы при посто­янной
площади поперечного сечения нормальная
сила на эпюре N
остава­лась
неизменной. С учетом этого на эпюре (σ)
будут три различных значения σ

(рис.
2.3, д):

σ1
=
N1/
S1
= F/S;

σ2
= N2/S2
= F/2S;

σ3
= N2/S2
= -2F/2S
= –F/S.

5.Строим
эпюру перемещений (U).
Начинать следует от неподвижного
се­чения,
т.е. от сечения О.
Выразим
перемещение сечения, находящегося от
неподвижного
на расстоянии z2:

Если
0
≤ z2
≤ l
, то для z2
= l
перемещение

Для
l
≤ z
≤ 2l

Или

при z
= 2l

Для 2l
≤ z1
≤ 3l

при z1
= 3
l

Откладываем
вычисленные перемещения на эпюре (U)
(рис. 2.3, e).

Диаграмма
растяжения. Наиболее
наглядно особенности диа­граммы
растяжения можно показать на примере
испытания образца из малоуглеродистой
стали (рис. 2.4). Диаграмма вы­черчена
в координатах F,Δl.
На кривой можно выделить четыре зоны.

Зона ОА
носит название
зоны упругости.
Здесь материал
подчиняется закону Гука и

.

На рис. 2.4 этот
участок для большей наглядности показан
с отступлением от масштаба. Уд­линения
на участке ОА
очень малы,
и прямая ОА,
будучи
вычер­ченной в масштабе, совпадала
бы в пределах ширины линии с осью ординат.
Значение силы, для которой справедлив
закон Гука, зависит от размеров образца
и физических свойств мате­риала,
поэтому при дальнейшем рассмотрении
диаграммы растя­жения ее перестраивают
в координатах σ
и ε

Зона АВ
называется
зоной общей
текучести, а
участок АВ
– площадкой
текучести. Здесь
происходит существенное изменение
длины образца без заметного увеличения
нагрузки. Не все метал­лы имеют площадку
текучести. Например, у алюминия,
отожжен­ной меди, легированных сталей
площадка текучести не обнару­живается.

З
она
ВС называется
зоной
упрочнения. Здесь
удлинение образца

сопровождается
возрастанием на-грузки. В стадии
упрочнения на

образце намечается
место будущего разрыва и начинает
образовы­ваться так называемая шейка
– мест­ное
сужение образца. При дальней­шем
растяжении образца шейка быст­ро
прогрессирует. Начиная с точки С

удлинение
образца происходит с

уменьшением
силы, но среднее напря­жение в поперечном
сечении шейки возрастает. Удлинение
образца носит в этом случае мест-ный
характер, по­ этому участок CD
называется
зоной местной
текучести
Рис.
2.4

Точка D
соответ­ствует
разрушению образца.


Относительная
поперечная дефор­мация.
При растяжении
(сжатии)

прямого бруса кроме продольной
деформации е происходит изменение
поперечных размеров бруса (рис.2.5). Ширина
бруса b
при
растяжении

уменьшается
на Δb.
Если Δb
отнести
к первоначальной ширине, то полу­чим
выражение для определения относительной
поперечной де­формации:


Отношение
относительной поперечной

деформации к
относи­тельной продольной деформации
называют коэффициентом
Пуас­сона и
обозначают

:

Рис. 2.5.

Коэффициент
Пуассона, так же как и модуль упругости
Е, ха­рактеризует
физические свойства материала; его
значение колеб­лется для металлов в
пределах от 0,25 до 0,35. Некоторые значе­ния
коэффициента и. приведены в табл. 2.1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

   Относительное удлинение — показывает на сколько процентов изменилось тело

  Относительное удлинение

   Единица измерения процент – [%]

Деформация растяжения

   Относительное удлинение показывает какую часть от первоначальной длины составляет абсолютное удлинение. Часто измеряется в процентах, для этого просто надо умножить на 100%.

   Относительное удлинению необходимо. С помощью него определяется, сможет ли материал при изменении своей длины разрушиться. Например: если взять металлическую трубку 10 метров и растянуть ее на 1метр, то она может разрушиться, но растянуть резиновую 100 метровую нить на 1 метр такого же сечения как и труба , то с ней ничего не произойдет. Относительное удлинение в первом случае будет 1/10*100%=10%, а во втором 1/10000*100%=0,01%

   Обозначения:

ε — относительное удлинение тела

Δl — абсолютное удлинение тела

l0  — первоначальная длина тела

Источник

Плис В. Упругие силы, деформации и закон Гука // Квант. — 2004. — № 1. — С. 35-39.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Под воздействием внешних сил тела в той или иной степени деформируются, т.е. изменяют свою форму и объем. При деформации молекулы тела смещаются, и тело выводится из состояния равновесия, в котором оно находилось первоначально. При этом, вследствие взаимодействия молекул, в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы действуют на каждый элемент поверхности произвольного объема, выделенного в теле, со стороны окружающих его частей.

Ограничимся рассмотрением деформаций однородных изотропных твердых тел. Если деформации исчезают после прекращения действия внешних сил, такие деформации называются упругими. О них и пойдет речь в статье.

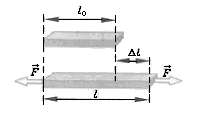
Простейшим видом деформации является растяжение (или сжатие) тонкого горизонтального стержня, один из концов которого закреплен, а к другому приложена сила , стремящаяся растянуть стержень. Изменением площади S поперечного сечения стержня мы будем пренебрегать. На рисунке 1 изображены внешние силы  и , действующие на весь стержень (  — это сила реакции со стороны закрепления), и сила , действующая со стороны правой части стержня на левую. 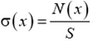Отношение  называется механическим напряжением в сечении х и измеряется в Паскалях (в СИ).

Рис. 1.

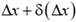
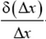
При деформации стержня изменяются расстояния между его частями. Если до деформации малый элемент стержня лежал между координатами х и х + Δх и, следовательно, имел длину Δх, то в деформированном состоянии его длина станет . Отношение  характеризует относительное удлинение элемента длиной Δх. Упругие деформации обычно невелики: величина относительного удлинения очень мала.

Для малых деформаций относительное удлинение пропорционально напряжению:

где постоянный коэффициент Е называется модулем Юнга (или модулем упругости) и определяется только свойствами материала стержня. Приведенный закон является основным законом теории упругости и известен под названием закона Гука. Современник Ньютона, Роберт Гук сформулировал этот закон в 1676 году.

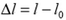
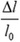
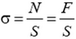
Величина деформации всего стержня характеризуется его полным удлинением  (здесь l и l0 — длины стержня до и после деформации) и относительным удлинением . Найдем связь величины F растягивающей стержень силы с удлинением Δl стержня. Для того чтобы найти полное удлинение стержня, следует просуммировать элементарные удлинения δ(Δx) всех его элементов. В равновесии величины F, T и N сил одинаковы. Из этого следует, что напряжение  однородно по длине стержня, поэтому полное удлинение стержня равно

Полученное соотношение можно переписать в виде

где 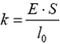 — жесткость стержня.

При упругих деформациях относительные удлинения, как правило, не превосходят 0,001. Это означает, что при межатомных расстояниях порядка 2  (1  = 10–10 м) положения равновесия атомов смещаются не более чем на 0,002 . При больших смещениях тело уже не возвращается к исходном виду при снятии внешних нагрузок, и в нем возникают заметные остаточные деформации. В таком случае закон Гука не выполняется.

Рассмотрим теперь некоторые конкретные задачи, иллюстрирующие технику вычисления упругих сил и деформаций.

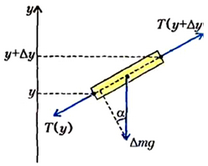
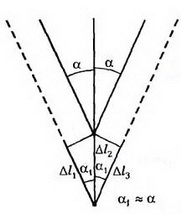
Задача 1. Одна из опор линии электропередачи в горах на Н выше другой (рис. 2). Длина однородного провода между опорами L, его масса М. На сколько натяжение провода вблизи одной опоры больше, чем вблизи другой? Ускорение свободного падения g.

Рис. 2.

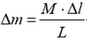
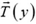
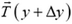
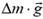
Рассмотрим произвольный элементарный участок провода длиной Δl и массой . К нему приложены силы натяжения  и  и сила тяжести  (рис. 3). Под действием этих сил выделенный участок покоится, следовательно,

Рис. 3.

Перейдем к проекциям сил на касательное к проводу направление:

откуда с учетом явного выражения для Δm получаем

Из геометрии следует

поэтому

т.е. приращение величины силы натяжения провода на любом его элементарном участке пропорционально проекции длины этого участка на вертикальную ось. Суммируя подобные соотношения вдоль всей длины провода между опорами, приходим к ответу на вопрос задачи:

Заметим, что для случая, когда опоры находятся вблизи одной вертикали, результат может быть получен без рассмотрения задачи «в малом». Действительно, в этом случае разность сил натяжения провода на уровнях A и В уравновешивает силу тяжести участка провода, находящегося выше горизонтали, проходящей через точку В.

Задача 2. Кабина лифта массой m = 1000 кг равномерно опускается со скоростью υ0 = 1,0 м/с с помощью троса, перекинутого через барабан. Когда кабина опустилась на l = 10 м, барабан заклинило. Найдите максимальную силу упругости Tmax, действующую на трос вследствие внезапной остановки лифта. Длина троса в момент остановки равна l = 10 м, площадь поперечного сечения троса S = 20 см2, модуль Юнга материала троса Е = 2,0·1011 Па. Ускорение свободного падения g = 10 м/с2.

При равномерном движении кабины действующие на нее силы упругости троса и тяжести кабины уравновешивают друг друга:

откуда найдем статическое удлинение троса:

После внезапной остановки барабана кабина будет двигаться по гармоническому закону (покажите это самостоятельно)

где 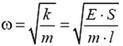 – частота гармонических колебаний, а амплитуда колебаний смещения в ω раз меньше амплитуды υ0 колебаний скорости. Максимальное удлинение троса будет равно сумме статического удлинения и амплитуды гармонических колебаний смещения:

В этот момент упругая сила достигнет своего наибольшего значения:

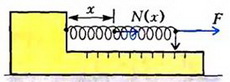
Задача 3. Динамометр, находящийся на гладкой горизонтальной поверхности, тянут с силой F = 5 Н. Что покажет динамометр, если масса его корпуса М = 0,2 кг, масса пружины m = 0,05 кг? Градуировка динамометра производилась при закрепленном корпусе.

Показание T динамометра, движущегося ускоренно, будет пропорционально удлинению Δl пружины:

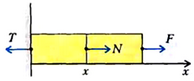
где k — жесткость пружины. Для определения удлинения заметим, что масса пружины не является пренебрежимо малой (по сравнению с массой корпуса), следовательно, упругая сила в любом ее сечении зависит от координаты этого сечения, отсчитанной, например, от точки закрепления пружины. Тогда из второго закона Ньютона для корпуса динамометра и части пружины длиной х (рис. 4):

и для оставшейся части пружины:

находим упругую силу N(x), а с ней и зависимость механического напряжения а от координаты х:

где L — длина пружины.

Рис 4

Удлинение δ(Δx) произвольного первоначально недеформированного элемента длиной Δx найдем по закону Гука

Полное удлинение пружины получим суммированием элементарных удлинений:

По условию, градуировка проводилась при закрепленном корпусе, следовательно, 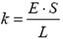. Тогда показание динамометра будет таким:

Задача 4. Мальчик стреляет из рогатки. Он медленно растягивает резиновый жгут так, что его длина L увеличивается вдвое, доводя усилие до F = 10 Н. Определите начальную скорость υ0 камешка массой m = 10 г, если длина растянутого резинового жгута 2L = 20 см, масса жгута М = 30 г.

При растяжении резинового жгута упругая сила растет пропорционально удлинению жгута и изменяется от нуля до F. Работа этой силы на перемещении L оказывается запасенной в виде потенциальной энергии пружины

При выстреле эта энергия переходит в кинетическую энергию камешка

и кинетическую энергию резинового жгута Wк2 (его масса не является пренебрежимо малой, а, наоборот, превышает массу камешка). Для определения кинетической энергии жгута заметим, что смещения сечений жгута, как и силы упругости, тоже распределены по линейному закону, следовательно, поэтому же закону будут распределены и скорости υ(x) элементарных масс жгута:

(здесь координата х отсчитывается от рогатки). Тогда кинетическая энергия двух одинаковых участков жгута, имеющих координаты от х до х + dx, равна

Суммируя эти величины по всей длине жгута, получаем

По закону сохранения энергии,

или

Отсюда находим начальную скорость камешка:

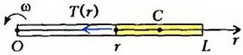
Задача 5. Однородный тонкий упругий стержень вращается в горизонтальной плоскости вокруг оси, проходящей через один из его концов, с постоянной угловой скоростью. В некоторый момент времени стержень срывается с оси. Во сколько раз изменится при этом его относительное удлинение?

Найдем распределение упругих напряжений 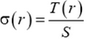 в равномерно вращающемся с угловой скоростью ω стержне длиной L (рис. 5).

Рис. 5

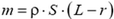
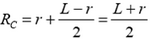
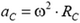
Под действием упругой силы T(r) центр масс С части бруска массой , где ρ — плотность материала стержня, равномерно движется по окружности радиусом . Ускорение центра масс направлено к оси вращения и равно по величине . По теореме о движении центра масс,

Переходя к проекциям силы и ускорения на радиальное направление и учитывая явные выражения для m и RC, получаем

Элементарное удлинение δ(Δx) произвольного первоначально недеформированного элемента длиной Δx найдем по закону Гука

Полное удлинение получим суммированием элементарных удлинений:

Относительное удлинение будет пропорционально квадрату угловой скорости и квадрату длины стержня:

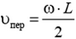
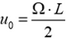
После отрыва стержня от оси его центр масс будет двигаться равномерно и прямолинейно со скоростью , a в системе центра масс стержень будет равномерно вращаться с угловой скоростью ω. Для нахождения этой скорости обратимся к закону сложения скоростей: в лабораторной системе отсчета скорость υ0 точки О стержня в момент отрыва равна нулю, а в системе центра масс ее скорость равна . По закону сложения скоростей,

Откуда

 или

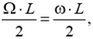
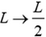
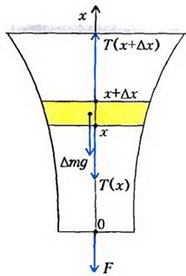
После отрыва оба конца стержня становятся свободными, растяжение стержня происходит относительно серединного сечения. В этом случае относительное удлинение каждой половины стержня, а, следовательно, и всего стержня, уменьшится в четыре раза, так как в формуле для относительного удлинения следует сделать замену , а угловая скорость остается неизменной.

Задача 6*. Осесимметричный стержень подвешен вертикально за один из концов. В нижнем сечении радиусом r0 стержень нагружен растягивающей силой F, равномерно распределенной по сечению. При какой зависимости радиуса r стержня от расстояния х до нижнего сечения напряжения во всех горизонтальных сечениях будут одинаковы? Плотность материала стержня ρ. Ускорение свободного падения g.

По условию, напряжения в горизонтальных сечениях одинаковы и равны напряжению в нижнем сечении:

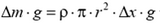
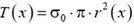
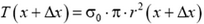
На любой элементарный горизонтальный слой толщиной Δх действует сила тяжести  и упругие силы  и  в нижнем сечении и в верхнем сечении соответственно (рис. 6).

Рис. 6

Под действием приложенных сил выделенный слой покоится, следовательно, по второму закону Ньютона,

Введем 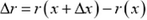, тогда полученное уравнение примет вид

или

Суммируя такие равенства от х = 0 до любого х в пределах стержня и переходя от логарифмов к основаниям, получаем искомую зависимость радиуса сечения стержня от координаты:

Задача 7. На астероиде Веста (радиус R = 280 км, ускорение свободного падения на поверхности g0 = 0,24 м/с2) решено установить межпланетную ретрансляционную станцию. Основой конструкции станции должна служить цилиндрическая труба, высота которой равняется радиусу планеты. На Весту завезли ровно 280 км титановых труб. На сколько ниже проектной окажется высота конструкции, когда она будет собрана в вертикальном положении? Считайте астероид однородным невращающимся шаром. Плотность титана ρ = 4500 кг/м3, модуль Юнга Е = 1,12·1011 Па.

Ускорение свободного падения над поверхностью планеты изменяется по закону 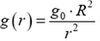 (координата r отсчитывается от центра планеты) и на высоте станции уменьшается в четыре раза. Следовательно, напряжения в конструкции и соответствующие им деформации не будут однородными.

Найдем зависимость упругой силы T от координаты r. Для этого рассмотрим находящийся в равновесии произвольный элементарный горизонтальный слой трубы толщиной Δr (рис. 7).

Рис. 7

Пусть площадь поперечного сечения стенки трубы равна S. На этот слой действует сила тяжести 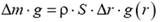 и упругие силы T(r) в нижнем сечении и T(r + Δr) в верхнем сечении. По второму закону Ньютона,

или

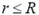
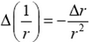
Суммируя такие равенства от r = 2R, где T(2R) = 0, до любого  в пределах стержня и учитывая равенство , получаем зависимость упругой силы от координаты:

Элементарные уменьшения длины δ(Δr) найдем по закону Гука

Полное уменьшение длины конструкции получим суммированием элементарных уменьшений:

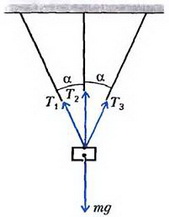
Задача 8. Груз массой m подвешен на трех тросах (рис. 8). Считая деформации малыми, найдите величину силы натяжения каждого троса, если они сделаны из одного материала и площади их поперечных сечений одинаковы. Ускорение свободного падения g.

Рис. 8

Эта задача статически неопределима, так как для нахождения трех неизвестных усилий T1, T2, T3 в тросах нам известны из статики лишь два уравнения. Это равенство нулю суммы проекций сил на вертикальное направление:

и на горизонтальное направление:

Чтобы найти недостающее третье уравнение, учтем упругие свойства материала, из которого сделаны тросы, и кинематическую связь. Так, малые деформации боковых тросов и центрального связаны соотношением (рис. 9)

Рис. 9

В свою очередь, для длин тросов справедливо равенство

Кроме того, считая деформации тросов упругими, по закону Гука находим

Подстановка полученных соотношений в первые два равенства приводит к следующим результатам:

Упражнения

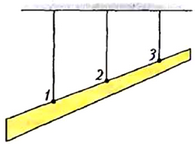
1. На гладком блоке радиусом R висит однородный гибкий канат массой m и длиной l. Найдите величину максимальной силы натяжения каната Fmax. Ускорение свободного падения g.

2. Груз массой m = 5000 кг равномерно опускается с некоторой скоростью с помощью троса и лебедки. Когда груз опустился на l = 2 м, лебедку заклинило, и трос оборвался. При какой скорости груза υ произойдет обрыв троса, если для него предел прочности на растяжение σр = 3,1·103 Па? Длина троса в момент остановки лебедки l = 2 м. Площадь поперечного сечения троса S = 5 см2, модуль Юнга материала троса E = 2,0·1011 Па. Ускорение свободного падения g = 10 м/с2.

3. Однородный стержень длиной l подвешен за один конец. Плотность материала стержня ρ, модуль Юнга Е, ускорение свободного падения g. Найдите удлинение Δl стержня. Как изменится ответ, если этот стержень будет размещен горизонтально и приведен в движение с горизонтальным ускорением а, сонаправленным со стержнем?

4. Определите период колебаний T груза массой m, подвешенного на пружине жесткостью k и массой М.

5. На верхний торец стоящей вертикально на жесткой опоре осесимметричной колонны высотой h действует сила F0 , однородно распределенная по горизонтальному сечению площадью S. При какой зависимости площади S поперечного сечения колонны от расстояния х до опоры напряжения во всех горизонтальных сечениях будут одинаковы? Найдите относительное уменьшение высоты колонны. Плотность материала колонны ρ, модуль Юнга Е. Ускорение свободного падения g.

6. В центре астероида Паллада (радиус R = 290 км, ускорение свободного падения на поверхности g0 = 0,17 м/с2) обнаружены залежи ценных ископаемых. Бурильщики затребовали ровно 290 км труб из вольфрамового сплава. Считая, что после завершения работ вся система труб свободно висит в канале, не касаясь его стенок, определите, какая часть труб будет сэкономлена вследствие растяжения конструкции под действием силы тяжести. Считайте астероид однородным невращающимся шаром. Плотность вольфрама ρ = 19,3·103 кг/м3, модуль Юнга E = 4,0·1011 Па.

7. Неоднородная балка массой m подвешена к потолку на трех одинаковых легких резиновых жгутах так, что жгуты вертикальны и лежат в одной плоскости (рис. 10). Расстояния между жгутами одинаковы. Считая деформации малыми, найдите упругие силы в жгутах. Ускорение свободного падения g.

Рис. 10

Ответы.

1.

2.

3.  удлинение изменится в  раз.

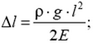
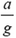
4.

5.

6.

7.

Источник

При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина еще называется абсолютной деформацией.

$Delta l = l-l_0$

Как показывают опыты, удлинение зависят от значения продольной силы, от площади сечения и от длины стержня.

При этом отмечено, что при увеличении силы или длины стержня удлинения увеличивается пропорционально.

При изменении площади удлинения, наоборот, обратно пропорционально площади сечения. Есть

$Delta l = frac{N l}{E A}$,

где Е – определенный коэффициент пропорциональности.

Записав по другому, получим

$frac{N}{A} = frac{Delta l}{l} E$

Введем следующее понятие.

Относительная деформация (относительное удлинение) – отношение удлинения к начальной длине стержня.

$epsilon=frac{Delta l}{l}$

Тогда, учтя что N/A = $sigma$, получим зависимость между напряжениями и относительными деформациями

sigma = Evarepsilon .  – закон Гука.

Закон Гука – утверждение, согласно которому деформация, возникающая в материале, пропорциональна напряжений. Открытый закон в 1660 году английским ученым Робертом Гуком.

Величина E называется модуль упругости (модуль Юнга). Это величина, характеризующая свойства материала сопротивляться растяжению или сжатию. Назван в честь английского физика XIX века Томаса Юнга.

Модуль упругости численно равен напряжению, которые могли бы возникнуть при единичных относительных деформациях (при $epsilon$ = 1).

Источник

Добавить комментарий