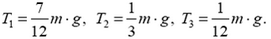Деформацией
называется такое изменение положений
точек тела, при котором изменяются
расстояния между любыми двумя его
точками.
Деформация
возникает вследствие нагрузки тела
или вследствие изменения температуры.
Изменение положений точек тела может
привести к изменению длин и к изменению
углов в теле. В первом случае возникает
линейная деформация, а во втором угловая
деформация. Линейная деформация
измеряется относительным удлинением,
а угловая деформация – углом сдвига.
Относительное
удлинение.
Рассмотрим
стержень, на котором сделаны две отметки
на расстоянии
друг от друга. Приложим к стержню
растягивающую нагрузку (рис.1)
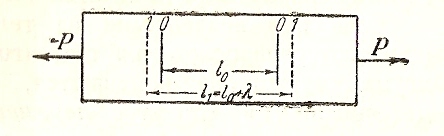
Рис.1.
Расстояние
между отметками увеличится и сделается
равным

Найдем
отношение

Т.е.
отношение изменения длины к первоначальной
длине называется относительным
удлинением.
Относительное удлинение является
безразмерной величиной.
Угол
сдвига.
Плоское напряженное состояние, при
котором на двух парах взаимно
перпендикулярных плоскостей имеются
только касательные напряжения, называется
чистым сдвигом. Возьмем частицу в форме
прямоугольного параллелепипеда и
закрепим неподвижно ее основание
(рис.2). Подвергнем параллелепипед
чистому сдвигу. Его углы из прямых
сделаются косыми.
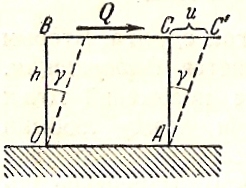
Рис.2
Величина
,
на которую изменился первоначально
прямой угол, называется углом сдвига.
Так как при малых углах
можно принять, что

,
то из рисунка видно, что:

При
рассмотрении этих примеров мы сделали
два важных допущения. Было принято, что
нормальные напряжения связаны только
с линейными деформациями, а касательные
напряжения только с угловыми деформациями.
Это допущение справедливо только для
малых деформаций и на нем основана
линейная теория упругости.
Если
при воздействии на тело внешних сил
его точки изменяют свои положения так,
что расстояния между любыми его двумя
точками не изменяются, то мы будем иметь
не деформацию, а жесткое перемещение
тела. В этом случае тело не деформируется,
а изменяет свое положение так, как если
бы оно было абсолютно твердое.
Вопрос 71. Компоненты тензора деформации
Формулы
относительного удлинения и сдвига
применимы к конечным по размерам частям
тела только в случае, если в этих частях
тела относительное удлинение и угол
сдвига одинаковы для всех отрезков во
всех плоскостях. В общем случае
относительное удлинение и угол сдвига
изменяются при переходе от одной точки
к другой.
Рассмотрим
деформацию тела в общем случае. Для
этого выделим внутри тела элементарный
объем в виде прямоугольного параллелепипеда
с ребрами

.
Деформация этого параллелепипеда будет
известна, если будут заданы изменения
длин трех его ребер и изменения трех
его углов, образуемых каждой парой
ребер, сходящихся в общей вершине.
Изменения длин ребер, разделенные на
первоначальные длины, называются
относительными удлинениями по
направлениям x,
y,
z
и обозначаются соответственно через

.
Изменения первоначально прямых углов,
образованных каждой парой ребер,
сходящихся в общей вершине, называются
углами сдвига в плоскостях yz,
zx,
xy
и обозначаются соответственно

.
Шесть
величин
,
называются компонентами тензора
деформации, и характеризуют деформацию
в точке, в которую стягивается
параллелепипед при переходе к пределам

.
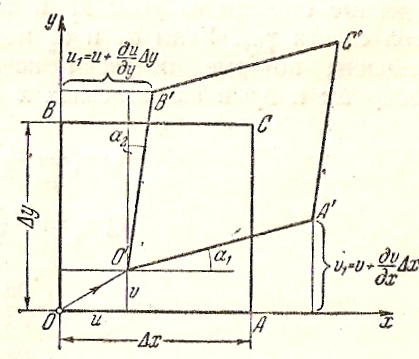
Рис.3
Положению
каждой точки в недеформированном
состоянии соответствует определенной
положение той же точки в деформированном
параллелепипеде. Пусть точка О в
результате деформации перешла в
положение О’ (рис.3). Вектор

будем называть вектором перемещений
(перемещением) точки О. Покажем, что
шесть компонентов тензора деформации
в точке О можно выразить через производные
от компонентов u,
v,
w
вектора перемещения точки О по координатам
x,
y,
z.
При этом будем предполагать, что
перемещение

и его компоненты u,
v,
w
по направлениям, совпадающим с ребрами
параллелепипеда, являются непрерывными
и дифференцируемыми функциями.
Пусть
компонент перемещения начальной точки
О ребра
в направлении х равен u,
тогда компонентом перемещения точки
А этого ребра в том же направлении
будет:

;

;
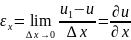
Относительным
удлинением

в направлении оси х будет предел
отношения изменения длины ребра в
направлении оси х к первоначальной
длине ребра. Аналогично, можно определить
относительные удлинения в двух других
направлениях.
Изменение
первоначального угла между ребрами
и
,
определяющее угол сдвига

,
происходит вследствие того, что грани
ОА и ОВ поворачиваются при деформации
в разные стороны на углы

и

,
в сумме составляющие угол сдвига
.
Углы
и
можно выразить через перемещения,
которые получают начальная и конечная
точки ребер
и
.

;

Где

;
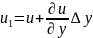
В
случае малых деформаций
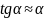
,
и поэтому для угла сдвига
в плоскости х у получим выражение:

Аналогично,
можно получить выражения для углов
сдвига

и
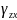
.
Таким
образом, мы получаем для шести компонентов
тензора деформации следующие выражения:
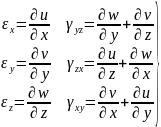
Компоненты
тензора деформации выражаются через
первые частные производные от трех
перемещений u,
v,
w
по координатам x,y,z.
Полученные равенства называют
соотношениями Коши.
Мы
можем говорить о деформации тела только
в том случае, если происходит относительные
перемещения точек друг относительно
друга. Но относительные перемещения
точек тела не изменяются, если расстояния
между ними остаются постоянными, т.е.
при жестком перемещении. Поэтому любая
деформация может быть определена с
точностью до жесткого перемещения.
При
трехосном деформированном состоянии
в каждой точке тела имеются три взаимно
перпендикулярные оси, углы между
которыми не изменяются при деформации.
Следовательно, для плоскостей,
определяемых этими осями углы сдвига
,
,
равны нулю и вся деформация определяется
только относительными удлинениями

,

,

.
Относительные удлинения
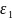
,

,

называют главными относительными
удлинениями, а соответствующие им оси
– главными осями деформации.
В
теории упругости показано, что в каждой
точке изотропного тела главные
направления напряжений совпадают с
главными осями деформаций.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
Определим по аналогии с теорией напряженного состояния в декартовой прямоугольной системе координат главные направления
тензора деформаций, как такие направления, для которых выполняются условия

Здесь  скаляр;
скаляр;  направляющие косинусы единичного вектора
направляющие косинусы единичного вектора 
Используя символы Кронекера, систему уравнений (3.35) запишем в виде

Так как все косинусы одновременно не могут быть равны нулю, то

Главные значения тензора деформаций, которые называются главными относительными удлинениями, являются корнями кубического уравнения (3.37). Направления, соответствующие главным удлинениям  взаимно перпендикулярны. Когда имеет место случай двух равных корней, тогда направления, соответствующие этим корням, лежат в плоскости, перпендикулярной направлению, соответствующему простому корню; в этом случае любые взаимно ортогональные направления, лежащие в этой плоскости, могут быть приняты за главные. Если все три корня равны, то любые перпендикулярные направления можно принять за главные.
взаимно перпендикулярны. Когда имеет место случай двух равных корней, тогда направления, соответствующие этим корням, лежат в плоскости, перпендикулярной направлению, соответствующему простому корню; в этом случае любые взаимно ортогональные направления, лежащие в этой плоскости, могут быть приняты за главные. Если все три корня равны, то любые перпендикулярные направления можно принять за главные.
Кубическое уравнение (3.37) запишем в форме

По свойству корней кубического уравнения соотношения между корнями и коэффициентами имеют вид

По аналогии с теорией напряженного состояния здесь  являются инвариантами. Таким образом,
являются инвариантами. Таким образом,

Первый инвариант тензора деформации в случае малых деформаций представляет собой относительное изменение объема. Действительно, возьмем в некоторой точке  среды главные оси тензора деформаций. На них построим параллелепипед, имевший до деформации ребра, равные
среды главные оси тензора деформаций. На них построим параллелепипед, имевший до деформации ребра, равные  После деформации рассматриваемый параллелепипед, оставаясь прямоугольным, будет иметь ребра
После деформации рассматриваемый параллелепипед, оставаясь прямоугольным, будет иметь ребра
Объем параллелепипеда до деформации  после деформации
после деформации

Отбрасывая малые величины высшего порядка, будем иметь

Обозначив изменение объема в точке  отнесенное к единице объема, или относительную объемную деформацию через
отнесенное к единице объема, или относительную объемную деформацию через  получим
получим

Учитывая, что  для относительной объемной деформации найдем
для относительной объемной деформации найдем

т. е.  есть относительная объемная деформация в точке
есть относительная объемная деформация в точке  Если координатные оси совместить с главными направлениями тензора деформации, то в этой системе координат компоненты
Если координатные оси совместить с главными направлениями тензора деформации, то в этой системе координат компоненты  обратятся в нуль, останутся лишь действующие на этих площадках удлинения
обратятся в нуль, останутся лишь действующие на этих площадках удлинения 

Относительными называют деформации определяемые отношением изменения размера (абсолютной деформации) к соответствующим начальным размерам тела.
Другими словами относительные деформации показывают насколько изменился размер тела в сравнении с его размерами до нагружения.
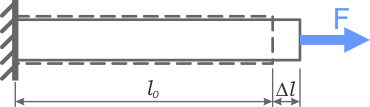
Например, при растяжении (сжатии) прямого стержня его относительное удлинение ε находится отношением абсолютного удлинения Δl к начальной длине l0.
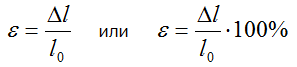
Относительная поперечная деформация
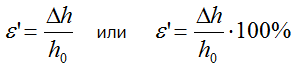
Здесь Δh – абсолютная поперечная деформация,
Δh0 – начальный поперечный размер (до деформации).
Измеряется в единицах или процентах [%]
При кручении — относительный угол закручивания
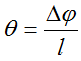
где, Δφ – угол закручивания участка вала,
l – длина рассматриваемого участка.
Единица измерения – радиан на метр [рад/м].
Примеры расчета деформаций >>
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Относительное удлинение — показывает на сколько процентов изменилось тело
![]()
Единица измерения процент – [%]
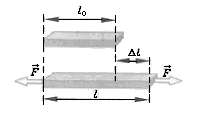
Относительное удлинение показывает какую часть от первоначальной длины составляет абсолютное удлинение. Часто измеряется в процентах, для этого просто надо умножить на 100%.
Относительное удлинению необходимо. С помощью него определяется, сможет ли материал при изменении своей длины разрушиться. Например: если взять металлическую трубку 10 метров и растянуть ее на 1метр, то она может разрушиться, но растянуть резиновую 100 метровую нить на 1 метр такого же сечения как и труба , то с ней ничего не произойдет. Относительное удлинение в первом случае будет 1/10*100%=10%, а во втором 1/10000*100%=0,01%
Обозначения:
ε — относительное удлинение тела
Δl — абсолютное удлинение тела
l0 — первоначальная длина тела
Плис В. Упругие силы, деформации и закон Гука // Квант. — 2004. — № 1. — С. 35-39.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Под воздействием внешних сил тела в той или иной степени деформируются, т.е. изменяют свою форму и объем. При деформации молекулы тела смещаются, и тело выводится из состояния равновесия, в котором оно находилось первоначально. При этом, вследствие взаимодействия молекул, в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы действуют на каждый элемент поверхности произвольного объема, выделенного в теле, со стороны окружающих его частей.
Ограничимся рассмотрением деформаций однородных изотропных твердых тел. Если деформации исчезают после прекращения действия внешних сил, такие деформации называются упругими. О них и пойдет речь в статье.
Простейшим видом деформации является растяжение (или сжатие) тонкого горизонтального стержня, один из концов которого закреплен, а к другому приложена сила ![]() , стремящаяся растянуть стержень. Изменением площади S поперечного сечения стержня мы будем пренебрегать. На рисунке 1 изображены внешние силы
, стремящаяся растянуть стержень. Изменением площади S поперечного сечения стержня мы будем пренебрегать. На рисунке 1 изображены внешние силы ![]() и
и ![]() , действующие на весь стержень (
, действующие на весь стержень (![]() — это сила реакции со стороны закрепления), и сила
— это сила реакции со стороны закрепления), и сила ![]() , действующая со стороны правой части стержня на левую. Отношение
, действующая со стороны правой части стержня на левую. Отношение 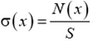 называется механическим напряжением в сечении х и измеряется в Паскалях (в СИ).
называется механическим напряжением в сечении х и измеряется в Паскалях (в СИ).
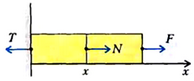
Рис. 1.
При деформации стержня изменяются расстояния между его частями. Если до деформации малый элемент стержня лежал между координатами х и х + Δх и, следовательно, имел длину Δх, то в деформированном состоянии его длина станет 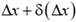 . Отношение
. Отношение 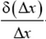 характеризует относительное удлинение элемента длиной Δх. Упругие деформации обычно невелики: величина относительного удлинения очень мала.
характеризует относительное удлинение элемента длиной Δх. Упругие деформации обычно невелики: величина относительного удлинения очень мала.
Для малых деформаций относительное удлинение пропорционально напряжению:
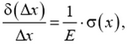
где постоянный коэффициент Е называется модулем Юнга (или модулем упругости) и определяется только свойствами материала стержня. Приведенный закон является основным законом теории упругости и известен под названием закона Гука. Современник Ньютона, Роберт Гук сформулировал этот закон в 1676 году.
Величина деформации всего стержня характеризуется его полным удлинением 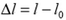 (здесь l и l0 — длины стержня до и после деформации) и относительным удлинением
(здесь l и l0 — длины стержня до и после деформации) и относительным удлинением 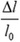 . Найдем связь величины F растягивающей стержень силы с удлинением Δl стержня. Для того чтобы найти полное удлинение стержня, следует просуммировать элементарные удлинения δ(Δx) всех его элементов. В равновесии величины F, T и N сил одинаковы. Из этого следует, что напряжение
. Найдем связь величины F растягивающей стержень силы с удлинением Δl стержня. Для того чтобы найти полное удлинение стержня, следует просуммировать элементарные удлинения δ(Δx) всех его элементов. В равновесии величины F, T и N сил одинаковы. Из этого следует, что напряжение 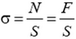 однородно по длине стержня, поэтому полное удлинение стержня равно
однородно по длине стержня, поэтому полное удлинение стержня равно
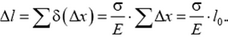
Полученное соотношение можно переписать в виде
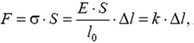
где 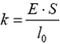 — жесткость стержня.
— жесткость стержня.
При упругих деформациях относительные удлинения, как правило, не превосходят 0,001. Это означает, что при межатомных расстояниях порядка 2 ![]() (1
(1 ![]() = 10–10 м) положения равновесия атомов смещаются не более чем на 0,002
= 10–10 м) положения равновесия атомов смещаются не более чем на 0,002 ![]() . При больших смещениях тело уже не возвращается к исходном виду при снятии внешних нагрузок, и в нем возникают заметные остаточные деформации. В таком случае закон Гука не выполняется.
. При больших смещениях тело уже не возвращается к исходном виду при снятии внешних нагрузок, и в нем возникают заметные остаточные деформации. В таком случае закон Гука не выполняется.
Рассмотрим теперь некоторые конкретные задачи, иллюстрирующие технику вычисления упругих сил и деформаций.
Задача 1. Одна из опор линии электропередачи в горах на Н выше другой (рис. 2). Длина однородного провода между опорами L, его масса М. На сколько натяжение провода вблизи одной опоры больше, чем вблизи другой? Ускорение свободного падения g.

Рис. 2.
Рассмотрим произвольный элементарный участок провода длиной Δl и массой 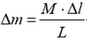 . К нему приложены силы натяжения
. К нему приложены силы натяжения 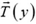 и
и 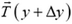 и сила тяжести
и сила тяжести 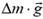 (рис. 3). Под действием этих сил выделенный участок покоится, следовательно,
(рис. 3). Под действием этих сил выделенный участок покоится, следовательно,
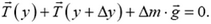
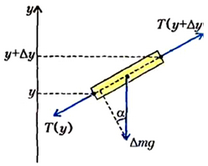
Рис. 3.
Перейдем к проекциям сил на касательное к проводу направление:

откуда с учетом явного выражения для Δm получаем
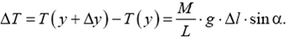
Из геометрии следует
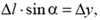
поэтому
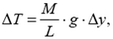
т.е. приращение величины силы натяжения провода на любом его элементарном участке пропорционально проекции длины этого участка на вертикальную ось. Суммируя подобные соотношения вдоль всей длины провода между опорами, приходим к ответу на вопрос задачи:
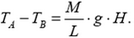
Заметим, что для случая, когда опоры находятся вблизи одной вертикали, результат может быть получен без рассмотрения задачи «в малом». Действительно, в этом случае разность сил натяжения провода на уровнях A и В уравновешивает силу тяжести участка провода, находящегося выше горизонтали, проходящей через точку В.
Задача 2. Кабина лифта массой m = 1000 кг равномерно опускается со скоростью υ0 = 1,0 м/с с помощью троса, перекинутого через барабан. Когда кабина опустилась на l = 10 м, барабан заклинило. Найдите максимальную силу упругости Tmax, действующую на трос вследствие внезапной остановки лифта. Длина троса в момент остановки равна l = 10 м, площадь поперечного сечения троса S = 20 см2, модуль Юнга материала троса Е = 2,0·1011 Па. Ускорение свободного падения g = 10 м/с2.
При равномерном движении кабины действующие на нее силы упругости троса и тяжести кабины уравновешивают друг друга:
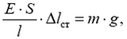
откуда найдем статическое удлинение троса:
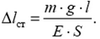
После внезапной остановки барабана кабина будет двигаться по гармоническому закону (покажите это самостоятельно)
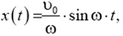
где 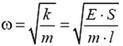 – частота гармонических колебаний, а амплитуда колебаний смещения в ω раз меньше амплитуды υ0 колебаний скорости. Максимальное удлинение троса будет равно сумме статического удлинения и амплитуды гармонических колебаний смещения:
– частота гармонических колебаний, а амплитуда колебаний смещения в ω раз меньше амплитуды υ0 колебаний скорости. Максимальное удлинение троса будет равно сумме статического удлинения и амплитуды гармонических колебаний смещения:
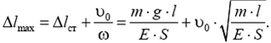
В этот момент упругая сила достигнет своего наибольшего значения:
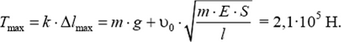
Задача 3. Динамометр, находящийся на гладкой горизонтальной поверхности, тянут с силой F = 5 Н. Что покажет динамометр, если масса его корпуса М = 0,2 кг, масса пружины m = 0,05 кг? Градуировка динамометра производилась при закрепленном корпусе.
Показание T динамометра, движущегося ускоренно, будет пропорционально удлинению Δl пружины:
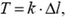
где k — жесткость пружины. Для определения удлинения заметим, что масса пружины не является пренебрежимо малой (по сравнению с массой корпуса), следовательно, упругая сила в любом ее сечении зависит от координаты этого сечения, отсчитанной, например, от точки закрепления пружины. Тогда из второго закона Ньютона для корпуса динамометра и части пружины длиной х (рис. 4):
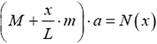
и для оставшейся части пружины:
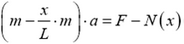
находим упругую силу N(x), а с ней и зависимость механического напряжения а от координаты х:
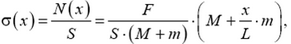
где L — длина пружины.
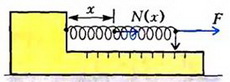
Рис 4
Удлинение δ(Δx) произвольного первоначально недеформированного элемента длиной Δx найдем по закону Гука
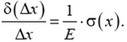
Полное удлинение пружины получим суммированием элементарных удлинений:
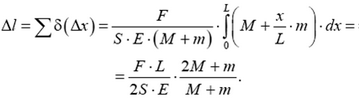
По условию, градуировка проводилась при закрепленном корпусе, следовательно, 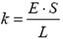 . Тогда показание динамометра будет таким:
. Тогда показание динамометра будет таким:
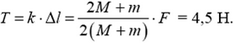
Задача 4. Мальчик стреляет из рогатки. Он медленно растягивает резиновый жгут так, что его длина L увеличивается вдвое, доводя усилие до F = 10 Н. Определите начальную скорость υ0 камешка массой m = 10 г, если длина растянутого резинового жгута 2L = 20 см, масса жгута М = 30 г.
При растяжении резинового жгута упругая сила растет пропорционально удлинению жгута и изменяется от нуля до F. Работа этой силы на перемещении L оказывается запасенной в виде потенциальной энергии пружины
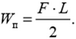
При выстреле эта энергия переходит в кинетическую энергию камешка
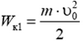
и кинетическую энергию резинового жгута Wк2 (его масса не является пренебрежимо малой, а, наоборот, превышает массу камешка). Для определения кинетической энергии жгута заметим, что смещения сечений жгута, как и силы упругости, тоже распределены по линейному закону, следовательно, поэтому же закону будут распределены и скорости υ(x) элементарных масс жгута:
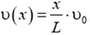
(здесь координата х отсчитывается от рогатки). Тогда кинетическая энергия двух одинаковых участков жгута, имеющих координаты от х до х + dx, равна
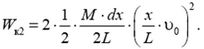
Суммируя эти величины по всей длине жгута, получаем
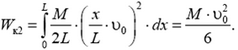
По закону сохранения энергии,
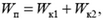
или
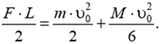
Отсюда находим начальную скорость камешка:
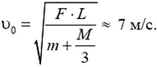
Задача 5. Однородный тонкий упругий стержень вращается в горизонтальной плоскости вокруг оси, проходящей через один из его концов, с постоянной угловой скоростью. В некоторый момент времени стержень срывается с оси. Во сколько раз изменится при этом его относительное удлинение?
Найдем распределение упругих напряжений 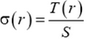 в равномерно вращающемся с угловой скоростью ω стержне длиной L (рис. 5).
в равномерно вращающемся с угловой скоростью ω стержне длиной L (рис. 5).
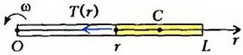
Рис. 5
Под действием упругой силы T(r) центр масс С части бруска массой 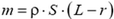 , где ρ — плотность материала стержня, равномерно движется по окружности радиусом
, где ρ — плотность материала стержня, равномерно движется по окружности радиусом 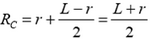 . Ускорение центра масс направлено к оси вращения и равно по величине
. Ускорение центра масс направлено к оси вращения и равно по величине 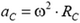 . По теореме о движении центра масс,
. По теореме о движении центра масс,
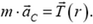
Переходя к проекциям силы и ускорения на радиальное направление и учитывая явные выражения для m и RC, получаем
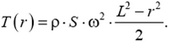
Элементарное удлинение δ(Δx) произвольного первоначально недеформированного элемента длиной Δx найдем по закону Гука
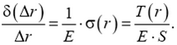
Полное удлинение получим суммированием элементарных удлинений:
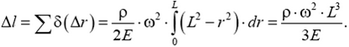
Относительное удлинение будет пропорционально квадрату угловой скорости и квадрату длины стержня:
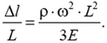
После отрыва стержня от оси его центр масс будет двигаться равномерно и прямолинейно со скоростью 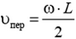 , a в системе центра масс стержень будет равномерно вращаться с угловой скоростью ω. Для нахождения этой скорости обратимся к закону сложения скоростей: в лабораторной системе отсчета скорость υ0 точки О стержня в момент отрыва равна нулю, а в системе центра масс ее скорость равна
, a в системе центра масс стержень будет равномерно вращаться с угловой скоростью ω. Для нахождения этой скорости обратимся к закону сложения скоростей: в лабораторной системе отсчета скорость υ0 точки О стержня в момент отрыва равна нулю, а в системе центра масс ее скорость равна 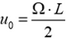 . По закону сложения скоростей,
. По закону сложения скоростей,
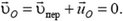
Откуда
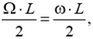 или
или 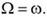
После отрыва оба конца стержня становятся свободными, растяжение стержня происходит относительно серединного сечения. В этом случае относительное удлинение каждой половины стержня, а, следовательно, и всего стержня, уменьшится в четыре раза, так как в формуле для относительного удлинения следует сделать замену 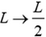 , а угловая скорость остается неизменной.
, а угловая скорость остается неизменной.
Задача 6*. Осесимметричный стержень подвешен вертикально за один из концов. В нижнем сечении радиусом r0 стержень нагружен растягивающей силой F, равномерно распределенной по сечению. При какой зависимости радиуса r стержня от расстояния х до нижнего сечения напряжения во всех горизонтальных сечениях будут одинаковы? Плотность материала стержня ρ. Ускорение свободного падения g.
По условию, напряжения в горизонтальных сечениях одинаковы и равны напряжению в нижнем сечении:
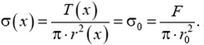
На любой элементарный горизонтальный слой толщиной Δх действует сила тяжести 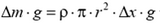 и упругие силы
и упругие силы 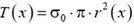 и
и 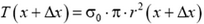 в нижнем сечении и в верхнем сечении соответственно (рис. 6).
в нижнем сечении и в верхнем сечении соответственно (рис. 6).
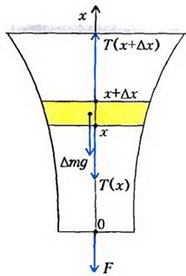
Рис. 6
Под действием приложенных сил выделенный слой покоится, следовательно, по второму закону Ньютона,
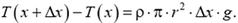
Введем 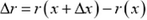 , тогда полученное уравнение примет вид
, тогда полученное уравнение примет вид
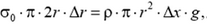
или
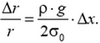
Суммируя такие равенства от х = 0 до любого х в пределах стержня и переходя от логарифмов к основаниям, получаем искомую зависимость радиуса сечения стержня от координаты:
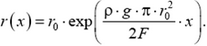
Задача 7. На астероиде Веста (радиус R = 280 км, ускорение свободного падения на поверхности g0 = 0,24 м/с2) решено установить межпланетную ретрансляционную станцию. Основой конструкции станции должна служить цилиндрическая труба, высота которой равняется радиусу планеты. На Весту завезли ровно 280 км титановых труб. На сколько ниже проектной окажется высота конструкции, когда она будет собрана в вертикальном положении? Считайте астероид однородным невращающимся шаром. Плотность титана ρ = 4500 кг/м3, модуль Юнга Е = 1,12·1011 Па.
Ускорение свободного падения над поверхностью планеты изменяется по закону 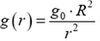 (координата r отсчитывается от центра планеты) и на высоте станции уменьшается в четыре раза. Следовательно, напряжения в конструкции и соответствующие им деформации не будут однородными.
(координата r отсчитывается от центра планеты) и на высоте станции уменьшается в четыре раза. Следовательно, напряжения в конструкции и соответствующие им деформации не будут однородными.
Найдем зависимость упругой силы T от координаты r. Для этого рассмотрим находящийся в равновесии произвольный элементарный горизонтальный слой трубы толщиной Δr (рис. 7).
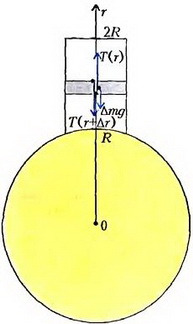
Рис. 7
Пусть площадь поперечного сечения стенки трубы равна S. На этот слой действует сила тяжести 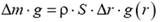 и упругие силы T(r) в нижнем сечении и T(r + Δr) в верхнем сечении. По второму закону Ньютона,
и упругие силы T(r) в нижнем сечении и T(r + Δr) в верхнем сечении. По второму закону Ньютона,
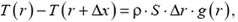
или
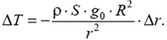
Суммируя такие равенства от r = 2R, где T(2R) = 0, до любого 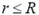 в пределах стержня и учитывая равенство
в пределах стержня и учитывая равенство 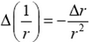 , получаем зависимость упругой силы от координаты:
, получаем зависимость упругой силы от координаты:
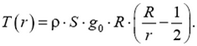
Элементарные уменьшения длины δ(Δr) найдем по закону Гука
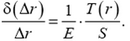
Полное уменьшение длины конструкции получим суммированием элементарных уменьшений:
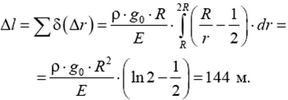
Задача 8. Груз массой m подвешен на трех тросах (рис. 8). Считая деформации малыми, найдите величину силы натяжения каждого троса, если они сделаны из одного материала и площади их поперечных сечений одинаковы. Ускорение свободного падения g.
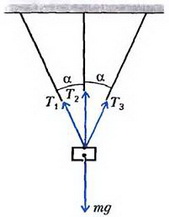
Рис. 8
Эта задача статически неопределима, так как для нахождения трех неизвестных усилий T1, T2, T3 в тросах нам известны из статики лишь два уравнения. Это равенство нулю суммы проекций сил на вертикальное направление:
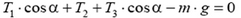
и на горизонтальное направление:
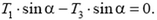
Чтобы найти недостающее третье уравнение, учтем упругие свойства материала, из которого сделаны тросы, и кинематическую связь. Так, малые деформации боковых тросов и центрального связаны соотношением (рис. 9)
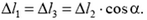
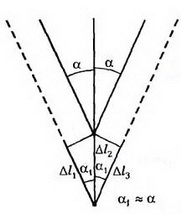
Рис. 9
В свою очередь, для длин тросов справедливо равенство
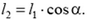
Кроме того, считая деформации тросов упругими, по закону Гука находим
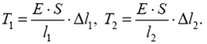
Подстановка полученных соотношений в первые два равенства приводит к следующим результатам:
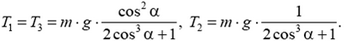
Упражнения
1. На гладком блоке радиусом R висит однородный гибкий канат массой m и длиной l. Найдите величину максимальной силы натяжения каната Fmax. Ускорение свободного падения g.
2. Груз массой m = 5000 кг равномерно опускается с некоторой скоростью с помощью троса и лебедки. Когда груз опустился на l = 2 м, лебедку заклинило, и трос оборвался. При какой скорости груза υ произойдет обрыв троса, если для него предел прочности на растяжение σр = 3,1·103 Па? Длина троса в момент остановки лебедки l = 2 м. Площадь поперечного сечения троса S = 5 см2, модуль Юнга материала троса E = 2,0·1011 Па. Ускорение свободного падения g = 10 м/с2.
3. Однородный стержень длиной l подвешен за один конец. Плотность материала стержня ρ, модуль Юнга Е, ускорение свободного падения g. Найдите удлинение Δl стержня. Как изменится ответ, если этот стержень будет размещен горизонтально и приведен в движение с горизонтальным ускорением а, сонаправленным со стержнем?
4. Определите период колебаний T груза массой m, подвешенного на пружине жесткостью k и массой М.
5. На верхний торец стоящей вертикально на жесткой опоре осесимметричной колонны высотой h действует сила F0 , однородно распределенная по горизонтальному сечению площадью S. При какой зависимости площади S поперечного сечения колонны от расстояния х до опоры напряжения во всех горизонтальных сечениях будут одинаковы? Найдите относительное уменьшение высоты колонны. Плотность материала колонны ρ, модуль Юнга Е. Ускорение свободного падения g.
6. В центре астероида Паллада (радиус R = 290 км, ускорение свободного падения на поверхности g0 = 0,17 м/с2) обнаружены залежи ценных ископаемых. Бурильщики затребовали ровно 290 км труб из вольфрамового сплава. Считая, что после завершения работ вся система труб свободно висит в канале, не касаясь его стенок, определите, какая часть труб будет сэкономлена вследствие растяжения конструкции под действием силы тяжести. Считайте астероид однородным невращающимся шаром. Плотность вольфрама ρ = 19,3·103 кг/м3, модуль Юнга E = 4,0·1011 Па.
7. Неоднородная балка массой m подвешена к потолку на трех одинаковых легких резиновых жгутах так, что жгуты вертикальны и лежат в одной плоскости (рис. 10). Расстояния между жгутами одинаковы. Считая деформации малыми, найдите упругие силы в жгутах. Ускорение свободного падения g.
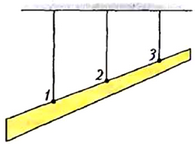
Рис. 10
Ответы.
1. 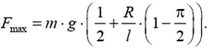
2. 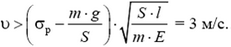
3. 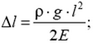 удлинение изменится в
удлинение изменится в 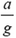 раз.
раз.
4. 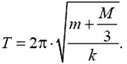
5. 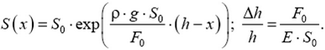
6. 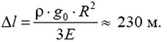
7.