
Рассмотрение уравнения относительного некоторой величины
Пусть имеется уравнение (неравенство), которое необходимо решить относительно неизвестной 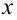 . Если в уравнении имеется параметр, то в некоторых случаях такое уравнение удобно решать относительно параметра (или какой-либо другой величины). Наиболее часто среди задач этой группы встречаются задачи, решаемые как квадратные относительно параметра.
. Если в уравнении имеется параметр, то в некоторых случаях такое уравнение удобно решать относительно параметра (или какой-либо другой величины). Наиболее часто среди задач этой группы встречаются задачи, решаемые как квадратные относительно параметра.
Пример №407.
Решить уравнение
Решение:
Рассмотрим данное уравнение как квадратное относительно 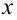 . Приведя его к стандартному виду, получим
. Приведя его к стандартному виду, получим
Чтобы уравнение имело решения, необходимо и достаточно, чтобы его дискриминант был неотрицателен:
![]()
Тогда 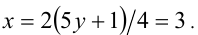
Ответ: 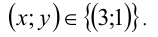
.
Пример 2 . При каких значениях 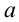 уравнение
уравнение 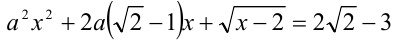 имеет решения?
имеет решения?
Решение:
ОДЗ: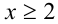 . Рассмотрим данное уравнение как квадратное относительно параметра
. Рассмотрим данное уравнение как квадратное относительно параметра 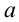 . Приведём его к стандартному виду
. Приведём его к стандартному виду
Квадратное уравнение (на ОДЗ 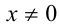 ) имеет решение тогда и только тогда, когда его дискриминант неотрицателен:
) имеет решение тогда и только тогда, когда его дискриминант неотрицателен:
![]()
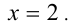 Тогда, подставляя это значение
Тогда, подставляя это значение 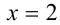 в уравнение, получим
в уравнение, получим 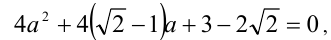 откуда находим
откуда находим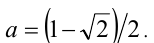
Замечание. Задачу можно было также решить, рассматривая данное уравнение как квадратное относительно выражения 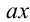 .
.
Пример №408.
Найти множество значений функции
Решение:
Рассмотрим данное равенство, которое задаёт функцию, как алгебраическое уравнение относительно 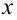 с параметром
с параметром 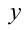 . Преобразуем его к виду:
. Преобразуем его к виду:
Сформулируем задачу в новой постановке: «При каких значениях 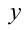 уравнение (1) имеет решения?»
уравнение (1) имеет решения?»
1) Если 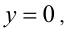 то, подставляя в уравнение (1), находим
то, подставляя в уравнение (1), находим 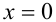 .
.
2) Если 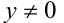 (тогда и
(тогда и 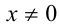 ), то уравнение является квадратным относительно
), то уравнение является квадратным относительно 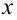 , и оно будет иметь решения тогда и только тогда, когда его дискриминант неотрицателен:
, и оно будет иметь решения тогда и только тогда, когда его дискриминант неотрицателен:
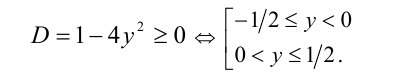
Объединяя все найденные значения 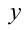 , получаем:
, получаем: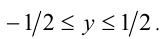 Следовательно, множество значений функции представляет собой отрезок
Следовательно, множество значений функции представляет собой отрезок 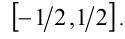
Ответ: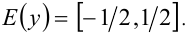
Пример №409.
Решить уравнение
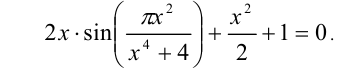
Решение:
Рассмотрим данное уравнение как квадратное относительно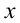 :
:
Необходимым и достаточным условием существования решений у этого уравнения является условие неотрицательности его дискриминанта:
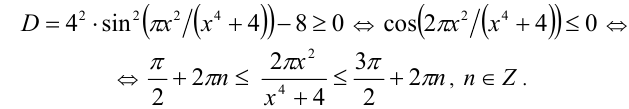
Оценим значения выражения 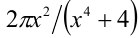 , при помощи неравенства
, при помощи неравенства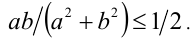 Тогда
Тогда 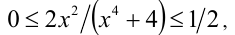 и, значит,
и, значит, 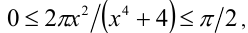 следовательно,
следовательно, 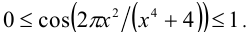 Поэтому
Поэтому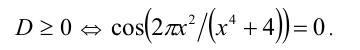
Отсюда находим
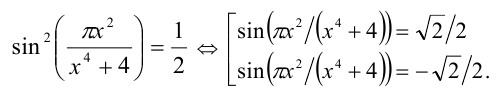
С учётом решаемого уравнения приходим к двум случаям:
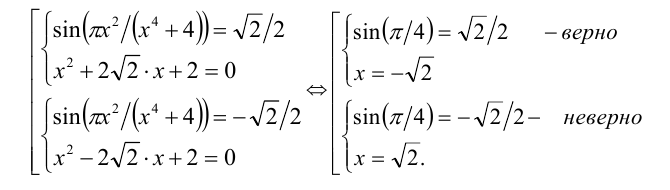
Ответ: 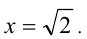
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:

Инвариантность или метод симметричных корней
Продолжаем знакомство с аналитическими способами решения сложных задач с параметрами, предлагающихся на различных пробниках и в настоящих вариантах ЕГЭ. В сегодняшнем материале будет рассмотрена новая группа задач, связанных с поиском значений параметра(ов), при которых имеется единственное решение задачи. Слово «единственное» в данной теме является ключевым. Один из самых распространённых методов решения таких задач — так называемый метод симметричных корней или, более научно, метод инвариантностей.
Типичные формулировки таких задач следующие: «Найдите все значения параметра а, при которых система уравнений имеет единственное решение.» Или: «Найдите все значения параметра а, при которых уравнение имеет единственный корень.»
Итак, пора познакомиться с инвариантностью. Что это за понятие? В переводе на русский язык слово «инвариантность» означает «неизменяемость». Неизменяемость чего-то по отношению к чему-то.)
В математике под инвариантностью понимается неизменяемость каких-либо выражений с переменными или функций по отношению к каким-либо преобразованиям над этими самыми переменными. Это может быть замена одной переменной на другую, смена знака и т.п. На словах, быть может, звучит не совсем понятно, но на деле всё гораздо проще.
Рассмотрим простой пример. Все мы с начальной школы знаем (я верю!) переместительное свойство сложения двух чисел:
Кто бы спорил, верно? От перестановки слагаемых сумма не меняется.) По-научному этот факт означает, что выражение a + b инвариантно относительно замены а на b и b на а. Можно сколько угодно менять буквы местами, а суть всего выражения от наших перестановок не изменится.)
Другой классический пример инвариантности – чётность. Если функция f(x) чётная, то, как мы знаем,
и тогда можно сказать, что функция f(x) инвариантна относительно замены x на –x.
Посмотрим на инвариантность в жизни?
Допустим у нас есть вот такое крутое уравнение:
Как нетрудно заметить, решений у него бесконечно много. Это, например, пары чисел (1;9), (5;5), (0;10), (-37;47), ну и так далее, можно писать до посинения.) Зачем, спрашивается? Пока — незачем. Бестолковое занятие, прямо скажем. Но, поскольку, как мы знаем, от перестановки слагаемых сумма не меняется, все эти решения объединяет одна важная особенность: если какая-то пара чисел (x0; y0) удовлетворяет данному уравнению, то автоматически и пара чисел (y0; x0) также обязательно ему удовлетворяет. Или в таких случаях говорят, что уравнение
инвариантно относительно замены x на y и y на x. Например, если пара (1;9) — решение, то автоматически и (9;1) — тоже решение. Понятно, я думаю.)
Идём дальше. Допустим, перед нами вот такая красивая система:
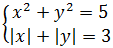
Кто умеет решать системы и в курсе, как раскрываются модули, тот без труда получит восемь её решений. Это пары:
Чем красива эта система? А тем, что она обладает сразу тремя типами инвариантностей!
Во-первых, суть системы не изменится от замены x на y и y на x. Это значит, что, помимо пары (x0; y0), система имеет своим решением и пару (y0; x0). Например, это пары (1; 2) и (2; 1) или (-1; -2) и (-2; -1). И так далее.
Во-вторых, квадрат и модуль — чётные функции. Это значит, что суть системы не изменится от замены, например, x на -х. Поэтому, помимо пары (x0; y0) решением системы будет являться и пара (-x0; y0). Что выражается, например, парами (1; 2) и (-1; 2). Или (2; 1) и (-2; 1).
То же самое можно сказать и про переменную игрек: суть системы не изменяется от замены y на -y, так как квадрат и модуль сжигают минус. И, помимо пары (x0; y0), решением нашей системы будет и пара (x0; -y0). Например пары (1; 2) и (1; -2).
А теперь представим, что у нас есть какая-нибудь ооочень страшная система. И мы каким-то чудом установили, что эта система инвариантна относительно, скажем, замены x на y. При этом в задаче требуется, чтобы решение было единственным. Тогда обязательно должно выполняться равенство x = y. То есть, таким единственным решением может быть только пара чисел (x0; x0) (или (y0; y0), что в данном случае одно и то же).
И теперь во всей задаче мы всюду можем смело заменить игрек на икс (или наоборот) и перейти к одной переменной, что, скорее всего, сильно упростит дальнейшие выкладки.)
Или если в какой-то задаче аргумент x всюду стоит под знаком чётной функции — квадрата, модуля, косинуса и т.п., а при этом требуется, чтобы решение задачи было единственным , то это будет возможно только в случае, когда
Почему? Да потому, что при всех остальных x, отличных от нуля, число –x автоматически тоже будет решением, т.е. задача заведомо будет иметь более одного решения . И теперь можно подставить x = 0 в исходную задачу и существенно упростить её. Таким образом, в случае чётности имеет место так называемая симметрия относительно нуля .
Но симметрия бывает не только относительно нуля. Если, скажем, уравнение не меняется относительно замены x на 2-x и должно иметь единственный корень, то обязательно должно выполняться равенство
x = 2 — x
То есть, этим единственным корнем может быть только единица. И теперьуже можно подставить x = 1 в исходное уравнение и определить все значения параметра, при которых единица является корнем.
А бывают и менее очевидные инвариантности. Например, относительно замены x на 1/x, откуда кандидатами на единственное решение могут быть только числа ±1. И так далее. Поиск таких закономерностей — порой процесс творческий и весьма интересный, и задачи такого типа предназначены для претендентов на высокие баллы.)
Сам процесс решения таких задач состоит из четырёх ключевых шагов.
1) Осмотр задачи и выявление инвариантных конструкций. Например, выражения x и -x, y и y-1 и т.п.
2) Нахождение решений-кандидатов на единственность. Делается это путём приравнивания этих самых инвариантных конструкций друг другу и решения получившегося уравнения.
3) Подстановка решений-кандидатов в исходную задачу и поиск соответствующих этим решениям значений параметра.
4) Проверка каждого найденных значений параметра на удовлетворение условий задачи.
Четвёртый шаг очень (ОЧЕНЬ!) важен в решении таких задач! Пояснения — ниже. На примерах.
Ну ладно, длинное вступительное повествование закончено, перейдём теперь к конкретным задачам (в т.ч. и из ЕГЭ) и будем решать их по мере возрастания сложности. Начнём с малого – с уравнений. 🙂
Пример 1

Итак, речь идёт о единственном корне. Это явный призыв поискать в уравнении инвариантные конструкции.)
От икса зависит только левая часть. Выпишем её отдельно:
А теперь рассуждаем примерно так:
«У нас слева стоит сумма двух показательных выражений. Основания у них одинаковые — тройка. Что очень хорошо.) А вот показатели — разные. «Икс» и «два минус икс». Но! Если в первом слагаемом показатель х заменить на 2-х, а во втором — наоборот, 2-х заменить на х, то слагаемые просто поменяются местами, а суть всего выражения при этом не изменится.»
Совершенно верно! Данное уравнение инвариантно относительно замены х на 2-х! Другими словами, если какое-то число х0 является корнем этого уравнения, то автоматически и число 2-х0 также будет его корнем. )
У нас же, по условию, корень должен быть единственным. Поэтому это возможно в том и только в том случае, когда
Здесь выявлена так называемая симметрия относительно единицы.
Это означает, что если данное уравнение имеет единственный корень, то им может быть только единица. И теперь уже можно подставить х = 1 в исходное уравнение и определить, при каких же значениях параметра а оно будет выполняться. Подставляем:
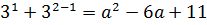
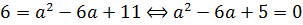
Решаем данное квадратное уравнение. Проще всего по теореме Виета:
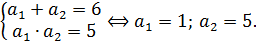
Получили два значения параметра — единицу и пятёрку. Но (внимание!) это пока что ещё не ответ, а лишь два возможных кандидата на ответ.) Теперь нам ещё предстоит сделать последний шаг — проверить каждое значение параметра а на выполнение условия единственности корня.
Специально акцентирую внимание на этом последнем шаге решения. Пропускать его ни в коем случае нельзя. Почему?
Казалось бы, всё классно: параметры найдены, и на этом решение задачи следовало бы закончить и записать ответ. Но… Вынужден открыть горькую правду. Всё дело в том, что найденные на третьем шаге значения параметра представляют собой лишь так называемое необходимое условие единственности решения. Но, к сожалению, не достаточное! Поясняю.
Найденные два числа (1 и 5) — это значения параметра, необходимые для того, чтобы единица только лишь была корнем данного уравнения . И всё! Единственный это корень будет или нет — совершенно не факт!
Поэтому последним (и обязательным!) шагом решения является проверка достаточности. Делается это так. Берётся каждое из найденных значений параметра и подставляется в исходную задачу. После чего решаем исходную задачу для каждого такого кандидата и устанавливаем, сколько решений в каждом случае получается. Тех кандидатов, при которых задача имеет более одного решения, безжалостно отсеиваем.)
Следует сказать, что последний шаг в подобных задачах зачастую наиболее трудоёмкий, потому что далеко не всегда при этом получаются уравнения и системы, решаемые стандартными алгебраическими преобразованиями — разложением на множители, приведением подобных, формулами тригонометрии, логарифмов и т.п. А требующие порой значительной изобретательности и искусства, я бы даже сказал. В чём мы лично убедимся на дальнейших примерах.)
Поэтому берём сейчас наши найденные значения параметра и подставляем в исходное уравнение.
Начнём с а = 1. Просто берём и подставляем в уравнение уже вместо «а» (а не икс!) единичку:
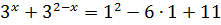
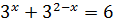
По правилам действий со степенями:
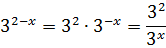
Перепишем наше уравнение с учётом данного факта:
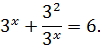
Умножим обе части на знаменатель 3 х (это вполне безобидно, поскольку выражение 3 х положительно при любом x и никогда не равно нулю) и перенесём всё влево:
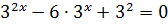
Получили квадратное уравнение относительно 3 х .
Здесь даже не нужно делать замену 3 х = t , а достаточно заметить, что слева стоит полный квадрат разности:
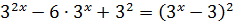
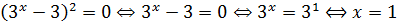 .
.
Итак, при a = 1 исходное уравнение действительно имеет своим единственным корнем единицу. Значит, a = 1 нас полностью устраивает и идёт в ответ.
Теперь разбираемся с пятёркой a = 5. Берём и подставляем в исходное уравнение пятёрку вместо a:
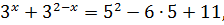
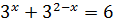
Получили уравнение, в точности эквивалентное случаю a = 1, имеющее, как уже установлено, единственный корень единицу. Значит, пятёрка нас также устраивает: a = 5.
Итак, мы полностью обосновали, что оба найденных значения параметра удовлетворяют условию достаточности, т.е. исходное уравнение действительно имеет единственный корень, и этот корень x = 1. И вот теперь можно с чистой совестью записывать окончательный ответ.)
Кстати, эту же задачу можно, конечно же, решить и через упомянутую выше замену переменной 3 х = t , выйти на квадратное (уже относительно t) уравнение с параметром и составить условие единственности корня. Какое? Конечно же, равенство нулю дискриминанта.) Но, поскольку темой данного урока является инвариантность, то и решили мы её, используя именно инвариантность.) Всё же хорошо иметь несколько способов решения одной и той же задачи, согласитесь.)
Здесь проверка достаточности никак не сказалась на ответе. Повезло, хороший пример.) Но, ещё раз повторю, что этот шаг является обязательной частью решения таких задач. На примерах ниже мы воочию в этом убедимся.)
Пример 2
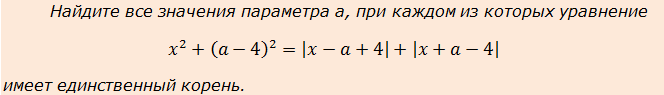
Здесь в нагрузку добавились ненавистные многими модули, но и мы тоже поднялись на следующий уровень.) Поскольку в задаче снова речь идёт о единственном корне, поищем инвариантности. Замечаем, что икс везде стоит внутри чётных функций — либо под модулем, либо в квадрате.
Напрашивается чётность. То есть, инвариантность относительно х и –х.)
Ну, с x 2 всё ясно — тут чётность очевидна. А вот с суммой модулей, стоящей в правой части, всё не так очевидно. Попробуем в выражение
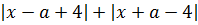
вместо «икс» подставить «минус икс» и посмотрим, что из этого выйдет:
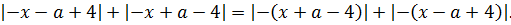
Как известно, модуль — тоже функция чётная и «сжигает» минус:
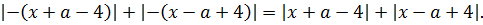
Итак, что мы видим? Мы видим, что от замены x на –x правая часть уравнения также не изменилась (просто модули поменялись местами :)). А это значит, что уравнение действительно инвариантно относительно х и –х. И, если оно имеет какой-то корень х0, то и число –х0 автоматически также будет корнем этого уравнения.
Поэтому для единственности эти два корня должны совпадать, т.е. необходимо выполнение условия
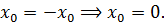
Значит, если данное уравнение имеет единственный корень, то им может быть только ноль. Подставляем число 0 в исходное уравнение вместо икса:
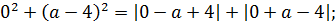
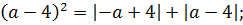
Для дальнейших упрощений воспользуемся чётностью квадрата и модуля:
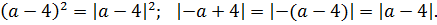
Перепишем наше уравнение с учётом этих фактов:
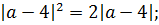
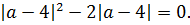
Выносим один модуль за скобку:
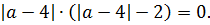
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
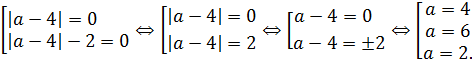
Итак, получены три кандидата на ответ. При этих значениях параметра a исходное уравнение обязательно будет иметь одним из своих корней число 0. А вот будет ли число 0 единственным корнем или нет, нам и предстоит сейчас проверить. Проверяем теперь достаточность: устраиваем нашим кандидатам конкурсный отбор. 🙂
Порядок здесь роли не играет. Давайте начнём с четвёрки: a = 4. Подставляем вместо а в исходное уравнение четвёрку:
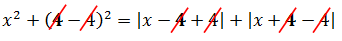
Все четвёрки благополучно посокращались и осталось лишь:
x 2 = |x| + |x| или x 2 — 2|x| = 0
Снова заменяем x 2 на |x| 2 и выносим один модуль за скобку:
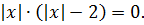
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
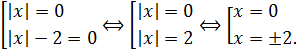
Итак, что мы видим? Мы видим, что при a = 4 наше уравнение имеет не только корень x = 0, но и ещё два корня — два и минус два! О чём это говорит? О том, что при a = 4 уравнение имеет более одного корня (а именно — целых три). Стало быть, первый кандидат a = 4 не прошёл наш кастинг, поэтому с треском вылетает из дальнейшей борьбы и в ответ не идёт. 🙂
Эстафета передаётся следующему претенденту a = 6. Подставляем в наше уравнение шестёрку вместо параметра a. Получаем:
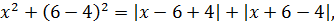
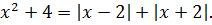
Получили типовое уравнение с модулями, решаемое путём раскрытия модулей по промежуткам. Предполагается, что народ, интересующийся нестандартными задачами с параметрами, решать такие уравнения уже умеет, поэтому здесь я опущу подробное описание решения этого уравнения (что, как, зачем и почему) и оформлю его достаточно сжато.
Как обычно, разбиваем числовую ось на промежутки, границами которых являются нули подмодульных выражений. В нашем случае это 2 и -2.
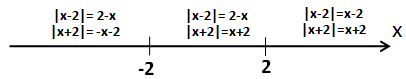
Раскроем модули на каждом промежутке и для наглядности подпишем их на рисунке.
1) x ≤ -2 . Оба модуля раскрываются со знаком «минус»:
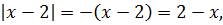
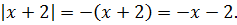
Тогда имеем следующее:
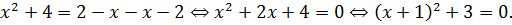
Очевидно, левая часть положительна при любых икс, а значит, данное уравнение действительных корней не имеет. Итак, на интервале (-∞; -2] корней у нашего уравнения нет.
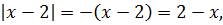
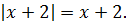
В этом случае наше уравнение станет таким:
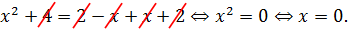
Ноль принадлежит рассматриваемому интервалу (-2; 2) и, стало быть, является первым корнем нашего уравнения.
И, наконец, на очереди третий случай.
3) x ≥ 2. В этом случае оба модуля раскрываются с плюсом:
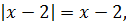
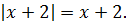
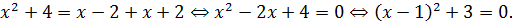
Понятно, что левая часть всегда положительна, а значит, как и в первом случае, корней при x ≥ 2 у нашего уравнения также нет.
Итак, все случаи разобраны, и единственным корнем нашего уравнения является x = 0.
А теперь вспоминаем, что это уравнение мы получили и решили для a = 6. А это значит, что при a = 6 исходное уравнение действительно имеет единственный корень x = 0, а других корней, кроме нуля, не имеет (мы только что это доказали). Всё, a = 6 нас полностью устраивает, и шестёрка пошла прямиком в ответ.)
Третий пошёл!) Подставляем теперь a = 2:
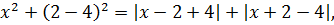
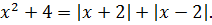
Кандидата a = 2 можно сразу принять на работу в ответ без предварительного собеседования решения полученного уравнения. Почему? А потому, что, если взглянуть на получившееся уравнение, то можно увидеть, что оно отличается от уравнения, полученного для a = 6 только порядком слагаемых в правой части. То есть, по своей сути — ничем.) И, ясное дело, оно также имеет своим единственным корнем число 0.
Итак, a = 2 тоже подходит.)
Всё, задача полностью решена! 🙂
Ответ: a = 2; a = 6.
Так, с уравнениями более-менее потренировались. Двигаемся на следующий уровень и переходим теперь к системам.)

«Так-с… Модуль, тригонометрия — всё намешано в одну кучу, что как-то не особо обнадёживает. Можно, конечно, напрямую выразить из первого уравнения игрек
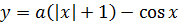
и подставить во второе, только что это даст? Всю эту белиберду ведь ещё и в квадрат возводить придётся!
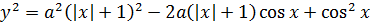
Ну, хорошо. Подставляем теперь всё это барахло во второе уравнение вместо «игрек квадрат»:
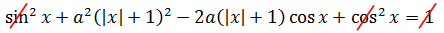
И что тут можно сделать? О-па! Да тут же основное тригонометрическое тождество sin 2 x + cos 2 x = 1, которое можно сократить с единичкой справа.)
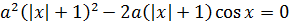
Ну, а потом что? Можно левую часть разложить на множители, отправив, к примеру, одну из скобок за скобки (да простит меня русский язык за тавтологию). Но что-то уж больно запутанно получается… Не факт, что удастся добраться до истины, совсем не факт… Стоп! Но у нас же говорится о единственном решении! А может, тут тоже есть что-то симметричное или инвариантное, что сделает решение куда проще?»
Немного присмотревшись к системе, можно снова заметить, что икс везде тусуется внутри чётных функций — модуль, косинус, квадрат синуса….
А это означает, что вместе с какой-то парой (x0; y0) данная система автоматически будет иметь своим решением и пару (-x0; y0). Что при требовании единственности решения означает, что
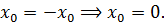
Далее по проторенной дорожке — подставляем в нашу систему х = 0 и ищем необходимые значения параметра a:
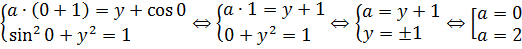
Получили два необходимых значения параметра a. Необходимых для чего? Для того, чтобы пара чисел (0; y0) была решением нашей системы. И не более того. Сколько этих решений окажется на самом деле, ещё непонятно. Что ж, снова тестируем наших кандидатов, подставляя каждого в исходную систему.)
Итак, проверяем a = 0.
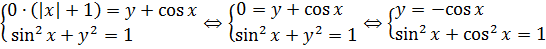
Ну,и что тут видно? Видно, что второе уравнение, после подстановки в него y = -cos x из первого уравнения, благополучно превратилось в основное тригонометрическое тождество, верное при любых значениях икса. О чём это говорит? Да! Система имеет бесконечно много решений: какой бы икс мы ни взяли, по нему всегда можно будет определить игрек из первого уравнения, а второе уравнение будет выполняться автоматически. Это значит, что при a = 0 наша система имеет бесконечно много решений. То есть, a = 0 нас заведомо не устраивает. Отметаем этого кандидата.)
Следующий клиент, a = 2.
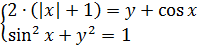
Здесь уже так просто не выкрутиться (а я предупреждал, что проверка достаточности — очень часто самая сложная часть решения задач). В таких нестандартных ситуациях, когда в уравнении слева и справа стоят какие-то разнородные (и обычно ограниченные) конструкции (в нашем случае это модуль и косинус), чаще всего применяется метод оценок или, более научно и красиво, метод мажорант. Что ж попробуем оценить каждое из уравнений.
Ну, во-первых, про модуль мы знаем, что он всегда неотрицателен:
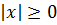 .
.
Значит, про левую часть первого уравнения можно сказать следующее:
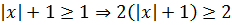 .
.
Итак, левая часть первого уравнения в любом случае не меньше двойки.
Что ещё в первом уравнении можно оценить? Ну, очевидно, косинус:
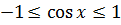 .
.
А вот всю правую часть первого уравнения мы пока оценить не можем: у нас ещё нет никакого ограничения на игрек. Ничего, сейчас получим.)
Для этого переключимся на второе уравнение:
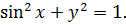
Смотрим на него и прикидываем: слева стоит сумма квадратов — двух неотрицательных слагаемых. И эта сумма квадратов даёт единицу.
А теперь подумаем: какие такие два неотрицательных числа в сумме могут давать единицу? Как нетрудно догадаться, это могут быть либо какие-то дроби от нуля до единицы (например, 0,5 или 1/3), либо же когда одно из слагаемых равно в точности нулю, а другое — в точности единице. Значит, по-любому
0 ≤ sin 2 x ≤ 1 и 0 ≤ y 2 ≤ 1.
Раз 0 ≤ y 2 ≤ 1 , то тогда про сам игрек можно сказать, что -1 ≤ y ≤ 1 .
Итак, мы установили ограничения на косинус и на игрек. Они таковы:
А это значит, что их сумма (т.е. вся правая часть первого уравнения) ограничена вот так:
А теперь смотрим на первое уравнение системы
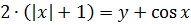
и на наши ограничения.
Для левой части: 2(|x|+1) ≥ 2, т.е. левая часть не меньше двойки.
Для правой части: -2 ≤ y + cos x ≤ 2 , т.е. правая часть не больше двойки.
Как вы думаете, когда возможно равенство обеих частей уравнения? Да! Когда каждая из них одновременно в точности равна двойке!
Значит, первое уравнение системы распадается на два условия:
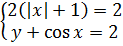
Вместе со вторым уравнением системы получим:
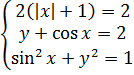
Нетрудно убедиться (а это достаточно просто), что единственным решением этой системы (а значит, и исходной) является пара чисел (0; 1). Это значит, что значение параметра a = 2 нас полностью устраивает. Всё, задача полностью решена, можно записывать окончательный ответ.
Кстати, стандартный способ подстановки (размышления синим цветом в самом начале решения этого примера), который был нами прерван, здесь со скрипом, но тоже действует.) Кому интересно, попробуйте довести решение до конца, продолжив разложение на множители и приравняв каждый к нулю. 🙂 А вот следующий пример уже куда серьёзнее будет.
Пример 4

Уже при первом взгляде на систему видно, что ничего никуда не преобразуется, переменные друг через друга «красиво» не выражаются — ни y через x, ни x через y. Значит, стандартные приёмы не катят. Но! Переменная икс у нас снова везде стоит под модулем или в квадрате, т.е. под чётными функциями! А это означает, что единственным решением данной системы может быть только пара вида (0; y0). Почему это именно так, объяснять, думаю, уже не нужно.) Если всё же непонятно, просмотрите ещё раз хотя бы предыдущий пример.
При подстановке x = 0 вся наша термоядерная система существенно упрощается:
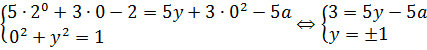
Если y = 1, то: Если y = -1 , то:
Итак, наши кандидаты — это две пятых и минус восемь пятых. Всего два.) Это – необходимые значения параметра «a» для того, чтобы пара (0; y) была одним из решений исходной системы. Теперь, как водится, проверяем достаточность, т.е. чтобы наша пара (0; y) была не просто одним из решений системы, а единственным её решением.
Поехали, подставляем в систему a = 2/5. В этом случае вся система примет вид:
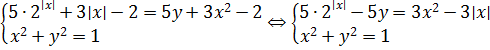
В первом уравнении я, во-первых, сократил двойки, а во-вторых, все члены с пятёркой собрал слева, а с тройкой — справа. Зачем — станет ясно ниже.)
Далее размышляем примерно так:
«Перед нами страшная система, которую как-то необходимо решить. Точнее не столько решить, сколько выяснить, сколько именно решений она имеет — единственное или нет. Или, возможно, вообще не имеет решений.) Но есть одна проблемка. Как к ней подступиться?
Если традиционно выразить y через x из второго уравнения, то будет
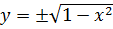
И что потом с этим плюс/минусом делать?! Непонятно…
А если выразить игрек из первого уравнения? Тогда вообще кошмар получится:
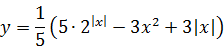
А если икс через игрек из второго? Тоже не фонтан. Значит, стандартные приёмы здесь явно не работают. Так… Но у нас в обоих уравнениях фигурируют модули и квадраты — ограниченные (снизу) конструкции. А что, если попробовать оценить левую и правую части первого (самого страшного) уравнения?»
Верные мысли! Итак, наша цель на данный момент – оценить обе части первого уравнения. Затяните потуже ремни на брюках, поскольку сейчас нам предстоит решать много неравенств. Точнее, не столько решать, сколько их выписывать, складывать, преобразовывать и т.д. Итак, перед оцениваем первое уравнение:
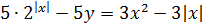 .
.
Но для начала обратим наш взор на второе уравнение:
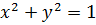
Снова, как и в примере 3, видим сумму квадратов, равную единице. О чём это говорит? О том, что каждый из этих квадратов сам по себе не превосходит 1.
То же самое можно сказать и про модули икса и игрека:
Поэтому про сами x и y можно сказать, что -1 ≤ x ≤ 1 и -1 ≤ y ≤ 1 .
А теперь с помощью данных неравенств оцениваем левую часть первого уравнения, равную сумме выражений 5·2 |x| и -5y:
Здесь мы воспользовались монотонным возрастанием функции f(x) = 2 x .
Если теперь все три части последнего неравенства помножить на 5, то получим:
Далее, раз -1 ≤ y ≤ 1 , то тогда
Возможно, кому-то непонятно, как именно из неравенства -1 ≤ 5y ≤ 1 получилось неравенство -1 ≤ -5y ≤ 1 . Поясняю.
-1 ≤ 5y ≤ 1 |·(-1) (умножаем обе части на -1);
1 ≥ -5y ≥ -1 (все знаки изменились на противоположные);
-5 ≤ -5y ≤ 5 (переписываем неравенство в привычной форме).
Итак, мы установили ограничения на выражения 5 ·2 |x| и -5y:
Теперь, сложив почленно эти два неравенства, получим ограничение на всю левую часть целиком:
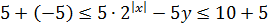
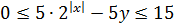
Запомним этот факт.) Обратимся теперь к правой части уравнения: 3x 2 — 3|x|.
А вот её будем оценивать немного иначе.
Как нами уже установлено, 0 ≤ x 2 ≤ 1 .
Далее воспользуемся одним весьма нетривиальным, но очень полезным сравнением:
Откуда я его взял? Как фокусник из рукава вытащил?)
Чтобы разобраться, почему это именно так, нарисуем графики модуля («уголок») и параболы у = x 2 . На отрезке [-1; 1] картинка будет вот такой:
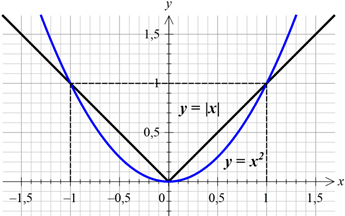
Видно, что на отрезке [-1; 1] «уголок» везде, кроме точек 0 и ±1 лежит выше параболы.
Тогда x 2 — |x| ≤ 0 (я просто перенёс модуль влево).
Значит, если это неравенство умножить на 3, то получим:
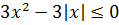
Таким образом, вся правая часть не больше нуля.
А теперь вспоминаем, что же у нас с левой частью:
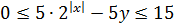
Таким образом, левая часть не меньше нуля.
Значит, равенство левой и правой частей возможно лишь в одном случае — когда каждая из них отдельно равна нулю:
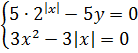
Решаем эту системку.)
Отсюда легко получаем три пары: (0; 1), (-1; 2), (1; 2).
Однако, решения этой системы — это на самом деле лишь решения первого уравнения нашей глобальной системы.) Вспоминаем про её второе уравнение: x 2 + y 2 = 1.
Нетрудно убедиться, что из этих трёх пар ему удовлетворяет лишь пара (0; 1). А что это означает? В дебрях долгих выкладок и рассуждений, неволей, и про основной вопрос забываешь… ) Да! При a = 2/5 наша исходная система и вправду имеет единственное решение.
Всё, a = 2/5 обводим как часть ответа.)
А что же с a = -8/5? Делать нечего, подставляем его в нашу систему:
А вот здесь так красиво провести оценку уже не получится: десятка справа всё испортила.( Как быть? В таких ситуациях, как правило, приходится прибегать к самой крайней мере — попытаться тупо подбором угадать два каких-нибудь решения и таким образом доказать, что система имеет более одного решения.) Как угадывать? Ну, тут уже всё от конкретного задания зависит. И немного от интуиции и иногда от везения. В нашем случае попробуем зацепиться за второе уравнение:
Понадеемся на гуманизм составителей задания и начнём с самого простого – поищем какие-нибудь целые решения этого уравнения и подставим их в первое. Их совсем немного. Ну, например, (1; 0):
Что ещё можно проверить? Ха! У нас же симметрия по икс! Мы же как раз этот факт использовали для решения всей задачи! И думать не надо — тут же всплывает решение (-1; 0)!
Всё! Мы подобрали два различных решения системы, а это значит, что второе значение параметра a = -8/5 нас точно не устраивает. Всё, задача решена! 🙂
Что ж, мы уже набрались достаточно опыта, чтобы рассмотреть какую-нибудь откровенную жесть. Берём быка за рога! 🙂
Пример 5
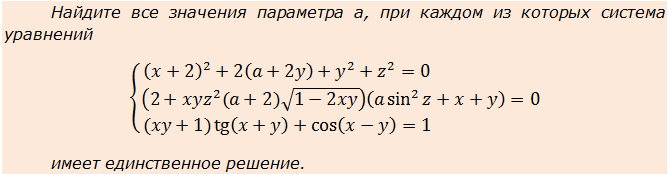
Ничего не боимся и стараемся при виде подобных монстров мыслить примерно следующим образом:
«Ух, наворотили, ужас! Корень, тангенс, синусы… Точно не решить… Так, стоп! От нас хотят найти единственное решение. Значит, скорее всего, нас просят отыскать какую-нибудь инвариантную конструкцию и с её помощью решить всю задачу.
Что тут сильнее всего бросается в глаза? Ну, во-первых, во втором и третьем уравнениях везде тусуются xy и x+y, а от перестановки множителей (слагаемых) результат не меняется. Это неспроста.) Так, ещё тут внутри косинуса затесалась разность x-y , которая от перемены икса и игрека местами сменит знак:
Плохо… Так, секундочку! Но ведь косинус – чётная функция и сжигает минус! Всё отлично, под косинусом тоже ничего не поменяется!)
Но есть ещё первое уравнение. В нём пока что никакой инвариантностью относительно перестановки икса и игрека и не пахнет. А вдруг, эту инвариантность и там удастся выявить? Ну-ка, посмотрим…
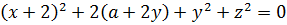
И что тут можно сделать? Можно хотя бы пораскрывать все скобки:
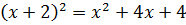
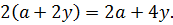
Вставляем всё в уравнение:
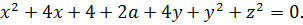
Ну, хорошо, а дальше? Сгруппируем-ка в кучку квадраты и первые степени. Хуже не будет. Будет либо хорошо, либо никак.)
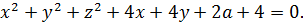
Кажется, уже что-то вырисовывается:
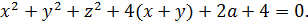
Ну, вот и выявилось то, чего мы так добивались: x 2 +y 2 и x+y – инвариантные конструкции. Относительно замены x на y и y на x. Ура!»
Итак, вся система инвариантна относительно замены x на y (и наоборот). Это значит, что, если какая-то тройка чисел (x; y; z) является решением этой злой системы, то автоматически и тройка (y; x; z) также будет её решением! И единственность решения системы возможна только при x = y. Теперь можно во всей системе смело исключить игрек, заменив его на икс: xy превратится в x 2 , x+y превратится в 2x. Ну, и так далее. )
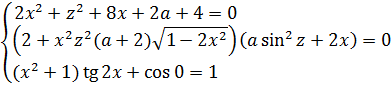
Так, система стала немного попроще, но ещё пока что довольно громоздка. Но… Переменная z везде тусуется под чётными функциями – либо в квадрате, либо внутри синуса в квадрате. А это значит, что единственность решения возможна только при z = 0. Прекрасно! Подставляем всюду ноль вместо z, и вся наша ужасная система ещё больше упростится и станет выглядеть вот так:
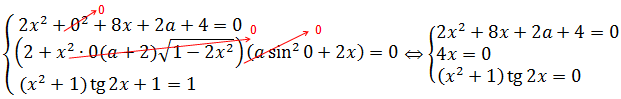
Из второго уравнения сразу ясно, что х = 0. Третье уравнение при х = 0, очевидно, выполняется. А из первого уравнения при х = 0 получим:
Ух ты, как интересно! Получено одно единственное допустимое значение параметра. Минус два. Но радоваться рано, т.к. это ещё не ответ: нам же ещё достаточность надо проверить (да-да!). Деваться некуда, подставляем минус двойку в исходную систему вместо «а»:
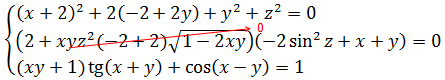
По максимуму упрощаем каждое из уравнений. В первом раскроем все скобки:
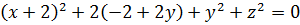
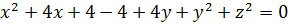
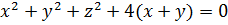
Во втором уравнении благополучно обнуляется самое ужасное слагаемое с корнем, сокращается двойка, оставшаяся от первой скобки, и остаётся лишь
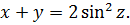
Ну, а третье уравнение так и оставим, без изменений. Итого:
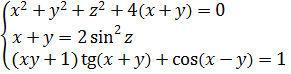
А теперь делаем такой финт ушами — подставляем в первое уравнение вместо x + y выражение 2sin 2 z из второго. Что получим:
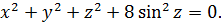
Проанализируем полученное уравнение. Чем оно примечательно? Тем, что слева стоит сумма каких-то квадратов, т.е. неотрицательных слагаемых! А когда возможно равенство нулю суммы неотрицательных слагаемых? Только в одном единственном случае — когда одновременно каждое слагаемое равно нулю! То есть:
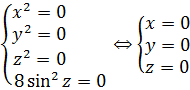
Итак, единственным решением первого уравнения является тройка чисел (0; 0; 0). Проверим эту тройку и по остальным уравнениям: вдруг, она там не пройдёт? Тогда ответом, очевидно, будет пустое множество.)
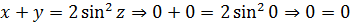
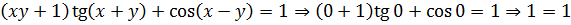
Все равенства выполнены. Итак, мы полностью обосновали, что при a = -2 наша система действительно имеет единственное решение, и это решение — «три бублика», т.е. (0; 0; 0).
Разумеется, эти рассмотренные пять примеров далеко не исчерпывают всего многообразия параметрических задач на единственное решение и инвариантность. ) Но в них я постарался максимально подробно и доходчиво изложить, как действовать в ситуации, если, вдруг, где-то (в пробнике или в настоящем ЕГЭ) вам попалась подобная задача. Итак, подытожим тему:
1) Как только видим словосочетание «единственный корень/единственное решение» – пробуем искать инвариантные конструкции или приходить к таковым путём предварительных преобразований. Чаще всего это чётность, симметрия относительно какого-нибудь числа, либо относительно перестановок (замен) переменных или выражений.
2) Выявив тип инвариантности, составляем необходимое условие единственности решения и ищем допустимые (необходимые) значения параметра. Как правило, вся задача при этом существенно упрощается, и их поиск не составляет особого труда.
3) Проверяем найденные допустимые значения параметра на достаточность . В случае, если получаемая задача не решается стандартными методами, применяем специальные приёмы — ограниченность, монотонность и т.п. Если и они не помогают — пробуем подобрать корень или решение. Чаще всего они лежат на поверхности и, как правило, являются целыми числами.
4) Не боимся. Пробуем различные варианты.) И побольше тренируемся.) Только так можно выработать необходимый опыт в решении таких (да и вообще любых) задач с параметрами.
Решение простых линейных уравнений

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = – 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Алгебраические уравнения в математике с примерами решения и образцами выполнения
Алгебраическое уравнение — это уравнение вида. где. — многочлен от переменных. , которые называются неизвестными.

Делимость многочлена
Делимость многочлена, целого относительно х, на разность x— а.
Теорема Безу:
Многочлен, целый относительно х: 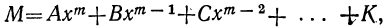 ,
,
при делении на разность х — а (где а есть произвольное число, положительное или отрицательное) даёт остаток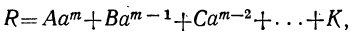
равный тому значению делимого, которое оно получает при х=а.
Доказательство:
Из процесса деления многочлена, расположенного по убывающим степеням буквы х, видно, что деление такого многочлена на х — а можно продолжать до тех пор, пока высший член остатка R не будет содержать в себе буквы х. Пусть при этом частное будет некоторый многочлен Q. Тогда мы можем написать равенство:
M=(x- a)Q+R.
Равенство это есть тождество, т. е. оно верно при всевозможных значениях буквы х, а потому оно должно быть верно и при х-а. Но при x=а оно даёт
M’ = (α — α) Q’ + R
если буквами М‘ и Q‘ обозначим те значения M и Q, которые эти многочлены принимают при х=а (остаток R, как не содержащий вовсе x, не изменится от подстановки а на место х). Так как a — α=0, то и произведение (а — a) Q‘ равно 0; значит, последнее равенство даёт M‘= R, т. е. 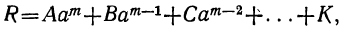
что и требовалось доказать.
Следствие:
Так как x+α=x— (—а), то, применяя доказанную теорему к сумме х+а, найдём:
многочлен 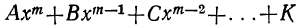
при делении на сумму x+α даёт в остатке число, равное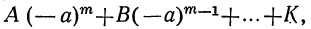
т. е. число, равное тому значению делимого, которое оно получает при x= —а.
Примеры:
1) Многочлен x⁵—3x²+5x—1 при делении на х—2 даёт остаток, равный
2⁵-3 ∙ 2²+5 ∙ 2—1=29.
2) Многочлен x⁵—3x²+5x—1 при делении на x+2 даёт остаток
(-2)⁵-3 (- 2)²+5 (-2)—1=-55.
Следствие:
Для того чтобы многочлен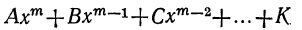
делился на разность х—а, необходимо и достаточно, чтобы при х=а он обращался в нуль.
Это необходимо, так как если указанный многочлен делится на x—а, то остаток от деления должен быть нуль, а этот остаток, по доказанному выше, есть то значение делимого, которое оно принимает при x=а. Это и достаточно, так как если многочлен обращается в нуль при x=a, то это значит, что остаток от деления этого многочлена на х—а равен нулю.
Следствие:
Для того чтобы многочлен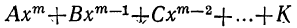
делился на сумму х+а, необходимо и достаточно, чтобы при х = —а он обращался в нуль, так как сумма х+а есть разность x—(— а).
Примеры:
1) Многочлен x³-4x²+9 делится на х—3, потому что
З³ — 4∙3²+9=0.
2) Многочлен 2x²+x-45 делится на x+5, так как
2 (-5)²+(-5)—45=0.
Делимость двучлена 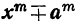 на
на 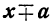 . 1) Разность одинаковых степеней двух чисел делится на разность тех же чисел, так как
. 1) Разность одинаковых степеней двух чисел делится на разность тех же чисел, так как 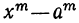 при делении на х—а даёт остаток
при делении на х—а даёт остаток 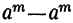 , т. е. 0.
, т. е. 0.
2) Сумма одинаковых степеней двух чисел не делится на разность этих чисел, так как 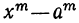 при делении на х—а даёт остаток
при делении на х—а даёт остаток 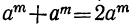 , а не 0.
, а не 0.
3) Разность одинаковых чётных степеней двух чисел делится, а нечётных не делится на сумму этих чисел, так как при делении разности 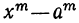 , на х+а остаток равен
, на х+а остаток равен 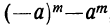 , что при m чётном равно нулю, а при tn нечётном составляет —
, что при m чётном равно нулю, а при tn нечётном составляет — 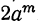 .
.
4) Сумма одинаковых нечётных степеней двух чисел делится, а чётных не делится на сумму этих чисел, так как. при делении суммы 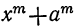 на x+α остаток равен
на x+α остаток равен 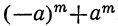 что при m нечётном равно 0, а при m чётном составляет
что при m нечётном равно 0, а при m чётном составляет 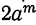 .
.
Примеры:
1) x¹+α¹ делится на x+α, но не делится на х—а.
2) x²- α² делится и на х—а, и на x+a.
3) x²+α² не делится ни на х—а, ни на x+a.
4) x³- α³ делится на х—а, но не делится на x+α.
5) x³+α³ делится на x+a, но не делится на х—а.
Частные, получаемые при делении 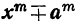 на
на 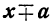 . Если произведём деление двучлена
. Если произведём деление двучлена 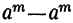 на двучлен х—а, то в частном получим многочлен:
на двучлен х—а, то в частном получим многочлен: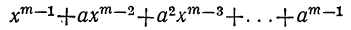
(остатки при этом делении идут в такой последовательности: 1-й остаток 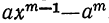 , 2-й остаток
, 2-й остаток 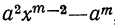 , 3-й остаток
, 3-й остаток 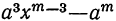 ,…, m-й остаток
,…, m-й остаток 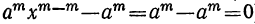 ).
).
Очевидно, что многочлен, получившийся в частном, содержит m членов; сумма показателей в каждом члене при а и х одна и та же, именно: m—1; показатели х идут, уменьшаясь на 1,от m—1 до 0, показатели же а идут, увеличиваясь на 1, от 0 до m—1; коэффициенты у всех членов равны 1; знаки все +; число членов в частном m.
Заметив это, можем прямо писать:
x³- α³=(x-a) (x²+αx+α²);
x⁴- α⁴=(x-α) (x³+αx²+α²x+ α³);
x⁵ — α⁵=(x-a) (x⁴+αx3+α²x²+α³x+α⁴) и т. п.
Чтобы получить частное от деления 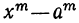 на x + a при m чётном или при делении
на x + a при m чётном или при делении 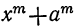 на x+a при m нечётном, достаточно в полученном выше частном заменить а на —а. Таким образом:
на x+a при m нечётном, достаточно в полученном выше частном заменить а на —а. Таким образом:
x³+α³=(x+α) (x²-αx+α²);
x⁴—α⁴=(x+α) (х³-αx²+α²x-α³);
x⁵+a⁵=(x+α) (х⁴ — αx³+α²x² — a³x+a⁴) и т.п.
Общий вид алгебраического уравнения
Мы ранее видели, что уравнение, содержащее неизвестное в знаменателях, может быть приведено к целому виду. Далее мы знаем, что уравнение, содержащее неизвестное под знаком радикала, может быть приведено к рациональному виду. Вследствие этого можем сказать, что всякое уравнение, в котором неизвестное связано с данными числами посредством конечного числа шести алгебраических действий (сложения, вычитания, умножения, деления, возвышения в степень и извлечения корня), может быть приведено к такому целому и рациональному виду: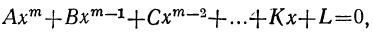
где коэффициенты А, В, С, … , K и L суть постоянные вещественные или комплексные числа, а m есть показатель степени уравнения. Некоторые коэффициенты, кроме первого, в частных случаях могут равняться нулю.
Уравнение такого вида называется алгебраическим. Алгебраические уравнения степени выше второй называются уравнениями высших степеней.
Некоторые свойства алгебраического уравнения
Уравнения высших степеней составляют предмет высшей алгебры. Элементарная же рассматривает только некоторые частные виды этих уравнений.
Высшая алгебра устанавливает следующую важную теорему:
Всякое алгебраическое уравнение имеет вещественный или комплексный корень (теорема Гаусса 2), 1799 г.).
Допустив эту истину (доказательство которой в элементарной алгебре было бы затруднительно), нетрудно показать, что:
Алгебраическое уравнение имеет столько корней, вещественных или комплексных, сколько единиц в показателе его степени.
Действительно, согласно теореме Гаусса, уравнение
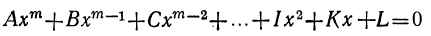 (1)
(1)
имеет вещественный или комплексный корень; пусть этот корень будет а. Тогда многочлен, стоящий в левой части уравнения (1), должен делиться на х—а. Если произвести это деление, то в частном получим многочлен степени m—1, у которого первый коэффициент будет А. Обозначив другие его коэффициенты соответственно буквами B₁, C₁ ,…, K₁ и приняв во внимание, что делимое равно делителю, умноженному на частное, можем представить уравнение (1) так:
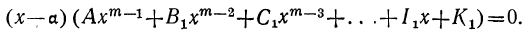 (2)
(2)
Приравняв нулю многочлен, стоящий во вторых скобках, получим новое уравнение, которое по той же теореме должно иметь некоторый корень β; вследствие этого левая его часть может быть разложена на два множителя: х—β и многочлен степени m—2, у которого первый коэффициент по-прежнему будет А. Поэтому уравнение (1) можно переписать так:
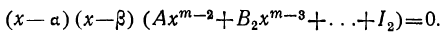 (3)
(3)
Продолжая эти рассуждения далее, дойдём, наконец, до того, что многочлен, заключённый в последних скобках, будет второй степени, причём первый его коэффициент останется А. Разложив этот трёхчлен на множители, приведём уравнение (1) к виду:
A(x- а) (х—β) (х— γ) . .. (х—λ)=0, (4)
где всех разностей: x-a, х- β,…, будет m. Очевидно, что уравнение (4) обращается в тождество при каждом из значений: x=α, x=β, x=γ, . x=λ и не удовлетворяется никакими иными значениями x (если A≠0); значит, уравнение (1) имеет m корней: a, β, γ ,…, λ. В частных случаях некоторые корни могут оказаться одинаковыми.
Полезно заметить ещё следующие истины, доказываемые в высшей алгебре.
Сумма корней всякого алгебраического уравнения 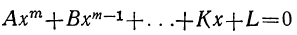
равна 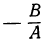 , а произведение корней равно
, а произведение корней равно 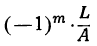 (примером может служить квадратное уравнение).
(примером может служить квадратное уравнение).
Если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то число этих корней — чётное (примером может служить биквадратное уравнение).
Если алгебраическое уравнение с вещественными коэффициентами имеет n корней вида p+qi, оно имеет ещё n корней вида p—qi (примером может служить биквадратное уравнение, комплексные корни которого всегда сопряжённые), и так как
[х—(p+qi)][x-(р— qi)]=[(x-p)- qi] (x-p)+qi] =
=(х—р)²—q²i²=(x-p)²+q²=x²-2 +(p²+q²),
то левая часть уравнения содержит в этом случае n вещественных множителей вида ax²+bx+c.
Алгебраическое уравнение нечётной степени с вещественными коэффициентами имеет, по крайней мере, один вещественный корень.
Уравнения с произвольными буквенными коэффициентами степени не выше четвёртой разрешены алгебраически, т. е. для корней этих уравнений найдены общие формулы, составленные из коэффициентов уравнения посредством алгебраических действий.
В этом смысле уравнения с произвольными коэффициентами степени выше четвёртой не могут быть разрешены алгебраически (теорема Абеля); однако, если коэффициенты уравнения какой угодно степени выражены числами, всегда есть возможность вычислить с желаемой степенью приближения все его корни как вещественные, так и мнимые. Способы такого вычисления излагаются в высшей алгебре.
Методы решения целых алгебраических уравнений
Разложение на множители
Часть целых алгебраических уравнений 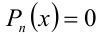 (или аналогичных неравенств) степени n выше 2-й могут быть решены путём разложения многочлена в левой части уравнения (неравенства) на множители с помощью таких известных приёмов, как группировка и вынесение общего множителя за скобки. Иногда для достижения цели приходится прибавлять и одновременно вычитать одно и то же выражение. Отметим, что порой разложение на множители этим способом требует определённого искусства.
(или аналогичных неравенств) степени n выше 2-й могут быть решены путём разложения многочлена в левой части уравнения (неравенства) на множители с помощью таких известных приёмов, как группировка и вынесение общего множителя за скобки. Иногда для достижения цели приходится прибавлять и одновременно вычитать одно и то же выражение. Отметим, что порой разложение на множители этим способом требует определённого искусства.
Если разложение на множители удалось выполнить, то решение алгебраического уравнения сводится к решению совокупности нескольких уравнений, но более низкой степени. Неравенство после разложения на множители можно решать методом интервалов.
Пример:
Решить уравнение 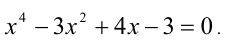
Решение:
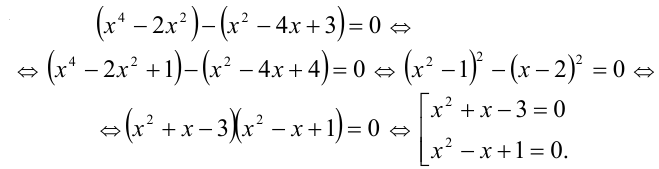
Из 1-го уравнения находим корни 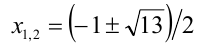 , а второе не имеет решений.
, а второе не имеет решений.
Пример:
Найти все положительные корни уравнения
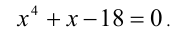
Решение:
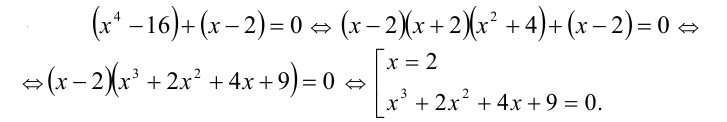
Покажем, что второе уравнение в совокупности не имеет положительных решений. Действительно, рассмотрим функцию 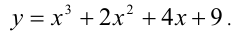 Её производная
Её производная 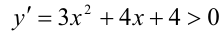 при всех действительных x, так как
при всех действительных x, так как 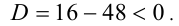 Следовательно, функция всюду монотонно возрастает, при этом y(0) = 5 . Отсюда следует, что при x > 0 её график не пересекает оси абсцисс.
Следовательно, функция всюду монотонно возрастает, при этом y(0) = 5 . Отсюда следует, что при x > 0 её график не пересекает оси абсцисс.
Ответ: 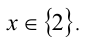
Подбор корня с последующим понижением степени уравнения
При решении алгебраических уравнений и неравенств степени выше второй можно использовать общий принцип последовательного понижения степени уравнения (неравенства).
Пусть требуется решить уравнение n -й степени
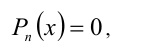
где 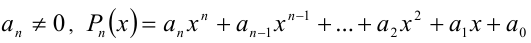 целый рациональный алгебраический многочлен n -й степени. Если удалось подобрать (любым способом) какой-либо корень
целый рациональный алгебраический многочлен n -й степени. Если удалось подобрать (любым способом) какой-либо корень 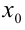 данного уравнения, то для нахождения остальных корней уравнения следует поделить многочлен
данного уравнения, то для нахождения остальных корней уравнения следует поделить многочлен  на разность X — Х0 (или целенаправленной группировкой слагаемых, выделяя разность
на разность X — Х0 (или целенаправленной группировкой слагаемых, выделяя разность 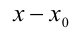 , разложить этот многочлен на множители). В результате деления образуется некоторый многочлен
, разложить этот многочлен на множители). В результате деления образуется некоторый многочлен 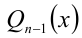 , степень которого на единицу меньше первоначальной. Таким образом, задача свелась к решению алгебраического уравнения степени n — 1 :
, степень которого на единицу меньше первоначальной. Таким образом, задача свелась к решению алгебраического уравнения степени n — 1 :
Пример:
Решить уравнение 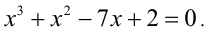
Решение:
Заметим, что x = 2 является корнем данного уравнения. Найдём другие корни этого уравнения:
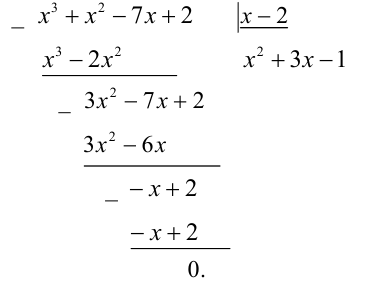
Решая уравнение 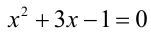 , находим ещё два корня
, находим ещё два корня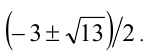
Эта ссылка возможно вам будет полезна:
Пример:
Решить уравнение 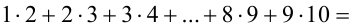
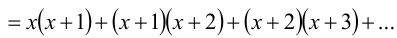
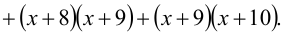
Решение:
Легко заметить, проанализировав структуру уравнения, что числа x = 0 и x = -10 являются решениями данного уравнения. С другой стороны, ясно, что это квадратное уравнение, а поэтому может иметь не более двух корней. Так как два корня уравнения уже подобраны, то других корней нет.
В некоторых случаях, для того чтобы не подбирать корень «вслепую», можно воспользоваться следующим методом.
Метод поиска рациональных корней у многочленов с целыми коэффициентами
Для решения такого рода уравнений и неравенств используется метод, в основе которого лежит Теорема 9 из предыдущего пункта. Рассмотрим подробнее суть этого метода. Пусть требуется найти рациональные корни уравнения n -й степени
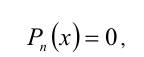
причём все коэффициенты 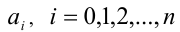 алгебраического многочлена
алгебраического многочлена  являются целыми числами. Поиск рациона-льных корней можно свести к перебору ограниченного количества вариантов. Для этого необходимо, во-первых, найти все целочислен-ные делители свободного члена
являются целыми числами. Поиск рациона-льных корней можно свести к перебору ограниченного количества вариантов. Для этого необходимо, во-первых, найти все целочислен-ные делители свободного члена 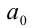 (их конечное число, однако если этот коэффициент содержит слишком много делителей, то это затрудняет поиск корней в уравнении). Обозначим, например, эти делители через
(их конечное число, однако если этот коэффициент содержит слишком много делителей, то это затрудняет поиск корней в уравнении). Обозначим, например, эти делители через 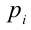 . Во-вторых, следует найти все натуральные делители старшего коэффициента уравнения
. Во-вторых, следует найти все натуральные делители старшего коэффициента уравнения 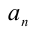 . Обозначим эти делители через
. Обозначим эти делители через 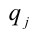 . В-третьих, надо составить всевозможные дроби вида
. В-третьих, надо составить всевозможные дроби вида 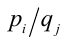 . Наконец, перебирая по очереди все такие дроби, проверить, является ли в действительности каждая из них корнем данного уравнения. Найдя таким образом первый корень
. Наконец, перебирая по очереди все такие дроби, проверить, является ли в действительности каждая из них корнем данного уравнения. Найдя таким образом первый корень 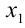 , вы или сразу понижаете степень уравнения делением многочлена
, вы или сразу понижаете степень уравнения делением многочлена 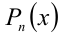 на разность
на разность 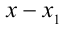 , (причём в силу следствия из теоремы Безу
, (причём в силу следствия из теоремы Безу  обязательно разделится нацело на этот линейный двучлен) и получаете некоторый многочлен
обязательно разделится нацело на этот линейный двучлен) и получаете некоторый многочлен 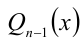 степени на единицу меньшей, чем первоначальная. Или, перебирая все дроби, находите все рациональные корни и уже затем понижаете степень уравнения сразу на столько порядков, сколько рациональных корней удалось найти, и ищете оставшиеся иррациональные корни. В любом случае задача сводится к решению уравнения более низкой степени.
степени на единицу меньшей, чем первоначальная. Или, перебирая все дроби, находите все рациональные корни и уже затем понижаете степень уравнения сразу на столько порядков, сколько рациональных корней удалось найти, и ищете оставшиеся иррациональные корни. В любом случае задача сводится к решению уравнения более низкой степени.
Пример:
При каких натуральных n уравнение 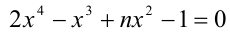 имеет рациональные корни?
имеет рациональные корни?
Решение:
Воспользуемся приведённым выше методом. Свободный член имеет два целочисленных делителя: ± 1, а старший коэффициент — два натуральных делителя: 1,2. Поэтому рациональные корни следует искать среди чисел 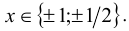 Подставим их поочерёдно в уравнение.
Подставим их поочерёдно в уравнение.
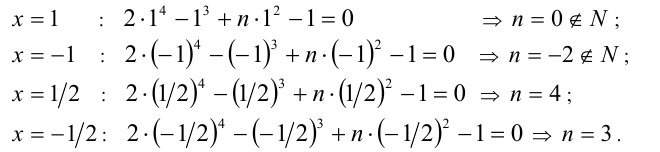
Ответ: 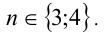
Метод неопределённых коэффициентов
Иногда для решения целых алгебраических уравнений (неравенств) с одной или несколькими неизвестными используют метод неопределённых коэффициентов. Пусть, например, решается уравнение
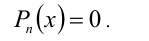
Суть метода состоит в том, что многочлен  в левой части уравнения представляется в виде произведения линейных
в левой части уравнения представляется в виде произведения линейных 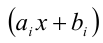 и(или) квадратичных
и(или) квадратичных 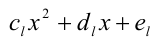 сомножителей с неизвестными (неопределёнными) коэффициентами
сомножителей с неизвестными (неопределёнными) коэффициентами 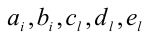
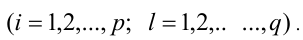 Чтобы найти эти коэффициенты, раскрывают скобки в указанном произведении и приводят образовавшийся при этом многочлен
Чтобы найти эти коэффициенты, раскрывают скобки в указанном произведении и приводят образовавшийся при этом многочлен 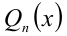 к стандарт-ному виду. Так как два многочлена
к стандарт-ному виду. Так как два многочлена 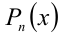 и
и 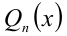 одной степени тождественно равны тогда и только тогда,
одной степени тождественно равны тогда и только тогда,
когда равны коэффициенты при одинаковых степенях переменной x, то, приравнивая эти коэффициенты, получают систему уравнений относительно неизвестных коэффициентов. Эту систему решают (или подбирают любое решение). Найденные таким способом коэффи-циенты 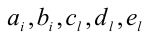 становятся определёнными и их значения подставляются в исходное разложение. К недостаткам метода можно отнести то, что получаемая система уравнений для нахождения коэффициентов может оказаться громоздкой и трудной даже в подборе решения.
становятся определёнными и их значения подставляются в исходное разложение. К недостаткам метода можно отнести то, что получаемая система уравнений для нахождения коэффициентов может оказаться громоздкой и трудной даже в подборе решения.
Рассмотрим применение этого метода на примере решения кубического уравнения. Допустим, требуется решить уравнение
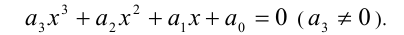
Известно, что многочлен третьей степени всегда можно представить в виде произведения многочленов первой и второй степеней. Таким образом, сразу для всех действительных значений переменной x должно выполняться равенство
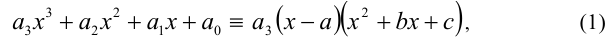
где числа а,b,c являются в данном случае искомыми неопределён-ными коэффициентами. Найдём их значения. После этого останется подставить их в правую часть (1) и, приравняв её к нулю, решить уравнение 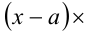
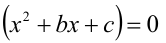 для нахождения всех корней уравнения.
для нахождения всех корней уравнения.
Чтобы найти коэффициенты а,b,c, раскроем скобки в правой части тождества (1) и приведём образовавшийся при этом многочлен к стандартному виду
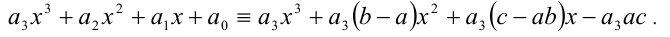
Многочлены третьей степени тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x . Приравнивая коэффициенты при 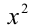 ,
, 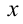 и свободные члены, получаем систему трёх алгебраических уравнений относительно трёх неизвестных а,b,c :
и свободные члены, получаем систему трёх алгебраических уравнений относительно трёх неизвестных а,b,c :
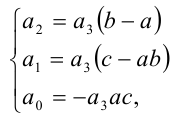
решая которую (можно даже просто подобрать любое решение этой системы) находим коэффициенты.
Пример:
Решить уравнение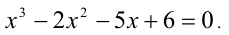
Решение:
Воспользуемся для решения методом неопределённых коэффициентов. Будем искать разложение многочлена, стоящего в левой части уравнения, в виде
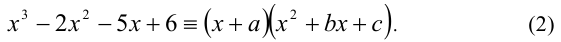
Раскрыв скобки, приведём многочлен в правой части к стандартному виду
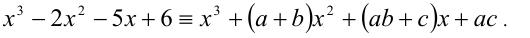
Приравнивая коэффициенты слева и справа при 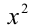 ,
,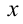 и свободные члены, получаем в итоге систему трёх уравнений с тремя неизвестными коэффициентами а,b,c:
и свободные члены, получаем в итоге систему трёх уравнений с тремя неизвестными коэффициентами а,b,c:
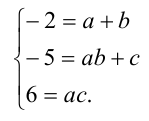
Найдя подбором решение 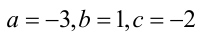 подставим найденные коэффициенты в разложение (2). Таким образом, исходное уравнение приобретает вид
подставим найденные коэффициенты в разложение (2). Таким образом, исходное уравнение приобретает вид 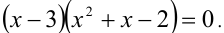 Оно имеет три корня
Оно имеет три корня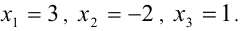
Пример:
При каких значениях а все корни уравнения 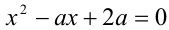 являются корнями уравнения
являются корнями уравнения
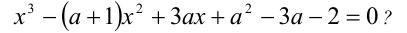
Решение:
Чтобы первое из уравнений имело корни, необходимо, чтобы его дискриминант был неотрицателен, т.е.
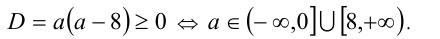
Далее, второй многочлен в силу теоремы Безу должен делиться нацело на первый многочлен. Иными словами, должно найтись такое b , что при всех действительных x справедливо тождество
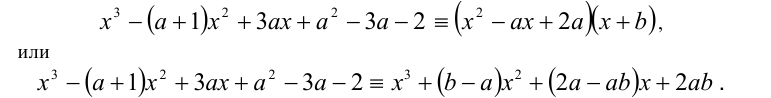
Для нахождения неопределённых коэффициентов (в данном случае в их роли выступают а и b ) воспользуемся известным фактом, что два кубических многочлена, стоящие по разные стороны от знака равенства, тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной x . Приравнивая эти коэффициенты, получаем систему уравнений

Метод умножения на функцию
Иногда, применяя приём умножения обеих частей уравнения (неравенства) на некоторую функцию, удаётся упростить уравнение (неравенство).
Пример:
Решить уравнение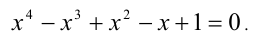
Решение:
Заметим, что x = — 1 (и вообще никакое отрицательное число) не является корнем данного уравнения. Домножим обе части данного уравнения на выражение (х +1). Получаем уравнение-следствие
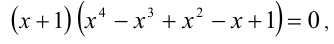
множество решений которого состоит из всех решений исходного уравнения и числа x = -1. Это число является посторонним корнем, возникшем как раз в результате умножения уравнения на функцию, имеющую действительный нуль. Применяя известную формулу сокращенного умножения, получаем существенно более простое уравнение 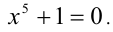 Поскольку уравнение не имеет других решений, кроме x = -1, то приходим к ответу.
Поскольку уравнение не имеет других решений, кроме x = -1, то приходим к ответу.
Ответ: уравнение не имеет решений.
Рассмотрим некоторые виды целых алгебраических уравнений, решаемые в основном при помощи специально подобранных подстановок.
Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения
Введем понятия алгебраического и трансцендентного уравнения.
Алгебраическое уравнение — уравнение, в котором переменная 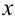 находится в основании степени с рациональным показателем.
находится в основании степени с рациональным показателем.
Примерами алгебраических уравнений могут служить уравнения вида: 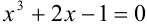 ,
, 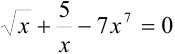 .
.
Уравнение, содержащее неизвестную переменную под знаком логарифма, тригонометрических функций, обратных тригонометрических функций или в показателе степени некоторого числа, называется трансцендентным.
Примерами трансцендентных уравнений могут служить уравнения вида:
Решить предложенное уравнение — значит найти все значения переменной  , обращающие его в верное тождество (корни уравнения), или доказать, что корней нет.
, обращающие его в верное тождество (корни уравнения), или доказать, что корней нет.
Из курса алгебры нам известны методы и приемы решения некоторых видов алгебраических и трансцендентных уравнений: например, квадратных уравнений; уравнений, решаемых методом группировки и вынесения за скобки общего множителя. Но даже решение несложного кубического уравнения вызовет у нас определенные сложности. Если нс удастся решить заданное уравнение привычными способами, существуют методы приближенного решения уравнений, состоящие из двух этапов:
1. отделение корней;
2. уточнение корней до заданной степени точности с помощью одного из следующих методов:
Этап отделения корней необходим для того, чтобы определить, какому промежутку принадлежат корни уравнения. На этом этапе обычно используется графический способ.
Пример:
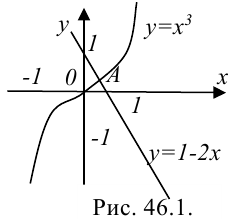
Определить промежуток, которому принадлежат корни уравнения 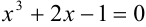 .
.
Решение:
Преобразуем данное уравнение к виду: 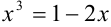 .
.
Построим графики функций 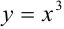 и
и 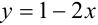 (рис. 46.1).
(рис. 46.1).
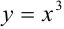 — кубическая парабола, строится по таблице значений:
— кубическая парабола, строится по таблице значений:
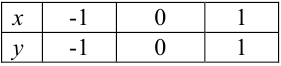
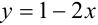 — прямая, строится по двум точкам:
— прямая, строится по двум точкам:
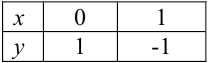
По рисунку видим, что графики функций 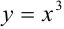 и
и 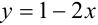 пересекаются в единственной точке
пересекаются в единственной точке 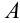 , координата
, координата 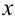 которой принадлежит отрезку
которой принадлежит отрезку 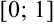 . Следовательно, уравнение
. Следовательно, уравнение 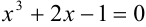 имеет ровно один корень на промежутке
имеет ровно один корень на промежутке 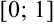 .
.
Ответ: 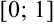 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Алгебраические уравнения и их геометрическое истолкование
Уравнение с одной буквой (неизвестным)
Один из основных вопросов, которыми занимается алгебра, заключается в решении уравнений нормального вида. Так называются уравнения, у которых в левой части стоит многочлен, расположенный по степеням неизвестной буквы, а в правой части — нуль.
Степень многочлена в левой части носит название степени уравнения.
Мы встречались не раз с уравнениями, которые не имели нормального вида: таковы, например, уравнения 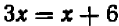 ,
, 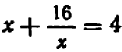 ,
, 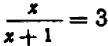 .
.
Подобного рода уравнения могут быть приведены к уравнениям нормального вида. Для этого до статочно освободиться от дробей, затем перенести на лево члены, стоящие в правой части, сделать приведение подобных членов и, наконец, правильно расположить члены.
Таким образом, привести заданное уравнение к уравнению нормального вида удается по большей части несложными приемами.
Напротив, нахождение всех корней уравнения представляет собою более трудную задачу, в особенности в том случае, если уравнение высокой степени.
Уравнение первой степени (линейное) имеет вид 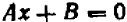 .
.
Уравнение второй степени (иначе квадратное) имеет вид 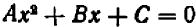 .
.
Уравнение третьей степени (иначе кубическое) имеет вид 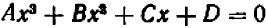 .
.
Так можно продолжать и дальше. Ради единообразия неизвестное здесь обозначено буквой 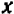 ; коэффициенты же
; коэффициенты же 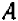 ,
, 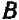 и т. д. — известные числа. В уравнении нормального вида старший коэффициент, конечно, следует считать отличным от нуля.
и т. д. — известные числа. В уравнении нормального вида старший коэффициент, конечно, следует считать отличным от нуля.
Уравнение первой степени мы решаем (см. гл. 6) следующим образом: свободный член переносим направо 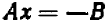 , затем делим уравнение на коэффициент при
, затем делим уравнение на коэффициент при 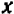 :
: 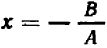 .
.
В случае уравнений второй степени или высших степеней решение уравнения тесно связано с разложением левой части на линейные множители. Так, например, уравнение 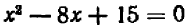 можно переписать в виде
можно переписать в виде 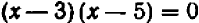 ; далее сошлемся на теорему: если произведение двух множителей равно нулю, то непременно один из множителей равен нулю. Поэтому или
; далее сошлемся на теорему: если произведение двух множителей равно нулю, то непременно один из множителей равен нулю. Поэтому или 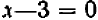 или
или 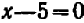 ; значит, или
; значит, или 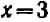 или
или 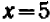 . Обратно, если
. Обратно, если 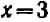 или
или 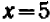 , то или первый множитель равен нулю или второй; но в обоих случаях произведение равно нулю, т. е. уравнение удовлетворяется. Итак, уравнение имеет два корня:
, то или первый множитель равен нулю или второй; но в обоих случаях произведение равно нулю, т. е. уравнение удовлетворяется. Итак, уравнение имеет два корня: 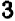 и
и 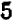 .
.
В отдельных примерах нам удавалось разлагать трехчлен второй степени на линейные множители; более полно общий прием разложения (по средствам «выделения квадрата») будет рассмотрен в главе 12.
Что касается уравнений третьей, четвертой и высших степеней, то, не говоря об отдельных частных случаях, разложить их левую часть на множители весьма трудно. С другой стороны, очень просто можно составить уравнение, имеющее наперед заданные корни; при этом степень уравнения в точности будет равняться числу корней.
Например, пусть заданы три числа: 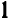 ,
, 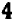 и
и 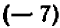 ; тогда уравнение, имеющее эти числа (и только их) своими корнями, таково:
; тогда уравнение, имеющее эти числа (и только их) своими корнями, таково: 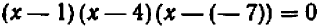 , или
, или 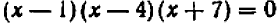 .
.
Производя умножение, получаем окончательно: 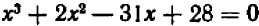 .
.
Можно доказать, что число корней уравнения никогда не превышает его степени. Но иногда оно бывает меньше степени уравнения.
Например, уравнение 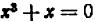 — третьей степени, но имеет только один корень
— третьей степени, но имеет только один корень  . Это сразу видно, если в левой части вынести
. Это сразу видно, если в левой части вынести 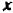 за скобку
за скобку 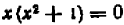 (здесь второй множитель
(здесь второй множитель 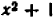 ни при каком значении
ни при каком значении 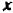 не обращается в нуль).
не обращается в нуль).
Совокупность точек на числовой оси, являющихся корнями уравнения (иначе, удовлетворяющих этому уравнению), дает нам геометрическое представление этого уравнения.
Уравнение с двумя буквами (переменными)
Нам хорошо известно, что решением (корнем) уравнения с одной неизвестной буквой называется всякое значение входящей буквы, удовлетворяющее уравнению.
Если уравнение содержит две неизвестные буквы, понятие решения должно быть обобщено и именно следующим образом: решением уравнения с двумя неизвестными буквами называется пара значений двух неизвестных, удовлетворяющая уравнению.
Так, пара чисел 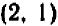 есть решение уравнения
есть решение уравнения 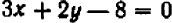 ; то же можно сказать о паре чисел
; то же можно сказать о паре чисел  ; но, например, пара
; но, например, пара 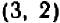 не есть решение.
не есть решение.
В случае уравнения с двумя неизвестными найти и перечислить все решения, как правило, невозможно. Уже простейшие примеры, вроде  или
или 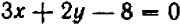 , показывают, что такое уравнение может иметь бесконечное множество решений.
, показывают, что такое уравнение может иметь бесконечное множество решений.
Поэтому, если в уравнение входят две (или более) неизвестных буквы, их называют обыкновенно не неизвестными, а переменными (переменными величинами).
Алгебраическое уравнение с двумя буквами считается нормальным, если в правой части стоит нуль, а в левой — многочлен, расположенный по обеим буквам.
Уравнения с двумя буквами (как и уравнения с одной буквой) классифицируются по степеням: степенью уравнения называется степень многочлена, стоящего в его левой части, причем обе буквы считаются главными.
Уравнения первой степени (линейные) имеют вид 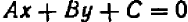 .
.
Уравнения второй степени (квадратные) имеют вид 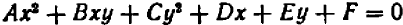 .
.
Отдать себе отчет в том, какова совокупность решений данного уравнения, нам помогает геометрическое представление уравнения: оно делает наглядной ту зависимость, которая существует между значениями букв, удовлетворяющими уравнению. Познакомимся ближе с этим геометрическим представлением.
Так как у нас имеется не одна, а две буквы, допустим, 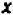 и
и 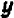 из которых каждая может принимать различные значения, то уже нельзя обойтись числовой прямой, а необходимо прибегнуть к числовой (координатной) плоскости. Проведем на листе клетчатой бумаги горизонтальную ось
из которых каждая может принимать различные значения, то уже нельзя обойтись числовой прямой, а необходимо прибегнуть к числовой (координатной) плоскости. Проведем на листе клетчатой бумаги горизонтальную ось 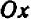 и вертикальную ось
и вертикальную ось 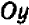 масштабы на осях будем брать одинаковые. Каждая пара значений букв
масштабы на осях будем брать одинаковые. Каждая пара значений букв 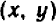 изображается, как нам известно, некоторой определенной точкой плоскости
изображается, как нам известно, некоторой определенной точкой плоскости 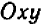 , именно — точкой с абсциссой
, именно — точкой с абсциссой 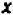 и ординатой
и ординатой 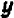 . Поэтому совокупность всех пар значений
. Поэтому совокупность всех пар значений 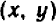 , удовлетворяющих уравнению, изображается также не которой совокупностью (геометрическим местом) точек на плоскости
, удовлетворяющих уравнению, изображается также не которой совокупностью (геометрическим местом) точек на плоскости 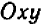 . Эта совокупность и дает геометрическое представление решений нашего уравнения; она называется графиком уравнения. Итак, график уравнения есть совокупность всех тех точек координатной плоскости, координаты которых удовлетворяют уравнению.
. Эта совокупность и дает геометрическое представление решений нашего уравнения; она называется графиком уравнения. Итак, график уравнения есть совокупность всех тех точек координатной плоскости, координаты которых удовлетворяют уравнению.
Пример:
Рассмотрим уравнение 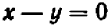 .
.
Его графиком является совокупность точек 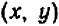 , у которых абсцисса
, у которых абсцисса 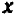 равна ординате
равна ординате 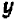 легко понять, что все такие точки лежат на биссектрисе первого и треть его координатных углов: эта биссектриса и представляет собой график нашего уравнения.
легко понять, что все такие точки лежат на биссектрисе первого и треть его координатных углов: эта биссектриса и представляет собой график нашего уравнения.
Пример:
Второй пример возьмем более сложный. Пусть нам дано уравнение второй степени: 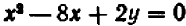 .
.
Посмотрим, как можно наметить его график.
Ничего не стоит решить уравнение относительно буквы 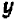 :
: 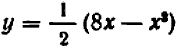
Дальше можно составить табличку числовых значений переменной 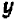 , соответствующих заранее назначенным значениям переменной
, соответствующих заранее назначенным значениям переменной  :
: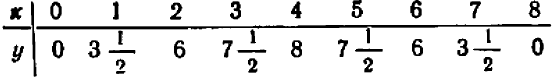
 Черт. 39
Черт. 39
Каждую полученную точку сейчас же отмечают на черте же. Точки располагаются с известной правильностью.
Чертеж 39 показывает, что при возрастании значений 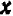 от
от 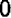 до
до 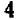 значения
значения 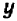 также возрастают от
также возрастают от 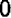 до
до 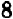 ; затем при дальнейшем возрастании
; затем при дальнейшем возрастании 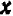 от
от 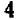 до
до 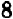 значения
значения 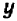 убывают от
убывают от  до
до  . При
. При 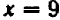 получаем уже отрицательное значение:
получаем уже отрицательное значение: 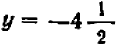 , придется поставить точку ниже оси
, придется поставить точку ниже оси  .
.
При  получаем
получаем 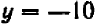 ; и еще дальше значения
; и еще дальше значения 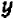 быстро убывают (в алгебраическом смысле).
быстро убывают (в алгебраическом смысле).
Можно букве  давать и отрицательные значения; например, при
давать и отрицательные значения; например, при 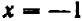 будем иметь
будем иметь 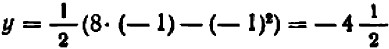 и т. д.
и т. д.
Полезло убедиться, что точки, получающиеся при подстановке дробных значений  , не нарушают общей правильности в расположении точек графика (например, при
, не нарушают общей правильности в расположении точек графика (например, при 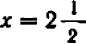 получаем
получаем 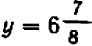 ).
).
Поставим себе еще и такой вопрос: имеет ли наш график какие-нибудь точки на оси 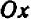 , кроме двух, уже найденных? Чтобы получить ответ, достаточно в уравнении положить
, кроме двух, уже найденных? Чтобы получить ответ, достаточно в уравнении положить 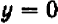 и решить полученное уравнение
и решить полученное уравнение  относительно
относительно 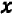 . Мы получаем два корня:
. Мы получаем два корня:  и
и 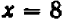 . Иных корней нет. Значит, график пересекается с осью
. Иных корней нет. Значит, график пересекается с осью 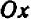 только в двух, уже ранее найденных точках.
только в двух, уже ранее найденных точках.
Хотя мы отметили на чертеже не свыше десятка точек, положение которых нам известно вполне точно, тем не менее правильность их расположения не оставляет сомнений в том, что все остальные, не отмеченные нами, точки графика лежат на некоторой плавной кривой, проходящей через отмеченные точки.
Эта кривая и есть график нашего уравнения. Провести ее от руки не представит труда.
Правда, полученная таким образом кривая даст возможность лишь приближенно судить о положении тех точек графика, координаты которых не были вычислены.
Использованный нами прием получения графика носит название построения графика по точкам.
Постараемся дать описание этого приема, не связывая его с каким-либо определенным примером. Пусть дано некоторое уравнение, содержащее буквы  и
и 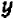 , мы хотим знать, каков его график.
, мы хотим знать, каков его график.
Посмотрим, существуют ли такие точки графика, которые имеют заранее назначенную абсциссу, скажем, 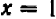 . Чтобы ответить на этот вопрос, достаточно подставить в уравнение вместо буквы
. Чтобы ответить на этот вопрос, достаточно подставить в уравнение вместо буквы  число
число  и решить полученное уравнение (содержащее теперь уже только одну букву) относительно буквы
и решить полученное уравнение (содержащее теперь уже только одну букву) относительно буквы 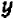 . Корни этого уравнения дают нам ординаты всех точек графика, имеющих абсциссу
. Корни этого уравнения дают нам ординаты всех точек графика, имеющих абсциссу 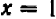 , т. е. лежащих на одной и той же вертикальной прямой, отстоящей вправо от оси
, т. е. лежащих на одной и той же вертикальной прямой, отстоящей вправо от оси 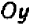 на расстоянии
на расстоянии  . Продолжая поступать таким же образом, т. е. давая абсциссе
. Продолжая поступать таким же образом, т. е. давая абсциссе 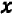 другие, заранее назначенные, значения, например,
другие, заранее назначенные, значения, например,  можно найти все точки графика, расположенные на других вертикальных прямых. Обыкновенно поступают именно таким образом; при этом стараются облегчить себе работу тем, что предварительно решают данное уравнение относительно буквы
можно найти все точки графика, расположенные на других вертикальных прямых. Обыкновенно поступают именно таким образом; при этом стараются облегчить себе работу тем, что предварительно решают данное уравнение относительно буквы 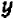 , т. е. приводят его к такому виду, чтобы в левой части была одна буква
, т. е. приводят его к такому виду, чтобы в левой части была одна буква 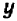 , а правая зависела только от
, а правая зависела только от  , но не от
, но не от  , Тогда нахождение точек графика сводится к выполнению числовых подстановок в правой части уравнения.
, Тогда нахождение точек графика сводится к выполнению числовых подстановок в правой части уравнения.
Разумеется, можно было бы также решить данное уравнение относительно буквы 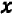 и затем придавать ряд значений букве
и затем придавать ряд значений букве 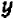 .
.
Примечание:
Иные уравнения — таковы, что не существует ни одной точки, координаты которой удовлетворяли бы уравнению.
Тогда график отсутствует или представляет собою «пустое место».
Этим свойством обладает, например, уравнение 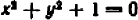 которого левая часть всегда положительна.
которого левая часть всегда положительна.
В редких случаях график может оказаться состоящим из одной точки или нескольких точек (в конечном числе). Так, уравнение 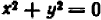 удовлетворяется только одной парой значений
удовлетворяется только одной парой значений  ,
, 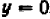 .
.
Действительно, каждый из квадратов 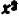 и
и 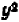 может быть или положительным числом, или нулем, но никак не отрицательным числом, сумма же
может быть или положительным числом, или нулем, но никак не отрицательным числом, сумма же 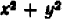 равна нулю только в том случае, если
равна нулю только в том случае, если 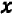 и
и 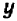 одновременно равны нулю. Следовательно, весь график сводится к одной точке — началу
одновременно равны нулю. Следовательно, весь график сводится к одной точке — началу 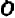 .
.
Линейное уравнение с двумя переменными
На чертеже 40 изображен график уравнения 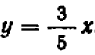 (1)
(1)
Это — прямая линия, проходящая через начало координат и расположенная в первой и третьей четвертях.
Уравнение показывает, что величина у прямо пропорциональна величине 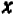 . Желая найти все точки графика с целыми координатами, мы даем букве
. Желая найти все точки графика с целыми координатами, мы даем букве  значения, кратные
значения, кратные  , и получаем точки:
, и получаем точки:  ,
, 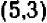 ,
, 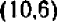 и т. д.
и т. д.
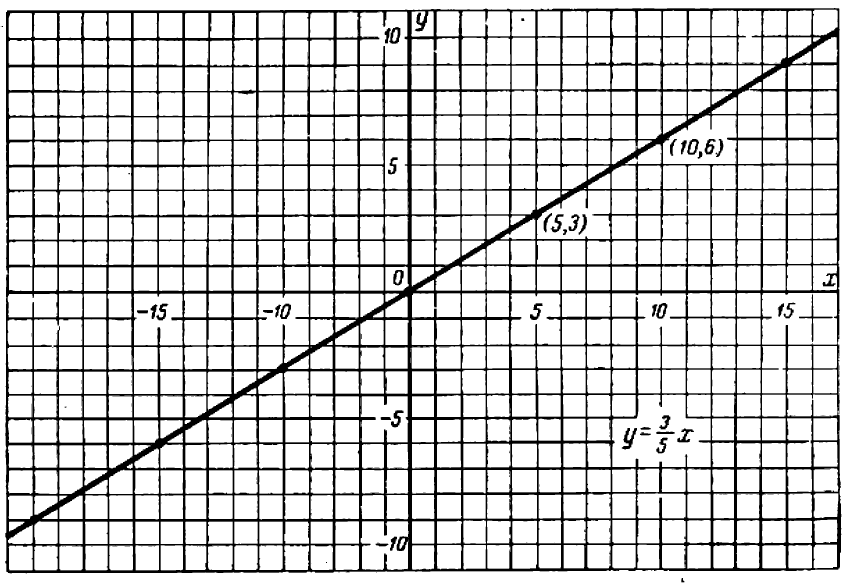 Черт. 40
Черт. 40
Эти точки отмечены на чертеже. Чтобы перейти от одной такой точки к следующей (считая вправо), достаточно отсчитать «  клеточек вправо и
клеточек вправо и 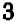 — вверх».
— вверх».
Коэффициент пропорциональности 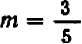 позволяет
позволяет
таким образом, определить направление нашей прямой.
Если бы вместо уравнения (I) было задано, например, уравнение 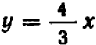 , (2) то мы получили бы точки графика (с целыми координатами):
, (2) то мы получили бы точки графика (с целыми координатами):  ,
, 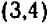 ,
, 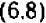 и т. д.; отмечая их одну за другой, мы отсчитывали бы «
и т. д.; отмечая их одну за другой, мы отсчитывали бы «  клетки вправо,
клетки вправо,  — вверх», Рассмотрим еще уравнение
— вверх», Рассмотрим еще уравнение 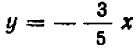 (3).
(3).
При значениях  , кратных
, кратных  , получаем точки:
, получаем точки:  ,
, 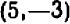 ,
, 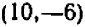 и т. д.
и т. д.
Отсчитывать нужно «  клеток вправо и
клеток вправо и  — вниз». Прямая, являющаяся графиком этого уравнения, расположена во второй и в четвертой четвертях. Из наших примеров можно сделать следующие общие заключения. Графиком уравнения вида
— вниз». Прямая, являющаяся графиком этого уравнения, расположена во второй и в четвертой четвертях. Из наших примеров можно сделать следующие общие заключения. Графиком уравнения вида 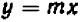 (4) является прямая линия, проходящая через начало
(4) является прямая линия, проходящая через начало  . Придавая уравнению вид
. Придавая уравнению вид 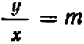 , мы убеждаемся, что коэффициент пропорциональности
, мы убеждаемся, что коэффициент пропорциональности 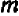 представляет собою отношение ординаты любой точки графика к ее абсциссе. Если
представляет собою отношение ординаты любой точки графика к ее абсциссе. Если 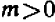 , то прямая проходит в первой и третьей четвертях; если
, то прямая проходит в первой и третьей четвертях; если  , то во второй и четвертой. При
, то во второй и четвертой. При 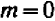 уравнение принимает вид
уравнение принимает вид 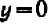 , и графиком тогда является ось
, и графиком тогда является ось  .
.
Чем меньше  по абсолютному значению, тем более полого расположена прямая (т. е. тем меньше острый угол, образованный ею с горизонтальной осью); напротив, чем больше
по абсолютному значению, тем более полого расположена прямая (т. е. тем меньше острый угол, образованный ею с горизонтальной осью); напротив, чем больше  по абсолютному значению, тем более круто расположена прямая (тем упомянутый острый угол ближе к прямому).
по абсолютному значению, тем более круто расположена прямая (тем упомянутый острый угол ближе к прямому).
Коэффициент 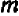 в уравнении (4) называется наклоном прямой, являющейся графиком этого уравнения.
в уравнении (4) называется наклоном прямой, являющейся графиком этого уравнения.
Обратим внимание на то, чем график уравнения 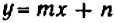 отличается от графика уравнения
отличается от графика уравнения 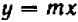 . При каждом данном значении абсциссы
. При каждом данном значении абсциссы 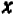 соответствующая ордината увеличена на
соответствующая ордината увеличена на 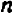 единиц (
единиц ( ,
,  или
или  ); значит, получается снова прямая линия, но «сдвинутая» на
); значит, получается снова прямая линия, но «сдвинутая» на  единиц в направлении оси
единиц в направлении оси 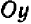 : она уже не проходит через начало
: она уже не проходит через начало  , а пересекает ось
, а пересекает ось  в точке
в точке 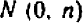 .
.
Таким образом, направление прямой 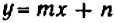 то же, что и направление прямой
то же, что и направление прямой 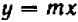 : оно зависит от коэффициента
: оно зависит от коэффициента 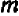 при
при 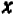 в уравнении прямой, решенном относительно
в уравнении прямой, решенном относительно 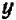 (называемого и в этом случае наклоном прямой).
(называемого и в этом случае наклоном прямой).
Другими словами, прямые 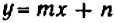 и
и 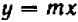 параллельны.
параллельны.
На черт. 41 изображен график уравнения 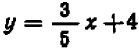 . Это — прямая, параллельная прямой
. Это — прямая, параллельная прямой 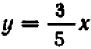 , но образующая на оси
, но образующая на оси 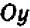 отрезок, равный
отрезок, равный  .
.
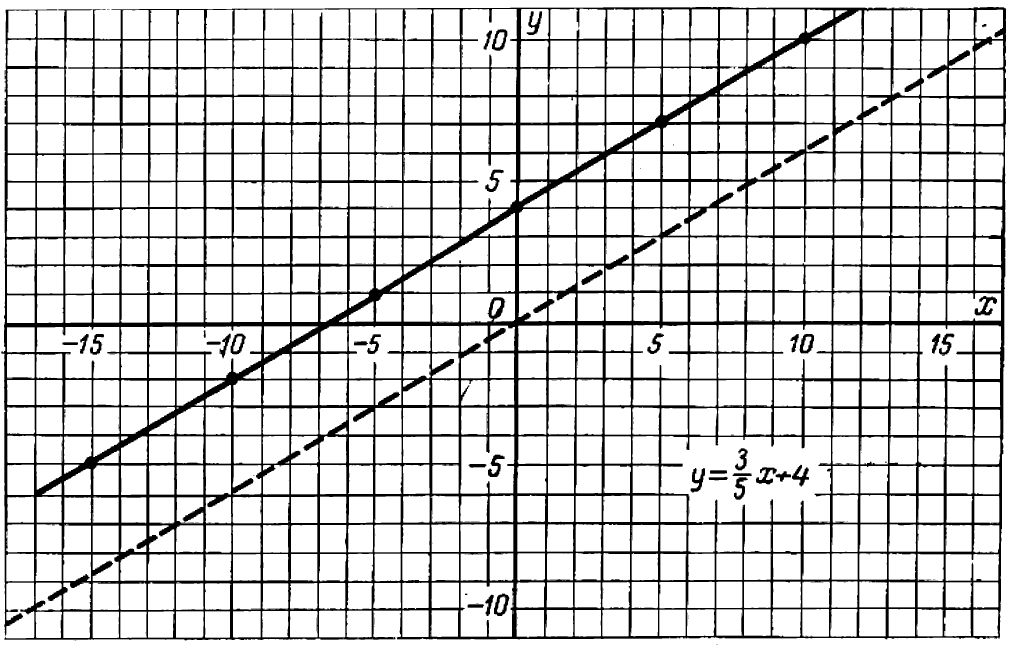 Черт. 41
Черт. 41
Пусть буква  обозначает какое угодно число. Постараемся уяснить себе, каков график уравнения
обозначает какое угодно число. Постараемся уяснить себе, каков график уравнения  .
.
Нам нужно установить, какова совокупность точек на плоскости  , координаты которых удовлетворяют уравнению. Уравнение не удовлетворяется, если значение абсциссы
, координаты которых удовлетворяют уравнению. Уравнение не удовлетворяется, если значение абсциссы 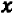 не равно
не равно 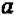 ; если же оно равно
; если же оно равно 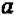 , то, како во бы ни было значение ординаты
, то, како во бы ни было значение ординаты 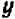 , уравнение удовлетворяется. Это значит, что уравнению удовлетворяют координаты любой точки на прямой, параллельной оси
, уравнение удовлетворяется. Это значит, что уравнению удовлетворяют координаты любой точки на прямой, параллельной оси 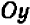 и отстоящей от этой оси вправо на расстоянии
и отстоящей от этой оси вправо на расстоянии 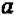 .
.
Итак, уравнение вида  имеет графиком прямую, параллельную оси
имеет графиком прямую, параллельную оси 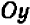 . Точно так же уравнение вида
. Точно так же уравнение вида 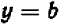 имеет графиком прямую, параллельную оси
имеет графиком прямую, параллельную оси  .
.
Из предыдущего следует весьма важное заключение: всякое уравнение, линейное относительно буквы 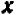 и
и 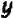 именно, уравнение вида
именно, уравнение вида 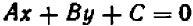 (где
(где  ,
,  и
и  — постоянные числа, причем
— постоянные числа, причем  и
и  не равны нулю одновременно), имеет своим графиком прямую линию .
не равны нулю одновременно), имеет своим графиком прямую линию .
Действительно, если буква 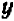 на самом деле входит в уравнение (это значит, что
на самом деле входит в уравнение (это значит, что  не равно нулю), то не представляет труда решить уравнение относительно
не равно нулю), то не представляет труда решить уравнение относительно  . Мы получим:
. Мы получим: 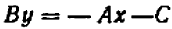 и далее, деля все уравнение на
и далее, деля все уравнение на 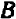 ,
, 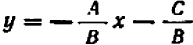 полагая затем
полагая затем
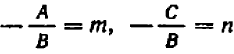 приходим к уравнению вида
приходим к уравнению вида 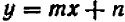 , которое, как нам уже известно, изображается прямой линией.
, которое, как нам уже известно, изображается прямой линией.
Если же буква  отсутствует в уравнении (т. е., если
отсутствует в уравнении (т. е., если  ), то тогда уравнение
), то тогда уравнение 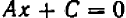 можно решить относительно буквы
можно решить относительно буквы  (раз
(раз  , то, по предположению,
, то, по предположению,  ), и мы получим:
), и мы получим: 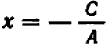 или
или  (где для краткости положено
(где для краткости положено 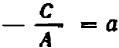 ). Графиком такого уравнения является совокупность точек, имеющих абсциссу
). Графиком такого уравнения является совокупность точек, имеющих абсциссу  ; это также прямая, но уже параллельная оси
; это также прямая, но уже параллельная оси  .
.
Рассматривать случай, когда  не представляет интереса. В этом случае, если
не представляет интереса. В этом случае, если 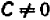 , заданное уравнение
, заданное уравнение 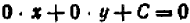 не удовлетворяется ни при каких значениях
не удовлетворяется ни при каких значениях  и
и  и, значит, график этого уравнения представляет собою «пустое место»; если же
и, значит, график этого уравнения представляет собою «пустое место»; если же 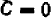 , то напротив, уравнение
, то напротив, уравнение 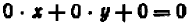 удовлетворяется при всех значениях
удовлетворяется при всех значениях  и
и  тогда его «график» — вся плоскость.
тогда его «график» — вся плоскость.
Раз известно, что линейное уравнение 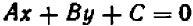 изображается прямой линией, то для того, чтобы начертить эту линию на координатной плоскости (на листе клетчатой бумаги), нет необходимости в больших вычислениях.
изображается прямой линией, то для того, чтобы начертить эту линию на координатной плоскости (на листе клетчатой бумаги), нет необходимости в больших вычислениях.
В самом деле, прямая определяется двумя точками: значит, достаточно сделать две числовые подстановки.
Проще всего установить точки пересечения прямой с осями  и
и  . Пусть, например, дано уравнение
. Пусть, например, дано уравнение 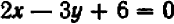 . Полагая
. Полагая 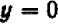 , получим уравнение относительно
, получим уравнение относительно 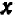 :
: 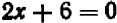 , из которого следует, что
, из которого следует, что  . Таким образом, найдена точка графика
. Таким образом, найдена точка графика  , лежащая на оси
, лежащая на оси  . Полагая
. Полагая  , получим таким же образом:
, получим таким же образом: 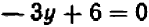 , откуда следует, что
, откуда следует, что 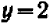 . Итак, найдена точка графика
. Итак, найдена точка графика  , лежащая на оси
, лежащая на оси  . Затем остается провести прямую через точки
. Затем остается провести прямую через точки 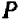 и
и 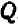 .
.
Указанный прием неудобен только в том случае, если точки  и
и  находятся очень близко одна от другой, т. е. близки к началу
находятся очень близко одна от другой, т. е. близки к началу  ; он непригоден вовсе, если график проходит через начала
; он непригоден вовсе, если график проходит через начала  . В этих случаях следует делать какие-нибудь другие подстановки.
. В этих случаях следует делать какие-нибудь другие подстановки.
Например, чтобы построить график прямой 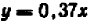 , заметим прежде всего, что она проходит через начало
, заметим прежде всего, что она проходит через начало  ; чтобы получить еще одну точку, положим
; чтобы получить еще одну точку, положим  и получим
и получим  ; итак, прямая проходит через точку
; итак, прямая проходит через точку 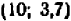 .
.
Нелинейные уравнения с двумя переменными
Мы видели, что если заданное уравнение — линейное (т. е. первой степени) относительно букв  и
и  , то его график — прямая линия.
, то его график — прямая линия.
Дальнейшие примеры покажут, что если заданное уравнение — не линейное (т. е. степени второй или выше) относительно букв  и
и  , то его графиком являются кривые линии.
, то его графиком являются кривые линии.
Степень уравнения относительно букв  и
и  называется порядком соответствующей кривой.
называется порядком соответствующей кривой.
Мы рассмотрим здесь только несколько наиболее простых и важных примеров кривых, преимущественно второго порядка.
Пример:
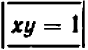
С этим уравнением мы уже встречались. Оно говорит о том, что переменные величины  и
и  обратно пропорциональны.
обратно пропорциональны.
Можно ли решить уравнение относительно  ? Ответ — утвердительный, если только
? Ответ — утвердительный, если только  имеет значение, не равное нулю. Но легко понять, что при
имеет значение, не равное нулю. Но легко понять, что при 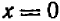 никакое значение
никакое значение  не может удовлетворить уравнению: это значит геометрически, что на оси
не может удовлетворить уравнению: это значит геометрически, что на оси  нет ни одной точки графика.
нет ни одной точки графика.
Итак, пусть теперь 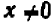 . Решим уравнение относительно у:
. Решим уравнение относительно у: 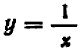 .
.
Это равенство свидетельствует, что  есть «величина, обратная величине
есть «величина, обратная величине  ». Посмотрим, как изменится величина, обратная
». Посмотрим, как изменится величина, обратная  , при изменении самого
, при изменении самого  .
.
Ограничиваясь пока положительными значениями величины  , станем составлять табличку и одновременно отмечать точки на чертеже. Ясно, что с увеличением
, станем составлять табличку и одновременно отмечать точки на чертеже. Ясно, что с увеличением  величина
величина  убывает, приближаясь к нулю. Но значения
убывает, приближаясь к нулю. Но значения  она не принимает.
она не принимает.

Попробуем взять и дробные значения  :
:
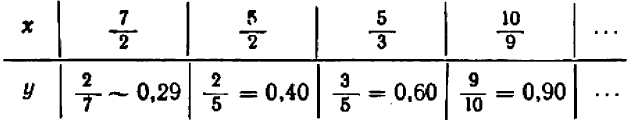
Получающиеся на чертеже точки имеют правильное расположение: через них можно с уверенностью про вести плавную кривую. Менее ясно пока, как вести кривую влево, в промежутке от  до
до  . Продолжим табличку:
. Продолжим табличку:
и станем отмечать новые точки. Теперь становится ясно, что с убыванием положительных значений  величина
величина  возрастает и притом не ограничено. Именно,
возрастает и притом не ограничено. Именно,  примет какое угодно большое значение, если только значение
примет какое угодно большое значение, если только значение  будет достаточно малым. Кривая (при движении справа налево) поднимается вверх, примыкая к оси
будет достаточно малым. Кривая (при движении справа налево) поднимается вверх, примыкая к оси 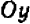 , хотя, как мы видели, с этой осью общих точек не имеет (см. черт. 42).
, хотя, как мы видели, с этой осью общих точек не имеет (см. черт. 42).
 Черт. 42
Черт. 42
Вся полученная кривая расположена в первой четверти. Если бы мы пожелали давать букве  отрицательные значения, то, составляя соответствующую таблицу и при этом производя деление по известным правилам, получили бы в третьей четверти другую «ветвь» кривой.
отрицательные значения, то, составляя соответствующую таблицу и при этом производя деление по известным правилам, получили бы в третьей четверти другую «ветвь» кривой.
Обе «ветви». рассматриваемые совместно, образуют кривую, называемую «гиперболой».
Гипербола — кривая второго порядка.
Пример:
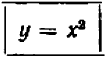
Подставляя положительные значения  , получаем таблицу:
, получаем таблицу:
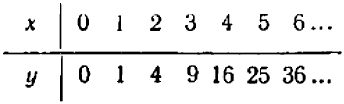
Отметив соответствующие точки на чертеже, мы видим, что при увеличении абсциссы  ордината
ордината  очень быстро возрастает, причем сам график (если попробовать его провести) все больше выпрямляется. Напротив, ближе к началу
очень быстро возрастает, причем сам график (если попробовать его провести) все больше выпрямляется. Напротив, ближе к началу  он довольно сильно искривлен. Подставляя еще значения
он довольно сильно искривлен. Подставляя еще значения 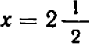 ,
, 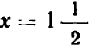 ,
, 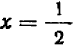 , мы получим:
, мы получим:
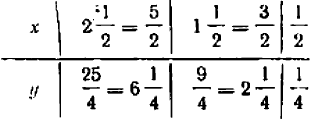
В первой клеточке  сделаем подстановки даже через одну десятую:
сделаем подстановки даже через одну десятую:
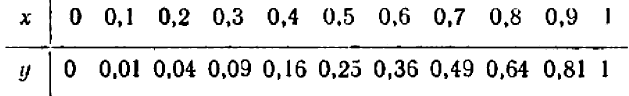
Последняя табличка позволяет заключить, что. под ходя к началу  . график тесно примыкает к оси
. график тесно примыкает к оси 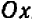 , касается ее.
, касается ее.
Обращаясь к отрицательным значениям  , мы видим, что при возведении в квадрат отрицательного числа знак минус будет уничтожаться. Отсюда ясно, что кривая продолжается из первой четверти во вторую симметрично относительно вертикальной оси.
, мы видим, что при возведении в квадрат отрицательного числа знак минус будет уничтожаться. Отсюда ясно, что кривая продолжается из первой четверти во вторую симметрично относительно вертикальной оси.
 Черт. 43
Черт. 43
Полученная кривая носит название параболы(см. черт. 43).
Парабола — кривая также второго порядка.
Пример:
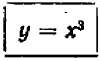
При подстановке больших значений  , как показывает следующая таблица, кубы возрастают гораздо быстрее, чем квадраты:
, как показывает следующая таблица, кубы возрастают гораздо быстрее, чем квадраты:
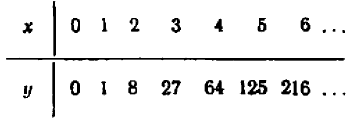
Напротив, при подстановке значений, близких к нулю, кубы убывают быстрее, чем квадраты:
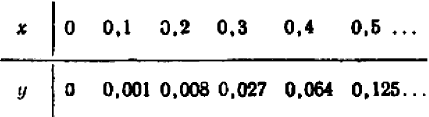
Поэтому кривая 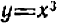 с возрастанием
с возрастанием 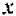 поднимается вверх гораздо круче, чем парабола
поднимается вверх гораздо круче, чем парабола 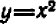 ; и при убывании
; и при убывании  до нуля гораздо теснее примыкает к оси
до нуля гораздо теснее примыкает к оси  .
.
На параболу 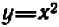 эта кривая не похожа еще и в том отношении, что у нее отсутствует вертикальная ось симметрии; но имеется центр симметрии в начале
эта кривая не похожа еще и в том отношении, что у нее отсутствует вертикальная ось симметрии; но имеется центр симметрии в начале  . Это зависит от того, что при возведении в куб отрицательного числа его абсолютное значение возводится в куб, но знак остается отрицательный.
. Это зависит от того, что при возведении в куб отрицательного числа его абсолютное значение возводится в куб, но знак остается отрицательный.
Общий вид кривой  (кубической параболы) показан на черт. 44.
(кубической параболы) показан на черт. 44.
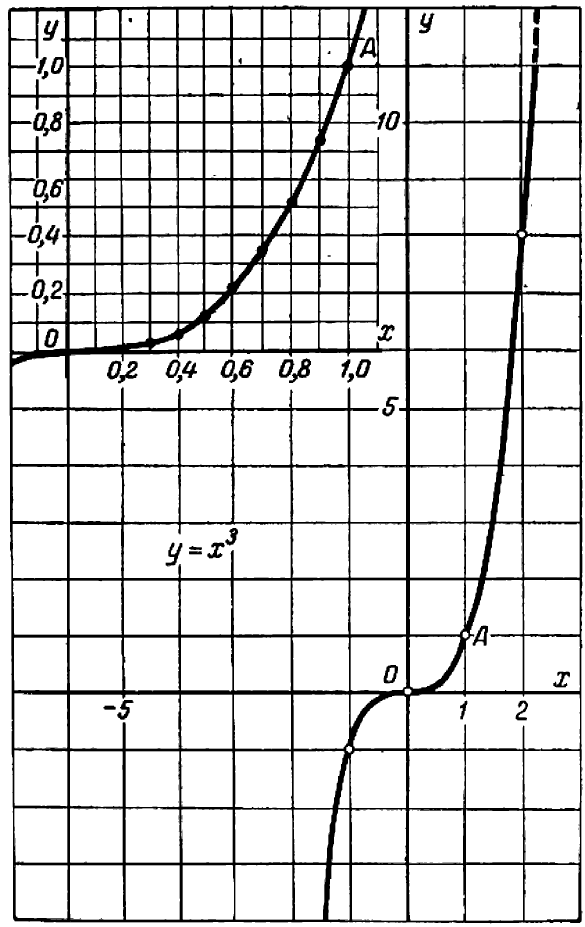 Черт. 44
Черт. 44
Это — кривая третьего порядка.
Алгебраические уравнения и алгоритм их решения
Общая теория уравнений
Тождества:
Введем понятие тождественного равенства функций на числовом множестве X.
Пусть функции у = f(х) и у = F(х) имеют области определения А и В соответственно, и X является подмножеством как A, так и В (но не обязательно совпадает с пересечением А и В). Тогда функции у = f(х) и у = F(х) определены на X.
Функции у=f(х) и у=F(х) называются тождественно равными на числовом множестве X, если для любого числа х из X выполняется равенство f(х)=F(х). В этом случае говорят, что равенство f(х)=F(х) является тождеством на множестве X.
Разумеется, равенство f(х)=F(х) может быть тождеством на некотором множестве X, но не быть тождеством на каком-нибудь другом множестве Y . Рассмотрим, например, функции у=х и у =|x|. На множестве X положительных чисел эти функции тождественно равны: если х — положительное число, то |х|=х. На множестве же Y всех действительных чисел эти функции не являются тождественно равными: при отрицательных значениях х равенство
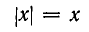
не имеет места, так как при этих значениях |x|= — х.
Совершенно так же определяется понятие тождественного равенства для функций нескольких переменных. Например, функции 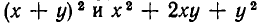 переменных х и у тождественно равны на множестве всех значений этих переменных: для любых значений х и у выполняется равенство
переменных х и у тождественно равны на множестве всех значений этих переменных: для любых значений х и у выполняется равенство
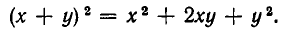
Функции же z=х+у и z =|х+у | тождественно равны лишь на множестве пар чисел х, у , для которых 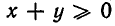 или, что то же самое,
или, что то же самое, 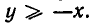
Область допустимых значений
Тождественные преобразования многочленов и алгебраических дробей изучались в начальной алгебре, и мы не будем подробно останавливаться на этом вопросе. Разберем лишь вопрос об области допустимых значений функционального равенства. Пусть дано равенство вида

Может случиться, что функции у=f(x) и у=F(x) определены не для всех значений х . Областью допустимых значений аргумента х для равенства (1) мы будем называть множество всех значений х, при которых определены и левая и правая части этого равенства.
Например, для тождества
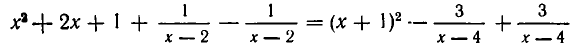
областью допустимых значений является совокупность всех действительных чисел, из которой исключены числа 2 и 4 (при х=2 не определена функция 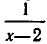 , а при х=4 — функция
, а при х=4 — функция 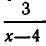 ).
).
Следует иметь в виду, что такие преобразования, как приведение подобных членов, могут привести к изменению области допустимых значений. Например, тождество (2) справедливо для всех значений х , кроме х=2 и х=4. Если же мы приведем подобные члены, то получим тождество
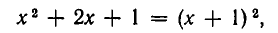
справедливое для всех без исключения значений х.
Уравнения
Обычно когда даны две функции у=f(х) и у=F(х), то неизвестно, каково множество, на котором эти функции тождественно равны. Поэтому возникает следующая задача: найти все значения х, для которых выполняется равенство

При такой постановке задачи (*) называют уравнением с неизвестным х , а все х , при которых функции у=f(х) и у=F(х) принимают одинаковые значения, — корнями или решениями этого уравнения.
Итак, уравнение f(x) =F(х) выражает задачу об отыскании таких значений переменного х, при которых функции f(x) и F(x) имеют одинаковые значения. Решить уравнение — это значит найти все такие значения х, т. е. все корни (решения) уравнения.
Областью допустимых значений для уравнения (1) называют множество всех х у при которых определены обе функции у=f(х) и у=F(х). Например, для уравнения
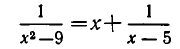
область допустимых значений определяется условиями:
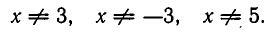
Область допустимых значений может заранее ограничиваться некоторыми условиями. Например, могут иметь смысл лишь положительные или лишь целые корни. В этом случае надо рассматривать уравнение лишь для положительных (или целых) значений х.
Тогда мы считаем, что функции f(x) и F(х) заданы на некотором множестве X, и рассматриваем уравнение лишь на этом множестве.
Пусть даны два уравнения


Обозначим множество корней уравнения (1) через M, а множество корней уравнения (2) через N. Если  (то есть, если всякий корень уравнения (1) является корнем уравнения (2)), то уравнение (2) называют следствием уравнения (1). Например, уравнение
(то есть, если всякий корень уравнения (1) является корнем уравнения (2)), то уравнение (2) называют следствием уравнения (1). Например, уравнение 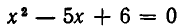 является следствием уравнения 2х—6= 0. В самом деле, корнем уравнения 2х — 6=0 является х=3, а при этом значении многочлен
является следствием уравнения 2х—6= 0. В самом деле, корнем уравнения 2х — 6=0 является х=3, а при этом значении многочлен 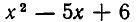 обращается в нуль.
обращается в нуль.
Если множества М и N корней уравнений (1) и (2) совпадают, то эти уравнения называются равносильными. Иными словами, уравнения

равносильны, если всякий корень уравнения (2) является корнем уравнения (3) и, обратно, всякий корень уравнения (3) является корнем уравнения (2).
В частности, уравнения равносильны, если множества М и N — пусты, то есть если каждое из уравнений не имеет решений.
Если уравнения (2) и (3) равносильны, то каждое из них является следствием другого.
Следует отметить, что понятие равносильности уравнений существенно зависит от того, какие значения корней считаются допустимыми. Рассмотрим, например, уравнения:

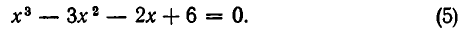
Корнями первого уравнения является число х=3, а второго — числа 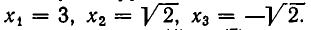 Так как эти множества различны, то уравнения (4) и (5) не являются равносильными. Но если рассматривать лишь рациональные значения корней уравнения, то уравнения (4) и (5) оказываются равносильными — ибо они имеют по единственному рациональному корню х = 3. Как правило, мы будем в дальнейшем рассматривать равносильность относительно множества всех действительных чисел. Иными словами, уравнения будут считаться равносильными, если они имеют одни и те же действительные корни.
Так как эти множества различны, то уравнения (4) и (5) не являются равносильными. Но если рассматривать лишь рациональные значения корней уравнения, то уравнения (4) и (5) оказываются равносильными — ибо они имеют по единственному рациональному корню х = 3. Как правило, мы будем в дальнейшем рассматривать равносильность относительно множества всех действительных чисел. Иными словами, уравнения будут считаться равносильными, если они имеют одни и те же действительные корни.
Совокупности уравнений
Пусть задано несколько уравнений

и требуется найти все значения х, которые удовлетворяют хотя бы одному из этих уравнений. Тогда говорят, что задана совокупность уравнений, а такие значения х называют решениями или корнями этой совокупности. Следует различать совокупность уравнений и систему уравнений — для системы уравнений требуется искать значения неизвестных, которые удовлетворяют всем уравнениям, а для совокупности — хотя бы одному из уравнений.
Чтобы отличать совокупность уравнений от системы уравнений, мы будем обозначать совокупность квадратными скобками, а систему — фигурными скобками.
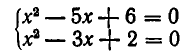
имеет одно решение 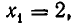 , а совокупность тех же уравнений
, а совокупность тех же уравнений
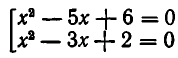
имеет три решения 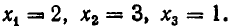
Обозначим множество решений уравнения 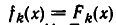 через
через 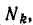 а множество решений совокупности уравнений (1) через N. Тогда
а множество решений совокупности уравнений (1) через N. Тогда 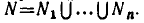 Например, множество решений совокупности
Например, множество решений совокупности
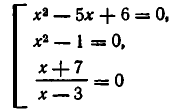
состоит из чисел 2, 3 (решений уравнения 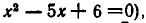 1, —1 (решений уравнения
1, —1 (решений уравнения 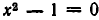 ) и —7 (решения уравнения
) и —7 (решения уравнения 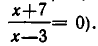 Число х=3 является решением, хотя при этом значении не определена функция
Число х=3 является решением, хотя при этом значении не определена функция 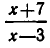
Две совокупности уравнений
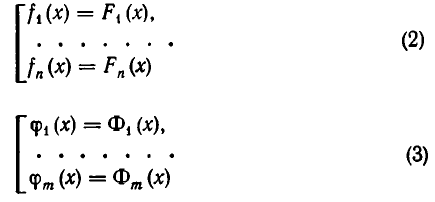
называются равносильными, если они имеют одно и то же множество корней.
Например, совокупности уравнений
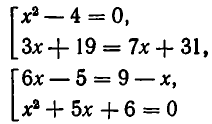
равносильны — их корнями являются числа 2, —2 и —3.
Преобразования уравнений
При решении уравнений мы переходим от одного уравнения к другому, пока не придем к уравнению вида х = а или совокупности уравнений такого вида. Возьмем, например, уравнение

Прибавляя к обеим частям этого уравнения (—Зх+3) и приводя подобные члены, получаем уравнение

А теперь умножим обе части уравнения (2) на и получим, что

В процессе решения этого уравнения мы прибавляли к обеим частям уравнения некоторое алгебраическое выражение (а именно, —Зх+3), умножали обе части уравнения на одно и то же число (а именно, на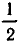 ). Кроме того, мы выполняли тождественные преобразования. Заметим, что уравнения (1), (2) и (3) имели одно и только одно решение х = 2. Таким образом, все проведенные преобразования приводили к уравнениям, равносильным первоначальному уравнению (1), имевшим с ним одно и то же решение.
). Кроме того, мы выполняли тождественные преобразования. Заметим, что уравнения (1), (2) и (3) имели одно и только одно решение х = 2. Таким образом, все проведенные преобразования приводили к уравнениям, равносильным первоначальному уравнению (1), имевшим с ним одно и то же решение.
Однако не всегда одинаковые преобразования обеих частей уравнения приводят к уравнению, равносильному первоначальному. Рассмотрим уравнение:

Его решением является х = 3. Если же мы умножим обе части уравнения на х — 2, то получим уравнение:
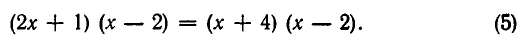
Это уравнение, кроме решения х=3, имеет еще решение х= 2— оно имеет лишний корень по сравнению с (4).
С другой стороны, если мы возьмем уравнение (5), имеющее решения х=2, х=3, и «сократим» его на х — 2 (то есть разделим обе части уравнения на х — 2), то получим уравнение 2х+1= =х+4 с единственным решением х=3. Значит, здесь мы в процессе решения потеряли корень х=2.
Не является «безобидным» и прибавление к обеим частям уравнения одного и того же алгебраического выражения. Например, уравнение

имеет решение х =2. Но если прибавить к обеим частям этого уравнения выражение 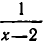 , то получим уравнение
, то получим уравнение
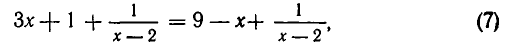
для которого х =2 не является решением — обе части этого уравнения не имеют смысла при х=2. Таким образом, произошла потеря решения.
Эти примеры наглядно показывают, что при преобразовании уравнений необходима осторожносгь — неправильно преобразуя уравнение, мы можем как приобрести лишние решения, так и потерять решения данного уравнения. При этом надо иметь в виду, что приобретение лишних решений не столь опасно, как потеря существующих. Ведь после того, как уравнение решено, можно подставить все найденные решения в заданное уравнение и отобрать те из решений, которые ему удовлетворяют. А потерянные решения восстановить уже нельзя.
Из изложенного видно, что, прежде чем решать конкретные виды уравнений, надо познакомиться с общей теорией уравнений, выяснить, какие преобразования приводят к равносильным уравнениям, какие дают посторонние решения, а при каких решения могут быть потеряны. Только после этого мы сможем решать уравнения «с открытыми глазами».
Теоремы о равносильности уравнений
Сформулируем сначала условия, при которых одно уравнение является следствием другого уравнения. Потом из этих условий будут получены условия равносильности уравнений.
Теорема:
Если к обеим частям уравнения

прибавить функцию  имеющую смысл при всех допустимых значениях неизвестного х, то получится новое уравнение
имеющую смысл при всех допустимых значениях неизвестного х, то получится новое уравнение
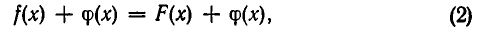
являющееся следствием данного.
Доказательство:
В самом деле, пусть а—корень уравнения (1). Тогда f(а)=F(а). Но  является некоторым числом, так как по условию функция
является некоторым числом, так как по условию функция  определена для всех допустимых значений х и, в частности, при х=а. Прибавим к обеим частям числового равенства f(a)=F(а) число
определена для всех допустимых значений х и, в частности, при х=а. Прибавим к обеим частям числового равенства f(a)=F(а) число  . Получим равенство
. Получим равенство
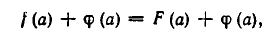
которое показывает, что число а является корнем уравнения (2). Таким образом, всякий корень уравнения (1) является корнем уравнения (2), то есть уравнение (2) является следствием уравнения (1).
Условие, что функция  определена при всех допустимых значениях х, существенно. Если
определена при всех допустимых значениях х, существенно. Если  не определено при х=а, где а — решение уравния (1), то уравнение (2) не является следствием уравнения (1) и уравнения (1) и (2) неравносильны: х = а является решением для (1), но не является решением для уравнения (2). Примером могут служить уравнения (6) и (7) из п. 5.
не определено при х=а, где а — решение уравния (1), то уравнение (2) не является следствием уравнения (1) и уравнения (1) и (2) неравносильны: х = а является решением для (1), но не является решением для уравнения (2). Примером могут служить уравнения (6) и (7) из п. 5.
Прибавление к обеим частям уравнения одного и того же выражения не может привести к приобретению посторонних корней, если это прибавление не сопровождается приведением подобных членов или иными преобразованиями, меняющими область определения уравнения (например, сокращением дробей). Рассмотрим, например, уравнение
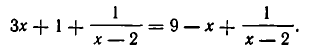
Если прибавить к обеим частям — 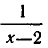 и привести подобные члены, то получим уравнение Зх +1= 9 — х, имеющее решение х = 2. Это решение не принадлежит области определения исходного уравнения и потому не удовлетворяет ему.
и привести подобные члены, то получим уравнение Зх +1= 9 — х, имеющее решение х = 2. Это решение не принадлежит области определения исходного уравнения и потому не удовлетворяет ему.
Перейдем к вопросу об умножении обеих частей уравнения на одно и то же выражение.
Теорема:
Если обе части уравнения

умножить на функцию  , имеющую смысл при всех допустимых значениях х, то получится новое уравнение
, имеющую смысл при всех допустимых значениях х, то получится новое уравнение

являющееся следствием уравнения (3).
Доказательство.
Пусть а — корень уравнения (3). Тогда справедливо равенство f(а)=F(а). Умножим обе части этого равенства на число  . Мы получим числовое равенство
. Мы получим числовое равенство 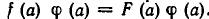 Оно показывает, что а является корнем и уравнения (4). Таким образом, всякий корень уравнения (3) является корнем уравнения (4), то есть (4) — следствие (3).
Оно показывает, что а является корнем и уравнения (4). Таким образом, всякий корень уравнения (3) является корнем уравнения (4), то есть (4) — следствие (3).
Из доказанных теорем следует, например, что уравнение
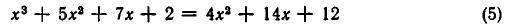
является следствием уравнения

Действительно, уравнение (5) получается из уравнения (6) прибавлением к обеим частям функции Зх+2 и умножением полученного уравнения на х + 2.
Многочлены определены при всех значениях х. Поэтому прибавление к обеим частям уравнения многочлена, равно как и умножение обеих частей
уравнения на многочлен, приводит к уравнению, являющемуся следствием исходного.
Оговорка о том, что  должно иметь смысл при всех допустимых значениях х, существенна для справедливости теоремы 2. Рассмотрим, например, уравнение
должно иметь смысл при всех допустимых значениях х, существенна для справедливости теоремы 2. Рассмотрим, например, уравнение

и умножим обе части этого уравнения на 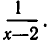 Мы получим уравнение
Мы получим уравнение 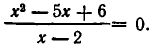 Оно уже не является следствием исходного: уравнение (7) имеет корни 2 и 3, а уравнение
Оно уже не является следствием исходного: уравнение (7) имеет корни 2 и 3, а уравнение 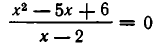 — лишь корень 3. Причиной потери корня явилось то, что функция
— лишь корень 3. Причиной потери корня явилось то, что функция 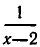 не определена при х = 2, а это значение как раз является корнем заданного уравнения.
не определена при х = 2, а это значение как раз является корнем заданного уравнения.
Докажем теперь теоремы о равносильности уравнений. Чтобы доказать равносильность двух уравнений, надо показать, что пер вое из них является следствием второго, а второе — следствием первого.
Теорема:
Если функция  определена при всех допустимых значениях неизвестного х, то уравнения
определена при всех допустимых значениях неизвестного х, то уравнения

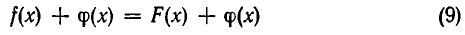
Доказательство:
Мы уже видели, что при условии теоремы уравнение (9) является следствием уравнения (8). Но уравнение (8) в свою очередь получается из уравнения (9) прибавлением к обеим частям функции — 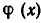 и приведением подобных членов.
и приведением подобных членов.
Так как функция 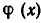 определена при всех допустимых значениях х, то уравнение (8) является следствием уравнения (9). Тем самым доказано, что уравнения (8) и (9) равносильны.
определена при всех допустимых значениях х, то уравнение (8) является следствием уравнения (9). Тем самым доказано, что уравнения (8) и (9) равносильны.
Из доказанной теоремы вытекает правило перенесения слагаемых из одной части уравнения в другую: если некоторое слагаемое данного уравнения перенести из одной части в другую, изменив знак этого слагаемого на противоположный, то получится уравнение, равносильное данному.
В самом деле, в силу теоремы 3 уравнения


равносильны: уравнение (11) получается путем прибавления функции — 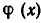 к обеим частям уравнения (10) и приведения подобных членов.
к обеим частям уравнения (10) и приведения подобных членов.
Кратко правило перенесения слагаемых формулируют так: всякое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.
Из доказанной теоремы вытекает, что всякое уравнение f(х) =F(х) можно заменить равносильным ему уравнением вида Ф(х) = 0. Для этого достаточно перенести F(х) в левую часть уравнения, заменив знак на противоположный, и положить f(х)— F(х) =Ф (х).
Теорема:
Если функция 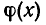 определена для всех допустимых значений х и ни при одном допустимом значении х не обращается в нуль, то уравнения
определена для всех допустимых значений х и ни при одном допустимом значении х не обращается в нуль, то уравнения


Доказательство:
Мы уже видели (теорема 2), что уравнение (13) является следствием уравнения (12). Докажем, что уравнение (12) в свою очередь является следствием уравнения (13). Уравнение (12) получается из уравнения (13) умножением обеих частей на функцию 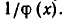 Так как по условию функция
Так как по условию функция 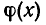 определена для всех допустимых значений х и не обращается при этих значениях в нуль, то функция
определена для всех допустимых значений х и не обращается при этих значениях в нуль, то функция 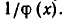 также определена при всех допустимых значениях х. Поэтому уравнение (12) является следствием уравнения (13), а значит, эти уравнения равносильны.
также определена при всех допустимых значениях х. Поэтому уравнение (12) является следствием уравнения (13), а значит, эти уравнения равносильны.
Из доказанной теоремы вытекает, например, что уравнения
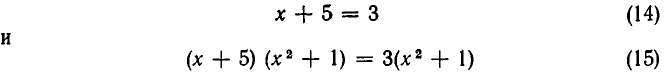
равносильны в области действительных чисел. В самом деле, уравнение (15) получается из уравнения (14) умножением на функцию 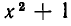 , а эта функция всюду определена и не обращается в нуль при действительных значениях х.
, а эта функция всюду определена и не обращается в нуль при действительных значениях х.
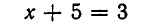
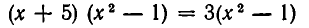
не являются равносильными — второе получается из первого умножением на функцию 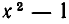 , а эта функция обращается в нуль при х = ± 1. Поэтому второе уравнение, кроме корня
, а эта функция обращается в нуль при х = ± 1. Поэтому второе уравнение, кроме корня 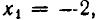 удовлетворяющего и первому уравнению, имеет еще и корни
удовлетворяющего и первому уравнению, имеет еще и корни 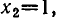
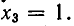
Уравнения (12) и (13) могут быть неравносильными и в том случае, когда множитель 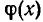 теряет смысл при некоторых допустимых значениях неизвестного. Например, уравнения
теряет смысл при некоторых допустимых значениях неизвестного. Например, уравнения
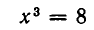
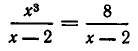
неравносильны: множитель 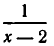 теряет смысл при х = 2, а x = 2 как раз является корнем уравнения
теряет смысл при х = 2, а x = 2 как раз является корнем уравнения 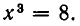
Если в ходе решения уравнения приходилось умножать обе части этого уравнения на выражение 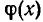 , содержащее неизвестное, то надо проверить две вещи: а) Не обращается ли
, содержащее неизвестное, то надо проверить две вещи: а) Не обращается ли 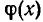 в нуль при допустимых значениях не известного? б) Не теряет ли
в нуль при допустимых значениях не известного? б) Не теряет ли 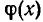 смысл при некоторых допустимых значениях неизвестного?
смысл при некоторых допустимых значениях неизвестного?
В первом случае среди найденных корней могут оказаться посторонние корни, и надо проверить все найденные корни, удовлетворяют ли они первоначально заданному уравнению. Во втором же случае возможна потеря корней, и мы должны подставить в заданное уравнение значения неизвестного, при которых теряет смысл 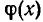 — среди этих значений могут оказаться потерянные в ходе решения корни уравнения.
— среди этих значений могут оказаться потерянные в ходе решения корни уравнения.
Из теоремы 4 непосредственно вытекает справедливость утверждения: если обе части уравнения умножить на произвольное отличное от нуля число, то получим уравнение, равносильное данному.
Это утверждение кратко формулируют так: обе части уравнения можно умножать на произвольное отличное от нуля число.
Уравнения с одним неизвестным
Алгебраические уравнения с одним неизвестным:
Рациональным алгебраическим уравнением с одним неизвестным называют уравнение вида

где R(х) — алгебраическая дробь относительно х. К такому виду можно в силу теорем 3 и 5, привести любое уравнение 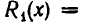
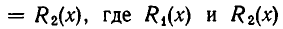 — алгебраические дроби. Например, уравнение
— алгебраические дроби. Например, уравнение
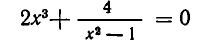
является рациональным алгебраическим. В дальнейшем мы будем называть такие уравнения просто алгебраическими.
Применяя теоремы о равносильности уравнений, можно заменить каждое уравнение вида (1) равносильным ему уравнением вида:

где f(x)— многочлен от х. Для этого надо записать дробь R(x) в виде отношения двух многочленов. Мы получим уравнение:
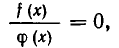
где f(х) и  — многочлены от х. Но дробь может равняться нулю лишь в случае, когда равен нулю ее числитель. Поэтому решение уравнения (1) сводится к решению уравнения f(x)=0, где f(х) — многочлен от х. При этом нужно иметь в виду, что решениями уравнения (1) являются лишь те корни уравнения (2), при которых дробь R(x) имеет смысл (то есть
— многочлены от х. Но дробь может равняться нулю лишь в случае, когда равен нулю ее числитель. Поэтому решение уравнения (1) сводится к решению уравнения f(x)=0, где f(х) — многочлен от х. При этом нужно иметь в виду, что решениями уравнения (1) являются лишь те корни уравнения (2), при которых дробь R(x) имеет смысл (то есть  отлично от нуля).
отлично от нуля).
Пример:
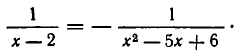
Перенесем 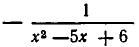 в левую часть уравнения и приведем получившуюся сумму к общему знаменателю. Получим уравнение:
в левую часть уравнения и приведем получившуюся сумму к общему знаменателю. Получим уравнение:
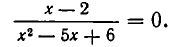
Приравнивая нулю числитель этой дроби, получаем уравнение х—2=0, корнем которого является число х=2. Однако при x=2 дробь 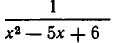 не определена. Поэтому заданное уравнение корней не имеет.
не определена. Поэтому заданное уравнение корней не имеет.
Метод разложения на множители
Рассмотрим некоторые методы решения алгебраических уравнений, а также отдельные виды таких уравнений.
Выше было сказано, что при решении уравнения его заменяют другими уравнениями или совокупностями уравнений, равносильными заданному, но более простыми
Рассмотрим следующий пример. Пусть надо решить уравнение:
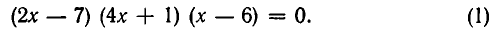
Мы знаем, что произведение может равняться нулю тогда и только тогда, когда хоть один из его сомножителей равен нулю. Поэтому, чтобы решить уравнение (1), надо найти все значения, при кототых хоть один из сомножителей равен нулю. А это все равно, что решить совокупность уравнений
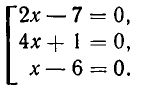
Решая ее, находим для х значения 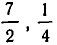 и 6. Они и дают корни уравнения (1).
и 6. Они и дают корни уравнения (1).
Метод, примененный для решения уравнения (1), в общем виде формулируется так.
Теорема:
Если функции  определены на некотором множестве М, то на этом множестве уравнение
определены на некотором множестве М, то на этом множестве уравнение
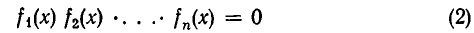
равносильно совокупности уравнений

Доказательство:
Пусть а — одно из решений совокупности (3). Это означает, что а является корнем одного из уравнений этой совокупности, например, уравнения 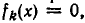 а все остальные функции
а все остальные функции 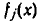 определены при х = а. Но тогда
определены при х = а. Но тогда
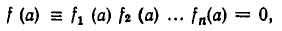
так как один из сомножителей 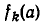 равен нулю. Следовательно, любое решение совокупности (3) является корнем уравнения (2).
равен нулю. Следовательно, любое решение совокупности (3) является корнем уравнения (2).
Наоборот, пусть а — корень уравнения (2). Тогда f (а)=0, то есть 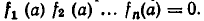 Но произведение равно нулю лишь в случае, когда хоть один из сомножителей равен нулю. Поэтому хотя бы одно из чисел
Но произведение равно нулю лишь в случае, когда хоть один из сомножителей равен нулю. Поэтому хотя бы одно из чисел  равно нулю. Это означает, что а является корнем хотя бы одного из уравнений
равно нулю. Это означает, что а является корнем хотя бы одного из уравнений 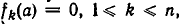 то есть одним из решений совокупности уравнений (3).
то есть одним из решений совокупности уравнений (3).
Пример:

Левая часть этого уравнения разлагается на множители следующим образом:
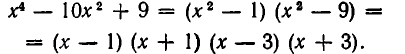
Отсюда следует, что уравнение (4) равносильно совокупности уравнений:

Решая уравнения этой совокупности, получаем корни уравнения (4):
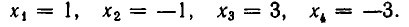
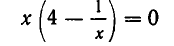
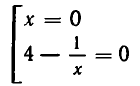
не равносильны, так как при х = 0 функция 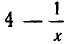 не определена. На множестве же
не определена. На множестве же 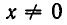 они равносильны.
они равносильны.
В некоторых случаях разложение на множители связано с искусственными преобразованиями. Рассмотрим, например, уравнение:

Нетрудно заметить, что
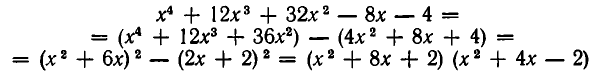
Поэтому уравнение (б) можно записать в виде:

Таким образом, все свелось к решению совокупности двух квадратных уравнений:
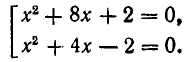
Решая их, находим корни уравнения (6):
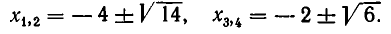
Метод введения нового неизвестного
Наряду с методом разложения на множители часто применяется другой метод — введение нового неизвестного.
Рассмотрим следующий пример:
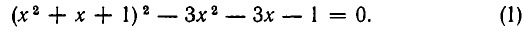
Если раскрыть скобки, то получится уравнение четвертой степени, решить которое довольно сложно. Мы поступим иначе. Обозначим 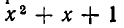 через r. Тогда
через r. Тогда 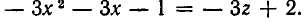
Поэтому уравнение (1) после введения нового неизвестного z принимает вид
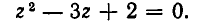
Решая это квадратное уравнение, получаем, что его корни равны: 
Но 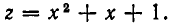 Поэтому х удовлетворяет или уравнению
Поэтому х удовлетворяет или уравнению  или уравнению
или уравнению 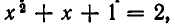 то есть совокупности уравнений:
то есть совокупности уравнений:
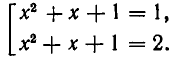
Решая ее, получаем:
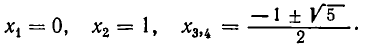
Метод, примененный для решения уравнения (1), в общем виде заключается в следующем.
Пусть дано уравнение F(х)=0 и пусть функцию F(х) можно представить в виде 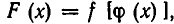 так что уравнение F (х)=0 записывается в виде
так что уравнение F (х)=0 записывается в виде

Введем новое неизвестное z, положив 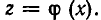 Тогда вместо уравнения (1) получаем уравнение относительно
Тогда вместо уравнения (1) получаем уравнение относительно 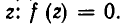 Докажем следующую теорему.
Докажем следующую теорему.
Теорема:
Если а — один из корней уравнения f(z) = 0, а b — один из корней уравнения  то b является одним из корней уравнения F(х)=0, где
то b является одним из корней уравнения F(х)=0, где 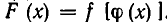 . Обратно, если b — корень уравнения F(х)=0, то
. Обратно, если b — корень уравнения F(х)=0, то 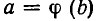 — один из корней уравнения f(z)= 0 .
— один из корней уравнения f(z)= 0 .
Доказательство. Пусть b — корень уравнения 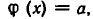 где а — корень уравнения f (z)=0; f(а) =0. Тогда
где а — корень уравнения f (z)=0; f(а) =0. Тогда 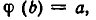 и потому
и потому
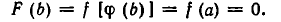
Таким образом, b удовлетворяет уравнению F (х) = 0.
Обратно, пусть b — корень уравнения F(х)=0 и 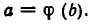 Тогда
Тогда
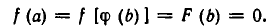
Следовательно, а — корень уравнения f(z)=0. Теорема доказана.
Из доказанной теоремы следует, что решение уравнения вида 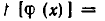
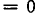 сводится к следующему: сначала находят корни
сводится к следующему: сначала находят корни  уравнения f(z) =0; после этого надо решить все уравнения
уравнения f(z) =0; после этого надо решить все уравнения 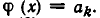 Совокупность корней этих уравнений и дает решение уравнения (2).
Совокупность корней этих уравнений и дает решение уравнения (2).
Биквадратные уравнения
Метод замены неизвестного при меняется для решения уравнений вида
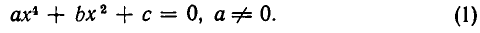
Такие уравнения называют биквадратными. Чтобы решить уравнение (1), положим 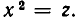 Тогда получим квадратное уравнение:
Тогда получим квадратное уравнение:

Его корнями являются числа:
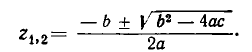
Поэтому корни уравнения (1) получаются путем решения уравнений 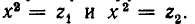 Значит, мы получаем четыре корня для уравнения (1)
Значит, мы получаем четыре корня для уравнения (1)
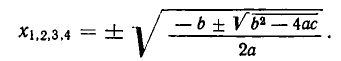
Четыре корня возникают при различных комбинациях знаков:

При решении биквадратных уравнений (как и при решении квадратных уравнений) иногда приходится извлекать квадратные корни из отрицательных чисел. Это приводит к так называемым комплексным числам, которые будут изучены в главе V.
Пример. Решить уравнение
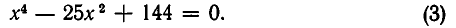
Полагая 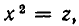 получаем квадратное уравнение:
получаем квадратное уравнение:
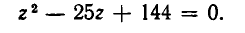
Его корнями являются числа 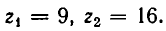 Значит, корни уравнения (8) имеют вид:
Значит, корни уравнения (8) имеют вид:

Возвратные уравнения 3-й и 4-й степеней
Многочлен n-й степени
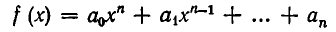
называется возвратным, если его коэффициенты, одинаково уда ленные от начала и от конца, равны между собой. Иными словами, коэффициенты возвратного многочлена n-й степени удовлетворяют условию 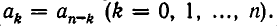
Алгебраическое уравнение вида f(х)=0, где f(х) — возвратный многочлен, называют возвратным уравнением. Примерами таких уравнений являются:
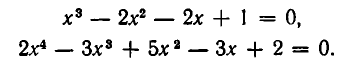
Рассмотрим решение возвратных уравнений третьей и четвертой степеней. Возвратное уравнение третьей степени имеет вид:
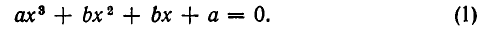
Группируя члены, разложим выражение в левой части уравнения на множители:
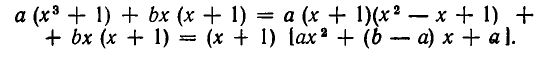
Отсюда видно, что одним из корней уравнения (1) является х=—1 . Два других корня получаются путем решения квадратного уравнения
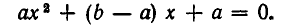
Пример:
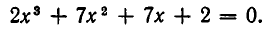
Разлагая левую часть уравнения на множители, получаем:
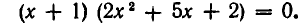
Корни квадратного уравнения 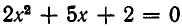 равны
равны 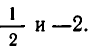 Поэтому корнями заданного уравнения являются числа
Поэтому корнями заданного уравнения являются числа 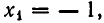
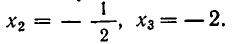
Приведем пример задачи, сводящейся к разобранному типу уравнений.
Задача:
Из квадратного листа жести со стороной а см вырезают по углам четыре квадратика со стороной х см и делают из получившейся фигуры коробку. При каком значении х объем коробки равен 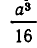 ?
?
Решение:
Основанием коробки является квадрат со стороной а-2x, а ее высота равна х. Значит, объем коробки равен 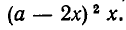 По условию имеем уравнение:
По условию имеем уравнение:
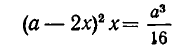
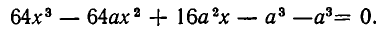
Положим 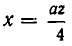 . Мы получим для z уравнение
. Мы получим для z уравнение
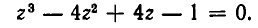
Разлагая на множители, получаем
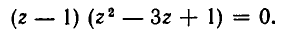
Поэтому корни нашего уравнения равны
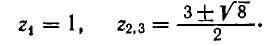
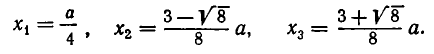
Из условия задачи следует, что  Поэтому
Поэтому  не удовлетворяет условию. Итак, либо
не удовлетворяет условию. Итак, либо 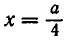 , либо
, либо 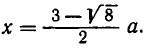
Теперь рассмотрим возвратное уравнение 4-й степени:
Так как  то х=0 не является корнем этого уравнения. Поэтому если разделить обе части уравнения (2) на
то х=0 не является корнем этого уравнения. Поэтому если разделить обе части уравнения (2) на 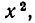 то получим равносильное уравнение:
то получим равносильное уравнение:
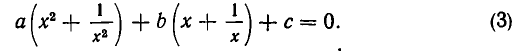
Введем новое неизвестное z, положив 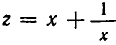 . Так как
. Так как 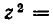
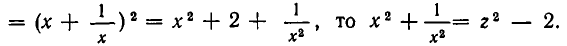
Следовательно, уравнение (3) превращается в квадратное уравнение относительно z

Решив это уравнение, найдем его корни 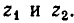 Чтобы найти х, остается решить совокупность уравнений:
Чтобы найти х, остается решить совокупность уравнений:
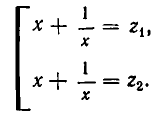
Она сводится к совокупности квадратных уравнений:
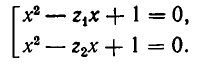
Пример. Решить уравнение
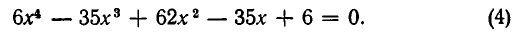
Перепишем это уравнение в виде
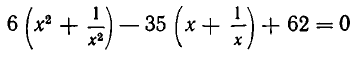
и введем новое неизвестное 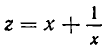 . Получим уравнение:
. Получим уравнение:
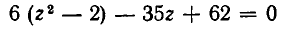
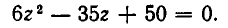
Решая его, находим: 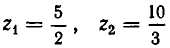 . Чтобы найти корни уравнения (4), надо решить уравнения:
. Чтобы найти корни уравнения (4), надо решить уравнения:

Из них получаем:
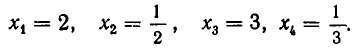
Наряду с уравнениями вида (1) и (2) рассматривают так называемые кососимметричные уравнения, или, иначе, возвратные уравнения второго рода. При n=4 они имеют вид:
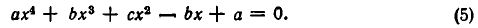
Это уравнение сводится к
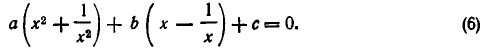
После этого вводят новое неизвестное по формуле 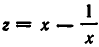 . Так как
. Так как 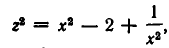 то уравнение (6) сводится к квадратному уравнению
то уравнение (6) сводится к квадратному уравнению 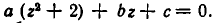 Дальнейшее решение ведется так же, как и для обычных возвратных уравнений.
Дальнейшее решение ведется так же, как и для обычных возвратных уравнений.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
http://lfirmal.com/ponyatie-algebraicheskogo-i-transtsendentnogo-uravneniya-i-metodov-ih-priblizhennogo-resheniya/
[/spoiler]
Дифференциальные уравнения первого порядка, приводящиеся к линейным
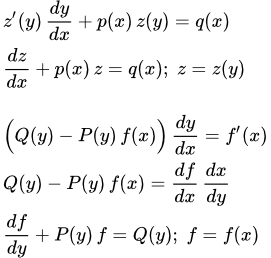
Метод решения
К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y ; p и q – функции от x .
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z :
.
Дифференциальные уравнения, линейные относительно переменной x
Ранее мы рассматривали уравнения, линейные относительно переменной y . То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x , а не y . В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y .
Покажем, что это уравнение линейно относительно переменной x . Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R ( y ) , приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.
Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка
Решить уравнение:
(П.1) .
Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y . Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y , .
Дифференцируем по y . По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z , дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y :
;
;
.
Интегрируем по частям:
;
;
;
.
Переходим к переменной x :
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 05-08-2012 Изменено: 26-06-2015
Обыкновенные дифференциальные уравнения
Содержание:
Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение
 (7.1)
(7.1)
Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или  . (7.4)
. (7.4)
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение  имеет решениями функции y = Cx, а дифференциальное уравнение
имеет решениями функции y = Cx, а дифференциальное уравнение  — функции
— функции  где C — произвольное число.
где C — произвольное число.
Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или  (7.7)
(7.7)
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение  имеет общее решение y = Cx. Зададим начальное условие
имеет общее решение y = Cx. Зададим начальное условие  . Подставим эти значения в общее решение, получим 6 = 2С, откуда С = 3. Следовательно, функция y = 3x удовлетворяет и дифференциальное уравнение, и начальное условие.
. Подставим эти значения в общее решение, получим 6 = 2С, откуда С = 3. Следовательно, функция y = 3x удовлетворяет и дифференциальное уравнение, и начальное условие.
Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная  определены и непрерывные в области G, которая содержит точку M0 (x0; y0) , то существует единственное решение y = φ (x) уравнения (7.4), которое удовлетворяет начальному условию: y (x0) = y0.
определены и непрерывные в области G, которая содержит точку M0 (x0; y0) , то существует единственное решение y = φ (x) уравнения (7.4), которое удовлетворяет начальному условию: y (x0) = y0.
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной  .
.
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение  имеет общее решение y = Cx, то ему соответствует семья прямых,
имеет общее решение y = Cx, то ему соответствует семья прямых,
которые проходят через начало координат (рис. 1).
Уравнение  имеет общее решение, ему соответствует семья равносторонних гипербол (рис. 2).
имеет общее решение, ему соответствует семья равносторонних гипербол (рис. 2). 
Если задано начальное условие  то это означает, что задана точка M0 (x0;y0), через которую должна проходить интегральная кривая, отвечающая искомому частному решению. Таким образом, отыскание частного решения дифференциального уравнения по заданному начальному условию геометрически означает, что из семьи
то это означает, что задана точка M0 (x0;y0), через которую должна проходить интегральная кривая, отвечающая искомому частному решению. Таким образом, отыскание частного решения дифференциального уравнения по заданному начальному условию геометрически означает, что из семьи
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части:  .
.
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение:  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 

 — это общее решение дифференциального уравнения.
— это общее решение дифференциального уравнения.
Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,
 является частным решением данного уравнения.
является частным решением данного уравнения.
Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными: 
Интегрируя это уравнение, запишем  .
.
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим  .
.
Интегрируя, получим



 — общий интеграл дифференциального уравнения.
— общий интеграл дифференциального уравнения.
Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение: 
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:
 откуда
откуда 
Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие 
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену  будем иметь:
будем иметь: 
Тогда уравнение (7.10) запишется в виде  (7.11)
(7.11)
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле
 или y = xu, (7.12)
или y = xu, (7.12)
то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение  примет вид: u + xu’ = φ (u),
примет вид: u + xu’ = φ (u),
то есть  , откуда
, откуда  .
.
После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить  вместо u.
вместо u.
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения

Решение. Заменой y = xu сведем заданное уравнение к уравнению
 или
или  .
.
Отделяя переменные, найдем
 откуда
откуда  или
или  , то есть
, то есть  .
.
Возвращаясь к переменной y, получим общее решение:  .
.
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем  , откуда
, откуда 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда 
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:
 (7.17)
(7.17)
При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение  .
.
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение:  или
или  . (7.18)
. (7.18)
Выражение, стоящее в скобках, приравниваем к нулю, имеем
 или
или 
Отделим переменные, домножив обе части уравнения на  , тогда
, тогда  .
.
После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18): 
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения  который удовлетворяет начальному условию y (0) = 0.
который удовлетворяет начальному условию y (0) = 0.
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 

Подставим v в уравнение и найдем u: 
Общее решение дифференциального уравнения будет: 
Подставляем начальные условия в найденное решение и находим С: 
Из общего решения получаем частное решение  .
.
Дифференциальное уравнение Бернулли
Определение. Уравнения вида
 (или
(или  )
)
называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»: 
Сделаем замену: 

Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 

Мы получили линейное дифференциальное уравнение относительно новой переменной 
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение.  .
.
Сделаем замену  Тогда
Тогда 

Данное уравнение решим, сделав замену z = u (x) ⋅ v (x). 
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения 
Тогда  .
.
Проинтегрировав правую часть этого уравнения по частям, получим  , а при y -1 = z = uv, имеем
, а при y -1 = z = uv, имеем 
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную  искомую функцию
искомую функцию  и производные искомой функции
и производные искомой функции  до некоторого порядка включительно.
до некоторого порядка включительно.
Обыкновенное дифференциальное уравнение может быть приведено к виду

Здесь  — известная функция, заданная в некоторой области
— известная функция, заданная в некоторой области 
Число  т. е. наивысший из порядков производных, входящих в (1), называется порядком уравнения.
т. е. наивысший из порядков производных, входящих в (1), называется порядком уравнения.
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид

В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:

Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение

используя последнее в окрестности тех точек, в которых  обращается в бесконечность.
обращается в бесконечность.
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение

Обе переменные  и
и  входят в это уравнение уже равноправно, и любую из них мы можем принять за независимую переменную.
входят в это уравнение уже равноправно, и любую из них мы можем принять за независимую переменную.
Умножая обе части уравнения (3) на некоторую функцию  получаем более симметричное уравнение:
получаем более симметричное уравнение:

где  Обратно, всякое уравнение вида (4) можно переписать в виде уравнений (2) или (2′), разрешая его относительно
Обратно, всякое уравнение вида (4) можно переписать в виде уравнений (2) или (2′), разрешая его относительно  или
или  так что уравнение (4) равносильно следующим двум уравнениям:
так что уравнение (4) равносильно следующим двум уравнениям:

Иногда уравнение записывают *з так называемой симметрической форме:

Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2),  определена на некотором подмножестве
определена на некотором подмножестве  вещественной плоскости
вещественной плоскости  Функцию
Функцию  определенную в интервале
определенную в интервале  мы будем называть решением уравнения (2) в этом интервале*, если:
мы будем называть решением уравнения (2) в этом интервале*, если:
- Существует производная
 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). - Функция
 обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 
справедливое для всех значений  из интервала
из интервала  Это означает, что при любом
Это означает, что при любом  из интервала
из интервала  точка
точка  принадлежит множеству
принадлежит множеству  и
и 
Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения  этого перевернутого уравнения естественно присоединять к решениям уравнения (2).
этого перевернутого уравнения естественно присоединять к решениям уравнения (2).
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.

является решением уравнения

в интервале  ибо она определена и дифференцируема в эгои интервале, и, подставляя се в уравнение (9), получаем тождество:
ибо она определена и дифференцируема в эгои интервале, и, подставляя се в уравнение (9), получаем тождество:

справедливое при всех значениях 
Пример 2.
Функция  есть решение равнения
есть решение равнения  в интервале
в интервале 
Пример 3.

является решением уравнения 
в интервале 
Иногда функцию  обращающую уравнение (2) в тождество (7), т. е. решение уравнения (2), называют интегралом этого уравнения. Мы будем употреблять термин интеграл только в смысле п. 16.
обращающую уравнение (2) в тождество (7), т. е. решение уравнения (2), называют интегралом этого уравнения. Мы будем употреблять термин интеграл только в смысле п. 16.
Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила  .
.
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила , а соответственно и ее проекции Fx, Fy, Fz зависят от времени t, от положения x, y, z точки и от скорости движения точки, то есть от
, а соответственно и ее проекции Fx, Fy, Fz зависят от времени t, от положения x, y, z точки и от скорости движения точки, то есть от  . Искомыми неизвестными функциями в этой задаче будут три функции x = x (t), y = y (t), z = z (t). Эти
. Искомыми неизвестными функциями в этой задаче будут три функции x = x (t), y = y (t), z = z (t). Эти
функции определяются из уравнений динамики: 
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t): 
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:
 (7.38)
(7.38)
где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:
 (7.39)
(7.39)
Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные
 их выражениями f1, f2, . fn из уравнений системы (7.38), получим уравнение
их выражениями f1, f2, . fn из уравнений системы (7.38), получим уравнение 
Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:
 (7.40)
(7.40)
Из первых (n-1) уравнений определим y2, y3, . yn:
 (7.41)
(7.41)
и подставим их значения в последнее уравнение системы (7.40) для определения y1: 
Продифференцируем это выражение (n-1) раз, определим
 как функции от x, C1, C2, . Cn. Подставим эти функции в (7.41), найдем
как функции от x, C1, C2, . Cn. Подставим эти функции в (7.41), найдем
 (7.43)
(7.43)
Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем:  . Подставляем сюда значение
. Подставляем сюда значение  и
и  из системы, получим
из системы, получим 

Из первого уравнения системы найдем  и подставим в полученное нами уравнение:
и подставим в полученное нами уравнение:
 или
или 
Общим решением этого уравнения является
 (*)
(*)
и тогда  (**)
(**)
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет: 
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:
 (7.44)
(7.44)
где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:
 (7.45)
(7.45)
Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44): 
Сократим на e kt и преобразуем систему, сведя ее к такой системе:
 (7.46)
(7.46)
Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы: 
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k: 
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде: 
Пример 2. Найти общее решение системы уравнений: 
Решение. Составим характеристическое уравнение:
 или k 2 – 5k + 4 = 0, корни которого k1 = 1, k2 = 4.
или k 2 – 5k + 4 = 0, корни которого k1 = 1, k2 = 4.
Решение системы ищем в виде 
Составим систему (7.46) для корня k1 и найдем  и
и  :
:
 или
или 
Откуда  Положив
Положив  получим
получим 
Итак, мы получили решение системы: 
Далее составляем систему (7.46) для k = 4: 
Откуда 
Получим второй решение системы: 
Общее решение системы будет: 
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:
 (7.47)
(7.47)
 (7.48)
(7.48)
Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:
 (7.49)
(7.49)
где  — действительные числа, которые определяются через
— действительные числа, которые определяются через  .
.
Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы 
Решение. Составляем характеристическое уравнение:
 или k 2 + 12k + 37 = 0, корни которого k1 = –6 + i, k2 = –6 – i .
или k 2 + 12k + 37 = 0, корни которого k1 = –6 + i, k2 = –6 – i .
Подставляем поочередно k1, k2 в систему (7.46), найдем 
Запишем уравнение (7.47) и (7.48) для наших данных 
Перепишем эти решения в таком виде:

За частные решения можно взять отдельно действительные и отдельно мнимые части: 
Общим решением системы будет



Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной
Уравнения 1-го порядка n-ой степени относительно производной
Пусть имеем дифференциальное уравнение
Решаем это уравнение относительно . Пусть
— вещественные решения уравнения (1).
Общий интеграл уравнения (1) выразится совокупностью интегралов:
где есть интеграл уравнения .
Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.
Пример 1. Решить уравнение .
Решение. Разрешим это уравнение относительно :
Пример 2. Решить уравнение .
Решение. Разрешим уравнение относительно переменной :
Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь
Рассмотрим два случая:
1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:
В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).
2) , откуда . Подставляя, получим еще одно решение .
Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь
откуда . Это значение постоянной подставим в . Тогда получим частное решение
которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.
2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0
Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .
А. Уравнение вида разрешимо относительно :
Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим
Получаем общее решение уравнения в параметрической форме
Пример 3. Решить уравнение , где — постоянные.
Решение. Положим , тогда , или . Отсюда и .
Общим решением будет .
Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :
то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда
Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме
Пример 4. Решить уравнение .
Решение. Полагаем , тогда имеем
Отсюда , общее решение .
В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .
Полагая , получим . Но и, следовательно, , так что
Таким образом — общее решение уравнения в параметрической форме ( — параметр).
Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.
Пример 5. Решить уравнение .
Решение. Положим , тогда
Итак, — общее решение.
Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .
3°. Уравнения Лагранжа
Уравнение Лагранжа имеет вид
Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:
Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .
Пример 6. Проинтегрировать уравнение .
Решение. Полагаем , тогда . Дифференцируя, находим
Получили уравнение первого порядка, линейное относительно ; решая его, находим
Подставляя найденное значение в выражение для , получим окончательно
Уравнения Клеро
Уравнение Клеро имеет вид .
Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид
Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .
Пример 7. Проинтегрировать уравнение .
Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем
Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).
С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).
источники:
http://natalibrilenova.ru/obyiknovennyie-differentsialnyie-uravneniya/
http://mathhelpplanet.com/static.php?p=differentsialnye-uravneniya-pervogo-poryadka—ne-razreshennye-otnositelno-proizvodnoi

Составление систем дифференциальных уравнений относительного движения точки массой m под действием сил.
Уравнение второго основного закона динамики для абсолютного движения точки массой m имеет вид

где a – абсолютное ускорение точки;
Fi – силы, действующие на точку, включая реакции связей.
Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма трех ускорений: переносного aпер , относительного aотн и кориолисова aкор, т.е.
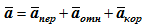
Подставляя это выражение в (7.1), получим
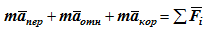
или
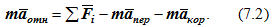
Введем в рассмотрение два вектора
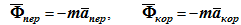
и назовем их переносной и кориолисовой силами инерции.
Подставим эти векторы в уравнение (7.2):
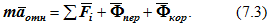
Уравнение (7.3) представляет собой основное уравнение динамики относительного движения материальной точки.
В случае равномерного и поступательного переносного движения Фпер= 0, Фкор= 0 и уравнение (7.3) ничем не отличается от уравнения (7.1). Во всех инерциальных системах отсчета уравнение движения точки записывается одинаково. В этом заключается принцип относительности классической механики.
Проецируя уравнение (7.3) на оси подвижной декартовой системы координат, получим дифференциальные уравнения относительного движения точки
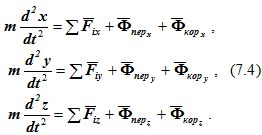
Дифференциальные уравнения относительного движения отличаются от дифференциальных уравнений абсолютного движения наличием в правой части уравнений проекций на соответствующие оси переносной и кориолисовой сил инерции.
Рассмотрим частные случаи относительного движения материальной точки:
- если подвижная система отсчета движется поступательно, то Фкор= 0, так как ωпер= 0, и уравнение относительного движения примет вид
maотн=ΣFi +Фпер (7.5)
- если точка по отношению к подвижным осям находится в покое, то для нее aотн=0, Vотн=0 и, следовательно, Фкор=0. Тогда уравнение (7.3) примет вид
ΣFi+Фпер=0 (7.6)
Уравнение (7.6) представляет собой уравнение относительного покоя точки.
Примеры решения задач >
Кинетическая энергия >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
123
Мастер
(1034),
на голосовании
11 лет назад
Голосование за лучший ответ
Сталин
Искусственный Интеллект
(243116)
11 лет назад
назначить Х переменной.
артем джигурда
Ученик
(97)
11 лет назад
найти такое значение х, при котором уравнение обращается в тождество
nikita Skladchikov
Ученик
(105)
11 лет назад
это значит найти все возможные значения Х.
Похожие вопросы

