17 авг. 2022 г.
читать 2 мин
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:
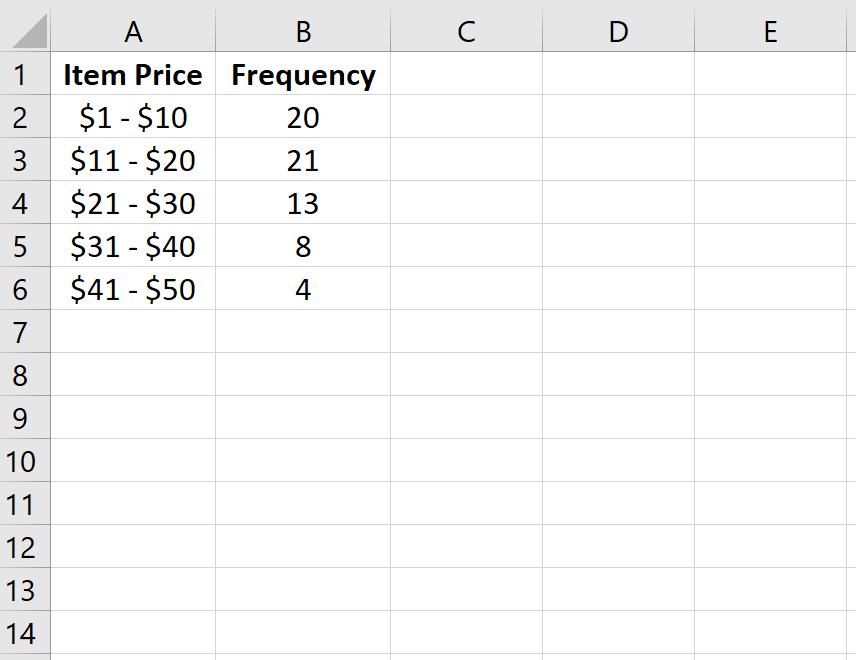
Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:
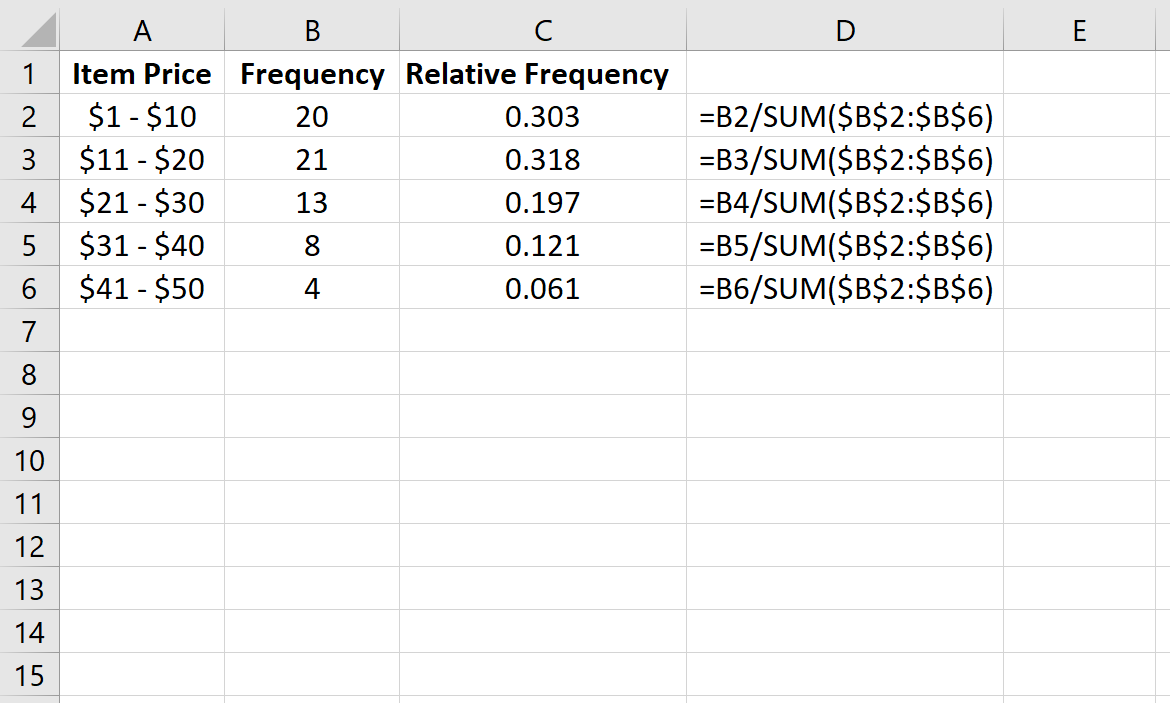
Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:
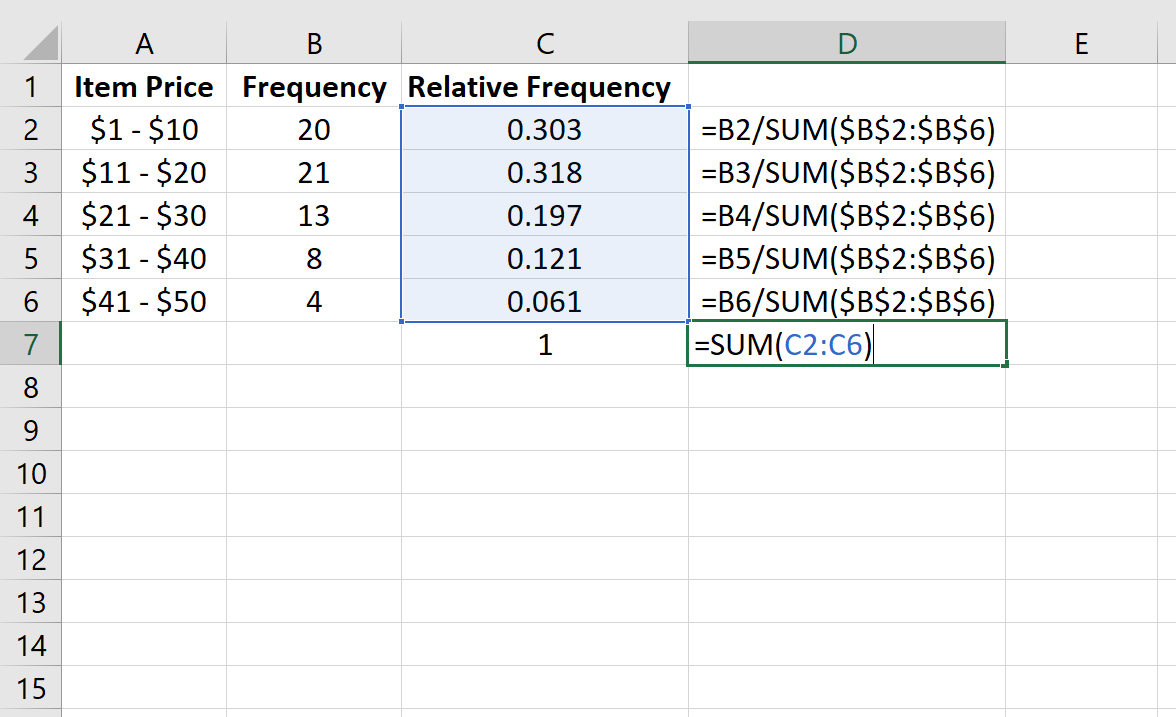
Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
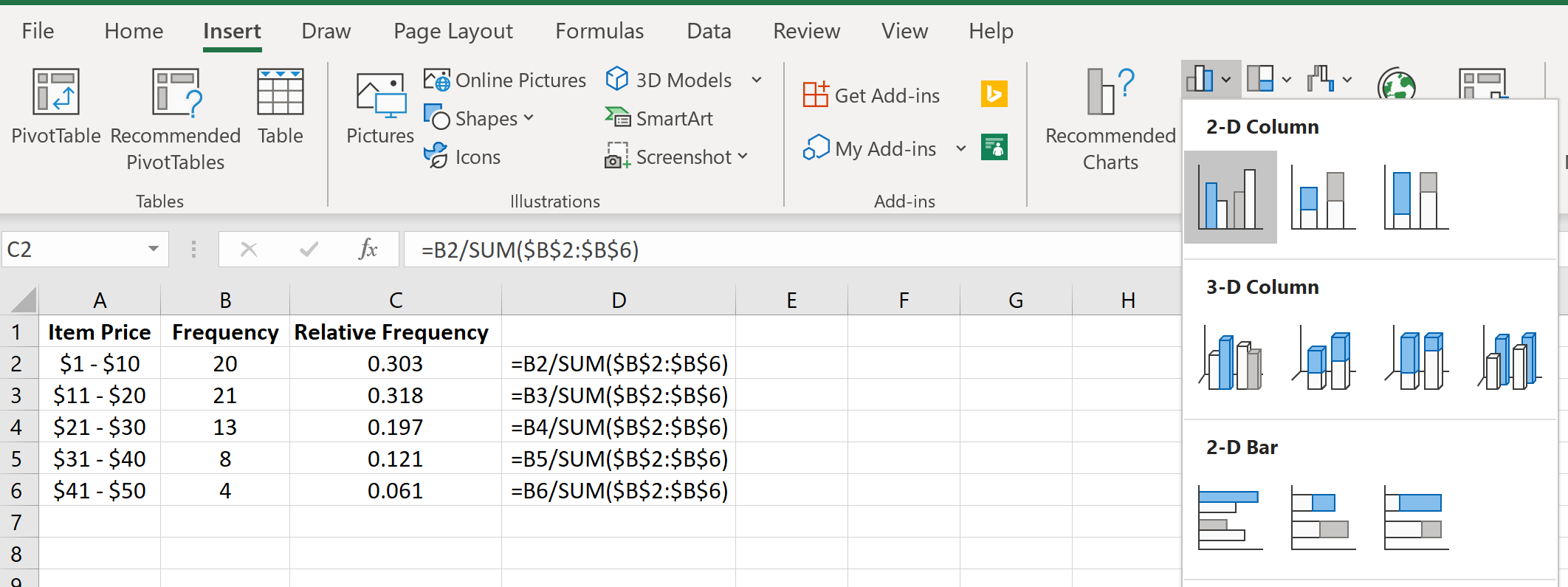
Автоматически появится гистограмма относительной частоты:
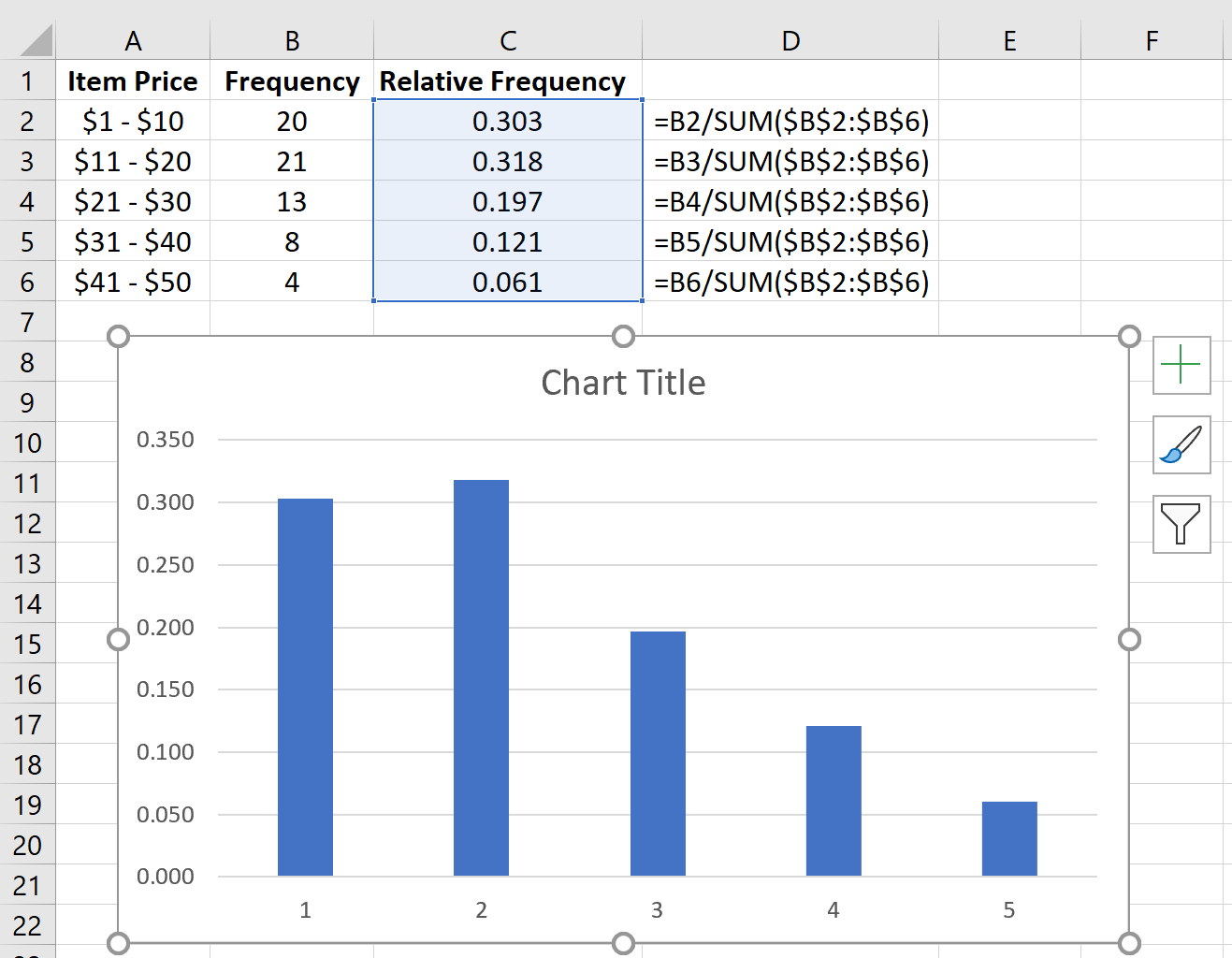
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
Дополнительные ресурсы
Калькулятор относительной частоты
Гистограмма относительной частоты: определение + пример
Содержание
- Как рассчитать относительную частоту в Excel
- Пример: относительные частоты в Excel
- Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
- Синтаксис функции
- Пример
- Функция ЧАСТОТА
- Пример
- Дополнительные сведения
- Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
- Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
- Пример использования функции ЧАСТОТА в Excel
- Пример определения вероятности используя функцию ЧАСТОТА в Excel
- Как посчитать неповторяющиеся значения в Excel?
- Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Как рассчитать относительную частоту в Excel
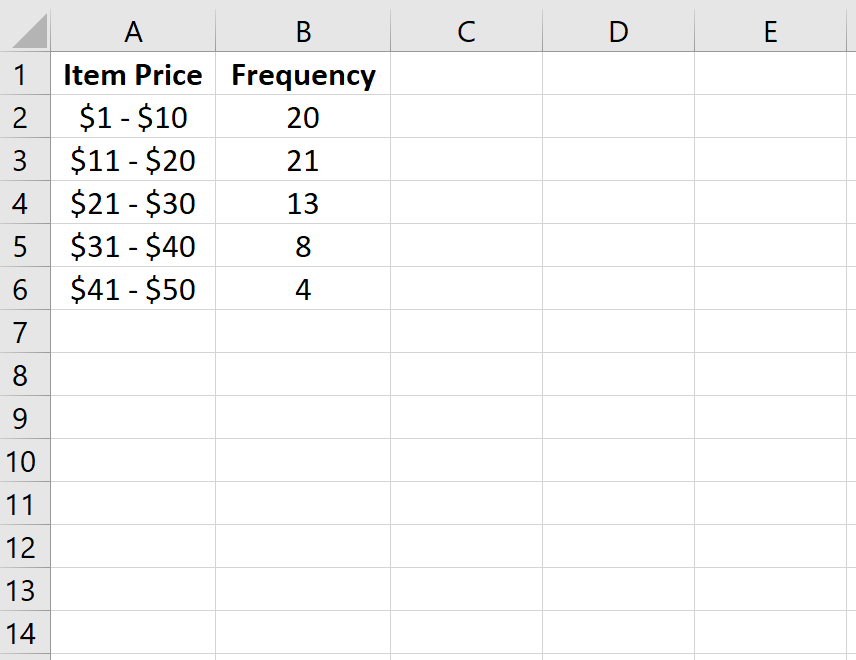
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:

Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:

Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:

Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :

Автоматически появится гистограмма относительной частоты:

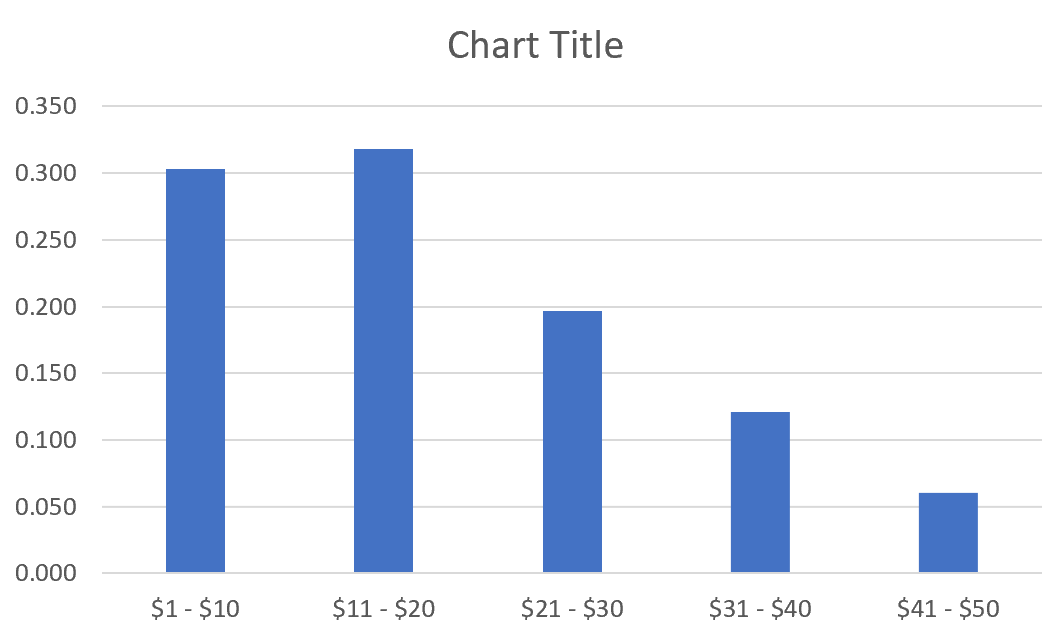
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
Источник
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
history 9 апреля 2013 г.
Функция ЧАСТОТА( ) , английская версия FREQUENCY() , вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА ( массив_данных ; массив_интервалов )
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER .
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве « массив_интервалов ». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
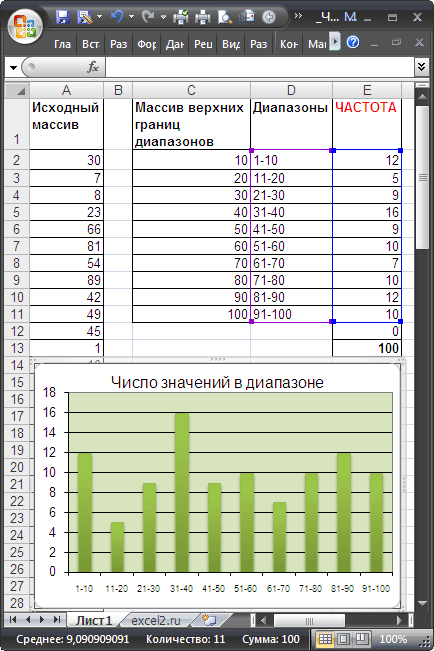
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12 , состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER . Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101 , которые меньше или равны 10;
- в Е3 — количество значений из А2:А101 , которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101 , которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101 , которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание . Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )
Источник
Функция ЧАСТОТА
Функция ЧАСТОТА вычисляет частоту ветвей значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
Аргументы функции ЧАСТОТА описаны ниже.
data_array — обязательный аргумент. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
bins_array — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Пример
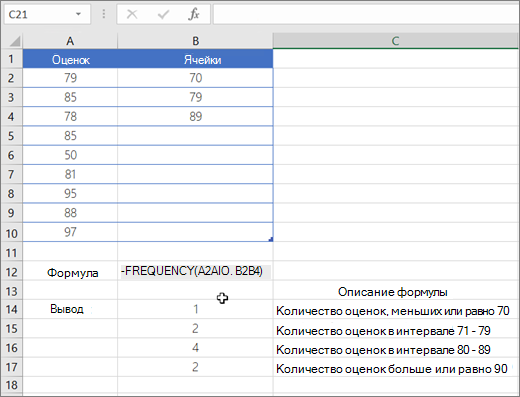
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Источник
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
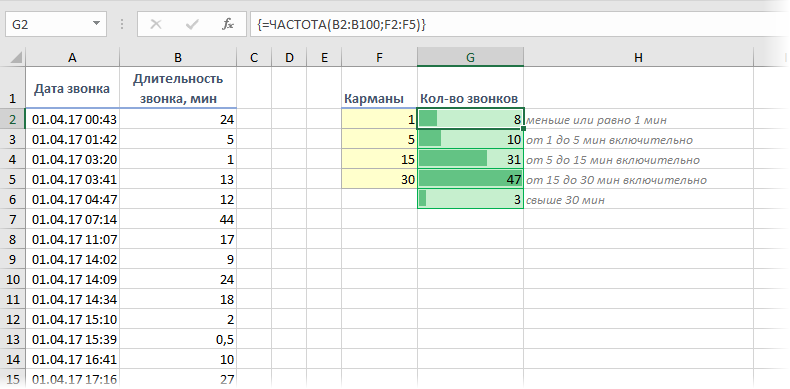
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Источник
Примеры функции ЧАСТОТА в Excel для расчета частоты повторений
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
- От 0 до 50 баллов – экзамен не сдан.
- От 51 до 65 баллов – оценка 3.
- От 66 до 85 баллов – оценка 4.
- Свыше 86 баллов – оценка 5.
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
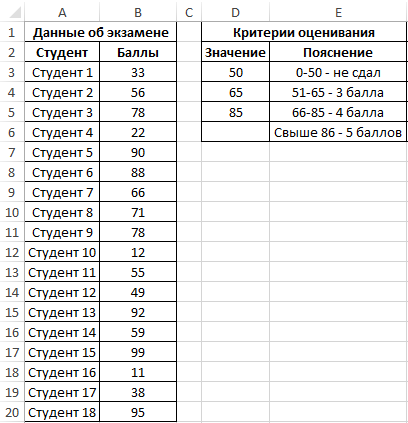
Для решения выделим области из 4 ячеек и введем следующую функцию:
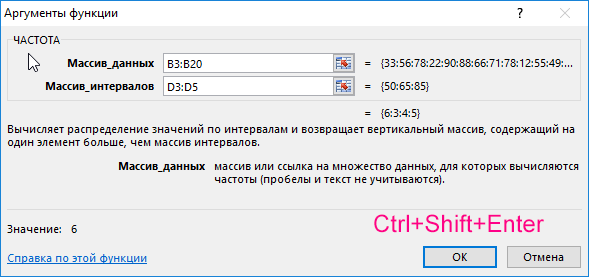
- B3:B20 – массив данных об оценках студентов;
- D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки <> в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
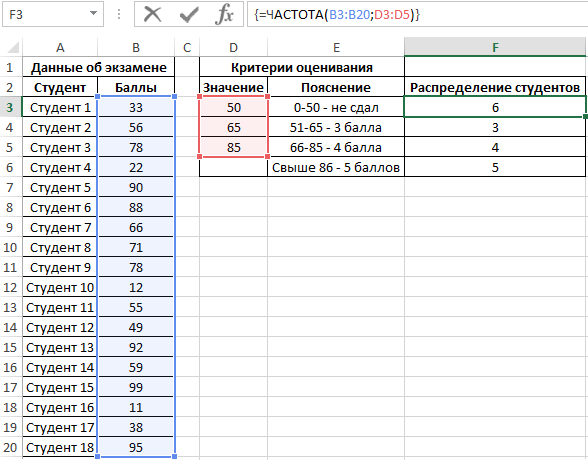
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
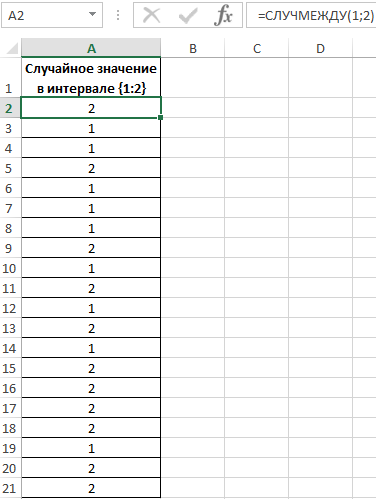
Для определения случайных значений в исходной таблице была использована специальная функция:
Для определения количества сгенерированных 1 и 2 используем функцию:
- A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
- 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).
В результате получим:
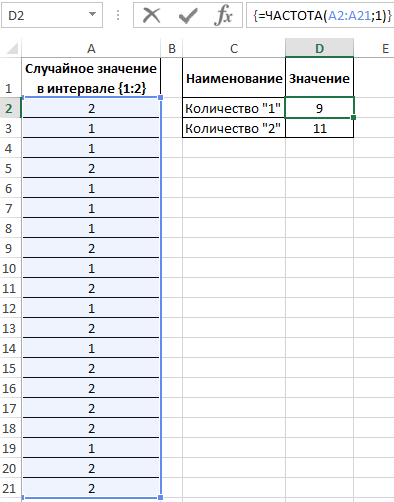
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
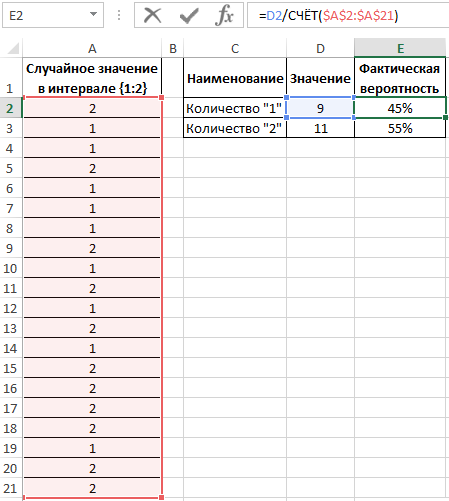
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» — 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
1)*СТРОКА($A$2:$A$21)))-1′ > 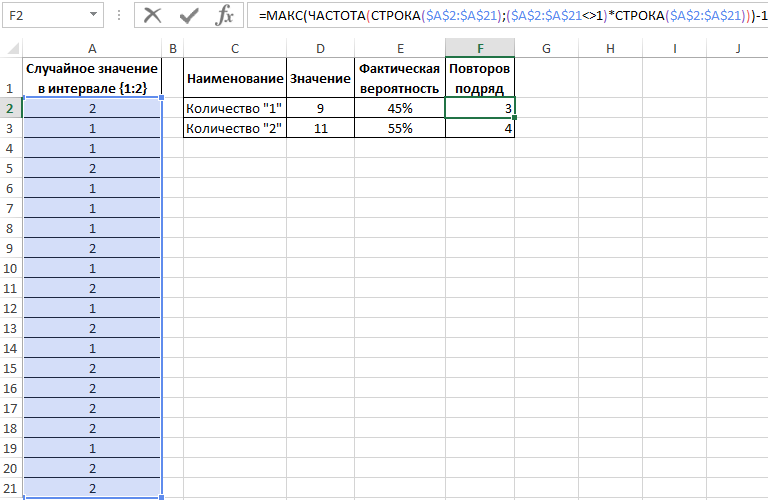
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
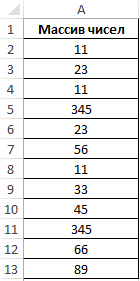
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
- Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
- Если искомого элемента нет – будет возвращен 0 (нуль).
Полученное значение (количество единиц) суммируется.
В результате получим:
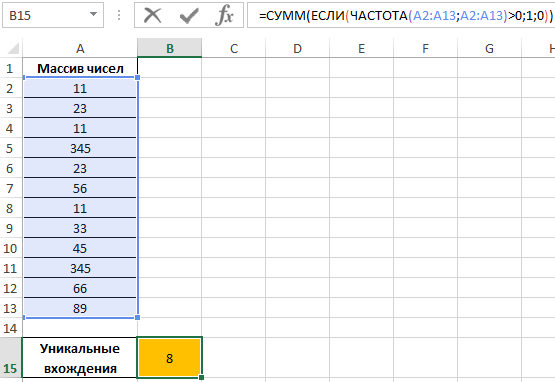
То есть, в указанном массиве содержится 8 уникальных значений.
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
- массив_интервалов — данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.
- Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
- При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
- Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА(<2;7;10;13;18;4;33;26>;<10;20;30>), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
- Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.
Источник
Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
- От 0 до 50 баллов – экзамен не сдан.
- От 51 до 65 баллов – оценка 3.
- От 66 до 85 баллов – оценка 4.
- Свыше 86 баллов – оценка 5.
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:

Для решения выделим области из 4 ячеек и введем следующую функцию:

Описание аргументов:
- B3:B20 – массив данных об оценках студентов;
- D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки {} в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:

То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:

Для определения случайных значений в исходной таблице была использована специальная функция:
=СЛУЧМЕЖДУ(1;2)
Для определения количества сгенерированных 1 и 2 используем функцию:
=ЧАСТОТА(A2:A21;1)
Описание аргументов:
- A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
- 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).
В результате получим:

Вычислим вероятности, разделив количество событий каждого типа на общее их число:

Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» – 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:

Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
Исходная таблица:

Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
- Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
- Если искомого элемента нет – будет возвращен 0 (нуль).
Полученное значение (количество единиц) суммируется.
В результате получим:

То есть, в указанном массиве содержится 8 уникальных значений.
Скачать пример функции ЧАСТОТА в Excel
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
- массив_интервалов – данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.
Примечания 1:
- Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
- При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
- Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА({2;7;10;13;18;4;33;26};{10;20;30}), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
- Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.
Примечания 2:
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.
- Данная функция должна быть использована как формула массива, поскольку возвращаемые ей данные имеют форму массива. Для выполнения обычных формул после их ввода необходимо нажать кнопку Enter. В данном случае требуется использовать комбинацию клавиш Ctrl+Shift+Enter.
=ЧАСТОТА(массив_данных;массив_интервалов)
Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неизвестных параметров. В частности, невозможно
рассчитать точное значение соответствующих вероятностей, так как нельзя
определить количество общих и благоприятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в которых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.
Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой события
и его вероятностью.
Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов).
Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
числа на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.
По
найденным относительным частотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.
Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того интервала
включительно, для которого определяется накопленная частота.
В Excel для построения выборочных функций распределения
используются специальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.
Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интервалах
значений и выводит их как массив цифр, где
•
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;
•
двоичный_массив
— это массив интервалов, по
которым группируются значения выборки.
Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:
•
Входной диапазон – диапазон исследуемых данных
(выборка);
•
Интервал карманов – диапазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в возрастающем порядке. Если
диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и
максимальным значениями данных, будет создан
автоматически.
•
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.
•
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму графика интегральных
процентов.
•
переключатель
Вывод графика позволяет установить режим автоматического создания встроенной диаграммы на листе, содержащем
выходной диапазон.
Пример 1. Построить эмпирическое распределение веса
студентов в килограммах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.
Решение
1. В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).
2.
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения интервалов (40, 45,
50, 55, 60, 65, 70).
3.
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные частоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накопленные частоты.(см. рис. 1).
4.
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
панели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появившемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться массив абсолютных частот (см. рис.1).
5.
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Автосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.
6.
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.
7.
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение относительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.

Рис. 1. Результат вычислений из
примера 1
8.
Постройте диаграмму относительных и накопленных частот. Щелчком указателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаграммы График/гистограмма. После
редактирования диаграмма будет иметь такой вид, как на рис. 2.

Рис. 2
Диаграмма относительных и накопленных частот из примера 1
Задания для самостоятельной работы
1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.
2. Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.
3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).
4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.
Обозначим
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).
Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания
|
№ п/п |
Варианты ответов |
Х |
|
1 |
Абсолютно неуспешно |
0,1 |
|
2 |
Неуспешно |
0,2 |
|
3 |
Успешно в очень |
0,3 |
|
4 |
В определенной |
0,4 |
|
5 |
В среднем успешно, |
0,5 |
|
6 |
Успешно с |
0,6 |
|
7 |
Успешно, но |
0,7 |
|
8 |
Достаточно успешно |
0,8 |
|
9 |
Очень успешно |
0,9 |
|
10 |
Абсолютно успешно |
1 |
При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.
Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).
Таблица 2.
Результаты опроса ста учителей

Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=

где
W(x) – относительная частота наступления события;

– стандартное
отклонение;

=3,14.
Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.
Решение математических задач
средствами Excel: Практикум/ В.Я. Гельман. – СПб.: Питер, 2003 – с. 168-172
2.1.2. Эмпирическая функция распределения
Это статистический аналог функции распределения из теорвера. Данная функция определяется, как отношение:
, где – количество вариант СТРОГО МЕНЬШИХ, чем ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Построим эмпирическую функцию распределения для нашей задачи. Чтобы было нагляднее, отложу варианты и их количество на числовой оси: 
На интервале – по той причине, что левее ЛЮБОЙ точки этого интервала вариант нет. Кроме того, функция равна нулю ещё и в точке . Почему? Потому, что значение определяет количество вариант (см. определение), которые СТРОГО меньше двух, а это количество равно нулю.
На промежутке – и опять обратите внимание, что значение не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению).
На промежутке – и далее процесс продолжается по принципу накопления частот:
– если , то ;
– если , то ;
– и, наконец, если , то – и в самом деле, для ЛЮБОГО «икс» из интервала ВСЕ частоты расположены СТРОГО левее этого значения «икс» (см. чертёж выше).
Накопленные относительные частоты удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева частоту (красная стрелка), и каждое следующее значение получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения): 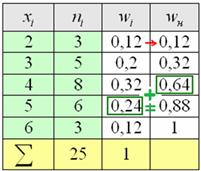
Вот ещё, кстати, один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Построенную функцию принято записывать в кусочном виде:
а её график представляет собой ступенчатую фигуру: 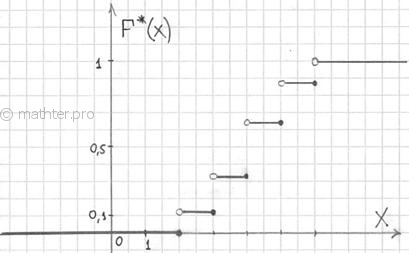
Эмпирическая функция распределения не убывает и принимает значения лишь из промежутка , и если у вас вдруг получится что-то не так, то ищите ошибку.
Теперь смотрим видео, о том, как построить эту функцию в Экселе (Ютуб).
И, конечно, вспомним основной метод математической статистики. Эмпирическая функция распределения строится по выборке и приближает теоретическую функцию распределения . Легко догадаться, что последняя появляется в результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была репрезентативна, дабы приближение было хорошим.
Миниатюрное задание для закрепления материала:
Пример 5
Дано статистическое распределение совокупности: 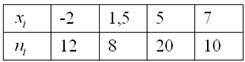
Составить эмпирическую функцию распределения, выполнить чертёж
Решаем самостоятельно – все числа уже в Экселе! Свериться с образцом можно в конце книги. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки 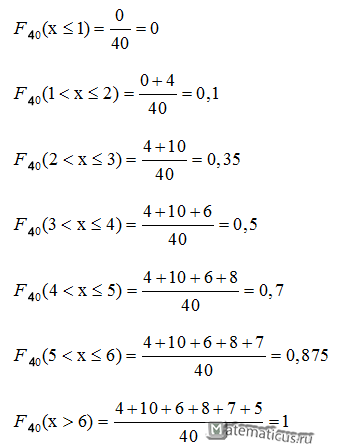
Эмпирическая функция распределения имеет вид

Построим график кусочно-постоянной эмпирической функции распределения
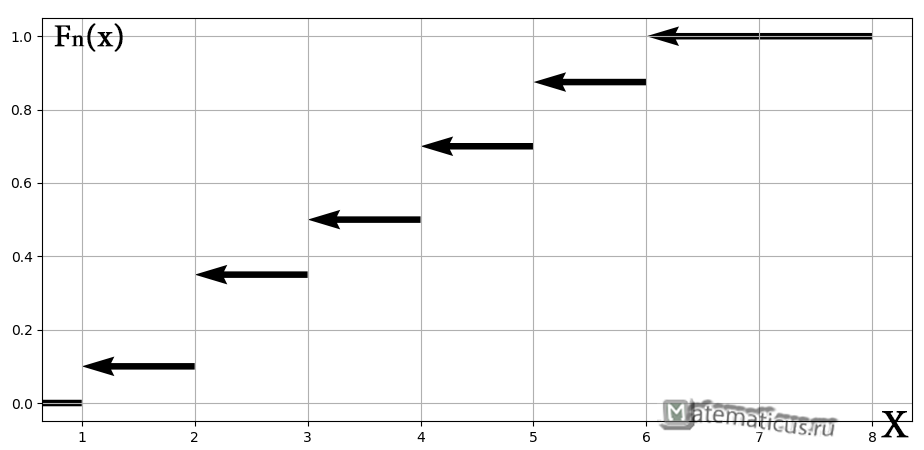
таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.
2 комментария
У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.
Построить эмпирическое распределение результатов тестирования в баллах для следующей выборки: 69, 85, 78, 85, 83, 81, 95, 88, 97, 92, 74, 83, 89, 77, 93.
В ячейку А1 введите слова Результаты, в диапазон А2:А16 – результаты тестирования.
Выберите ширину интервала 5 баллов. Тогда при крайних результатах 69 и 97 баллов, получится 7 интервалов. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.
Введите заголовки создаваемой таблицы: в ячейку D1 – Абсолютные частоты, в ячейку Е1 – Относительные частоты, в F1 – Накопленные частоты.
Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек D2:D8, вызовите Мастер функций, категория – Статистические, функция – Частота, в поле Массив данных введите диапазон данных тестирования А2:А16, в поле Массив интервалов введите диапазон интервалов С2:С8, нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D8 появится массив абсолютных частот.
В ячейке D9 найдите общее количество результатов тестирования, с помощью Автосумма.
Заполните столбец относительных частот. В ячейку Е2 введите формулу =$D2/$D$9 .
Протягиванием скопируйте полученное значение в диапазон Е3:Е8. Получим массив относительных частот.
Заполните столбец накопленных частот. В ячейку F2 скопируйте значение относительной частоты из ячейки Е2. В ячейку F3 введите формулу =F2+E3. Протягиванием скопируйте полученное значение в диапазон F4:F8. Получим массив накопленных частот.
В результате получим таблицу, представленную на рисунке 1.
Пусть Nх — число наблюдений, при которых значение признака Х меньше Х. При объеме выборки, равном П, относительная частота события Х XK.
Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.
Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х 6. Напишем формулу искомой эмпирической функции:
4. Рассмотрим любой из критериев оценки качеств педагога-профессионала, например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку такого измерения, необходимо увеличить число возможных ответов на конкретный критериальный вопрос. В табл. 1 представлены возможные варианты ответов.
Обозначим этот параметр через х. Тогда в процессе ответа на вопрос величина х примет дискретное значение х, принадлежащее определенному интервалу значений. Поставим в соответствие каждому из ответов определенное числовое значение параметра х (см. табл. 1).

