Теория вероятностей – это раздел математики, который
изучает закономерности случайных событий.
События
можно считать случайными – это те, которые могут произойти, а могут и не
произойти.
Примерами
таких событий являются: выпадение орла или решки при подбрасывании монеты;
поражение мишени или промах при стрельбе; выпадение того или иного количества
очков при бросании игрального кубика.
Пример.
Провели
испытания. 100 раз бросали игральный кубик и подсчитали, что 6 очков выпало 17
раз – частота рассматриваемого события, то есть выпадения очков.
Отношение
частоты к общему числу испытаний называют относительной частотой этого
события.
Пусть
некоторое испытание проводилось многократно в одних и тех же условиях. При этом
фиксировалось, произошло или нет некоторое интересующее нас событие А.
Если
общее число испытаний – n,
а число испытаний, при которых произошло событие А, – m. То m называют
частотой события А, частное m и n –
относительной
частотой.
Определение:
Относительной
частотой случайного события в серии испытаний называется
отношение числа испытаний, в которых это событие наступило, к числу всех
испытаний.
В
ходе исследований выяснилось, что относительная частота появления ожидаемого
события при повторении опытов в одних и тех же условиях, может оставаться
примерно одинаковой, незначительно отличаясь от некоторого числа р.
Пример.
При
подбрасывании монеты отмечают те случаи, когда выпадает орёл.
Если
монета однородна и имеет правильную геометрическую форму, то шансы выпадения
орла или решки будут примерно одинаковы. Но при
небольшом количестве бросков такой результат может не получиться.
А
вот если испытание проводиться большое количество раз, то относительная частота
выпадения орла близка к относительной частоте выпадения решки.
Многие
учёные проводили такой эксперимент.
Так,
например, английский математик Карл Пирсон бросал монету 24 тысячи раз, и
относительная частота выпадения орла оказалось равной 0,5005.
А
наш соотечественник, Всеволод Иванович Романовский, подбрасывая монету 80 тысяч
640 раз, нашёл, что относительная частота выпадения орла в его испытании была
равна 0,4923.
Заметим,
что в обоих случаях относительная частота выпадения орла очень близка к .
Говорят,
что вероятность выпадения орла при подбрасывании монеты правильной
геометрической формы равна .
Пример.
В
непрозрачном мешке лежит 7 зелёных и 12 синих кубиков. За раз можно доставать
только 1 из них. Какова вероятность того, что из мешка достанут синий кубик?
Всего
в мешке 19 кубиков. Значит, n=19.
Синий
кубик мы можем достать 12 раз. Получаем, что m=12.
Относительная
частота равна:
Вероятность
того, что из мешка достанут синий кубик, равна .
Пример.
Определить
относительную частоту появления буквы «о» в слове «достопримечательность».
Общее
число букв, то есть n=21.
А количество букв «о», то есть m=3.
Значит
относительная частота:
Пример.
Отмечая
число попаданий в корзину в каждой серии из 40 бросков, которые совершал
баскетболист, получили такие данные:
Какова
относительная вероятность попадания мяча в корзину для данного баскетболиста?
Определим
общее число бросков. Было 5 серий по 40 бросков, то есть n=200.
Сосчитаем
число попаданий в корзину:
Получили,
что m=184.
Относительная
вероятность попадания в корзину будет:
Пример.
Стрелок
совершил 50 выстрелов. Относительная частота попадания в цель оказалась равной
0,88. Сколько раз он промахнулся?
Зная
общее число выстрелов n=50
и относительную вероятность попадания p=0,88.
Найдем число попаданий в цель:
Стрелок
попал в цель 44 раза.
Найдём
число промахов
Стрелок
промахнулся 6 раз.
Относительная частота появления в тексте букв русского алфавита
|
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
|
а |
0,075 |
К |
0,034 |
Ф |
0,002 |
|
б |
0,017 |
л |
0,042 |
X |
0,011 |
|
в |
0,046 |
м |
0,031 |
ц |
0,005 |
|
г |
0,016 |
и |
0,065 |
ч |
0,015 |
|
д |
0,030 |
о |
0,110 |
ш |
0,007 |
|
е, ё |
0,087 |
II |
0,028 |
щ |
0,004 |
|
ж |
0,009 |
р |
0,048 |
ь, ъ |
0,017 |
|
3 |
0,018 |
с |
0,055 |
ы |
0,019 |
|
и |
0,075 |
т |
0,065 |
э |
0,003 |
|
и |
0,012 |
у |
0,025 |
ю |
0,022 |
|
я |
0,022 |
Из таблицы следует,
что на каждую тысячу букв в среднем
приходится 75 букв а, 17 букв б, 46 букв в и
т. д.
Получив шифрованное
письмо, вам придется лишь подсчитать
частоты появления в нем различных
секретных значков и сопоставить их с
теми частотами, что в таблице. Так, если
на тысячу восемьсот букв письма окажется
135 «треугольников», то это означает, что
данный значок
![]()
А вот еще один
эксперимент – специально для любителей
«счастливых» билетов. (Как известно,
«счастливым» считается такой трамвайный,
автобусный, троллейбусный билет, у
которого сумма первых трех цифр равна
сумме трех последних). В теории вероятностей
существует формула, в соответствии с
которой на каждые 100 билетов в среднем
5–6 должны оказаться «счастливыми». И
если не полениться собрать необходимую
пачку в сто билетов, то можно легко в
этом убедиться.
«Обязательность»
случая была давно подмечена предприимчивыми
людьми.
В чем смысл игры
для хозяина рулетки? Главный «секрет
производства» здесь в том, что выпадение
цифры 0 – ее называют «зеро» – всегда
в пользу хозяина, независимо от того,
на «красное» или «черное» поставил
игрок свои деньги. За счет этой единственной
цифры и существует хозяин рулетки. И не
только он. Целое государство Монако
живет за счет доходов знаменитого
игорного дома в Монте-Карло, где идет
крупная игра в рулетку. Трудно придумать
более яркий пример использования
закономерностей случайных явлений:
выход «зеро» определенное число раз
столь же обязателен, как, скажем, падение
подброшенного камня на землю, хотя
каждая отдельная цифра появляется
случайно и никакими силами заранее
угадана быть не может.
И все же Смок
Беллью, герой повести Джека Лондона,
если вы помните, научился почти безошибочно
предугадывать, где остановится шарик.
Как ему это удавалось делать?
Джек Лондон
раскрывает секрет своего любимого
героя. Наблюдая за игрой, Смок подметил,
что колесо останавливалось не как попало
– этого, казалось бы, следовало ожидать,
– а по определенным правилам. «Случайно
я дважды отметил, где остановился шарик,
когда вначале против него был номер
девять. Оба раза выиграл двадцать
шестой». Столь странное поведение колеса
объяснялось тем, что рулетка стояла
недалеко от печки: ее деревянное колесо
рассохлось и покоробилось. Смоку удалось
уловить скрытую от других закономерность
поведения колеса.
Стоит
ли, однако, утверждать, что можно выявить
систему у любых – всех проявлений
случая? Попробуйте, например, установить
общие закономерности изменения моды,
формы одежды,
которая, безусловно, относится к случайным
явлениям. На рис. 8.1 показаны колебания
мод женской одежды почти за 50 лет XX
века. Срок вполне достаточный, чтобы
найти хоть какие-нибудь основательные
регулярности. Однако их нет. Все – и
форма шляпок, и силуэт платья – меняются
«как попало». Остается незыблемым лишь
общий принцип: «новое – это прочно
забытое старое». Предпринимавшиеся
попытки связать капризы моды с мировыми
катаклизмами – войнами, экономическими
кризисами, даже с солнечной активностью
– ни к чему не привели.
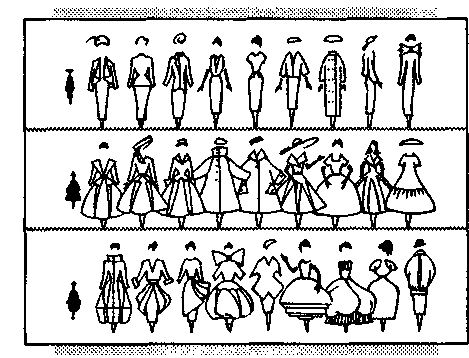
Рис.
8.1. Динамика
дамской моды
Возможность
установления определенного порядка,
закономерностей в случайных явлениях,
как правило, связана с наличием в них
так называемой «устойчивой частоты»:
появление интересующего нас события,
например рождение младенца мужского
пола, при многократном повторении
происходит в одинаковой доле от общего
числа рождений.
Поисками
закономерностей в случайных явлениях
занимается специальная, хорошо
разработанная в наши дни наука –
статистика. Именно статистика после
многих наблюдений над случаем делает
заключение о том, устойчива ли частота
его появления. Когда такую устойчивость
удается обнаружить, статистики говорят
о наличии статистического ансамбля.
Изучением
закономерностей в случайных явлениях
занимается теория
вероятностей.
Познакомимся с основами этой науки.
Как и многие другие
понятия, слово «вероятность» с его
производным «вероятно» входит в нашу
жизнь с детства. Мы говорим: вероятно,
вечером будет дождь; я, вероятно,
простудился и т. п.
« Вероятно» в этих
привычных фразах означает «возможно»
– этим словом субъективно оценивается
возможность наступления интересующего
нас случайного события в будущем. Если
же появляется необходимость показать
степень этой возможности, мы уточняем:
«весьма вероятно», «маловероятно»,
«совершенно невероятно». Более четкие
градации, чем «много» и «мало», в обиходном
языке не предусмотрены. Между тем
жизненные задачи требуют оценки
вероятности более конкретной, чем
«много» или «мало». Сегодня на морском
транспорте сказать: вероятно, будет
(или не будет) происшествие – это значит
не сказать почти ничего. Степень
возможности появления будущего случайного
события – вероятность – должна быть
оценена объективно точно, определенным
числом.
Самый старый, так
называемый классический способ измерения
вероятности – по частоте наступления
интересующего нас события. Это можно
сделать весьма просто: прийти в тир,
выстрелить все 100 раз и сосчитать число
попаданий в мишень. Доля, которую это
число составит от общего числа выстрелов,
и есть частота попаданий. Скажем, попали
70 раз – частота равна 0,7, или семидесяти
процентам. Вот эта самая частота и
принимается за вероятность.
Но что
значит «принимается»? Почему не сказать
просто: вероятность – это и есть частота
интересующего нас события? По той же
самой причине, по которой мы различаем
вчерашнюю сводку погоды и прогноз на
завтра. Частота
-это
результат события, которое уже произошло,
вероятность
–
предсказание того, что должно случиться
в будущем. Сказать: «Вероятность попадания
70 процентов» – значит предположить,
что при очередной стрельбе 70 пуль из
ста попадут в мишень. Это предположение
мы делаем в уверенности, что соотношение
шансов попасть – не попасть, которое
определилось во время уже состоявшейся
стрельбы, сохранится и на будущее. При
этом, разумеется, предполагается, что
условия стрельбы: оружие, расстояние
до мишени, размеры мишени и т. д. –
останутся неизменными.
Применительно к
бизнесу это означает, что если при
определенных условиях в прошлом мы
получали, на каждые 100 рублей 30 рублей
прибыли, то при повторении ситуации в
будущем сохранится и прибыль.
Откуда, однако, у
нас берется уверенность, что «дальше
будет, как раньше»? К этому нас подводит
весь многовековой коллективный опыт
человечества. Когда народ говорит,
например, «У семи нянек дитя без глаза»,
«Тише едешь – дальше будешь» или
утверждается, что «бутерброд падает
маслом вниз», – это не только о прошлом,
но и о будущем.
Если
в течение многих лет люди наблюдают,
как из 100 куриных яиц появляется примерно
поровну петушков и курочек, то нет
основания не верить, что и на следующий
год шансы появления петушка останутся
прежними. В слове «вероятно» явственно
прослушивается «надеюсь». Это дало
основание магистру философии Вильнюсского
университета Сигизмунду Ревковскому
– первому, кто в 1829– 1830 годах стал
преподавать в России (тогдашней) теорию
вероятностей, – определить вероятность
как «меру надежды».
Итак, для того
чтобы рассчитать вероятность во многих
распространенных жизненных задачах,
достаточно произвести весьма элементарное
арифметическое вычисление – разделить
число случаев, благоприятствующих
интересующему нас событию, на общее
число всех возможных случаев.
![]()
Важно
отметить, что чем больше опытов проведено
при определении частоты, тем точнее,
объективнее получается вероятность.
Это проявление одного из важнейших
законов, управляющих случаем, – так
называемого закона
больших чисел.
Классический
способ определения вероятностей и его
формула и сегодня находят широкое
применение. Если нам, скажем, известно,
что среди тридцати экзаменационных
билетов три очень трудных, то можно
быстро прикинуть вероятность вытащить
трудный билет, как
![]() = 0,1, или 10 процентов. И если бы можно было
= 0,1, или 10 процентов. И если бы можно было
таким простым способом рассчитывать
вероятности во всех случаях, то учебники
по теории вероятностей (а заодно и данная
глава) были бы много тоньше. К большому
сожалению, столь просто рассчитывать
вероятность удается далеко не всегда.
Представьте себе,
что вы получили перед какой-либо
жеребьевкой весьма обнадеживающую
информацию: организатор кладет плохие
билеты не как попало, а снизу, видно
стараясь, чтобы они оказались подальше
от испытуемых. Это, конечно, хорошо:
стоит теперь вытянуть билет сверху –
и вероятность заполучить выгодный номер
резко увеличится. Но вот какой она
станет? Узнать это с помощью классической
формулы невозможно. Формула применима
лишь тогда, когда все рассматриваемые
случаи равновозможны – любой билет
должен иметь одинаковые шансы попасть
в руки испытуемого. Стоит исключить эту
равновозможность, и классическая формула
перестает работать. Следовательно,
правильно эту формулу записать так:
![]()
Откуда
же мы знаем, равновозможны случаи или
нет? На этот вопрос отвечает опыт.
Причем
опыт, который не обязательно ставить.
Бывает, вполне достаточно провести его
мысленно. Допустим, вы собрались сыграть
с товарищем в шахматы. Кому играть
белыми, должен решить жребий. Ваш партнер
в одной руке зажимает белую фигуру, в
другой – черную. Какова вероятность,
что вы будете играть белыми? Каждый из
нас, не задумываясь, назовет 50 процентов.
Но почему? Это результат мысленного
опыта: мы инстинктивно оцениваем шансы
отгадать любую фигурку как равновероятные,
и поскольку белых фигур ровно половина,
то это и будет интересующая нас
вероятность.
Вот еще один пример.
Многим читателям, видимо, доводилось
слышать о такой дикой игре армейского
захолустья царской России. В барабан
многозарядного револьвера закладывается
лишь один патрон, после чего барабан
несколько раз проворачивается. Затем
участники игры по очереди приставляют
револьвер к виску и нажимают на спуск.
Так вот, для того чтобы сказать, чему
равна при этом вероятность проигрыша,
явно нет необходимости ставить
эксперимент. Так же как и при отгадывании
шахматной фигуры, равновозможность
шансов здесь очевидна из соображения
о симметрии возможных исходов. И
вероятность проигрыша – получения пули
– для того, кто стреляет первым, в расчете
на 5 патронов равна:
![]()
Вполне можно
ограничиться мысленным экспериментом
и там, где равновозможность шансов
очевидна из геометрического представления
задачи. Скажем, в офисе проложен телефонный
кабель длиной 60 метров, из которых 3
метра приходится на труднодоступное
место. Спрашивается, какова вероятность
в случае выхода кабеля из строя, что
повреждение случится именно на
труднодоступном участке?
![]()
Такую
вероятность иногда называют геометрической
– ведь
она получена путем сопоставления длин
двух отрезков. И соображение о
равновозможности шансов (уверенность
в том, что появление неисправности
возможно в любом месте кабеля) в этом
случае исходит из наглядных, геометрических
представлений.
Интуитивное
определение
вероятности, выработанное человеком и
ходе многовековой эволюции, не раз
выручало его в сложных ситуациях.
Принимая решение «что лучше», «что
быстрее», «какова мера опасности», люди,
сами того не ведая, часто основывают
свой выбор на интуитивной вероятной
оценке. «Лучше поездом, чем самолетом»,
«Поеду-ка я трамваем, автобуса не
дождаться», «Сегодня стоит надеть плащ»
– во всех этих решениях явно просматривается
учет возможности случая.
С
интуитивным определением вероятности
тесно связан так называемый принцип
практической уверенности. Принцип
этот можно сформулировать так: «Если
вероятность события мала, то следует
считать, что в однократном опыте – в
данном конкретном случае – это событие
не произойдет. И наоборот – при большой
вероятности событие следует ожидать».
В повседневной
жизни мы широко, сами то не подозревая,
пользуемся этим важным принципом.
Скажем, собираясь лететь в отпуск
самолетом, мы уверены в том, что нас
доставят на места в целости и сохранности:
не пишем завещание, даем телеграмму с
просьбой встретить т. п. Тем самым мы
интуитивно принимаем, что вероятность
аварии самолета равна нулю – событие
невозможное, хотя эта вероятность всегда
имеет некоторое, правда весьма небольшое,
но все же отличное от нуля значение.
Вероятность же нашей доставки до места
соответственно но принимается равной
единице – событие это считается
достоверным.
Оценивая практическую
невозможность или достоверность события
и принимая на этой основе решение, мы,
однако, далеко не всегда связываем свой
выбор с предельными, крайним значениями
вероятности. Величина вероятности,
которая нас практически устраивает,
зависит от того, какова важность
последствий принятого нами решения.
Решение надеть плащ может быть принято
и в том случае, если вероятность дождя,
скажем, 70–80 %. Но вряд ли мы решимся
прыгнуть с парашютом, узнав, что у него
такая же (70–80 %) надежность.
Итак,
вероятность
–
это степень возможности появления
будущего случайного события Руководствуясь
этим определением, решим несколько
примеров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Частотный анализ текста онлайн
| Результат частотного анализа введенного текста |
Частотный анализ – это один из методов криптоанализа, основывающийся на предположении о существовании нетривиального статистического распределения отдельных символов и их последовательностей как в открытом тексте, так и шифрованном тексте, которое с точностью до замены символов будет сохраняться в процессе шифрования и дешифрования.
Кратко говоря, частотный анализ предполагает, что частота появления заданной буквы алфавита в достаточно длинных текстах одна и та же для разных текстов одного языка. При этом в случае моно алфавитного шифрования, если в шифрованном тексте будет символ с аналогичной вероятностью появления, то можно предположить, что он и является указанной зашифрованной буквой. Аналогичные рассуждения применяются к биграммам (двухбуквенным последовательностям), триграммам в случае поли алфавитных шифров.
Метод частотного анализа известен с еще IX-го века и связан и именем Ал-Кинди. Но наиболее известным случаем применения такого анализа является дешифровка египетских иероглифов Ж.-Ф. Шампольоном в 1822 году.
Данный вид анализа основывается на том, что текст состоит из слов, а слова из букв. Количество различных букв в каждом языке ограничено и буквы могут быть просто перечислены. Важными характеристиками текста являются повторяемость букв, пар букв (биграмм) и вообще m-ок (m-грамм), сочетаемость букв друг с другом, чередование гласных и согласных и некоторые другие.
Идея состоит в подсчете чисел вхождений каждой nm возможных m-грамм в достаточно длинных открытых текстах T=t1t2…tl, составленных из букв алфавита {a1, a2, …, an}. При этом просматриваются подряд идущие m-граммы текста:
t1t2…tm, t2t3… tm+1, …, ti-m+1tl-m+2…tl.
Если – число появлений m-граммы ai1ai2…aim в тексте T, а L – общее число подсчитанных m-грамм, то опыт показывает, что при достаточно больших L частоты
для данной m-граммы мало отличаются друг от друга.
В силу этого, относительную частоту считают приближением вероятности P (ai1ai2…aim) появления данной m-граммы в случайно выбранном месте текста (такой подход принят при статистическом определении вероятности).
В представленной ниже таблице приводятся частоты встречаемости букв в русском языке (в процентах):
| Буква алфавита | Показатель частоты встречаемости | Буква алфавита | Показатель частоты встречаемости |
|---|---|---|---|
| А | 0,062 | Р | 0,04 |
| В | 0,038 | Т | 0,053 |
| Д | 0,025 | Ф | 0,002 |
| Ж | 0,007 | Ц | 0,004 |
| И | 0,062 | Ш | 0,006 |
| К | 0,028 | Ъ, Ь | 0,014 |
| М | 0,026 | Э | 0,003 |
| О | 0,09 | Я | 0,018 |
Имеется мнемоническое правило запоминания десяти наиболее частых букв русского алфавита. Эти буквы составляют слово СЕНОВАЛИТР.
Устойчивыми являются также частотные характеристики биграмм, триграмм и четырехграмм осмысленных текстов. Существуют специальные таблицы с указанием частоты биграмм некоторых алфавитов. По результатам исследований с помощью таких таблиц ученые определили наиболее часто встречаемые биграммы и триграммы для русского алфавита:
СТ, НО, ЕН, ТО, НА, ОВ, НИ, РА, ВО, КО, СТО, ЕНО, НОВ, ТОВ, ОВО, ОВА.
Из таблиц биграмм можно также легко извлечь информацию о сочетаемости букв, т.е. о предпочтительных связях букв друг с другом.
Результатом таких исследований является таблица, в которой слева и справа от каждой буквы расположены наиболее предпочтительные «соседи» (в порядке убывания частоты соответствующих биграмм). В таких таблицах обычно указывается также доля гласных и согласных букв (в процентах), предшествующих (или следующих за) данной букве.
| Г | С | Слева | Справа | Г | С | |
|---|---|---|---|---|---|---|
| 3 | 97 | л, д, к, т, в, р, н | А | л, н, с, т, р, в, к, м | 12 | 88 |
| 80 | 20 | я, е, у, и, а, о | Б | о, ы, е, а, р, у | 81 | 19 |
| 68 | 32 | я, т, а, е, и, о | В | о, а, и, ы, с, н, л, р | 60 | 40 |
| 78 | 22 | р, у, а, и, е, о | Г | о, а, р, л, и, в | 69 | 31 |
| 72 | 28 | р, я, у, а, и, е, о | Д | е, а, и, о, н, у, р, в | 68 | 32 |
| 19 | 81 | м, и, л, д, т, р, н | Е | н, т, р, с, л, в, м, и | 12 | 88 |
| 83 | 17 | р, е, и, а, у, о | Ж | е, и, д, а, н | 71 | 29 |
| 89 | 11 | о, е, а, и | З | а, н, в, о, м, д | 51 | 49 |
| 27 | 73 | р, т, м, и, о, л, н | И | с, н, в, и, е, м, к, з | 25 | 75 |
| 55 | 45 | ь, в, е, о, а, и, с | К | о, а, и, р, у, т, л, е | 73 | 27 |
| 77 | 23 | г, в, ы, и, е, о, а | Л | и, е, о, а, ь, я, ю, у | 75 | 25 |
| 80 | 20 | я, ы, а, и, е, о | М | и, е, о, у, а, н, п, ы | 73 | 27 |
| 55 | 45 | д, ь, н, о | Н | о, а, и, е, ы, н, у | 80 | 20 |
| 11 | 89 | р, п, к, в, т, н | О | в, с, т, р, и, д, н, м | 15 | 85 |
| 65 | 35 | в, с, у, а, и, е, о | П | о, р, е, а, у, и, л | 68 | 32 |
| 55 | 45 | и, к, т, а, п, о, е | Р | а, е, о, и, у, я, ы, н | 80 | 20 |
| 69 | 31 | с, т, в, а, е, и, о | С | т, к, о, я, е, ь, с, н | 32 | 68 |
| 57 | 43 | ч, у, и, а, е, о, с | Т | о, а, е, и, ь, в, р, с | 63 | 37 |
| 15 | 85 | п, т, к, д, н, м, р | У | т, п, с, д, н, ю, ж | 16 | 84 |
| 70 | 30 | н, а, е, о, и | Ф | и, е, о, а, е, о, а | 81 | 19 |
| 90 | 10 | у, е, о, а, ы, и | Х | о, и, с, н, в, п, р | 43 | 57 |
| 69 | 31 | е, ю, н, а, и | Ц | и, е, а, ы | 93 | 7 |
| 82 | 18 | е, а, у, и, о | Ч | е, и, т, н | 66 | 34 |
| 67 | 33 | ь, у, ы, е, о, а, и, в | Ш | е, и, н, а, о, л | 68 | 32 |
| 84 | 16 | е, б, а, я, ю | Щ | е, и, а | 97 | 3 |
| 0 | 100 | м, р, т, с, б, в, н | Ы | л, х, е, м, и, в, с, н | 56 | 44 |
| 0 | 100 | н, с, т, л | Ь | н, к, в, п, с, е, о, и | 24 | 76 |
| 14 | 86 | с, ы, м, л, д, т,, р, н | Э | н, т, р, с, к | 0 | 100 |
| 58 | 42 | ь, о, а, и, л, у | Ю | д, т, щ, ц, н, п | 11 | 89 |
| 43 | 57 | о, н, р, л, а, и, с | Я | в, с, т, п, д, к, м, л | 16 | 84 |
Пример: Проведем анализ текста следующего содержания
“СОКРАТ из Афин (469–399 до н.э.) – знаменитый античный философ, учитель Платона, воплощенный идеал истинного мудреца в исторической памяти человечества. С именем Сократа связано первое фундаментальное деление истории античной философии на до- и после-Сократовскую («Досократики»), отражающее интерес ранних философов VI–V вв. к натурфилософии, а последующего поколения софистов V в. – к этико-политическим темам, главная из которых – воспитание добродетельного человека и гражданина. Сократу был близок софистическому движению. Учение Сократа было устным; все свободное время он проводил в беседах с приезжими софистами и местными гражданами, политиками и обывателями, друзьями и незнакомыми на темы, ставшими традиционными для софистической практики: что есть добро и что – зло, что прекрасно, а что безобразно, что добродетель и что порок, можно ли научиться быть хорошим и как приобретается знание. Об этих беседах мы знаем в основном благодаря ученикам Сократа – Ксенофонту и Платону. Кроме их сочинений, имеются также фрагменты и свидетельства о содержании «сократических диалогов» других сократиков, пародийное изображение Сократа в комедии Аристофана Облака и ряд замечаний о Сократе у Аристотеля. Проблема достоверности изображения личности Сократа в сохранившихся произведениях – ключевой вопрос всех исследований о нем.”
Пишем
в поле ввода этот текст и получаем ответ
Проведен анализ текста
Количество символов в тексте 1329
Количество пробелов 179
Количество цифр 6
Количество точек и запятых 25
Количество английских букв 4
Количество русских букв 1094
Посимвольная статистика и частотный анализ
Символ встречается 179 раз. Частота 13.47%
Символ о встречается 130 раз. Частота 9.78%
Символ и встречается 117 раз. Частота 8.80%
Символ а встречается 88 раз. Частота 6.62%
Символ е встречается 86 раз. Частота 6.47%
Символ с встречается 70 раз. Частота 5.27%
Символ н встречается 70 раз. Частота 5.27%
Символ т встречается 70 раз. Частота 5.27%
Символ р встречается 55 раз. Частота 4.14%
Символ к встречается 42 раз. Частота 3.16%
Символ л встречается 38 раз. Частота 2.86%
Символ в встречается 38 раз. Частота 2.86%
Символ м встречается 38 раз. Частота 2.86%
Символ д встречается 34 раз. Частота 2.56%
Символ ч встречается 24 раз. Частота 1.81%
Символ п встречается 21 раз. Частота 1.58%
Символ б встречается 20 раз. Частота 1.50%
Символ з встречается 17 раз. Частота 1.28%
Символ ф встречается 17 раз. Частота 1.28%
Символ я встречается 17 раз. Частота 1.28%
Символ у встречается 17 раз. Частота 1.28%
Символ ы встречается 15 раз. Частота 1.13%
Символ , встречается 14 раз. Частота 1.05%
Символ х встречается 13 раз. Частота 0.98%
Символ . встречается 11 раз. Частота 0.83%
Символ й встречается 11 раз. Частота 0.83%
Символ ж встречается 10 раз. Частота 0.75%
Символ г встречается 10 раз. Частота 0.75%
Символ ь встречается 9 раз. Частота 0.68%
Символ – встречается 8 раз. Частота 0.60%
Символ ю встречается 6 раз. Частота 0.45%
Символ v встречается 3 раз. Частота 0.23%
Символ – встречается 3 раз. Частота 0.23%
Символ 9 встречается 3 раз. Частота 0.23%
Символ щ встречается 3 раз. Частота 0.23%
Символ э встречается 3 раз. Частота 0.23%
Символ ш встречается 3 раз. Частота 0.23%
Символ » встречается 2 раз. Частота 0.15%
Символ ( встречается 2 раз. Частота 0.15%
Символ ц встречается 2 раз. Частота 0.15%
Символ « встречается 2 раз. Частота 0.15%
Символ ) встречается 2 раз. Частота 0.15%
Символ 3 встречается 1 раз. Частота 0.08%
Символ : встречается 1 раз. Частота 0.08%
Символ ; встречается 1 раз. Частота 0.08%
Символ i встречается 1 раз. Частота 0.08%
Символ 4 встречается 1 раз. Частота 0.08%
Символ 6 встречается 1 раз. Частота 0.08%
Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-

2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-

3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-

2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-

3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-

2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-

3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 144 719 раз.
Была ли эта статья полезной?
Неужели ты думаешь что какой то дурак будет ВРУЧНУЮ считать буквы?
Твое счастье Что задание в инете есть
***************************
По этим приметам немудрено будет вам отыскать Дубровского. Да кто
же не среднего роста, у кого не русые волосы, не прямой нос, да не карие
глаза! Бьюсь об заклад, три часа будешь говорить с самим Дубровским, а не
догадаешься, с кем бог тебя свел. Нечего сказать, умные головушки приказные!
Рассеянные жители столицы не имеют понятия о многих впечатлениях,
столь известных жителям деревень или городков, например об ожидании по-
чтового дня: во вторник и пятницу полковая наша канцелярия бывала полна
офицерами: кто ждал денег, кто письма, кто газет.
Вскоре все заговорили о Пугачеве. Толки были различны. Комендант послал
урядника с поручением разведать хорошенько обо всем по соседним селениям и
крепостям. Урядник возвратился через два дня и объявил, что в степи верст за
шестьдесят от крепости видел он множество огней и слышал от башкирцев,
что идет неведомая сила.
**************
Результат частотного анализа введенного текста
Проведен анализ текста
Количество символов в тексте 737
Количество пробелов 123
Количество цифр 0
Количество точек и запятых 7
Количество английских букв -120
Количество русских букв 589
Посимвольная статистика и частотный анализ
Символ пробел/space встречается 123 раз. Частота 16.69%
Символ о встречается 75 раз. Частота 10.18%
Символ е встречается 69 раз. Частота 9.36%
Символ и встречается 52 раз. Частота 7.06%
Символ а встречается 50 раз. Частота 6.78%
Символ н встречается 43 раз. Частота 5.83%
Символ т встречается 42 раз. Частота 5.70%
Символ с встречается 40 раз. Частота 5.43%
Символ р встречается 34 раз. Частота 4.61%
Символ в встречается 32 раз. Частота 4.34%
Символ д встречается 28 раз. Частота 3.80%
Символ к встречается 27 раз. Частота 3.66%
Символ м встречается 25 раз. Частота 3.39%
Символ п встречается 19 раз. Частота 2.58%
Символ г встречается 17 раз. Частота 2.31%
Символ у встречается 14 раз. Частота 1.90%
Символ б встречается 14 раз. Частота 1.90%
Символ ь встречается 13 раз. Частота 1.76%
Символ ы встречается 12 раз. Частота 1.63%
Символ . встречается 7 раз. Частота 0.95%
Символ э встречается 1 раз. Частота 0.14%
Символ встречается 0 раз. Частота 0.00%
****************
abakbot.ru/online-5/97-freq-letter
