Как найти относительную частоту появления шара - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.^[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
3

Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:^[2]

Реклама

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.^[3]
- В нашем примере набор данных содержит 16 чисел.
2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.^[4]
- Например, в нашем примере число встречается в наборе данных три раза.
3

Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.^[5]

Реклама

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.^[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама

Советы

Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.

Источники

Об этой статье

Эту страницу просматривали 144 126 раз.

Была ли эта статья полезной?

Источник

Относительная частота и статистическая вероятность. Основные формулы и решения типовых задач
Относительная частота (частость) события А определяется равенством

$W(A)=frac{m}{n},; ; ; ; (5)$

где n – общее число проведенных испытаний; m – число испытаний, в которых событие А наступило (иначе – частота события А).
При статистическом определении за вероятность события принимают его относительную частоту, найденную по результатам большого числа испытаний.
Задача №1. При определении всхожести партии семян взяли пробу из 1000 единиц. Из отобранных семян не взошло 90. Какова относительная частота появления всхожего семени?
Решение. Обозначим событие: А – отобрано всхожее семя. Найдем относительную частоту события А, применив формулу (5). Общее число проведенных испытаний n = 1000. Число испытаний, в которых событие А наступило, равно m = 1000 – 90 = 910.
Относительная частота события А равна $W(A)=frac{m}{n}=frac{910}{1000}=0,91.$

Задача №2. Для проведения исследований на некотором поле взяли случайную выборку из 200 колосьев пшеницы. Относительная частота (частость) колосьев, имеющих по 12 колосков в колосе, оказалась равной 0,123, а по 18 колосков – 0,05. Найти для этой выборки частоты колосьев, имущих по 12 и по 18 колосков.
Решение. Рассмотрим события: A – взят колос, имеющий 12 колосков; В – взят колос, имеющий 18 колосков.
Найдем частоты $m_{1}$ и $m_{2}$ событий А и В применив формулу (5).
Обозначим через $W_{1}(A)=frac{m_{1}}{n}$ относительную частоту события A, а через $W_{2}(B)=frac{m_{2}}{n}$ относительную частоту события В. Так как число проведенных испытаний n = 200, то $m_{1}=W_{1}(A)cdot n=0,125cdot 200=25,; m_{2}=W_{2}(B)cdot n=0,05cdot 200=10.$

Задача №3. Многолетними наблюдениями установлено, что в некоторой области ежегодно в среднем в тридцати хозяйствах из каждых ста среднегодовой удой молока от одной коровы составляет 4 100 – 4 300 кг. Какова вероятность того, что в текущем году в одном из хозяйств этой области, отобранном случайным образом, будет получен такой среднегодовой удой?
Решение. Обозначим событие: А – в текущем году в хозяйстве области, отобранном случайным образом, среднегодовой удой молока от одной коровы составит 4 100 – 4 300 кг.
Вероятность события А найдем, воспользовавшись ее статистическим определением.
Располагая статистическими данными, найдем, что относительная частота хозяйств области, в которых ежегодно имеют указанный средне-годовой удой молока от одной коровы, равна 0,3. Так как эти данные получены в результате проведения большого числа наблюдений, выполняемых в течение многих лет, то можно принять, что вероятность события А равна Р(А) = 0,3.

Источник

Теория вероятностей – это раздел математики, который
изучает закономерности случайных событий.

События
можно считать случайными – это те, которые могут произойти, а могут и не
произойти.

Примерами
таких событий являются: выпадение орла или решки при подбрасывании монеты;
поражение мишени или промах при стрельбе; выпадение того или иного количества
очков при бросании игрального кубика.

Пример.

Провели
испытания. 100 раз бросали игральный кубик и подсчитали, что 6 очков выпало 17
раз – частота рассматриваемого события, то есть выпадения очков.

Отношение
частоты к общему числу испытаний называют относительной частотой этого
события.

Пусть
некоторое испытание проводилось многократно в одних и тех же условиях. При этом
фиксировалось, произошло или нет некоторое интересующее нас событие А.

Если
общее число испытаний – n,
а число испытаний, при которых произошло событие А, – m. То m называют
частотой события А, частное m и n –
относительной
частотой.

Определение:

Относительной
частотой случайного события в серии испытаний называется
отношение числа испытаний, в которых это событие наступило, к числу всех
испытаний.

В
ходе исследований выяснилось, что относительная частота появления ожидаемого
события при повторении опытов в одних и тех же условиях, может оставаться
примерно одинаковой, незначительно отличаясь от некоторого числа р.

Пример.

При
подбрасывании монеты отмечают те случаи, когда выпадает орёл.

Если
монета однородна и имеет правильную геометрическую форму, то шансы выпадения
орла или решки будут примерно одинаковы. Но при
небольшом количестве бросков такой результат может не получиться.

А
вот если испытание проводиться большое количество раз, то относительная частота
выпадения орла близка к относительной частоте выпадения решки.

Многие
учёные проводили такой эксперимент.

Так,
например, английский математик Карл Пирсон бросал монету 24 тысячи раз, и
относительная частота выпадения орла оказалось равной 0,5005.

А
наш соотечественник, Всеволод Иванович Романовский, подбрасывая монету 80 тысяч
640 раз, нашёл, что относительная частота выпадения орла в его испытании была
равна 0,4923.

Заметим,
что в обоих случаях относительная частота выпадения орла очень близка к .

Говорят,
что вероятность выпадения орла при подбрасывании монеты правильной
геометрической формы равна .

Пример.

В
непрозрачном мешке лежит 7 зелёных и 12 синих кубиков. За раз можно доставать
только 1 из них. Какова вероятность того, что из мешка достанут синий кубик?

Всего
в мешке 19 кубиков. Значит, n=19.

Синий
кубик мы можем достать 12 раз. Получаем, что m=12.

Относительная
частота равна:

Вероятность
того, что из мешка достанут синий кубик, равна .

Пример.

Определить
относительную частоту появления буквы «о» в слове «достопримечательность».

Общее
число букв, то есть n=21.
А количество букв «о», то есть m=3.

Значит
относительная частота:

Пример.

Отмечая
число попаданий в корзину в каждой серии из 40 бросков, которые совершал
баскетболист, получили такие данные:

Какова
относительная вероятность попадания мяча в корзину для данного баскетболиста?

Определим
общее число бросков. Было 5 серий по 40 бросков, то есть n=200.

Сосчитаем
число попаданий в корзину:

Получили,
что m=184.

Относительная
вероятность попадания в корзину будет:

Пример.

Стрелок
совершил 50 выстрелов. Относительная частота попадания в цель оказалась равной
0,88. Сколько раз он промахнулся?

Зная
общее число выстрелов n=50
и относительную вероятность попадания p=0,88.
Найдем число попаданий в цель:

Стрелок
попал в цель 44 раза.

Найдём
число промахов

Стрелок
промахнулся 6 раз.

Источник

Относительная частота события. Статистическое определение вероятности

Недостатком
классического определения вероятности
является то, что не всегда удается
узнать, являются исходы испытания
равновозможными или не являются.

Относительной
частотой р^*
случайного события А
называется отношение числа m^*
появления данного события к общему
числу n^*
проведенных одинаковых испытаний, в
каждом из которых могло появиться или
не появиться данное событие.

Оказывается,
что при большом числе испытаний n,
относительная частота появления события
А
в различных сериях отличается друг от
друга мало и это отличие тем меньше, чем
больше испытаний в сериях.

При
статистическом определении вероятностью
события называют относительную частоту
события при большом числе испытаний
или число близкое к ней:

Сложение вероятностей

Суммой
двух событий А
и B
называется событие С,
состоящее в появлении хотя бы одного
из этих событий. Сумма обозначается:
С=А+В=АилиВ.

Теорема
о сложении вероятностей.
Вероятность появления одного из двух
несовместных
событий равна сумме вероятностей этих
событий.

Р(АилиВ)=Р(А)+Р(В).

Заметим, что
сформулированная теорема справедлива
для любого числа слагаемых:

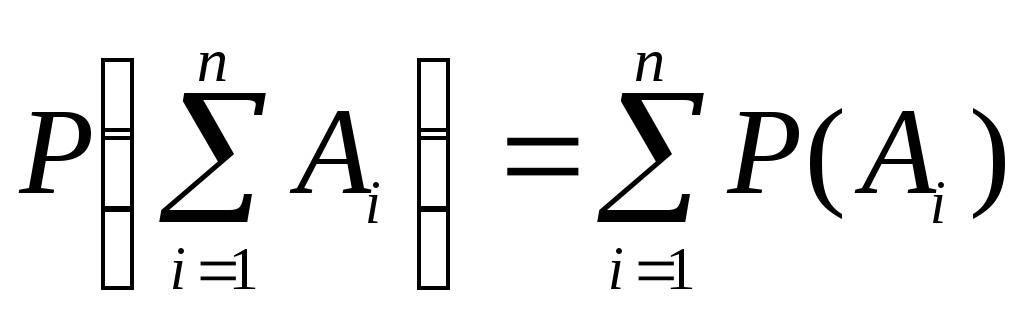Два
события называются противоположными,
если они несовместны и образуют полную
группу. Если событие обозначим через
А,
то противоположное ему – через
.

Так
как при испытании обязательно произойдет
или событие А
или событие
,
то согласно теореме о сложении вероятностей
получаем
.

Если
случайные события А₁,
А₂,…,
А_n
образуют полную группу несовместных
событий, то имеет место равенство

Случайные
события А и B
называются совместными, если при
данном испытании могут произойти оба
эти события. Событие, заключающееся в
совмещении событий А и B,
будем обозначать АиВ или АВ.

Теорема.
Вероятность
суммы совместных событий вычисляется
по формуле

Примеры.
1. В урне 10
белых, 15 черных, 20 синих и 25 красных
шаров. Вынули один шар. Найти вероятность
того, что вынутый шар а) синий или черный;
б) белый, черный или синий.

Обозначим следующие
события:

Б
– вынули белый шар,
;

Ч
– вынули черный шар,
;

С
– вынули синий шар,
;

К
– вынули красный шар,
.

Тогда
искомые вероятности будут:

а)
.

б)

или

2.
На стеллаже в библиотеке стоит 15
учебников, причем 5 из них в переплете.
Библиотекарь берет три учебника. Найти
вероятность того, что хотя бы один из
взятых учебников окажется в переплете.

Рассмотрим два
способа решения задачи.

Первый
способ. Пусть
события А
– хотя бы один учебник в переплете;

В
– один из взятых учебников в переплете,
два – без переплета;

С
– два в переплете, один без переплета;

D
– все три учебника в переплете.

Очевидно,
А=В+С+D.
Найдем вероятности событий В,
С,
и D.

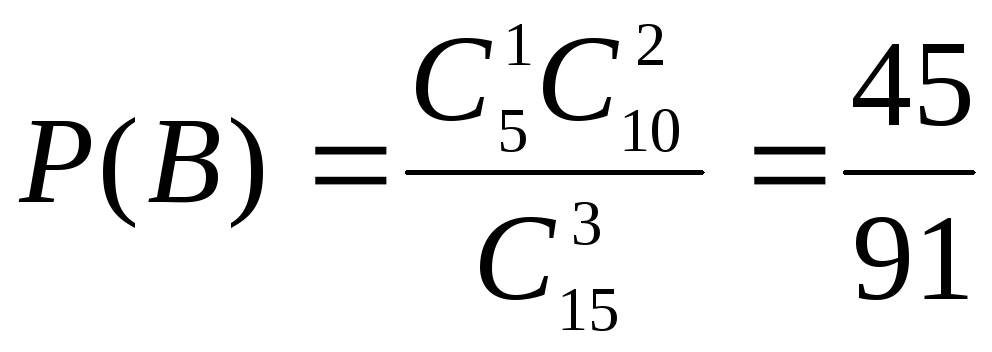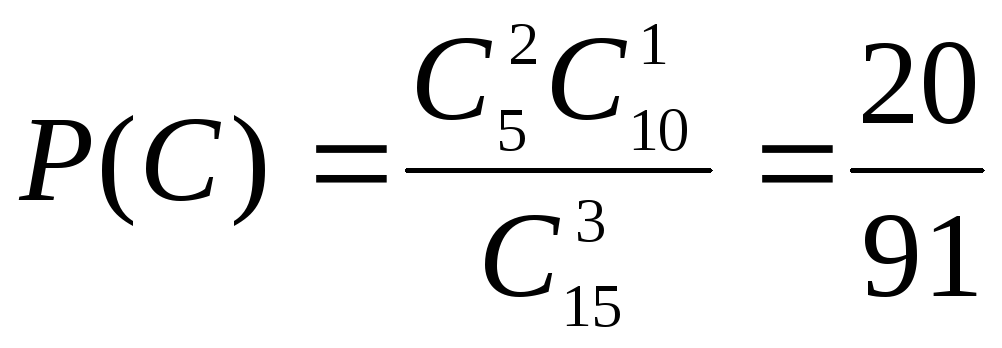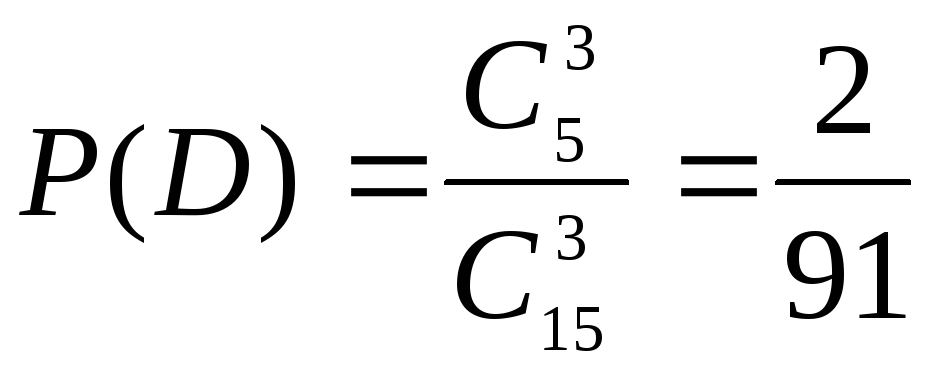Тогда

Второй
способ. Вновь
А
– хотя бы один учебник в переплете;

–
ни один из взятых учебников не имеет
переплета.

Так
как события А
и

противоположные, то

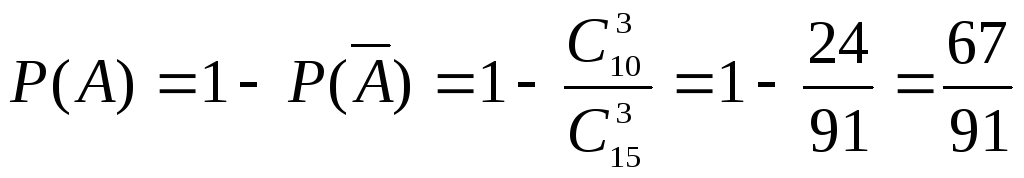Умножение вероятностей независимых событий

Событие
А
называется независимым
от события В,
если вероятность появления события А
не зависит от того, произошло событие
В
или нет.

Теорема.
Вероятность совместного появления двух
независимых событий равна произведению
вероятностей этих событий

Р(АВ)=Р(А)·Р(В).

Заметим, что
теорему о вероятности суммы совместных
событий можно записать теперь в виде:

Примеры.
1. В первом
ящике 2 белых и 7 черных шаров, во втором
8 белых и 4 черных шара. Из каждого ящика
вынули по шару. Найти вероятность того,
что один из вынутых шаров белый, а другой
– черный.

Обозначим
события: А
– вынули белый шар из первого ящика,
;

–
вынули черный шар из первого ящика,
;

В
– белый шар из второго ящика,
;

–
черный шар из второго ящика,
.

Нам
нужно, чтобы произошло одно из событий

или
.
По теореме об умножении вероятностей
,

.
Тогда искомая вероятность по теореме
сложения будет

2.
Вероятность попадания в цель у первого
стрелка 0,8, у второго – 0,9. Стрелки делают
по выстрелу. Найти вероятность: а)
двойного попадания; б) хотя бы одного
попадания; г) одного попадания.

Пусть
А
– попадание первого стрелка, Р(А)=0,8;

В
– попадание второго стрелка, Р(В)=0,9.

Тогда

– промах первого,
;

–
промах второго,
.

Найдем нужные
вероятности.

а)
АВ
– двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.

б)

– двойной промах,
.

в)
А+В
– хотя бы одно попадание,

г)

– одно попадание,

3.
Студент разыскивает нужную ему формулу
в трех справочниках. Вероятности того,
что формула содержится в первом, втором
и третьем справочниках равны 0,6; 0,7 и
0,8. Найти вероятности того, что формула
содержится 1) только в одном справочнике;
2) только в двух справочниках; 3) во всех
трех справочниках.

А
– формула содержится в первом справочнике;

В
– формула содержится во втором
справочнике;

С
– формула содержится в третьем
справочнике.

Воспользуемся
теоремами сложения и умножения
вероятностей.

=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.

2.
.

3.З(АВС)=0,6·0,7·0,8=0,336.

4.
Из 10 деталей
7 – стандартные. Наудачу берут 6 деталей.
Найти вероятность того, что среди них:
а) не более одной нестандартной; б) не
более двух нестандартных.

а)
Обозначим события А
– среди взятых 6 деталей нестандартных
нет;

В
– в 6 выбранных деталях одна нестандартная.
Тогда А+В
– среди 6 деталей не более одной
нестандартной. Найдем Р(А+В).
Заметим, что

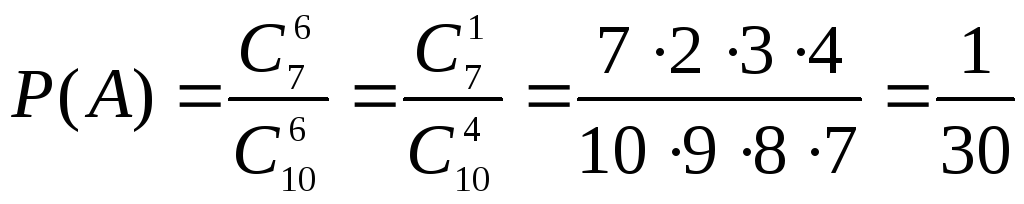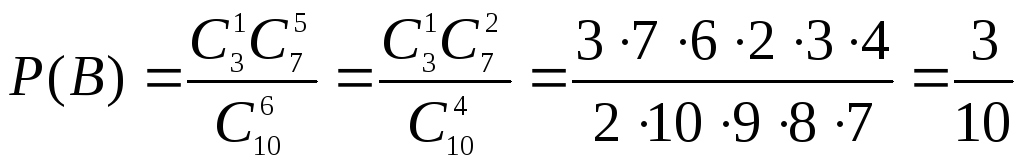Откуда

б)
Пусть теперь событие А
– в шести взятых деталях не более двух
нестандартных. Тогда

– в выбранных деталях более двух
нестандартных, т.е. три.

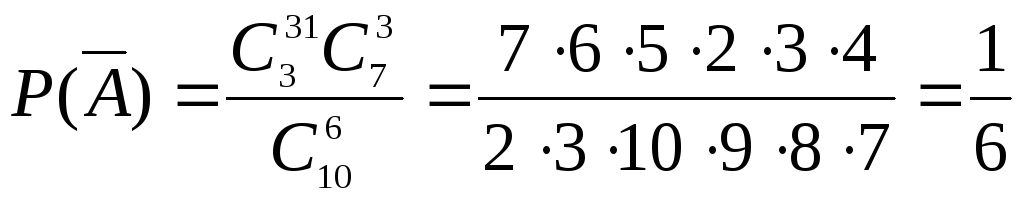Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В отличии от классического определения вероятности, постулирующего, что все результаты равновероятны, статистический подход к формулированию вероятности более приближен к реальности. Действительно при использовании теории вероятности для работы с прикладными задачами очень редко встречаются исходы, вероятности которых одинаковы, и такие результаты, вероятности которых легко предсказать.

Для реальных явлений часто требуется учесть слишком много факторов для верного прогноза вероятности. Чтобы рассмотреть возможность оценки вероятности, исходя из других вводных, необходимо ввести определение относительной частоты вероятности.

Определение 1

Отношение количества появления события к суммарному количеству проведённых испытаний называется относительной частотой события.

$W(X)= frac{k}{m}$

Где k — число результатов благоприятствующих событию Х, m — суммарное количество проведённых экспериментов, в результате которых могло наступить событие Х.

Параметр относительная частота применяется в тех случаях, когда сложно или невозможно выявить всё множество элементарных результатов эксперимента.

Пример 1

Рассмотрим ограниченную территорию, на которой в течение последних 50 лет происходили цунами. Всего было зафиксировано 20 мощных явлений и 40 слабых. Необходимо вычислить величину относительной частоты появления мощных цунами.

Вычислим суммарное количество всех цунами, которые происходили в рассматриваемом регионе:

m=20+40=60, при этом, сильных цунами было 20.

Исходя из определения вычислим значение относительной частоты

$W(A)=frac{20}{60}=0,33$

Получили, что относительная частота сильных цунами составляет 0,33.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример 2

Рассмотрим событие — появление какого-либо конкретного числа при подбрасывании шестигранного кубика. Выделим среди прочих два события:

• появление двойки,

• появление тройки или четвёрки.

В ходе проведения эксперимента кубик бросили 120 раз. При этом двойка появилась 22 раза — событие Х, а тройку, либо четвёрку наблюдали 39 раз — событие Y.

Согласно классическому определению вероятности, появление одного любого числа при бросании кубика будет в одном случае из шести $P=frac {1}{6}=0,167$. А значит мы могли предсказать появление двойки в $frac{120}{6}=20$ случаях, а появление тройки, либо четвёрки в $2 cdot frac{120}{6}$=40 случаях.

Однако, было проведено испытание и можно вычислить экспериментальное значение вероятности, точнее аналогичную ему величину — относительную частоту события.

$W(X)=frac{22}{120}=0,183$

$W(Y)=frac{39}{120}=0,325$

Итак, относительная частота появления двойки в данном эксперименте составила $W(X)=0,183$ (классическая вероятность 0,167), а относительная частота появления тройки или четвёрки составила $W(Y)=0,325$ (классическая вероятность 0,334). При увеличении числа экспериментов значение относительной частоты будет приближаться к значению классической вероятности.

Относительная частота обладает тем недостатком, что сильно варьируется при проведении различных экспериментов, является неоднозначной. Однако её колебания происходят в пределах около значения фактической вероятности. И чем больше проведено экспериментов, тем ближе лежит относительная частота к вероятности.

В теории вероятности относительная частота имеет значение как оценка вероятности статистическими методами по всей совокупности исходов конкретного эксперимента. При этом она будет достаточна близка к оцениваемому параметру, который принято называть статистическая вероятность.

Определение 2

Отношение количества конкретных экспериментов к общему числу испытаний (относительная частота) характеризует статистическую вероятность тем точнее, чем большее количество экспериментов было проведено, а значит можно записать следующее определение для статистической вероятности:

$P(X)= lim_{m rightarrow infty} frac{k}{m}$

Покажем, что значение относительной частоты стремится к значению вероятности.

Пример 3

Рассмотрим простой пример с подбрасыванием монетки. Классическая вероятность того, что выпадет любая из сторон составляет 0,5. Пусть событие Х — выпадение «орла». Вычислим относительную частоту выпадения «орла» при разном количестве подбрасываний монетки.

Монетку бросили 3 раза — орел выпал 2 раза;
Монетку подбросили 10 раз — орёл выпал 6 раз;
Монетку подбросили 100 раз — орёл выпал 56 раз;
Монетку подбросили 10000 раз — орёл выпал 5135 раз.

Вычислим относительную частоту

$W(X_1)=frac{2}{3}=0,67$

$W(X_2)=frac{6}{10}=0,6$

$W(X_3)=frac{56}{100}=0,56$

$W(X_4)=frac{5135}{10000}=0,5135$

Чем больше будет сделано бросков, тем реже будут встречаться аномальные результаты, такие как повторное выпадение «орла» и тем меньшее значение они будут иметь для вычисления.

Классическое определение вероятности является именно теоретическим, вероятность в этом случае вычисляется с помощью анализа предполагаемых обстоятельств события, то есть даётся прогноз о том, насколько ожидаемо выполнение этого события. Ключевое же отличие относительной частоты от вероятности в том, что её значение получается экспериментально и её нельзя определить заранее, а можно вычислить только после завершения эксперимента.

Так, например, если взять выпуск деталей на производстве, то предварительно оценить процент брака можно основываясь на состоянии оборудования, на квалификации персонала, на качестве сырья. Однако, фактические сведения о браке будут получены только после начала процесса производства.

Пример 4

На заводе было изготовлено 10000 деталей. Отдел технического контроля изучил продукцию и установил, что из всего количества 100 изделий являются бракованными, а 2000 следует отнести ко второму сорту.

Необходимо вычислить относительную частоту появления бракованных деталей, изделий первого и второго сорта.

Решение

Сначала следует вычислить количество изделий первого сорта.

$k_1=m-k_2-k_br=10000-2000-100=7900$

Определим требуемые параметры:

$W(k_1)=frac{7900}{10000}=0,79$

$W(k_2)=frac{2000}{10000}=0,2$

$W(k_3)=frac{100}{10000}=0,01$

В результате получим относительную частоту деталей первого сорта $W(k_1)=0,79$, второго сорта$W(k_2)=0,2$ , брака$W(k_3)=0,01$.

Источник

Советы

Источники

Об этой статье

Была ли эта статья полезной?

Относительная частота события. Статистическое определение вероятности

Сложение вероятностей

Умножение вероятностей независимых событий

Вам также может понравиться

Нужны друзья как найти

Как найти файл деинсталляции

Как найти хорошего достойного парня

Добавить комментарий Отменить ответ