Ответ:
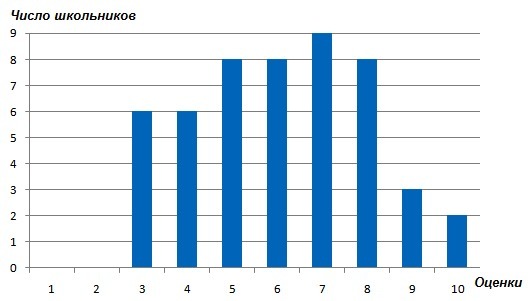
Количество – сколько учеников получило данную оценку. На графике видно:
- оценка 1 – 1 ученик
- оценка 2 – никто
- оценка 3 – 6 учеников
- и т.д. см. таблицу ниже
оценки кол-во
1 – 2
2 – 0
3 – 6
4 – 2
5 – 7
6 – 8
7 – 9
8 – 9
9 – 1
10 – 6
сумма =50
Относительная частота – как часто встречается оценка среди учеников. Общее количество оценок (сумма в данной задаче 50) делится на Количество.
Часта получения оценок:
оценка 1 = 1/50 * 100% = 2%
оценка 2 = 0/50 =0
оценка 3 = 6/50 * 100% = 12%
оценка 4 = 2/50 * 100% = 4%
оценка 5 = 7/50 * 100% = 14%
оценка 6 = 8/50 * 100% = 16%
оценка 7 = 9/50 * 100% = 18%
оценка 8 = 9/50 * 100% = 18%
оценка 9 = 1/50 * 100% = 2%
оценка 10 = 6/50 * 100% = 12%
Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-
1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-
2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-
3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-
1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-
2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-
3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-
1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-
2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-
3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 144 719 раз.
Была ли эта статья полезной?
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Частоты и относительные частоты
На чтение 3 мин. Просмотров 31 Опубликовано 02.06.2021
При построении гистограммы мы должны выполнить несколько шагов, прежде чем мы начнем рисовать наш график. После настройки классов, которые мы будем использовать, мы назначаем каждое из наших значений данных одному из этих классов, затем подсчитываем количество значений данных, которые попадают в каждый класс, и рисуем высоты столбцов. Эти высоты могут быть определены двумя разными способами, которые взаимосвязаны: частота или относительная частота.
Частота класса – это количество выпавших значений данных. в определенный класс, в котором классы с более высокими частотами имеют более высокие столбцы, а классы с меньшими частотами имеют более низкие столбцы. С другой стороны, относительная частота требует одного дополнительного шага, поскольку это мера того, какая доля или процент значений данных попадает в определенный класс.
A при прямом вычислении относительная частота определяется по частоте путем сложения частот всех классов и деления количества по каждому классу на сумму этих частот.
Разница между частотой и относительной частотой
Чтобы увидеть разницу между частотой и относительной частотой, мы рассмотрим следующий пример. Предположим, мы смотрим на оценки учащихся 10-го класса по истории и имеем классы, соответствующие буквенным оценкам: A, B, C, D, F. Число каждой из этих оценок дает нам частоту для каждого класса:
- 7 студентов с F
- 9 студентов с D
- 18 студентов с оценкой C
- 12 учеников с оценкой B
- 4 ученика с отличием
Чтобы определить относительную частоту для каждого класса, мы сначала складываем общее количество точек данных: 7 + 9 + 18 + 12 + 4 = 50. Затем мы делим каждую частоту на эту сумму 50.
- 0,14 = 14% учащихся с оценкой F
- 0,18 = 18% учащихся с оценкой D
- 0,36 = 36% учащихся с оценкой C
- 0,24 = 24% учащихся с оценкой B
- 0,08 = 8% учащихся с оценкой A
Приведенный выше набор исходных данных с количеством студентов, попадающих в каждый класс (буквенная оценка), будет показывать частоту, в то время как процент во втором наборе данных rep возмущается относительной частотой этих оценок.
Простой способ определить разницу между частотой и относительной частотой состоит в том, что частота зависит от фактических значений каждого класса в набор статистических данных, в то время как относительная частота сравнивает эти отдельные значения с общими итогами всех классов в наборе данных.
Гистограммы
Для гистограммы можно использовать либо частоты, либо относительные частоты. Хотя числа по вертикальной оси будут другими, общая форма гистограммы останется неизменной. Это связано с тем, что высоты относительно друг друга одинаковы, независимо от того, используем ли мы частоты или относительные частоты..
Гистограммы относительной частоты важны, потому что высоты можно интерпретировать как вероятности. Эти гистограммы вероятностей обеспечивают графическое отображение распределения вероятностей, которое можно использовать для определения вероятности получения определенных результатов в данной совокупности.
Гистограммы – это полезные инструменты для быстрого наблюдения за тенденциями в популяциях, чтобы статистики, законодатели и общественные организаторы могли определить наилучший курс действий, чтобы повлиять на большинство людей в данной популяции.
Предмет: Алгебра,
автор: polinafirsova1
Приложения:
Ответы
Автор ответа: armanelaoztl7s
27
1)0%
2)0%
3)12%
4)12%
5)16%
6)16%
7)18%
8)16%
9)6%
10)4%
polinafirsova1:
а количество???
armanelaoztl7s:
Сколько их всего имеешь ввиду?
armanelaoztl7s:
50
polinafirsova1:
вот вы написали относительная чистота столбик,а столбик количество ?
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Биология,
автор: zelenskiyyevgeniy
Подумайте, каково значение плода покрытосеменных, кроме защиты семени
4 года назад
Предмет: Математика,
автор: girl66669
Срочно помогите!!! Пожалуйста
4 года назад
Предмет: Математика,
автор: gabitzhansabina
Номер 641 только можно обратную задачу?:
4 года назад
Предмет: Математика,
автор: vladah
1.Раскройте скобки:
1)2,2*(x-4)
2)-2*(1,2n-m)
3)(4с-d)*(-0,5y)
4)6*(-p+0,3к-1,2t)
7 лет назад
Предмет: Математика,
автор: maxlbedvskiy
Найти сумму корней (в градусах ) уравнения корень cos2х=COSx+SINx
7 лет назад









