Выделим
из стержня на участке, где действует
постоянная продольная
сила N,
некоторую его часть длиной l
и шириной b
(см. рис. 4.3, а). Опыты показывают,
что при растяжении резинового стержня
его длина увеличивается, а ширина
уменьшается. Пусть
l1
и b1 –
длина и ширина стержня после деформации
соответственно.
Изменение
длины стержня при растяжении (сжатии)
называется абсолютной продольной
деформацией и определяется по формуле
∆l
= l1
– l2.
Отношение
абсолютной продольной деформации к
первоначальной длине стержня называется
относительной продольной деформацией
и определяется по формуле
.
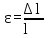По
аналогии с продольными деформациями
имеем:
∆b
= b1
– b,
∆h
= h1
– h
– абсолютные
поперечные деформации;
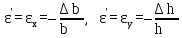
– относительные
поперечные деформации.
При
растяжении: N
0, ∆l
0, ε
0, ∆b
< 0, ε‘
<
0; при сжатии:
N
< 0, ∆l
< 0, ε
<
0, ∆b
0, ε‘
0.
Закон
Гука –
относительная продольная деформация
прямо пропорциональна нормальному
напряжению, а именно:
,
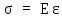где
Е
– модуль
Юнга или модуль упругости первого рода
(кН/см2,
МПа).
Используя
зависимости
,
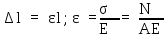получим
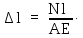
Абсолютная
продольная деформация прямо пропорциональна
продольной силе в пределах участка
длиной l
при
постоянных N
и
EА,
где EА
– жесткость поперечного сечения при
растяжении (сжатии).
Коэффициент
Пуассона
– безразмерная величина, характеризующая
упругие свойства и способность материала
деформироваться в поперечном направлении
при его растяжении или сжатии в продольном
направлении.
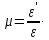
Для
реальных материалов коэффициент Пуассона
изменяется в очень узких пределах:
= 0…0,5.
Значение
для некоторых
материалов:
–
пробка –
;
–
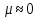резина –
;
–
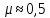сталь –
;
–
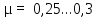свинец –
;
–
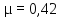бетон –
;
–
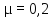каучук –
0,5.
Значение
коэффициента Пуассона определяется
опытным путем в результате специальных
испытаний материала.
4.4. Условия прочности и жесткости
Условие
прочности элементов конструкций и
сооружений рассмотрено в главе 3.
В
некоторых случаях для обеспечения
нормальной работы машин, конструкций
и сооружений требуется проектировать
размеры деталей и элементов таким
образом, чтобы обеспечивалось условие
жесткости:
,
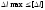где
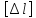
– допускаемое удлинение, задается
техническими условиями.
Удлинение
ступенчатых стержней, а также когда
внешние силы приложены в разных точках
продольной оси стержня, определяется
суммированием удлинений отдельных
участков.
,
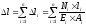где
Ni,
li,
Ei,
Аi
– нормальная сила, длина, модуль упругости
и площадь поперечного сечения і–го
участка соответственно.
Условие
жесткости позволяет выполнять три вида
расчетов:
1)
проверочный:
;
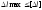2)
проектировочный: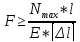 
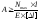(стержень
постоянного сечения);
3)
расчет грузоподъемности или несущей
способности:
.
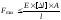4.5. Потенциальная энергия упругой деформации
Внешние
силы, приложенные к упругому телу и
вызывающие изменение его геометрии,
совершают работу АF
на соответствующих перемещениях. В
упругом теле накапливается потенциальная
энергия деформации U.
При действии динамических нагрузок
часть работы внешних сил превращается
в кинетическую энергию движения частиц
тела К.
Уравнение
баланса энергии можно записать в
следующем виде:
АF = U + K.
При
статическом нагружении упругого тела
работа внешних сил полностью преобразуется
в потенциальную энергию деформации,
следовательно, АF = U.
При разгрузке тела производится работа
за счет потенциальной энергии деформации,
накопленной телом. При этом упругое
тело является аккумулятором энергии.
Это свойство упругого тела широко
используется в заводных пружинах часовых
механизмов, в конструкции лука и т. д.
Для вывода необходимых расчетных
зависимостей потенциальной энергии
деформации рассмотрим простейший случай
– растяжение стержня.
На
рис. 4.5, а изображен стержень,
растягиваемый силой F,
удлинение которого соответствует l.
График изменения величины удлинения
стержня l
в зависимости от силы F
показан на рис. 4.5, б.
В соответствии
с законом Гука этот график носит линейный
характер.
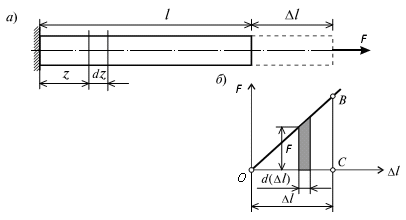
Рис.
4.5. а
– схема растягиваемого стержня; б
– график зависимости F
– ∆l
Пусть
некоторому значению силы F соответствует
удлинение стержня l.
Дадим некоторое приращение силе
F соответствующее
приращение удлинения составит d (l ).
Элементарная работа на этом приращении
удлинения составит:
.
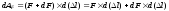Вторым
слагаемым, в силу его малости, можно
пренебречь, и тогда
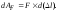
Полная
работа равна сумме элементарных работ,
тогда при линейной зависимости работа
внешней силы F
на перемещении l
будет равна площади треугольника ОСВ
(рис. 4.5, б), т. е.
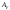
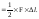
Если
напряжения
и деформации
распределены по объему тела V
равномерно, то потенциальную энергию
деформации стержня можно записать в
следующем виде:
,
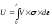где
V = А l,
F =
A,
= Е ;
А
– площадь поперечного сечения стержня.
Тогда
окончательно
.
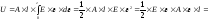
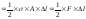С
учетом
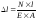
для
однородного стержня с постоянным
поперечным сечением при F = const
получим:
.
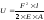Относительными называют деформации определяемые отношением изменения размера (абсолютной деформации) к соответствующим начальным размерам тела.
Другими словами относительные деформации показывают насколько изменился размер тела в сравнении с его размерами до нагружения.
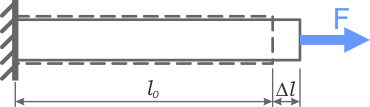
Например, при растяжении (сжатии) прямого стержня его относительное удлинение ε находится отношением абсолютного удлинения Δl к начальной длине l0.
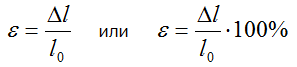
Относительная поперечная деформация
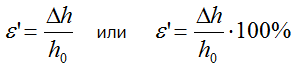
Здесь Δh – абсолютная поперечная деформация,
Δh0 – начальный поперечный размер (до деформации).
Измеряется в единицах или процентах [%]
При кручении — относительный угол закручивания
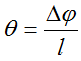
где, Δφ – угол закручивания участка вала,
l – длина рассматриваемого участка.
Единица измерения – радиан на метр [рад/м].
Примеры расчета деформаций >>
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Лекция 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ – СЖАТИЕ
Внутренние силы в поперечных сечениях стержня. Построение эпюр
внутренних сил от действия внешних сил. Напряжения в поперечных сечениях
стержня. Деформации продольные и поперечные, коэффициент Пуассона.
Закон Гука. Модуль упругости. Определение перемещений поперечных сечений
стержня. Построение эпюр напряжений и перемещений.
Растяжение – сжатие. Растяжение и сжатие – это наиболее простые
и часто встречающиеся виды деформации. На растяжение и сжатие работают
многие элементы конструкций: стержни ферм, колонны, канаты лебедок,
штоки паровых машин, лонжероны крыла самолетов. Растяжение и сжатие –
это наиболее простые виды деформации, поэтому изучение курса сопромата
начинается именно с изучения этих видов деформации.
Внутренняя продольная сила (или нормальная сила). При растяжении
или сжатии в поперечных сечениях бруса возникает только один внутренний
силовой фактор – внутренняя продольная сила N (рис. 5). Брус имеет два
характерных участка. Для определения продольной силы N воспользуемся
методом сечения. На расстоянии y1 проведем сечение на первом участке
и рассмотрим равновесие отсеченной части. Продольную силу будем всегда
показывать от сечения, что будет соответствовать растяжению бруса.
Составим условие равновесия на ось y
N1 – F = 0,
откуда
N1 = F.
Проведем на втором участке сечение на расстоянии y2. Рассматривая
равновесие отсеченной части, получаем N2 = F. Строим эпюру продольных
сил.
Нормальные напряжения. Исходя из определения напряжения, можно записать
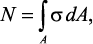(1)
где σ – нормальное напряжение в произвольной точке сечения.
Согласно гипотезе плоских сечений (гипотезаБернулли) все
продольные волокна бруса деформируются одинаково, а это означает, что
напряжения в поперечных сечениях одинаковы, т.е. σ = const.
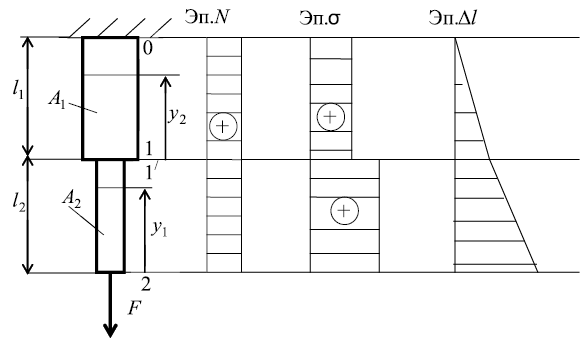
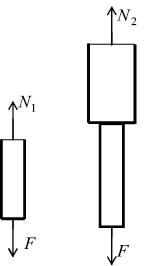
Рис. 5. Построение эпюр N, σт, Δl
В этом случае получаем
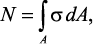
откуда .
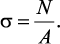
Рассчитывая напряжения в каждом сечении, строим эпюру нормальных напряжений (рис. 5).
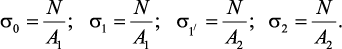
Деформации и перемещения.
Величина, на которую изменится длина бруса (или одного из его
участков) под действием продольных сил, называется продольной
деформацией (рис. 6). Относительная продольная деформация – отношение
абсолютной продольной деформации Dl к первоначальной длине стержня l:
ε = Dl/l0
Величина Δа (Δb), на которую изменится размерпоперечного сечениябруса а (b) под действием продольной силы, называется поперечной деформацией.
Отношение абсолютной поперечной деформации, Dа (Db)
к первоначальному размеру сечения бруса а (b), называется относительной
поперечной деформацией:
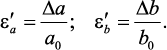
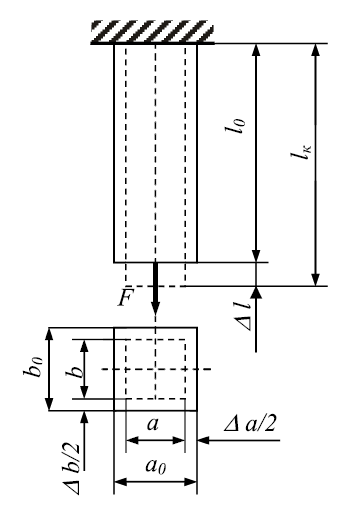
Рис. 6. Схема деформирования стержня
